У любого вектора есть 2 главные характеристики:
- длина (математики говорят «модуль вектора»)
- направление (в какую сторону вектор на рисунке направлен)
Третья характеристика вектора – это его координаты.
Примечание:
Зная координаты вектора, можно найти его длину и направление. Поэтому, задавать информацию о векторе можно двояко: либо указав его длину и направление, либо его координаты.
Что такое координаты вектора
Координаты вектора – это длины его теней на осях координат (его проекции на оси).
Координаты вектора указывают так:
[vec{a} = left{ a_{x}; a_{y} right}]
( a_{x} ) – это «x» координата вектора, проекция вектора ( vec{a} ) на ось Ox;
( a_{y} ) — это «y» координата вектора, проекция вектора ( vec{a} ) на ось Oy;
Рис. 1. Обозначения вектора и его проекций на координатные оси
Координаты вектора можно получить из координат его начальной и конечной точек:
«координата вектора» = «конец» — «начало»
Пример:
( A left( 1;1 right) ) — начальная точка,
( B left( 4;3 right) ) — конечная точка,
Рис. 2. На плоскости отмечены две точки
( overrightarrow {AB} ) – вектор.
[ overrightarrow {AB} = left{ AB_{x}; AB_{y} right} ]
[ begin{cases} AB_{x} = 4 – 1; AB_{x} = 3 \ AB_{y} = 3 – 1; AB_{y} = 2 end{cases} ]
[ overrightarrow {AB} = left{ 3; 2 right} ]
Рис. 3. Вектор и его координаты
Длина вектора (в чем измеряется, как посчитать)
Длину вектора (его модуль) обозначают так:
( left| vec{a} right| ) – длина вектора ( vec{a} ).
Как вычислить длину вектора по его координатам
Когда известны координаты вектора, его длину считают так:
( a_{x} ) и ( a_{y} ) — это числа, координаты вектора ( vec{a} )
Для двухмерного вектора:
[ large boxed { left| vec{a} right| = sqrt{ a_{x}^{2} + a_{y}^{2} } }]
Для трехмерного вектора:
[ large boxed { left| vec{a} right| = sqrt{ a_{x}^{2} + a_{y}^{2} + a_{z}^{2} } } ]
Как вычислить длину вектора с помощью рисунка
Если вектор нарисован на клетчатой бумаге, длину считаем так:
1). Если вектор лежит на линиях клеточек тетради:
— считаем количество клеточек.
Зная масштаб клеток, легко получить длину вектора – умножаем масштаб на количество клеток.
Рис. 4. Вектор располагается вдоль линий, на листке в клетку
2). Если вектор не лежит вдоль линий:
— проводим вертикаль и горизонталь пунктиром.
Рис. 5. Вектор не расположен вдоль линий, разграничивающих листок в клетку
( Delta x ) — горизонталь; ( Delta y ) — вертикаль;
— затем применяем формулу:
[ left| vec{a} right| = sqrt { left(Delta x right)^{2} + left( Delta y right)^{2} } ]
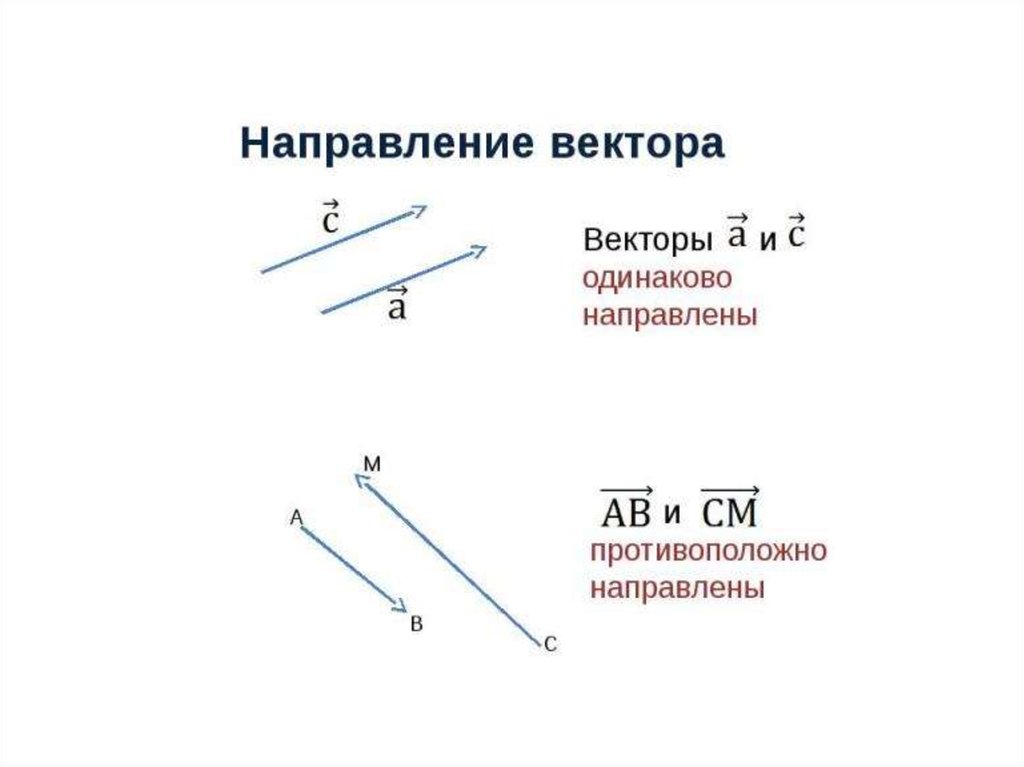
Как указать направление вектора
Указать направление вектора можно с помощью его координат. Так как в его координатах уже содержится информация о длине и направлении вектора.
Бывает так, что координаты вектора неизвестны, а известна только лишь его длина. Тогда направление можно указать с помощью угла между вектором и какой-либо осью.
Для двумерного вектора
Если вектор двумерный, то для указания направления (см. рис. 10) можно использовать один из двух углов:
- угол ( alpha ) между вектором и горизонталью (осью Ox),
- или угол ( beta ) вежду вектором и вертикалью (осью Oy).
Рис. 6. Углы между вектором и осями на плоскости
Словами указать направление вектора можно так:
- вектор длиной 5 единиц направлен под углом 30 градусов к горизонтали;
- Или же: вектор длиной 5 единиц направлен под углом 60 градусов к вертикали.
Такой способ указания координат используют в полярной системе координат.
Для трехмерного вектора
Когда вектор располагается в трехмерном пространстве, чтобы указать, куда вектор направлен, используют два угла.
- угол между вектором и осью Oz;
- и один из углов: между вектором и осью Oy, или между вектором и осью Ox;
Такой способ указания координат используют в сферической системе координат.
Считаем Землю шаром. Расположим ее центр в начале трехмерной системы координат – точке (0 ; 0 ; 0).
Тогда координаты любой точки на поверхности планеты можно указать с помощью радиус-вектора этой точки.
Для указания сферических координат принято использовать:
- длину вектора,
- угол между осью Ox и вектором и
- угол между осью Oz и вектором.
Download Article
Quickly get the angle and magnitude of a vector
Download Article
Finding the direction of a vector in a 2-dimensional plane is easy! You’ll just need a little trigonometry. The x and y components of a vector form a right triangle. You can use the tangent function to find the angle between the x-axis and the vector. This wikiHow guide will show you how to find the direction of a vector and walk through four examples. Additionally, we’ll review how to find the magnitude of a vector.
Things You Should Know
- For this method, the vector’s tail will be located at the origin of an xy coordinate plane, and the tip will be at an (X, Y) coordinate.
- Use tan(𝛉) = Y/X to find the direction angle 𝛉 of the vector. Apply arctan to both sides to solve for 𝛉.
- If your vector is in the second, third, or fourth quadrant, you’ll need to apply an adjustment. Add 180 degrees to your answer for quadrants II and III. Add 360 for quadrant IV.
- Use||a|| = sqrt(X^2 + Y^2) to calculate the magnitude of vector a.
-
Use 𝛉 = arctan(Y/X). This formula calculates 𝛉 (the greek symbol, theta), which is the angle measuring the degrees between the positive x-axis and the vector.
- Where Y is the Y component of the vector and X is the X component of the vector.
- “arctan” is the inverse tangent function.
- This assumes the vector’s tail is located at the origin (0, 0).
- If the vector is in the second or third quadrant, add 180 degrees to your result.
- If the vector is in the fourth quadrant, add 360 degrees to your result.
- Make sure your calculator is set to degrees mode, usually called “deg.”
Advertisement
-
Use ||a|| = sqrt(X^2 + Y^2). This formula calculates ||a||, the magnitude of vector a.[1]
- Where Y is the Y component of the vector and X is the X component of the vector.
- “sqrt” is the square root of what’s in the parentheses.
- This assumes the vector’s tail is located at the origin (0, 0).
- Check out the full wikiHow guide on finding the magnitude of a vector for more details and examples.
-
1
There are a few coordinate plane terms you’ll need to know. A Cartesian 2-dimensional coordinate plane specifies points in a plane by assigning distances from the origin.
- A 2-dimensional plane is a flat surface consisting of two directions, x and y. It extends infinitely in the x and y direction.
- The x-axis is a horizontal line that measures distance in space in the x direction. Positive values point right from the origin (positive x-axis), negative point left (negative x-axis).
- The y-axis is a vertical line that measures distance in space in the x direction. It is perpendicular to the x-axis. Positive values point up from the origin (positive y-axis), negative point down (negative y-axis).
- The origin is where the x and y axes intersect. It has coordinates of (0, 0).
- Coordinates are where a point is located. They are written as (x, y) where x is the distance you need to move in the horizontal direction and y is the distance you need to move in the vertical direction to get to the point from the origin.
-
2
You’ll also need to know the four quadrants. The quadrants are four spaces in the coordinate plane defined by the x and y axes.
- The space above the x-axis and to the right of the y-axis is the first quadrant. Everything in this quadrant is a positive value. It’s the upper right space of the plane.
- The quadrants are then ordered counterclockwise starting at the first quadrant.
- So, the second quadrant is above the x-axis and to the left of the y-axis.
- The third quadrant is below the x-axis and to the left of the y-axis.
- The fourth quadrant is below the x-axis and to the right of the y-axis.
-
3
Vectors are defined by two parameters, magnitude and direction. The magnitude is represented by the length of the vector. Direction is which way the vector is pointed in a given coordinate plane.[2]
- Vectors are often illustrated as an arrow on a coordinate plane. The tail of the vector is at the origin of the plane.
- For example, a 2-dimensional vector may have a length of 3 and point 45 degrees counterclockwise from the positive X axis.
- Note: this wikiHow guide will discuss vectors in a 2-dimensional space, but these principles apply to 3-dimensional spaces as well.
-
4
There are two common ways to represent vector components. You can use coordinates or unit vector notation.
- Coordinate notation tells you where the tip of the vector arrow is located. It’s often written as two vertically-stacked numbers within square brackets. The x coordinate is on top while the y is on the bottom.
- If you don’t know them, you can resolve a vector into components.
-
5
Unit vector notation represents the vector as an equation. This is also sometimes called engineering notation. The equation is
- u = Xî + Yĵ
- where u is the vector (this can be any letter, and usually has an arrow pointing right over the letter), X is the x coordinate, and Y is the y coordinate.
- For example, u = 3î + 4ĵ would be a vector with the tip pointed at the coordinate (3, 4).
Advertisement
-
1
Locate the angle 𝛉 you’re trying to find. The direction of a vector can be defined as the angle between the positive x-axis and the vector.[3]
- Find the angle by starting at the positive x-axis (0 degrees), and then moving counterclockwise until you get to the vector.
- The vector can point in any direction in the plane, 0 to 360 degrees.
- This angle will be referred to as 𝛉 (the greek symbol theta).
-
2
Identify the triangle created by the vector. The vector is defined by its X and Y components. You can use these two numbers to make a right triangle.
- One side of the triangle will be in line with the x-axis. This side’s length X is the X component of the vector. We’ll refer to this as the adjacent side.
- The second side is perpendicular to the x-axis. This side’s length Y is the Y component of the vector. We’ll refer to this as the opposite side.
- The third side of the triangle is the hypotenuse and also the vector itself.
-
3
Use the definition of the trigonometric function, tangent. Tangent (tan) is defined as[4]
- tan(𝛉) = opposite/adjacent
- where
- “opposite” is the length of the side farthest from the angle 𝛉
- and “adjacent” is the length of the side closest to the angle 𝛉 (that isn’t the hypotenuse)
-
4
Insert the vector components into the tangent equation. The tangent equation will use the triangle created by the x and y components of the vector. The equation will be formatted as
- tan(𝛉) = Y/X
-
5
Solve for 𝛉. To find 𝛉, you’ll need to apply the inverse tangent (written as tan^-1 or arctan) to both sides of the equation. We’ll use arctan in this guide, but it’s common to see tan^-1 on calculators. This will result in
- 𝛉 = arctan(Y/X)
- To use your calculator for solving this, first divide Y by X, then press the arctan button. You may need to press the shift or 2nd key on your calculator to access the arctan function.
- Note: Make sure your calculator is in degrees mode (usually labeled “Deg”). If you’re in radians mode (“Rad”), the answer will be in radians instead of degrees.
-
6
Apply an angle adjustment to get the correct measurement. Calculators only output angles in the first and fourth quadrants (negative 90 degrees to positive 90 degrees). This is because the calculator doesn’t evaluate where the negatives are when solving for 𝛉. To get the correct 𝛉 for each quadrant, you’ll need to identify which quadrant your vector is in, and then apply an adjustment:
- The first quadrant doesn’t need an adjustment.
- For vectors in the second quadrant, the arctan function will result in a negative angle pointing down and to the right (in the fourth quadrant). This angle points directly opposite to the vector, so you’ll need to add 180 degrees to the angle to get 𝛉.
- For vectors in the third quadrant, the arctan function will result in a positive angle pointing up and to the right (in the first quadrant). This angle points directly opposite to the vector, so you’ll need to add 180 degrees to the angle to get 𝛉.[5]
- For vectors in the fourth quadrant, the arctan function will result in a negative angle pointing down and to the right (in the fourth quadrant). This angle points in the correct direction, but the angle is negative (measured clockwise from the positive x-axis) instead of positive (measured counterclockwise from the positive x-axis). You’ll need to add 360 degrees to the angle to get 𝛉.
Advertisement
-
There are a few cases where you don’t need to use trigonometry to find the angle of the vector. These are cases in which the angle of the vector is apparent by looking at it on the graph.
- If one of the vector’s x or y components is 0, then the vector is pointing directly in line with an axis.
- For example, if you have the vector u = 0î + 5ĵ, the vector is pointing straight up along the positive y-axis. This means it has an angle of 90 degrees since the y-axis is perpendicular to the x-axis.
- If the vector’s x and y components are the same number, the vector is pointing at an increment of 45 degrees.
- For example, if you have the vector u = -3î + 3ĵ, the vector is pointing up and to the left, 45 degrees counterclockwise from the positive y-axis. Since the axes are perpendicular, we can add 90 degrees (positive x-axis to positive y-axis) plus 45 degrees to get 135 degrees.
-
Here’s a step-by-step example of a vector in the first quadrant.
- You’re given the vector u = 2î + 5ĵ
- Insert the components into the tangent equation tan(𝛉) = Y/X
- tan(𝛉) = 5/2
- 𝛉 = arctan(5/2)
- 𝛉 = arctan(2.5)
- 𝛉 = 68.20 degrees
Advertisement
-
Here’s a step-by-step example of a vector in the second quadrant.
- You’re given the vector u = -3î + 6ĵ
- Insert the components into the tangent equation tan(𝛉) = Y/X
- tan(𝛉) = 6/-3
- 𝛉 = arctan(6/-3)
- 𝛉 = arctan(-2)
- 𝛉 = -63.43 degrees
- This angle points in the fourth quadrant. Apply an adjustment to get the vector angle.
- 𝛉 = -63.43 + 180
- 𝛉 = 116.57
-
Here’s a step-by-step example of a vector in the third quadrant.
- You’re given the vector u = -1î + -7ĵ
- Insert the components into the tangent equation tan(𝛉) = Y/X
- tan(𝛉) = -7/-1
- 𝛉 = arctan(-7/-1)
- 𝛉 = arctan(7)
- 𝛉 = 81.87 degrees
- This angle points in the first quadrant. Apply an adjustment to get the vector angle.
- 𝛉 = 81.87 + 180
- 𝛉 = 261.87
Advertisement
-
Here’s a step-by-step example of a vector in the fourth quadrant.
- You’re given the vector u = 12î + -4ĵ
- Insert the components into the tangent equation tan(𝛉) = Y/X
- tan(𝛉) = -4/12
- 𝛉 = arctan(-4/12)
- 𝛉 = arctan(-0.33)
- 𝛉 = -18.43 degrees
- This angle points in the fourth quadrant, but is negative. Apply an adjustment to get the positive vector angle.
- 𝛉 = -18.43 + 360
- 𝛉 = 341.57
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Thanks to all authors for creating a page that has been read 9,405 times.
Did this article help you?
Координаты вектора. Направляющие косинусы, формулы и онлайн калькуляторы
Содержание:
- Координаты вектора
- Направляющие косинусы
- Сумма двух векторов, заданных координатами
- Умножение вектора на число
- Основное свойство направляющих косинусов
Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении
и длине.
Координаты вектора
Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$
и произвольный вектор $overline{a}$, начало которого совпадает
с началом системы координат (рис. 1).
Определение
Координатами вектора $overline{a}$ называются проекции
$a_{x}$ и $a_{y}$
данного вектора на оси $O x$ и
$O y$ соответственно:
$$a_{x}=Пр_{O x} bar{a}, a_{y}=Пр_{O y} bar{a}$$
Величина $a_{x}$ называется абсциссой вектора
$overline{a}$, а число $a_{y}$
— его ординатой.
То, что вектор $overline{a}$ имеет координаты
$a_{x}$ и $a_{y}$,
записывается следующим образом: $overline{a}=left(a_{x} ; a_{y}right)$.
Пример
Запись $overline{a}=(5 ;-2)$ означает, что вектор $overline{a}$
имеет следующие координаты: абсцисса равна 5, ордината равна -2.
Сумма двух векторов, заданных координатами
Пусть заданы $overline{a}=left(a_{x} ; a_{y}right)$ и $overline{b}=left(b_{x} ; b_{y}right)$,
тогда вектор $overline{c}=overline{a}+overline{b}$ имеет координаты
$left(a_{x}+b_{x} ; a_{y}+b_{y}right)$ (рис. 2).
Определение
Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание.
Заданы $overline{a}=(-3 ; 5)$
и $overline{b}=(0 ;-1)$. Найти координаты вектора $overline{c}=overline{a}+overline{b}$
Решение. $overline{c}=overline{a}+overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)$
Умножение вектора на число
Если задан $overline{a}=left(a_{x} ; a_{y}right)$, то тогда вектор
$m overline{a}$ имеет координаты
$m overline{a}=left(m a_{x} ; m a_{y}right)$, здесь
$m$ — некоторое число (рис. 3).
Определение
Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное
число.
Пример
Задание. Вектор $overline{a}=(3 ;-2)$.
Найти координаты вектора 2$overline{a}$
Решение. $2 overline{a}=2 cdot(3 ;-2)=(2 cdot 3 ; 2 cdot(-2))=(6 ;-4)$
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две
точки $Aleft(a_{x} ; a_{y}right)$ и $Bleft(b_{x} ; b_{y}right)$.
Тогда координаты вектора $overline{A B}=left(x_{1} ; y_{1}right)$ находятся по формулам (рис. 4):
$x_{1}=b_{x}-a_{x}, y_{1}=b_{y}-a_{y}$
Определение
Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат
конца отнять соответствующие координаты начала.
Пример
Задание. Найти координаты вектора $overline{A B}$,
если $A(-4 ; 2), B(1 ;-3)$
Решение. $overline{A B}=(1-(-4) ;-3-2)=(5 ;-5)$
Направляющие косинусы
Определение
Направляющими косинусами вектора называются косинусы углов, образованных вектором с
положительными направлениями осей координат.
Направление вектора однозначно задается направляющими косинусами. Для
единичного вектора направляющие косинусы
равны его координатам.
Если в пространстве задан вектор $overline{a}=left(a_{x} ; a_{y} ; a_{z}right)$, то
его направляющие косинусы вычисляются по формулам:
$cos alpha=frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}, cos beta=frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}, cos gamma=frac{a_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}$
Здесь $alpha$, $beta$ и
$gamma$ — углы, которые составляет вектор с положительными
направлениями осей $O x$, $O y$ и
$O z$ соответственно.
Если известны направляющие косинусы вектора $overline{a}=left(a_{x} ; a_{y}right)$,
то его координаты могут быть найдены по формулам:
$a_{x}=|overline{a}| cos alpha, a_{y}=|overline{a}| cos beta$
Аналогичные формулы имеют место и в трехмерном случае — если известны направляющие косинусы вектора
$overline{a}=left(a_{x} ; a_{y} ; a_{z}right)$,
то его координаты могут быть найдены по формулам:
$a_{x}=|overline{a}| cos alpha, a_{y}=|overline{a}| cos beta, a_{z}=|overline{a}| cos gamma$
Читать дальше: длина (модуль) вектора.
Направляющие косинусы вектора.
Направляющие косинусы вектора.
Навигация по странице:
- Определение направляющих косинусов
- Формулы для направляющих косинусов
- для плоских задач
- для пространственных задач
- Примеры задач с направляющими косинусами вектора
- плоские задачи
- пространственные задачи
Смотрите также онлайн калькулятор для вычисления направляющих косинусов вектора.
Определение направляющих косинусов
Определение. Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат.
Направляющие косинусы однозначно задают направление вектора.
Основное соотношение. Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора.
Соответственно, координаты единичного вектора равны его направляющим косинусам.
Свойство направляющих косинусов. Сумма квадратов направляющих косинусов равна единице.
Формулы вычисления направляющих косинусов вектора
Формула вычисления направляющих косинусов вектора для плоских задач
В случае плоской задачи (рис. 1) направляющие косинусы вектора a = {ax ; ay} можно найти воспользовавшись следующей формулой
| cos α = | ax | ; | cos β = | ay |
| |a| | |a| |
Свойство:
cos2 α + cos2 β = 1
рис. 1 1 |
Формула вычисления направляющих косинусов вектора для пространственных задач
В случае пространственной задачи (рис. 2) направляющие косинусы вектора a = {ax ; ay ; az} можно найти воспользовавшись следующей формулой
| cos α = | ax | ; | cos β = | ay | ; | cos γ = | az |
| |a| | |a| | |a| |
Свойство:
cos2 α + cos2 β + cos2 γ = 1
Примеры задач с направляющими косинусами вектора
Примеры плоских задач с направляющими косинусами вектора
Пример 1. Найти направляющие косинусы вектора a = {3; 4}.
Решение:
Найдем модуль вектора a:
|a| = √32 + 42 = √9 + 16 = √25 = 5.
Найдем направляющие косинусы вектора a:
| cos α = | ax | = | 3 | = 0.6 |
| |a| | 5 |
| cos β = | ay | = | 4 | = 0.8 |
| |a| | 5 |
Ответ: направляющие косинусы вектора cos α = 0.6, cos β = 0.8.
Пример 2. Найти значение векора a если его длина равна 26, а направляющие косинусы cos α = 5/13, cos β = -12/13.
Решение:
ax = |a| · cos α = 26 ·
513
= 10
ay = |a| · cos β = 26 · (-
1213
) = -24
Ответ: a = {10; -24}.
Примеры пространственных задач с направляющими косинусами вектора
Пример 3.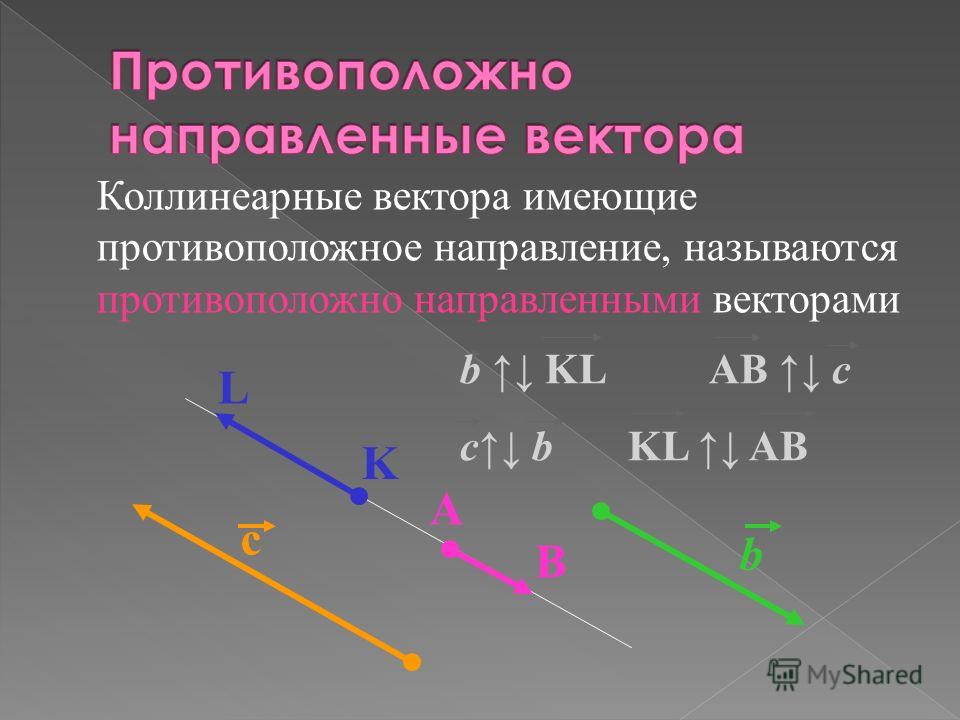
Решение:
Найдем модуль вектора a:
|a| = √22 + 42 + 42 = √4 + 16 + 16 = √36 = 6.
Найдем направляющие косинусы вектора a:
| cos α = | ax | = | 2 | = | 1 |
| |a| | 6 | 3 |
| cos β = | ay | = | 4 | = | 2 |
| |a| | 6 | 3 |
| cos γ = | az | = | 4 | = | 2 |
| |a| | 6 | 3 |
Ответ: направляющие косинусы вектора cos α =
13
, cos β =
23
, cos γ =
23
.
Вектора
Вектор: определение и основные понятия
Определение координат вектора заданного координатами его начальной и конечной точки
Модуль вектора. Длина вектора
Направляющие косинусы вектора
Равенство векторов
Ортогональность векторов
Коллинеарность векторов
Компланарность векторов
Угол между векторами
Проекция вектора
Сложение и вычитание векторов
Умножение вектора на число
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Линейно зависимые и линейно независимые вектора
Разложение вектора по базису
Онлайн калькуляторы с векторами
Онлайн упражнения с векторами на плоскости
Онлайн упражнения с векторами в пространстве
§2. Проекция вектора на заданное направление — ЗФТШ, МФТИ
1. Проекция вектора на заданное направление.
Пусть заданы два вектора `vec a` и `vec b`.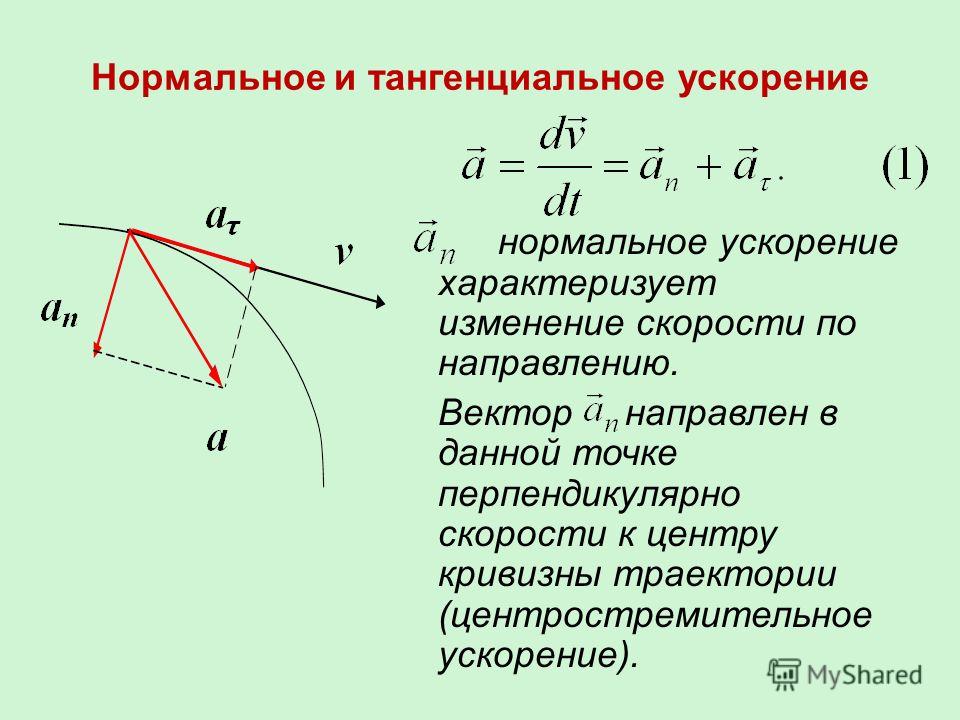
Проекция равна нулю, если направления векторов `vec a` и `vec b` взаимно перпендикулярны (см. рис. 12).
Проекции равных векторов на любые направления равны друг другу. Проекции противоположных векторов отличаются знаком.
Легко показать, что проекция суммы векторов равна алгебраической сумме их проекций и что при умножении вектора на число его проекция умножается на то же число.
2. Разложение вектора.
До сих пор мы говорили о сложении векторов. Для решения многих задач бывает необходимо произвести обратную процедуру — разложить вектор на составляющие, например, найти несколько сил, которые своим совместным действием могли бы заменить одну данную силу. Такая операция называется разложением сил.
Пусть на плоскости задан вектор `vec a` и две пересекающиеся в точке `O` прямые `AO` и `OB` (см. рис. 13).
Вектор `vec a` можно представить в виде суммы двух векторов, направленных вдоль заданных прямых.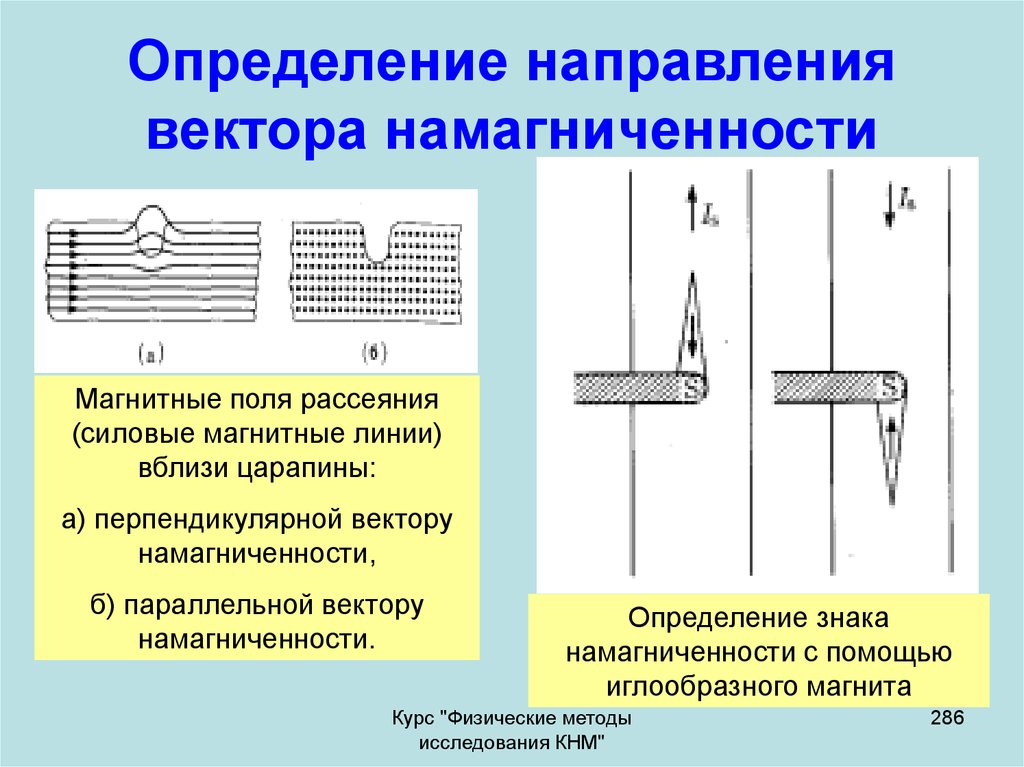
Векторы `vec(a_1)` и `vec(a_2)` называются составляющими вектора `vec a` по заданным направлениям, а само представление вектора в виде суммы (*) — разложением вектора по двум направлениям.
3. Проектирование вектора на оси координат.
Особенно важен частный случай разложения вектора по двум взаимно перпендикулярным направлениям. Пусть на плоскости задана прямоугольная система координат `xOy` и некоторый вектор `vec a`. Отложим из начала координат вдоль положительного направления осей `Ox` и `Oy` векторы `vec i` и `vec j` соответственно такие, что `|vec i| = 1` и `|vec j| = 1`. Векторы `vec i` и `vec j` назовём единичными векторами.
Перенесём вектор `vec a` так, чтобы его начало совпало с началом координат.
Опустим из точки `A` перпендикуляры на оси `Ox` и `Oy`. Тогда векторы `vec(a_x)` и `vec(a_y)` будут составляющими вектора `vec a` по координатным осям, причём вектор `vec(a_x)` будет коллинеарен вектору `vec i`, а вектор `vec(a_y)` — коллинеарен вектору `vecj`. Следовательно, существуют такие числа `a_x` и `a_y`, что `vec(a_x) = a_x vec i` и `vec(a_y) = a_y vec j`. Таким образом, вектор `vec a` может быть представлен в виде разложения по осям:
Числа `a_x` и `a_y` суть проекции вектора `vec a` на направления векторов `vec i` и `vec j` соответственно, то есть на оси `Ox` и `Oy`. Используется и иная, чем (3), форма записи векторов, а именно `vec a = (a_x ; a_y)`.
Иногда говорят о составляющей вектора вдоль одной единственной оси — без указания второй. Просто молчаливо предполагается, что вторая ось перпендикулярна первой (но почему-то не нарисована).
Пусть угол между положительным направлением оси `Ox` и вектором `vec a` равен `alpha` (рис.14). Тогда `a_x = a cos alpha`, `a_y = a sin alpha`.
В зависимости от значения угла `alpha` проекции вектора `vec a` на оси прямоугольной системы координат могут быть положительными, отрицательными или равными нулю.
Зная проекции вектора `vec a` на оси координат, можно найти его величину и направление по формулам:
причём знаки `a_x` и `a_y` будут указывать на то, какому квадранту принадлежит значение `alpha`.
4. Пусть теперь нам задано векторное равенство `vec a + vec b = vec c` (рис. 15).
Проектируя все векторы на оси координат, получим очевидные равенства
т. е. по проекциям векторов `vec a` и `vec b` легко находятся проекции суммарного вектора `vec c`.
Как определить направление вектора магнитной индукции
Содержание:
Физический смысл магнитной индукции
Физически это явление объясняется следующим образом.
В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.
При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.
Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.
Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.
Формула магнитной индукции
где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.
Вектор магнитной индукции
Определение
Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как →B. Единица измерения — Тесла (Тл).
За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B=FAmaxIl..
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Направление вектора магнитной индукции и способы его определения
Чтобы определить направление вектора магнитной индукции, нужно:
- Расположить в магнитном поле компас.
- Дождаться, когда магнитная стрелка займет устойчивое положение.
- Принять за направление вектора магнитной индукции направление стрелки компаса «север».
В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:
При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:
При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора →B магнитной индукции.
Отсюда следует, что:
- Если по витку ток идет против часовой стрелки, то вектор магнитной индукции →B направлен вверх.
- Если по витку ток идет по часовой стрелке, то вектор магнитной индукции →B направлен вниз.
Способы обозначения направлений векторов:
| Вверх | |
| Вниз | |
| Влево | |
| Вправо | |
| На нас перпендикулярно плоскости чертежа | |
| От нас перпендикулярно плоскости чертежа |
Пример №1.
Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.
Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.
Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.
С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.
В начале 19 века ученые обнаружили, что магнитное поле создается вокруг проводника с протекающим по нему током. Возникшие силовые линии ведут себя по таким же правилам, как и с природным магнитом. Больше того, взаимодействие электрического поля проводника с током и магнитного поля послужило основой электромагнитной динамики.
Понимание ориентации в пространстве сил во взаимодействующих полях позволяет рассчитать осевые вектора:
- Магнитной индукции;
- Величины и направления индукционного тока;
- Угловой скорости.
Такое понимание было сформулировано в правиле буравчика.
Совместив поступательное движение правостороннего буравчика с направлением тока в проводнике получаем направление линий магнитного поля, на которое указывает вращение рукоятки.
Не являясь законом физики, правило буравчика в электротехнике применяется для определения не только направления силовых линий магнитного поля зависящего от вектора тока в проводнике, но и наоборот, определение направления тока в проводах соленоида в связи с вращением линий магнитной индукции.
Понимание этой взаимосвязи позволило Амперу обосновать закон вращающихся полей, что привело к созданию электрических двигателей различного принципа. Вся втягивающая аппаратура, использующая катушки индуктивности, соблюдает правило буравчика.
Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.
Закон Био-Савара-Лапласа
Формула ЭДС индукции
Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.
Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB:
dB = µ0 *I*dl*sin α /4*π*r2,
где:
- dB – магнитная индукция, Тл;
- µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
- I – сила тока, А;
- dl – отрезок проводника, м;
- r – расстояние до точки нахождения магнитной индукции, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме.
Закон Био-Савара-Лапласа
Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого перемещения электронов;
- поля кругового движения заряженных частиц.
Формула для МП первого типа имеет вид:
В = µ* µ0*2*I/4*π*r.
Для кругового движения она выглядит так:
В = µ*µ0*I/4*π*r.
В этих формулах µ – это магнитная проницаемость среды (относительная).
Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:
B→= B1→+ B2→+ B3→… + Bn→
Принцип суперпозиции
Теорема о циркуляции
Изначально в 1826 году Андре Ампер сформулировал данную теорему. Он разобрал случай с постоянными электрическими полями, его теорема применима к магнитостатике. Теорема гласит: циркуляция МП постоянного электричества по любому контуру соразмерна сумме сил всех токов, которые пронизывают этот контур.
Стоит знать! Тридцать пять лет спустя Д. Максвелл обобщил это утверждение, проведя параллели с гидродинамикой.
Другое название теоремы – закон Ампера, описывающий циркуляцию МП.
Математически теорема записывается следующим образом.
Математическая формула теоремы о циркуляции
где:
- B→– вектор магнитной индукции;
- j→ – плотность движения электронов.
Это интегральная форма записи теоремы. Здесь в левой части интегрируют по некоторому замкнутому контуру, в правой части – по натянутой поверхности на полученный контур.
Магнитный поток
Одна из физических величин, характеризующих уровень МП, пересекающего любую поверхность, – магнитный поток. Обозначается буквой φ и имеет единицу измерения вебер (Вб). Эта единица характерна для системы СИ. В СГС магнитный поток измеряется в максвеллах (Мкс):
108 Мкс = 1 Вб.
Магнитный поток φ определяет величину МП, пронизывающую определённую поверхность. Поток φ зависит от угла, под которым поле пронизывает поверхность, и силы поля.
Формула для расчёта имеет вид:
φ = |B*S| = B*S*cosα,
где:
- В – скалярная величина градиента магнитной индукции;
- S – площадь пересекаемой поверхности;
- α – угол, образованный потоком Ф и перпендикуляром к поверхности (нормалью).
Внимание! Поток Ф будет наибольшим, когда B→ совпадёт с нормалью по направлению (угол α = 00). Аналогично Ф = 0, когда он проходит параллельно нормали (угол α = 900).
Магнитный поток
Вектор магнитной индукции, или магнитная индукция, указывает направление поля. Применяя простые методы: правило буравчика, свободно ориентирующуюся магнитную стрелку или контур с током в магнитном поле, можно определить направление действия этого поля.
Другие формулы, где встречается B
Эти формулы также можно использовать для её расчёта.
Сила Ампера:
Сила Ампера: Fa=IBL sinα
Где:
- Fa — сила Ампера (в Н — ньютон)
- I — сила тока (в А — ампер)
- B — индукция магнитного поля (в Тл)
- L — длина проводника (в м)
- α — угол между вектором В и одним из направлений (силы тока, скорости или др.
; измеряется в рад. или град.)
Сила Лоренца:
Сила Лоренца: Fл = qvB sinα
Где:
- Fл — сила Лоренца (в Н — ньютон)
- q — заряд частицы (в Кл — кулон)
- v — скорость (в м/с)
- B — индукция (в Тл)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Магнитный поток:
Магнитный поток: Ф = BS cosα
Где:
- Ф — магнитный поток (в Вб – вебер)
- B — индукция (в Тл)
- S — площадь рамки (в м²)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Электромагнитная индукция и магнитная индукция: какая между ними разница?
Электромагнитная индукция — это производство электродвижущей силы, создаваемой в результате относительного движения между магнитным полем и проводником.
Магнитная индукция может производить постоянный магнит, но может и не производить.
Электромагнитная индукция создаёт ток, но таким образом, что этот созданный ток противодействует изменению магнитного поля.
В электромагнитной индукции используются магниты и электрические цепи, а в магнитной индукции используются только магниты и магнитные материалы.
Предыдущая
РазноеЭлектротехника для чайников. Как научиться разбираться в электрике: уроки для начинающих
Следующая
РазноеАвтоматический выключатель — от чего защищает и как он устроен
Векторы, графическое изображение векторов, величина вектора, направление вектора
Векторы могут быть графически представлены направленными отрезками. Длина выбирается по определенной шкале, чтобы обозначить
величину вектора, а направление отрезка представляетнаправление вектора. Например, если мы примем, что 1 см представляет 5 км/час, тогда северо-восточный ветер со скоростью 15 км/час будет представлен направленным отрезком длиной 3 cм, как показано на рисунке.
Вектор на плоскости это направленный отрезок. Два вектора равны если они имеют одинаковуювеличину и направление.
Рассмотрим вектор, нарисованный из точки A к точке B. Точка называется начальной точкой вектора, а точка B называется конечной точкой. Символическим обозначением для этого вектора есть (читается как “вектора AB”). Векторы также обозначается жирными буквами, такими как U, V и W. Четыре вектора на рисунке слева имеют одинаковую длину и направление. Поэтому они представляют
равные веторы; то есть,
В контексте векторов мы применяем = чтобы обозначить их равность.
Длина, или величина выражается как ||. Для того, чтобы определить, равны ли векторы, мы находим их величины и направления.
Пример 1 Векторы u, , w показаны на рисунке внизу. Докажите, что u = = w.
Решение Сначала мы находим длину каждого вектора с использованием формулы расстояния:
|u| = √[2 — (-1)]2 + (4 — 3)2 = √9 + 1 = √10,
|| = √[0 — (-3)]2 + [0 — (-1)]2 = √9 + 1 = √10,
|w| = √(4 — 1)2 + [-1 — (-2)]2 = √9 + 1 = √10.
Отсюда
|u| = | = |w|.
Векторы u, , и w, как видно из рисунка, вроде бы имеют одно и то же направление, но мы проверим их наклон. Если прямые, на которых они находятся, имеют одинаковые наклоны, то векторы имеют одно и то же направление. Рассчитываем наклоны:
Так как u, , и w имеют равные величины и одно и то же напраывление,
u = = w.
Имейте в виду, что равность векторов требует только одинаковой величины и одинакового направления, а не расположения в одном месте. На самом верхнем рисунке — пример равности векторов.
Предположим, что человек делает 4 шага на восток, а затем 3 шага на север. Тогда человек будет в 5 шагах от начальной точки в направлении, показанном слева. Вектор в 4 единицы длиной и с направление направо представляет 4 шага на восток и вектор 3 единицы длиной направление вверх представляет 3 шага на север.
Сумма двух этих векторов есть вектор 5-ти шагов величины и в показанном направлении. Сумма также называется результирующим двух векторов.
В общем, два ненулевых вектора u и v могут быть сложены геометрически расположением начальной точки вектора v в конечную точку вектора u, и затем нахождением ветора, который имеет ту же самую начальную точку, что и вектор u и ту же самую конечную точку что и вектор v, как показано на рисунке внизу.
Суммой есть вектор, представленный направленным отрезком из точки A вектора u в конечную точку C вектора v. Таким образом, если u = и v = , тогда
u + v = + =
Мы также можем описать сложение векторов как совместное размещение начальных точек векторов, построением параллелограмма и нахождением диагонали параллелограмма. (на рисунке внизу.) Это сложение иногда называется как правило параллелограмма сложения векторов. Векторное сложение коммутативно. Как показано на рисунке, оба вектора u + v и v + u представлены одним и тем же направленным отрезком.
Если две силы F1 и F2 действуют на один объект, результирующая сила есть сумма F1
+ F2 этих двух отдельных сил.
Пример Две силы в 15 ньютонов и 25 ньютонов действуют на один объект перпендикулярно друг другу. Найдите их сумму, или результирующую силу и угол, которая она образовывает с большей силой.
Решение Нарисуем условие задачи, в этом случае — прямоугольник, используя v или для представления результирующей. Чтобы найти ее величину, используем теорему Пифагора:
|v|2 = 152 + 252 Здесь |v| обозначает длину или величину v.
|v| = √152 + 252
|v| ≈ 29,2.
Чтобы найти направление, отметим, что так как OAB есть прямым углом,
tanθ = 15/25 = 0,6.
Используя калькулятор, мы находим θ, угол, который большая сила образует с результирующей силой:
θ = tan— 1(0,6) ≈ 31°
Результирующая имеет величину 29,2 и угол 31° с большей силой.
Пилоты могут корректировать направление их полёта, если есть боковой ветер. Ветер и скорость самолёта могут быть изображены как веторы.
Пример 3. Скорость самолёта и направление. Самолёт движется по азимуту 100° со скоростью 190 км/час, в то время как скорость ветра 48 км/ч, а его азимут — 220°. Найдите абсолютную скорость самолета и направление его движения с учетом ветра.
Решение Сначала сделаем рисунок. Ветер представлен и вектор скорости самолета есть . Результирующий вектор скорости есть v, сумма двух векторов. Угол θ между v и называется угол сноса.
Обратите внимание, что величина COA = 100° — 40° = 60°. Тогда величина CBA также равна 60° (противоположные углы параллклограмма равны). Так как сумма всех углов параллелограмма равна 360° и COB и OAB имеют одну и ту же величину, каждый должен быть 120°. По правилу косинусов в OAB, мы имеем
|v|2 = 482 + 1902 — 2.48.190.cos120°
|v|2 = 47,524
|v| = 218
Тогда, |v| равно 218 км/ч. Согласно правилу синусов, в том же самом треуголнике,
48/sinθ = 218/sin120°,
или
sinθ = 48.
θ ≈ 11°
Тогда, θ = 11°, к ближайшему целому углу. Абсолютная скорость равна 218 км/ч, и направление его движения с учетом ветра: 100° — 11°, или 89°.
Если нам задан вектор w, мы можем найти два других вектора u и v, сумма которых есть w. Векторы u и v называются компонентами w и процесс их нахождения называется разложением, или представлением вектора его векторными компонентами.
Когда мы раскладываем вектор, обычно мы ищем перпендикулярные компоненты. Очень часто, однако, одна компонента будет параллельной оси x, и другая будет параллельна оси y. Поэтому, они часто называются горизонтальными и вертикальными компонентами вектора. На рисунке внизу вектор w = разложен как сумма u = и v = .
Горизонтальная компонента w есть u и вертикальная компонента — v.
Пример 4 Вектор w имеет величину 130 и наклон 40° относительно горизонтали. Разложите вектор на горизонтальные и вертикальные компоненты.
Решение Сначала мы нарисуем рисунок с горизонтальными и вертикальными векторами u и v, чья сумма есть w.
Из ABC, мы находим |u| и |v|, используя определения косинуса и синуса:
cos40° = |u|/130, или |u| = 130.cos40° ≈ 100,
sin40° = |v|/130, или |v| = 130.sin40° ≈ 84.
Тогда, горизонтальная компонента w есть 100 направо и вертикальная компонента w есть 84 вверх.
Как определить направление вектора напряженности
1
.Два
рода электрических зарядов и их
свойства. Наименьший неделимый
электрический заряд. Закон сохранения
электрических зарядов. Закон Кулона.
Единица заряда. Электростатическое
поле. Способ обнаружения поля.
Напряженность как характеристика
электростатического поля. Вектор
напряженности, его направление.
Напряженность электрического поля
точечного заряда. Единицы напряженности.
Принцип суперпозиции полей.
Электрический
заряд
—
величина
инвариантная, т.е. не зависит от системы
отсчета, а потому не зависит от того,
движется заряд или он покоится.
два
рода (типа) эл.зарядов
: заряды положительные и заряды
отрицательные.
Экспериментально
установили, что одноименные заряды
отталкиваются, а разноименные
притягиваются.
Электрически
нейтральное тело должно иметь равное
количество положительных и отрицательных
зарядов, но и их распределение по
объему тела должно быть равномерным.
Закон
сохранения эл. заряда
:
алгебраическая
сумма элек. зарядов любой замкнутой
системы (системы не обменивающейся
зарядами с внешними тепами) остается
неизменной, какие бы процессы не
происходили внутри этой системы.
Элек.
заряды самопроизвольно не создаются
и не возникают, они лишь могут разделяться
и передаваться от одного тела к другому.
Существует
наименьший
заряд, его назвали элементарным зарядом
—
это
заряд, который имеет электрон и заряд
на теле кратен этому элементарному
заряду: е=1,6*10
-19
Кл
.
Отрицательный элементарный заряд
связан с электроном, а положительный-
с позитроном, у которого заряд и масса
количественно совпадают с зарядом и
массой электрона.
что время жизни позитрона мало, на
телах они отсутствуют и поэтому
положительную или отрицательную
заряженность тел объясняют или
недостатком или избытком электронов
на телах.
Закон
Кулона:
силы
взаимодействия двух точечных зарядов,
находящихся в однородной и изотропной
среде, прямо пропорциональны произведению
этих зарядов и обратно пропорциональны
квадрату расстояния между ними, равны
между собой и направлены по прямой,
проходящей через эти заряды.
г- расстояние
между зарядами q 1
и q 2 ,
k-коэффициент
пропорциональности, зависящий от
выбора системы физических единиц.
м/Ф,
а
=8,85*10 -12
Ф/м —
диэлектрическая постоянная
Под
точечным зарядом следует понимать
заряды, сосредоточенные на телах,
линейные размеры которых малы по
сравнению с расстояниями между ними.
При
этом заряд измеряется в кулонах —
количество электричества, протекающее
через поперечное сечение проводника
в одну секунду при токе в 1 ампер.
Сила
F
направлена вдоль прямой, соединяющей
заряды, т.е. является центральной силой
и соответствующей притяжению (F0)
в случае одноименных зарядов. Эту силу
называют кулоновская
сила.
Позднейшие
исследования Фарадея показали, что
электрическое взаимодействие между
заряженными телами зависят от свойств
среды, в которой происходят эти
взаимодействия.
Заряженные тела могут воздействовать друг на друга без соприкосновения через электрическое поле. Поле, которое создается неподвижными электрическими частицами, называется электростатическим.
Спонсор размещения P&G
Статьи по теме «Как определить направление вектора напряженности»
Как найти напряженность магнитного поля
Как определить направление момента силы
Как определить направление вектора магнитной индукции
Инструкция
Если в электрическое поле, создаваемое зарядом Q, поместить еще один заряд Q0, то оно будет воздействовать на него с определенной силой.
В зависимости от конкретной точки пространства, значение напряженности поля E может меняться, что выражается формулой Е = Е (x, y, z, t). Поэтому напряженность электрического поля относится к векторным физическим величинам.
Поскольку напряженность поля зависит от силой, действующей на точечный заряд, то вектор напряженности электрического поля E одинаков с вектором силы F. Согласно закону Кулона, сила, с которой взаимодействуют две заряженные частицы в вакууме, направлена по прямой линии, которая соединяет эти заряды.
Майкл Фарадей предложил наглядно изображать напряженность поля электрического заряда с помощью линий напряженности. Эти линии совпадают с вектором напряженности во всех точках по касательной. На чертежах их принято обозначать стрелками.
В том случае, если электрическое поле однородно и вектор его напряженности постоянен по своему модулю и направлению, то линии напряженности параллельны с ним. Если электрическое поле создается положительно заряженным телом, линии напряженности направлены от него, а в случае с отрицательно заряженной частицей — по направлению к нему.
Как просто
Другие новости по теме:
Силовое поле, часть пространства, в каждой точке которого действует некоторая сила, зависящая только от положения выбранной точки. Если например мы имеем какое-нибудь заряженное тело, то на заряд, помещенный в любую точку около него, будет действовать сила электрического притяжения (или
Потенциал является энергетической характеристикой электрического поля. Для того чтобы найти его значение, нужно потенциальную энергию заряда в данной точке электрического поля поделить на сам заряд. Для различных типов полей используются разные формулы расчета потенциала. Вам понадобится —
Найти значение электрического заряда можно двумя способами.
Для того чтобы найти напряженность электрического поля, внесите в него известный пробный заряд. Измерьте силу, которая действует на него со стороны поля и рассчитайте значение напряженности. Если электрическое поле создается точечным зарядом или конденсатором, рассчитайте его по специальным
В задачах по физике иногда нужно найти заряд какого-либо тела на основе его взаимодействия с электрическим полем или другими телами. В большинстве случаев размерами самого тела пренебрегают, чтобы не рассчитывать распределение элементарных зарядов по его массе или поверхности. Спонсор размещения
Для того чтобы определить модуль точечных зарядов одинаковой величины, измерьте силу их взаимодействия и расстояние между ними и произведите расчет.
Напряженность магнитного поля H – векторная физическая величина, результат разности вектора магнитной индукции и вектора намагниченности. В системе СИ измеряется в амперах на метр, в СГС – в эрстедах. Спонсор размещения P&G Статьи по теме «Как найти напряженность магнитного поля» Как определить
Сила Лоренца определяет интенсивность воздействия электрического поля на точечный заряд. В одних случаях под ней подразумевается сила, с которой на заряд q, который движется со скоростью V, действует магнитное поле, в других имеется ввиду суммарное воздействие электрического и магнитного полей.
Электромагнитные волны (ЭМВ).
Электрическое поле, созданное неподвижными электрическими зарядами, с течением времени остается неизменным. Такое поле получило название потенциального электрического поля (электростатическое поле).
и наоборот, изменяющееся со временем магнитное поле, являющееся по самой своей природе вихревым
, создает вихревое электрическое поле
(силовые линии, т. е. линии напряженности такого электрического поля, являются замкнутыми) (рис.1).
Рис. 1. Графическое представление взаимосвязи вихревых электрического и магнитного полей.
вектор напряженности электрического поля
— вектор индукции магнитного поля, связан с вектором напряженности магнитного поля соотношением ( — магнитная проницаемость среды).
Согласно Максвеллу, переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.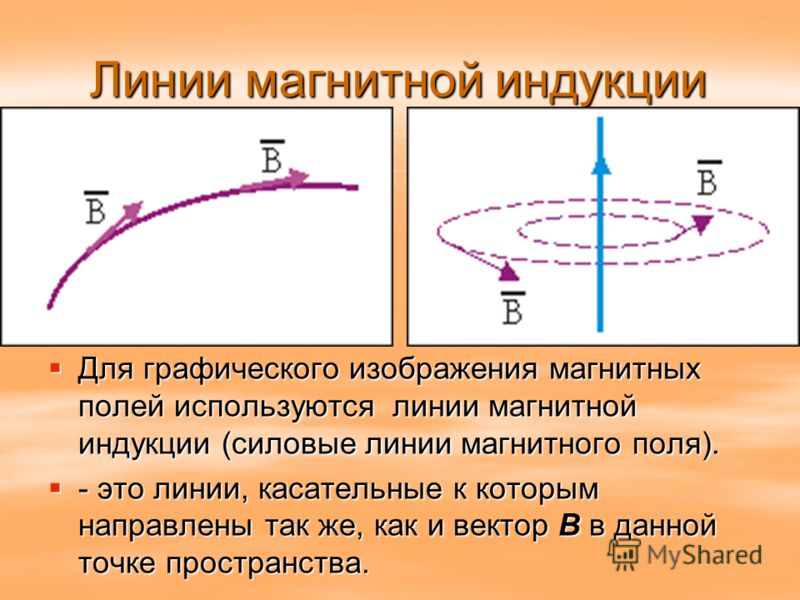
.
Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение, так называемый, ток смещения
. Током смещения объяснялось протекание переменного электрического тока через конденсатор между его обкладками, т. е. через те участки цепи, где отсутствуют проводники. Максвелл высказал предположение, что ток смещения, как и ток проводимости создает магнитное поле. Ток смещения по своей сути – это изменяющееся со временем электрическое поле, поэтому ток смещения существует и в вакууме. Введя понятие тока смещения, Максвелл по-новому подошел к рассмотрению замкнутых цепей переменного тока. Там, где на концах проводника обрывается ток проводимости, продолжается ток смещения и т. д. Следовательно, полный ток
в цепи переменного тока может быть представлен суммой токов проводимости и токов смещения.
При неравномерном движении электрических зарядов, в частности, при их колебательном движении, а значит и при всяком переменном токе, электрическое и магнитное поле будут меняться с течением времени; эти изменения будут передаваться от одной точки пространства к другой, образуя, предсказанную Максвеллом, электромагнитную
(ЭМ
) волну
. В дальнейшем было показано, что скорость распространения электромагнитных волн (ЭМВ
) в вакууме имеет значение , совпадающее с экспериментально полученным значением скорости света. Обобщение экспериментальных данных (опыты Эрстеда, сила Ампера, закон Био-Савара-Лапласа, основной закон электромагнитной индукции) привело к заключению, что при распространении ЭМВ электрические и магнитные поля имеет взаимно перпендикулярную ориентацию. В направлении распространения ЭМ волну можно представить с помощью двух синусоид, лежащих во взаимно перпендикулярных плоскостях. Одна из них изображает колебания вектора напряженности электрического поля , а другая – вектора напряженности магнитного поля .
скорости ) определяется правилом правого винта (буравчика) (рис. 2). Рисунок хорошо иллюстрирует тот факт, что ЭМ волны являются поперечными
, поскольку колебания векторов и происходят в плоскостях, перпендикулярных направлению распространения волны
(ось OY
).
Рис.2. Графическое представление электромагнитной волны. Электромагнитная теория Максвелла была блестяще подтверждена опытами Герца по распространению ЭМВ.
Общие свойства ЭМВ.
1. ЭМВ поперечные. Векторы напряженностей электрического и магнитного полей взаимно перпендикулярны и образуют правовинтовую систему с направлением распространения волны.
2. Скорость распространения (фазовая) в непроводящей среде , где
Направление векторного калькулятора
Если вы хотите рассчитать направление вектора , вы попали по адресу.
Векторы — это мощный инструмент для представления многих физических величин в нашем физическом мире. Они представляют собой силы, скорости и многие другие производные от них величины.
Помимо направления, также возможно найти величину вектора, если вы выберете расширенный режим калькулятора. Таким образом, с помощью этого инструмента вы можете найти величину и угол направления любого вектора.
Как рассчитать направление вектора?
Вы можете выразить или вычислить направление вектора v⃗ двумя способами:
- Вычисление угла направления вектора
v⃗. Направляющий угол — это угол, которыйv⃗образует с положительной осью x, считая против часовой стрелки. - Вычисление единичного вектора в направлении того же вектора. Этот единичный вектор называется вектором направления .
Как найти угол направления вектора?
Чтобы вычислить угол θthetaθ, который двумерный вектор v⃗=(x,y)vec{v} = (x, y)v=(x,y) образует с горизонтальной осью, используйте это уравнение:
θ=arctan(yx) theta = arctanleft(frac{y}{x}right)θ=arctan(xy)
Единственная проблема с этим уравнением заключается в том, что оно не дает нам угол относительно положительной оси x, но только относительно ближайшей горизонтальной оси. Если ваш вектор лежит в первом квадранте декартовой плоскости, как вектор, указывающий на P(3,5)P(3,5)P(3,5) на изображении, это не проблема. 9circ — gammaθ=180∘−γ. Мы можем распространить это рассуждение на другие случаи и составить следующие уравнения для вычисления направления вектора в каждом квадранте:
- В первом квадранте , } = arctan(frac{y}{x})θI=arctan(xy).
- Во втором квадранте , θII=180°-arctan(yx)theta_text{II} = 180° — arctan(frac{y}{x})θII=180°-arctan(xy ).
- В третьем квадранте , θIII=180°+arctan(yx)theta_text{III} = 180° + arctan(frac{y}{x})θIII=180°+arctan(xy ).
- В четвертом квадранте , θIV=360°−arctan(yx)theta_text{IV} = 360° — arctan(frac{y}{x})θIV=360°−arctan(xy ).
🙋 Термин arctan(yx)arctan(frac{y}{x})arctan(xy) дает угол в радианах, и вы должны преобразовать его в градусы, прежде чем использовать его во втором, третьем или уравнения четвертого квадранта. Посетите наш конвертер углов, чтобы узнать, как это сделать.
Как вычислить единичный вектор в направлении другого вектора?
Чтобы найти единичный вектор û в направлении другого вектора v⃗ = (x, y, z) , выполните следующие действия:
- Найдите модуль вектора
v⃗:
|v⃗| = √(x² + y² + z²) - Разделить каждый коэффициент вектора
v⃗на величинуv⃗:
û = v⃗/|v⃗| = (х/|v⃗|, у/|v⃗|, z/|v⃗|). - Вот и все.
û— единичный вектор в направленииv⃗.
Как найти вектор одной величины в направлении другой?
Чтобы найти вектор определенной величины в направлении другого вектора v⃗ = (x, y, z) :
- Найти модуль вектора
v⃗:
|v⃗| = √(x² + y² + z²) - Найдите единичный вектор
ûв направленииv⃗. Для этого каждый коэффициент вектораv⃗разделим на модуль вектора:
û = v⃗/|v⃗| = (х/|v⃗|, у/|v⃗|, z/|v⃗|) - Умножить величину желаемого вектора на единичный вектор
х. Это приведет к желаемому вектору.
Как найти величину и направление двух векторов?
Чтобы найти величину и направление двух векторов, необходимо найти результирующий вектор (для этого можно использовать наш калькулятор сложения векторов) и применить к нему описанные выше действия.
Теперь, когда вы знаете, как найти величину и угол направления вектора, давайте рассмотрим некоторые числовые примеры и ответы на часто задаваемые вопросы.
FAQ
Как найти вектор величины 3 в направлении v = 12i — 5k?
Чтобы найти вектор величины 3 в направлении v⃗ = 12i − 5k :
- Найдите величину
v⃗:
|v⃗| = √(12² + (-5)²) = 13 - Найдите единичный вектор
ûв направленииv⃗. Для этого нужно разделитьv⃗на его величину:
û = v⃗/|v⃗| = (12/13)i - (5/13)k - Умножьте желаемую величину
3на единичный векторû. Получаем векторw⃗:
w⃗ = 3û = (36/13)i − (15/13)k
, которое имеет желаемое направление и величину.
Как вычислить единичный вектор в направлении v = i + j + 2k
Чтобы вычислить единичный вектор в направлении v⃗ = i + j + 2k :
- Найти модуль
v⃗:
|v⃗| = √(1² + 1² + 2²) = √6 ≈ 2,4495 - Разделить вектор
v⃗на его модуль:
û = v⃗/|v⃗| = (1/√6)i + (1/√6)j + (2/√6)k - Вот и все.
û— единичный вектор в направленииv⃗.
Является ли скалярное произведение двух векторов в одном направлении положительным или отрицательным?
Скалярное произведение двух векторов в одном направлении всегда положительно. Это потому, что скалярное произведение двух векторов в одном направлении равно произведению их величин, а их величины всегда положительны.
Как найти величину и направление суммы двух векторов?
Чтобы найти величину и направление суммы двух векторов:
- Найдите равнодействующую двух векторов.
- Просуммируйте квадрат каждого из компонентов результирующего вектора.
- Возьмите квадратный корень из предыдущего результата, и это будет величина суммы ваших двух векторов!
- Чтобы вычислить направление вектора
v⃗ = (x, y), используйте формулуθ = arctan(y/x), гдеθ— наименьший угол, который вектор образует с горизонтальной осью, а x и y компоненты результирующего вектора.
Направление вектора — формула
Направление вектора — это угол, образуемый вектором с горизонтальной осью, то есть с осью X. Направление вектора задается вращением против часовой стрелки угла вектора вокруг его хвоста строго на восток. Например, вектор с направлением 45 градусов — это вектор, повернутый на 45 градусов против часовой стрелки относительно строго на восток. Еще одно соглашение для выражения направления вектора — это угол поворота вектора вокруг его хвоста с востока, запада, севера или юга. Например, если вектор направлен на 60 градусов к северу от запада, это означает, что вектор, указывающий на запад, был повернут на 60 градусов в северном направлении.
Направление действия вектора определяется как направление вектора. Давайте узнаем направление векторной формулы и как определить направление вектора в разных квадрантах вместе с несколькими решенными примерами.
1. |
Каково направление вектора? |
| 2. | Направление векторной формулы |
| 3. | Как найти направление вектора? |
| 4. | Часто задаваемые вопросы о направлении вектора |
Каково направление вектора?
Направление вектора — это ориентация вектора, то есть угол, который он образует с осью x. Вектор рисуется линией со стрелкой наверху и фиксированной точкой на другом конце. Направление, в котором направлена стрелка вектора, дает направление вектора. Например, скорость — это вектор. Он дает величину, с которой движется объект, а также направление, в котором движется объект. Точно так же направление приложения силы задается вектором силы. Направление вектора обозначается (overrightarrow{a} = |a|hat{a}), где |a| обозначает величину вектора, тогда как (hat{a}) является единичным вектором и обозначает направление вектора a.
Направление векторной формулы
Направление векторной формулы связано с наклоном линии.
Шаги для нахождения направления вектора (x, y):
- Найдите α, используя α = tan -1 |y/x|.
- Найдите направление вектора θ, используя следующие правила, в зависимости от того, в каком квадранте (x, y) лежит:
| Квадрант, в котором (x, y) лежит | θ (в градусах) |
|---|---|
| 1 | α |
| 2 | 180° — α |
| 3 | 180° + α |
| 4 | 360° — α |
Чтобы найти направление вектора, концы которого заданы векторами положения (x 1 , y 1 ) и (x 2 , y 2 ), затем найти его направление:
- Найдите вектор (x, y) по формуле (x, y) = (x 2 — x 1 , y 2 — y 1 )
- Найдите α и θ, как описано выше.
Давайте теперь рассмотрим несколько примеров, чтобы понять, как найти направление вектора.
Как найти направление вектора?
Теперь, когда мы знаем формулы для определения направления вектора в разных квадрантах, давайте рассмотрим пример, чтобы понять применение формулы.
Пример 1: Определить направление вектора с начальной точкой P = (1, 4) и Q = (3, 9).
Для определения направления вектора PQ сначала определим координаты вектора PQ
(x, y) = (3-1, 9-4) = (2, 5). Направление вектора определяется формулой
θ = tan -1 |5/2|
= 68,2° [Поскольку (2, 5) лежит в первом квадранте]
Направление вектора равно 68,2°.
Пример 2: Рассмотрим изображение, приведенное ниже.
Вектор на изображении выше образует угол 50° против часовой стрелки с востоком. Следовательно, направление вектора составляет 50° с востока.
Важные примечания о направлении вектора
- Направление вектора можно выразить углом, который образует его хвост с востоком, севером, западом или югом.
- После определения значения тангенса -1 |y/x| мы можем применить соответствующую формулу для каждого квадранта.
- Направление вектора также может быть задано углом, образуемым вектором в направлении против часовой стрелки с востока.
Связанные темы по направлению вектора
- Векторы
- Векторные формулы
- Перекрестное произведение
Часто задаваемые вопросы о направлении вектора
Каково направление вектора?
Направление вектора — это угол, образуемый вектором с горизонтальной осью, то есть с осью X.
Каково направление векторной формулы?
Чтобы найти направление вектора (x, y):
- Найдите α, используя α = tan -1 |г/х|
- Направление вектора (x, y) определяется как:
- α, если (x, y) лежит в первом квадранте
- 180° — α, если (x, y) лежит во втором квадранте
- 180° + α, если (x, y) лежит в третьем квадранте
- 360° — α, если (x, y) лежит в четвертом квадранте
Как найти направление вектора?
Направление вектора можно вычислить, используя формулы для каждого квадранта.
Что представляет собой направление вектора?
Направление вектора представляет направление, в котором движется объект.
Как найти направление вектора, зная его компоненты?
Направление вектора можно определить, проверив квадрант, в котором находится вектор, и затем применив соответствующую формулу.
Направление вектора – объяснение и примеры
В области векторной геометрии направление вектора играет фундаментальную роль. Направление вектора определяется как:
«Направление вектора — это направление, в котором он действует».
Помня о важности направления, давайте двигаться вперед.
В этом разделе мы рассмотрим следующие темы:
- Каково направление вектора?
- Как найти направление вектора?
- По какой формуле найти направление вектора?
- Примеры
- Практические задачи
Каково направление вектора?
Вектор — это физическая величина, описываемая величиной и направлением.
По соглашению, если его векторная диаграмма представляет собой вектор, его направление определяется углом против часовой стрелки, который он образует с положительной осью x. По масштабу векторная диаграмма представляет собой линию со стрелкой, обозначающей направление вектора.
А = |А|
|А| представляет величину, а представляет единичный вектор.
Например, чтобы полностью описать скорость тела, нам придется указать ее величину и направление. Это означает, что мы должны указать, насколько быстро он движется в единицах времени, и описать, в каком направлении он движется.
Итак, если мы говорим, что автомобиль движется со скоростью 40 км/ч. Это утверждение описывает только скорость тела. Если кто-то скажет, что машина движется со скоростью 40 км/ч и движется на север.
Вот почему для описания вектора нам столь же важны направление и величина. Если бы мы сказали, что конфеты находятся в 3 метрах от классной комнаты к северу, это имело бы больше смысла.
В приведенном выше примере мы видели, как важно направление для векторной величины.
Наконечник указывает направление вектора, а хвост представляет собой точку действия. Есть два обычных способа описать направление вектора.
- Направление вектора можно описать углом, который образует его хвост с востоком, севером, западом или югом. Например, при описании вектора можно сказать, что вектор направлен на 80° к югу от востока. Это означает, что вектор повернулся на 80° с востока на юг. Фиолетовый вектор представляет это.
Точно так же другой вектор может находиться в 65° к югу от запада. Это означает, что он направлен на 65° вокруг хвоста с запада на юг.
- Другой способ описать вектор — это угол поворота против часовой стрелки от точного «востока». В соответствии с этим вектор с направлением 50° направлен на 50° от востока.
Давайте посмотрим на эту векторную диаграмму. Если говорят, что вектор имеет направление 50°. Хитрость, чтобы понять это, состоит в том, чтобы закрепить хвост вектора, выровненный с прямым востоком или осью x. Теперь поверните вектор на 50° против часовой стрелки вокруг его хвоста.
Теперь возьмем другой пример. Предположим, что вектор имеет направление 200°. Это означает, что хвост вектора прижат к востоку, а затем повернут на 200° против часовой стрелки.
Точно так же можно использовать прямоугольную систему координат. В этом случае угол будет рассчитываться от положительной оси x.
Теперь давайте рассмотрим несколько примеров, чтобы лучше понять эту концепцию.
Пример 1
Нарисуйте вектор в 30° к северу от запада.
Решение
Пример 2
Нарисуйте вектор с направлением 60° к востоку от севера.
Решение
Как найти направление вектора?
Направление вектора определяется углом, который он образует с горизонтальной линией.
Существует два метода определения направления вектора:
- Графический метод
- Использование формулы арктангенса нарисуйте вектор графически, а затем вычислите угол. Шаги для графического метода следующие:
- Нарисуйте отдельные векторы с хвостами в начале координат и в соответствии с их углами.
- Используя правило «голова к хвосту», сложите векторы.
- Результирующий вектор R направлен от конца первого вектора A к началу второго вектора B .
- Затем с помощью линейки и транспортира определяются величина и направление вектора. Длина результирующего вектора R даст его величину.
- Для направления нарисуйте линию, параллельную оси x, проходящую через начальную точку результирующего вектора R .
Измерьте угол между горизонтальной линией и равнодействующей.
Однако вот в чем проблема: Этот метод предназначен только для базового понимания. Это усложняется, если вам нужно добавить несколько векторов, и не всегда дает самый точный результат. Всегда есть вероятность человеческой ошибки. Следовательно, у нас есть второй метод:
Формула арктангенса
Мы используем функцию арктангенса, чтобы найти угол, который он образует с горизонтальной линией .
Это возможно, если у вас есть начальная и конечная координаты вектора на плоскости. Он определяется как:
θ = tan-1 (y/x)
Пример 3
Вектор направлен от начала координат к (3,5). Определите его направление.
Решение
Здесь мы видим, что
a = x = 3
b = y = 5
θ = tan-1 (a/b)
θ = tan-1 (3/5)
θ = 30,9°
Вектор направлен под углом 30,9° от оси x.
Теперь рассмотрим случай, когда хвост не расположен в начале координат, а вектор расположен где-то еще на плоскости.
В этом случае формула видоизменяется следующим образом:
По свойству Пифагора мы знаем: y2 – y1)/(x2 – x1)
Таким образом, формула изменяется следующим образом:
θ = tan-1 (y1 – y0)/(x1 – x0)
Заданный здесь угол от горизонтальной линии, идущей параллельно оси x.
Давайте решим несколько примеров, чтобы понять эту концепцию.
Пример 4
Найти направление вектора, проходящего от A(2,1) до B(6,9)
Δx = x1 – x0 = 6 -2 = 4 9 -1 = 8
Решение
Используя формулу:
θ = tan-1 (y1 – y0)/(x1 – x0)
θ = tan-1 (8/4)
θ = 63,4°
Условные обозначения для направления вектора
Давайте перейдем к более сложному случаю.
Мы видели, что в приведенном выше примере вектор лежит в первом квадранте. Давайте посмотрим, как это работает для остальных квадрантов. Это можно определить по знакам координат вектора, которые определяют квадрант, в котором лежит угол.
Для этого необходимо соблюдать определенные соглашения:
- Если обе координаты положительны, то угол существует в первом квадранте и считается стандартным углом. θ = Ⲫ
- Если координата y положительна, а координата x отрицательна, то угол существует во 2-м квадранте, тогда стандартный угол равен: θ = 180 + Ⲫ
- Если обе координаты отрицательны, то угол существует в 3-м квадранте, тогда стандартный угол равен: θ = 270 + Ⲫ
- Если координата x положительна, а координата y отрицательна, то стандартный угол равен: θ = 360 + Ⲫ.
Поясним это на примерах.
Пример 5
Найти направление вектора, направленного из начала координат в координаты (6, -7).
Решение
Воспользуемся формулой арктангенса:
θ = tan-1 (-7/6)
θ = -49,23° лежащий в квадранте IV.
Теперь дело в том, что:
Формула дает кратчайший угол от положительной или отрицательной оси x. Соглашение состоит в том, чтобы представлять угол с положительным знаком от положительной оси x.
Для этого от 360° отнимаем от полученного угла.
θ’ = -49,23 + 360
θ = 310,77°
Пример 6
Найти направление вектора (-4,3).
Решение
Глядя на координаты, мы знаем, что вектор лежит в квадранте II:
θ = tan-1 (3/-4)
θ = -36,87° ось х. Теперь, чтобы получить положительный ответ и рассчитать от положительной оси x против часовой стрелки:
θ = -36,87 + 180
θ = 143,13°
от положительной оси x против часовой стрелки.
Для нахождения направления равнодействующего вектора
Двигаясь дальше, давайте посмотрим, как мы можем найти направление равнодействующего двух или более векторов.
Как вы знаете, чтобы вычислить результирующий вектор двух или более отдельных векторов, мы сначала находим их соответствующие прямоугольные координаты. Затем мы добавляем x-компоненту и y-компоненту двух векторов. Результирующие компоненты x и компоненты y фактически являются компонентами результирующего вектора.
Ниже приведен шаг для вычисления направления равнодействующей двух или более векторов:
Допустим, у вас есть векторы A и B, , и вы хотите найти их равнодействующую и направление.
- Разложите оба вектора на их прямоугольные компоненты.
- Мы знаем, R = A + B. Аналогично, Rₓ = Aₓ + Bₓ и R𝚢 = Bₓ и R𝚢 = Bₓ .0460
- Теперь, используя свойство арктангенса, замените x и y на x, y-компоненты равнодействующей, т.е. результирующую и изменить тета в соответствии с ней.
Практические задачи
- Найдите направление вектора, начальная и конечная точки которого равны (5, 2) и (4, 3) соответственно.
- Найдите направление вектора, начальная и конечная точки которого равны (2, 3) и (5,
соответственно.
- Вектор направлен из начала координат в (7, 4). Найдите его направление.
- Найдите направление вектора с координатами (-7, -5).
- Найдите направление вектора с координатами (1, -1).
Answers
- -45° or 135°
- 59°
- 29.74°
- 234°
- -45° or 135°
All the vector diagrams are constructed by using GeoGebra .
Предыдущий урок | Главная страница | Следующий урок
MathScene — Векторы — Урок 5
MathScene — Векторы — Урок 5
2008 Расмус Эф и Джанн Сак
Урок
5
Векторы и
прямые
Пример 1:Найдите один вектор, параллельный прямой y = 3x + 2, и второй вектор,
перпендикулярна прямойМы
начните с поиска двух точек, лежащих на прямой.Выберите x = 0 и найдите соответствующее значение y.
y = 30 + 2 = 2. Точка (0, 2) лежит на прямой.Выбирать
х = 1 и найти у.y = 31 + 2 = 5. Точка (1, 5) лежит на прямой.
Найдите вектор, который соединяет эти две точки и может назвать его
.
имеет
в том же направлении, что и линия, и называется вектором направления.Если мы повернем вектор на 90, мы получим вектор, перпендикулярный
линия. Это называется вектором нормали и помечен
.На диаграмме показаны эти два вектора.
Мы можем переписать уравнение прямой в примере y = 3x + 2
в виде 3x y + 2 = 0, переместив y через знак равенства и расположив
так, чтобы первым стоял член по х, затем член по у и, наконец,
постоянный срок. Обратите внимание, что коэффициенты x и y, 3 и 1 такие же, как и
координаты вектора нормали
.Теперь покажем, что это верно для всех прямых.
Мы используем общую форму для прямой линии, ax + by + c = 0,
.
Найдите две точки на прямой, сначала выбрав x = 0 и найдя
y, а затем выбрав y = 0 и найдя x.а0 + by + с = 0
у = с/б, если
х = 0топор + b0
+ с = 0х = с/а, если
у = 0Точки (0, c/b) и (c/a, 0) лежат на прямой.
Таким образом, вектор направления
а вектор нормали
.Привычно и проще работать с целыми числами, а
чем дроби, поэтому мы умножаем координаты векторов на ab/c. При выполнении
это мы меняем только длину векторов, а не направление. Векторы
по-прежнему параллельны или перпендикулярны прямой.Новый вектор направления будет
и новый вектор нормали будетЧтобы найти вектор направления или вектор нормали для прямой линии
все, что нам нужно сделать, это записать уравнение в общем виде. Затем мы можем прочитать
непосредственно из уравнения.Общее уравнение прямой:
ах + бай + с = 0,Нормальный вектор
Вектор направления
Мы можем использовать эти векторы, чтобы найти угол между прямыми линиями, используя
скалярное произведение векторов.Угол между линиями такой же, как и
угол между их направляющими векторами. Простая геометрия показывает, что угол
между прямыми также равен углу между их векторами нормалей.
Пример 2:Найдите угол v между прямыми l 1
, с уравнением y = 3x + 2 и линией l 2 с уравнением y = x
+ 4 (см. схему).Приведя уравнения к общему виду, получим: 3x y + 2 = 0 и x y + 2 = 0,
нормальные векторы
иДлины векторов нормалей:
Мы
теперь у нас есть вся информация, необходимая для использования скалярного произведения для нахождения угла
v между векторами нормалей, которые
равен углу между прямыми.v ≈
26,6Найдите вектор, начинающийся в точке (1,
2) и
перпендикулярно векторуЕсли мы укажем конечную точку векторных координат (x, y), то увидим, что
все векторы вида
перпендикулярны данному вектору.Скалярное произведение перпендикулярных векторов равно 0, что означает, что мы можем записать
следующее уравнение:3(х
1) + (1)(у
2) = 03x 3 года + 2 = 0
3x у 1 = 0
Это уравнение прямой, проходящей через точку (1, 2)
с нормальным векторомЭто дает нам метод нахождения уравнения прямой линии, если мы знаем
одна точка на прямой и вектор нормали.Уравнение прямой, проходящей через точку (x 1 ,
y 1 ) и имеет вектор нормали
это:а(х
— х 1 )
+ б(х — у 1 ) = 0
Пример 3:Найдите уравнение двух прямых l 1 и l 2
пересекающиеся в точке (3,
3). l 1 параллельный и l 2
перпендикулярна прямой 3x y + 2 = 0 .Вектор нормали l 1 такой же, как нормаль 3x y
+ 2 = 0, т.е.
.Мы можем поместить эту информацию прямо в уравнение
а(х
х 1 )
+ б(х
у 1 ) = 03(х
3) + (1)(у
3) = 03x 9 у + 3 = 0
3x y 6 = 0 (уравнение
линии л 1 )Нормальный вектор для l 2 совпадает с вектором направления
3x y + 2 = 0 , то есть
.Опять же, мы можем поместить эти значения в базовое уравнение линии
.
а(х
х 1 )
+ б(х
у 1 ) = 01(х
3) + 3(у
3) = 0х 3 + 3у 9 = 0
х + 3у 12 = 0
(уравнение прямой l 2 )Наконец, давайте посмотрим на схему.
Пример 4:Найдите расстояние между параллельными прямыми 3x y + 2 = 0 и 3x y 6 = 0.
(см. схему).Выбираем любую точку, например (1, 5), на прямой 3x y + 2 = 0 и находим
кратчайшее расстояние точки от другой линии
3x y 6 = 0.Это даст нам необходимое расстояние между двумя линиями.
Длина вектора нормали обычно не является требуемым расстоянием.
Из диаграммы видно, что в этом примере вектор нормали,
,
больше, чем расстояние между двумя линиями. Поэтому нам необходимо найти
число t, которое при умножении на
,
дает нам вектор точно правильной длины.
Назовите конечную точку вектора (на второй линии) (x, y). Теперь мы можем написать
следующее векторное уравнение:Это дает нам два уравнения, которые можно решить относительно x и y.
3т =
х 1
а также
т =
у 5х =
3т
+ 1
у =
т + 5Точка ( x, y ) лежит на второй линии, поэтому мы можем поместить эти значения x и y
в уравнение прямой.3x
у
6 = 03(3т
+ 1) (т
+ 5) 6 = 09т + 3 + т
5 6 = 010т = 8
т = 0,8
В
примере 2 мы обнаружили, что длина была
.Следовательно, расстояние между двумя прямыми равно t
или же
требуемое расстояние 0,8Теперь мы сделаем приведенный выше пример с буквами вместо цифр. Это ведет к
очень полезная формула для расстояния точки от линии.Общее уравнение прямой: ax + by + c = 0, и мы выбираем точку
с координатами (x 1 , у 1 ).
Теперь мы можем написать следующее уравнение:Решим это векторное уравнение относительно x и y.
та =
х х 1
и tb =
г г 1х =
та
+ х 1
у
знак равно
ТВ
+ у 1Ввод этих значений в уравнение и решение для t:
топор + по + с = 0
а(та
+ х 1 ) + б(тб
+ у 1 ) + с =
0та 2
+ топор 1 + тб 2
+ по 1 + с = 0та 2 + тб 2
= топор 1 по 1
ст(а 2 + б 2 )
= топор 1 по 1
сДлина вектора нормали определяется как || 2
= a 2 + b 2 , поэтому мы можем переписать уравнение как:т|| 2
= топор 1 на 1
сЕсли мы разделим на || 2
мы получаем значение для t, которое мы можем умножить на длину нормали
вектор
.
Нам нужно помнить, что длина не может быть отрицательной, поэтому мы используем абсолютное значение
знак.т = |ах 1
по 1 с| /|| 2Если мы умножим на ||
получаем следующую формулу:Расстояние до точки (x 1 , y 1 )
с линии
топор + by + c = 0 этоили же
Пример 5:Теперь мы собираемся отразить точку (3, 5) на линии 3x y 6 = 0 и
найти точку отражения.План следующий. Сначала найдите вектор, который перпендикулярен прямой 3x
y 6 = 0, идущих из точки (3, 5) в точку
P = (x, y), лежащий на прямой. Это будет вектор нормали t
(видеть
диаграмму). Отраженную точку S находим добавлением вектора t
к
вектор положения P.Начнем с нахождения значения t тем же методом, что и в предыдущем
пример:Решая эти два уравнения относительно x и y, мы получаем:
3т =
х + 3
а также
т =
у 5х =
3т
3
у =
т
+ 5Подставляя эти значения x и y в уравнение, мы можем найти t.
3x
у 6 = 03(3т
3) (т
+ 5) 6
= 09т 9 + т 5 6 = 0
10т = 20
т = 2
Этот
дает нам вектор
а также
мы можем найти координаты вектора положения P.В настоящее время
мы добавляем 2
(
т)
к этому и получить вектор положения для S.Координаты точки отражения:
S = (9, 1)
Пример 6:Найдите уравнения двух прямых l 1 и l 2
пересекающиеся в точке (3,
4) и
параллельны векторам
и соответственно.Затем найдите уравнение биссектрисы угла между двумя прямыми.
Векторы нормалей к l 1 и l 2 равны
иТаким образом, уравнение l 1 выглядит следующим образом:
1(х
3) 3(у
4) = 0х 3 3у + 12 = 0
х 3у + 9 = 0
и уравнение l 2 равно
3(х
3) 1(у
4) = 03x
9 г + 4 = 03x у 5 = 0,
Все точки (x, y) на биссектрисе угла равноудалены от прямых l 1
и л 2 .Таким образом, мы можем найти уравнение угла
биссектрисы, найдя расстояние (x, y) от каждой линии и приравняв их.х + 3у 9= (3x
+ у + 5)из-за абсолютного
значениеЭто дает нам два уравнения.
х + 3х + 3у у 9 5 = 0
или же
х 3х + 3у + у
9 + 5 = 02х + 2у 14 = 0
4x + 4y 4 = 0x + y 7 = 0 x
у + 1 = 0Есть два ответа, потому что есть два угла между линиями и
следовательно, две биссектрисы угла (см. схему).
Попробуйте Викторина
5
на Векторы.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.Векторные операции
В физическом мире некоторые величины, такие как масса, длина, возраст и стоимость, могут быть представлены только величиной.
Другие величины, такие как скорость и сила, также включают направление. Вы можете использовать векторы для представления тех величин, которые включают в себя как величину, так и направление. Одно из распространенных применений векторов включает определение фактической скорости и направления самолета с учетом его воздушной скорости и направления, а также скорости и направления попутного ветра. Другое распространенное использование векторов связано с нахождением результирующей силы, действующей на объект, на который действуют несколько отдельных сил.
Любая величина, имеющая как размер, так и направление, называется векторной величиной . Если A и B — две точки, расположенные на плоскости, то направленный отрезок от точки A до точки B обозначается . Точка A — это начальная точка , а точка B — конечная точка .
Геометрический вектор — это величина, которая может быть представлена отрезком направленной линии.
С этого момента вектор будет обозначаться жирной буквой, например 9.0003 и или и . Величина вектора — это длина направленного отрезка. Величину иногда называют нормой . Два вектора имеют одинаковое направление , если они параллельны и указывают в одном и том же направлении. Два вектора имеют противоположных направлений , если они параллельны и направлены в противоположные стороны. Вектор, который не имеет величины и указывает в любом направлении, называется нулевым вектором . Говорят, что два вектора равны эквивалентны векторам , если они имеют одинаковую величину и одинаковое направление.
На рис. 1 показано добавление вектора с использованием правила – кончика хвоста – . Чтобы сложить векторы v и u , переместите вектор u так, чтобы начальная точка u находилась в конечной точке u .
Результирующий вектор от начальной точки v до конечной точки u есть вектор v + u и называется результатом . Векторы v и u называются компонентами вектора v + u . Если два добавляемых вектора не параллельны, то также можно использовать правило параллелограмма . В этом случае начальные точки векторов совпадают, а результирующая является диагональю параллелограмма, образованного использованием двух векторов в качестве смежных сторон параллелограмма.
Рисунок 1
Пример сложения векторов.
Чтобы умножить вектор u на действительное число q , умножьте длину u на | q | и изменить направление u , если q < 0.
Это называется скалярным умножением . Если вектор u умножить на -1, результирующий вектор обозначается как — u . Он имеет ту же величину, что и u , но имеет противоположное направление. На рис. 2 показано использование скаляров.
Рисунок 2
Примеры векторов.Пример 1: Самолет летит строго на запад со скоростью 400 миль в час. Попутный ветер дует в юго-западном направлении со скоростью 50 миль в час. Нарисуйте диаграмму, отображающую путевую скорость и направление движения самолета (рис. 3 ).
Рисунок 3
Рисунок для примера 1 — векторное представление.Вектор, представленный в предыдущем примере, известен как вектор скорости . Азимут вектора v представляет собой угол, измеренный по часовой стрелке от точного севера до v .
В примере пеленг самолета составляет 270°, а пеленг ветра — 225°. Перерисовав фигуру в виде треугольника с использованием правила кончика хвоста, можно рассчитать длину (путевую скорость самолета) и пеленг равнодействующей (рис. 4).
Рисунок 4
Чертеж для примера 1 — представление угла.Во-первых, используйте закон косинусов, чтобы найти величину равнодействующей.
Затем используйте закон синусов, чтобы найти азимут.
Азимут β, таким образом, составляет 270° − 4,64° или приблизительно 265,4°.
Пример 2: Самолет летит со скоростью 300 миль в час. Ветер дует с юго-востока со скоростью 86 миль в час и азимутом 320°. В каком азимуте должен направиться самолет, чтобы его истинный азимут (относительно земли) составлял 14°? Какова будет путевая скорость самолета (рис. 5)?
Рисунок 5
Чертеж для примера 2.Используйте закон синусов для расчета азимута и скорости относительно земли. Поскольку эти чередующиеся внутренние углы конгруэнтны, угол 54° является суммой угла 14° и угла 40°.
Следовательно, пеленг самолета должен быть 14° + 13,4° = 27,4°. Наземная скорость самолета составляет 342,3 мили в час.
Любой вектор можно разбить на два составляющих вектора , горизонтальная составляющая и вертикальная составляющая. Эти вектора компонентов называются проекциями (рис. 6).
Рисунок 6
Пример прогнозов.Пример 3: Сила в 11 фунтов и сила в 6 фунтов действуют на объект под углом 41° друг к другу. Какова величина результирующей силы и какой угол образует результирующая сила с силой 11 фунтов (рис. 7)?
Рисунок 7
Чертеж для примера 3.Во-первых, используйте закон косинусов, чтобы найти величину равнодействующей силы.
Затем используйте закон синусов.
Таким образом, результирующая сила равна 16,02 фунта, и эта сила составляет угол 14,24° с силой 11 фунтов.
Направление косинусов вектора
Направление косинусов вектора
Навигация по страницам:
- Направление косинусов вектора — определение
- Направление косинусов векторных формул
- для плоскостных задач
- для пространственных задач
- Примеры задач
- плоские задачи
- пространственные задачи
Онлайн калькулятор. Направление косинусов вектора
Направление косинусов вектора — определение
Определение. направляющие косинусы вектора а — это косинусы углов, которые вектор образует с осями координат.
Косинусы направления однозначно задают направление вектора.
Основное отношение. Чтобы найти направляющих косинусов вектора а, нужно соответствующую координату вектора разделить на длину вектора.
Координаты единичного вектора равны его направляющим косинусам.
Свойство направляющих косинусов. Сумма квадратов направляющих косинусов равна единице.
Направляющие косинусы векторной формулы
Направляющие косинусы векторной формулы для двумерного вектора
В случае плоской задачи (рис. 1) направляющие косинусы вектора a = {a x ; a y } можно найти по следующей формуле
cos α = a x ; cos β = а у |а| |а| Property:
cos
2 α + cos 2 β = 1
Direction cosines of a vector formula для трехмерного вектора
В случае пространственной задачи (рис.
2) направляющие косинусы вектора a = {a x ; а и ; a z } можно найти по следующей формуле
cos α = a x ; cos β = a y ; cos γ = a z |a| |а| |а| Свойство:
COS 2 α + COS 2 β + COS 2 γ = 1
75 2 γ = 1733333333333333333333333333333333333333333333333333333333333333333333333333333ня0240
Примеры задач
Примеры плоскостных задач
Пример 1. Найти направляющие косинусы вектора a = {3; 4}.
Решение:
Вычислить длину вектора a:
|а| = √3 2 + 4 2 = √9 + 16 = √25 = 5.Вычислить направляющие косинусы вектора a:
cos α = a x = 3 = 0,6 |a| 5 cos β = a y = 4 = 0.8 |a| 5 Ответ: направляющие косинусы вектора a равны cos α = 0,6, cos β = 0,8.
Пример 2. Найти вектор a, если его длина равна 26, а направление косинусов cos α = 5/13, cos β = -12/13.
Решение:
а х = |а| · cos α = 26 · 5/13 = 10
а у = |а| · cos β = 26 · (-12/13) = -24Ответ: а = {10; -24}.
Примеры пространственных задач
Пример 3.
Найти направляющие косинусы вектора a = {2; 4; 4}.
Решение:
Вычислить длину вектора a:
|а| = √2 2 + 4 2 + 4 2 = √4 + 16 + 16 = √36 = 6.Вычислить направляющие косинусы вектора a:
COS α = A x = 2 = 1 1 1 1 6 3 899 8 8 899 .
cos β = a y = 4 = 2 |a| 6 3 .
COS γ = A Z = 4 = 4 = 4
Нахождение координат вектора через координаты точек
Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .
Векторы i → и j → называют координатными векторами.
Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.
Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .
Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .
Таким образом, координаты равных векторов соответственно равны.
Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.
Изобразим координатную ось.
Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .
O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .
По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .
Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.
Для нахождения координат вектора, необходимо найти разность его точек конца и начала.
Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .
Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.
Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .
Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .
Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .
Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .
По условию известно, что A B → = ( 2 , 0 , — 2 ) .
Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2
Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5
Ответ: B ( 5 , 5 , 5 ) .
Как найти вектор по точкам
Формула
Чтобы найти координаты вектора $overline$ на плоскости, если он задан координатами своих начала $Aleft(x_ <1>; y_<1>right)$ и конца $Bleft(x_ <2>; y_<2>right)$, необходимо от координат конца отнять соответствующие координаты начала, то есть
Чтобы найти координаты вектора $overline$, заданного в пространстве координатами $Aleft(x_ <1>; y_ <1>; z_<1>right)$ и $Bleft(x_ <2>; y_ <2>; z_<2>right)$, необходимо, по аналогии с плоским случаем, из координат конца вычесть координаты начала:
Примеры нахождения координат вектора по точкам
Задание. Даны точки $A(4;-1)$ и $B(2;1)$. Найти координаты векторов $overline$ и $overline$
Решение. Для вектора $overline$ точка $A$ является началом, а точка $B$ — концом. Тогда координаты вектора $overline$ равны
Для вектора 
Ответ. $overline=(-2 ; 2), overline=(2 ;-2)$
Задание. Даны три точки в пространстве точки $A(1;-2;0,5)$, $B(3;2;1,5)$ и $C(0;-1;1)$. Найти координаты векторов $overline$, $overline$, $overline$
Решение. Для искомого вектора $overline$ точка $A$ является началом, а точка $B$ — концом. Тогда координаты вектора $overline$ соответственно равны:
$$overline=(3-1 ; 2-(-2) ; 1,5-0,5)=(2 ; 4 ; 1)$$
Для вектора $overline$ точка $A$ является началом, а точка $C$ — концом. Тогда его координаты соответственно равны
Для вектора $overline$ точка $B$ является началом, а точка $C$ — концом. Его координаты равны
Ответ. $overline=(2 ; 4 ; 1), overline=(-1 ; 1 ; 0,5), overline=(-3 ;-3 ;-0,5)$
Как найти длину вектора
Чтобы найти длину вектора, определяемого его координатами, вам нужно извлечь квадратный корень из суммы квадратов его координат. Если вектор определен на плоскости и имеет координаты ( overline=left(a_ ; a_right) ), его длина рассчитывается по формуле:
ПРИМЕРЫ РАСЧЕТА ВЕКТОРНОЙ ДЛИНЫ
Задание: Найти длину вектора ( overline=(-3 ; 4) )
Решение: Чтобы найти длину вектора, определенного на плоскости, мы используем формулу
Подставляя в него координаты заданного вектора, получаем:
Задание: В пространстве заданы точки ( A(3 ;-2 ;-1)quad<и>quad B(1 ; 2 ;-5) ). Найти длину вектора ( overline )
Решение: Сначала мы находим координаты вектора ( overline ). Для этого из координат конца мы вычисляем соответствующие координаты начала, получаем:
Находя длину вектора ( overline ) мы используем формулу:
Подставляя в эту формулу координаты вектора, получим
http://www.webmath.ru/poleznoe/formules_13_0.php
http://www.homework.ru/spravochnik/kak-najti-dlinu-vektora/
Направление вектора
Направление вектора: основные понятия и определения
Первая точка называется началом вектора, а вторая – его концом.
Расстояние между началом и концом вектора называется длиной или модулем вектора.
Вектор, начало и конец которого совпадают, называется нулевым и обозначается ; его длина считается равной нулю. В противном случае, если длина вектора положительна, то его называют ненулевым.
Замечание. Если длина вектора равна единице, то он называется ортом или единичным вектором и обозначается .
Ненулевой вектор также можно определить как направленный отрезок.
Замечание. Направление нулевого вектора не определено.
Направляющие косинусы вектора
Замечание. Однозначно направление вектора задают его направляющие косинусы.
Чтобы найти направляющие косинусы вектора необходимо вектор нормировать (то есть вектор поделить на его длину):
Замечание. Координаты единичного вектора равны его направляющим косинусам.
| Понравился сайт? Расскажи друзьям! | |




























 ; измеряется в рад. или град.)
; измеряется в рад. или град.)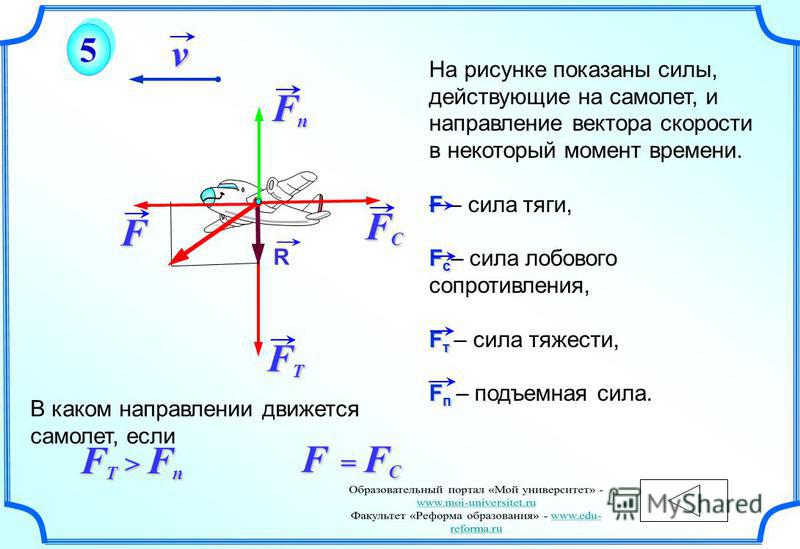

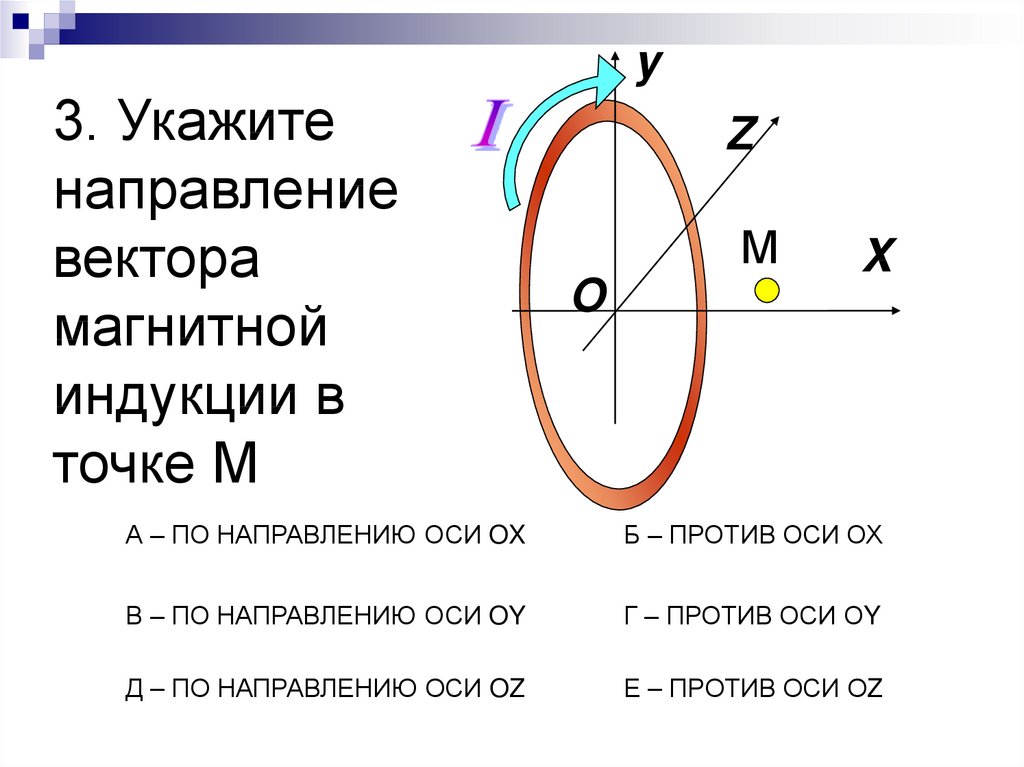

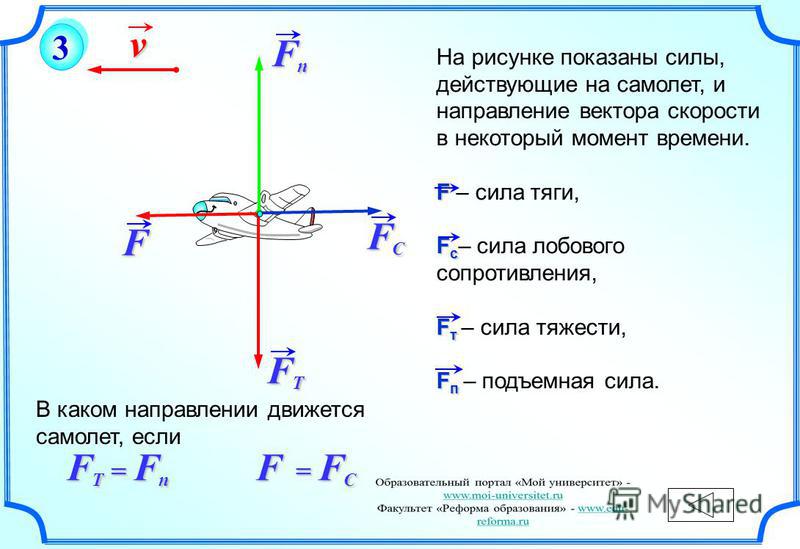


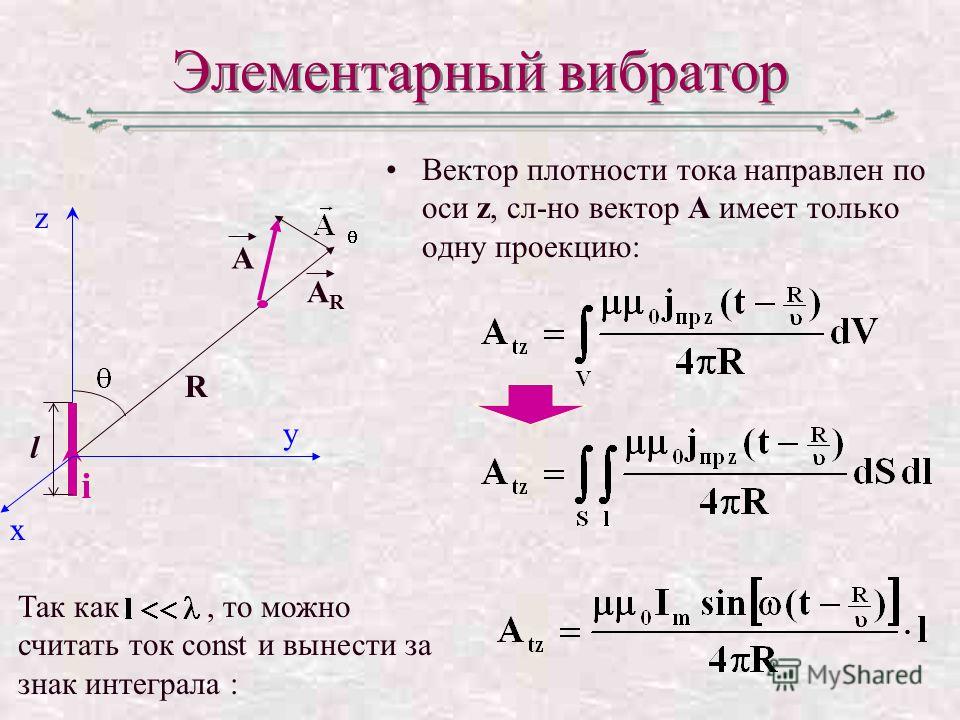
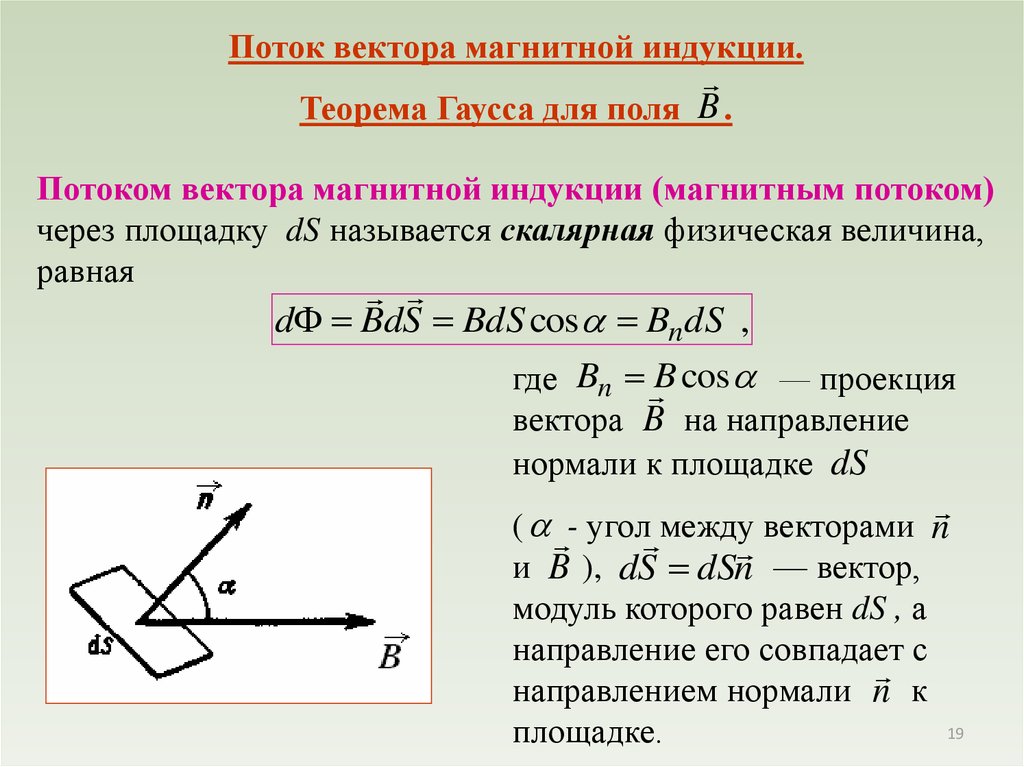
 Измерьте угол между горизонтальной линией и равнодействующей.
Измерьте угол между горизонтальной линией и равнодействующей.  В этом случае формула видоизменяется следующим образом:
В этом случае формула видоизменяется следующим образом: 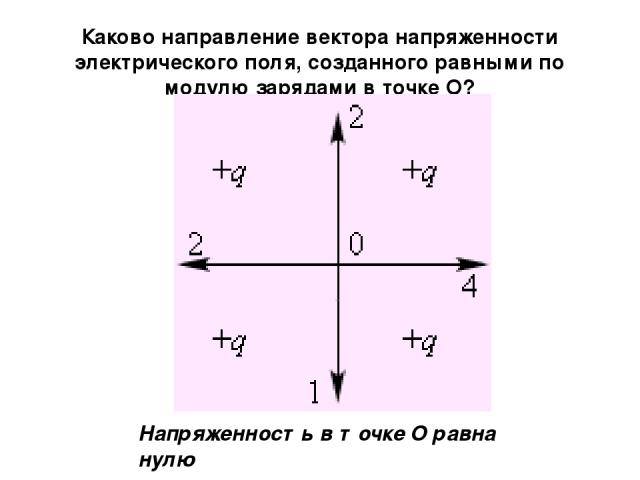
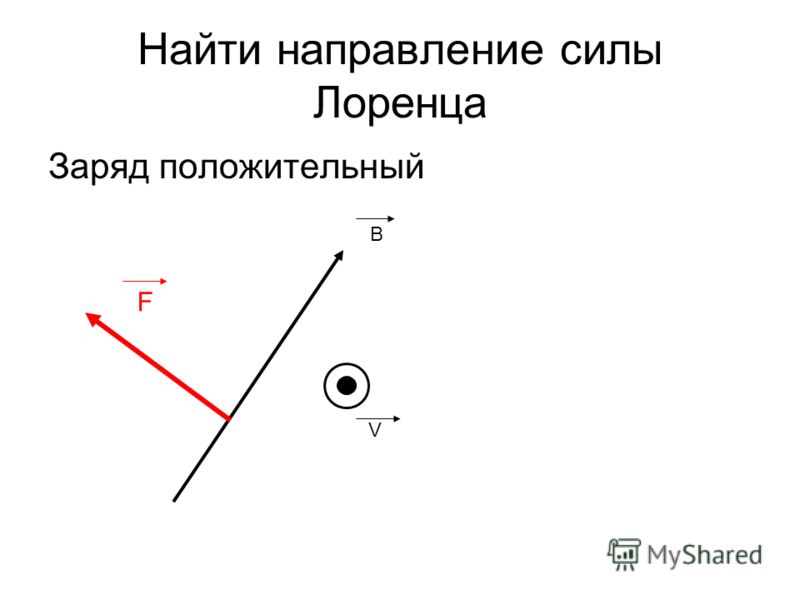 Для этого от 360° отнимаем от полученного угла.
Для этого от 360° отнимаем от полученного угла. 
 соответственно.
соответственно. 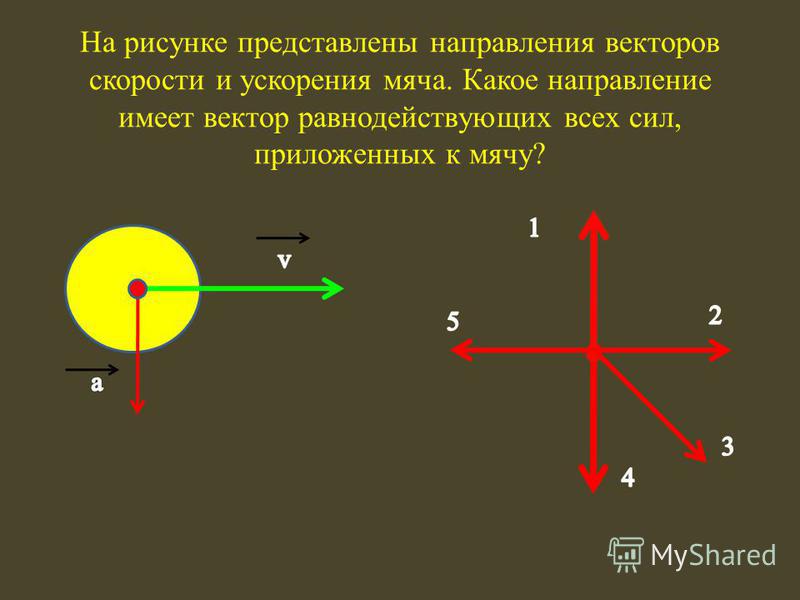


 Угол между линиями такой же, как и
Угол между линиями такой же, как и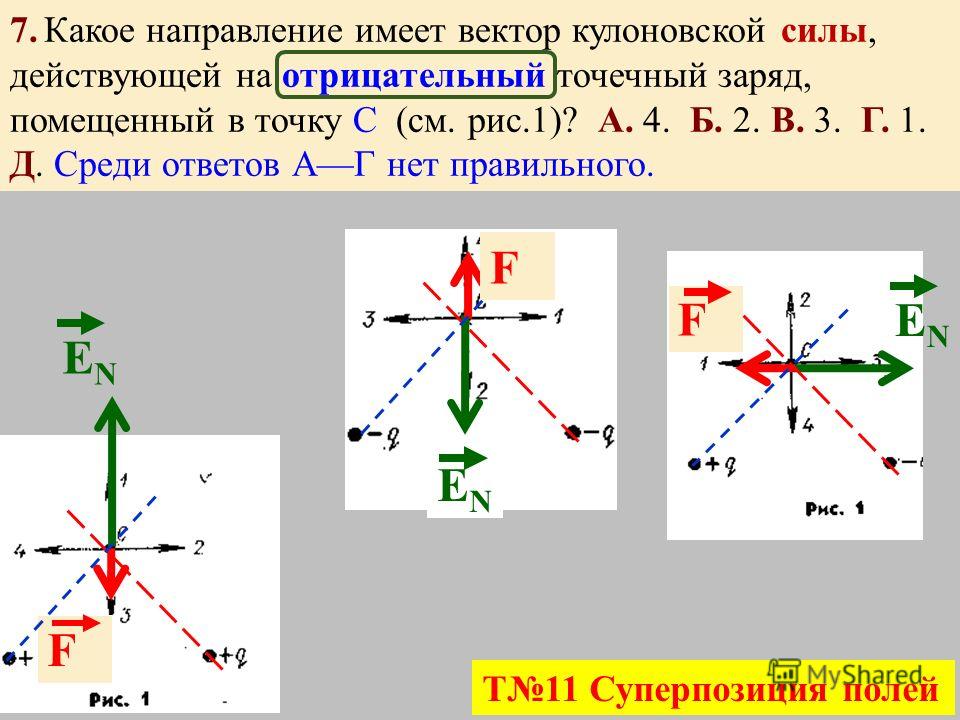
 е.
е.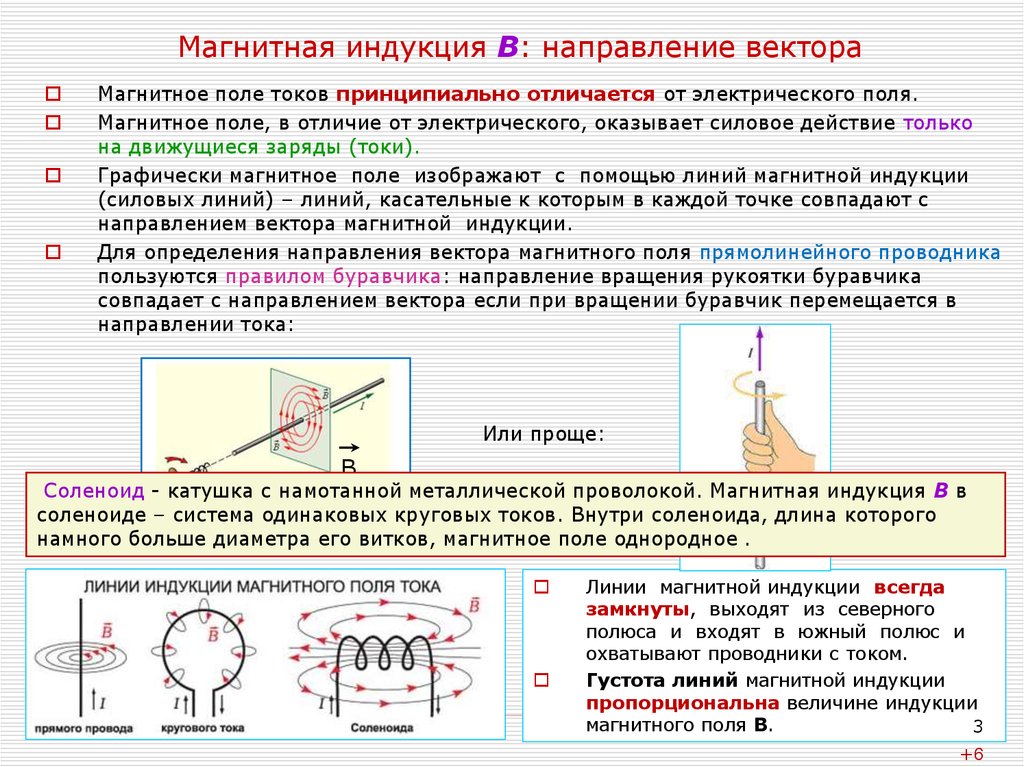 Это даст нам необходимое расстояние между двумя линиями.
Это даст нам необходимое расстояние между двумя линиями. 
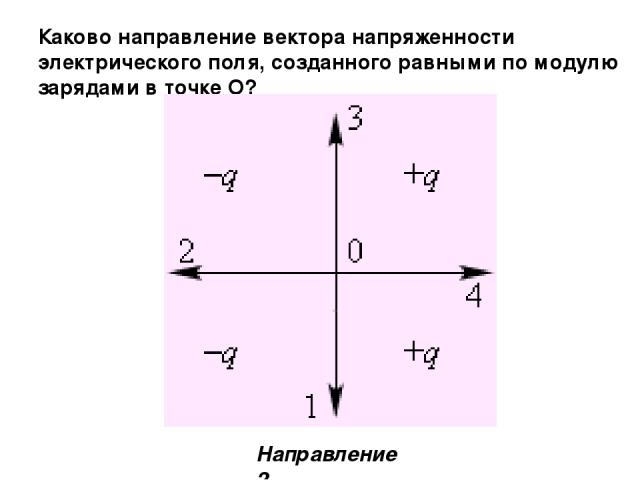
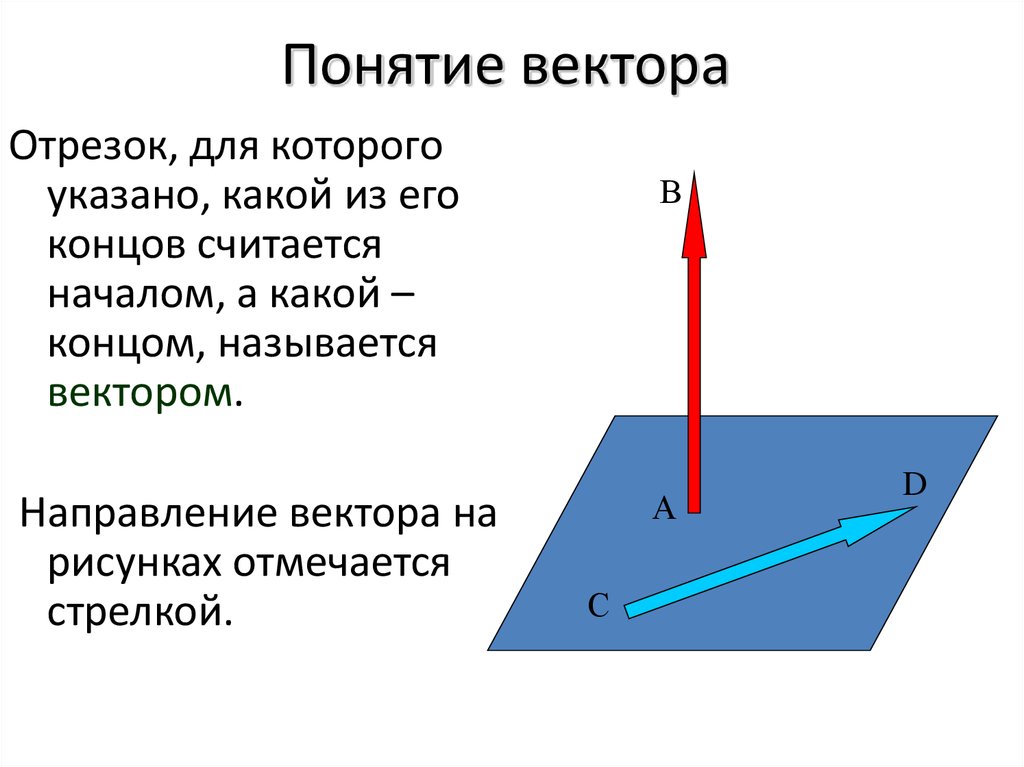
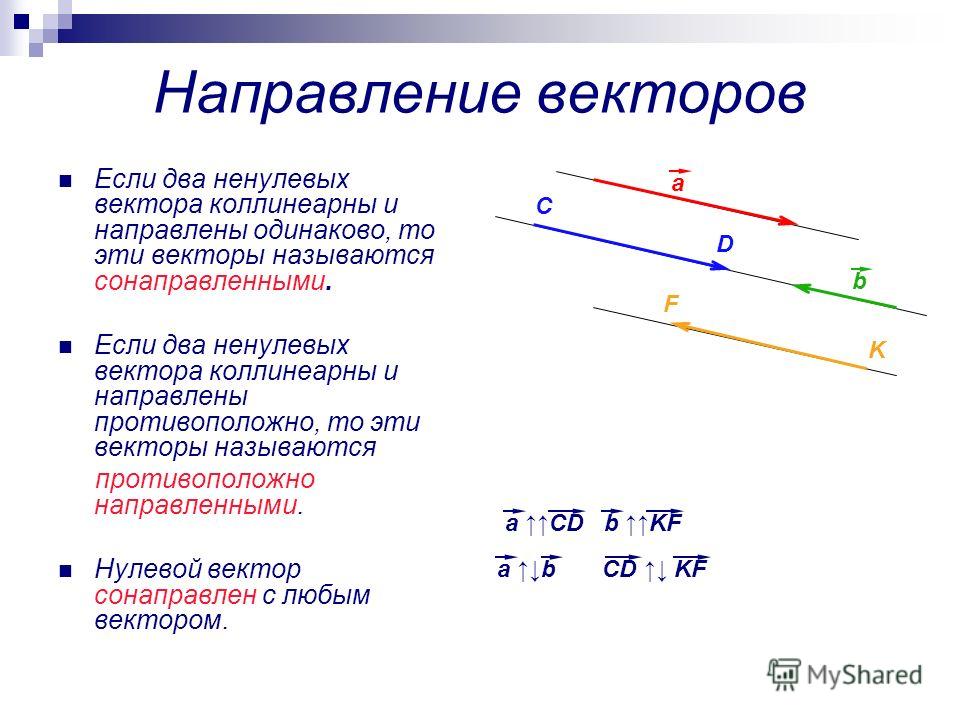 Таким образом, мы можем найти уравнение угла
Таким образом, мы можем найти уравнение угла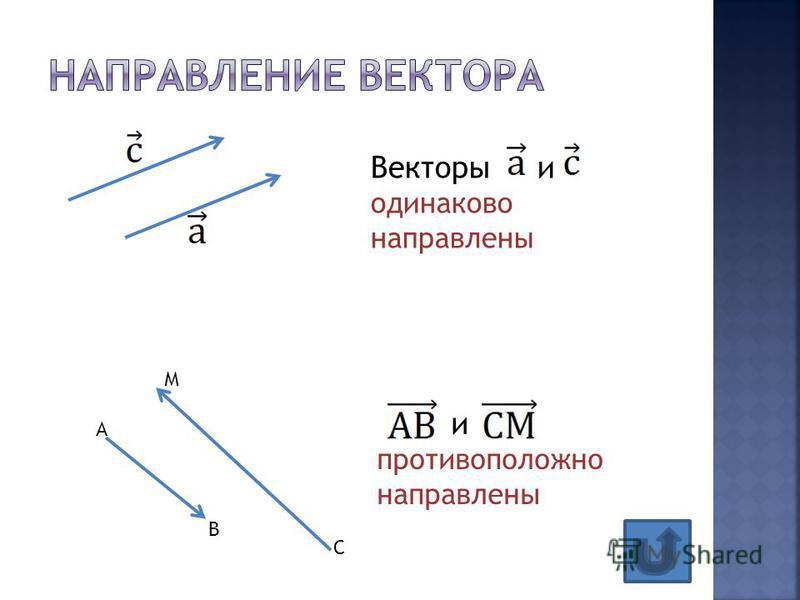 Другие величины, такие как скорость и сила, также включают направление. Вы можете использовать векторы для представления тех величин, которые включают в себя как величину, так и направление. Одно из распространенных применений векторов включает определение фактической скорости и направления самолета с учетом его воздушной скорости и направления, а также скорости и направления попутного ветра. Другое распространенное использование векторов связано с нахождением результирующей силы, действующей на объект, на который действуют несколько отдельных сил.
Другие величины, такие как скорость и сила, также включают направление. Вы можете использовать векторы для представления тех величин, которые включают в себя как величину, так и направление. Одно из распространенных применений векторов включает определение фактической скорости и направления самолета с учетом его воздушной скорости и направления, а также скорости и направления попутного ветра. Другое распространенное использование векторов связано с нахождением результирующей силы, действующей на объект, на который действуют несколько отдельных сил. 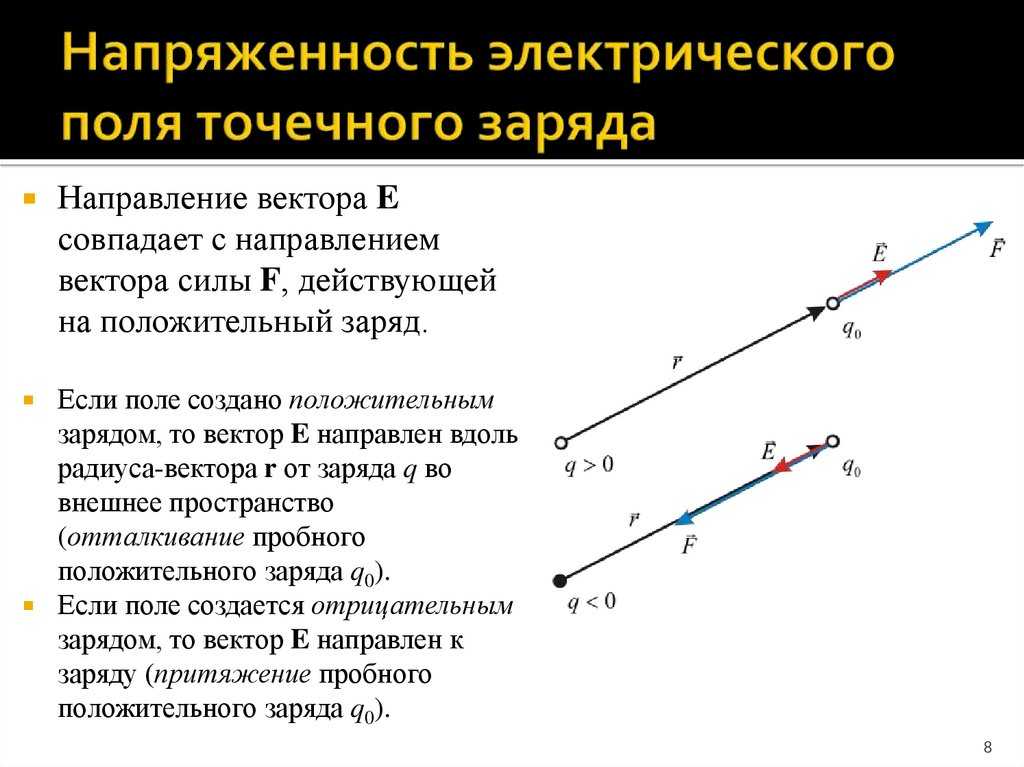 С этого момента вектор будет обозначаться жирной буквой, например 9.0003 и или и . Величина вектора — это длина направленного отрезка. Величину иногда называют нормой . Два вектора имеют одинаковое направление , если они параллельны и указывают в одном и том же направлении. Два вектора имеют противоположных направлений , если они параллельны и направлены в противоположные стороны. Вектор, который не имеет величины и указывает в любом направлении, называется нулевым вектором . Говорят, что два вектора равны эквивалентны векторам , если они имеют одинаковую величину и одинаковое направление.
С этого момента вектор будет обозначаться жирной буквой, например 9.0003 и или и . Величина вектора — это длина направленного отрезка. Величину иногда называют нормой . Два вектора имеют одинаковое направление , если они параллельны и указывают в одном и том же направлении. Два вектора имеют противоположных направлений , если они параллельны и направлены в противоположные стороны. Вектор, который не имеет величины и указывает в любом направлении, называется нулевым вектором . Говорят, что два вектора равны эквивалентны векторам , если они имеют одинаковую величину и одинаковое направление.  Результирующий вектор от начальной точки v до конечной точки u есть вектор v + u и называется результатом . Векторы v и u называются компонентами вектора v + u . Если два добавляемых вектора не параллельны, то также можно использовать правило параллелограмма . В этом случае начальные точки векторов совпадают, а результирующая является диагональю параллелограмма, образованного использованием двух векторов в качестве смежных сторон параллелограмма.
Результирующий вектор от начальной точки v до конечной точки u есть вектор v + u и называется результатом . Векторы v и u называются компонентами вектора v + u . Если два добавляемых вектора не параллельны, то также можно использовать правило параллелограмма . В этом случае начальные точки векторов совпадают, а результирующая является диагональю параллелограмма, образованного использованием двух векторов в качестве смежных сторон параллелограмма. 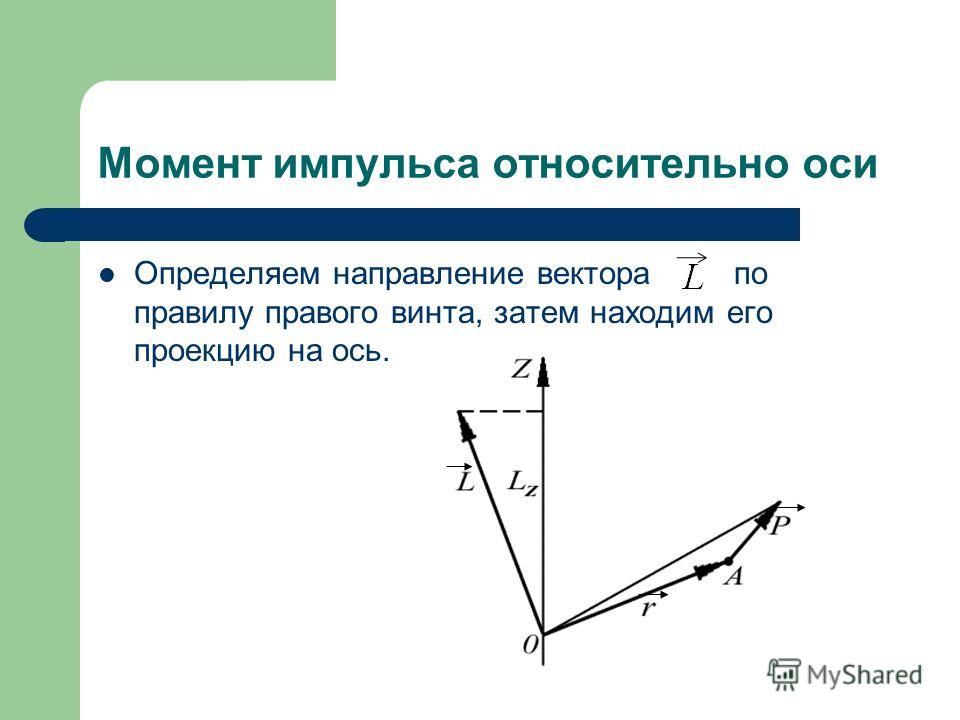 Это называется скалярным умножением . Если вектор u умножить на -1, результирующий вектор обозначается как — u . Он имеет ту же величину, что и u , но имеет противоположное направление. На рис. 2 показано использование скаляров.
Это называется скалярным умножением . Если вектор u умножить на -1, результирующий вектор обозначается как — u . Он имеет ту же величину, что и u , но имеет противоположное направление. На рис. 2 показано использование скаляров.  В примере пеленг самолета составляет 270°, а пеленг ветра — 225°. Перерисовав фигуру в виде треугольника с использованием правила кончика хвоста, можно рассчитать длину (путевую скорость самолета) и пеленг равнодействующей (рис. 4).
В примере пеленг самолета составляет 270°, а пеленг ветра — 225°. Перерисовав фигуру в виде треугольника с использованием правила кончика хвоста, можно рассчитать длину (путевую скорость самолета) и пеленг равнодействующей (рис. 4). 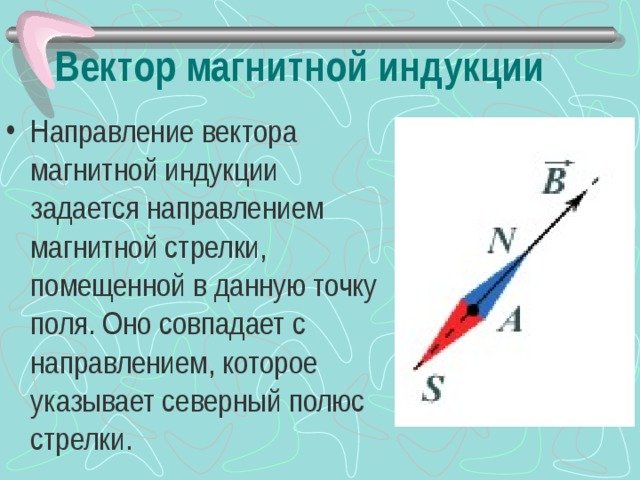
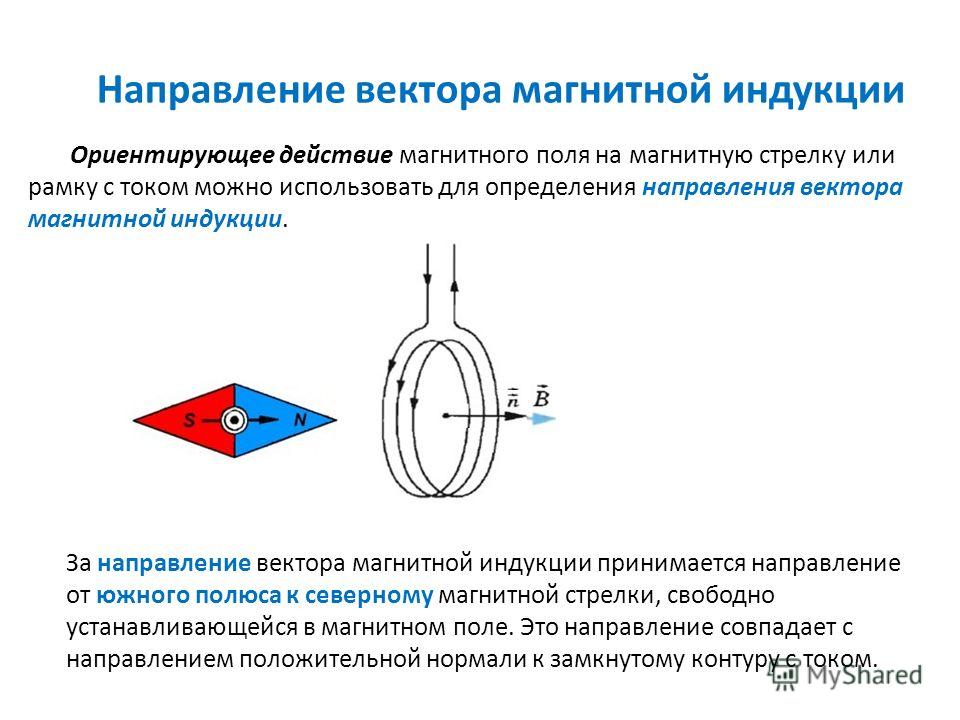

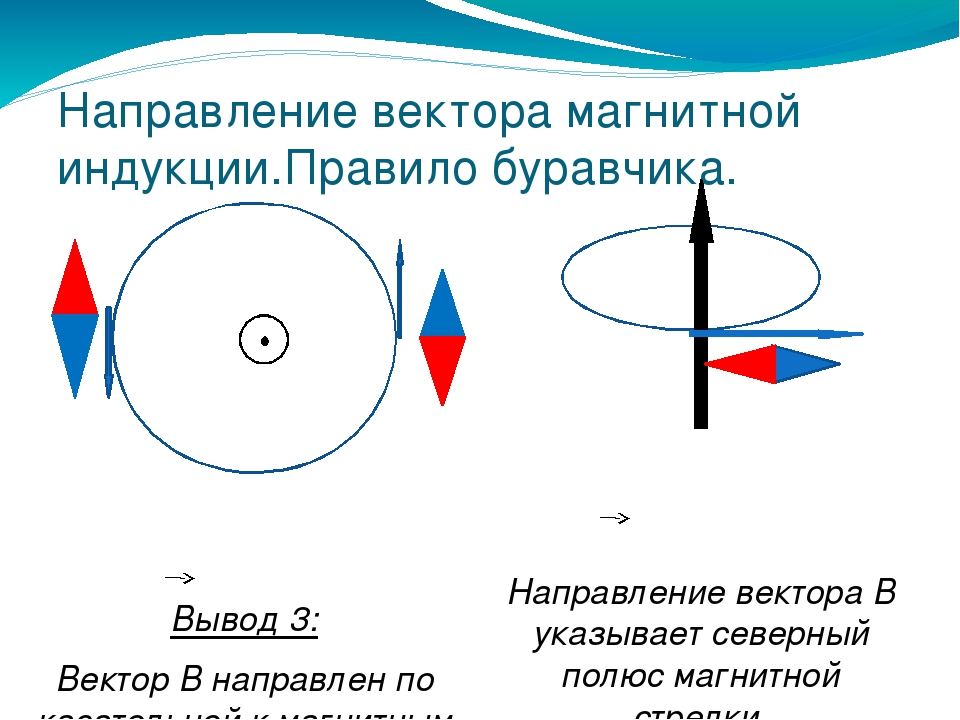 2) направляющие косинусы вектора a = {a x ; а и ; a z } можно найти по следующей формуле
2) направляющие косинусы вектора a = {a x ; а и ; a z } можно найти по следующей формуле 
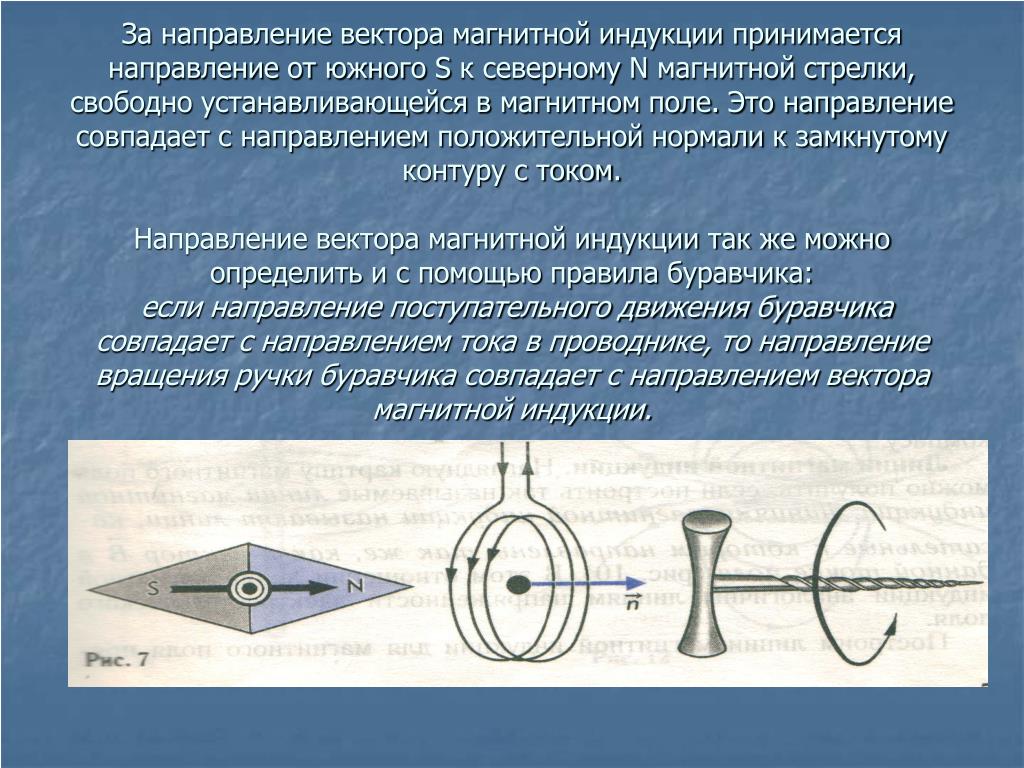 Найти направляющие косинусы вектора a = {2; 4; 4}.
Найти направляющие косинусы вектора a = {2; 4; 4}.