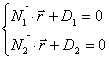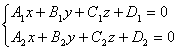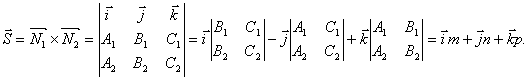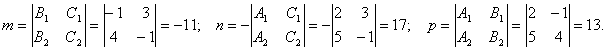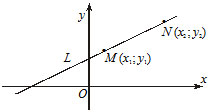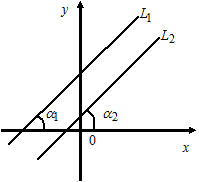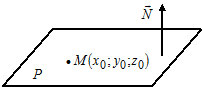Как найти направляющие косинусы прямой - Исправление недочетов и поиск решений вместе с Examum.ru

Уравнение линии в пространстве.

Как на плоскости, так и в пространстве, любая линия может быть определена как
совокупность точек, координаты которых в некоторой выбранной в пространстве
системе координат удовлетворяют уравнению:

F(x, y, z) = 0.

Это уравнение называется уравнением линии в пространстве.

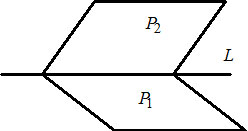
Кроме того, линия в пространстве может быть определена и иначе. Ее можно
рассматривать как линию пересечения двух поверхностей, каждая из которых задана
каким- либо уравнением.

Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 –
уравнения поверхностей, пересекающихся по линии L.

Тогда пару уравнений

назовем
уравнением линии в пространстве.

Уравнение прямой в
пространстве по точке и

направляющему вектору.

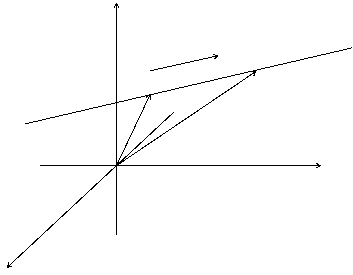
Возьмем произвольную прямую и вектор (m, n, p), параллельный данной прямой. Вектор называется
направляющим вектором прямой.

На прямой возьмем две произвольные точки М₀(x₀, y₀, z₀) и M(x, y, z).

M₁

M₀

0
          y

Обозначим радиус- векторы этих точек как и ,
очевидно, что — = .

Т.к. векторы и коллинеарны,
то верно соотношение = t, где t – некоторый
параметр.

Итого, можно записать: = + t.

Т.к. этому уравнению удовлетворяют координаты любой
точки прямой, то полученное уравнение – параметрическое
уравнение прямой.

Это векторное уравнение может быть представлено в координатной форме:

Преобразовав
эту систему и приравняв значения параметра t, получаем канонические уравнения прямой
в пространстве:

Определение. Направляющими косинусами
прямой называются направляющие косинусы вектора , которые могут
быть вычислены по формулам:

; .

Отсюда получим: m : n : p = cosa : cosb : cosg.

Числа
m, n, p называются угловыми
коэффициентами прямой. Т.к. — ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два
из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.

Уравнение прямой в
пространстве, проходящей

через две точки.

Если на прямой в пространстве отметить две произвольные точки
M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), то координаты
этих точек должны удовлетворять полученному выше уравнению прямой:

Кроме того, для точки М₁ можно записать:

Решая совместно эти уравнения, получим:

Это уравнение прямой, проходящей через две точки в
пространстве.

Общие уравнения прямой в
пространстве.

Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух
плоскостей.

Как было рассмотрено выше, плоскость в векторной форме может быть задана
уравнением:

×+ D = 0, где

— нормаль плоскости; — радиус- вектор произвольной точки плоскости.

Пусть в пространстве заданы две плоскости: ×+ D₁ = 0 и ×+ D₂ = 0, векторы нормали имеют координаты: (A₁, B₁, C₁), (A₂, B₂, C₂); (x, y, z).

Тогда общие уравнения прямой в векторной форме:

Общие уравнения прямой в координатной форме:

Практическая задача часто состоит в приведении уравнений прямых в общем виде к
каноническому виду.

Для этого надо найти произвольную точку прямой и числа m, n, p.

При этом направляющий вектор прямой может быть найден как векторное
произведение векторов нормали к заданным плоскостям.

Пример. Найти каноническое уравнение, если прямая
задана в виде:

Для
нахождения произвольной точки прямой, примем ее координату х
= 0, а затем подставим это значение в заданную систему уравнений.

, т.е.
А(0, 2, 1).

Находим компоненты направляющего вектора прямой.

Тогда канонические уравнения прямой:

Пример.
Привести к каноническому виду уравнение прямой, заданное в виде:

Для
нахождения произвольной точки прямой, являющейся линией пересечения указанных
выше плоскостей, примем z = 0. Тогда:

;

2x – 9x – 7 = 0;

x = -1; y = 3;

Получаем: A(-1; 3; 0).

Направляющий
вектор прямой: .

Итого:

Источник

Решение типовых задач по теме «Задание плоскости в пространстве». Часть 2
Задача №1. Определить направляющие косинусы вектора, направленного из начала координат перпендикулярно к плоскости x-2y+2z-9=0.
Решение. Приводим уравнение плоскости к нормальному виду. Нормирующий множитель:

$M=frac{1}{sqrt{1^{2}+(-2)^{2}+2^{2}}}=frac{1}{sqrt{9}}=frac{1}{3}.$

Умножая данное уравнение на $M=frac{1}{3}$ , получим нормальное уравнение плоскости:

$frac{1}{3}x-frac{2}{3}y+frac{2}{3}z-3=0.$

Здесь $cos alpha =frac{1}{3},; cos beta =-frac{2}{3},; cos gamma =frac{2}{3}$
суть направляющие косинусы нормального вектора

vec{n}left{A;B;C right}=vec{n}left{1;-2;2 right}

данной плоскости.
Ответ: vec{n}left{1;-2;2 right} .
Задача №2. Найти расстояние плоскости left(6vec{i}-7vec{j}-6vec{k} right)vec{r}-33=0 от начала координат и углы, которые образует с осями координат перпендикуляр, опущенный из начала координат на плоскость.
Решения задач №1 и №2 подробно изложены в следующем видео

Задача №3. Уравнение плоскости 11х-7у-9z+15=0 написать в векторной форме в общем и в нормальном видах.
Задача №4. Составить уравнение плоскости, перпендикулярной к вектору vec{n}left{3;4;12 right} и отстоящей от начала координат на расстояние р=3.
Решение. Уравнение плоскости, параллельной искомой и проходящей через начало координат, имеет вид: Зх+4у+12z=0.
Отклонение любой точки М(х;у;z) искомой плоскости Зх+4у+12z=0 равно ±3.
Тогда, воспользовавшись формулой

$delta =frac{Ax_{1}+By_{1}+Cz_{1}+D}{sqrt{A^{2}+B^{2}+C^{2}}},$

будем иметь:

$pm 3 =frac{3x+4y+12z}{sqrt{3^{2}+4^{2}+12^{2}}},; pm 3 =frac{3x+4y+12z}{13}.$

Откуда Зх+4у+12z±39=0 — искомые уравнения плоскости.
Ответ: Зх+4у+12z±39=0.
Решения задач №3 и №4 подробно изложены в следующем видео

Задача №5. Через точки М(3;-2;1) и N(0;3;5) провести плоскость, которая отсекала бы на осях Ох и Оу равные положительные отрезки.
Задача №6. Найти направляющие косинусы прямой, перпендикулярной к плоскости, которая отсекает на осях координат отрезки а=-18, b=-9, с=9.
Решение. Воспользовавшись уравнением плоскости в отрезках $frac{x}{a}+frac{y}{b}+frac{z}{c}=1,$
составим уравнение плоскости: $frac{x}{-18}+frac{y}{-9}+frac{z}{9}=1,$
или

x+2y-2z+18=0. (1)

Приведем общее уравнение плоскости к нормальному виду: нормирующий множитель

$M=frac{1}{pm sqrt{A^{2}+B^{2}+C^{2}}}$

берем со знаком минус, так как в уравнении плоскости D= 18>0:

$M=frac{1}{- sqrt{1+4+4}}=-frac{1}{3}.$

Теперь умножим уравнение (1) на $-frac{1}{3}$ . Получим:

$-frac{1}{3}x-frac{2}{3}y+frac{2}{3}z-6=0.$

Направляющие косинусы перпендикуляра к плоскости имеют следующие значения:

$cos alpha =-frac{1}{3},; cos beta =-frac{2}{3},; cos gamma =frac{2}{3}.$

Ответ: $cos alpha =-frac{1}{3},; cos beta =-frac{2}{3},; cos gamma =frac{2}{3}.$
Решения задач №6 и №7 подробно изложены в следующем видео

Источник

Прямая на плоскости, всевозможные уравнения.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Существуют такие формы записи уравнения прямой:

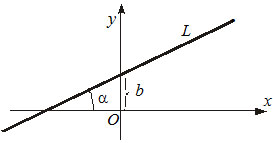
1) $y=kx+b,$ где $k -$ угловой коэффициент, $b-$ отрезок, который прямая отсекает на оси $OY.$

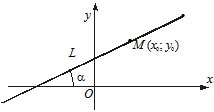
2) $y-y_0=k(x-x_0) $ — уравнение прямой, которая проходит через заданную точку $P(x_0, y_0)$ под заданным углом $alpha$ к оси $OX$ $(k=tgalpha).$

3) $frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1} $ — уравнение прямой, которая проходит через две точки $M(x_1, y_1)$ и $N(x_2, y_2).$

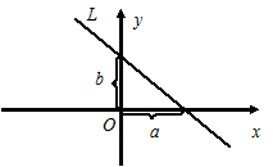
4) $frac{x}{a}+frac{y}{b}=1 $ — уравнение прямой в отрезках на осях, где $a$ и $b -$ величины отрезков, которые прямая отсекает на осях координат.

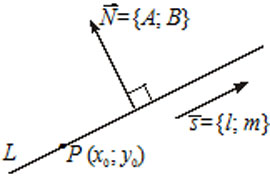
5) $frac{x-x_0}{l}=frac{y-y_0}{m} $ — каноническое уравнение прямой, где $overline{S}=(l, m) -$ направляющий вектор прямой, то есть вектор параллельный прямой $(overline{S}parallel L),$ точка $P(x_0, y_0)in L.$

{jumi[*4]}

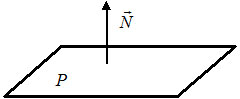
6) $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $overline{N}=(A, B).$ Вектор $overline N$ называется нормальным вектором прямой.

7) $Ax+By+C=0 -$ общее уравнение прямой $L,$ где $overline{N}=(A, B) -$ нормальный вектор прямой $L.$

$xcosalpha+ycosbeta-p=0 -$ нормальное уравнение прямой, где $cosalpha$ и $cosbeta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.

Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $mu=-frac{sgn C}{sqrt{A^2+B^2}}.$

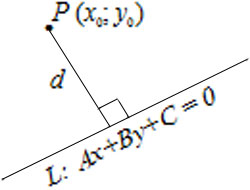
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac{Ax_0+By_0+C}{sqrt{A^2+B^2}}right|.$$

Расположение двух прямых на плоскости.

Условия параллельности двух прямых:

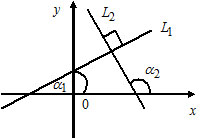
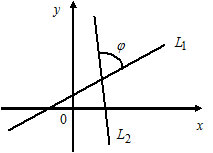
1) Пусть $L_1: k_1x+b_1,$ $k_1=tgalpha_1;$

$L_2: k_2x+b_2,$ $k_2=tgalpha_2.$

Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $k_1=k_2.$

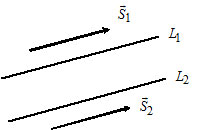
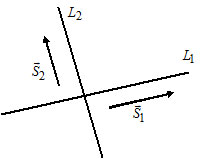
2) Пусть $L_1:$ $frac{x-x_1}{l_1}=frac{y-y_1}{m_1},$ $overline{S}_1=(l_1, m_1);$

$L_2:$ $frac{x-x_2}{l_2}=frac{y-y_2}{m_2},$ $overline{S}_2=(l_2, m_2).$

Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $overline{S}_1paralleloverline{S}_2Leftrightarrow$ $frac{l_1}{l_2}=frac{m_1}{m_2}.$

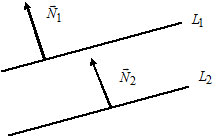
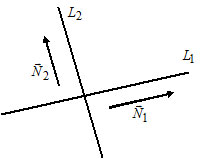
3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $overline{N}_1=(A_1, B_1);$

$L_2: A_2x+B_2y+C_2=0,$ $overline{N}_2=(A_2, B_2).$

Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $overline{N}_1paralleloverline{N}_2Leftrightarrow$ $frac{A_1}{A_2}=frac{B_1}{B_2}.$

Условия перпендикулярности двух прямых:

1) Пусть $L_1: k_1x+b_1,$ $k_1=tgalpha_1;$

$L_2: k_2x+b_2,$ $k_2=tgalpha_2.$

$L_1perp L_2Leftrightarrow$ $k_1cdot k_2=-1.$

perp1

2) Пусть $L_1:$ $frac{x-x_1}{l_1}=frac{y-y_1}{m_1},$ $overline{S}_1=(l_1, m_1);$

$L_2:$ $frac{x-x_2}{l_2}=frac{y-y_2}{m_2},$ $overline{S}_2=(l_2, m_2).$

$L_1perp L_2Leftrightarrow$ $overline{S}_1perpoverline{S}_2Leftrightarrow$ ${l_1}cdot{l_2}+{m_1}cdot{m_2}=0.$

3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $overline{N}_1=(A_1, B_1);$

$L_2: A_2x+B_2y+C_2=0,$ $overline{N}_2=(A_2, B_2).$

$L_1perp L_2Leftrightarrow$ $overline{N}_1perpoverline{N}_2Leftrightarrow$ ${A_1}cdot{A_2}+{B_1}cdot{B_2}=0.$

perp3

Угол между прямыми:

1) Пусть $L_1: k_1x+b_1,$ $k_1=tgalpha_1;$

$L_2: k_2x+b_2,$ $k_2=tgalpha_2.$

$tgwidehat{(L_1, L_2)}=$ $frac{k_1-k_2}{1+k_1cdot k_2}.$

ugol1

2) Пусть $L_1:$ $frac{x-x_1}{l_1}=frac{y-y_1}{m_1},$ $overline{S}_1=(l_1, m_1);$

$L_2:$ $frac{x-x_2}{l_2}=frac{y-y_2}{m_2},$ $overline{S}_2=(l_2, m_2).$

$coswidehat{(L_1, L_2)}=$ $frac{{l_1}cdot{l_2}+{m_1}cdot{m_2}}{sqrt{l_1^2+m_1^2}cdotsqrt{l_2^2+m_2^2}}.$

ugol2

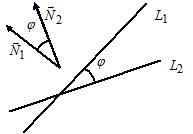
3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $overline{N}_1=(A_1, B_1);$

$L_2: A_2x+B_2y+C_2=0,$ $overline{N}_2=(A_2, B_2).$

$coswidehat{(L_1, L_2)}=$ $frac{{A_1}cdot{A_2}+{B_1}cdot{B_2}}{sqrt{A_1^2+B_1^2}cdotsqrt{A_2^2+B_2^2}}.$

ugol3

Примеры:

2.141.

а) Прямая $L$ задана точкой $M_0(-1; 2)in L$ и нормальным вектором $overline N(2; 2).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.

Решение.

Подставим в формулу 6) для уравнения прямых ($A(x-x_0)+B(y-y_0)=0$) соответственно координаты точки $(x_0; y_0)=M_0(-1; 2)$ и вектора $(A; B)=overline N(2; 2):$

$2(x+1)+2(y-2)=0.$ Далее, приведем это уравнение к общему виду:

$2x+2+2y-4=0Rightarrow$

$2x+2y-2=0Rightarrow$

$x+y-1=0.$

Нормальное уравнение прямой имеет вид $xcosalpha+ycosbeta-p=0,$ где $cosalpha$ и $cosbeta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.

Для нашей прямой имеем $A=1; B=1; C=-1 Rightarrow sgn C=-1.$ Таким образом, $mu=-frac{-1}{sqrt{1+1}}=frac{1}{sqrt 2}.$

Запишем нормальное уравнение прямой:

$x+y-1=0 |cdotfrac{1}{sqrt 2}Rightarrow$

$frac{1}{sqrt 2}x+frac{1}{sqrt 2}y-frac{1}{sqrt 2}=0.$

Расстояние от начала координат $p=frac{1}{sqrt 2}.$

Ответ: $2(x+1)+2(y-2)=0;$ общее уравнение $x+y-1=0;$ нормальное уравнение прямой $frac{1}{sqrt 2}x+frac{1}{sqrt 2}y-frac{1}{sqrt 2}=0;$ $p=frac{1}{sqrt 2}.$

2.142.

а) Прямая $L$ задана точкой $M_0(-1; 2)in L$ и направляющим вектором $overline S(3; -1).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.

Решение.

Подставим в формулу 5) для уравнения прямых ($frac{x-x_0}{l}=frac{y-y_0}{m}$) соответственно координаты точки $(x_0; y_0)=M_0(-1; 2)$ и вектора $(l; m)=overline S(3; -1):$ $frac{x+1}{3}=frac{y-2}{-1}$

Далее, приведем это уравнение к общему виду:

$-1(x+1)=3(y-2)Rightarrow$

$-x-1-3y+6=0Rightarrow$

$x+3y-5=0.$

Для нашей прямой имеем $A=1; B=3; C=-5 Rightarrow sgn C=-1.$ Таким образом, $mu=-frac{-1}{sqrt{1+9}}=frac{1}{sqrt{10}}.$

Запишем нормальное уравнение прямой:

$x+y-1=0 |cdotfrac{1}{sqrt {10}}Rightarrow$

$frac{1}{sqrt {10}}x+frac{3}{sqrt {10}}y-frac{5}{sqrt {10}}=0.$

Расстояние от начала координат $p=frac{5}{sqrt {10}}.$

Ответ: $frac{x+1}{3}=frac{y-2}{-1};$ общее уравнение $x+3y-5=0;$ нормальное уравнение прямой $frac{1}{sqrt {10}}x+frac{3}{sqrt {10}}y-frac{5}{sqrt {10}}=0;$ $p=frac{5}{sqrt {10}}.$

2.143.

а) Прямая $L$ задана двумя своими точками $M_1(1; 2)in L$ и $M_2(-1; 0)in L.$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.

Решение.

Подставим в формулу 3) для уравнения прямых ($frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}$) соответственно координаты точек $M_1(1; 2)=(x_1; y_1)$ и $M_2(-1; 0)=(x_2; y_2):$ $frac{x-1}{-1-1}=frac{y-2}{0-2}Rightarrow frac{x-1}{-2}=frac{y-2}{-2}.$

Далее, приведем это уравнение к общему виду:

$-2(x-1)=-2(y-2)Rightarrow$

$x-1=y-2Rightarrow$

$x-y+1=0.$

Для нашей прямой имеем $A=1; B=-1; C=1 Rightarrow sgn C=1.$ Таким образом, $mu=-frac{1}{sqrt{1+1}}=-frac{1}{sqrt{2}}.$

Запишем нормальное уравнение прямой:

$x-y+1=0 |cdot-frac{1}{sqrt {2}}Rightarrow$

$-frac{1}{sqrt {2}}x+frac{1}{sqrt {2}}y-frac{1}{sqrt {2}}=0.$

Расстояние от начала координат $p=frac{1}{sqrt {2}}.$

Ответ: $frac{x-1}{-2}=frac{y-2}{-2};$ общее уравнение $x-y+1=0;$ нормальное уравнение прямой $-frac{1}{sqrt {2}}x+frac{1}{sqrt {2}}y-frac{1}{sqrt {2}}=0;$ $p=frac{1}{sqrt {2}}.$

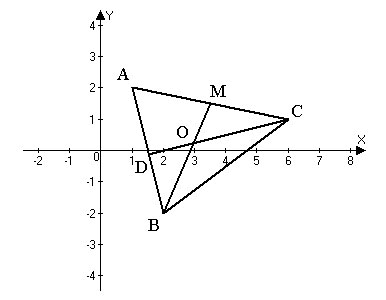
2.150. Треугольник $ABC$ задан координатами своих вершин $A(1; 2), B(2; -2), C(6; 1).$ Требуется:

1) Найти уравнение стороны $AB;$

2) найти уравнение высоты $CD$ и вычислить ее длину $h=|CD|;$

3) найти угол между высотой $CD$ и медианой $BM.$

Решение.

Сделаем рисунок:

1) Уравнение прямой $AB$ найдем по формуле уравнения прямой, проходящей через две точки $frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}. $

В нашем случае $(x_1; y_1)=A(1; 2);$ $(x_2; y_2)=B(2; -2).$

Подставляем координаты точек в уравнение прямой. Получаем $$frac{x-1}{2-1}=frac{y-2}{-2-2}Rightarrow x-1=frac{y-2}{-4}.$$ Запишем общее уравнение прямой $AB$:

$-4(x-1)=y-2Rightarrow$ $-4x+4=y-2Rightarrow$ $4x+y-6=0.$

2) Уравнение прямой $CD$ найдем, пользуясь уравнением (6): $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $overline{N}=(A, B).$

В нашем случае, высота $CD$ это прямая, которая проходит через точку $C$ перпендикулярно вектору $AB.$

Таким образом, $$(x_0; y_0)=C=(6; 1);quadoverline{N}=overline{AB}=(2-1; -2-2)=(1; -4).$$

Подставляем эти координаты в уравнение прямой:

$1(x-6)-4(y-1)=0Rightarrow x-6-4y+4=0 Rightarrow x-4y-2=0.$

То есть, уравнение прямой $CD:$ $x-4y-2=0.$

Чтобы найти длину высоты $h=|CD|,$ найдем координаты точки $D,$ как точки пересечения прямых $CD$ и $AB:$

$left{begin{array}{lcl}x-4y-2=0\4x+y-6=0.end{array}right. $

Решим систему методом исключений:

$left{begin{array}{lcl}x-4y-2=0\4x+y-6=0.end{array}right. Rightarrow$ $left{begin{array}{lcl}x=4y+2\4x+y-6=0.end{array}right. Rightarrow$

$left{begin{array}{lcl}x=4y+2\4(4y+2)+y-6=0.end{array}right. Rightarrow$ $left{begin{array}{lcl}x=4y+2\16y+8+y-6=0.end{array}right. Rightarrow$

$left{begin{array}{lcl}x=-8/17+2=26/17\y=-2/17.end{array}right. .$

Следовательно имеем $D(26/17; -2/17).$ Теперь можем найти длину высоты $CD:$

$h=|CD|=sqrt{(x_d-x_c)^2+(y_d-y_c)^2}=sqrt{(26/17-6)^2+(-2/17-1)^2}=$ $sqrt{left(frac{26-102}{17}right)^2+left(frac{-2-17}{17}right)^2}=sqrt{frac{76^2+19^2}{17^2}}=sqrt{frac{6137}{17^2}}=frac{19}{17}sqrt{17}=frac{19}{sqrt{17}}.$

3) Уравнение высоты $CD$ мы уже нашли в пункте 2). Найдем уравнение медианы $BM.$ Будем его искать, используя форумулу уравнения прямой, проходящей через две точки.

Координаты точки $B=(2, -2); $ координаты точки $M$ найдем как середину стороны $AC:$ $x_M=frac{x_A+x_C}{2}; y_M=frac{y_A+y_C}{2}.$

$x_M=frac{1+6}{2}=3.5;$ $y_M=frac{2+1}{2}=1.5.$

Подставляем координаты точек $B(2; -2)$ и $M(3.5; 1.5)$ в уравнение прямой

$frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}:$

$frac{x-2}{3.5-2}=frac{y-(-2)}{1.5-(-2)}Rightarrow frac{x-2}{1.5}=frac{y+2}{3.5}Rightarrow$

$3.5(x-2)=1.5(y+2)Rightarrow 3.5x-7=1.5y+3 Rightarrow 3.5x-1.5y-10=0.$

Далее, зная общие уравнения двух прямых $CD: x-4y-2=0$ и $BM: 3.5x-1.5y-10=0$ можно найти угол между ними по формуле

$coswidehat{(L_1, L_2)}=$ $frac{{A_1}cdot{A_2}+{B_1}cdot{B_2}}{sqrt{A_1^2+B_1^2}cdotsqrt{A_2^2+B_2^2}},$

где $L_1: A_1x+B_1y+C_1=0,$ $overline{N}_1=(A_1, B_1);$

$L_2: A_2x+B_2y+C_2=0,$ $overline{N}_2=(A_2, B_2).$

Для наших прямых имеем: $(A_1, B_1)=(1; -4);$ $(A_2; B_2)=(3.5; -1.5).$

Отсюда

$coswidehat{(CD, BM)}=$ $frac{{1}cdot{3.5}+{(-4)}cdot{(-1.5)}}{sqrt{1^2+(-4)^2}cdotsqrt{3.5^2+(-1.5)^2}}=frac{9.5}{sqrt{17}cdotsqrt{14.5}}=frac{19}{sqrt{986}}.$

Ответ: 1) $AB: 4x+y-6=0.$

2) $CD:$ $x-4y-2=0; $ $h=|CD|=frac{19}{sqrt{17}};$

3) $coswidehat{(CD, BM)}=$ $frac{19}{sqrt{986}}.$

2.160. В равнобедренном треугольнике $ABC$ заданы вершина $C(4; 3),$ уравнение $2x-y-5=0$ основания $AC$ и уравнение $x-y=0$ боковой стороны $AB.$ Найти уравнение стороны $BC.$

Решение.

Найдем координаты вершины треугольника $A,$ как точки пересечения прямых $AB$ и $AC:$

$$left{begin{array}{lcl}x-y=0\2x-y-5=0end{array}right.Rightarrowleft{begin{array}{lcl}x=y\2y-y-5=0end{array}right.Rightarrowleft{begin{array}{lcl}x=y\y=5end{array}right.Rightarrowleft{begin{array}{lcl}x=5\y=5end{array}right. $$

Таким образом, мы имеем координаты вершин при основании равнобедренного треугольника $A(5; 5)$ и $C(4; 3).$ Найдем координаты вершины $B(x, y).$ Мы знаем, что эта точка принадлежит прямой $AB: x-y=0$ и что $AB=BC.$ Запишем формулы для длин сторон $AB$ и $BC:$

$|AB|=sqrt{(x-5)^2+(y-5)^2};$

$|BC|=sqrt{(x-4)^2+(y-3)^2}.$

Далее, чтобы найти координаты точки $B,$ решим систему уравнений:

$$left{begin{array}{lcl}x-y=0\sqrt{(x-5)^2+(y-5)^2}=sqrt{(x-4)^2+(y-3)^2}end{array}right.Rightarrow$$ $$left{begin{array}{lcl}x-y=0\x^2-10x+25+y^2-10y+25=x^2-8x+16+y^2-6y+9end{array}right.Rightarrow $$

$$left{begin{array}{lcl}x-y=0\-2x-4y+25=0end{array}right.Rightarrowleft{begin{array}{lcl}x=y\-2y-4y+25=0end{array}right.Rightarrow $$

$$Rightarrowleft{begin{array}{lcl}x=y\y=frac{25}{6}.end{array}right.$$ Мы нашли координаты точки $Bleft(frac{25}{6}, frac{25}{6}right).$

Зная координаты точек $B$ и $C$ можно записать уравнение прямой $BC,$ как прямой проходящей через две точки $left(frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1} right):$

$$frac{x-4}{frac{25}{6}-4}=frac{y-3}{frac{25}{6}-3}Rightarrow frac{x-4}{frac{25-24}{6}}=frac{y-3}{frac{25-18}{6}}Rightarrow $$

$$Rightarrowfrac{x-4}{1}=frac{y-3}{7}Rightarrow 7x-28=y-3Rightarrow 7x-y-25=0.$$

Ответ: $7x-y-25=0.$

2.165. Даны две противоположные вершины квадрата $A(1; 3)$ и $C(-1; 1).$ Найти координаты двух его других вершин и написать уравнения его сторон.

Решение:

Найдем уравнение диагонали $AC:$

$frac{x-1}{-1-1}=frac{y-3}{1-3} Rightarrow frac{x-1}{-2}=frac{y-3}{-2}Rightarrow x-y+2=0.$

Найдем ее середину: $$x_O=frac{x_A+x_C}{2}; y_O=frac{y_A+y_C}{2}.$$

$$x_O=frac{1-1}{2}=0;,,, y_O=frac{3+1}{2}=2,, Rightarrow,, O=(0; 2).$$

Далее, найдем уравнение второй диагонали квадрата — прямой, проходящей через точку $O$ перпендикулярно прямой $AC.$ Для прямой $AC$ нормальный вектор имеет координаты $overline{N}=(1; -1).$ Прямая, перпендикулярная прямой $AC$ является параллельной нормальному вектору $overline{N}$. Таким образом, уравнение прямой $BD$ запишем по формуле 5) $left(frac{x-x_0}{l}=frac{y-y_0}{m}right),$ где $(x_0, y_0)=O(0; 2),$ $(l, m)=overline{N}=(1, -1):$

$$frac{x}{1}=frac{y-2}{-1}Rightarrow x=-y+2 Rightarrow x+y-2=0.$$

Ясно, что $AO=CO=BO=DO.$ Найдем длину отрезка $AO:$ $AO=sqrt{(0-1)^2+(2-3)^2}=sqrt{2}.$

Далее, будем искать координаты точек $B$ и $D,$ принадлежащих прямой $BD$ и таких, что $BO=DO=AO.$

$$left{begin{array}{lcl}x+y-2=0\sqrt{(0-x)^2+(2-y)^2}=sqrt{2}end{array}right.Rightarrow$$

$$left{begin{array}{lcl}x=2-y\sqrt{(y-2)^2+(2-y)^2}=sqrt{2}end{array}right.Rightarrow$$

$$left{begin{array}{lcl}x=2-y\|2-y|sqrt{2}=sqrt{2}end{array}right.Rightarrowleft{begin{array}{lcl}x=2-y\|2-y|=1end{array}right.Rightarrowleft{begin{array}{lcl}x=2-y\left[begin{array}{lcl}2-y_1=1\2-y_2=-1end{array}right.end{array}right.Rightarrow$$

$Rightarrowleft{begin{array}{lcl}x=2-y\left[begin{array}{lcl}y_1=1\y_2=3end{array}right.end{array}right.Rightarrow$ $left{begin{array}{lcl}left[begin{array}{lcl}x_1=1\x_2=-1end{array}right.\left[begin{array}{lcl}y_1=1\y_2=3end{array}right.end{array}right.$

Таким образом, мы нашли координаты вершин $B(1; 1)$ и $D(-1; 3).$ Зная координаты вершин квадрата, запишем уравнения его сторон, пользуясь формулой (3) — $frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1} $ — уравнение прямой, которая проходит через две точки $M(x_1, y_1)$ и $N(x_2, y_2).$

$A(1; 3),$ $B(1; 1),$ $C(-1; 1),$ $D(-1; 3).$

$AB:$ $frac{x-1}{1-1}=frac{y-3}{1-3}Rightarrowfrac{x-1}{0}=frac{y-3}{-2}Rightarrow $ $-2(x-1)=0Rightarrow x=1.$

$BC:$ $frac{x-1}{-1-1}=frac{y-1}{1-1}Rightarrowfrac{x-1}{-1}=frac{y-1}{0}Rightarrow $ $0(x-1)=-1(y-1)Rightarrow y=1.$

$CD:$ $frac{x+1}{-1+1}=frac{y-1}{3-1}Rightarrowfrac{x+1}{0}=frac{y-1}{2}Rightarrow $ $2(x+1)=0(y-1)Rightarrow x=-1.$

$DA:$ $frac{x-1}{-1-1}=frac{y-3}{3-3}Rightarrowfrac{x-1}{-2}=frac{y-3}{0}Rightarrow $ $0(x-1)=-2(y-3)Rightarrow y=3.$

Ответ: $A(1; 3),$ $B(1; 1),$ $C(-1; 1),$ $D(-1; 3);$ $AB:$ $x=1;$ $BC:$ $y=1;$ $CD:$ $x=-1;$ $DA:$ $y=3.$

Деление отрезка в заданном отношении (векторный и координатный способы).

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $lambda,$ в котором точка $M$ делит направленный отрезок $overline{M_1M_2},$ найдем координаты точки $M.$

Пусть $O -$ начало координат. Обозначим $overline{OM_1}=r_1,$ $overline{OM_2}=r_2,$ $overline{OM}=r.$ Так как, $$overline{M_1M}=r-r_1, overline{MM_2}=r_2-r,$$ то $r-r_1=lambda(r_2-r),$ откуда (так как $lambdaneq -1$) $$r=frac{r_1+lambda r_2}{1+lambda}.$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=frac{x_1+lambda x_2}{1+lambda}, y=frac{y_1+lambda y_2}{1+lambda}, z=frac{z_1+lambda z_2}{1+lambda}.$$

Примеры.

2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.

Решение.

Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$lambda_1=frac{AC}{CB}=frac{1}{2};$$ $$x_C=frac{x_A+lambda_1x_B}{1+lambda_1}=frac{3+frac{1}{2}cdot 6}{1+frac{1}{2}}=4;$$

$$y_C=frac{y_A+lambda_1y_B}{1+lambda_1}=frac{-2+frac{1}{2}cdot 4}{1+frac{1}{2}}=0.$$

Далее находим координаты точки $D:$

$$lambda_2=frac{AD}{DB}=frac{2}{1}=2;$$ $$x_D=frac{x_A+lambda_2x_B}{1+lambda_2}=frac{3+2cdot 6}{1+2}=5;$$

$$y_D=frac{y_A+lambda_2y_B}{1+lambda_2}=frac{-2+2cdot 4}{1+2}=2.$$

Ответ: $(4, 0)$ и $(5, 2).$

2.58.Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.

Решение.

Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.

Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:

$$lambda_1=frac{AC}{CB}=frac{1}{2};$$ $$x_C=frac{x_A+lambda_1x_B}{1+lambda_1}Rightarrow 2=frac{x_A+frac{1}{2}cdot x_B}{1+frac{1}{2}}=2frac{x_A+frac{1}{2}cdot x_B}{3}Rightarrow $$ $$Rightarrow 3=x_A+frac{1}{2}cdot x_B;$$

$$y_C=frac{y_A+lambda_1y_B}{1+lambda_1}Rightarrow 0=frac{y_A+frac{1}{2}cdot y_B}{1+frac{1}{2}}Rightarrow 0=y_A+frac{1}{2}cdot y_B;$$

$$z_C=frac{z_A+lambda_1z_B}{1+lambda_1}Rightarrow 2=frac{z_A+frac{1}{2}cdot z_B}{1+frac{1}{2}}=2frac{z_A+frac{1}{2}cdot z_B}{3}Rightarrow$$ $$Rightarrow 3=z_A+frac{1}{2}cdot z_B.$$

Аналогичные равенства запишем для точки $D:$

$$lambda_2=frac{AD}{DB}=frac{2}{1}=2;$$ $$x_D=frac{x_A+lambda_2x_B}{1+lambda_2}Rightarrow 5=frac{x_A+2cdot x_B}{1+2}=frac{x_A+2cdot x_B}{3}Rightarrow $$ $$Rightarrow 15=x_A+2cdot x_B;$$

$$y_D=frac{y_A+lambda_2y_B}{1+lambda_2}Rightarrow -2=frac{y_A+2cdot y_B}{1+2}Rightarrow -6=y_A+2cdot y_B;$$

$$z_D=frac{z_A+lambda_2z_B}{1+lambda_2}Rightarrow 0=frac{z_A+2cdot z_B}{1+2}Rightarrow 0=z_A+2cdot z_B.$$

Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$ и $z_A, z_B$ попарно в виде систем и решим их:

$$left{begin{array}{lcl}x_A+frac{1}{2}x_B=3\x_A+2x_B=15end{array}right.Rightarrowleft{begin{array}{lcl}x_A=3-0,5x_B\3-0,5x_B+2x_B=15end{array}right.Rightarrow$$ $$Rightarrowleft{begin{array}{lcl}x_A=3-0,5cdot8=-1\x_B=frac{12}{1,5}=8end{array}right.$$

$$left{begin{array}{lcl}y_A+frac{1}{2}y_B=0\y_A+2y_B=-6end{array}right.Rightarrowleft{begin{array}{lcl}y_B=-2y_A\y_A-4y_A=-6end{array}right.Rightarrow$$ $$Rightarrowleft{begin{array}{lcl}y_B=-4\y_A=2end{array}right.$$

$$left{begin{array}{lcl}z_A+frac{1}{2}z_B=3\z_A+2z_B=0end{array}right.Rightarrowleft{begin{array}{lcl}-2z_B+0,5z_B=3\z_A=-2z_Bend{array}right.Rightarrow$$ $$Rightarrowleft{begin{array}{lcl}z_B=-2\z_A=4end{array}right.$$

Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$

Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$

Взаимное расположение плоскостей, угол между плоскостями.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Условие параллельности двух плоскостей:

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline{N}_1=(A_1, B_1, C_1);$

$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline{N}_2=(A_2, B_2, C_2).$

Плоскости $P_1$ и $P_2$ параллельны тогда и только тогда, когда $overline{N}_1paralleloverline{N}_2Leftrightarrow$ $frac{A_1}{A_2}=frac{B_1}{B_2}=frac{C_1}{C_2}.$

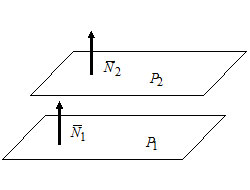
Условия перпендикулярности двух плоскостей:

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline{N}_1=(A_1, B_1, C_1);$

$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline{N}_2=(A_2, B_2, C_2).$

$P_1perp P_2Leftrightarrow$ $overline{N}_1perpoverline{N}_2Leftrightarrow$ ${A_1}cdot{A_2}+{B_1}cdot{B_2}+C_1cdot C_2=0.$

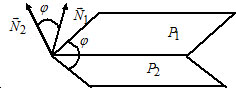
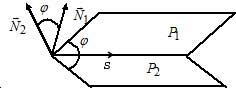
Угол между плоскостями:

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline{N}_1=(A_1, B_1, C_1);$

$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline{N}_2=(A_2, B_2, C_2).$

$coswidehat{(P_1, P_2)}=$ $frac{overline N_1cdot overline N_2}{|overline N_1||overline N_2|}=$ $frac{{A_1}cdot{A_2}+{B_1}cdot{B_2}+C_1cdot C_2}{sqrt{A_1^2+B_1^2+C_1^2}cdotsqrt{A_2^2+B_2^2+C_2^2}}.$

Примеры.

В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1parallel P_2$ то найти расстояние между плоскостями, а в случае — косинус угла между ними.

2.185. $P_1: -x+2y-z+1=0;$ $P_2: y+3z-1=0.$

Решение.

Вычислим угол между заданными плоскостями.

$P_1: -x+2y-z+1=0, Rightarrowoverline{N}_1=(-1, 2, -1);$

$P_2: y+3z-1=0, Rightarrowoverline{N}_2=(0, 1, 3).$

Отсюда

$coswidehat{(P_1, P_2)}=$ $frac{overline N_1cdot overline N_2}{|overline N_1||overline N_2|}=$ $frac{-1cdot 0+2cdot1-1cdot 3}{sqrt{(-1)^2+2^2+(-1)^2}cdotsqrt{0^2+1^2+3^2}}=frac{-1}{sqrt{60}}=frac{-1}{2sqrt{15}}.$

Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями

$coswidehat{(P_1, P_2)}=frac{1}{2sqrt{15}}.$

Ответ: Плоскости пересекаются. $coswidehat{(P_1, P_2)}=frac{1}{2sqrt{15}}.$

2.187. $P_1: x-y+1=0;$ $P_2: y-z+1=0.$

Решение.

Вычислим угол между заданными плоскостями.

$P_1: x-y+1=0, Rightarrowoverline{N}_1=(1, -1, 0);$

$P_2: y-z+1=0, Rightarrowoverline{N}_2=(0, 1, -1).$

Отсюда

$coswidehat{(P_1, P_2)}=$ $frac{overline N_1cdot overline N_2}{|overline N_1||overline N_2|}=$ $frac{1cdot 0+(-1)cdot1+0cdot (-1)}{sqrt{(1)^2+(-1)^2+0^2}cdotsqrt{0^2+1^2+(-1)^2}}=frac{-1}{sqrt{4}}=frac{-1}{2}.$

Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями

$coswidehat{(P_1, P_2)}=frac{1}{2}.$

Ответ: Плоскости пересекаются. $coswidehat{(P_1, P_2)}=frac{1}{2}.$

2.196. Составить уравнение плоскости $P,$ проходящей через точку $A(1, 1, -1)$ и перпендикулярной к плоскостям $P_1: 2x-y+5z+3=0$ и $P_2: x+3y-z-7=0.$

Решение.

Для того, чтобы плоскость $P$ была перпендикулярно плоскостям $P_1$ и $P_2,$ достаточно, чтобы она была параллельна их нормалям $N_1$ и $N_2.$ Или, что тоже самое, перпендикулярна векторному произведению $[N_1, N_2]$

$P_1: 2x-y+5z+3=0, Rightarrowoverline{N}_1=(2, -1, 5);$

$P_2: x+3y-z-7=0, Rightarrowoverline{N}_2=(1, 3, -1).$

$[N_1, N_2]=begin{vmatrix}i&j&k\2&-1&5\1&3&-1end{vmatrix}=i(1-15)-j(-2-5)+k(6+1)=$ $=-14i+7j+7k.$

Теперь выпишем уравнение плоскости, проходящей через заданную точку $A(1, 1, -1)$ и перпендикулярной вектору $[N_1, N_2]=(-14, 7, 7):$

$-14(x-1)+7(y-1)+7(z+1)=0 |:7$

$-2(x-1)+y-1+z+1=0$

$-2x+y+z+2=0.$

Ответ: $-2x+y+z+2=0.$

Домашнее задание.

2.186. $P_1: 2x-y+z-1=0;$ $P_2: -4x+2y-2z-1=0.$

2.188. $P_1: 2x-y-z+1=0;$ $P_2: -4x+2y+2z-2=0.$

Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Существуют такие формы записи уравнения плоскости:

1) $Ax+By+Cz+D=0 -$ общее уравнение плоскости $P,$ где $overline{N}=(A, B, C) -$ нормальный вектор плоскости $P.$

2) $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости $P,$ которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $overline{N}=(A, B, C).$ Вектор $overline N$ называется нормальным вектором плоскости.

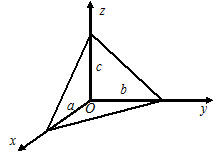
3) $frac{x}{a}+frac{y}{b}+frac{z}{c}=1 -$ уравнение плоскости в отрезках на осях, где $a,$ $b$ и $c -$ величины отрезков, которые плоскость отсекает на осях координат.

4) $begin{vmatrix}x-x_1&y-y_1&z-z_1\x_2-x_1&y_2-y_1&z_2-z_1\x_3-x_1&x_2-x_1&x_3-x_1end{vmatrix}=0 — $ уравнение плоскости, которая проходит через три точки $A(x_1, y_1, z_1), B(x_2, y_2, z_2)$ и $C(x_3, y_3, z_3).$

5) $xcosalpha+ycosbeta+zcosgamma-p=0 -$ нормальное уравнение плоскости, где $cosalpha, cosbeta$ и $cosgamma -$ направляющие косинусы нормального вектора $overline{N},$ направленного из начала координат в сторону плоскости, а $p>0 -$ расстояние от начала координат до плоскости.

Общее уравнение плоскости приводится к нормальному, путем умножения на нормирующий множитель $mu=-frac{sgn D}{sqrt{A^2+B^2+C^2}}.$

Расстояние от точки $M(x_0, y_0, z_0)$ до плоскости $P: Ax+By+Cz+D=0$ вычисляется по формуле $$d=left|frac{Ax_0+By_0+Cz_0+D}{sqrt{A^2+B^2+C^2}}right|.$$

{jumi[*3]}

Примеры:

2.180.

а) Заданы плоскость $P: -2x+y-z+1=0$ и точка $M(1, 1, 1).$ Написать уравнение плоскости $P’,$ проходящей через точку $M$ параллельно плоскости $P$ и вычислить расстояние $rho(P, P’).$

Решение.

Так как п.лоскости $P$ и $P’$ параллельны, то нормальный вектор для плоскости $P$ будет также нормальным вектором для плоскости $P’.$ Из уравнения плоскости получаем $overline{N}=(-2, 1, -1).$

Далее запишем уравнение плоскости по формуле (2): $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости, которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $overline{N}=(A, B, C).$

$-2(x-1)+(y-1)-(z-1)=0Rightarrow -2x+y-z+2=0.$

Ответ: $-2x+y-z+2=0.$

2.181.

а) Написать уравнение плоскости $P’,$ проходящей через заданные точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ перпендикулярно заданной плоскости $P: -x+y-1=0.$

Решение.

Из уравнения плоскости $P,$ находим ее нормальный вектор $overline{N}=(-1, 1, 0).$ Плоскость, перпендикулярная плоскости $P,$ параллельна ее нормальному вектору. Отсюда следует, что можно выбрать точку $M_3(x, y, z)in P’$ такую, что что $overline{M_1M_3}||overline{N}.$

$overline{M_1M_3}=(x-1, y-2, z).$

Условие коллинеарности векторов $overline{M_1M_3}$ и $overline{N}:$ $frac{x_{M_1M_3}}{x_N}=frac{y_{M_1M_3}}{y_N}=frac{z_{M_1M_3}}{z_N}.$

Поскольку $z_N=0,$ то есть вектор $Nin XoY,$ то $z_{M_1M_3}=0.$

$frac{x-1}{-1}=frac{y-2}{1}.$ Пусть $x=2,$ тогда $y=1.$

Мы нашли точку $M_3=(2, 1, 0).$

Так как точка $M_1in P’,$ то и $M_3in P’.$ Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(2, 1, 0).$

$begin{vmatrix}x-1&y-2&z\2-1&1-2&1\2-1&1-2&0-0end{vmatrix}=0 Rightarrow $

$begin{vmatrix}x-1&y-2&z\1&-1&1\1&-1&0end{vmatrix}=0 Rightarrow $

$(x-1)(-1)0+(-1)z+(y-2)-(-1)z-(-1)(x-1)-(y-2)0=0Rightarrow$ $Rightarrow-z+y-2+z+x-1=0Rightarrow x+y-3=0.$

Ответ: $x+y-3=0.$

2.182.

а) Написать уравнение плоскости $P,$ проходящей через точку $M(1, 1, 1)$ параллельно векторам $a_1(0, 1, 2)$ и $a_2(-1, 0, 1).$

Решение.

Поскольку вектор $[a_1, a_2]$ перпендикулярен плоскости векторов $a_1$ и $a_2$ (см. векторное произведение), то он будет также перпендикулярен искомой плоскости. То есть вектор $[a_1, a_2]$ является нормальным для плоскости $P.$ Найдем этот вектор:

$[a_1, a_2]=begin{vmatrix}i&j&k\0&1&2\-1&0&1end{vmatrix}=i(1-0)-j(0+2)+k(0+1)=i-2j+k.$

Таким образом $overline{N}=[a_1, a_2]=(1, -2, 1).$

Теперь можно найти уравнение плоскости $P,$ по формуле (2), как плоскости, проходящей через точку $M(1, 1, 1)$ перпендикулярно вектору $overline N=(1, -2, 1):$

$1(x-1)-2(y-1)+1(z-1)=0Rightarrow$

$x-2y+z=0.$

Ответ: $x-2y+z=0.$

2.183.

а) Написать уравнение плоскости $P,$ проходящей через точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ параллельно вектору $a=(3, 0, 1).$

Решение.

Поскольку вектор $a$ параллелен плоскости $P,$ то для всякого вектора $overline{M_1M_3},$ параллельного вектору $a,$ точка $M_3in P.$

Пусть $M_3=(x, y, z).$ Тогда $overline{M_1M_3}=(x-1, y-2, z).$ Так как $overline{M_1M_3}||a,$ то $frac{x_{M_1M_3}}{x_а}=frac{y_{M_1M_3}}{y_а}=frac{z_{M_1M_3}}{z_а}.$ $y_a=0,$ то есть вектор $ain XoZ$ и всякий параллельный ему вектор так же будет принадлежать этой плоскости. Таким образом, $y_{M_1M_3}=y-2=0Rightarrow y=2.$

Из условия параллельности векторов имеем $frac{x-1}{3}=frac{z}{1}.$ Пусть $x=4,$ тогда $z=1.$

Мы получили точку $M_3=(4, 2, 1).$

Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(4, 2, 1).$

$begin{vmatrix}x-1&y-2&z\2-1&1-2&1\4-1&2-2&1end{vmatrix}=0 Rightarrow $

$begin{vmatrix}x-1&y-2&z\1&-1&1\3&0&1end{vmatrix}=0 Rightarrow $

$(x-1)(-1)1+1cdot zcdot 0+(y-2)3-3(-1)z-0cdot 1cdot(x-1)-1(y-2)1=0Rightarrow$

$Rightarrow -x+1+3y-6+3z-y+2=0Rightarrow -x+2y+3z-3=0.$

Ответ: $-x+2y+3z-3=0.$

2.184.

а) Написать уравнение плоскости, проходящей через три заданные точки $M_1(1, 2,0),$ $M_2(2, 1, 1)$ и $M_3(3, 0, 1).$

Решение.

Воспользуемся формулой (4):

$begin{vmatrix}x-1&y-2&z\2-1&1-2&1\3-1&0-2&1end{vmatrix}=0 Rightarrow $

$begin{vmatrix}x-1&y-2&z\1&-1&1\2&-2&1end{vmatrix}=0 Rightarrow $

$(x-1)(-1)1+z(-2)+2(y-2)1-2(-1)z-(-2)(x-1)-1(y-2)1=0Rightarrow$

$Rightarrow -x+1+-2z+2y-4+2z+2x-2-y+2=0Rightarrow x+y-3=0.$

Ответ: $x+y-3=0.$

{jumi[*4]}

Прямая в пространстве, всевозможные уравнения.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Существуют такие формы записи уравнения прямой в пространстве:

1) $left{begin{array}{lcl}A_1x+B_1y+C_1z+D_1=0quad (P_1)\ A_2x+B_2y+C_2z+D_2=0quad (P_2)end{array}right. — $ общее уравнение прямой $L$ в пространстве, как линии пересечения двух плоскостей $P_1$ и $P_2.$

2) $frac{x-x_0}{m}=frac{y-y_0}{n}=frac{z-z_0}{p} -$ каноническое уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0, z_0)$ параллельно вектору $overline{S}=(m, n, p).$ Вектор $overline S$ является направляющим вектором прямой $L.$

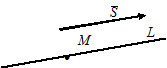
3) $frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}=frac{z-z_1}{z_2-z_1} -$ уравнение прямой, которая проходит через две точки $A(x_1, y_1, z_1)$ и $B(x_2, y_2, z_2).$

4) Приравнивая каждую из частей канонического уравнения 2 к прараметру $t,$ получаем параметрическое уравнение прямой:

$$left{begin{array}{lcl}x=x_0+mt\ y=y_0+nt\z=z_0+ptend{array}right. $$

Расположение двух прямых в пространстве.

Пусть $L_1:$ $frac{x-x_1}{m_1}=frac{y-y_1}{n_1}=frac{z-z_1}{p_1}$ $overline{S}_1=(m_1, n_1, p_1);$

$L_2:$ $frac{x-x_2}{m_2}=frac{y-y_2}{n_2}=frac{z-z_2}{p_2},$ $overline{S}_2=(m_2, n_2, p_2).$

Условие параллельности двух прямых: Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $overline{S}_1paralleloverline{S}_2Leftrightarrow$ $frac{m_1}{m_2}=frac{n_1}{n_2}=frac{p_1}{p_2}.$

Условие перпендикулярности двух прямых: $L_1perp L_2Leftrightarrow$ $overline{S}_1perpoverline{S}_2Leftrightarrow$ ${m_1}cdot{m_2}+{n_1}cdot{n_2}+p_1cdot p_2=0.$

Угол между прямыми:

$coswidehat{(L_1, L_2)}=$ $frac{overline{S}_1cdotoverline{S}_2}{|overline S_1|cdot|overline S_2|}=frac{{m_1}cdot{m_2}+{n_1}cdot{n_2}+p_1cdot p_2}{sqrt{m_1^2+n_1^2+p_1^2}cdotsqrt{m_2^2+n_2^2+p_2^2}}.$

ugol2

Расстояние от точки до прямой равно длине перпендикуляра, опущенного из точки на данную прямую.

Пусть прямая $L$ задана уравнением $frac{x-x_0}{m}=frac{y-y_0}{n}=frac{z-z_0}{p},$ следовательно $overline S=(m, n, p).$ Пусть также $M_2=(x_2, y_2, z_2) -$ произвольная точка, принадлежащая прямой $L.$ Тогда расстояние от точки $M_1=(x_1, y_1, z_1)$ до прямой $L$ можно найти по формуле: $$d(M_1, L)=frac{|[overline{M_1M_2}, overline S]|}{|overline S|}.$$

dist

Примеры.

2.198. Написать каноническое уравнение прямой, проходящей через точку $M_0(2, 0, -3)$ параллельно:

а) вектору $q(2, -3, 5);$

б) прямой $frac{x-1}{5}=frac{y+2}{2}=frac{z+1}{-1};$

в) оси $OX;$

д) прямой $left{begin{array}{lcl}3x-y+2z-7=0,\ x+3y-2z-3=0; end{array}right. $

е) прямой $x=-2+t, y=2t, z=1-frac{1}{2}t.$

Решение.

а) Воспользуемся формулой (2) уравнения прямой в пространстве:

$frac{x-x_0}{m}=frac{y-y_0}{n}=frac{z-z_0}{p} -$ каноническое уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0, z_0)$ параллельно вектору $overline{S}=(m, n, p).$

По условию $M_0(2, 0, -3)$ и $overline{S}=q(2,-3,5).$

Таким образом, $frac{x-2}{2}=frac{y-0}{-3}=frac{z-(-3)}{5}Rightarrowfrac{x-2}{2}=frac{y}{-3}=frac{z+3}{5}.$

Ответ: $frac{x-2}{2}=frac{y}{-3}=frac{z+3}{5}.$

б) Прямая, параллельная заданной прямой, должна быть параллельна ее направляющему вектору. Направляющий вектор прямой $frac{x-1}{5}=frac{y+2}{2}=frac{z+1}{-1}$ имеет координаты $overline S(5, 2, -1).$ Далее, находим уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(5, 2, -1)$ как и в пункте а):

$frac{x-2}{5}=frac{y-0}{2}=frac{z-(-3)}{-1}Rightarrowfrac{x-2}{5}=frac{y}{2}=frac{z+3}{-1}.$

Ответ: $frac{x-2}{5}=frac{y}{2}=frac{z+3}{-1}.$

в) ось OX имеет направляющий вектор $i=(1, 0, 0).$ Таким образом, ищем уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $i(1, 0, 0):$

$frac{x-2}{1}=frac{y-0}{0}=frac{z-(-3)}{0}Rightarrowfrac{x-2}{1}=frac{y}{0}=frac{z+3}{0}.$

Ответ: $frac{x-2}{1}=frac{y}{0}=frac{z+3}{0}.$

д) Прямая, заданная как пересечение двух плоскостей перпендикулярна нормалям обеих плоскостей, поэтому Направляющий вектор прямой

$left{begin{array}{lcl}3x-y+2z-7=0,\ x+3y-2z-3=0; end{array}right.$ можно найти как векторное произведение нормалей заданных плоскостей.

Для плоскости $P_1:$ $3x-y+2z-7=0$ нормальный вектор имеет координаты $N_1(3, -1, 2);$

для плосости $P_2:$ $x+3y-2z-3,$ нормальный вектор имеет координаты $N_2(1, 3, -2).$

Находим векторное произведение:

$[N_1, N_2]=begin{vmatrix}i&j&k\3&-1&2\1&3&-2end{vmatrix}=i(2-6)-j(-6-2)+k(9+1)=-4i+8j+10k.$

Таким образом, направляющий вектор прямой $left{begin{array}{lcl}3x-y+2z-7=0,\ x+3y-2z-3=0; end{array}right.$ имеет координаты $overline S (-4, 8, 10).$

Далее нам необходимо найти уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(-4, 8, 10):$

$frac{x-2}{-4}=frac{y-0}{8}=frac{z-(-3)}{10}Rightarrowfrac{x-2}{-4}=frac{y}{8}=frac{z+3}{10}.$

Ответ: $frac{x-2}{-4}=frac{y}{8}=frac{z+3}{10}.$

{jumi[*4]}

е) Найдем направляющий вектор прямой $x=-2+t, y=2t, z=1-frac{1}{2}t.$ Для этого запишем уравнение этой прямой в каноническом виде:

$left{begin{array}{lcl}x=-2+t,\ y=2t,\z=1-frac{1}{2}t end{array}right.Rightarrow$ $left{begin{array}{lcl}t=x+2,\ t=frac{y}{2},\t=frac{z-1}{-frac{1}{2}} end{array}right.$ $Rightarrowfrac{x+2}{1}=frac{y}{2}=frac{z-1}{-frac{1}{2}}.$

Отсюда находим направляющий вектор $overline Sleft(1, 2, -frac{1}{2}right).$ Умножим координаты направляющего вектора на 2 (чтобы избавиться от дроби): $overline S_1(2, 4, -1).$

Далее нам необходимо найти уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(2, 4, -1):$

$frac{x-2}{2}=frac{y-0}{4}=frac{z-(-3)}{-1}Rightarrowfrac{x-2}{2}=frac{y}{4}=frac{z+3}{-1}.$

Ответ: $frac{x-2}{2}=frac{y}{4}=frac{z+3}{-1}.$

2.199(a). Написать уравнение прямой, проходящей через две заданные точки $M_1 (1, -2, 1)$ и $M_2(3, 1, -1).$

Решение.

Воспользуемся формулой (3) уравнения прямой в пространстве:

$frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}=frac{z-z_1}{z_2-z_1} -$ уравнение прямой, которая проходит через две точки $A(x_1, y_1, z_1)$ и $B(x_2, y_2, z_2).$

Подставляем заданные точки:

$frac{x-1}{3-1}=frac{y+2}{1+2}=frac{z-1}{-1-1} Rightarrow$ $frac{x-1}{2}=frac{y+2}{3}=frac{z-1}{-2}.$

Ответ: $frac{x-1}{2}=frac{y+2}{3}=frac{z-1}{-2}.$

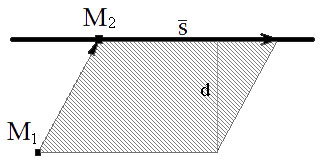
2.204. Найти расстояние между параллельными прямыми

$frac{x-2}{3}=frac{y+1}{4}=frac{z}{2}$ и $frac{x-7}{3}=frac{y-1}{4}=frac{z-3}{2}.$

Решение.

Расстояние между параллельными прямыми $L_1$ и $L_2$ равно расстоянию от произвольной точки прямой $L_1$ до прямой $L_2.$ Следовательно, его можно найти по формуле $$d(L_1, L_2)=d(M_1, L_2)=frac{|[overline{M_1M_2}, overline S]|}{|overline S|},$$ где $M_1-$ произвольная точка прямой $L_1,$ $M_2 — $произвольная точка прямой $L_2,$ $overline S -$ направляющий вектор прямой $L_2.$

Из канонических уравнений прямых берем точки $M_1=(2, -1, 0)in L_1,$ $M_2=(7, 1, 3)in L_2,$ $overline S=(3, 4, 2).$

Отсюда находим $overline{M_1M_2}=(7-2, 1-(-1),3-0)=(5, 2, 3);$

$[overline{M_1M_2}, overline S]=begin{vmatrix}i&j&k\5&2&3\3&4&2end{vmatrix}=i(4-12)-j(10-9)+k(20-6)=$ $=-8i-j+14k.$

$|[overline{M_1M_2},overline S]|=sqrt{8^2+1+14^2}=sqrt{64+1+196}=sqrt{261}=sqrt{9* 29}=3sqrt{29}.$

$|overline S|=sqrt{3^2+4^2+2^2}=sqrt{9+16+4}=sqrt{29}$

$$d(L_1, L_2)=frac{|[overline{M_1M_2}, overline S]|}{|overline S|}=frac{3sqrt{29}}{sqrt{29}}=3.$$

Ответ: 3.

2.205 (а). Найти расстояние от точки $A(2, 3, -1)$ до заданной прямой $L:$ $left{begin{array}{lcl}2x-2y+z+3=0,\ 3x-2y+2z+17=0 end{array}right.$

Решение.

Для того, чтобы найти расстояние от точки $A$ до прямой $L,$ нам необходимо выбрать произвольную точку $M,$ принадлежащую прямой $L$ и найти направляющий вектор этой прямой.

Выбираем точку $M.$ Пусть координата $z=0.$ Подставим это значение в данную систему:

$left{begin{array}{lcl}2x-2y+0+3=0,\ 3x-2y+0+17=0 end{array}right.Rightarrow$ $left{begin{array}{lcl}2x-2y+3=0,\ 3x-2y+17=0 end{array}right.-Rightarrow$ $left{begin{array}{lcl}x+14=0,\ 2x-2y+3=0 end{array}right.Rightarrow$ $left{begin{array}{lcl}x=-14,\ -28-2y+3=0 end{array}right.Rightarrow$ $left{begin{array}{lcl}x=-14,\ y=-frac{25}{2}. end{array}right.$

Таким образом, $M=(-14, -frac{25}{2}, 0)$

Направляющий вектор найдем, как векторное произведение нормалей заданных плоскостей:

Для плоскости $P_1:$ $2x-2y+z+3=0$ нормальный вектор имеет координаты $N_1(2, -2, 1);$

для плосости $P_2:$ $3x+2y+2z+17=0,$ нормальный вектор имеет координаты $N_2(3, -2, 2).$

Находим векторное произведение:

$[N_1, N_2]=begin{vmatrix}i&j&k\2&-2&1\3&-2&2end{vmatrix}=i(-4+2)-j(4-3)+k(-4+6)=-2i-j+2k.$

Таким образом, направляющий вектор прямой $left{begin{array}{lcl}2x-2y+z+3=0,\ 3x-2y+2z+17=0 end{array}right.$

имеет координаты $overline S (-2, -1, 2).$

Теперь можно воспользоваться формулой $$d(A, L)=frac{|[overline{AM}, overline S]|}{|overline S|}.$$

$overline{AM}=left(2-(-14),3-left(-frac{25}{2}right),-1-0right)=left(16, 15frac{1}{2}, -1right)$

$[overline{AM}, overline S]=begin{vmatrix}i&j&k\16&15,5&-1\-2&-1&2end{vmatrix}=i(31-1)-j(32-2)+k(-16+31)=$ $=30i-30j+15k.$

$|[overline{AM},overline S]|=sqrt{30^2+30^2+15^2}=sqrt{900+900+225}=sqrt{2025}=45.$

$|overline S|=sqrt{2^2+1^2+2^2}=sqrt{4+1+4}=3$

$$d(A, L)=frac{|[overline{AM}, overline S]|}{|overline S|}=frac{45}{3}=15.$$

Ответ: $d(A, L)=15.$

2.212. Написать каноническое уравнение прямой, которая проходит через точку $M_0(3, -2, -4)$ параллельно плоскости $P: 3x-2y-3z-7=0$ и пересекает прямую $L: frac{x-2}{3}=frac{y+4}{-2}=frac{z-1}{2}.$

Решение.

Запишем уравнение плоскости $P_1,$ которая проходит через точку $M_0(3, -2, -4)$ параллельно плоскости $3x-2y-3z-7=0:$

$P: 3x-2y-3z-7=0Rightarrow overline N=(3; -2; -3).$ Искомая плоскость проходит через точку $M_0(3, -2, -4)$ перпендикулярно вектору $overline N(3, -2, -3).$

$P_1: 3(x-3)-2(y+2)-3(z+4)=0Rightarrow $

$P_1: 3x-9-2y-4-3z-12=0 Rightarrow$

$P_1: 3x-2y-3z-25=0.$

Далее найдем точку пересечения плоскости $P_1$ и прямой $L.$ Для этого запишем уравнение прямой $L$ в параметрической форме:

$L: frac{x-2}{3}=frac{y+4}{-2}=frac{z-1}{2}=tRightarrow$

$left{begin{array}{lcl}x=3t+2,\ y=-2t-4,\z=2t+1. end{array}right.$

Далее, подставим значения $x, y$ и $z,$ выраженные через $t$ в уравнение плоскости $P_1,$ и из полученного уравнения выразм $t:$

$3x-2y-3z-25=0$

$3(3t+2)-2(-2t-4)-3(2t+1)-25=0$

$9t+6+4t+8-6t-3-25=0$

$7t-14=0$

$t=frac{14}{7}=2$

Подставляя найденное занчение $t$ в уравнение прямой $L,$ найдем координаты точки пересечения:

$left{begin{array}{lcl}x=3t+2,\ y=-2t-4,\z=2t+1. end{array}right.Rightarrow $ $left{begin{array}{lcl}x=6+2=8,\ y=-4-4=-8,\z=4+1=5. end{array}right.$

Таким образом, прямая $L$ и плоскость $P_1$ пересекаются в точке $M_1(8, -8, 5).$

Теперь запишем уравнение прямой, проходящей через точки $M_0(3, -2. -4)$ и $M_1(8, -8, 5)$— это и будет искомая прямая. Воспользуемся формулой (3) $frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}=frac{z-z_1}{z_2-z_1} :$

$frac{x-3}{8-3}=frac{y+2}{-8+2}=frac{z+4}{5+4}Rightarrow$ $frac{x-3}{5}=frac{y+2}{-6}=frac{z+4}{9}.$

Ответ: $frac{x-3}{5}=frac{y+2}{-6}=frac{z+4}{9}.$

Домашнее задание.

2.199.

б) Написать уравнение прямой, проходящей через две заданные точки $M_1 (3, -1, 0)$ и $M_2(1, 0, -3).$

Ответ: $frac{x-3}{-2}=frac{y+1}{1}=frac{z}{-3}.$

2.205.

б) Найти расстояние от точки $A(2, 3, -1)$ до заданной прямой $L:$ $left{begin{array}{lcl}x=3t+5,\ y=2t,\z=-2t-25. end{array}right.$

Ответ: 21.

2.206. Доказать, что прямые $L_1: left{begin{array}{lcl}2x+2y-z-10=0,\ x-y-z-22=0, end{array}right.$ и $L_2: frac{x+7}{3}=frac{y-5}{-1}=frac{z-9}{4}.$ параллельны и найти расстояние $rho(L_1, L_2)$

Ответ: 25.

2.207. Составить уравнения прямой, проходящей через точки пересечения плоскости $x-3y+2z+1=0$ с прямыми $frac{x-5}{5}=frac{y+1}{-2}=frac{z-3}{-1}$ и $frac{x-3}{4}=frac{y+4}{-6}=frac{z-5}{2}.$

Ответ: $frac{x+1}{7}=frac{y-2}{-1}=frac{z-3}{-5}.$

2.211. Написать уравнение прямой, проходящей через точку $M_0(7, 1, 0)$ параллельно плоскости $2x+3y-z-15=0$ и пересекающей прямую $frac{x}{1}=frac{y-1}{4}=frac{z-3}{2}.$

Ответ: $frac{x-7}{67}=frac{y-1}{-28}=frac{z}{70}.$

{jcomments on}

Источник

Напомним, что любой геометрический вектор характеризуется его модулем и направлением. Направление вектора = на плоскости определяется углами и (см. рис. 23), образованными им с осями координат и . Косинусы этих углов (так называемые Направляющие косинусы вектора) определяются по формулам:

= = , = = . (12)

Направляющие косинусы вектора на плоскости связаны соотношением

Пример 28. Пусть = . Найти направляющие косинусы данного вектора, а также углы и .

Решение. Имеем:

= , = , = = = 3;

= = , = = . Отсюда = , = .

Утверждение 10. Координаты единичного вектора совпадают с его направляющими косинусами. Направляющие косинусы любого вектора совпадают с координатами его Орт-вектора (единичного вектора, имеющего то же направление, что и исходный вектор).

При решении задач по аналитической геометрии часто используют Нормальное уравнение прямой на плоскости (рис. 24)

. (13)

Здесь — угол между вектором и осью где — проекция точки (начала координат) на эту прямую, — длина вектора .

Таким образом, — вектор, выходящий из начала координат и перпендикулярный к прямой, а — расстояние от начала координат до прямой. Заметим еще, что и суть направляющие косинусы нормального вектора этой прямой.

Из общего уравнения прямой легко получить нормальное, если его разделить на коэффициент (Нормирующий множитель). Следует правильно выбирать знак коэффициента ; он должен быть противоположен знаку свободного члена .

С помощью нормального уравнения прямой легко вычисляется Отклонение точки от прямой:

. (14)

При решении задач полезно иметь в виду, что по разные стороны от прямой отклонение имеет разный знак.

С помощью отклонения легко найти расстояние от произвольной точки до прямой :

. (15)

Напомним еще, что = = = — единичная нормаль прямой. Пусть и — координаты текущей точки прямой , т. е. = — Радиус-вектор этой точки. Нормальное уравнение прямой может быть записано в векторном виде (Векторное уравнение прямой):

: . (16)

Здесь = = = , — угол между векторами и ; — проекция вектора на направление нормали ;

, если , , если ;

— длина проекции , равная расстоянию от начала координат до прямой .

Пример 29. Уравнение прямой, заданной общим уравнением , привести к нормальному виду и найти расстояние от начала координат до этой прямой.

Решение. Найдем коэффициент . Поскольку , то

Разделив общее уравнение прямой на нормирующий множитель , получим нормальное уравнение прямой:

Или

Здесь , — направляющие косинусы нормального вектора прямой; — расстояние от начала координат до прямой .

Пример 30. Стороны треугольника заданы уравнениями: Составить уравнение биссектрисы внутреннего угла треугольника, лежащего против стороны (рис. 25).

Решение. Из систем уравнений

Находим координаты двух вершин , .

Подставляя координаты каждой из вершин и в левую часть уравнения соответствующей противоположной стороны, получим:

Пусть — произвольная точка искомой биссектрисы, расположенная внутри треугольника. Эта точка лежит по ту же сторону от прямой , что и точка , и поэтому . Она лежит по ту же сторону от прямой , что и точка , и поэтому .