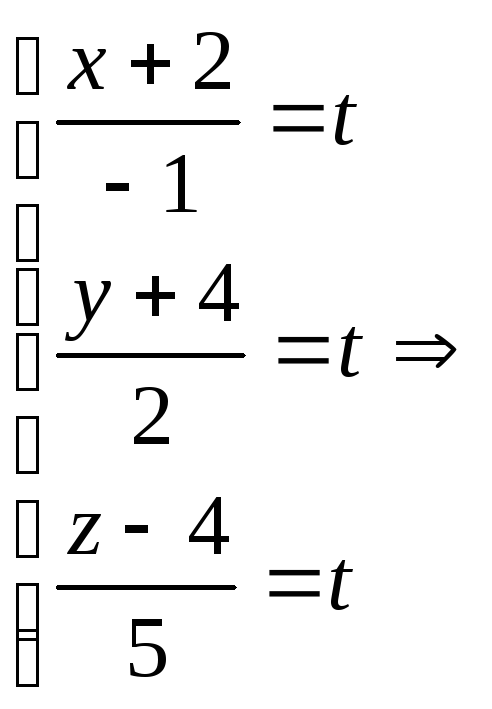Как найти направляющий вектор прямой в пространстве

1. Общее уравнение прямой.

Прямая в пространстве
может быть задана как пересечение двух
плоскостей:

.
(1)

О1.
Геометрическое место точек пространства,
удовлетворяющих системе уравнений (1),
называется
прямой
в пространстве,
а
система уравнений (1) называется общим
уравнением прямой.

З1. Для того чтобы
система уравнений (1) определяла прямую
в пространстве необходимо и достаточно,
чтобы нормальные вектора плоскостей,

определяющих
прямую,
ибыли неколлинеарными, т.е. выполняется
одно из неравенств:или.

Пусть прямая
проходит через точку

параллельно вектору
,
который называется направляющим
вектором прямой
(см. Лекцию
№ 7),
тогда ее уравнение называется каноническим
и имеет вид:

.
(2)

З2. Если в уравнении
(2) одна из проекций направляющего вектора
равна 0, то это означает, что прямая
перпендикулярна соответствующей
координатной оси.

Пример 1.
Как расположена прямая
относительно координатных осей.

Согласно замечанию
2 эта прямая будет перпендикулярна осям
абсцисс и ординат (параллельна оси
аппликат) и будет проходить через точку

.

Приравняв каждую
дробь уравнения (2) параметру
,
получимпараметрическое
уравнение прямой:

Пример 2.
Записать уравнение прямой
в параметрическом виде.

Приравняем каждую
дробь к параметру
:.
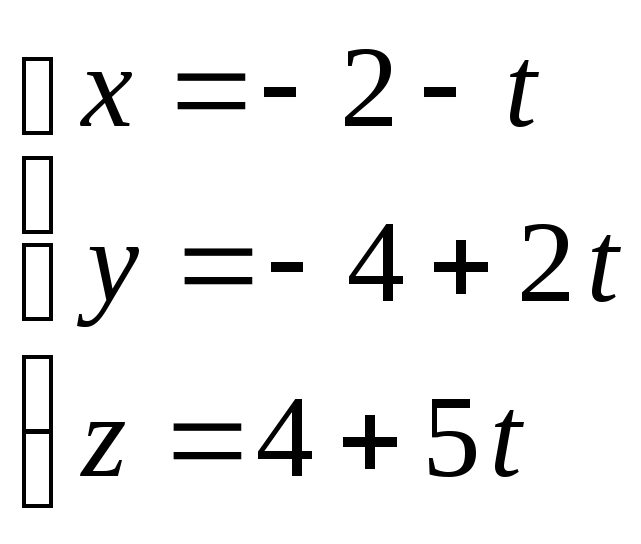
Если пря-

мая проходит через
две известные точки
и,
то ее уравнение имеет вид (см.Лекцию
№ 7):
и назы-ваетсяуравнением
прямой,
проходящей
через две заданные точки.

2. Основные задачи.

а) Переход
от общего уравнения прямой к каноническому.
Пусть прямая задана общим уравнением
.
Для того, чтобы перейти от этого уравнения
прямой к каноническому, поступают
следующим образом:

– находят
координаты любой точки, удовлетворяющие
приведенной системе, для чего одну из
переменных величин, например
,
полагают равной нулю и решают систему
линейных алгебраических уравнений
относительно оставшихся переменных
величин;

– направляющий
вектор
прямой находят как векторное произведение
нормальных векторов
и
:

;

– зная
точку, через которую проходит прямая,
и направляющий вектор прямой записывают
каноническое уравнение прямой.

Пример 3.
Записать уравнение прямой
в каноническом и параметрическом виде.

Положив
,
получим СЛАУСкладывая уравнения, найдем.
Подставив это значение переменнойво второе уравнение системы, по-лучим.
Таким образом, прямая проходит через
точку
.
Найдем направляющий вектор прямой как
векторное произведение нормальных
векторов заданных плоскостей:

б)
Угол
между пересекающимися прямыми.
Угол
между двумя пересека-ющимися прямыми
определяется как угол между их
направляющими векторами.
Если прямые
иимеют направляющие вектора

и
,

соответственно,
то угол между прямыми определяется по
формуле:

.

Сл1.
Если
прямые перпендикулярны (),
тоусловием
перпен-дикулярности
прямых является
равенство:
.

Сл2.
Если прямые параллельны, то направляющие
вектора коллинеарны, следовательно,
условие
параллельности прямых:

.

в)
Координаты
точки пересечения прямой и плоскости.
Пусть прямая
задана общим уравнением,
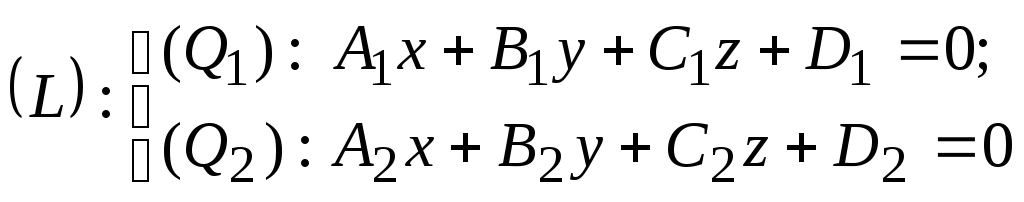
а плоскостьуравнением.Так
как точка пересечения прямой и плоскости
принадлежит одновременно обоим этим
объектам, то ее координаты находят из
решения системы уравнений:

.

Если прямая
задана
каноническим уравнением,

а плоскость
уравнением,
то поступают по следующей

схеме:

– переходят
от канонического уравнения прямой к
параметрическому, т.е. записывают
уравнение прямой в виде
;

– полученные
выражения подставляют в уравнение
заданной плоскости

и
находят параметр
:.

Рассмотрим возможные
случаи:

1) если
выполняются условия
,
то прямая не пересекает плоскость
(прямая параллельна плоскости);

2) при
условиях
прямая лежит на плоскости;

3) если
,
прямая пересекает плоскость в одной
точке.

– вычисляют
координаты точки пересечения, подставив
найденное значение
в параметрическое уравнение прямой

.

г)
Угол
между прямой и плоскостью.
Пусть дана плоскость
с нормальным вектороми пересекающая ее прямаяс направляющим вектором

(Рис.
53).

Рис.
53.
Угол между
прямой

и
плоскостью.

Угол
является углом между прямойи плоскостью.
Угол между нормальным вектором плоскости
и прямой обозначим через.
Из рисунка видно, что.
Следовательно,

.

Сл1.
Если прямая
перпендикулярна плоскости (),
тоусловие
перпендикулярности прямой и плоскости
имеет вид:

.

Сл2.
Если прямая
параллельна плоскости (),
то направляющий вектор прямой и нормальный
вектор плоскости перпендикулярны (),
следовательно,условие
параллельности прямой и плоскости:

.

21

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Уравнения прямых в пространстве

Уравнение прямой как линии пересечения двух плоскостей

Пусть в координатном пространстве (в прямоугольной системе координат) две плоскости заданы общими уравнениями

в которых коэффициенты при неизвестных непропорциональны, т.е. . Это условие означает, что плоскости и пересекаются (см. условие (4.25)), поскольку их нормали и неколлинеарны (рис.4.25). Тогда линия пересечения плоскостей описывается системой уравнений

Система (4.31) называется общим уравнением прямой в пространстве.

---

Пример 4.13. В координатном пространстве (в прямоугольной системе координат) заданы вершины треугольника (рис.4.26). Требуется составить уравнение прямой, содержащей высоту треугольника.

Решение. Прямая является линией пересечения двух плоскостей: плоскости , треугольника и плоскости , проходящей через точку перпендикулярно вектору (рис.4.26). По формуле (4.21) составим уравнение плоскости проходящей через три точки

По формуле (4.14) составим уравнение плоскости , проходящей через точку перпендикулярно вектору

Следовательно, общее уравнение (4.31) прямой имеет вид

---

Параметрическое уравнение прямой в пространстве

Напомним, что направляющий вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.

Пусть в координатном пространстве заданы точка и ненулевой вектор (рис.4.27). Требуется составить уравнение прямой, коллинеарной вектору и проходящей через точку .

Выберем на прямой произвольную точку . Обозначим — радиус-векторы точек и (рис.4.28).

Точка принадлежит заданной прямой тогда и только тогда, когда векторы и коллинеарны. Запишем условие коллинеарности: , где — некоторое действительное число (параметр). Учитывая, что , получим векторное параметрическое уравнение прямой в пространстве:

где — направляющий вектор прямой, а — радиус-вектор заданной точки принадлежащей прямой.

Координатная форма записи уравнения (4.32) называется параметрическим уравнением прямой в пространстве

где — координаты направляющего вектора прямой. Параметр в уравнениях (4.32),(4.33) имеет следующий геометрический смысл: величина пропорциональна расстоянию от заданной точки до точки . Физический смысл параметра в параметрических уравнениях (4.32),(4.33) — это время при равномерном и Прямолинейном движении точки по прямой. При точка совпадает с заданной точкой . При возрастании параметра движение происходит в направлении направляющего вектора.

---

Каноническое уравнение прямой в пространстве

Выразим параметр из каждого уравнения системы (4.33): , а затем исключим этот параметр:

Уравнение (4.34) называется каноническим уравнением прямой в пространстве. В этом уравнении коэффициенты не равны нулю одновременно, так как это координаты направляющего вектора прямой.

---

Замечания 4.6.

1. Если один или два из трех знаменателей дробей в (4.34) равны нулю, то считается, что соответствующий числитель дроби равен нулю. Например:

а) каноническое уравнение — это уравнение прямой, параллельной оси аппликат (рис.4.29,а);

б) каноническое уравнение — это уравнение прямой, параллельной координатной плоскости (рис.4.29,б).

2. Направляющий вектор прямой определяется неоднозначно. Например, любой ненулевой вектор , где , также является направляющим вектором для той же прямой.

Переход от общего уравнение к каноническому

3. Для перехода от общего уравнения прямой (4.31) к каноническому (4.34) нужно выполнить следующие действия:

1) найти любое решение системы определяя тем самым координаты точки , принадлежащей прямой;

2) найти направляющий вектор прямой как векторное произведение нормалей заданных плоскостей:

3) записать каноническое уравнение (4.34) с учетом пунктов 1 и 2.

4. Чтобы перейти от канонического уравнения к общему, достаточно двойное равенство (4.34) записать в виде системы

и привести подобные члены.

5. Чтобы перейти от канонического уравнения к параметрическому, следует приравнять каждую дробь в уравнении (4.34) параметру t и записать полученные равенства в виде системы (4.33):

6. Если в каноническом уравнении (4.34) прямой фиксировать координаты точки , а коэффициентам придавать произвольные значения (не равные нулю одновременно), то получим уравнение связки прямых с центром в точке , т.е. совокупность всех прямых, проходящих через точку .

7. Параметрическое (4.33) и каноническое (4.34) уравнения прямой, полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним.

---

Пример 4.14. В координатном пространстве (в прямоугольной системе координат) заданы вершины треугольника (рис. 4.30). Требуется:

а) составить каноническое уравнение прямой, содержащей высоту треугольника;

б) составить общее уравнение прямой, содержащей биссектрису треугольника.

Решение. а) Общее уравнение прямой получено в примере 4.13: Перейдем от общего уравнения к каноническому.

1) Найдем любое решение системы, например, (это координаты точки ).

2) Найдем направляющий вектор прямой как векторное произведение нормалей заданных плоскостей

3) Запишем каноническое уравнение (4.34): .

б) Сначала составим каноническое уравнение прямой . Для этого нужно найти направляющий вектор этой прямой. Учитывая, что диагональ ромба является биссектрисой, , где и — единичные векторы, одинаково направленные с векторами и соответственно. Находим

Составляем каноническое уравнение прямой .

Записывая двойное равенство в виде системы, получаем общее уравнение прямой

---

Расстояние от точки до прямой в пространстве

Найдем расстояние от точки до прямой , заданной каноническим уравнением (рис.4.31)):

Искомое расстояние равно высоте параллелограмма, построенного на векторах

и , то есть.

---

Уравнение прямой, проходящей через две заданные точки

Пусть в координатном пространстве заданы две точки и . Требуется составить уравнение прямой, проходящей через заданные точки.

Как показано в разд., точка принадлежит прямой тогда и только тогда, когда ее радиус-вектор удовлетворяет условию (рис.4.32): , где — некоторое действительное число (параметр). Это уравнение, а также его координатную форму

будем называть аффинным уравнением прямой, проходящей через две точки и .

Выражая параметр из каждого уравнения системы (4.36), получаем: . Исключая параметр , приходим к уравнению прямой, проходящей через две точки и :

Уравнение (4.37) можно получить из канонического уравнения (4.34), выбирая в качестве направляющего вектора вектор т.е. подставляя

---

Пример 4.15. В координатном пространстве (в прямоугольной системе координат) заданы вершины треугольника (рис.4.33). Требуется:

а) составить уравнение прямой ;

б) составить уравнение прямой, содержащей медиану треугольника;

в) найти высоту треугольника, опущенную на сторону .

Решение. а) Записываем уравнение (4.37) прямой, проходящей через точки

б) Находим координаты середины стороны . Составляем уравнение (4.37) прямой

в) Искомую высоту находим по формуле (4.35), полагая и

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

(схема 27)

         Пусть задан
вектор , параллельный заданной прямой l (без учета направления) и точка M₀, лежащая на данной прямой. Таким образом, прямая l
однозначно определяется в пространстве точкой  M₀(x₀;y₀;z₀) и вектором , называемым для l направляющим.
Обозначим
  и определим его
с точностью до коллинеарности (рис. 2.21).

      Пусть точка M(x;y;z) – текущая точка прямой l,
тогда   текущий вектор прямой имеет координаты . Значит, векторы  и  коллинеарны. По
следствию из теоремы 2.5 данное  условие
можно записать в виде:

    –                                                 (2.43)

канонические уравнения прямой в
пространстве. Равенство нулю одного из знаменателей означает обращение
в нуль соответствующего числителя.

Пусть прямая l проходит через две точки,
одна из которых  – уже введенная в
рассмотрение точка M₀(x₀;y₀;z₀). Другую точку обозначим  M₁(x₁;y₁;z₁). Тогда в качестве направляющего вектора  прямой  можно взять вектор . При этом уравнения (2.43) принимают вид:  

   –                                                                                                                                                    (2.44) 

уравнения прямой в пространстве, проходящей
через две заданные точки.

Все
соотношения (2.43) равны между собой, следовательно, может быть введен
коэффициент пропорциональности t,
называемый параметром прямой:

    – параметрические уравнения прямой.                                                  (2.45) 

Можно записать
частный случай уравнений (2.45) для плоскости: . Они представляют собой параметрические уравнения
прямой линии на плоскости. Проводя аналогичные рассуждения, в качестве
направляющего вектора прямой на плоскости можно взять вектор , параллельный прямой (без учета направления), а точку
M₀(x₀;y₀) – в качестве произвольной точки
прямой. Заметим, что канонические уравнения (2.4) прямой на плоскости
представляют собой частный случай уравнений (2.44).

         Чтобы задать прямую l в пространстве в общем виде
надо рассмотреть её как линию пересечения  двух
плоскостей, которые обозначим через α
и β, и зададим уравнениями соответственно:        . Это
означает, что прямая задается системой, состоящей из уравнений плоскостей α и β:

                                                                                                                                                             (2.46)

–
общее уравнение прямой в пространстве.
Здесь  (в противном случае плоскости параллельны
или совпадают).             

Поставим
задачу – привести общее уравнение (2.46) прямой к  ее каноническим уравнениям (2.43). Решение
состоит из трех этапов.

1.   Отыскание точки  M₀(x₀;y₀;z₀), лежащей на данной прямой.

Координаты
точки  M₀ должны удовлетворять системе (2.46), так как
точка  принадлежит обеим плоскостям  α и β.

Ранг
системы (2.46) равен 2, сама система является совместной неопределенной.
Объявим  базисными  переменными, например, x и y,
тогда z – свободная переменная. Придадим ей конкретное
значение z=z₀. Система примет вид:  при условии, что главный  определитель .  Так как надо знать только одну точку прямой (одно решение системы (2.46)), то
достаточно найти одно ее частное решение. 
Для простоты вычислений можно придать свободной переменной  нулевое значение, то есть z₀=0.  После этого определенную систему уравнений  решают известными методами. Решение
системы  x=x₀; y=y₀
в совокупности со значением свободной переменной представляет собой координаты
искомой точки  M₀(x₀;y₀;z₀).

2.  Рассмотрим нахождение  направляющего вектора  прямой. Так как  перпендикулярен  нормальным векторам  и  плоскостей α и β,
то его можно найти по теореме 2.5 как векторное произведение указанных
векторов:  

.                                                                                                         (2.47)

3. Найденную точку M₀ и вектор  подставляем в
уравнение (2.43). Таким образом, задача о приведении общего уравнения прямой к
каноническому виду решена.

Пример 2.16.
Привести общее уравнение прямой в
пространстве     к
каноническому виду.

Решение. Найдем точку M₀(x₀;y₀;z₀), принадлежащую данной прямой. Достаточно найти одно
частное решение заданной системы, например, при  z₀=0. Решение будет представлять собой координаты точки M₀:  
 

. Используем  метод Крамера – вычислим главный и
вспомогательные определители системы:  .

По формулам (1.6):        

. Следовательно, точка   – искомая точка
заданной прямой.

Найдем направляющий вектор  прямой. Нормальные векторы плоскостей,
пересечением которых задана прямая, есть . Тогда по теореме
2.5: 

.

Подставляя координаты точки M и вектора
 в (2.43), получим искомое каноническое
уравнение прямой l:

Вопросы
для самопроверки

Рассмотрим прямую $L$, заданную точкой $M_0$, лежащей на ней, и направляющим вектором $overline{S}$ с координатами $(l;m)$, при этом вектор $overline{S}$ — ненулевой. Обозначим на прямой произвольную точку $M$ с координатами $(x, y)$, не совпадающую с точкой $M_0$. Радиус-векторы этих точек назовём $overline{r_0}$ и $overline{r}$. Вектор $overline{MM_0}$ при этом будет колинеарен вектору $overline{S}$.

Вектор $overline{r}$ можно выразить через сумму векторов $overline{MM_0}$:

$overline{r} = overline{r_0} + overline{MM_0}left(1right).$

Вектор $overline{MM_0}$ лежит на прямой $L$, поэтому он по условию является параллельным направляющему вектору $overline{S}$ и связан с ним соотношением $overline{MM_0}= toverline{S}left(2right)$, где $t$ — множитель, являющийся скалярной величиной и зависящий от позиции точки $M$ на прямой.

Учитывая равенство $(2)$, формулу $(1)$ можно переписать следующим образом:

Возможны следующие варианты задания уравнения прямой на плоскости:

• Общее уравнение прямой;
• Уравнение с угловым коэффициентом;
• Через параметрические уравнения;
• Каноническое уравнение;
• С помощью двух точек, через которые проходит прямая.

Для каждого из этих вариантов подходит свой способ нахождения направляющего вектора.

Направляющий вектор из канонического уравнения прямой и через две точки

«Направляющий вектор прямой» 👇

Каноническое уравнение прямой выглядит так:

$frac{x-x_0}{l}= frac{y-y_0}{m}left(4right)$

Из канонического уравнения выразить координаты направляющего вектора проще всего: достаточно выписать знаменатели из уравнения следующим образом:

$overline{S}=(l; m)$.

Уравнение прямой, проходящей через 2 точки, имеет вид, очень похожий на каноническое уравнение:

$frac{x-x_1}{x_2 — x_1}= frac{y-y_1}{y_2-y_1}left(5right)$, где $(x_1; y_1)$ и $(x_2; y_2)$ — координаты точек, через которые проходит прямая.

В этом случае координаты направляющего вектора $overline{S}$ равны $((x_2 – x_1); (y_2-y_1))$.

Направляющий вектор из параметрических уравнений

Параметрические уравнения имеют следующий вид:
$begin{cases} x=x_0 + lt \ y=y_0 + mt end{cases}$

Для того чтобы выразить координаты направляющего вектора из параметрических уравнений, нужно выписать коэффициенты, стоящие перед параметром $t$, т.е. $overline{S}=(l; m)$.

Координаты направляющего вектора из общего уравнения

Общее уравнение имеет следующий вид:

$Ax + By + C = 0left(6right)$

Для того чтобы получить координаты направляющего вектора, нужно от общего уравнения прямой перейти к каноническому.

Сделаем это в общей форме.

Сначала перенесём часть $By + C$ в правую часть:

$Ax = — By – C$

Теперь разделим всё на $A$:

$x=-frac{By}{A} — frac{C}{A}$

А после этого всё уравнение разделим на $B$:

$frac{x}{B}=-frac{y}{A} — frac{C}{AB}$

$frac{x}{B} = frac{y + frac{C}{B}}{-A}left(7right)$

Из вышеизложенного следует, что координаты направляющего вектора $overline{S}$ будут равны $(B; -A)$.

Координаты направляющего вектора из уравнения с угловым коэффициентом

Уравнение с угловым коэффициентом имеет вид:

$y = kx + b$

Для того чтобы получить из него координаты направляющего вектора, необходимо сначала привести его к общему виду, для этого переносим всё в левую часть:

$y — kx – b= 0$

Затем нужно воспользоваться алгоритмом для общего уравнения.

Уравнение с угловым коэффициентом, приведённое к каноническому, выглядит так:

$frac{x}{1}=frac{y-b}{k}$,

то есть координаты направляющего вектора в данном случае будут $overline{S}= (1;k)$.

Направляющий вектор прямой

В геометрии можно встретить множество задач на изучение прямой в пространстве и ее свойств. В трехмерном пространстве рассматривают не только прямую, но и плоскость. Данные объекты достаточно просто задать, используя направляющие векторы.

Направляющим вектором прямой является любой ненулевой вектор, находящийся на рассматриваемой прямой или на прямой, параллельной ей.

Согласно определению, можно сделать вывод о существовании бесконечного множества направляющих векторов прямой, которая задана. Кроме того, какой-либо направляющий вектор прямой расположен либо на рассматриваемой прямой, либо на прямой, которая ей параллельна. Таким образом, все направляющие векторы заданной прямой коллинеарны.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Отсюда следует, что при (vec{a}) направляющем векторе прямой а, каждое из направлений (t*vec{a}), где t определяется некоторым ненулевым действительным значением, также представляет собой направляющий вектор прямой а, что следует из условия коллинеарности векторов.

Исходя из термина направляющего вектора прямой, следует, что множества направляющих векторов параллельных прямых совпадают. По-другому, данное утверждение можно сформулировать так: в том случае, когда прямые а и а1 параллельны, вектор (vec{a}) является направляющим вектором прямой а, при этом вектор (vec{a}) также является направляющим вектором прямой а1.

Кроме того, из определений направляющего вектора прямой и нормального вектора прямой следует, что каждый нормальный вектор прямой а является перпендикуляром каждому направляющему вектору прямой а.

На примере можно рассмотреть направляющий вектор прямой. Предположим, что в трехмерном пространстве имеется прямоугольная система координат Охуz. Координатные векторы ( vec{i}, vec{j}, vec{k}) представляют собой направляющие векторы координатных прямых Ох, Оу, Оz соответственно.

Можно рассмотреть другой пример, где задан вектор (vec{v}). Его координаты известны (а; b; с). Так как имеется три координаты, то можно заключить, что вектор задан в пространстве. Для того чтобы изобразить рассматриваемый вектор в прямоугольной системе координат, на каждой из трех осей требуется отложить прямую, ограниченную двумя точками, то есть отрезок с длиной, равной соответствующей координате сектора.

Три перпендикуляра, которые восстановлены к плоскостям xy, yz и xz, будут пересекаться в точке, являющейся концом вектора. Начало вектора совпадает с точкой (0; 0; 0). Однако рассматриваемое положение вектора не единственное. Таким же образом можно задать вектор (vec{v}) с началом в произвольной точке пространства.

Отсюда следует вывод о невозможности задания конкретной прямой с помощью вектора. С его помощью можно определить комплекс из бесконечного числа параллельных прямых.

Далее можно отметить в пространстве какую-либо точку P(x0; y0; z0). Следует определить условие, что через данную точку должна проходить прямая. Таким образом, заданная точка будет располагаться на векторе (vec{v}). Исходя из этого, можно сделать вывод, что прямая, заданная с помощью (Р) и (vec{v}), является единственной. Уравнение данной прямой будет иметь вид:

(Q=P+lambda*vec{v})

 где Q является любой точкой, которая принадлежит рассматриваемой прямой.

Данная точка получается путем подбора соответствующего параметра (lambda). Представленная запись уравнения является векторной, а (vec{v}) представляет собой направляющий вектор прямой. В том случае, когда этот вектор пересекает Р и изменяется в длине по параметру (lambda), получается какая-либо точка Q прямой. Координатная форма уравнения:

((x;y;z) = (x_{0};y_{0};z_{0})+lambda*(a;b;c))

Параметрический вид уравнения:

(x=x_{0}+lambda*a;)

(y = y_{0}+lambda *b;)

(z = z_{0} + lambda *c)

Когда нужно знать направляющий вектор

Данные знания пригодятся при решении задач на определение параллельности и перпендикулярности прямых. Кроме того, направляющий вектор используют для расчета расстояния между прямыми, а также точкой и прямой, описания поведения прямой относительно плоскости.

Одна прямая будет параллельна второй прямой в том случае, когда их направляющие вектора параллельны. Аналогично, перпендикулярность прямых доказывают через перпендикулярность их векторов. Подобные задачи предполагают необходимость определения скалярного произведения рассматриваемых векторов для получения ответа.

Когда требуется вычислить расстояние между прямыми и точками, целесообразно использовать формулу с направляющим вектором:

(d=frac{left|left[vec{P_{1}P_{2} }*vec{v}right]right|} {left| vec{v}right|})

В данном случае (vec{P_{1}P_{2} }) является построенным на точках P1 и P2 направленным отрезком. Точка P2 произвольно расположена на прямой с вектором (*vec{v}), а до точки Р1 требуется определить расстояние. Данная точка является самостоятельной, либо расположена на другой прямой или находится в другой плоскости.

Следует заметить, что рассчитывать расстояние целесообразно только между параллельными или скрещивающимися прямыми. В том случае, когда прямые пересекаются, d обладает нулевым значением. Записанная формула для d справедлива и для расчета дистанции между плоскостью и параллельной ей прямой. Но при этом P1 расположена в рассматриваемой плоскости.

Задача на составление векторного уравнения

Представим, что имеется следующее уравнение прямой:

(y = 3 × x – 4)

Необходимо записать векторное уравнение данной прямой.

Допустимо переписать выражение в виде:

((x; y) = (x; 3 × x — 4))

При раскрытии данного уравнения будет получено выражение из условия.

Далее можно разделить правую часть уравнения на вектора таким образом, чтобы лишь один из них включал неизвестные:

((x; y) = (x; 3 × x) + (0; -4))

Затем следует вынести х за скобки, обозначить его (lambda) и поменять вектора правой части местами:

((x; y) = (0; -4) + lambda * (1; 3))

Таким образом, получена векторная форма уравнения прямой из условия. Координаты ее направляющего вектора равны (1; 3).

Задача на определение взаимного расположения прямых

Представим, что в пространстве задана пара прямых:

((x; y; z) = (1; 0; -2) + lambda * (-1; 3; 1);)

((x; y; z) = (3; 2; 2) + lambda * (1; 2; 0))

Необходимо определить, какие эти прямые: параллельные, скрещивающиеся или пересекающиеся. При этом ненулевые вектора (-1; 3; 1) и (1; 2; 0) являются направляющими для заданных прямых. Можно выразить в параметрической форме рассматриваемые уравнения и подставить координаты первого во второе:

(x = 1 — lambda;)

(y = 3 * lambda;)

(z = -2 + lambda;)

(x = 3 + gamma = 1 — lambda => gamma = -2 — lambda;)

(y = 2 + 2 * gamma = 3 * lambda => gamma = 3 / 2 * lambda — 1;)

(z = 2 = -2 + lambda => lambda = 4)

При подстановке определенного параметра (lambda )в два уравнения выше, получится:

(gamma = -2 — lambda = -6;)

(gamma = 3 / 2 *lambda — 1 = 5)

Для параметра (gamma) не предусмотрено наличие сразу двух значений. Таким образом, прямые не обладают ни одной общей точкой, то есть являются скрещивающимися. Параллельность данных прямых исключается, так как ненулевые векторы не параллельны друг другу, то есть для их параллельности должно существовать число, которое бы путем умножения на один вектор приводило к координатам второго.

Математическое описание плоскости

Задать плоскость в пространстве можно путем приведения уравнения общего вида:

(A * x + B * y + C * z + D = 0)

В данном случае латинскими большими буквами обозначают конкретные числа. Первая тройка таких чисел определяет координаты нормального вектора плоскости. В том случае, когда он обозначен (vec{n}), можно записать: (vec{n} = (A; B; C)). Рассматриваемый вектор перпендикулярен к плоскости, поэтому его называют направляющим.

Его знание, а также известные координаты любой точки, находящейся на плоскости, однозначно задают последнюю. Если точка P (x1; y1; z1) плоскости принадлежит, то свободный член D рассчитывается следующим образом:

(D = -1 * (A * x1 + B * y1 + C * z1))

Уравнение прямой по направляющему вектору

Любой ненулевой вектор (vec{a} (а1; а2)) с компонентами, соответствующими условию А а1 + В а2 = 0, представляет собой направляющий вектор прямой.

Ах + Ву + С = 0

В качестве примера можно вывести уравнение прямой, которая проходит через точку А (1, 2) с направляющим вектором (vec{a} ) (1, -1). Для этого требуется записать уравнение в виде:

Ax + By + C = 0

Согласно определению, коэффициенты должны соответствовать следующим условиям:

1 * A + (-1) * B = 0, то есть А = В

В таком случае:

Ax + Ay + C = 0, или x + y + C / A = 0

Если х = 1, у = 2 получаем:

С/ A = -3

Таким образом:

х + у — 3 = 0

Общее уравнение прямой в декартовой системе координат имеет вид:

Ax + By + C = 0

где x, y – являются координатами точек прямой, A, B, C – определяются, как действительные числа при условии ({A^2} + {B^2} ne 0).

В том случае, когда прямая задана общим уравнением:

Ax + By + C = 0

В таком случае вектор:

(mathbf{n}left( {A,B} right))

Его координаты соответствуют коэффициентам A, B. Данный вектор представляет собой вектор нормали к данной прямой.

Уравнение прямой по точке и направляющему вектору представляет собой каноническое уравнение прямой и имеет вид:

(largefrac{{x — {x_1}}}{X}normalsize = largefrac{{y — {y_1}}}{Y}normalsize)

где вектор (mathbf{s}left( {X,Y} right)) направлен вдоль прямой, а точка (Pleft( {{x_1},{y_1}} right)) расположена на этой прямой.

Координаты направляющего вектора из общего уравнения

При рассмотрении данной темы стоит привязать рассматриваемую прямую и ее направляющие векторы к прямоугольной системе координат. Алгоритм действий:

• рассмотреть прямую и ее направляющие векторы в прямоугольной декартовой системе координат Oxy на плоскости;
• рассмотреть прямую и ее направляющие векторы в прямоугольной системе координат Oxyz, принадлежащей трехмерному пространству.

Прямая линия в прямоугольной системе координат Oxy определяется некоторым уравнением прямой на плоскости. При этом направляющие вектора прямой в системе координат Oxy соответствуют координатам направляющих векторов.

Определить координаты направляющего вектора прямой при известном уравнении рассматриваемой прямой можно в том случае, когда прямая линия задана каноническим уравнением или параметрическими уравнениями.

Каноническое уравнение прямой на плоскости можно записать в виде:

(frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}})

Один из направляющих векторов этой прямой можно записать так:

(vec{a}(a_{x}; a_{y}))

Отсюда следует вывод о том, что числа в знаменателях канонического уравнения прямой соответствуют координатам направляющего вектора рассматриваемой прямой.

(frac{x-1}{4}=frac{y+1/2}{-3})

Необходимо рассчитать координаты любого направляющего вектора данной прямой.

Решение

Согласно каноническому уравнению прямой на плоскости, координаты какого-то из направляющих векторов рассматриваемой прямой соответствуют числам в знаменателях. Таким образом, искомый направляющий вектор обладает координатами (4; -3).

Ответ: (4; -3)

Подобным образом можно определить прямую с направляющим вектором (vec{a}(a_{x}; a_{y})) с помощью параметрических уравнений прямой на плоскости:

(x=x_{1}+a_{x}*lambda)

(y=y_{1}+a_{y}*lambda)

Таким образом, коэффициенты при параметре в параметрических уравнениях прямой представляют собой соответствующие координаты направляющего вектора прямой.

(x=-1)

(y=7-5*lambda)

При этом (lambda in R). Требуется определить координаты направляющих векторов заданной прямой.

Решение

В первую очередь следует преобразовать уравнение прямой:

(x=-1+0*lambda)

(y=7-5*lambda)

Коэффициенты с параметром (lambda) соответствуют координатам направляющего вектора прямой:

(vec{a}(0; -5))

Данный вектор является одним из направляющих векторов исходной прямой. Так как направляющие вектора прямой коллинеарны, их можно записать в виде: (t*vec{a}). В координатной форме запись будет иметь вид: ((0; -5*t)). В данном случае t является любым действительным числом, которое не равно нулю.

Ответ: ((0; -5*t), t in R, tneq 0)

Далее можно рассмотреть принцип поиска координат направляющего вектора прямой, заданной общим уравнением прямой вида: (Ax + By + C = 0.)

Ели А=0 в выражении Ах + Ву + С = 0, то уравнение будет записано в виде:

Ву + С = 0

Данное уравнение определяет прямую, которая параллельна оси абсцисс. Таким образом, направляющим вектором прямой (Ву + С = 0) является координатный вектор (vec{i}(1; 0).)

Если В=0, то запись общего уравнения прямой будет следующая:

(Ах + С = 0)

Данная прямая параллельна оси ординат. В связи с этим, ее направляющим вектором будет координатный вектор (vec{j}(1; 0).)

Решение

С помощью уравнения х-2=0 в прямоугольной системе координат Oxy можно задать прямую, которая будет параллельна оси Oy. Таким образом, роль ее направляющего вектора играет координатный вектор (vec{j}(0; 1).)

Ответ: (0; 1)

В том случае, когда общее уравнение прямой имеет вид (Ах + Ву + С = 0) с коэффициентами А и В, не равными нулю, координаты направляющего вектора находят одним из следующих методов:

• приведение заданного уравнения в канонический вид, что позволит распознать координаты направляющего вектора;
• поиск координат пары не совпадающих точек на данной прямой, принятие их в качестве начала и конца направляющего вектора прямой и определение его координат;
• поиск координат любого вектора, который перпендикулярен к нормальному вектору (vec{n}(A; B)) прямой (Ах + Ву + С = 0.)

(3х + 2у – 10 = 0)

Решение

В первую очередь необходимо привести общее уравнение прямой к каноническому виду. В данном случае в левой части выражения остается лишь слагаемое 3х, а остальные компоненты следует перенести в правую часть, меняя знак на противоположный:

(3х + 2у – 10 = 0)

(3х = -2у + 10)

Преобразованное равенство имеет вид:

(3х = -2у + 10)

(3х = -2(у -5))

(frac{x}{-2}=frac{y-5}{3})

Полученное уравнение позволяет сделать вывод о том, что координаты направляющего вектора равны (2;-3).

Ответ: (2;-3)

Координаты направляющего вектора из уравнения с угловым коэффициентом

Уравнение с угловым коэффициентом записывают в таком виде:

(y=kx+b)

Определить координаты направляющего вектора прямой, описанной данным уравнением, можно с помощью приведения рассматриваемого уравнения к общему виду. В процессе требуется перенести компоненты в левую часть:

(y−kx–b=0)

Далее можно прибегнуть к алгоритму, характерному для общего уравнения. Уравнение с угловым коэффициентом, преобразованное в каноническое, запишем следующим образом:

(x1=y−bk)

Таким образом, координаты направляющего вектора для данного случая равны:

(vec{S}=(1;k))

Уравнение прямой с угловым коэффициентом:

(y = kx + b)

где (k = tanalpha) представляет собой угловой коэффициент прямой, число b определяется, как координата точки пересечения прямой с осью Oy.

Угловой коэффициент прямой рассчитывают с помощью уравнения:

(k = tan alpha = largefrac{{{y_2} — {y_1}}}{{{x_2} — {x_1}}}normalsize,)

где (Aleft( {{x_1},{y_1}} right), Bleft( {{x_2},{y_2}} right)) – являются координатами двух точек, расположенных на прямой.

Уравнение прямой по точке и угловому коэффициенту имеет вид:

(y = {y_0} + kleft( {x — {x_0}} right),)

где k – является угловым коэффициентом, а точка (Pleft( {{x_0},{y_0}} right) ) расположена на рассматриваемой прямой.