Главная
→
Примеры решения задач ТОЭ
→
Расчет электрической цепи постоянного тока с конденсаторами
Расчет электрической цепи постоянного тока с конденсаторами
Расчет электрической цепи постоянного тока с конденсаторами
Основные положения и соотношения
1. Общее выражение емкости конденсатора
C= Q U .
2. Емкость плоского конденсатора
C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d ,
здесь
S — поверхность каждой пластины конденсатора;
d — расстояние между ними;
εa = εr·ε0 — абсолютная диэлектрическая проницаемость среды;
εr — диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);
ε 0 = 1 4π⋅ с 2 ⋅ 10 −7 ≈8,85418782⋅ 10 −12 Ф м – электрическая постоянная.
3. При параллельном соединении конденсаторов С1, С2, …, Сn эквивалентная емкость равна
C= C 1 + C 2 +…+ C n = ∑ k=1 n C k .
4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы
1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .
Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:
C= C 1 ⋅ C 2 C 1 + C 2 ,
а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:
U 1 =U⋅ C 2 C 1 + C 2 ; U 2 =U⋅ C 1 C 1 + C 2 .
5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)
Рис. 0
осуществляется по формулам:
Y→Δ { C 12 = C 1 ⋅ C 2 ΣC ; C 13 = C 1 ⋅ C 3 ΣC ; C 23 = C 2 ⋅ C 3 ΣC , где ΣC= C 1 + C 2 + C 3 , Δ→Y { C 1 = C 12 + C 13 + C 12 ⋅ C 13 C 23 ; C 2 = C 12 + C 23 + C 12 ⋅ C 23 C 13 ; C 3 = C 13 + C 23 + C 13 ⋅ C 23 C 12 .
6. Энергия электростатического поля конденсатора:
W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C .
7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:
1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:
ΣQ=Σ Q ′ .
2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:
∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k .
Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.
Решение задач на расчет электрической цепи постоянного тока с конденсаторами
Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).
Рис. 1
Решение
На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U12, то на левую пластину конденсатора С1 перейдет заряд +q, на правую пластину конденсатора С3 заряд –q.
Вследствие электризации через влияние правая пластина конденсатора С1 будет иметь заряд –q, а так как пластины конденсаторов С1 и С2 соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C2 будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.
Найти эквивалентную емкость — это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.
Разность потенциалов U12 = φ1 — φ2 складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов
U 12 = φ 1 − φ 2 =( φ 1 − φ A )+( φ A − φ B )+( φ B − φ 2 )= U 1A + U AB + U B2 .
Воспользовавшись формулой напряжения на конденсаторе
U= q C ,
запишем
q C = q C 1 + q C 2 + q C 3 .
Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов
1 C = 1 C 1 + 1 C 2 + 1 C 3 .
В общем случае эквивалентная емкость при последовательном соединении конденсаторов
1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .
Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.
Рис. 2
Емкости конденсаторов: C1 =50 мкФ; C2 =150 мкФ; C3 =300 мкФ.
Решение
Эквивалентная емкость конденсаторов C1 и C2, соединенных параллельно
C12 = C1 + C2 = 200 мкФ,
эквивалентная емкость всей цепи равна
C= C 12 ⋅ C 3 C 12 + C 3 = 200⋅300 500 =120 мкФ.
Заряд на эквивалентной емкости
Q = C·U = 120·10–6·240 = 288·10–4 Кл.
Той же величине равен заряд Q3 на конденсаторе C3, т.е. Q3 = Q = 288·10–4 Кл; напряжение на этом конденсаторе
U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96 В.
Напряжение на конденсаторах C1 и C2 равно
U1 = U2 = U — U3 = 240 — 96 = 144 В.
их заряды имеют следующие значения
Q1 = C1·U1 = 50·10–6·144 = 72·10–4 Кл;
Q2 = C2·U2 = 150·10–6·144 = 216·10–4 Кл.
Энергии электростатического поля конденсаторов равны
W 1 = Q 1 ⋅ U 1 2 = 72⋅ 10 −4 ⋅144 2 ≈0,52 Дж; W 2 = Q 2 ⋅ U 2 2 = 216⋅ 10 −4 ⋅144 2 ≈1,56 Дж; W 3 = Q 3 ⋅ U 3 2 = 288⋅ 10 −4 ⋅96 2 ≈1,38 Дж.
Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см2, имеет диэлектрик, состоящий из слюды (εr1 = 6) толщиною d1 = 0,3 мм и стекла (εr2 = 7) толщиною d2 =0,4 мм.
Пробивные напряженности слюды и стекла соответственно равны E1 = 77 кВ/мм, E2 = 36 кВ/мм.
Рис. 3
Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.
Решение
Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов
C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .
Подставляя сюда числовые значения, предварительно заменив εa1 = εr1·ε0 и εa2 = εr2·ε0, получим
C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12 Ф.
Обозначим общее напряжение, подключаемое к слоистому конденсатору, через Uпр, при этом заряд конденсатора будет равен
Q = C·Uпр.
Напряжения на каждом слое будут равны
U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .
Напряженности электростатического поля в каждом слое
E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .
Здесь U’np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U»np — общее напряжение, при котором происходит пробой второго слоя.
Из последнего выражения находим
U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5 кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0 кВ.
Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное
27,0 кВ / 2 = 13,5 кВ.
Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d1 = 1 см друг от друга. Площадь обкладок S = 50 см2. Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.
Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d2 = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.
Решение
Энергия заряженного плоского конденсатора равна
W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,
где С1 — емкость до раздвижения обкладок.
Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения
Q = C2·U2,
где C2 — емкость конденсатора после раздвижения обкладок, следует, что, так как C2 = ε0·S/d2 стало меньше в 10 раз (d2 увеличилось в 10 раз), то напряжение на конденсаторе U2 увеличилось в 10 раз, т. е. U2 = 10U.
Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d2 будет больше первоначальной
W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .
Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.
Таким образом, надо совершить работу, равную
W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7 Дж.
Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.
Даны: C1 = 30 мкФ; C2 = 20 мкФ; r1 = 100 Ом. r2 = 400 Ом. r3 = 600 Ом, U = 20 В.
Решение
Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям
U 1 = C 2 C 1 + C 2 ⋅U= 20⋅ 10 −6 30⋅ 10 −6 +20⋅ 10 −6 ⋅20=8 В; U 2 =U− U 1 =20−8=12 В.
Рис. 4
Ключ К замкнут. Через сопротивления r1 и r2 протекает ток
I= U r 1 + r 2 = 20 500 =0,04 А,
а через сопротивление r3 ток не протекает.
Поэтому точки c и d равнопотенциальны (φc = φd). Следовательно, напряжение между точками a и c (Uac = φa — φc) равно напряжению между точками a и d (Uad = φa — φd).
Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r1
UC1 = I·r1 = 0,04·100 = 4 В.
Аналогично напряжение на втором конденсаторе равно
UC2 = I·r2 = 0,04·400 = 16 В.
Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C1 = 5 мкФ; C2 = 120 мкФ. Конденсатор C2 предварительно не был заряжен.
Рис. 5
Решение
Когда рубильник находится в положении 1, то конденсатор C1 заряжен до напряжения U и его заряд равен
Q = C1·U = 5·10–6·25 = 125·10–6 Кл.
После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C1 и C2 (рис. 5). Обозначим эти заряды через Q’1 и Q’2.
На основании закона сохранения электричества имеем
Q = Q’1 + Q’2 = 125 10–6 Кл. (1)
По второму закону Кирхгофа имеем
0= U C1 − U C2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,
или
Q ′ 1 5⋅ 10 −6 − Q ′ 2 120⋅ 10 −6 =0. (2)
Решая уравнения (1) и (2), найдем
Q’1 = 5 10–6 Кл; Q’2 = 120 10–6 Кл.
Доставка свежих и аппетитных японских суши в Новороссийске — ям ям..
Напряжение на зажимах конденсаторов станет равным
U C1 = Q ′ 1 C 1 = U C2 = Q ′ 2 C 2 = 5⋅ 10 −6 5⋅ 10 −6 =1 В.
Энергия обоих конденсаторов будет равна
W= C 1 ⋅ U C1 2 2 + C 2 ⋅ U C2 2 2 =62,5⋅ 10 −6 Дж.
Подсчитаем энергию, которая была запасена в конденсаторе С1, при его подключении к источнику электрической энергии
W нач = C 1 ⋅U 2 = 5⋅ 10 −6 ⋅ 25 2 2 =1562,5⋅ 10 −6 Дж.
Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10–6 — 62,5·10–6 = 1500·10–6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C1 в конденсатор C2 после перевода рубильника в положение 2.
Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.
Емкости конденсаторов равны: C1 = 10 мкФ; C2 = 30 мкФ; C3 = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.
Рис. 6
Решение
Рубильник находится в положении 1. Заряд конденсатора C1 равен
Q1 = C1·U = 10·10–6·30 = 0,3·10–3 Кл.
В указанном положении рубильника конденсаторы C2 и C3 соединены последовательно друг с другом, поэтому их заряды равны: Q2 = Q3. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем
E= U C2 + U C3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,
откуда
Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅E= 30⋅ 10 −6 ⋅60⋅ 10 −6 90⋅ 10 −6 ⋅50=1⋅ 10 −3 Кл.
При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’1, Q’2 и Q’3. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.
Для узла a
Q’1 + Q’2 — Q’3 = Q1 + Q2 — Q3. (1)
Для контура 2ebda2
0= U ′ C1 − U ′ C2 = Q ′ 1 C 1 − Q ′ 2 C 1 .
Для контура bcadb
E= U ′ C2 − U ′ C3 = Q ′ 2 C 2 + Q ′ 3 C 3 .
Уравнения (1) — (3), после подстановки числовых значений величин, примут вид
Q’1 + Q’2 — Q’3 = 0,3·10–3; (4)
3Q’1 — Q’2 = 0; (5)
2Q’2 + Q’3 = 3·10–3. (6)
Решая совместно уравнения (4) — (6), получим
Q’1 = 0,33·10–3 Кл; Q’2 = 0,99·10–3 Кл; Q’3 = 1,02·10–3 Кл.
Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.
Напряжения на конденсаторах после перевода рубильника будут равны
U C1 = Q ′ 1 C 1 = 0,33⋅ 10 −3 10⋅ 10 6 =33 В; U C2 = Q ′ 2 C 2 = 0,99⋅ 10 −3 30⋅ 10 6 =33 В; U C3 = Q ′ 3 C 3 = 1,02⋅ 10 −3 60⋅ 10 6 =17 В.
Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C1 = 5 мкФ; C2 = 4 мкФ; C3 = 3 мкФ; э. д. с. источников E1 = 20 В и E2 = 5 В.
Рис. 7
Решение
Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках
− Q 1 + Q 2 − Q 3 =0; E 1 = U C1 − U C3 = Q 1 C 1 − Q 3 C 3 ; E 2 =− U C2 − U C3 =− Q 2 C 2 − Q 3 C 3 .
Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q1 = 50 мкКл; Q2 = 20 мкКл; Q3 = –30 мкКл.
Таким образом, истинная полярность зарядов на обкладках конденсаторов C1 и C2 соответствует выбранной, а у конденсатора C3 — противоположна выбранной.
Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C1 = 2 мкФ; C2 = 3 мкФ; C3 = 5 мкФ; C4 = 1 мкФ; C5 = 2,4 мкФ.
Рис. 8
Индивидуалка Дана (34 лет) т.8 926 650-82-63 Москва, метро Сокол.
Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.
Решение
1-й способ. Звезду емкостей C1, C2 и C3 (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)
C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 =0,6 мкФ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 =1,0 мкФ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 =1,5 мкФ.
Емкости C12 и C5 оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость
C6 = C12 + C5 = 3 мкФ.
Аналогично
C7 = C13 + C4 = 2 мкФ.
Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется
C ab = C 23 + C 6 ⋅ C 7 C 6 + C 7 =2,7 мкФ.
Вычислим напряжение на каждом из конденсаторов.
На конденсаторе C7 напряжение равно
U 7 = C 6 C 6 + C 7 ⋅U=6 В.
Таково же напряжение и на конденсаторах C4 и C13
U4 = U31 = 6 В.
Напряжение на конденсаторе C6 равно
U6 = U — U7 = 4 В;
U5 = U12 = 4 В.
Вычислим заряды
Q4 = C4·U4 = 6·10–6 Кл;
Q5 = C5·U5 = 9,6·10–6 Кл;
Q12 = C12·U12 = 6·10–6 Кл;
Q13 = C13·U31 = 2,4·10–6 Кл.
По закону сохранения электричества для узла 1 схем 8, а и б имеем
–Q4 — Q1 + Q5 = –Q4 — Q13 + Q12 + Q5,
отсюда
Q1 = Q13 — Q12 = 3,6·10–6 Кл,
а напряжение на конденсаторе, емкостью C1 составляет
U 1 = Q 1 C 1 =1,8 В.
Далее находим напряжения и заряды на остальных конденсаторах
U31 = U1 + U3,
отсюда
U3 = U31 — U1 = 4,2 В;
Q3 = C3·U3 = 21·10–6 Кл,
также
U12 = U2 — U1 = 4,2 В,
откуда
U2 = U12 + U1 = 5,8 В;
Q2 = C2·U2 = 17,4·10–6 Кл.
Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.
2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)
для узла 1
Q5 — Q1 — Q4 = 0; (1)
для узла О
Q1 + Q2 — Q3 = 0; (2)
для контура О13О
Q 1 C 1 − Q 4 C 4 + Q 3 C 3 =0; (3)
для контура О12О
Q 1 C 1 + Q 5 C 5 − Q 2 C 2 =0; (4)
для контура a3О2b
Q 3 C 3 + Q 2 C 2 =U. (5)
Система уравнений (1) — (5) — содержит пять неизвестных: Q1, Q2, Q3, Q4 и Q5. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы Сab можно найти из отношения
C ab = Q U ,
где Q = Q3 + Q4, или Q = Q2 + Q5.
Задача 9. В схеме рис. 9 найти распределение зарядов, если E1 = 20 В; E2 = 7 В; C1 = 7 мкФ; C2 = 1 мкФ; C3 = 3 мкФ; C4 = 4 мкФ; C5 = C6 = 5 мкФ.
Рис. 9
Решение
При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:
для узла а
Q1 + Q2 + Q3 = 0;
для узла b
–Q3 — Q4 — Q5 = 0;
для узла c
–Q1 + Q4 + Q6 = 0;
для контура afcba
E 1 = U C1 + U C4 − U C3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;
ля контура gdbag
E 2 = U C5 − U C3 + U C2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;
для контура cbdc
0= U C4 − U C5 − U C6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .
Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды
Q1 = 35 мкКл; Q2 = –5 мкКл; Q3 = –30 мкКл;
Q4 = 20 мкКл; Q5 = 10 мкКл; Q6 = 15 мкКл.
Таким образом, истинные знаки зарядов Q1, Q4, Q5 и Q6 соответствуют выбранным, а знаки Q2 и Q3 противоположны выбранным.
Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.
Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C1 = 6 мкФ; C2 = 2 мкФ; C3 = 3 мкФ; r1 = 500 Ом; r2 = 400 Ом; U = 45 В.
Рис. 10
Решение
Через сопротивления протекает ток
I= U r 1 + r 2 =0,05 А.
Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:
− Q 1 + Q 2 + Q 3 =0; U= U C1 + U C2 = Q 1 C 1 + Q 2 C 2 ; I⋅ r 1 = U C1 + U C3 = Q 1 C 1 + Q 3 C 3 ,
или
Q 1 = Q 2 + Q 3 ; 45= Q 1 6⋅ 10 −6 + Q 2 2⋅ 10 −6 ; 25= Q 1 6⋅ 10 −6 + Q 3 3⋅ 10 −6 .
Решив эту систему уравнений, найдем, что
Q1 = 90 мкКл; Q2 = 60 мкКл; Q3 = 30 мкКл.

параллельное соединение конденсаторов,
Расчет цепи конденсаторов,
Конденсатор в цепи постоянного тока,
Цепи с конденсаторами
Комментарии
Методика расчёта электрических цепей с конденсаторами.
Краткие теоретические сведения:
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
|
В системе СИ единица электроемкости называется фарад (Ф):
|
|
Конденсаторы могут соединяться между собой, образуя батареи конденсаторов. При параллельном соединении конденсаторов (рис. 1.) напряжения на конденсаторах одинаковы: U1 = U2 = U, а заряды равны q1 = С1U и q2 = C2U. Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q1 + q2при напряжении между обкладками равном U. Отсюда следует
|
Таким образом, при параллельном соединении электроемкости складываются.
|
|
При последовательном соединении (рис.2.) одинаковыми оказываются заряды обоих конденсаторов: q1 = q2 = q, а напряжения на них 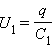
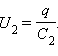
|
При последовательном соединении конденсаторов складываются обратные величины емкостей.
Пример расчёта:На рисунке 2 приведена схема соединения конденсаторов. Определить эквивалентнуюемкостьСэкв батареи конденсаторов, общий заряд Q, напряжение сети U, напряжение и заряд на каждом конденсаторе, если дано: C1=24 мкФ; С2=С3=8 мкФ; С4=12 мкФ; С5=6 мкФ; напряжение на пятом конденсаторе U5=30 В.
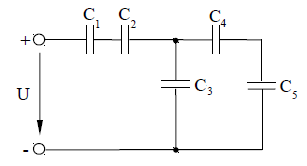
Рисунок 3
Дано: C1=24 мкФ; С2=С3=8 мкФ; С4=12 мкФ; С5=6 мкФ; U5=30 ВОпределить: U, Q, Сэкв, U1, U2, U3, U4, Q1.
Решение: 1. Общая емкость последовательно соединенных конденсаторов С4 и С5:
2. Общая емкость параллельно соединенных конденсаторов С3 иС4,5:
3. Общая емкость последовательно соединенных конденсаторов С1, С2 и С3,4,5, которая и является эквивалентной емкостью батареи конденсаторов:
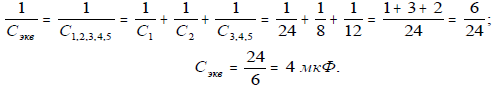
4. По заданному напряжению U5 и емкости конденсатора С5 определяем заряд, накапливаемый этим конденсатором:
5. Заряд конденсатора С4 Q4=Q5=Q4,5=180・10-6 Кл, т. к. конденсаторы С4 и С5 соединены последовательно. 6. Напряжение на четвертом конденсаторе:
7. Напряжение на третьем конденсаторе:
8. Заряд конденсатора С3:
9. Общий заряд батареи и заряды конденсаторов С1 и С2:
10. Напряжение на первом и втором конденсаторах:
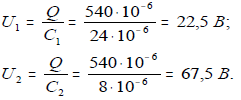
11. Напряжение сети (напряжение последовательно соединенных конденсаторов С1, С2, С3,4,5):
12. Энергия электрического поля батареи:
Выполнить задание:
На рисунке 4 дана схема соединения конденсаторов. Значение емкостей конденсаторов и значение одного из напряжений или зарядов для своего варианта взять из таблицы 1.Вычислить эквивалентную емкость батареи конденсаторов; напряжение сети, напряжение на каждом конденсаторе; общий заряд и заряд на каждом конденсаторе; энергию, накопленную батареей, а также потенциал заданной точки.
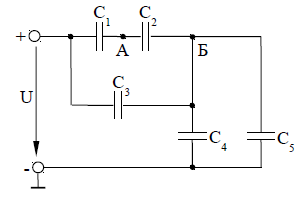
Рисунок 4.
Таблица 1
|
№ вар. |
Емкость конденсатора, мкФ |
Напряжение, заряд |
Точка, потенциал которой следует вычислить |
||||
|
С1 |
С2 |
С3 |
С4 |
С5 |
|||
|
1 |
120 |
280 |
16 |
80 |
70 |
U=20 В |
Б |
|
2 |
600 |
200 |
150 |
400 |
200 |
Q3=72∙10-4 Кл |
Б |
|
3 |
24 |
12 |
2 |
16 |
14 |
U5=25 В |
А |
|
4 |
30 |
20 |
12 |
20 |
16 |
Q4=4∙10-4 Кл |
Б |
|
5 |
10 |
15 |
24 |
6 |
9 |
U1=15 В |
А |
|
6 |
12 |
6 |
5 |
9 |
9 |
Q2=282∙10-6Кл |
А |
|
7 |
30 |
15 |
10 |
65 |
15 |
Q5=6∙10-4 Кл |
А |
|
8 |
18 |
9 |
12 |
15 |
21 |
U2=84 В |
Б |
|
9 |
140 |
60 |
6 |
30 |
18 |
U3=50 В |
А |
|
10 |
150 |
50 |
37,5 |
30 |
20 |
Q1=3∙10-4 Кл |
Б |
Ответить на контрольные вопросы:
1.От чего зависит ёмкость конденсатора ?
2.Как изменится ёмкость батареи конденсаторов, если вместо последовательного соединения их соединили параллельно?
3.Изменится ли ёмкость воздушного конденсатора, если раздвинуть пластины так, чтобы расстояние между ними увеличилось с 5 до 14 мм?
Иногда в наличии нет конденсатора с нужными параметрами. В таком случае, можно соединить несколько конденсаторов так, чтобы полученная система обладала необходимой электрической емкостью. Существуют два основных способа соединений:
- параллельный;
- последовательный;
Комбинируя эти способы, можно получить смешанное соединение.
Для каждого способа применяют специальные формулы, описывающие распределение заряда и напряжения на конденсаторах, а, так же, получаемую итоговую электроемкость системы.
Параллельное соединение
Этот способ соединения получаем, соединяя каждый вывод одного прибора с соответствующим ему выводом другого (рис. 1).
Рис. 1. Параллельный способ соединения
Емкость для параллельного включения можно определить так:
[large boxed { C_{1} + C_{2} = C_{text{общ}} } ]
При этом, общая (large C_{text{Общ}} ) электроемкость получится больше самой большой емкости, входящей в соединение.
(large C_{1}, C_{2} left( text{Ф} right) ) – электроемкости конденсаторов.
Общая электроемкость включенных параллельно конденсаторов больше емкости большего из них.
Напряжение на конденсаторах
Напряжения, приложенные к параллельно подключенным обкладкам, равны.
[large boxed { U_{1} = U_{2} = U_{text{общ}} } ]
(large U_{1}, U_{2}left( Bright) ) – напряжения на обкладках.
Рис. 2. Равенство напряжений на параллельно соединенных обкладках
Правило для зарядов
Общий заряд системы разделится на части. Каждая из параллельно соединенных емкостей получит свой заряд.
[large boxed { q_{1} + q_{2} = q_{text{общ}} } ]
(large q_{1}, q_{2}left( text{Кл} right) ) – заряды на конденсаторах.
Рис. 3. Заряды, содержащиеся на каждом параллельно включенном элементе, складываются
При этом, из формулы емкости (ссылка), связывающей ее с напряжением на обкладках и зарядом, следует (рис. 4):
При параллельном соединении меньшая емкость содержит меньший заряд.
Рис. 4. Пример распределения зарядов на конденсаторах при их параллельном включении
Из рисунка 4 следует, в параллельной части цепи конденсатор с наименьшей (0,1 Ф) электроемкостью накапливает меньший (1 Кулон) заряд. А набиольший заряд 4 Кулона содержится на приборе, обладающем максимальной емкостью 0,4 Ф.
Последовательное соединение
Для такого способа соединения складываются величины, обратные емкостям.
[large boxed { frac {1}{C_{1}} + frac {1}{C_{2}} = frac {1}{C_{text{общ}}} } ]
Примечание: Величина, обратно пропорциональная емкости, измеряется в обратных Фарадах.
(large displaystyle frac {1}{C} left( frac {1}{text{Ф}} right) ) – величину, обратную электроемкости в некоторых источниках называют электрической эластичностью (эластансом).
(large C_{1}, C_{2}left( text{Ф}right) ) – емкости конденсаторов.
При последовательном включении общая (large C_{text{Общ}} ) электроемкость цепочки окажется меньше самой маленькой емкости включенной в цепочку.
Рис. 5. Последовательный способ соединения емкостей
Общая емкость системы меньше меньшей из включенных последовательно емкостей.
Правило для напряжений
Приложенное к концам последовательной цепочки напряжение распределится между элементами.
[large boxed { U_{1} + U_{2} = U_{text{общ}} } ]
где (large U_{1}, U_{2}left( Bright) ) — это напряжения на обкладках.
Чем больше емкость конденсатора, тем меньшее напряжение будет наблюдаться на его обкладках при последовательном соединении.
Рис. 6. Способ определить общее напряжение на последовательно включенных емкостях
Общее напряжение разделится на части. Большее напряжение будет на конденсаторе с меньшей электроемкостью.
На рисунке 7 представлена цепочка, состоящая из 4-ех емкостей, соединенных последовательно. На конденсаторе с наименьшей емкостью 0,3 Ф напряжение составляет 4 Вольта.
Рис. 7. Пример распределения напряжений на элементах последовательной цепи
А наименьшее напряжение 1 Вольт, находится на обкладках конденсатора с наибольшей емкостью 1,2 Ф. Общее напряжение на концах цепочки равняется 10-и Вольтам.
Заряд на конденсаторах
Зарядив одну из обкладок конденсатора, мы получим на второй его обкладке такой же (по модулю) заряд противоположного знака. Поэтому, все конденсаторы, соединенные последовательно, будут иметь одинаковые заряды на обкладках.
[large boxed { q_{1} = q_{2} = q_{text{общ}} } ]
где (large q_{1}, q_{2}left( text{Кл} right) ) – заряды, накопленные конденсаторами.
В последовательно включенной цепочке все конденсаторы обладают равными зарядами.
Рис. 8. Равенство зарядов на обкладках последовательно включенных емкостей
Выводы
- Правила, приведенные в статье, будут справедливы не только для двух, но и для любого количества включенных конденсаторов.
- Связывающие напряжения и заряды формулы для последовательно и параллельно включенных элементов, можно получить из принципа сложения емкостей и обратных емкостей, а, так же, отношения между приложенным напряжением и зарядом.
Рис. 9. Основные формулы для различных способов соединения
Положим
теперь, что участок цепи содержит
конденсатор емкости C
,
причем сопротивлением и индуктивностью
участка можно пренебречь, и посмотрим,
по какому закону будет изменяться
напряжение на концах участка в этом
случае. Обозначим напряжение между
точками а
и b
через u
и будем
считать заряд конденсатора q
и силу тока i
положительными, если они соответствуют
рис.4.
Тогда
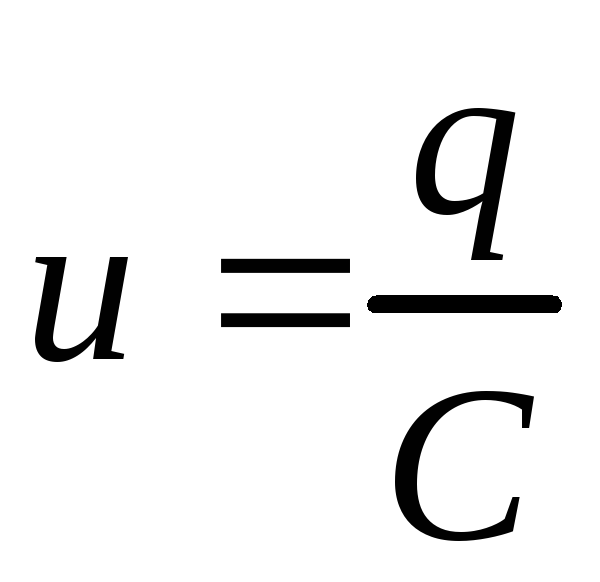
и,
следовательно,
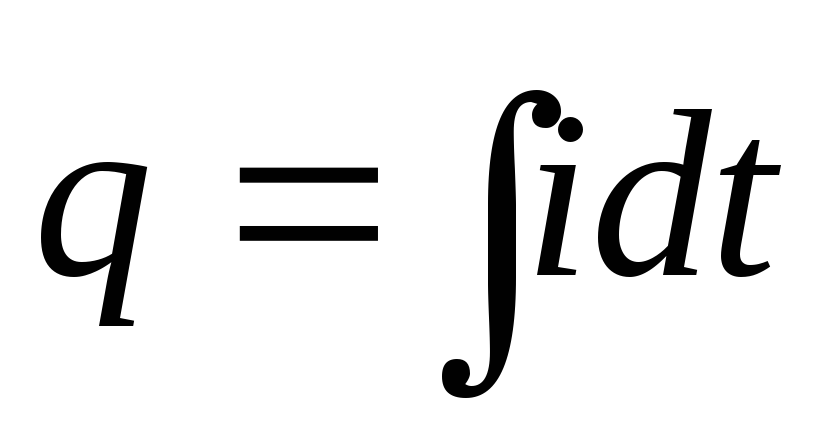

(1)
то заряд конденсатора
равен

Постоянная
интегрирования q
0
здесь обозначает произвольный постоянный
заряд конденсатора, не связанный с
колебаниями тока, и поэтому мы положим

Следовательно,

(2)
|
Рис.4. Конденсатор |
Рис.5. Зависимости |
Сравнивая
(1) и (2), мы видим, что при синусоидальных
колебаниях тока в цепи напряжение на
конденсаторе изменяется также по закону
косинуса. Однако колебания напряжения
на конденсаторе отстают по фазе от
колебаний тока на /2.
Изменения тока и напряжения во времени
изображены графически на рис.5. Полученный
результат имеет простой физический
смысл. Напряжение на конденсаторе в
какой-либо момент времени определяется
существующим зарядом конденсатора. Но
этот заряд был образован током, протекавшим
предварительно в более ранней стадии
колебаний. Поэтому и колебания напряжения
запаздывают относительно колебаний
тока.
Формула
(2) показывает, что амплитуда напряжения
на конденсаторе равна
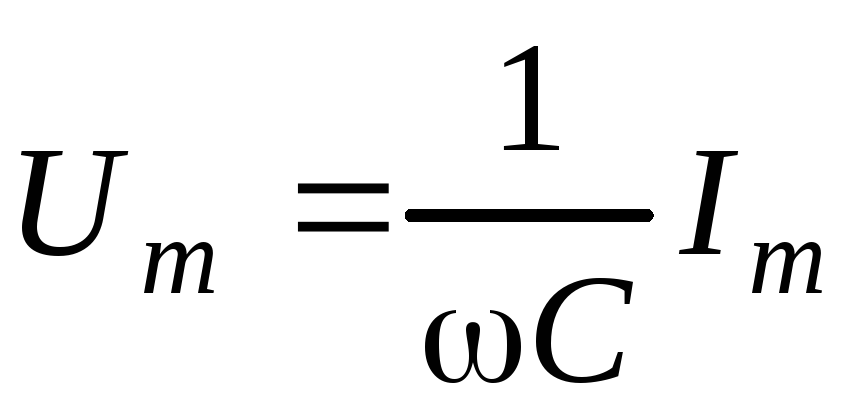
Сравнивая
это выражение с законом Ома для участка
цепи с постоянным током (
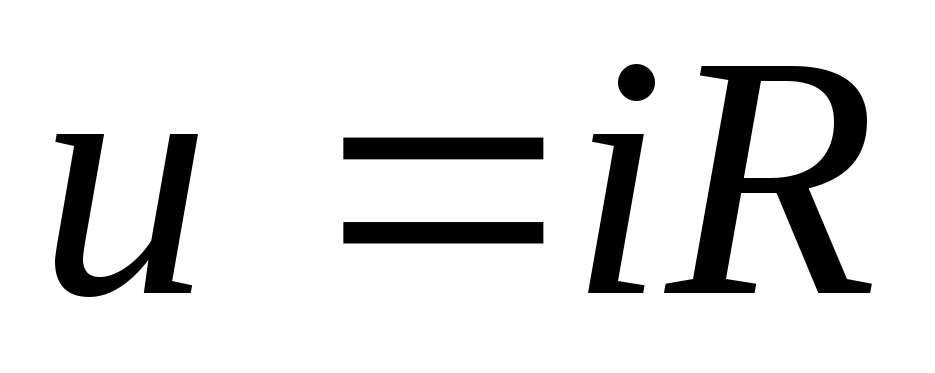
мы видим, что величина
играет
роль сопротивления участка цепи, она
получила название емкостного сопротивления.
Емкостное сопротивление зависит от
частоты и
при высоких частотах даже малые емкости
могут представлять совсем небольшое
сопротивление для переменного тока.
Важно отметить,
что емкостное сопротивление определяет
связь между амплитудными, а не мгновенными
значениями тока и напряжения.
меняется
со временем по синусоидальному закону
с удвоенной частотой. В течение времени
от 0 до T
/4
мощность
положительна, а в следующую четверть
периода ток и напряжение имеют
противоположные знаки и мощность
становится отрицательной.
Поскольку
среднее значение за период колебаний
величины
равно нулю, то средняя мощность переменного
тока на конденсаторе
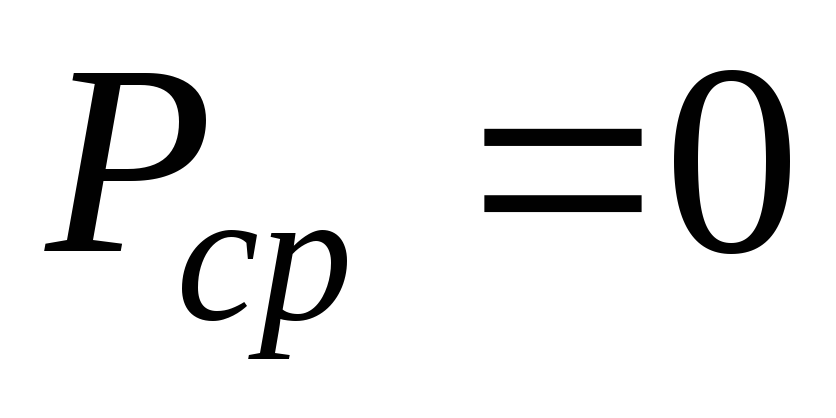
Катушка индуктивности в цепи переменного тока
Рассмотрим,
наконец, третий частный случай, когда
участок цепи содержит только индуктивность.
Обозначим по-прежнему через U
напряжение между точками а
и б
и будем считать ток I
положительным, если он направлен от а
к б
(рис.6). При наличии переменного тока в
катушке индуктивности возникнет ЭДС
самоиндукции, и поэтому мы должны
применить закон Ома для участка цепи,
содержащего эту ЭДС:

В
нашем случае R
= 0, а ЭДС самоиндукции


(3)
Если сила тока в
цепи изменяется по закону

|
Рис.6. Катушка переменного |
индуктивности |
Видно,
что колебания напряжения на индуктивности
опережают по фазе колебания тока на
/2.
Когда сила тока, возрастая, проходит
через нуль, напряжение уже достигает
максимума, после чего начинает уменьшаться;
когда сила тока становится максимальной,
напряжение проходит через нуль, и т.д.
(рис.7).
Из
(4) следует, что амплитуда напряжения
равна

и, следовательно,
величина
играет
ту же роль, что сопротивление участка
цепи. Поэтому

Индуктивное сопротивление пропорционально
частоте переменного тока, и поэтому при
очень больших частотах даже малые
индуктивности могут представлять
значительное сопротивление для переменных
токов.
Мгновенная
мощность переменного тока
также,
как и в случае идеальной емкости, меняется
со временем по синусоидальному закону
с удвоенной частотой. Очевидно, что
средняя за период мощность равна нулю.
Таким
образом, при протекании переменного
тока через идеальные емкость и
индуктивность обнаруживается ряд общих
закономерностей:
Колебания
тока и напряжения происходят в различных
фазах — сдвиг по фазе между этими
колебаниями равен /2.
Амплитуда
переменного напряжения на емкости
(индуктивности) пропорциональна
амплитуде протекающего через этот
элемент переменного тока
где
X
— реактивное (емкостное или индуктивное
сопротивление). Важно иметь в виду, что
это сопротивление связывает между собой
не мгновенные значения тока и напряжения,
а только их максимальные значения.
Реактивное сопротивление отличается
от омического (резистивного) сопротивления
еще и тем, что оно зависит от частоты
переменного тока.
На
реактивном сопротивлении не рассеивается
мощность (в среднем за период колебаний),
это означает, что, например, через
конденсатор может протекать переменный
ток очень большой амплитуды, но
тепловыделение на конденсаторе будет
отсутствовать. Это является следствием
фазового сдвига между колебаниями тока
и напряжения на реактивных элементах
цепи (индуктивности и емкости).
Резистивный
элемент, который описывается в
рассматриваемом частотном диапазоне
законом Ома для мгновенных
токов и напряжений

называют омическим
или активным сопротивлением. На активных
сопротивлениях происходит выделение
мощности.
Лабораторная работа 6
Конденсатор в цепи переменного тока
Цель работы.
Исследование зависимости проводимости конденсатора от частоты синусоидального тока. Определение емкости конденсатора и диэлектрической проницаемости вещества, заполняющего конденсатор.
Приборы и оборудование.
Плоский конденсатор, диэлектрическая пластина, генератор синусоидального напряжения, два цифровых вольтметра.
Теоретическая часть
В работе исследуется плоский конденсатор, который представляет собой две плоские проводящие пластины (обкладки), расположенные параллельно друг другу, причем заряд одной пластины q
, а другой пластины (-q
). Расстояние между пластинами d
предполагается малым по сравнению с линейными размерами пластин. В этом случае электрическое поле между пластинами можно считать однородным (рис.1), а распределение зарядов по пластинам равномерным:
, , (1)
где — разность потенциалов между пластинами – напряжение на конденсаторе, — поверхностная плотность заряда, S
— площадь пластины.
Для напряженности электрического поля в конденсаторе при помощи теоремы Гаусса можно найти
где — диэлектрическая проницаемость вещества между пластинами, — электрическая постоянная, и тогда из формул (1), (2) следует, что заряд конденсатора пропорционален приложенному к нему напряжению
Коэффициент пропорциональности
называют электроемкостью (или просто емкостью) конденсатора.
Заметим, что, строго говоря, поверхностная плотность заряда s не является постоянной по всей поверхности пластины, а увеличивается вблизи ее краев. Вблизи краев нарушается также предположение об однородности электрического поля, поэтому формулы (1), использованные при выводе (4), являются приближенными. Они выполняются тем точнее, чем меньше отношение d
к линейным размерам пластин конденсатора.
Схематически поле плоского конденсатора с учетом отмеченных выше краевых эффектов изображено на рис. 2. Как видно из рисунка, линии поля сгущаются вблизи краев конденсатора, что связано с концентрацией заряда у краев пластин. Кроме того, некоторые линии поля начинаются и заканчиваются не на внутренних, а на внешних поверхностях пластин. Это означает, что некоторая часть заряд располагается на внешних поверхностях пластин конденсатора. Заметим, что общее число линий поля на рис.1 и рис.2 одинаково, если одинаковы заряды соответствующих пластин на рис.1 и рис. 2.
Строгий расчет емкости плоского конденсатора с учетом краевых эффектов представляет собой сложную задачу. Приведем без вывода приближенную формулу, учитывающую краевые эффекты для плоского конденсатора с круглыми
пластинами:
, (5)
где — емкость конденсатора без учета краевых эффектов, r
— радиус пластины (). Второе слагаемое в (5) учитывает оттеснение заряда к краям пластин, третье слагаемое – частичное вытеснение заряда на внешние поверхности пластин.
Если в пространство между обкладками конденсатора параллельно им ввести плоскую пластину толщиной из диэлектрика с проницаемостью , то емкость конденсатора будет равна
, (6)
где C
— емкость конденсатора без диэлектрика.
Отметим, что любую пару проводников, независимо от их формы и расположения, можно считать конденсатором. И в этом случае емкостью конденсатора называют коэффициент пропорциональности между зарядом конденсатора (так называют заряд положительной обкладки, заряд другой обкладки конденсатора такой же по величине, но отрицательный) и разностью потенциалов между обкладками. Емкость конденсатора зависит от геометрических размеров обкладок, их взаимного расположения и диэлектрической проницаемости среды.
Рассмотрим теперь случай, когда конденсатор включен в цепь переменного тока. Одно из направлений тока примем за положительное (оно обозначено на рис.3 стрелкой). Обозначим через
заряд той из обкладок конденсатора, направление от которой к другой обкладке совпадает с положительным направлением тока. Напряжение между точками а
и b
обозначим через u
. Тогда
и, следовательно,
Если сила тока в цепи изменяется по закону
( — амплитуда тока, — циклическая частота), то заряд конденсатора равен
.
Постоянная интегрирования q
0 обозначает произвольный постоянный заряд конденсатора, не связанный с колебаниями тока, и поэтому мы положим . Следовательно,
. (8)
Сравнивая (7) и (8), видим, что при синусоидальных колебаниях тока в цепи колебания напряжения на конденсаторе отстают по фазе от колебаний тока на p/2. Изменения тока и напряжения во времени изображены графически на рис.4.
Формула (8) показывает, что амплитуда напряжения на конденсаторе равна
Сравнивая это выражение с законом Ома для участка цепи с постоянным током (), видим, что величина
играет роль сопротивления участка цепи, она получила название емкостного сопротивления. Емкостное сопротивление зависит от частоты w, поэтому при очень высоких частотах даже малые емкости могут представлять совсем небольшое сопротивление для переменного тока. Важно отметить, что емкостное сопротивление определяет связь между амплитудными
, а не мгновенными значениями тока и напряжения.
В цепях переменного тока обычно измеряют не амплитудные, а эффективные значения тока и напряжения:
,
.
где — частота. Это соотношение проверяется в работе экспериментально.
Постоянный ток не может существовать в цепи, содержащей конденсатор. Цепь при этом оказывается разомкнутой, так как обкладки конденсатора разделены слоем диэлектрика.
Переменный ток способен течь в цепи, содержащей конденсатор. В этом можно убедиться с помощью простого опыта.
Возьмем источники постоянного и переменного напряжения, причем постоянное напряжение на зажимах источника пусть будет равно действующему значению переменного на-пряжения. Цепь состоит из конденсатора и лампы накаливания (рис. 2.14), соединенных последовательно. При включении с помощью переключателя постоянного напряжения лампа не светится. Но при включении переменного напряжения лампа начинает светиться, если емкость конденсатора достаточно велика.
Как же переменный ток может течь по разомкнутой цепи? Здесь происходит периодическая перезарядка конденсатора под действием переменного напряжения. Ток, текущий при перезарядке, нагревает нить лампы.
Найдем, как меняется со временем сила тока в цепи, содержащей только конденсатор, если сопротивлением проводников и обкладок конденсатора можно пренебречь (рис. 2.15). + о
¦о
С
С Напряжение на конденсаторе % -U.
равно напряжению на зажимах цепи. Следовательно,
sin cof. Заряд конденсатора меняется по гармоническому закону:
q = CUm sin cof. (2.7.1)
Сила тока представляет собой производную заряда по времени. Если заряд q в формуле (2.7.1) — это заряд той пласти-ны конденсатора, которая встречается первой при выбранном направлении обхода контура, то (см. с. 64, § 2.3)
і =
Рис. 2.16
Следовательно, колебания силы тока опережают по фазе колебания напряжения на л/2 (рис. 2.16). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того как напряжение достигает максимума, сила тока становится равной нулю и т. д.
Амплитуда силы тока равна: (2.7.3)
I = U (аС.
т т Если ввести обозначение (2.7.4)
со С ЛС и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим:
U
/ =
(2.7.5)
Величину Хс, обратную произведению циклической частоты на емкость конденсатора, называют емкостным сопротивлением. Роль этой величины подобна роли активного сопротивления R в законе Ома (2.6.3). Действующее значение силы тока связано с действующим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение на участке цепи постоянного тока. Это и позволяет рассматривать величину Хс как сопротивление конденсатора переменному току — емкостное со-противление.
Чем больше емкость конденсатора, тем больше согласно формуле (2.7.3) сила тока перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Хс. Оно уменьшается с
увеличением емкости и увеличением частоты.
Это можно увидеть, если для питания цепи, изображенной на рисунке 2.14, использовать генератор переменного тока регулируемой частоты. Плавно увеличивая частоту переменного тока, можно наблюдать увеличение накала лампы. Оно вызвано увеличением силы тока за счет уменьшения емкостного сопротивления конденсатора.
Если на один вход двухлучевого осциллографа подать напряжение с конденсатора, а на другой вход — напряжение, мгновенное значение которого пропорционально силе тока в цепи (это напряжение снимается с активного сопротивления), то на экране будут одновременно наблюдаться осциллограммы (временные развертки) обоих колебаний: напряжения и силы тока. Такие наблюдения подтверждают полученный выше вывод о том, что колебания силы тока в цепи конденсатора сдвинуты по фазе относительно колебаний напряжения на л/2, как это показано на рисунке 2.16.
Найди разность потенциалов между точками (A) и (B) батареи конденсаторов известной ёмкости, подключённой к источнику постоянного тока с напряжением (U) (рис. (1)).
Рис. (1). Физическая ситуация задачи
1. Физическая модель задачи:
— конденсаторы (C_1) и (C_2) соединены последовательно (Rightarrow) заряд на каждом их них равен (Q_{1});
— конденсаторы (C_3) и (C_4) соединены последовательно (Rightarrow) заряд на каждом их них равен (Q_{2});
— левые обкладки конденсаторов (C_{1}) и (C_{3}) соединены с положительной клеммой источника тока (Rightarrow) их заряд положительный;
— правые обкладки конденсаторов (C_{2}) и (C_{4}) соединены с отрицательной клеммой источника тока (Rightarrow) их заряд отрицательный;
— введём дополнительные обозначения узлов (a) и (b) (рис. (2)).
Рис. (2). Физическая модель задачи
2. Физические законы:
— разность потенциалов (varphi_a) и (varphi_b):
(varphi_a — varphi_b=U); ((1))
— ёмкость конденсатора (C_{1}):
(C_{1}=frac{Q_{1}}{varphi_a-varphi_A}); ((2))
— ёмкость конденсатора (C_{2}):
(C_{2}=frac{Q_{1}}{varphi_A-varphi_b}); ((3))
— ёмкость конденсатора (C_{3}):
(C_{3}=frac{Q_{2}}{varphi_a-varphi_B}); ((4))
— ёмкость конденсатора (C_{4}):
(C_{4}=frac{Q_{2}}{varphi_B-varphi_b}). ((5))
3. Математическое решение задачи:
— выражаем разности потенциалов из формул ((2))–((5)):
(varphi_a-varphi_A=frac{Q_1}{C_1}); ((6))
(varphi_A-varphi_b=frac{Q_1}{C_2}); ((7))
(varphi_a-varphi_B=frac{Q_2}{C_3}); ((8))
(varphi_B-varphi_b=frac{Q_2}{C_4}); ((9))
— складываем левые и правые части уравнений ((6)) и ((7)) с учётом формулы ((1)):
(U=frac{Q_{1}}{C_1}+frac{Q_1}{C_{2}}); ((10))
— складываем левые и правые части уравнений ((8)) и ((9)) с учётом формулы ((1)):
(U=frac{Q_{2}}{C_3}+frac{Q_2}{C_{4}}); ((11))
— выражаем заряды (Q_1) и (Q_2) из формул ((10)) и ((11)) соответственно:
(Q_{1}=frac{C_1 C_2}{(C_1+C_2)}U); ((12))
(Q_{2}=frac{C_3 C_4}{(C_3+C_4)}U); ((13))
— подставляем формулы ((12)) и ((13)) в ((6)) и ((8)) соответственно (или в ((7)) и ((9)):
(varphi_a-varphi_A=frac{C_2 U}{C_1+C_2}); ((14))
(varphi_a-varphi_B=frac{C_4 U}{C_3+C_4}); ((15))
— вычитаем левые и правые части формул ((15)) и ((14)) друг из друга и находим искомую разность потенциалов:
(varphi_A-varphi_B=left(frac{C_4}{C_3+C_4}-frac{C_2}{C_1+C_2}right) U;) ((16))
— проверяем размерность формулы ((16)):
(varphi_A-varphi_B=left( frac{Ф}{Ф}-frac{Ф}{Ф}right)В=В).
Источники:
Рис. 1. Физическая ситуация задачи. © ЯКласс.
Рис. 2. Физическая модель задачи. © ЯКласс.

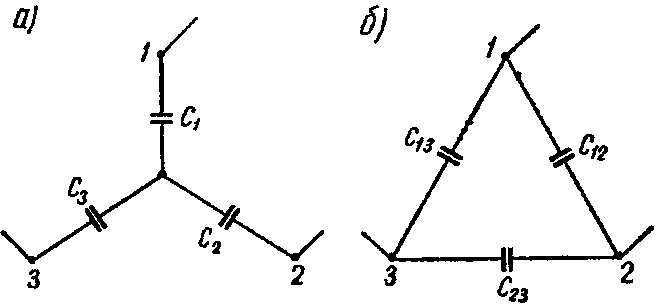
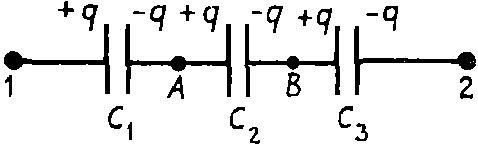
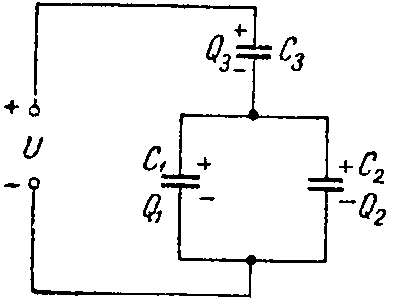
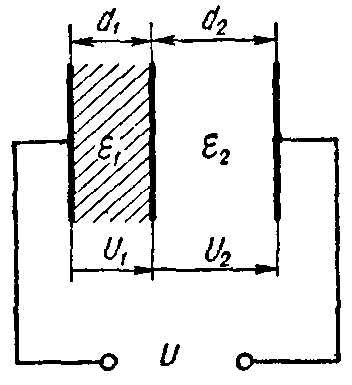
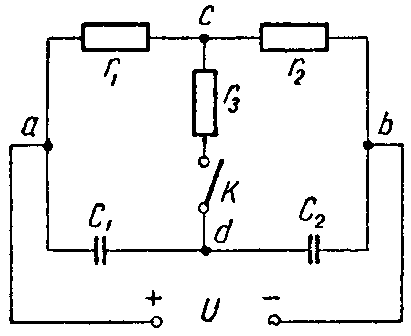
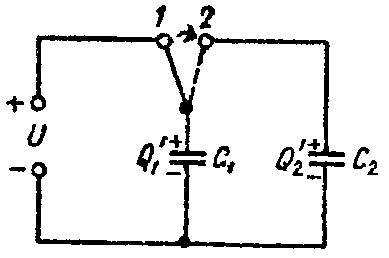
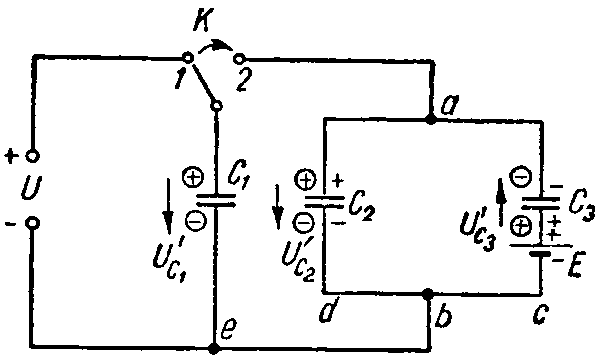
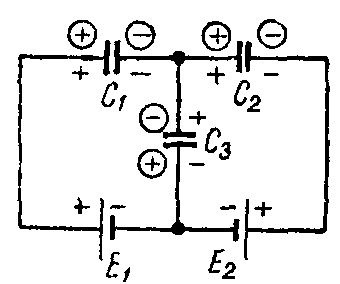
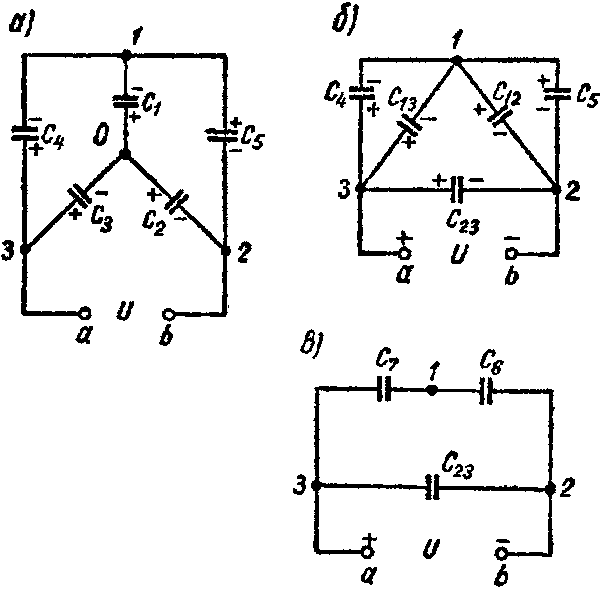
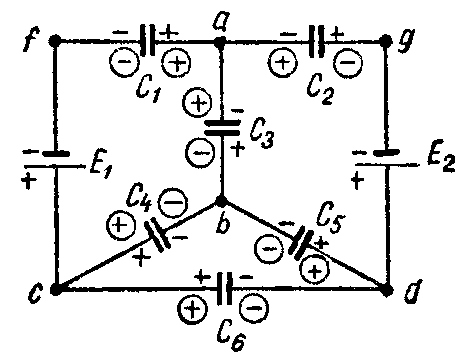
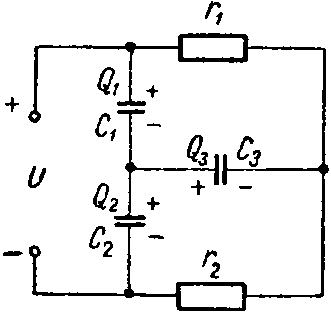
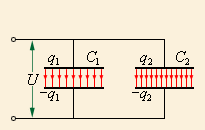
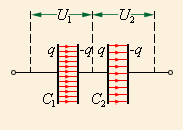
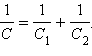











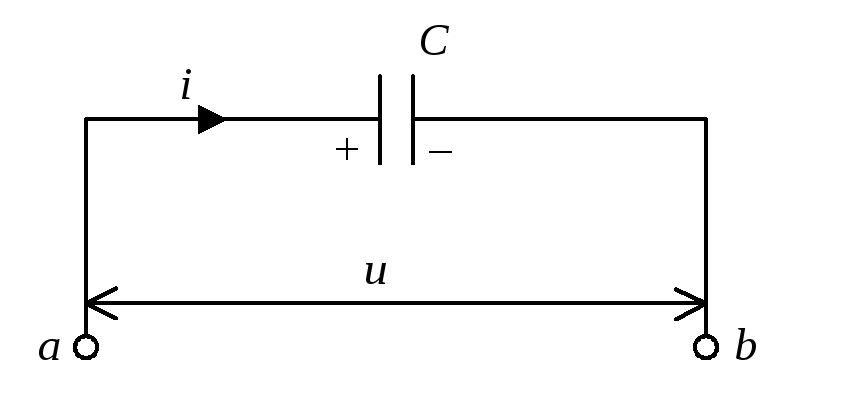

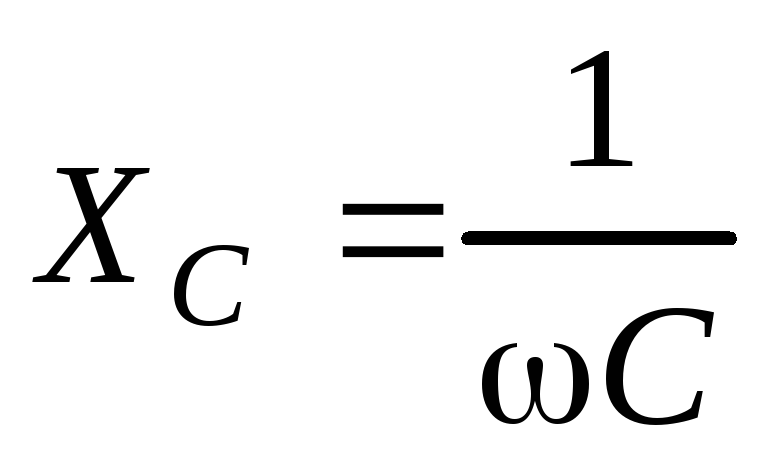

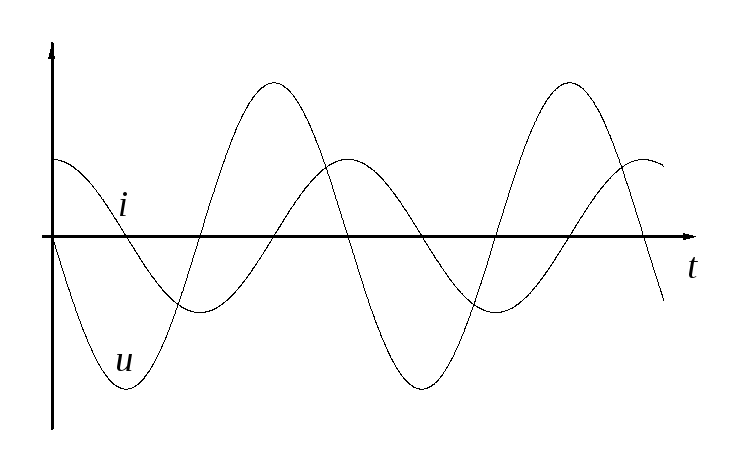 Рис.7.
Рис.7.


