Как найти напряжение на последовательном участке цепи

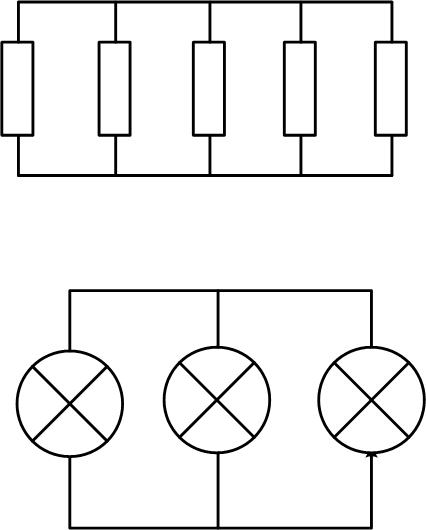
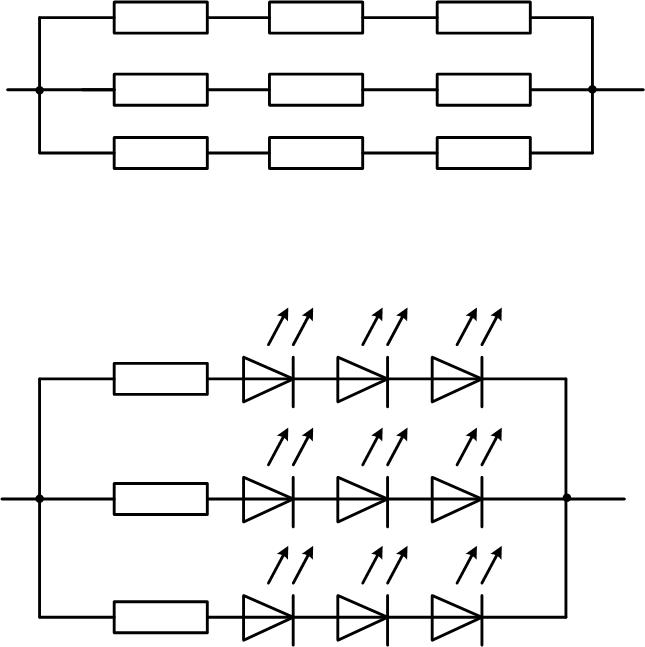
Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей — проводников.

Для начала давайте вспомним, что такое проводник? Проводник — это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:

ρ – это удельное сопротивление, Ом × м

R – сопротивление проводника, Ом

S – площадь поперечного сечения, м²

l – длина проводника, м

Более подробно об этом я писал здесь.

Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.

Последовательное соединение проводников

Сопротивление при последовательном соединении проводников

Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

Пример

У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.

Решение

R_общее =R₁ + R₂ + R₃ = 3+5+2=10 Ом.

То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор R_AB .

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:

Сила тока через последовательное соединение проводников

Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор R_AB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R₁ , R₂ , R₃ , то получится, что через них течет та же самая сила тока, которая текла через резистор R_AB .

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R₁ течет такая же сила тока, как и через резистор R₂ и такая же сила тока течет через резистор R₃ .

Напряжение при последовательном соединении проводников

Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?

Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на  любом резисторе. Давайте так и сделаем.

Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае R_AB =R₁ + R₂ + R₃ = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.

Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения U_R1 , U_R2 , U_R3  . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.

Следовательно,

U_R1 = IR₁ =1×2=2 Вольта

U_R2 = IR₂ = 1×3=3 Вольта

U_R3 = IR₃ =1×5=5 Вольт

Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.

Получается

U=U_R1+U_R2+U_R3

Мы получили самый простой делитель напряжения.

Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.

Параллельное соединение проводников

Параллельное соединение проводников выглядит вот так.

Ну что, думаю, начнем с сопротивления.

Сопротивление при параллельном соединении проводников

Давайте пометим клеммы как А и В

В этом случае общее сопротивление R_AB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников

Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.

Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников

Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.

Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что

I₁ = U/R₁

I₂ = U/R₂

I₃ = U/R₃

Если бы у нас еще были резисторы, соединенные параллельно, то для них

I_n = U/R_n

В этом случае, сила тока в цепи будет равна:

Задача

Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Решение

Воспользуемся формулами, которые приводили выше.

I₁ = U/R₁

I₂ = U/R₂

I₃ = U/R₃

Если бы у нас еще были резисторы, соединенные параллельно, то для них

I_n = U/R_n

Следовательно,

I₁ = U/R₁ = 10/2=5 Ампер

I₂ = U/R₂ = 10/5=2 Ампера

I₃ = U/R₃ = 10/10=1 Ампер

Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи

I=I₁ + I₂ + I₃ = 5+2+1=8 Ампер

2-ой способ найти I

I=U/R_общее

Чтобы найти R_общее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них — «калькулятор резисторов«. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть R_общее = 1,25 Ом.

I=U/R_общее = 10/1,25=8 Ампер.

Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.

Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.

Подробное объяснение на видео:

Прикольный набор радиолюбителя по ссылке <<<

Похожие статьи по теме «последовательное и параллельное соединение»

Закон Ома

Проводник (электрический проводник)

Что такое резистор

Делитель напряжения

Делитель тока

Что такое напряжение

Что такое сила тока

Вы уже знаете, что есть два типа соединения элементов электрической цепи: последовательный и параллельный. Последовательно мы подключали в цепь амперметр, а параллельно — вольтметр.

На данном уроке мы более подробно рассмотрим последовательное соединение. Мы будем использовать сразу несколько потребителей электроэнергии и узнаем, каким закономерностям подчиняются уже известные нам величины (сила тока, сопротивление и напряжение) при таком соединении элементов в цепи.  

Последовательное включение элементов в электрическую цепь

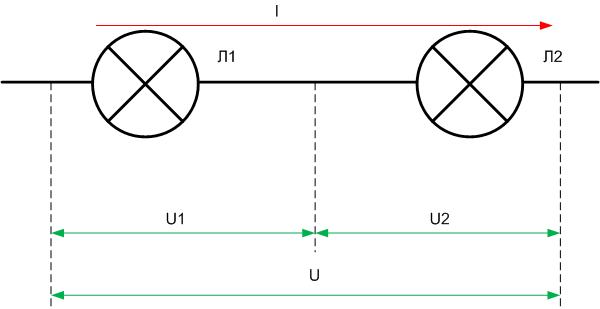
Соберем электрическую цепь. Последовательно соединим две электролампы, два источника тока и ключа (рисунок 1).

Обратите внимание, что при таком подключении аккумуляторов соблюдается определенная полярность подключения: провод, идущий от положительного полюса одного аккумулятора необходимо соединить с отрицательным полюсом другого аккумулятора. И, наоборот, провод идущий от отрицательного полюса одного аккумулятора соединяется с положительным полюсом другого.

Если в такой цепи попытаться выключить только одну лампу, то погаснет и вторая.

Схема этой электрической цепи показана на рисунке 2.

В такую цепь мы можем подключить еще несколько ламп или некоторое количество других потребителей электроэнергии. Поэтому все закономерности, которые мы рассмотрим далее, будут справедливы для любого количества последовательно подключенных в цепь проводников.

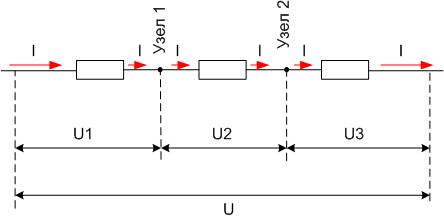
Сила тока в цепи при последовательном соединении проводников

При изучении силы тока мы измеряли ее на различных участках электрической цепи (рисунок 3). Полученные с помощью амперметра значения силы тока были одинаковы.

При этом все элементы у нас были соединены последовательно. Сделаем вывод.

При последовательном соединении сила тока в любых частях цепи одна и та же:
$I = I_1 = I_2 = … = I_n$.

Сопротивление в цепи при последовательном соединении проводников

Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?

Давайте порассуждаем. В цепи был один проводник с определенным сопротивлением. Мы последовательно подключаем второй. Представим эти два проводника в виде одного элемента цепи. Тогда получается, что, подсоединив второй проводник, мы увеличили длину первого.

Сопротивление же зависит от длины проводника. Поэтому суммарное сопротивление цепи будет точно больше сопротивления одного проводника.

Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):
$R = R_1 + R_2 + … + R_n$.

На схемах электрических цепей последовательное соединение нескольких проводников изображается так, как показано на рисунке 4.

Напряжение в цепи при последовательном соединении проводников

Используя закон Ома для участка цепи, мы можем найти напряжение и на концах этих участков:
$U_1 = IR_1$,
$U_2 = IR_2$,
…
$U_n = IR_n$.

Получается, что напряжение будет тем больше, чем больше сопротивление на участках цепи. Сила тока же везде будет одинакова.

Как найти напряжение участка цепи, состоящего из последовательно соединенных проводников, зная напряжение на каждом?

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
$U = U_1 + U_2 + … + U_n$.

Полное напряжение в цепи и закон сохранения энергии

Давайте вспомним, что напряжение определяется работой электрического тока. Эта работа совершается при прохождении по участку цепи электрического заряда, равного $1 space Кл$:
$U = frac{A}{q}$.

За счет чего совершается эта работа? Мы уже говорили, что электрическое поле обладает некоторой энергией. Именно за счет нее и идет совершение работы.

Такая работа совершается на каждом участке цепи, которую мы рассматриваем. Пользуясь законом сохранения энергии, мы можем сделать следующий вывод.

Энергия, израсходованная на всей цепи, равна сумме энергий, которые расходуются на отдельных ее участках (проводниках).

Пример задачи

Два проводника сопротивлением $R_1 = 2 space Ом$ и $R_2 = 3 space Ом$ соединены последовательно. Сила тока в цепи равна $1 space А$. Определите сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.

Так как проводники соединены последовательно, мы будем использовать формулы, полученные на данном уроке.

Дано:
$R_1 = 2 space Ом$
$R_2 = 3 space Ом$
$I = 1 space А$

$R — ?$
$U_1 — ?$
$U_2 — ?$
$U — ?$

Решение:

Общее сопротивление цепи будет равно сумме сопротивлений составляющих ее проводников:
$R = R_1 + R_2$.

Рассчитаем его:
$R = 2 space Ом + 3 space Ом = 5 space Ом$.

Сила тока на всех участках цепи будет одинакова и равна $1 space А$.

Запишем закон Ома для участка цепи с первым проводником и выразим из него напряжение на концах первого проводника:
$I = frac{U_1}{R_1}$,
$U_1 = IR_1$.

Рассчитаем его:
$U_1 = 1 space А cdot 2 space Ом = 2 space В$.

Так же рассчитаем напряжение на концах второго проводника:
$I = frac{U_2}{R_2}$,
$U_2 = IR_2$,
$U_2 = 1 space А cdot 3 space Ом = 3 space В$.

При последовательном соединении проводников полное напряжение в цепи мы можем рассчитать двумя способами.

Способ №1
Напряжение на всей цепи равно сумме напряжений на концах проводников в этой цепи:
$U = U_1 + U_2$,
$U = 2 space В + 3 space В = 5 space В$.

Способ №2
Мы уже знаем общее сопротивление двух проводников. Получается, что эти два проводника мы можем представить как один целый. Используем закон Ома для участка цепи:
$I = frac{U}{R}$,
$U = IR$,
$U = 1 space А cdot 5 space Ом = 5 space В$.

Ответ: $R = 5 space Ом$, $U_1 = 2 space В$, $U_2 = 3 space В$, $U = 5 space В$.

Упражнения

Дано:
$R_1 = 4 space Ом$
$R_2 = 6 space Ом$

$I = 0.2 space А$

$U_1 — ?$
$U_2 — ?$
$U — ?$

Показать решение и ответ

Скрыть

Такие лампы можно соединить последовательно в одну цепь. Главное, чтобы их суммарное напряжение не превышало общее. Рассчитаем количество таких ламп, которое мы можем включить в цепь.

Дано:
$U = 3000 space В$
$U_1 = 50 space В$

$n — ?$

Показать решение и ответ

Скрыть

Дано:

$U = 220 space В$

$U_1 — ?$
$U_2 — ?$

Показать решение и ответ

Скрыть

Схема такой цепи изображена на рисунке 5.

Дано:
$U = 6 space В$
$R_1 = 13.5 space Ом$
$R_2 = 3 space Ом$
$R_3 = 2 space Ом$

$I — ?$
$U_1 — ?$
$U_2 — ?$
$U_3 — ?$

Показать решение и ответ

Скрыть

• 

Напряжение при параллельном и последовательном соединении

Напряжение при параллельном и последовательном соединении: в первом случае одинаково для всей цепи, а во втором – равно сумме значений для каждого потребителя.

Напряжение при параллельном соединении

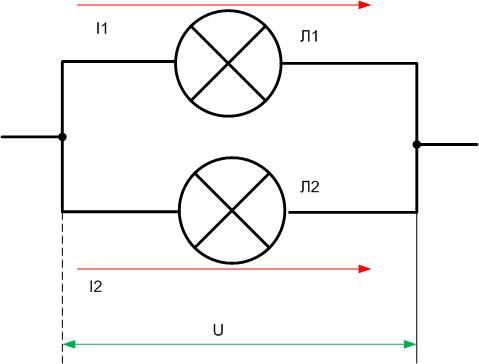
В параллельном соединении все ветви потребителей энергии сходятся в двух точках цепи, что изображено на схеме.

При таком соединении напряжение U₁, U₂ и U₃ для трех компонентов цепи одинаково. То есть общее равно напряжению для любой ветки цепи:

U = U₁ = U₂ = … = U_n

Напряжение при последовательном соединении

При последовательном соединении потребители энергии соединены друг с другом в виде цепочки, как показано в схематическом рисунке.

При последовательном соединении общее напряжение будет равно сумме значений для каждого ее звена:

U = U₁ + U₂ + … + U_n

Общие сведения о напряжении

Напряжение обозначается буквой U. Единица в системе СИ – Вольт. Измеряется специальным прибором – вольтметром. Формула напряжения:

U = I*R,

где I – сила тока, А;

R – сопротивление проводника, Ом.

Примеры вычисления напряжения при параллельном и последовательном соединении

Возьмем для примера цепь с двумя резисторами. Если их соединение параллельно, на вольтметре будут показаны одни и те же значения для любого участка цепи:

U = U1 = U2 = 10 Вольт

При последовательном соединении общее напряжение равно сумме показателей обоих приборов, т.е.

U = 10 + 10 = 20 Вольт.

Применение двух типов соединений на практике

Так как при параллельном соединении напряжение для любой ветки цепи одинаково, его часто применяют на практике. Например, чтобы включить сразу несколько приборов, которым требуется одинаковое напряжение, а работа каждого не зависит от остальных приборов: холодильник, утюг, микроволновая печь и другие. Выключение утюга или холодильника никак не скажется на работе микроволновки. При последовательном соединении выключение одного из участников цепи ведет к обесточиванию всех приборов. Например: в елочной гирлянде при перегорании одной лампочки перестает работать вся гирлянда.

При разработке электрических цепей применяется последовательное и параллельное соединение проводников. Умение анализировать (как количественно, так и качественно) и рассчитывать такие схемы является базовым принципом знаний электротехники.

Виды соединений электрических проводников

Основными схемами подключения являются параллельное и последовательное соединение. Также существуют комбинации из этих двух включений.

Последовательное

При последовательном (в зарубежной терминологии serial) соединении выводы элементов соединяются так, чтобы получилась цепочка. Один вывод устройства подключается к одному соседнему звену, а второй – к другому, с противоположной стороны.

Параллельное

При параллельном (parallel) включении одноименные выводы элементов цепи соединяются между собой. Практический пример – лампы в многорожковой люстре или повторители светового сигнала поворота в автомобиле.

Смешанное

В одной цепи схема подключения может быть комбинированной – serial+parallel. Часть элементов подключена в параллель, образуя звенья. Эти звенья могут быть включены в последовательную цепочку. Или наоборот – последовательные цепи включаются параллельно.

Как вычисляются напряжение, сила тока и электрическая мощность в зависимости от подключения

Параметры электрической цепи рассчитываются по-разному в зависимости от типа подключения. Чтобы разобраться, какова будет сила тока, проходящего через каждое сопротивление, можно воспользоваться первым законом Кирхгофа. Одна из его формулировок гласит, что алгебраическая сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла. Остальные зависимости будут вытекать из данного рассуждения.

При параллельном соединении

Если рассмотреть параллельное соединение, например, трех резисторов, то можно отметить, что втекающий ток I в узле 1 распадается на три ветви I₁, I₂, I₃, причем Кирхгоф утверждает, что их сумма I₁+ I₂+ I₃ = I. В узле 2 все токи стекаются в один ток, и снова I= I₁+ I₂+ I₃.

Очевидно, что напряжение на каждом резисторе одинаково и равно U, следовательно, по закону Ома:

• I₁=U/R₁;
• I₂=U/R₂;
• I₃=U/R₃;
• I=U/R_общ.

Отсюда U/R_общ= U/R₁+ U/R₂+ U/R₃, после сокращения обеих частей на U получается формула для нахождения общего сопротивления при параллельном соединении резисторов:

1/R_общ= 1/R₁+ 1/R₂+ 1/R_3.

Отсюда следует, что при параллельном соединении общее сопротивление будет меньше наименьшего сопротивления в наборе. При соединении двух резисторов формула принимает вид R_общ=R₁* R₂/(R₁+ R₂).

Также из равенства I=U/R₁+U/R₂+U/R₃ следует, что токи через параллельно включенные резисторы распределяются обратно пропорционально значениям их сопротивлений – чем выше сопротивление, тем ниже ток, и наоборот. Если все резисторы имеют одинаковый номинал, то ток, текущий через каждый из них, находится делением общего тока на количество сопротивлений. Если элементов в сборке три, то через каждый течет треть общего тока, а если параллельно включены n одинаковых резисторов, то через каждый протекает I/n.

Так как электрическая мощность равна P=U*I, а напряжение на каждом резисторе равно, то мощность, выделяемая на каждом элементе, распределяется пропорционально току и обратно пропорционально сопротивлению резистора. Если все элементы одинаковы, то и мощность на них будет рассеиваться одинаковая.

Для наглядности видео.

При последовательном соединении

Если рассматривать последовательную цепь из трех элементов, можно заметить, что ток, втекающий в узел 1 будет равен вытекающему. В узле 2 выполняется то же самое соотношение и так до бесконечности.

Отсюда сила тока в последовательном соединении будет одинакова для любого элемента и равна I. Напряжение, приложенное к цепи и равное I*R, распределится между резисторами:

U=U₁+U₂+U₃=I*R₁+I*R₂+I*R₃ = I* R_общ

После сокращения на I можно найти общее сопротивление цепи. Оно равно сумме составляющих, и общее значение сопротивления будет выше сопротивления любого элемента:

R_общ=R₁+R₂+R₃

Очевидно, что падение напряжения в последовательной цепи прямо пропорционально сопротивлению каждого элемента – чем выше сопротивление, тем выше на нем напряжение. Точно так же, эти соотношения выполняются для цепи из n элементов.

Примеры расчетов

В качестве практических примеров можно рассмотреть несколько вариантов расчетов параметров цепи в разных схемах соединения.

Для резисторов

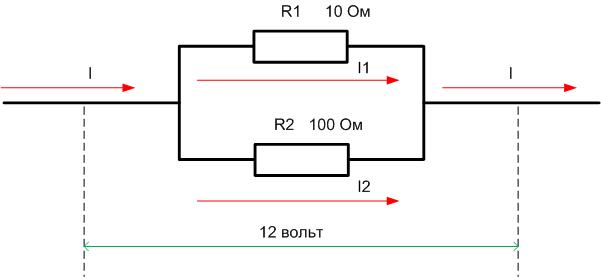
Самым простым примером расчета будет цепь из двух сопротивлений – 10 Ом и 100 Ом, соединенных в цепочку. К цепи приложено 12 вольт.

Сначала надо найти R_общ, оно равно сумме R₁ и R₂. R_общ=100+10=110 Ом. Отсюда ток в цепи I=U/R=12/110=0,109 ампер. Падение на каждом элементе можно вычислить исходя из равенств U₁=I*R₁ и U₂=I*R₂. Отсюда U₁=1,1 В, а U₂=10,9 В. Очевидно, что U₁/U₂=R₁/R₂. На первом элементе будет рассеиваться мощность P₁=U₁*I=1,1*0,109=0,12 ватт (для практики подойдет стандартный компонент на 0,125 ватт), а на втором – P₂=U₂*I=10,9*0,109=1,19 ватт (для практической реализации понадобится двухваттник).

Если соединить эти же два резистора параллельно и подать то же самое напряжение, то параметры распределятся по-другому.

Сначала надо определить R_общ=R₁*R₂/(R₁+R₂)=110*10/(110+10)=1100/120=9,17 Ом (меньше наименьшего значения в 10 Ом). Общий ток составит I=U/Rобщ=12/9,17=1,31 ампер. Через первый элемент потечет I₁=U/R₁=12/10=1,2 ампер, через второй I₂=U/R₂=12/100=0,12. Очевидно, что I₁+I₂=I (с учетом погрешностей округления). Мощности потребуются такие:

• P₁=I₁*U=1,2*12=14,2 ватт;
• P₂=I₂*U=0,12*12=1,42 ватт.

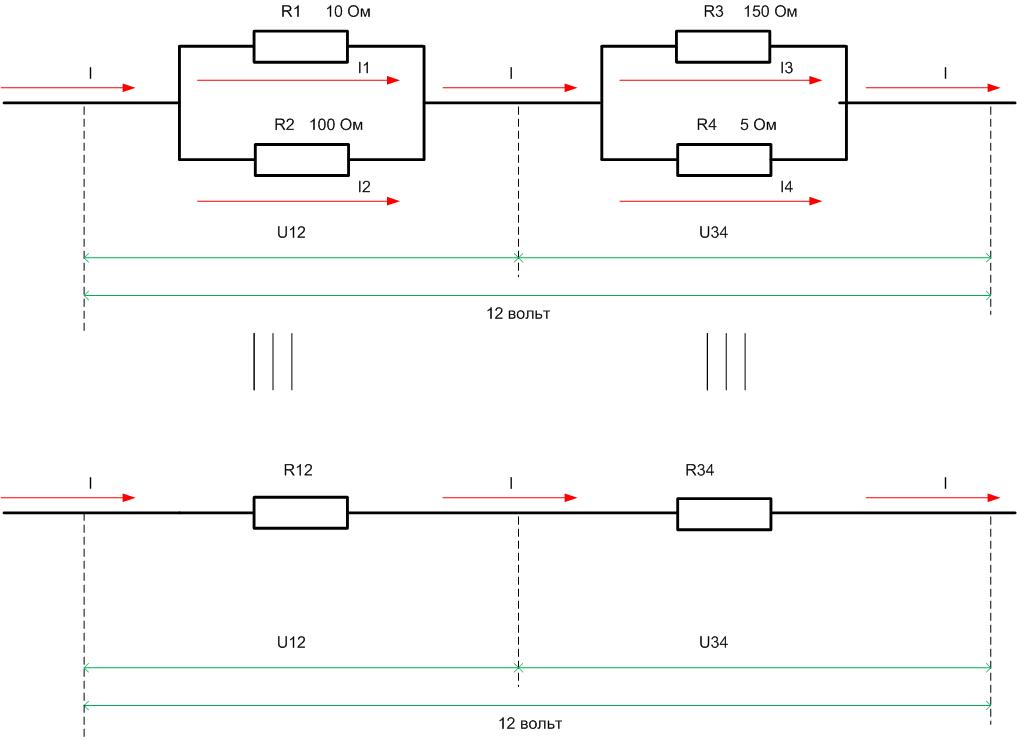
Если имеется смешанное соединение элементов, надо сначала преобразовать схему к однотипному виду – параллельному или последовательному. Пусть имеется схема следующего вида.

В данном случае удобно заменить параллельную сборку R₁ и R₂ на резистор с эквивалентным сопротивлением R₁₂, а R₃ и R₄ – на R₃₄. Сначала находится R₁₂=R₁*R₂/(R₁+R₂)=9,17 Ом. Тем же способом рассчитывается R₃₄=150*5/(150+5)=4,8 Ом. Тогда общее сопротивление эквивалентной цепи будет равно R₁₂+R₃₄=9,17+4,8=13,97 Ом.

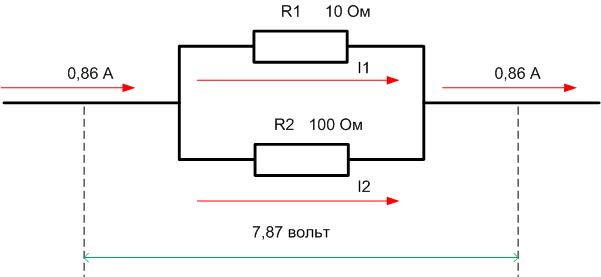
Отсюда I=U/R=12/13,97=0,86 ампер. На “гирлянде» R₁R₂ падает U₁₂=I*R₁₂=0,86*9,17=7,87 вольт, а на R₃R₄ падение составит U₃₄= I*R₃₄=0,86*4,8=4,13 вольт. Дальше надо вернуться к исходной схеме и рассмотреть отдельно участок схемы R₁R₂ с найденными параметрами.

Отсюда I₁=U/R₁=7,87/10=0,787 ампер, I₂=U/R₂=7,87/100=0,0787 ампер. По мощностям – P₁=U*I₁=7,87*0,787=6,2 ватт, P₂= U*I₂=7,87*0,0787=0,62 ватт.

Аналогично рассчитывается и участок, содержащий элементы R₃R₄.

Для лампочек

Точно такими же способами можно рассчитать параметры цепи, состоящей из двух или более лампочек накаливания – на практике с такой ситуацией можно столкнуться чаще. Но есть две проблемы. Первая из них – на лампочках и в технических данных на них не указывается сопротивление нити. Его придется пересчитывать исходя из номинального напряжения и мощности. Так как P=U*I, а I=U*R, то P=U²/R, а R=U²/P. Так, для 10-ваттной лампочки на 12 вольт сопротивление нити будет равно 12²/10=144/10=14,4 Ом. Можно рассчитать характеристики цепи для двух последовательно и параллельно соединенных лампочек.

В первом случае ток, текущий через каждую лампу будет общим, и равным I=U/Rобщ=12/(14,4+14,4)=12/28,8=0,42 А. На каждой лампе упадет U/2=6 вольт. А электрическая мощность каждого элемента составит 0,42*6=2,5 Вт, что составляет ¼ от номинала лампочки. Такое уменьшение произошло из-за двукратного снижения тока и двукратного снижения напряжения. Естественно, лампочки будут светиться далеко не в полный накал. Чтобы довести яркость свечения до нормальной, придется вдвое увеличивать напряжение, что одновременно вдвое увеличит ток.

Если лампочки соединить в параллель, то на каждой из них упадет номинальный уровень в 12 вольт. Через каждый элемент потечет I=U/R= 12/14,4=0,83 А, а мощность на каждой лампочке будет равна P=U*I=12*0,83=10 ватт, то есть, номинал. И каждая нить будет светить в полный накал. Но вся цепь будет потреблять 20 ватт и через нее потечет 0,83*2=1,66 А, что вдвое больше значения для одной лампы.

Есть и вторая проблема. В общем случае сопротивление зависит от тока и приложенного напряжения, но у ламп накаливания эта зависимость выражена ярко. Нить в холодном состоянии имеет низкое сопротивление, а номинального значения достигает при прогреве в номинальном режиме. Поэтому данные выше расчеты верны лишь для штатного напряжения 12 вольт. В других условиях характеристики лампы будут другими, и, по большому счету, расчет для параллельного случая неточен – сопротивление нити будет меньше 14,4 Ом. Зато это свойство позволяет применять лампу в качестве стабилизатора тока – при увеличении его значения нить нагреется, сопротивление вырастет, ток упадет примерно до прежнего уровня. При его уменьшении произойдет обратный процесс со снижением уровня накала нити лампочки.

Рекомендуем посмотреть видео урок «Просто физика»

Для светодиодов

Еще сложнее ситуация со светодиодами. В отличие от лампочек они стабилизируют напряжение, причем не всегда, а только после открывания. Иными словами, сначала при росте напряжения на последовательной цепочке (LED+резистор), она ведет себя согласно закону Ома. После того, как светодиод открылся (и начал светиться), увеличение падения на нем прекратилось, и рост напряжения на цепочке ведет к росту тока и увеличению U на резисторе. На полупроводниковом приборе напряжение остается стабильным (в зависимости от технологии изготовления – от 1,2 до 3 вольт или выше), хотя ток через него также растет.

По мере освоения приемов расчета можно научиться анализировать все более сложные схемы, содержащие как параллельное, так и последовательное подключение элементов. Потом можно переходить к следующему этапу – анализ и расчет устройств, содержащих реактивные (а впоследствии – и нелинейные) компоненты.

Во многих электрических схемах мы можем обнаружить последовательное и параллельное соединение резисторов. Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление.

Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи.

Последовательное соединение резисторов

На рисунке ниже, резисторы R1, R2 и R3 связаны друг с другом последовательно между точками А и В с общим током I, который протекает через них.

Эквивалентное сопротивление нескольких последовательно соединенных резисторов можно определить по следующей формуле:

R = R1 + R2 + R3

То есть, в нашем случае общее сопротивление цепи будет равно:

R = R1 + R2 + R3 = 1 кОм + 2 кОм + 6 кОм = 9 кОм

Таким образом, мы можем заменить эти три резистора всего лишь одним «эквивалентным» резистором, который будет иметь значение 9 кОм.

Там, где четыре, пять или более резисторов связаны вместе в последовательную цепь, общее или эквивалентное сопротивление всей цепи так же будет равно сумме сопротивлений отдельных резисторов.

Следует отметить, что общее сопротивление любых двух или более резисторов, соединенных последовательно всегда будет больше, чем самое большое сопротивление резистора входящего в эту цепь. В приведенном выше примере R = 9 кОм, тогда как наибольшее значение резистора только 6 кОм (R3).

Блок питания 0…30В/3A

Набор для сборки регулируемого блока питания…

Напряжение на каждом из резисторов, соединенных последовательно, подчинено другому правилу, нежели протекающий ток. Как известно, из приведенной выше схемы, что общее напряжение питания на резисторах равно сумме разности потенциала на каждом из них:

Используя закон Ома для участка цепи, напряжение на отдельных резисторов может быть вычислена следующим образом:

В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи, нашем примере это 9В.

В частности, ряд резисторов, соединенных последовательно, можно рассматривать как делитель напряжения:

Пример № 1

Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:

Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:

Пример № 2

Необходимо рассчитать падение напряжения на выводах «А» и «В»:

а) без подключенного резистора R3

б) с подключенным резистором R3

Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью потенциометра установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.

Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) — то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R).