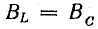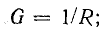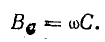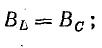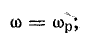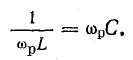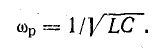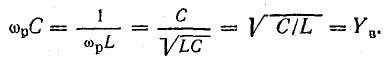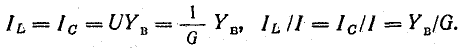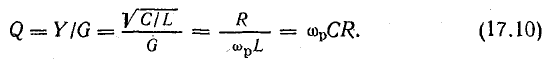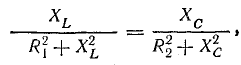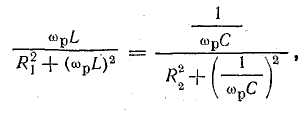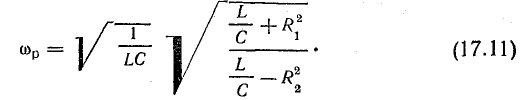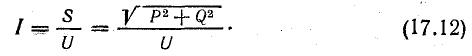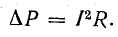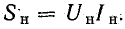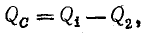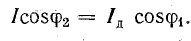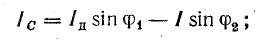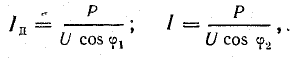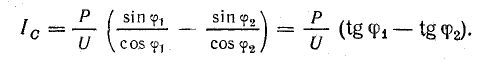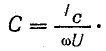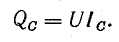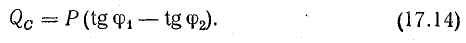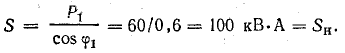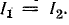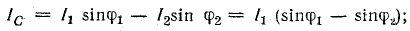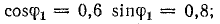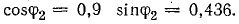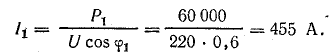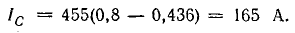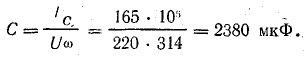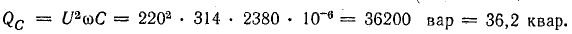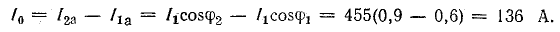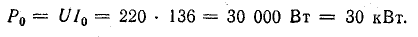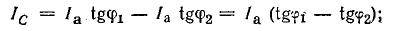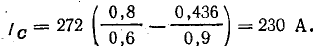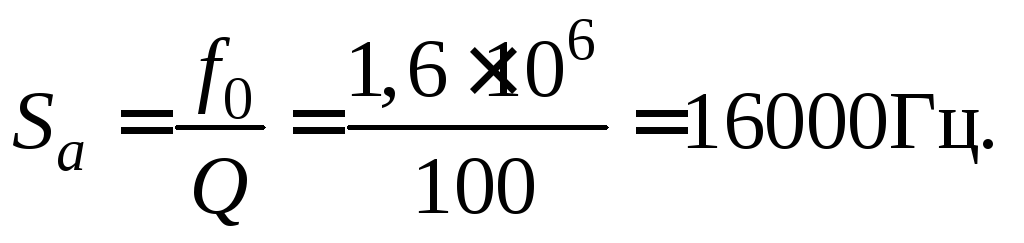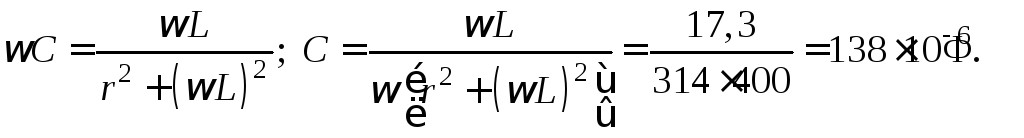Как найти напряжение при резонансе токов

Резонанс напряжений и резонанс токов

В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений и резонанс токов.

Резонанс напряжений

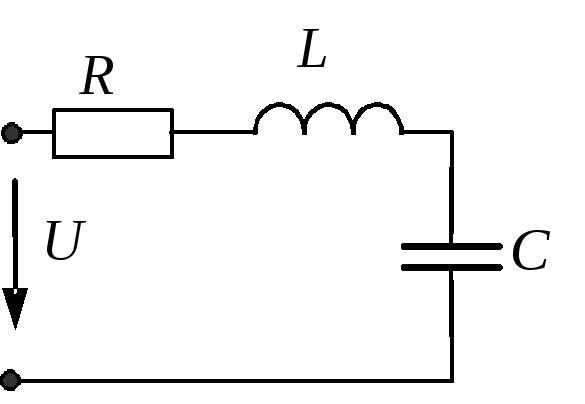
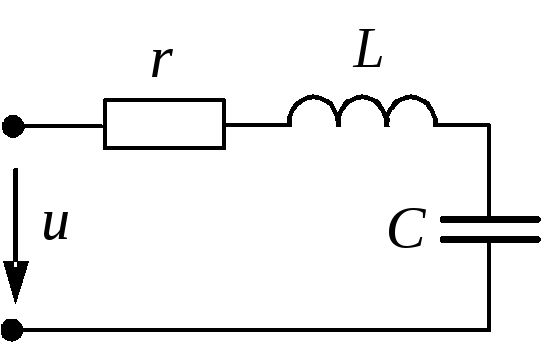
Резонанс напряжений возникает в последовательной RLC-цепи.

 

Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=w_р, а следовательно и индуктивного и емкостного сопротивлений x_L=x_C. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке U_L и на конденсаторе U_C будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.

При резонансе напряжения U_C и U_L могут быть намного больше, чем напряжение источника, что опасно для цепи.

 

С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.

 

Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту 

Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.

Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.

Резонанс токов

Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.

 

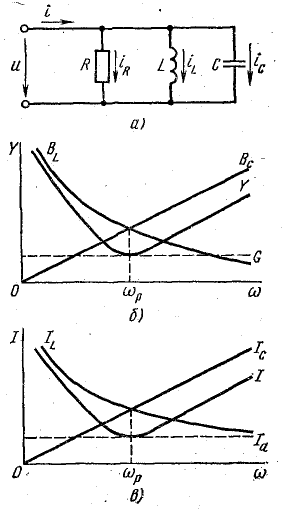
Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=w_р, следовательно проводимости B_L=B_C. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.

Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.

 

Выразим резонансную частоту 

Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.

Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к аварии.

Просмотров: 129554

Резонансом называется такой режим работы цепи, включающей в себя индуктивные
и емкостные элементы, при котором ее входное сопротивление (входная проводимость)
вещественно. Следствием этого является совпадение по фазе тока на входе цепи
с входным напряжением.

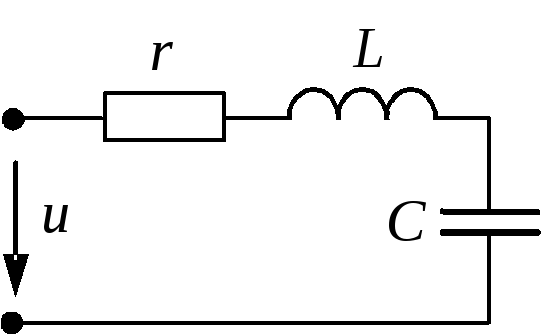
Резонанс в цепи с последовательно соединенными элементами
(резонанс напряжений)

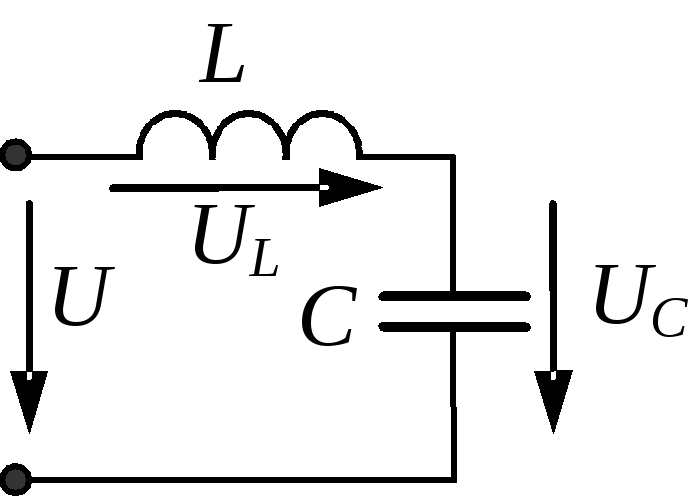
Для цепи на рис.1 имеет место

где

;

(1)

.

(2)

В зависимости от соотношения величин и возможны три различных случая.

1. В цепи преобладает индуктивность, т.е. , а следовательно,

. Этому режиму соответствует векторная
диаграмма на рис. 2,а.

2.В цепи преобладает емкость, т.е. , а значит, . Этот случай отражает векторная
диаграмма на рис. 2,б.

3. — случай резонанса напряжений
(рис. 2,в).

Условие резонанса напряжений

.

(3)

При этом, как следует из (1) и (2), .

При резонансе напряжений или режимах, близких к нему, ток в цепи резко возрастает.
В теоретическом случае при R=0 его величина стремится к бесконечности. Соответственно
возрастанию тока увеличиваются напряжения на индуктивном и емкостном элементах,
которые могут во много раз превысить величину напряжения источника питания.

Пусть, например, в цепи на рис. 1 . Тогда , и, соответственно, .

Явление резонанса находит полезное применение на практике, в частности в радиотехнике.
Однако, если он возникает стихийно, то может привести к аварийным режимам вследствие
появления больших перенапряжений и сверхтоков.

Физическая сущность резонанса заключается в периодическом обмене энергией между
магнитным полем катушки индуктивности и электрическим полем конденсатора, причем
сумма энергий полей остается постоянной.

Суть дела не меняется, если в цепи имеется несколько индуктивных и емкостных
элементов. Действительно, в этом случае , и соотношение (3) выполняется
для эквивалентных значений L_Э и C_Э .

Как показывает анализ уравнения (3), режима резонанса можно добиться путем
изменения параметров L и C, а также частоты. На основании (3) для резонансной
частоты можно записать

.

(4)

Резонансными кривыми называются зависимости тока и напряжения от частоты.
В качестве их примера на рис. 3 приведены типовые кривые I(f); и для цепи на рис. 1 при U=const.

Важной характеристикой резонансного контура является добротность Q,
определяемая отношением напряжения на индуктивном (емкостном) элементе к входному
напряжению:

,

(5)

— и характеризующая “избирательные” свойства резонансного контура, в частности
его полосу пропускания .

Другим параметром резонансного контура является характеристическое сопротивление,
связанное с добротностью соотношением

,

(6)

или с учетом (4) и (5) для можно записать:

.

(7)

Резонанс в цепи с параллельно соединенными элементами

(резонанс токов)

Для цепи рис. 4 имеем

,

где

;

(8)

.

(9)

В зависимости от соотношения величин и , как и в рассмотренном выше случае
последовательного соединения элементов, возможны три различных случая.

В цепи преобладает индуктивность, т.е. , а следовательно, . Этому режиму соответствует векторная
диаграмма на рис. 5,а.

В цепи преобладает емкость, т.е. , а значит, . Этот случай иллюстрирует векторная
диаграмма на рис. 5,б.

— случай резонанса токов (рис.
5,в).

Условие резонанса токов или

.

(10)

При этом, как следует из (8) и (9), . Таким образом, при резонансе
токов входная проводимость цепи минимальна, а входное сопротивление, наоборот,
максимально. В частности при отсутствии в цепи на рис. 4 резистора R ее входное
сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе
токов ток на входе цепи минимален.

Идентичность соотношений (3) и (5) указывает, что в обоих случаях резонансная
частота определяется соотношением (4). Однако не следует использовать выражение
(4) для любой резонансной цепи. Оно справедливо только для простейших схем с
последовательным или параллельным соединением индуктивного и емкостного элементов.

При определении резонансной частоты в цепи произвольной конфигурации или, в
общем случае, соотношения параметров схемы в режиме резонанса следует исходить
из условия вещественности входного сопротивления (входной проводимости) цепи.

Например, для цепи на рис. 6 имеем

Поскольку в режиме резонанса мнимая часть должна быть равна нулю, то условие резонанса имеет
вид

,

откуда, в частности, находится резонансная частота.

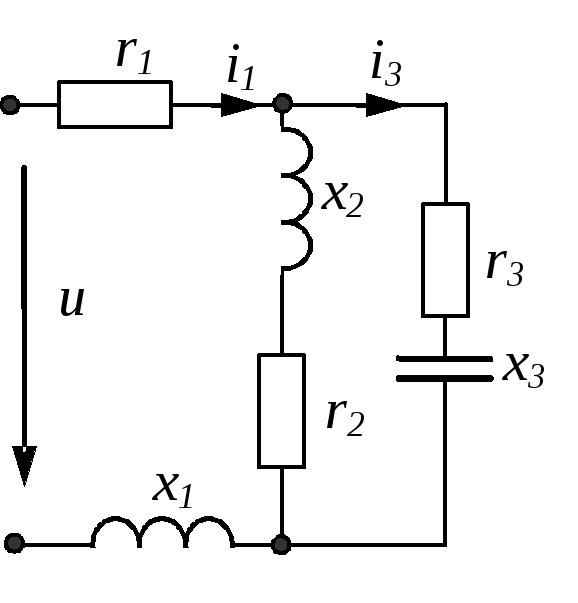
Резонанс в сложной цепи

Условие резонанса для сложной цепи со смешанным соединением нескольких индуктивных
и емкостных элементов, заключающееся в равенстве нулю мнимой части входного
сопротивления или входной проводимости , определяет наличие у соответствующих
этому условию уравнений относительно нескольких вещественных корней,
т.е. таким цепям соответствует несколько резонансных частот.

При определении резонансных частот для реактивного двухполюсника аналитическое
выражение его входного реактивного сопротивления или входной реактивной проводимости
следует представить в виде отношения
двух полиномов по степеням , т.е. или . Тогда корни уравнения дадут значения частот, которые
соответствуют резонансам напряжений, а корни уравнения — значения частот, при которых
возникают резонансы токов. Общее число резонансных частот в цепи на единицу
меньше количества индуктивных и емкостных элементов в схеме, получаемой из исходной
путем ее сведения к цепи (с помощью эквивалентных преобразований) с минимальным
числом этих элементов. Характерным при этом является тот факт, что режимы резонансов
напряжений и токов чередуются.

В качестве примера определим резонансные частоты для цепи рис. 7. Выражение
входного сопротивления данной цепи имеет вид

Из решения уравнения получаем частоту , соответствующую резонансу напряжений,
а из решения уравнения — частоту , соответствующую резонансу токов.

Литература

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
   С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические
   цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
   специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. Что такое резонанс напряжений, чем он характеризуется?
2. Что такое резонанс токов, чем он характеризуется?
3. В чем физическая сущность резонансных режимов?
4. На основании каких условий в общем случае определяются резонансные частоты?
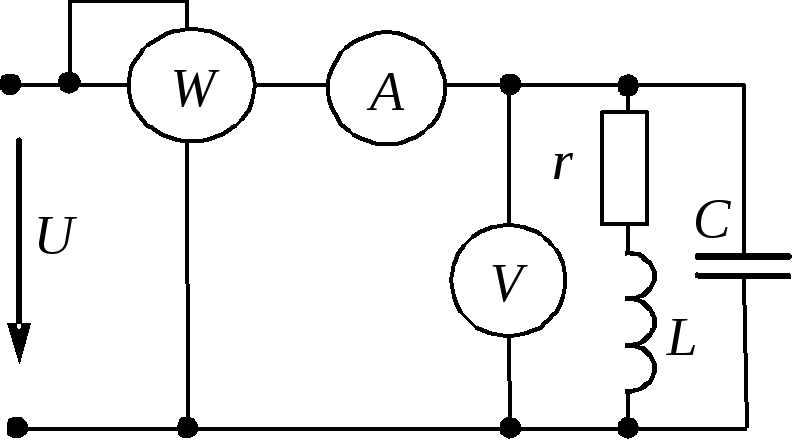
5. В цепи на рис. 1 R=1 Ом; L=10 мГн; С=10 мкФ. Определить резонансную частоту
   и добротность контура.

Ответ: .

6. Какие условия необходимы и достаточны, чтобы в цепи на рис. 1 выполнялось
   соотношение ?
7. Определить резонансную частоту для цепи на рис. 7, если в ней конденсатор
   С3 заменен на резистор R3.

Ответ: .

Содержание:

Резонанс токов:

При рассмотрении параллельного соединения катушки и конденсатора был отмечен случай равенства активной и реактивной проводимостей

Условия возникновения резонанса

Так же как и резонанс напряжений, резонанс токов возникает, когда частота источника энергии равна резонансной частоте ω_р, а

Режим электрической цепи при параллельном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивной и емкостной проводимостей, называют резонансом токов.

Сначала рассмотрим этот режим для схемы идеализированной цепи (рис. 17.6, а). В этой схеме параллельно резистору R включены идеальные катушки L и конденсатор С, потери энергии в которых не учитываются.

Рис. 17.6. К вопросу о резонансе токов

Реактивные проводимости зависят от частоты вынужденных колебаний. Для рассматриваемой схемы:
активная проводимость

реактивные проводимости
 
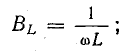
При резонансе токов

Отсюда определяют резонансную частоту:

Выражение для резонансной частоты в данном случае такое же, какое было получено при рассмотрении резонанса напряжений [см. формулу (17.8)] и для частоты собственных колебаний в контуре без потерь.
Резонанс токов, так же как и резонанс напряжений, можно получить изменением параметров L и С или изменением частоты источника энергии.

Резонансные кривые

На рис. 17.6, б показаны зависимости проводимостей от частоты. Полная проводимость цепи Y при резонансной частоте ω_р оказывается наименьшей, равной активной проводимости G. При изменении частоты в обе стороны от резонансной полная проводимость увеличивается.

При заданном напряжении источника энергии ток в цепи пропорционален проводимости (рис. 17.6, в): 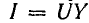, поэтому кривая I(ω) по форме повторяет кривую Y(ω). Состояние резонанса токов характеризуется наименьшей величиной тока в цепи и равенством нулю угла сдвига фаз между напряжением и током (φ_р = 0).

При резонансе токов отношение тока индуктивного или емкостного к току в неразветвленной части цепи равно отношению волновой проводимости 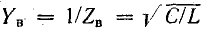к активной проводимости цепи G.
Реактивные проводимости при резонансе

Поэтому

Добротность контура

При параллельном соединении элементов качество резонансной цепи считается тем выше, чем больше отношение 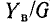, которое и в этом случае называется добротностью:

Чем меньше потери энергии в цепи (этому соответствует большая величина R), тем больше добротность.

Параметры реальных катушек и конденсаторов (R, L, С) измеряются и задаются в справочниках применительно к их схемам замещения с последовательным соединением активных и реактивных элементов (см. рис. 14.11, б).
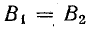
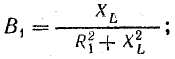
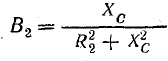
Условие резонанса токов — равенство реактивных проводимостей обеих ветвей — остается справедливым, и в этом случае
  ,
где R₁ и R₂ — активные сопротивления катушки и конденсатора с потерями.
Приравнивая реактивные проводимости, получим исходное уравнение для определения резонансной частоты

или

откуда

Из «того выражения видно, что резонансная частота зависит от активных сопротивлений катушки и конденсатора. Если потери энергии в катушке и конденсаторе малы (R₁ и R₂ малы) и ими можно пренебречь, для резонансной частоты получается выражение, найденное раньше для идеализированной цепи.

Компенсация реактивной мощности в электрических сетях с помощью конденсаторов

Было отмечено, что в электрической цепи переменного тока, в которой имеются катушка индуктивности и конденсатор, включенные последовательно или параллельно, общая реактивная мощность цепи всегда меньше, чем реактивная мощность каждого из элементов.

Благодаря взаимному обмену энергией между катушкой и конденсатором и рис. 14.5 источник частично или полностью освобождается от поставки реактивной энергии в цепь.

В этом случае говорят о компенсации реактивной мощности катушки реактивной мощностью конденсатора и наоборот (реактивные мощности Q_L и Q_С имеют противоположные знаки). Полная компенсация реактивной мощности имеет место при резонансе.

Компенсация реактивной мощности в электрических сетях имеет большое технико-экономическое значение. Далее кратко рассмотрены общие сведения по этому вопросу и принцип применения конденсаторов для компенсации реактивной мощности.

Реактивная мощность электрических установок

Энергетический процесс в катушке индуктивности, включенной в цепь переменного тока, характеризуется активной мощностью  и реактивной мощностью .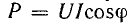

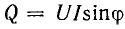
В электрической схеме замещения такая катушка представлена активным сопротивлением R и индуктивностью L, или активной проводимостью G и реактивной проводимостью Y.

В этом отношении катушке индуктивности подобны многочисленные устройства переменного тока: асинхронные двигатели, индукционные нагревательные установки, трансформаторы, воздушные линии и др.
Получая от генераторов электрическую энергию, эти устройства передают или преобразуют ее в другие виды энергии (активная мощность Р), т. е. выполняют те функции, для которых созданы.

Одновременно они обмениваются энергией с источниками (реактивная мощность Q), что является процессом хотя и нежелательным, но неизбежным, так как без магнитного поля и периодического накопления энергии в нем перечисленные устройства работать не могут.

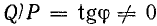
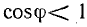
Если реактивная мощность устройства не равна нулю, то отношение , а коэффициент мощности .

На каждом предприятии одновременно работают электродвигатели (их может быть десятки и сотни), трансформаторы и другие устройства. Чем больше их число и чем меньше их коэффициент мощности, тем больше общая реактивная мощность электрооборудования производственного участка, цеха, всего предприятия.

Величина общей реактивной мощности электрической установки или электрооборудования предприятия в целом зависит еще и от правильного выбора, степени загрузки электродвигателей, трансформаторов, от соблюдения правил эксплуатации электрооборудования.

Далее будет показано, что за счет реактивной мощности потребителей электрический ток в сетях оказывается больше, чем требуется по величине активной нагрузки. С этим связана одна из проблем проектирования и эксплуатации электрических сетей. При передаче электрической энергии, особенно на большие расстояния, из-за наличия индуктивных и емкостных сопротивлений в элементах сети переменного тока возникает также проблема поддержания заданного уровня напряжения на всех приемниках.
Для обеспечения оптимальной величины тока и требуемых величин напряжения в сети необходимо иметь оптимальный баланс реактивных мощностей (индуктивной и емкостной).

Влияние величины реактивной мощности на технико-экономические показатели электроустановок

Для выяснения влияния величины реактивной мощности на экономические показатели электротехнических установок рассмотрим приемник энергии (например, асинхронный электродвигатель), работающий с постоянной активной мощностью при постоянном напряжении в сети.
Ток в приемнике, а следовательно, и в проводах, соединяющих его с источником энергии, при этих условиях зависит от величины реактивной мощности Q:

Чем больше реактивная мощность приемника, тем больший ток должен быть в самом приемнике, в генераторе, соединительных проводах, трансформаторе и других элементах сети электроснабжения.
Мощность тепловых потерь, согласно закону Ленца — Джоуля, пропорциональна квадрату тока и сопротивлению проводов:

Очевидно, чем больше ток приемника, тем больше потери энергии во всех элементах электрической цепи.

Стоимость потерянной энергии входит в эксплуатационные расходы. Уменьшение реактивной мощности приемников ведет к уменьшению их токов, сокращению потерь энергии и эксплуатационных расходов.
Если электрическая установка спроектирована с относительно большей величиной реактивной мощности, то оборудование (коммутационная аппаратура, приборы контроля и т. д.) и провода необходимо выбрать на большие токи, чем при меньшей величине реактивной мощности.
Это значит, что оборудование должно быть установлено относительно больших размеров, а провода — большего сечения. Последнее повлечет за собой увеличение объема зданий, утяжеление фундаментов и опор и т. п.
Уменьшение реактивной мощности приемников энергии сокращает капитальные затраты.

Генераторы электрической энергии и трансформаторы характеризуются номинальной мощностью — произведением номинальных величин напряжения и тока:

Наиболее полное использование генераторов и трансформаторов соответствует режиму работы с номинальным током при номинальном напряжении (особые случаи, когда допускается некоторая перегрузка оборудования при эксплуатации, здесь не учитываются).

Величина активной мощности генератора равна активной мощности питающихся от него приемников.

Если реактивная мощность приемников равна нулю, то генератор может развивать активную мощность, равную его номинальной мощности , т. е. основная функция генератора — преобразование энергии — может быть выполнена наиболее полно, а первичный двигатель (например, турбина), также рассчитанный на номинальную мощность, будет работать с полной нагрузкой.
При наличии у приемников реактивной мощности активная мощность генератора меньше номинальной, хотя он работает при номинальных напряжении и токе. Таким образом, генератор и первичный двигатель по мощности недогружены, что приводит к снижению их коэффициента полезного действия.

Компенсация реактивной мощности

Из приведенных рассуждений следует, что реактивную мощность установок, потребляющих электрическую энергию, надо по возможности сокращать.
На практике это достигается путем правильного выбора мощности электродвигателей переменного токаи трансформаторов, рациональной эксплуатации их без недогрузки и работы вхолостую. Эти и некоторые другие меры уменьшения реактивной мощности, связанные с выбором и эксплуатацией электрооборудования, называют естественными.

В тех случаях, когда естественные меры не могут обеспечить оптимальной величины реактивной мощности установки, принимают искусственные меры для ее компенсации.

Одной из таких мер является включение параллельно к приемникам батареи конденсаторов.

Для определения мощности и емкости батареи конденсаторов должны быть известны величины напряжения сети U, реактивной мощности установки до компенсации (Q₁) и после компенсации (Q₂).

Можно установить батарею конденсаторов мощностью Q_C = Q₁, тогда Q₂ = 0. Полная компенсация реактивной мощности освобождает полностью сеть от реактивного тока.

Однако технико-экономические расчеты показывают, что полная компенсация в большинстве случаев не является оптимальным решением вопроса, так как компенсационное устройство оказывается более сложным и дорогим, чем при некоторой оптимальной величине реактивной мощности Q₂, которую определяют на основе технико-экономического сопоставления вариантов (Определение оптимальной величины Q₂, выбор вида компенсирующего устройства и места его установки в сети рассматриваются в специальных курсах).

Мощность батареи конденсаторов

а емкость


Рис. 17.7. К вопросу о компенсации реактивной мощности

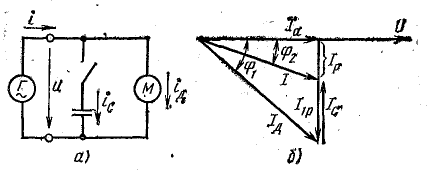
Сущность компенсации реактивной мощности с помощью конденсаторов видна из векторной диаграммы (рис. 17.7, б), построенной для схемы (рис. 17.7, а), на которой параллельно приемнику, например асинхронному двигателю (группе двигателей), может быть включена конденсаторная батарея. До включения конденсаторов ток в подводящих проводах I_д отстает по фазе от напряжения на угол φ₁. После включения батареи реактивная составляющая I_1р тока двигателя частично компенсируется емкостным током I_C, в связи с чем ток в подводящих проводах уменьшается до I, а угол сдвига фаз — до φ₂ (в обменном энергетическом процессе между генератором и приемником участвует меньшее количество электромагнитной энергии).

Активная составляющая тока в проводах не изменяется, следовательно, по активной мощности режим цепи остается прежним:

Ток батареи конденсаторов имеет величину


где Р — активная мощность приемника (в данном случае двигателя);

Емкость батареи конденсаторов

Мощность батареи конденсаторов

Нетрудно заметить, что мощность конденсаторов можно найти, не подсчитывая тока I_C:

 

Задача 17.7.

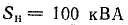
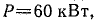
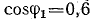
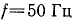
К трансформатору номинальной мощностью и номинальным напряжением 220 В подключена группа электродвигателей, общая активная мощность которых   при частоте  (рис. 17.8, а). Если параллельно группе двигателей включить батарею конденсаторов, реактивная мощность установки (двигатели — батарея конденсаторов) уменьшится и соответственно уменьшится нагрузка трансформатора.
Определить емкость и мощность батареи конденсаторов и дополнительную осветительную нагрузку, которые нужно подключить к трансформатору так, чтобы реактивная мощность установки уменьшилась до величины, при которой коэффициент мощности 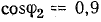при полной загрузке трансформатора.
Определить емкость и мощность батареи конденсаторов в том случае, когда 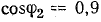при отсутствии дополнительной осветительной нагрузки.
Решение. 1. В первоначальном режиме трансформатор был загружен до номинальной мощности

Дополнительную осветительную нагрузку можно присоединить только за счет разгрузки трансформатора от части реактивной мощности путем включения батареи конденсаторов.
Согласно условию задачи, трансформатор после компенсации части реактивной мощности остается полностью загруженным, следовательно, при неизменном напряжении ток трансформатора должен остаться прежним:

Рис. 17.8. К задаче 17.7

Из векторной диаграммы (рис. 17.8, б) следует выражение для тока конденсатора:

при

при 

Ток установки до компенсации реактивной мощности

Ток батареи конденсаторов

Емкость батареи конденсаторов

Мощность батареи конденсаторов

Активный ток дополнительной осветительной нагрузки

Мощность осветительной нагрузки

2. При отсутствии дополнительной осветительной нагрузки необходимый ток в батарее конденсаторов (рис. 17.8, в)


Емкость батареи конденсаторов

Мощность батареи конденсаторов

Режим
при котором в цепи, содержащей реактивные
элементы, ток и напряжение совпадают
по фазе, называется резонансным, т.е.
эквивалентное сопротивление цепи
является чисто активным.

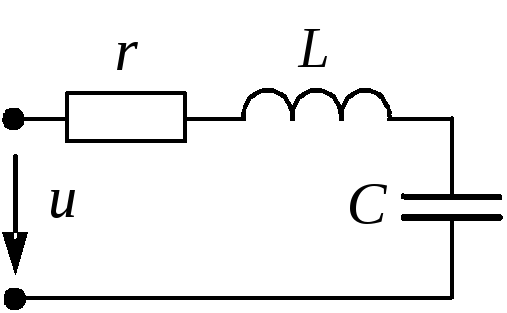
2.10.3.1. Резонанс напряжений

Резонанс
напряжений возможен при (Рис.8)
последовательном соединении R,L,Cэлементов.

Условие
резонанса напряжений:

Угловая
резонансная частота

.

При
резонансе напряжений ток в контуре
.

Коэффициент
мощности
.

Напряжение
на емкости и на индуктивности одинаковы:
.

При
резонансе напряжений применяются
следующие соотношения и формулы:

характеристическое
сопротивление контура – сопротивление
каждого из реактивных элементов при
резонансе
;

• добротность
  контура
  ;

• затухание
  контура
  ;

• абсолютная
  расстройка
  ;

• относительная
  расстройка
  .

2.10.3.2. Резонанс токов

Резонанс
токов возможен в цепи, содержащей
параллельно соединенные индуктивности
и емкости (Рис. 9)

Условие
резонанса токов:

Угловая
резонансная частота:
,

где
характеристическое сопротивление
;

добротность
контура
;

сопротивление
контура при резонансе токов
;

ток
неразветвленной части цепи при резонансе
;

полоса
пропускания определяется из условия,
что ток на частотах f₁иf₂,
соответствующих границы полосы
пропускания, уменьшается в;

абсолютное
значение полосы пропускания:
;

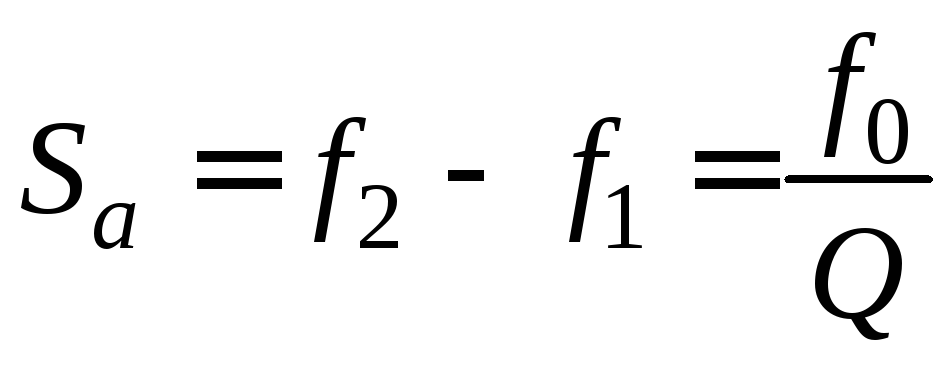
относительное
значение полосы пропускания:
.

Пример
3.1

Электрическая
цепь состоит из последовательно
соединенных активного сопротивления
Ом,
катушки индуктивностьюмкГн
и конденсатора емкостьюпФ.

Определить
резонансную частоту
,
характеристическое сопротивление,
затухание и добротность контура. Чему
равны ток, расходуемая в цепи мощность,
напряжение на индуктивности и емкости,
если контур включен на напряжении 1 В?
Вычислить абсолютное значение полос
пропускания контура.

Решение:

Пример 3.2

На
зажимах цепи поддерживается постоянное
по действующему значению напряжение
В,Ом,Ом,Ом.

Определить
,
при котором цепь будет находиться в
резонансе.

Решение:

Условие
резонанса напряжений
,

;

Ток
при резонансе

Пример
3.3

В схеме
без емкости приборы показывают
Вт,А,В,Гц.

Определить
величину емкости, необходимую для
повышения коэффициента мощности ()
до 1.

Решение:

Определим
параметры катушки по схеме без емкости

Ом;

при резонансе.

Условия
резонанса токов:

;

§2.11. Вопросы для самопроверки

1. Какой
ток называется переменным? Дайте
определение синусоидального тока.

2. Что
такое максимальное, действующее и
среднее значения синусоидальных величин
тока, напряжения, ЭДС. Запишите формулы,
связывающие действующие значения с
максимальными, средние значения с
максимальными?

3.
Назовите известные вам способы выражения
синусоидальных величин.

4. Дайте
определение векторной диаграмме.

5. Как
определяются знаки углов на векторной
диаграмме?

6. Дайте
определение индуктивности, емкости,
запишите выражения индуктивного,
емкостного сопротивления.

7. Чем
отличается реальная катушка индуктивности
от идеальной?

8.
Изобразите схему замещения реальной
катушки индуктивности и начертите для
нее векторную диаграмму.

9.
Начертите векторную диаграмму для цепи
с резистивным и емкостным элементом.

10.
Запишите закон Ома в комплексной форме
для резистивного, индуктивного и
емкостного элементов.

11. Как
определить угол сдвига фаз
по треугольнику напряжений, сопротивлений,
мощностей.

12. В
чем смысл символического метода расчета
цепей синусоидального тока?

13. В
каких электрических цепях и при каком
условии возникает резонанс напряжений?

14.
Запишите условие возникновения резонанса
токов.

Задачи
для самостоятельного решения:

Задачи

1.1. Ток
изменяется по синусоидальному закону.
Периодc,
амплитудаA,начальная фаза.
Токизменяется по синусоидальному закону
с той же частотой и амплитудой.

Записать
выражения
идля случаев:

опережает токна угол;

отстает от токана угол;

находится в противофазе с током;

совпадает по фазе с током.

1.2. Ток
изменяется по синусоидальному закону.
ЧастотаГц,
амплитудаА,
начальная фаза.
Токизменяется по синусоидальному закону
с той же частотой и амплитудой.

Записать
выражения
идля случаев:

совпадает по фазе с током;

отстает от токана угол;

опережает токна угол;

находится в противофазе с током.

Построить
графики
.

1.3. Ток
изменяется по синусоидальному закону.
Периодмс,
амплитудаA,
начальная фаза
.
Токизменяется по синусоидальному закону
с той же частотой, но амплитуда в два
раза больше.

Записать
выражения
идля случаев:

опережает тока угол;

отстает от токана угол;

находится в противофазе с током;

совпадает по фазе с током.

Построить
графики
.

1.4. Ток
изменяется по синусоидальному закону.
Периодмс,
амплитудаI_m1
= 2,8A,начальная фаза.
Токизменяется по синусоидальному закону
с той же частотой и амплитудой.

Записать
выражения
идля случаев:

опережает токна угол;

отстает от токана угол;

находится в противофазе с током;

совпадает по фазе с током.

Построить
графики
.

1.5.
Заданы мгновенные значения токов:

,

,

,

,

.

Записать
комплексные мгновенные, амплитудные и
действующие значения токов в алгебраической
и показательной формах.

Построить
векторы комплексных действующих значений
токов на комплексной плоскости.

1.6.
Заданы мгновенные значения токов:

,

,

,

,

.

Записать
комплексные мгновенные, амплитудные и
действующие значения токов в алгебраической
и показательной формах.

Построить
векторы комплексных действующих значений
токов на комплексной плоскости.

1.7.
Заданы мгновенные значения токов:

,

,

,

,

.

Записать
комплексные мгновенные, амплитудные и
действующие значения токов в алгебраической
и показательной формах.

Построить
векторы комплексных действующих значений
токов на комплексной плоскости.

1.8.
Заданы мгновенные значения токов:

,

,

,

,

.

Записать
комплексные мгновенные, амплитудные и
действующие значения токов в алгебраической
и показательной формах.

Построить
векторы комплексных действующих значений
токов на комплексной плоскости.

1.9.
Заданы комплексные действующие значения
токов и напряжений:

,

,

,

.

Построить
векторы токов и напряжений на комплексной
плоскости.

Записать
мгновенные значения
и.

1.10.
Заданы комплексные действующие значения
токов и напряжений:

,

,

,

.

Построить
векторы токов и напряжений на комплексной
плоскости.

Записать
мгновенные значения
и.

1.11.
Заданы комплексные действующие значения
токов и напряжений:

,

,

,

.

Построить
векторы токов и напряжений на комплексной
плоскости.

Записать
мгновенные значения
и.

1.12.
Заданы комплексные действующие значения
токов и напряжений:

,

,

,

.

Построить
векторы токов и напряжений на комплексной
плоскости.

Записать
мгновенные значения
и.

1.13.
Заданы комплексные действующие значения
токов и напряжений:

,

,

,

.

Построить
векторы токов и напряжений на комплексной
плоскости.

Записать
мгновенные значения
и.

1.14.
Заданы комплексные действующие значения
токов и напряжений:

,

,

,

.

Построить
векторы токов и напряжений на комплексной
плоскости.

Записать
мгновенные значения
и.

Задачи

2.1. Определить напряжение, приложенное к цепи, если действующее значение синусоидального напряжения В,В.
Построить векторную диаграмму напряжений и тока.

2.2. Определить напряжение , если действующее значение синусоидального напряженияВ,В.
Построить векторную диаграмму напряжений и тока.

2.3. Определить мгновенное напряжение, приложенное к цепи, если действующие значения напряжений В,В,В.
Построить векторную диаграмму напряжений и тока

2.4.  Ом, мГн, Ом, .
Определить ,,,. Построить векторную диаграмму напряжений и тока.

2.5. Ом, Ом, мкФ, В, .
Определить ,,. Построить векторную диаграмму напряжений и тока

2.6. мГн, Ом, мГн, Ом, В, Гц.
Определить ,,,. Построить векторную диаграмму напряжений и тока.

2.7. А, Ом, Ом, Ом, Ом.
Определить напряжение . Построить векторную диаграмму напряжений и тока.

2.8. Ом,Ом,Ом,Ом,В.
Определить ,. Построить векторную диаграмму напряжений и тока.

2.9. Ом,мГн,Ом,мГн,Ом,В,Гц.
Определить ,и мощность, расходуемую в цепи. Построить векторную диаграмму напряжений и тока.

2.10. Ом,МкФ,Ом,мкФ,,В.
Определить . Построить векторную диаграмму напряжений и тока.

2.11., .
Определить емкость конденсатора С.

2.12. При разомкнутом ключе Sсдвиг фаз междуи .
Определить сдвиг фаз при замкнутом ключе S.

2.13. В, Гц, В, В.
Вычислить, пользуясь векторной диаграммой и.

2.14. , Ом, Ом.
Определить , а такжеP,QиS. Найти проводимость .

2.15. При Гц, В, А, а при Гц, В, А.
Вычислить ,.

2.16. Ом, Ом, мГн, Гц. При каком значении емкости ток в ветви с катушкой будет в три раза больше тока в ветви с конденсатором.
Определить цепи.

2.17. Ом,Ом,Ом,Ом,Ом,Ом,В.
Определить токи в ветвях и написать их мгновенные значения. Определить PиQ. Построить векторную диаграмму напряжений и токов.
2.18. ,,,.
Определить токи в ветвях методом узловых потенциалов.

2.19. ,,Ом,Ом.
Найти мгновенное значение тока через методом эквивалентного генератора.

2.20. А,А,А.
Определить показания амперметров А2,А4.

2.21. Ом,Ом,Ом,Ом,Ом. К зажимам цепи включено синусоидальное напряжение,В.
Найти токи в ветвях схемы. Построить векторную диаграмму.

2.22. Ом, Ом, Ом, Ом, Ом, Ом. К зажимам цепи включено синусоидальное напряжение,В.
Найти токи в ветвях системы. Построить векторную диаграмму.

2.23. , Ом, Ом, Ом, Ом.
Определить токи в ветвях системы, напряжение и. Построить векторную диаграмму.

2.24. В, Ом, Ом, Ом, Ом.
Определить токи в ветвях схемы. Построить векторную диаграмму.

2.25. Ом, Ом, Ом, Ом, Ом, Ом, А.
Определить напряжение и. Построить векторную диаграмму.

2.26. Ом, Ом, Ом, В.
Определить токи в ветвях схемы. Построить векторную диаграмму токов и напряжений.

2.27. ,Гн,мкФ,Ом.
Определить токи в ветвях схемы и мощность Р. Построить векторную диаграмму токов и напряжений.

3.1. При
резонансе:
В,В,В,А,Гц.

Определить
.

3.2.
Ом,Ом,Ом,Гц.

При
каком значении L наступит резонанс

.

3.3. При
резонансе:
В,В,Ом,Гц.

Определить
показания приборов, значения L и С.

3.4.
Ом,Ом,Ом.

Определить значение
при котором наступает резонанс токов.

3.5.
,Ом.
Определить показания приборов.

3.6. При
резонансе:
Вт,В,Ом.

Определить
r и
.

3.7. При
резонансе:
В,Гц,Ом,В.

Определить
показания
,и добротность цепи.

3.8.
В,мкФ,мГн,Дж.

Определить
ток при резонансе, добротность цепи и
сопротивление.

3.9.
мкГн,,Ом,пФ.

Определить
добротность контура и резонансную
частоту
и.

3.10.
Ом,Ом.

При
каком значении
в цепи наступит резонанс.

3.11.
Определить r и L контура, если при
резонансной частоте
кГц
отношение напряжения на конденсаторе
к напряжению на входе равно 50. Емкость
конденсаторамкФ.

3.12.
Гн,Ом,мкФ.

Определить
частоту
при которой в цепи наступит резонанс
токов.

3.13.
Ом,мГн,мкФ,.

Определить
резонансную частоту, волновое сопротивление
и затухание контура, напряжения
и.

3.14.
Ом,В,Ом.

Определить
сопротивление
и все токи при резонансе.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #