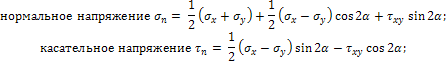Напряжением называется
интенсивность действия внутренних сил
в точке тела,
то есть, напряжение — это внутреннее
усилие, приходящееся на единицу площади.
По своей природе напряжение —
это поверхностная
нагрузка,
возникающая на внутренних поверхностях
соприкасания частей тела.
Деформацией называется
изменение размеров и формы тела под
действием приложенных сил.
Напряжением называется
отношение действующего усилия к площади
поперечного сечения тела или образца σ
= P/F.
В
зависимости от направления действия
силы нормальные напряжения подразделяют
на растягивающие и сжимающие.
Различают временные и остаточные напряжения.
Временные
напряжения возникают
под действием внешней нагрузки и исчезают
после ее снятия, остаточные —
остаются в теле после прекращения
действия нагрузки.
Если
после прекращения действия внешних сил
изменения формы, структуры и свойств
тела полностью устраняются, то такая
деформация называется упругой.
При
возрастании напряжений выше предела
упругости деформация становится
необратимой. При снятии нагрузки
устраняется лишь упругая составляющая
деформации, оставшаяся часть
называется пластической
деформацией.
Норм
напряжение:
Составляющая
напряжений, направленных по нормали к
площадке ее действия.
Касат
напряжение:
Составляющая
напряжений, лежащих в плоскости сечения.
Правила
знаков:
Нормальные
напряжения σ принимаются
положительными (т.е. σ>0),
если они растягивают выделенный элемент
бруса.
Касательные
напряжения τ принимаются
положительными (т.е. τ>0),
если они стремятся повернуть рассматриваемый
элемент бруса по ходу часовой стрелки.
При
растяжении-сжатии
Внутренняя
продольная сила N,
которая стремится растянуть рассматриваемую
частьбруса,
считается положительной. Сжимающая
продольная сила имеет отрицательный
знак.
При
кручении
Внутренний
скручивающий момент T считается
положительным, если он стремится
повернуть рассматриваемую часть бруса
против хода часовой стрелки, при взгляде
на него со стороны внешней нормали.
При
изгибе
Внутренняя
поперечная сила Q считается
положительной, в случае, когда она
стремится повернуть рассматриваемую
часть бруса по ходу часовой стрелки.
Внутренний
изгибающий момент M положителен, когда
он стремится сжать верхние волокна
бруса.
Деформация
при растяжении-сжатии Δl считается
положительной, если длина стержняпри
этом увеличивается.
При
плоском поперечном изгибе
Вертикальное
перемещение сечения бруса принимается
положительным, если оно направлено
вверх от начального положения.
Правило
знаков при составлении уравнений статики
—
для проекций сил на оси системы координат
Проекции
внешних сил на оси системы координат
принимаются положительными, если их
направление совпадает с положительным
направлением соответствующей оси.
—
для моментов
Сосредоточенные
моменты и моменты сил в уравнениях
статики записываются с положительным
знаком, если они стремятся повернуть
рассматриваемую систему против хода
часовой стрелки.
Правило
знаков при составлении уравнений статики
для неподвижных систем
При
составлении уравнений равновесия
статичных (неподвижных) систем (например,
приопределении
опорных реакций),
последние два правила упрощаются до
вида:
Проекции
сил и моменты, имеющие одинаковое
направление принимаются положительными,
а соответственно проекции сил и моменты
обратного направления – отрицательными.
ПЛОСКОЕ
НАПРЯЖЕННОЕ СОСТОЯНИЕ
Если
все векторы напряжений параллельны
одной и той же плоскости, напряженное
состояние называется плоским (рис. 1).
Иначе: напряженное состояние является
плоским, если одно из трех главных
напряжений равно нулю.
Рисунок
1.
Плоское
напряженное состояние реализуется в
пластине, нагруженной по ее контуру
силами, равнодействующие которых
расположены в ее срединной плоскости
(срединная плоскость — плоскость, делящая
пополам толщину пластины).
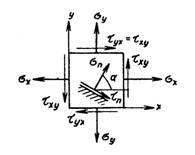
Направления
напряжений на рис. 1 приняты за
положительные. Угол α положителен, если
он откладывается от оси х к оси у. На
площадке с нормалью n:
|
|
(1) |
при 
.
Нормальное
напряжение σn положительно,
если оно растягивающее. Положительное
напряжение 
показано
на рис. 1. Правило знаков для
по
формуле (1) то же самое, что для
напряжений
по
формуле (1).
Данное
здесь правило знаков относится к
наклонным площадкам. В статье «Объёмное
напряженное состояние» сформулировано
правило знаков для компонентов напряжений
в точке, т. е. для напряжений на площадках,
перпендикулярных осям координат. Это
правило знаков принято в теории упругости.
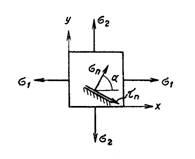
Главные
напряжения на площадках, перпендикулярных
плоскости напряжений:
|
|
(2) |
(Поскольку
здесь рассматриваются только два главных
напряжения, они обозначены через σ1 и
σ2,
хотя может оказаться, что σ2<0,
т. е. σ2 не
будет средним из трех главных напряжений).
Угол α1 составляемый
нормалью к первой главной площадке с
осью х, находится из равенства:
|
|
(3) |
Наибольшее
и наименьшее касательные напряжения
|
|
(4) |
Эти
напряжения действуют на площадках,
расположенных под углом 45° к первой и
второй главным площадкам.
Если
главные напряжения σ1 и
σ2 имеют
одинаковый знак, то наибольшее касательное
напряжение действует на площадке,
расположенной под углом 45° к плоскости
напряжений (плоскости ху). В этом случае:
В
стенке балки (здесь имеется в виду
обычная балка, а не балка-стенка) при
ее изгибе силами реализуется частный
случай плоского напряженного состояния.
В стенках балки одно из нормальных
напряжений σy равно
нулю. В этом случае напряжения получатся
по формулам (1), (2) и (4), если в этих формулах
положить σy=0.
Положение первой главной площадки
определяется формулой (3).
РАСТЯЖЕНИЕ
ПО ДВУМ НАПРАВЛЕНИЯМ (рис
2):
Рисунок
2.
При
σ1>0
и σ2<0 
При
σ1>0
и σ2>0 
При
σ1<0
и σ2<0 
ЧИСТЫЙ
СДВИГ (рис.
3)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
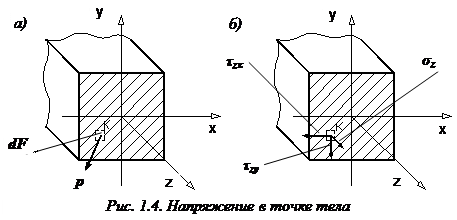
Напряжение в точке тела
Напряженное состояние в точке тела является ключевым понятием в сопромате. Необходимость введения понятия напряжения в точке для суждения об интенсивности внутренних сил в некоторой точке сечения стержня вызвана неравномерным распределением внутренних сил по длине и поперечному сечению в общем случае нагружения.
Напряжение в точке тела K (обозначено буквой p) – это интенсивность внутренней силы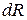 
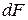
, возникающей на бесконечно малой площадке 
в окрестности данной точки (рис. 1.4, а).
В количественном выражении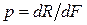 
.
|
|
Понятие о напряжении в точке твердого тела в некотором смысле напоминает понятие о давлении, действующем, например, внутри жидкости. Однако давление в точке жидкости одинаково во всех направлениях. Если проведем через точку K тела другое сечение, иной будет внутренняя сила. Следовательно, иным будет и напряжение, хотя оно возникает в той же самой точке K.
Напряжение в точке тела в разных направлениях (на разных площадках, проходящих через данную точку тела) может быть различным (в частности, оно может возникать только в одном направлении).
Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши.
Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат x, y и z: нормальное напряжение (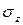
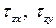
– сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения (
– тау), лежащие в плоскости сечения и направленные, соответственно, вдоль осей x и y (рис. 1.4, б). Первый индекс у касательных напряжений характеризует нормаль к площадке z, на которой они возникают.
Между полным (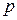
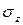
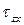
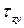
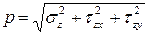
), нормальным () и касательными напряжениями (
и 
) существует зависимость:
.
Касательные напряжения служат мерой тенденции одной части сечения смещаться (или скользить) относительно другой его части.
Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону (то есть равная, приблизительно, весу одного яблока). Как мы увидим в дальнейшем, эта единица напряжения мизерно мала. В сопромате чаще используются другие единицы:
1 МПа = 106 Па; 1 кН/см2 = 107 Па.
В технической системе единиц напряжения измеряются в килограммах силы на миллиметр (сантиметр) в квадрате (кгс/мм2 или кгс/см2) . Следует запомнить, что 1 кН/см2 » 1 кгс/мм2.
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
1.5. ПОНЯТИЕ О НАПРЯЖЕНИЯХ Напряжение в точке по сечению – внутренняя сила взаимодействия, приходящаяся на единицу площади у этой точки. Напряжение – величина, характеризующая интенсивность внутренних усилий в точке. Рассмотренные ранее усилия N, Qy, Qz, My, Mz, T являются интегральным эквивалентом внутренних сил, распределенных по площади сечения. Эти силы характеризуются их интенсивностью (рис. 1.11) Напряжение нормальное σ – перпендикулярное к сечению, характеризует интенсивность сил отрыва или сжатия частиц элементов конструкции. Напряжение касательное τ – действующее в плоскости сечения, характеризует интенсивность сил, сдвигающих эти части в плоскости сечения. Напряжение полное p=σ +τ22 . Суммируя элементарные усилия σ•dA, τy•dA, τz•dA (рис. 1.12), распределенные по сечению и их моменты относительно координатных осей, получим (рис. 1.14) Единица измерения давления и механического напряжения паскаль (обозначение Па). Паскаль – давление, вызываемое силой 1 Н, равномерно распределенной по поверхности площадью 1 м2. 1 Па = 1 Н/м2; 1 МПа = 0,102 кгс/мм2; 1 МПа = 10,2 кгс/см2; 1 МПа = 1 Н/мм2; 1 кгс/мм2 = 9,81 МПа.