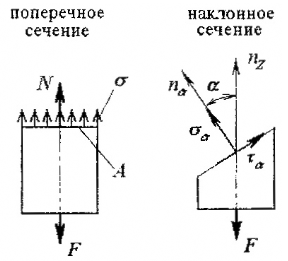
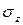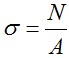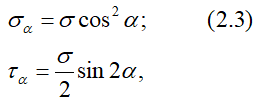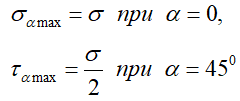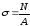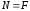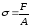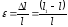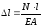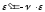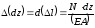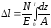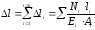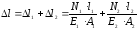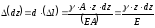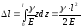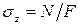В поперечных сечениях при растяжении-сжатии имеют место только нормальные напряжения σ, которые определяются отношением внутренней силы N к площади A соответствующего поперечного сечения стержня.
Вывод формулы
Знак напряжений зависит от знака внутренней продольной силы на рассматриваемом участке стержня.
Опытным путем показано, что при растяжении-сжатии, на достаточном удалении от точки приложения сил, вследствие равномерного распределения внутренних сил по сечению стержня в каждой его точке возникают напряжения одинаковой величины (σ=const).
Для обеспечения необходимой прочности элементов и конструкций напряжения не должны превышать допустимых значений.
Напряжения в наклонных сечениях
В наклонных сечения бруса одновременно с изменением величины нормальных напряжений появляются касательные.
при этом
Деформации при осевом растяжении-сжатии >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
-
Определение
внутренних сил в растягиваемых и
сжимаемых стержнях. -
напряжения
при растяжении (сжатии) прямого стержня.
Понятие о допускаемом напряжении. -
Определение
деформаций и перемещений. Закон Гука. -
Опытное
изучение свойств материалов.
Растяжение
и сжатие – это простой и часто встречающийся
случай напряженного состояния элементов
конструкции и деталей машин.
В
таких условиях работает буксировочный
канат или трос подъемного механизма,
колонна здания.
Чистое
(центральное) растяжение или сжатие
возникает в элементе конструкции, если
внешняя нагрузка вызывает в нем только
одно
внутреннее усилие,
которое сопротивляется этой внешней
нагрузке, — нормальную
продольную силу.
При
определении значений внутренних
нормальных сил, действующих в поперечных
сечениях стержней, примем следующее
правило
знаков:
—
нормальная сила положительна, если
сопротивляется растяжению стержня;
—
нормальная сила отрицательна – если
сопротивляется сжатию.
Для
определения значений внутренней
нормальной силы в любом из поперечных
сечений используется метод
сечений.
Пусть
прямой стержень постоянной толщиной в
одном конце закреплен, а к его другому
торцу приложена растягивающая его вдоль
оси стержня внешняя сила F.
Какое
по величине внутреннее продольное
усилие возникает в некотором поперечном
сечении стержня n—n?
Прежде
всего, отметим, что под действием
закрепления и внешней силы стержень
растягивается (деформируется), но никуда
не движется, т.е. остается в равновесии.
Удобно
вначале мысленно «снять» со стержня
закрепление. Заменим его влияние на
стержень эквивалентно действующей
внешней силой. Эта сила равна реакции
закрепления.
Т.е.
в закреплении возникает некоторое
усилие, благодаря которому верхний край
стержня остается неподвижным. Это усилие
называют реакцией
закрепления на внешнюю нагрузку,
передающееся на это закрепление через
деформируемый стержень.
Незакрепленный
стержень, теперь уже под действием двух
внешних воздействий: известной силы и
неизвестной пока реакции также никуда
не движется, т.е. находится в равновесии.
Определить
величину реакции поможет математическая
формулировка этого факта.
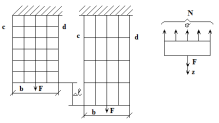
Проведем
координатную ось Оz,
для удобства совпадающую с осью стержня.
Стержень никуда не движется под действием
силы и реакции в частности, не движется
и вдоль оси, потому что проекции этих
внешних сил на ось уравновешивают друг
друга.
Такого
рода факт в механике формулируется
уравнением
общего равновесия стержня:
суммарная проекция на ось Оz
всех
действующих на стержень внешних сил,
равна нулю:
При
построении уравнений общего равновесия
механики принято использовать следующее
правило
знаков:
-
Проекция
усилия на ось положительна, если ее
направление совпадает с выбранным
направлением этой оси; -
И
наоборот – проекция отрицательна, если
направлена в противоположную сторону.
Эпюры
– графики
внутренних усилий, напряжений, перемещений,
деформаций, возникающих в элементах
конструкций и деталях машин под
воздействием внешней нагрузки.
Напряжения
при растяжении (сжатии) прямого стержня
Предположим,
растягивающую брус внешнюю силу удалось
распределить равномерно по его торцам.
Опыты
показывают. Что в этом случае каждое
продольное волокно бруса подвержено
только растяжению и в любом его поперечном
сечении внутренние силы действуют
только по нормали к этим сечениям.
Поперечные
сечения бруса, плоские до деформации,
под действием внешних сил перемещаются
параллельно своему начальному положению
и остаются постоянными.
Растягивающие
стержень внешние силы не всегда удается
распределить по площади стержня
равномерно.
Но
опыты показывают, что поведение поперечных
сечений растягиваемых стержней,
расположенных на некотором расстоянии
от места приложения внешней нагрузки,
уже не зависит от способа приложения
этих сил и всегда соответствует гипотезе
плоских сечений.
При
рассмотрении деформаций растяжения
или сжатия, а также при рассмотрении
последующих простых деформаций нами
будет рассматриваться принцип
Сен-Венана,
названный по имени французского ученого
XIX
века, который заключается в том, что
внутренние
силовые факторы, возникающие в результате
действия внешних сил, распределяются
по сечениям рассматриваемого тела
равномерно.
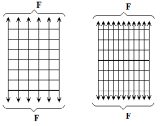
Рассмотрим
стержень, подверженный действию
продольных сил
Если
на поверхность призматического стержня
нанести сетку линий параллельных и
перпендикулярных оси стержня, и приложить
к нему растягивающую силу, то можно
убедиться в том, что линии сетки и после
деформации останутся взаимно-перпендикулярными,
но расстояние между ними изменятся.
Все
горизонтальные линии, например, cd,
переместятся вниз, оставаясь горизонтальными
и прямыми.
Можно
предположить, что и внутри стержня будет
происходить то же самое, т.е. поперечные
сечения стержня плоские и нормальные
к его оси до деформации, останутся
плоскими и нормальными к оси и после
деформации.
Эту
гипотезу называют гипотезой
плоских сечений (гипотезой Бернулли).
Продольная
сила N
есть равнодействующая нормальных
напряжений в поперечном сечении:
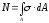
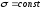
то

отсюда
В
частном случае, когда на стержень
действует одна внешняя сила, из уравнения
равновесия получим:
И
вместо общей формулы получим частный
вид формулы для растяжения:
Эти
формулы справедливы и для сжатия, с той
только разницей, что сжимающие напряжения
считаются отрицательными.
Кроме
того, сжатые стержни помимо расчета на
прочность рассчитываются также и на
устойчивость.
Очевидно,
что эти напряжения в реальных условиях
нельзя создавать больше или много меньше
определенной величины. Поэтому вводится
понятие допускаемого
напряжения:
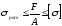
прочности.
Определение
деформаций и перемещений. Закон Гука.
Опыты
показывают, что при растяжении длина
стержня увеличивается, а поперечные
размеры уменьшаются, при сжатии –
наоборот.
Для
многих материалов при нагружении до
определенных пределов опыты показали
следующую зависимость между относительным
удлинением стержня

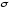
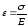
где
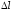
абсолютное удлинение стержня
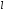
длина образца до деформации
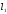
длина образца после деформации
Эта
зависимость носит название закона
Гука и
формулируется следующим образом:
линейные
деформации прямо пропорциональны
нормальным напряжениям.
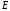
коэффициент, зависящий от материала,
т.е. его способность сопротивляться
деформированию. Он характеризует
жесткость материала, т.е. его способность
сопротивляться деформированию.
Для
ст.3
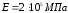
Для
других материалов значение
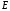
Имея
ввиду, что для стержня постоянного
сечения:
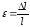
а
Можно
получить формулу для определения полного
(абсолютного) удлинения (укорочения)
стержня:
Между
продольным удлинением

Здесь

поперечной деформации (коэффициент
Пуассона),который
характеризует способность материала
к поперечным деформациям.
При
пользовании этой формулой удлинение
считается положительным, а укорочение
– отрицательным.
Для
всех материалов
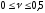
Для
стали при упругих деформациях можно
принимать

Зная
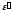
сужение или расширение стержня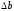
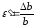
где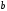
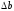
поперечный размер стержня после
деформации.
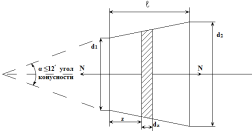
В
стержнях переменного сечения напряжения
в поперечных сечениях можно считать
распределенными равномерно (если угол
конусности
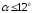
и определять их по той же формуле, что
и для стержня постоянного сечения.
Для
определения деформаций стержня
переменного сечения, в поперечных
сечениях которого действует продольная
сила N,
найдем сначала удлинение
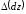
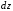
которое является дифференциалом полного
удлинения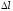
Согласно
закону Гука, имеем:
Полное
удлинение стержня получим, интегрируя
выражение в пределах
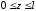
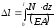
если
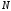
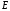
Чтобы
воспользоваться этой формулой, необходимо
знать закон изменения
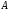

Для
ступенчатых стержней интегрирование
заменяется суммирование, и полное
изменение длины бруса определяется как
алгебраическая сумма деформаций его
отдельных частей, в пределах которых
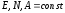
Например,
для стержня изображенного на схеме,
имеем:
Определим
теперь удлинение стержня постоянного
сечения под действием силы тяжести,
которая представляет собой нагрузку,
равномерно распределенную вдоль стержня.
Удельный
вес материала обозначим через
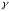
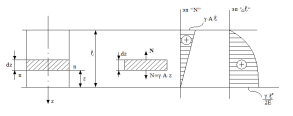
Рассмотрим
деформацию элемента
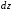
выделенного на расстоянии
Удлинение
элемента равно:
Интегрируя
это выражение в пределах, получим
Это
выражение можно представить в другом
виде, если учесть, что сила тяжести бруса
равна:
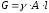
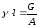
тогда получим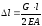
определению перемещения с учетом
собственного веса при известной длине
Следовательно,
удлинение бруса постоянного сечения
от собственной силы тяжести в два раза
меньше удлинения от действия силы,
равной силе тяжести и приложенной к его
концу.
Опытное
изучение свойств материалов
Для
изучения свойств материалов и установления
значения предельных (по разрушению или
по пластическим деформациям) производят
испытания образцов материала вплоть
до разрушения. По виду деформации
различают испытания на растяжение,
сжатие, кручение и изгиб.
Испытания
производят при статической и ударной
(испытание на усталость и выносливость)
нагрузках на ГМС – 50.
Цель
испытания на растяжение – определение
механических характеристик материала.
При
проведении испытания автоматически
записывается диаграмма зависимости
между растягивающей силой и удлинением
образца.
Условия
и порядок выполнения работы
-
Стальной
стержень ступенчатого сечения находится
под действием внешней силы и собственного
веса.
-
Необходимо
построить эпюры:
-
нормальных
продольных сил
-
нормальных
напряжений
-
перемещения
сечений стержня относительно жесткой
заделки.
Площадь
большего поперечного сечения стержня
в 2 раза превышает меньшую.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Методология
расчетов стержней на растяжение (сжатие)
Центральным растяжением (сжатием) называется такой вид
деформации, при котором в поперечном сечении бруса возникает только продольная
сила
(растягивающая или сжимающая), а все остальные внутренние усилия равны нулю.
ПОСТРОЕНИЕ
ЭПЮР ПРОДОЛЬНЫХ СИЛ N
Рисунок
Продольная сила — это внутреннее усилие, которое возникает между
отдельными частями элемента под действием внешних сип (центрально-сжимающих или
центрально-растягивающих).
Для определения продольной силы используется метод сечений. Растяжение
обозначается плюсом (+), сжатие минусом (-). (рис. 1).
В соответствии с методом сечений; разрезаем, отбрасываем, заменяем,
уравновешиваем:
1. Скачок в эпюре N равен приложенной в этом сечении
сосредоточенной силе.
2. В сечении ‘А’ (заделка) есть реакция Ra, которую
можно найти из формулы:
Но проще идти со свободного конца, и затем найти реакцию Ra по эпюре в точке А:
Ra = P.
Рисунок 1
При центральном растяжении (сжатии) в поперечном
сечении возникают нормальные напряжения:
где N — продольная сила;
F — площадь поперечного сечения.
Эти
напряжения распределены по поперечному сечению равномерно (рис. 2).

Рисунок 2
Проверка прочности центрально растянутого стержня
выполняется по условию:
При растяжении и сжатии бруса меняются его продольные
и поперечные размеры (рис. 3).
Рисунок 3
При растяжении:
Длина бруса меняется на (удлинение), Ширина
бруса меняется на (сужение). При сжатии:
(укорочение)
(увеличение)
Закон Гука выражает прямо пропорциональную зависимость между нормальным
напряжением и относительной деформацией:
или, если представить в другом виде:
где Е — модуль продольной упругости.
Это физическая постоянная материала, характеризующая его
способность сопротивляться упругому деформированию.
EF — жесткость поперечного сечения бруса при
растяжении-сжатии.
|
абсолютная |
относительная деформация безразмерная |
|
|
|
|
|
|
|
|
Деформация бруса (растяжение или сжатие) вызывает перемещение
поперечных сечений.
Рассмотрим три случая нагружения при растяжении.
В первом случае при растяжении бруса сечение n-n
перемещается в положение n1-n1 на величину . Здесь: перемещение
сечения равно деформации (удлинению) бруса =
l.
Рисунок 4
Во втором случае растяжения (рис. 5)
Рисунок 5
I-ый
участок бруса деформируется (удлиняется) на величину l1, сечение n-n
перемещается в положение n1-n1 на величину лев = l1.
II-ой
участок бруса не деформируется, так как здесь отсутствует продольная сила N,
сечение m-m перемещается в положение m1-m1 на величину
В третьем случае рассмотрим деформации бруса при схеме нагружения, представленной
на рисунке (рис. 6).
Рисунок 6
В этом примере: перемещение сечения n-n (лев)
равно удлинению 1-ого участка бруса:
Сечение m-m переместится в положение m1-m1 за счет деформации 1-ого участка
бруса, а в положение m2-m2 за счет своего собственного удлинения:
Суммарное перемещение сечения m-m:
В данном случае:
Рисунок 7
С использованием эпюры N получаем такой же результат (снимаем N с эпюры) (рис. 8).
Рисунок 8
Перемещение конца консоли можно получить, используя
только внешние силы (2Р,Р). Тогда
Для решения статически неопределимых задач необходимо
получить столько дополнительных уравнений, сколько имеется лишних неизвестных
(т.е. сколько раз статически неопределима задача).
Эти дополнительные уравнения получают из
рассмотрения деформации системы — составляют условие совместности деформаций
(рис. 9).
Рисунок 9
В этой системе мы можем взять следующие условия
совместности деформаций:
(перемещение
сечения А равно нулю, т.к. в этом сечении — заделка), (то
же).
(т.е. общее удлинение бруса
равно нулю)
Нам нужно выбрать только одно условие. Допустим, мы
выбрали . Тогда отбросим заделку В’ и заменим ее
реакцией Rb, которая должна обеспечить неподвижность этого сечения (рис. 9).
Получили необходимое дополнительное уравнение, из которого определяем Rb
Строим эпюру N.
В статически неопределимых задачах эпюры внутренних
усилий (у нас это — эпюра N) всегда двузначные, т.е. переходят с плюса на минус
(или наоборот).
Пример решения работы
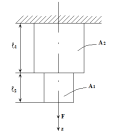
Условие задачи:
Стальной стержень (модуль Юнга кН/см2) с
размерами см;
см,
см и площадью
поперечного сечения нижнего участка см2, а
верхнего – см2 нагружен
внешними осевыми силами кН и
кН. Построить
эпюры продольных сил и нормальных
напряжений . Оценить
прочность стержня, если предельное напряжение (предел текучести) кН/см2, а
допускаемый коэффициент запаса . Найти
удлинение стержня .
Расчетная схема для задачи:
Рисунок
10
Решение задачи:
Определяем
значение опорной реакции , возникающей
в заделке
Учитывая, что , направим
опорную реакцию вниз. Тогда из
уравнения равновесия находим:
кН.
Строим
эпюру продольных сил
Разбиваем длину стержня на три участка. Границами
участков являются сечения, в которых приложены внешние силы и (или) изменяется
размер поперечного сечения стержня.
Воспользуемся методом сечений. Делаем по одному
сечению в произвольном месте каждого из трех участков стержня.
Cечение 1 – 1. Отбросим
(или закроем листком бумаги) верхнюю часть стержня (рис. б). Само сечение 1 – 1
мысленно считаем неподвижным. Мы видим, что внешняя сила растягивает
рассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня
противодействует этому растяжению. Это противодействие мы заменим внутренней
продольной силой , направленной
от сечения и соответствующей растяжению. Разрушения стержня не произойдет
только в том случае, если возникающая в сечении 1 – 1 внутренняя продольная
сила уравновесит
внешнюю силу . Поэтому
очевидно, что
кН.
Сечение 2 – 2. Внешняя
сила растягивает
рассматриваемую нами нижнюю часть стержня, а сила ее сжимает
(напомним, что 2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию
задачи, . Чтобы
уравновесить эти две силы, в сечении 2 – 2 должна возникнуть внутренняя
сила , противодействующая
сжатию, то есть направленная к сечению. Она равна:
кН.
Сечение 3 – 3. Отбросим
теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная
сила должна
уравновесить внешнюю (реактивную) сжимающую силу . Поэтому она
направлена к сечению и равна:
кН.
Легко убедиться в том, что полученный результат не
изменится, если мы отбросим не нижнюю, а верхнюю часть стержня. В этом случае
продольная сила также
противодействует сжатию. Она равна:
кН.
При построении эпюры продольных сил будем
пользоваться следующим правилом знаков: внутренняя продольная сила, возникающая
в поперечном сечении стержня, считается положительной, если она
противодействует растяжению стержня, и отрицательной, если она противодействует
его сжатию. Оно вводится для того, чтобы можно было наглядно видеть, какая
часть стержня испытывает деформацию растяжения, а какая часть – деформацию
сжатия. Это обстоятельство может оказаться крайне важным, в частности для
стержней из хрупкого материала, которые имеют разные допускаемые напряжения на
растяжение и на сжатие.
Таким образом, мы установили, что в любом сечении
нижнего участка стержня внутренняя продольная сила противодействует растяжению
и равна кН. В любом
сечении среднего и верхнего участков стержня имеет место деформация сжатия,
поэтому кН.
Для построения эпюры продольных сил проводим
тонкой линией ось, параллельную оси стержня z (рис. д). Вычисленные значения
продольных сил в выбранном масштабе и с учетом их знака откладываем от этой
вертикальной оси. В пределах каждого из участков стержня продольная сила
остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями
соответствующий участок.
Отметим, что каждая линия «штриховки» (то есть
ордината эпюры) в принятом масштабе дает значение продольной силы в
соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Анализируя полученную эпюру, мы видим, что в местах
приложения внешних сил на эпюре имеет место
скачкообразное изменение продольной силы на величину, равную значению
соответствующей внешней силы. Причем изменение поперечного размера стержня, как
это видно из рис. д, никак не сказывается на характере эпюры .
Строим
эпюру нормальных напряжений
Нормальное напряжение, возникающее в k–м поперечном
сечении стержня при растяжении (сжатии), вычисляется по следующей формуле
,
где и
– продольная
сила и площадь k–го поперечного сечения стержня соответственно.
В первом поперечном сечении стержня нормальное
напряжение равно

во втором –

в третьем –

Строим по вычисленным значениям эпюру (рис. е). В
пределах каждого из участков стержня напряжения постоянны, то есть эпюра
напряжений параллельна оси. Заметим, что в отличие от эпюры N, на эпюре «скачок» имеет
место не только в местах приложения внешних сил, но и там, где происходит
изменение размеров поперечного сечения стержня.
Оцениваем
прочность стержня
Сопоставляем наибольшее (по модулю) нормальное
напряжение , которое в
нашем примере возникает во втором сечении стержня, с допускаемым
напряжением . Напомним,
что допускаемое напряжение представляет собой долю от предельного
напряжения , то есть от
напряжения, при котором начинается разрушение материала. Разрушение стали, как
пластичного материала, начинается при появлении значительных остаточных деформаций.
Поэтому для стали предельное напряжение равно пределу текучести: . Тогда
кН/см2.
Условие прочности имеет вид . В нашем
случае
кН/см2
> кН/см2,
следовательно, прочность стержня на втором участке не
обеспечена.
Таким образом, площадь поперечного сечения стержня на
втором участке, равную см2, нам
необходимо увеличить.
Несложный анализ показывает, что на других участках
стержня условие прочности выполняется.
Из условия прочности определяем требуемую площадь
поперечного сечения стержня на втором участке:
см2.
Принимаем на втором участке см2.
Вычисляем
удлинение всего стержня
При переменных по длине стержня значениях продольной
силы и площади поперечного сечения удлинение вычисляется по формуле

где E – модуль Юнга, а – длина
соответствующего участка стержня.
Тогда

Таким образом, длина стержня уменьшается на мм.
Задания для решения работы
Условие задачи:
Стальной стержень (модуль Юнга кН/см2)
находится под действием внешних осевых сил и
.
Построить эпюры продольных сил и нормальных напряжений
.
Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2,
а допускаемый коэффициент запаса . Найти удлинение стержня
.
Схемы для задачи:
Рисунок
11
Исходные данные к задаче:
|
Номер схемы |
F, см2 |
a, м |
b, м |
c, м |
P, кН |
|
1 |
2,0 |
1,2 |
1,4 |
1,6 |
11 |
|
2 |
2,2 |
1,4 |
1,6 |
1,4 |
12 |
|
3 |
2,4 |
1,8 |
1,6 |
1,2 |
13 |
|
4 |
2,6 |
1,6 |
2,0 |
1,0 |
14 |
|
5 |
2,8 |
2,0 |
1,8 |
1,2 |
15 |
|
6 |
3,0 |
2,2 |
1,6 |
1,4 |
16 |
|
7 |
3,2 |
2,4 |
1,4 |
1,6 |
17 |
|
8 |
3,4 |
2,6 |
1,2 |
1,8 |
18 |
|
9 |
3,6 |
2,8 |
1,0 |
1,4 |
19 |
|
0 |
3,8 |
2,4 |
1,6 |
1,2 |
20 |
Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.
Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!
Что же давай приступим к изучению!
Построение эпюры продольных сил
В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.
Что такое эпюра?
Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.
Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.
Что такое продольная сила?
Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.
Расчёт эпюры продольных сил
Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.
То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.
Правило знаков для продольных сил
Правило знаков для продольных сил следующее:
- если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
- если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках
На первом участке сила F1 растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F1, также действует сила F2, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:
Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке
Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.
Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.
Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:
То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.
Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:
А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.
Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.
Построение эпюры нормальных напряжений
В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.
Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.
Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A1=2 см2, а на втором и третьем A2 = A3 = 4 см2.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.
Построение эпюры осевых перемещений поперечных сечений
Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.
Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:
Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.
Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:
А также удлинения (или укорочения) участка между расчетными сечениями:
В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).


Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.
Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.
Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину WD (т. к. значение WD — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.
Учёт распределённой нагрузки
А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил
На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:
Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:
Рассчитываем продольную силу на третьем участке:
Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений
Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений
Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче:


Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):


Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.



Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.
То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.
Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:


Отмечаем найденное значение на эпюре перемещений:

Распределение и формула нормальных напряжений
Из гипотезы плоских сечений следует: все продольные волокна стержня деформируются одинаково. Поэтому можно считать, что при растяжении (сжатии) напряжения во всех точках поперечного сечения стержня одинаковы и направлены по нормали к сечению. Такие напряжения, как уже отмечалось, называются нормальными напряжениями.
Из вышеизложенного вытекает формула нормальных напряжений при растяжении (сжатии):
где N – продольное усилие, возникающее в данном поперечном сечении стержня, а F – площадь этого поперечного сечения.
Правило знаков для нормального напряжения (