Содержание:
- Определение и формула напряженности магнитного поля
- Закон Био-Савара-Лапласа
- Единицы измерения
- Примеры решения задач
Определение и формула напряженности магнитного поля
Определение
Напряженностью магнитного поля $bar{H}$ называют
векторную физическую величину, направленную по касательной к силовым линиям поля, являющуюся характеристикой магнитного поля, равную:
$$bar{H}=frac{bar{B}}{mu_{0}}-bar{J}(1)$$
где $bar{B}$ – вектор магнитной индукции,
$mu_{0}=4 pi cdot 10^{-7}$ Гн/м(Н/А2)- магнитная постоянная,
$bar{j}$ – вектор намагниченности среды в исследуемой точке поля.
Для магнитного поля в вакууме напряженность магнитного поля определяется выражением:
$$bar{H}=frac{bar{B}}{mu_{0}}$$
В изотропной среде формула (1) преобразуется к виду:
$$bar{H}=frac{bar{B}}{mu_{0} mu}$$
где $mu$ – скалярная величина, называемая
относительной магнитной проницаемостью среды (или просто магнитной проницаемостью). В изотропной среде векторы напряженности
магнитного поля и магнитной индукции совпадают по направлению.
Иногда напряженность магнитного поля $d bar{H}$ определяют как
векторную величину, направленную по касательной к силовой линии поля, по модулю равной отношению силы (dF), с которой поле
воздействует на единичный элемент тока (dl), который расположен перпендикулярно полю в вакууме, к магнитной постоянной:
$$d H=frac{d F}{mu_{0} I d l}$$
Закон Био-Савара-Лапласа
Это важнейший в электромагнетизме закон. Он определяет вектор напряженности $d bar{H}$
в произвольной точке магнитного поля, которое создает в вакууме элементарный проводник длинны dl с постоянным током I:
$$d bar{H}=frac{1}{4 pi} frac{I}{r^{3}} d bar{l} times bar{r}(5)$$
где $d bar{l}$ – вектор элемента проводника, который по модулю равен длине
проводника, направление совпадает с направлением тока; $bar{r}$ – радиус–вектор,
который проводят от рассматриваемого элементарного проводника к точке рассмотрения поля;
$r=|bar{r}|$ .
Вектор $d bar{H}$ – перпендикулярен плоскости, в которой находятся
векторы $d bar{l}$ и
$bar{r}$, и направлен так, что из его конца вращение вектора
$d bar{l}$ по кратчайшему пути до совмещения с вектором
$bar{r}$ происходило по часовой стрелке. Для нахождения направления вектора
$d bar{H}$ можно использовать правило буравчика (Буравчик (винт) вращаем так,
чтобы его поступательное движение совпадало с направлением тока, тогда направление, по которому вращается ручка винта, совпадает с направлением
вектора напряженности поля, которое создает рассматриваемый ток).
Закон Био-Савара-Лапласа дает возможность вычислять величину полной напряженности магнитного поля, которое создает ток, текущий по проводнику любой формы.
Для нахождения полной напряженности магнитного поля, которое создает в исследуемой точке ток I, который течет по проводнику l, следует
векторно суммировать все элементарные напряженности $d bar{H}$, порождаемые
элементами проводника и найденные по формуле (4).
Единицы измерения
Основной единицей измерения момента силы в системе СИ является: [H]=А/м
Примеры решения задач
Пример
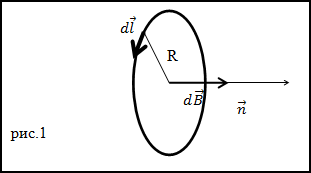
Задание. Чему равна напряженность (H) в центре кругового витка (R — радиус витка) с током I.
Решение. Каждый элементарный ток витка магнитное поле в центре окружности, напряженность которого направлена по
положительной нормали к плоскости контура витка (рис.1). Поэтому, если элементарную напряженность поля найти по закону Био-Савара –
Лапласа, то векторное сложение элементарных полей можно будет заменить на алгебраическое.
В соответствии с законом Био-Савара – Лапласа dH равно:
$$d bar{H}=frac{1}{4 pi} frac{I}{r^{3}} d bar{l} times bar{r}(1.1)$$
Применяя выражение (1.1) к нашему случаю, получим:
$$d H=frac{1}{4 pi} frac{I d l}{R^{2}}(1.2)$$
Возьмем интеграл по контуру, получим:
$$H=oint_{L} frac{1}{4 pi} frac{I d l}{R^{2}}=frac{1}{4 pi} I cdot frac{2 pi R}{R^{2}}=frac{I}{2 R}$$
Ответ. $H=frac{I}{2 R}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова напряженность магнитного поля, которую создает электрон, движущийся прямолинейно и равномерно со
скоростью v? Если точка, в которой исследуется поле, находится на расстоянии r от электрона на перпендикуляре к вектору скорости,
если перпендикуляр провести через мгновенное положение частицы.
Решение. Сделаем рисунок.
Напряженность магнитного поля будем искать, применяя закон Био – Савара – Лапласа:
$$d bar{H}=frac{1}{4 pi} frac{I}{r^{3}} d bar{l} times bar{r}(2.1)$$
Учтем, что:
$$I d l=S j d l(2.2)$$
Если все заряды одинаковы (q), то плотность тока равна:
$$bar{j}=q n bar{v}(2.3)$$
заряд отрицательный, следовательно, направления векторов
$bar{j}$ и
$bar{v}$ противоположны. n – концентрация зарядов. Подставим формулу (2.3)
в (2.2), результат в (2.1) получаем:
$$d bar{H}=frac{1}{4 pi} frac{S q n d l}{r^{3}} bar{v} times bar{r}(2.4)$$
где dN=Sdln — количество заряженных частиц в отрезке dl. В таком случае, напряженность поля, которое создает один заряд:
$$bar{H}=frac{d bar{H}}{d N}=frac{1}{4 pi} frac{q}{r^{3}} bar{v} times bar{r}(2.4)$$
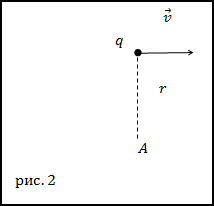
По условию задачи $bar{v} perp bar{r}$ , значит модуль напряжённости магнитного поля в точке А (рис.2) будет равен:
$$H=frac{1}{4 pi} frac{q v}{r^{2}}$$
Ответ. $H=frac{1}{4 pi} frac{q v}{r^{2}}$
Читать дальше: Формула напряженности электрического поля.
Принцип суперпозиции
(примеры решения задач)
Закон Кулона.
Электростатическое поле системы точечных
зарядов
Пример 1.1
В однородном электрическом поле
напряженностью
закреплен точечный отрицательный заряд
.
В точкеA, положение
которой определяется расстояниеми углом
(см.
рис.), модуль вектора напряженности
результирующего электрического поля.
Определите угол.
Решениe.
Напряженность результирующего поля
согласно принципу суперпозиции равна
,
гденапряженность
поля, создаваемого точечным зарядомqв точкеА(рис.)
|
|
.
По теореме косинусов
.
Учитывая, что по условию задачи,
получим для искомого угла:
.
Пример 1.2
Два
одинаковых небольших металлических
шарика с зарядами и
,
находящихся на расстоянии l = 0,2 м
друг от друга притягиваются с силой
H.
После того как шарики привели в
соприкосновение и опять развели на то
же расстояниеl,
они стали отталкиваться с силой
Н.
Найдитеи
.
Решение.
Так как в начале
шарики притягивались, то их заряды
противоположны по знаку и по закону
Кулона
(1)
После
того, как шарики были приведены в
соприкосновение, заряды перераспределяются,
и на каждом из шариков заряд, согласно
закону сохранения заряда, становится
равным
Поэтому они стали взаимодействовать с
силой
(2)
Уравнения
(1) и (2), дают систему уравнений для
неизвестных и
решив которую,
находим искомые заряды
Кл,
Кл.
Заметим,
что в соответствии с симметрией задачи
возможны и
такие значения зарядов:
Кл,
Кл.
Пример 1.3
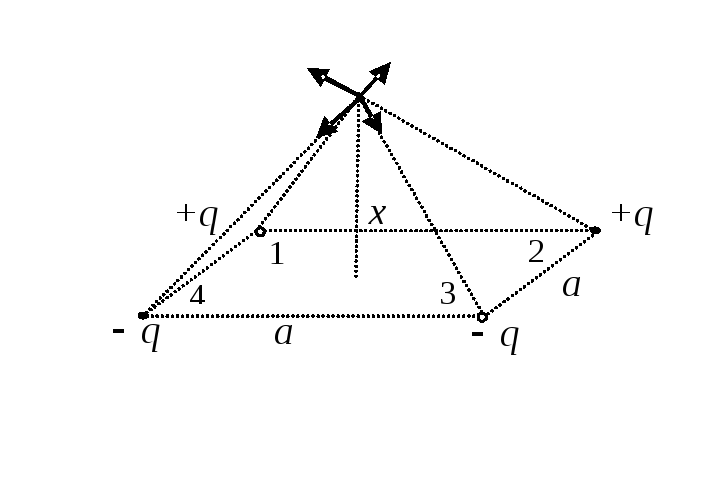
В вершинах квадрата, со стороной а,помещены четыре зарядаq(см. рис.).
Найдите напряженность электрического
поля на перпендикуляре, восстановленном
из центра квадрата, как функцию его
длины x.
Решение.
Из принципа суперпозиции полей,
результирующее поле, создаваемое
зарядами, равно:
|
|
|
=
,
где.
Задача сводится к суммированию четырех
равных по величине, но разных по
направлению векторов
.Найдем векторную сумму полей положительного
и отрицательного зарядов 1 и 3. Из подобия
треугольников на рисунке получим:
,
т.е..
Аналогично, складывая поля 2-го и 4-го
зарядов найдем
.
Для сложения векторови
учтем
их равенство по величине и взаимную
перпендикулярность. По теореме Пифагора,
получим
.
Пример 1.4
На рисунке изображена одна из линий
напряженности электрического поля двух
неподвижных точечных зарядов
и
.
Известно, что нКл.
Определите.
|
|
Решение.
Введем систему координат, выбрав ее,
как показано на рисунке, т.е. ось xпроходит через заряды, а осьyпроходит через «вершину» линии поля.
Так как вектор поля направлен по
касательной к линии поля, то в точке
«вершины»Еy= 0. По принципу суперпозиции для поля
в этой точке имеем:
,
где
,
.
После подстановки и преобразований,
найдем, взяв значения геометрических
параметров из рисунка в условии задачи
a1 =2, a2
= 8, b = 4:

Электростатическое
поле заряженных тел (непрерывное
распределение зарядов)
Пример 1.5
На единицу длины
тонкого однородно заряженного стержня
АВ,имеющего форму дуги окружностирадиуса R
с центром в точке О,
приходится заряд
.
Найдите модуль напряженности электрического
поля в точкеО,
если угол АОВ
равен
.
Решение.
Выберем оси координат так, чтобы начало
координат совпадало с точкой О, а
осьубыла симметрично расположена
относительно концов дугиАВ(рис.).
Разобьем стержень на элементарные
участки длины dl с зарядом,
который можно рассматривать как точечный.
|
|
Найдем напряженность поля, создаваемого
зарядом этого элементарного участка
стержня в точке 0:
,
где
—
радиус вектор, направленный от элементаdlк точке, напряженность
которой вычисляется. Напряженность
результирующего поля найдем,
воспользовавшись принципом суперпозиции.
В силу симметрии результирующее поле
будет направлено вдоль осиу(рис.).
Запишем выражение для проекции:
.
Приведем правую часть последнего
уравнения к одной переменной интегрирования
– углу
(учитывая, что
)
.
Проинтегрировав левую часть полученного
уравнения от
доE, а правую от
до
,
найдем модуль напряженности электрического
поля, создаваемого в точкеОдугойАВ:
.
Рассмотрим специальные случаи
использования формулы для
расчета поля, создаваемого частью дуги
окружности в ее центре
:
а) Модуль напряженности электрического
поля, создаваемого 1/4 части дуги окружности
радиуса Rв ее центре:
.
б) Модуль напряженности электрического
поля, создаваемого тонким полукольцом
радиуса Rв его центре:
.
в) Модуль напряженности электрического
поля, создаваемого тонким кольцом
радиуса Rв его центре:
.
г) Модуль напряженности электрического
поля в центре тонкого кольца радиуса
R, если половины этого
кольца заряжены разноименными зарядами
с линейными плотностями зарядаи
.
Напряженность электрического поля,
создаваемого каждой из половинок равна:
,
.
С
принципу суперпозиции найдем результирующее
поле в центре
.
Из рисунка видно, что направления
векторов
и
совпадают,
поэтому результирующее поле в центре
такого кольца равно
.
Соседние файлы в папке Примеры решений
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вы здесь
Напряженность магнитных полей токов
СОДЕРЖАНИЕ
- Напряженность магнитных полей токов
- Литература
Напряженность магнитных полей токов
Силовыми линиями магнитного поля называют такие линии, касательные к которым совпадают с направлением напряженности этого поля в данной точке. Магнитные силовые линии поля замкнуты (и отличие от силовых линий электростатического поля); такие поля называют вихревыми (рис.1, 2).
Рис.1. Силовые линии магнитного поля кругового тока обнаруживаемые по действию поля на железные опилки
Рис.2. Силовые линии магнитного поля соленоида, обнаруживаемые по действию поля на железные опилки
Силовые линии прямолинейного тока представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной к проводнику (рис.3). Направление силовой линии магнитного поля определяется по правилу правого винта: если винт поворачивать так, чтобы он поступательно перемещался по направлению тока, то направление вращения его головки будет совпадать с направлением силовых линии.
Рис.3. К закону Био-Савара-Лапласа. Правило винта
Напряженность магнитного поля, отдаваемая элементом тока i·Δl равна в системе СГСМ (рис.3)
 |
1) |
 |
2) |
где
| r | — | расстояние от элемента тока до точки, в которой определяйся напряженность; |
| α | — | угол между r и i·Δl. |
Напряженность магнитного поля прямого длинного провода с током (эта и нижеследующие формулы даны в системах СГСМ и СИ):
 |
3) |
где
| а | — | расстояние от проводника до точки поля, в которой определяется напряженность. |
Напряженность магнитного поля в центре кругового тока:
 |
4) |
где
Напряженность поля внутри тороидальной катушки (рис.4):
 |
5) |
где
| N | — | полное число витков; |
| r | — | средний радиус тороида. |
Рис.4. Тороидальная катушка (тороид)
Напряженность поля внутри прямого соленоида, длина которого значительно больше диаметра витков:
где
| n | — | число витков на единицу длины соленоида. |
Напряженность поля в таком соленоиде имеет одинаковые величину и направление во всех точках, т. е. поле однородно.
Напряженность поля движущейся заряженной частицы (рис.5):
 |
7) |
где
| v | — | скорость частицы; |
| r | — | расстояние от частицы до точки поля, в которой определяется напряженность; |
| υ | — | угол между направлением скорости и прямой, проведен¬ной от частицы в данную точку поля. |
Рис.5. Магнитное поле движущейся частицы
Единицей напряженности магнитного поля в системе СГСМ является эрстед (Э), в системе СИ – ампер на метр (А/м). 1 А/м – это напряженность магнитного поля, создаваемого прямолинейным бесконечно длинным проводником с током в 4π А на расстоянии 2 м от него. 1 Э – это напряженность магнитного поля, создаваемого прямолинейным бесконечно длинным проводником с током 1 ед. СГСМ (10 А) на расстоянии 2 см от него:
ЛИТЕРАТУРА
- Справочник по элементарной физике / Н.И. Кошкин, М.Г. Ширкевич. М.: Наука. 1976. 255 с.
- 6716 просмотров
Напряженность поля: задачи второго уровня.
В этой статье собраны не очень сложные задачи, однако тем, кто только начинает разбираться с этой темой, я рекомендую начать с задач попроще. Для решения предложенных в этой статье задач понадобится знание элементарной геометрии.
Задача 1.
Найти напряженность электрического поля в точке, находящейся посередине между точечными зарядами нКл и
нКл. Расстояние между зарядами
см. В какой точке прямой, проходящей через оба заряда, напряженность электрического поля равна
?
Задача 1.
Первый вопрос задачи. Напряженность, создаваемая первым зарядом:
Напряженность, создаваемая вторым зарядом:
Обратим внимание на то, что вектор напряженности направлен от первого заряда, а вектор
— ко второму.
Итоговая напряженность поля в данной точке – векторная сумма напряженностей и
. Но, так как направлены вектора будут в данном случае по одной прямой, можно просто сложить их модули (заряды разноименные и оба вектора имеют одно и то же направление):
Ответ: кВ/м
Второй вопрос задачи: обозначим расстояние до искомой точки . Тогда, поскольку, повторюсь, заряды разноименные и суммарная напряженность – векторная сумма двух разнонаправленных векторов, то очевидно, что эти вектора обязаны быть равными по длине, чтобы друг друга полностью компенсировать (погасить):
Можно воспользоваться свойством пропорции:
Решим квадратное уравнение:
Отрицательный корень отбрасываем, он не имеет физического смысла:
Ответ: 64,7 см – от второго заряда.
Задача 2.
Два заряда Кл и
Кл помещены на расстоянии
см друг от друга. Определить напряженность поля в точке, удаленной от первого заряда на
см, и от второго на расстояние
см.
Задача 2.
Точки расположения зарядов и точка, в которой будем определять напряженность, образуют прямоугольный (египетский) треугольник. Поэтому суммарную напряженность можно найти по теореме Пифагора (между векторами и
угол в
), кроме того, оба вектора направлены от зарядов, так как оба они положительные.
Напряженность, создаваемая первым зарядом:
Напряженность, создаваемая вторым зарядом:
Теперь определим суммарную напряженность:
Ответ: В/м.
Задача 3.
Электрическое поле создано двумя одинаковыми зарядами, находящимися на некотором расстоянии друг от друга. На таком же расстоянии от одного из них по прямой линии, проходящей через оба заряда, напряженность электрического поля В/м. Определить напряженность электрического поля в точках пространства, находящихся на одинаковых расстояниях от зарядов, равных расстоянию между зарядами.
Задача 3.
Так как оба заряда одноименные, то напряженность поля в точке 3 является суммой векторов напряженностей и
.
Найдем теперь напряженности поля в точках 1 и 2. Очевидно, что направления векторов различны, но модули напряженностей одинаковы.
Ответ: 0,346 В/м
Задача 4.
Диполь образован двумя разноименными зарядами, по нКл каждый. Расстояние между зарядами
см. Найти напряженность электрического поля: a) на продолжении оси диполя на расстоянии
см от его центра; б) на перпендикуляре к оси диполя, проведенном через его середину, на том же расстоянии. Как убывает поле диполя при
?
На рисунке вектора изображены с учетом того, что заряд положительный, а
— отрицательный.
Задача 4.
а)
Разность напряженностей (вектора направлены в разные стороны):
При
б) Определим сначала расстояния от зарядов до точки наблюдения:
Модули напряженностей:
Чтобы сложить вектора, понадобится знать косинус угла , а он равен синусу
:
Тогда векторная сумма напряженностей равна:
При
Ответ: а) В/м, б) 1080 В/м
Задача 5.
Тонкий стержень согнут в виде окружности радиусом м так, что между его концами остался воздушный промежуток
м. По стержню равномерно распределен заряд
Кл. Определить напряженность поля в центре окружности.
Задача 5.
Так как стержень согнут в кольцо, то вектора напряженностей ото всех элементарных элементов этого кольца направлены внутрь, поэтому вектора напряженностей от противолежащих элементов друг друга компенсируют. Только вектора элементов, находящихся напротив разрыва, не будут скомпенсированы. Длина участка кольца, где находятся эти элементы, равна . Так как заряд равномерно распределен по кольцу, найдем, какая часть заряда приходится на этот участок:
Тогда напряженность поля равна:
Ответ: 0,0761 В/м
Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
В соответствии с теорией близкодействия, взаимодействия между заряженными телами, которые удалены друг от друга, осуществляется посредством полей (электромагнитных), создаваемых этими телами в окружающем их пространстве. Если поля создаются неподвижными частицами (телами), то поле является электростатическим. Если поле не изменяется во времени, то его называют стационарным. Электростатическое поле является стационарным. Это поле — частный случай электромагнитного поля. Силовой характеристикой электрического поля служит вектор напряженности, который можно определить как:
где $overrightarrow{F}$- сила, действующая со стороны поля на неподвижный заряд q, который называют иногда «пробным». При этом необходимо, чтобы «пробный» заряд был мал, чтобы не искажал поле, напряженность которого с его помощью измеряют. Из уравнения (1) видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный «пробный заряд».
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Напряженность электростатического поля не зависит от времени. Если напряженность во всех точках поля одинакова, то поле называют однородным. В противном случае поле неоднородно.
Силовые линии
Для графического изображения электростатических полей используют понятие силовых линий.
Определение
Силовыми линиями или линиями напряженности поля, называются линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.
Силовые линии электростатического поля являются разомкнутыми. Они начинаются на положительных зарядах и заканчиваются на отрицательных. Иногда они могут уходить в бесконечность или приходить из бесконечности. Силовые линии поля не пересекаются.
Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:
[overrightarrow{E}=sumlimits^n_{i=1}{{overrightarrow{E}}_i(2)}.]
Результирующий вектор напряженности поля может быть найден как векторная сумма напряженностей составляющих его «отдельных» полей. Если заряд распределен непрерывно (нет необходимости учитывать дискретность), то суммарная напряженность поля найдется как:
[overrightarrow{E}=int{doverrightarrow{E}} left(3right).]
В уравнении (3) интегрирование проводят по области распределения зарядов. Если заряды распределены по линии ($tau =frac{dq }{dl}$ -линейная плотность распределения заряда), то интегрирование в (3) проводят по линии. Если заряды распределены по поверхности и поверхностная плотность распределения $sigma=frac{dq }{dS}$, то интегрируют по поверхности. Интегрирование проводят по объему, если имеют дело с объемным распределением заряда: $rho =frac{dq }{dV}$, где $rho $ — объемная плотность распределения заряда.
Напряженность поля
«Вектор напряженности электрического поля» 👇
Напряжённость поля в диэлектрике равна векторной сумме напряженностей полей, которые создают свободные заряды ($overrightarrow{E_0}$) и связанные заряды ($overrightarrow{E_p}$):
[overrightarrow{E}=overrightarrow{E_0}+overrightarrow{E_p}left(4right).]
Очень часто в примерах мы сталкиваемся с тем, что диэлектрик является изотропным. В таком случае, напряжённость поля может быть записана как:
[overrightarrow{E}=frac{overrightarrow{E_0}}{varepsilon } left(5right),]
где $varepsilon $- относительная диэлектрическая проницаемость среды в рассматриваемой точке поля. Таким образом, из (5) очевидно, что однородном в изотропном диэлектрике напряженность электрического поля в $varepsilon $ раз меньше, чем в вакууме.
Напряженность электростатического поля системы точечных зарядов равна:
[overrightarrow{E}=frac{1}{4pi {varepsilon }_0}sumlimits^n_{i=1}{frac{q_i}{varepsilon r^3_i}}overrightarrow{r_i} left(6right).]
В системе СГС напряженность поля точечного заряда в вакууме равна:
[overrightarrow{E}=frac{qoverrightarrow{r}}{r^3}left(7right).]
Пример 1
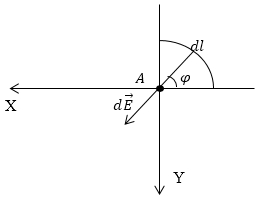
Задание: Заряд равномерно распределен по четверти окружности радиуса R с линейной плотностью $tau $. Найти напряженность поля в точке (А), которая была бы центром окружности.
Решение:
Рис. 1
Выделим на заряженной части окружности элементарный участок ($dl$), который будет создавать элемент поля в точке А, для него запишем выражение для напряженности (будем использовать систему СГС), в таком случае выражение для $doverrightarrow{E}$ имеет вид:
[doverrightarrow{E}=frac{dq}{R^3}frac{overrightarrow{R}}{R} left(1.1right).]
Проекция вектора $doverrightarrow{E}$ на ось OX имеет вид:
[{dE}_x=dEcosvarphi =frac{dqcosvarphi }{R^2}left(1.2right).]
Выразим dq через линейную плотность заряда $tau $:
[dq=tau dl=tau cdot 2pi RdR left(1.3right).]
Используя (1.3) преобразуем (1.2), получим:
[{dE}_x=frac{2pi Rtau dRcosvarphi }{R^2}=frac{2pi tau dRcosvarphi }{R}=frac{tau cosvarphi dvarphi }{R} left(1.4right),]
где $2pi dR=dvarphi $.
Найдем полную проекцию $E_x$, интегрированием выражения (1.4) по $dvarphi $, где угол изменяется $0le varphi le 2pi $.
[E_x=intlimits^{2pi }_0{frac{tau cosvarphi d varphi }{R}}=frac{tau }{R}intlimits^{2 pi}_0{cosvarphi d varphi=}frac{tau}{R}left({left.sinvarphi right|}^{2pi }_0right)=frac{tau }{R} left(1.5right).]
Займемся проекцией вектора напряженности на ос OY, по аналогии без особых пояснений запишем:
[{dE}_y=dEsinvarphi =frac{tau }{R}sinvarphi d varphi left(1.6right).]
Интегрируем выражение (1.6), угол изменяется $frac{pi }{2}le varphi le 0$, получаем:
[E_y=intlimits^0_{frac{pi }{2}}{frac{tau }{R}sinvarphi dvarphi =frac{tau }{R}intlimits^0_{frac{pi }{2}}{sinvarphi dvarphi =- frac{tau }{R}} }{left.cosvarphi right|}^0_{frac{pi }{2}}=- frac{tau }{R} left(1.7right).]
Найдем модуль вектора напряженности в точке А, используя теорему Пифагора:
[E=sqrt{{E_x}^2+{E_y}^2}=sqrt{{left(frac{tau }{R}right)}^2+{left(-frac{tau }{R}right)}^2}=frac{tau }{R}sqrt{2}]
Ответ: Напряженность поля в точке (А) равна $E=frac{tau }{R}sqrt{2}.$
Пример 2
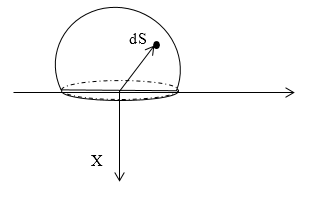
Задание: Найдите напряженность электростатического поля равномерно заряженной полусферы, радиус которой равен R. Поверхностная плотность заряда равна $sigma$.
Решение:
Рис. 2
Выделим на поверхности заряженной сферы элементарный заряд $dq$, который расположен на элементе площади $dS.$ В сферических координатах $dS$ равен:
[dS=R^2sintheta dtheta dvarphi left(2.1right),]
где $0le varphi le 2pi , 0le theta le frac{pi }{2}.$
Запишем выражение для элементарной напряженности поля точечного заряда в системе СИ:
[doverrightarrow{E}=frac{dq}{{4pi {varepsilon }_0R}^3}frac{overrightarrow{R}}{R} left(2.2right).]
Проектируем вектор напряженности на ось OX, получим:
[{dE}_x=frac{dqcostheta }{4 pi varepsilon_0R^2}left(2.3right).]
Элементарный заряд выразим через поверхностную плотность заряда, получим:
[dq=sigma dS left(2.4right).]
Подставляем (2.4) в (2.3), используем (2.1) интегрируем, получаем:
[E_x=frac{sigma R^2}{4pi {varepsilon }_0R^2}intlimits^{2pi }_0{dvarphi intlimits^{frac{pi }{2}}_0{costheta }}sintheta dtheta =frac{sigma}{4pi {varepsilon }_0}left(2pi cdot frac{1}{2}right)=frac{sigma}{4{varepsilon }_0}.]
Легко получить, что $E_Y=0.$
Следовательно, $E=E_x.$
Ответ: Напряженность поля полусферы заряженной по поверхности в ее центре равна $E=frac{sigma}{4{varepsilon }_0}.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме