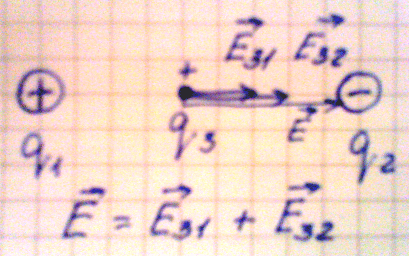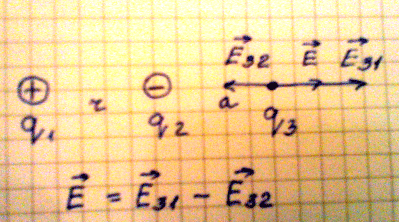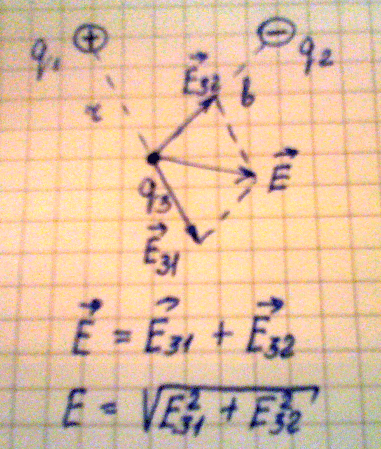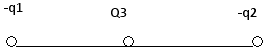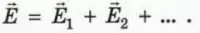Как найти напряженность поля в этой точке

Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.

Задачи урока:

• формирование понятия напряжённости электрического поля; дать понятие о
  линиях напряжённости и графическое представление электрического поля;
• научить учащихся применять формулу E=kq/r² в решении
  несложных задач на расчёт напряжённости.

Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.

Графически изображая поле, следует помнить, что линии напряженности
электрического поля:

1. нигде не пересекаются друг с другом;
2. имеют начало на положительном заряде (или в бесконечности) и конец на
   отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями;
3. между зарядами нигде не прерываются.

Рис.1

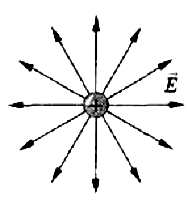
Силовые линии положительного заряда:

Рис.2

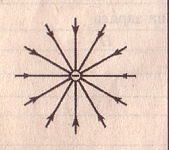
Силовые линии отрицательного заряда:

Рис.3

Силовые линии одноименных взаимодействующих зарядов:

Рис.4

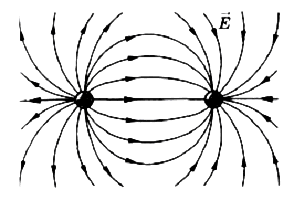
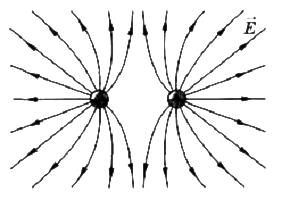
Силовые линии разноименных взаимодействующих зарядов:

Рис.5

Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
или
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда

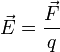
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда

где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.

В системе СИ
Н·м²/Кл²,

где ε₀ – электрическая
постоянная, равная 8,85·10^-12 Кл²/Н·м²;

q – электрический заряд (Кл);

r – расстояние от заряда до точки в которой определяется напряженность.

Направление вектора напряженности совпадает с направлением силы Кулона.

Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.

Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:

Рассмотрим несколько случаев определения напряженности.

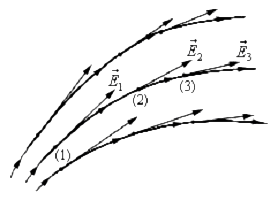
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:

Е₃₁ – напряженность точечного заряда 3 со стороны заряда 1;

Е₃₂ – напряженность точечного заряда 3 со стороны заряда 2.

Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е₃₁ и Е₃₂.

Напряженность в данной точке определяется по формуле:

Е = kq₁/x² + kq₂/(r – x)²

где: r – расстояние между первым и вторым зарядом;

х – расстояние между первым и точечным зарядом.

Рис.6

2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е₃₁ и Е₃₂.

Формула напряженности в данной точке равна:

Е = kq1/(r + a)² – kq₂/a²

Где: r – расстояние между взаимодействующими зарядами;

а – расстояние между вторым и точечным зарядом.

Рис.7

3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:

Е = (Е₃₁² +Е₃₂²)^1/2

Следовательно:

Е = ((kq₁/r² )² + (kq₂/b²)²)^1/2

Рис.8

Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.

4. Закрепление темы.

Проверочная работа.

Вариант № 1.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: электрическое поле – это ….

3. Как направлены силовые линии напряженности данного заряда?

4. Определить знаки зарядов:

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Вариант № 2.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: напряженностью называется …

3. Как направлены силовые линии напряженности данного заряда?

4. Определить заряды.

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Задачи на дом:

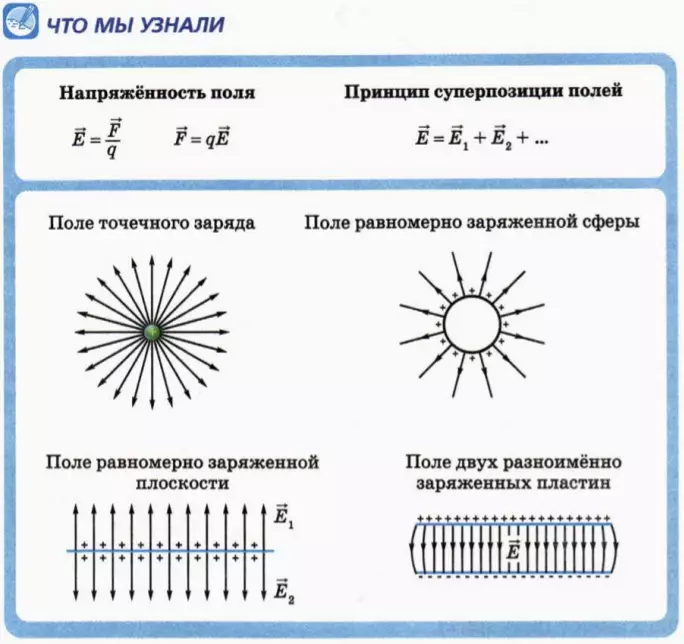
1. Определение напряженности

Как вы уже знаете из курса физики основной школы, электрическое взаимодействие заряженных тел осуществляется посредством электрического поля: каждое заряженное тело создает вокруг себя электрическое поле, которое действует на другие заряженные тела. Представление об электрическом поле ввел английский ученый Майкл Фарадей в первой половине 19-го века.

Электрическое поле в данной точке пространства можно охарактеризовать с помощью силы, действующей со стороны этого поля на точечный заряд, помещенный в данную точку. (Этот заряд должен быть достаточно мал, чтобы создаваемое им поле не изменяло распределения зарядов, которые создают данное поле.)

Как показывает опыт, сила 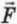, действующая на заряд q, пропорциональна величине этого заряда. Следовательно, отношение силы к заряду не зависит от величины заряда и характеризует само электрическое поле.

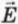
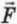
Напряженностью электрического поля в данной точке называют физическую величину, равную отношению силы , действующей со стороны поля на заряд q, помещенный в данную точку поля, к величине этого заряда:

Напряженность поля – векторная величина. Ее направление в каждой точке совпадает с направлением силы, действующей на положительный заряд, помещенный в эту точку.

Единицей напряженности поля является 1 Н/Кл. 1 Н/Кл – небольшая напряженность. Например, напряженность электрического поля вблизи поверхности Земли, обусловленная электрическим зарядом Земли, составляет примерно 130 Н/Кл.

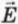
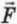
Если известна напряженность поля в данной точке, то можно найти силу , действующую на заряд q, помещенный в эту точку, по формуле

Из формул (1) и (2) следует, что направление напряженности поля в данной точке совпадает с направлением силы, действующей на положительный заряд, помещенный в эту точку.

Напряженность поля точечного заряда

Если внести в поле положительного точечного заряда Q другой положительный заряд, он будет отталкиваться от заряда Q.

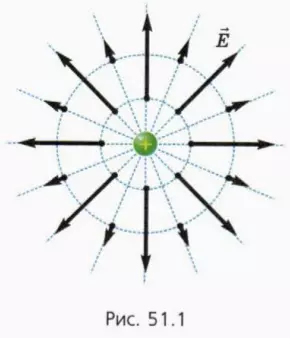
Следовательно, напряженность поля положительного точечного заряда во всех точках пространства направлена от этого заряда. На рисунке 51.1 изображены векторы напряженности поля точечного заряда в некоторых точках. Видно, что при удалении от заряда модуль напряженности поля уменьшается.

? 1. Объясните, почему модуль напряженности поля точечного заряда Q на расстоянии r от заряда выражается формулой

Подсказка. Воспользуйтесь законом Кулона и определением напряженности поля.

? 2. Чему равна напряженность поля точечного заряда 2 нКл на расстоянии 2 м от него?

? 3. Модуль напряженности поля точечного заряда на расстоянии 0,5 м от него равен 90 Н/Кл. Чему может быть равен этот заряд?

Принцип суперпозиции полей

Если заряд находится в поле, созданном несколькими зарядами, то каждый из этих зарядов действует на данный заряд независимо от других.

Отсюда следует, что равнодействующая сил, действующих на данный заряд со стороны других зарядов, равна векторной сумме сил, действующих на данный заряд со стороны каждого из остальных зарядов.

Это означает, что справедлив принцип суперпозиции полей:

напряженность поля, созданного несколькими зарядами, равна векторной сумме напряженностей полей, созданных каждым из зарядов:

Используя принцип суперпозиции, можно найти напряженность поля, создаваемого несколькими зарядами.

? 4. Два точечных заряда расположены на расстоянии 60 см друг от друга. Модуль каждого заряда равен 8 нКл. Чему равен модуль напряженности поля, создаваемого этими зарядами:
а) в точке, расположенной на середине отрезка, соединяющего заряды, если заряды одноименные? разноименные?
б) в точке, находящейся на расстоянии 60 см от каждого заряда, если заряды одноименные? разноименные?

Для каждого из этих случаев сделайте в тетради чертеж, поясняющий решение.

2. Линии напряженности

На примере поля точечного заряда (рис. 51.1) можно заметить, что векторы напряженности электрического поля в разных точках пространства выстраиваются вдоль некоторых линий.

В случае точечного заряда эти линии представляют собой прямые лучи, проведенные из точки, в которой находится заряд. В поле, созданном несколькими зарядами, зти линии будут некоторыми кривыми, причем напряженность поля в каждой точке будет направлена по касательной к одной из таких линий.

Воображаемые линии, касательные к которым в каждой точке совпадают с направлением напряженности электрического поля, называют линиями напряженности электрического поля.

Линии напряженности начинаются на положительных зарядах и заканчиваются на отрицательных. Густота линий напряженности пропорциональна модулю напряженности.

? 5. Объясните, почему линии напряженности электрического поля не могут пересекаться.

Поля точечных зарядов

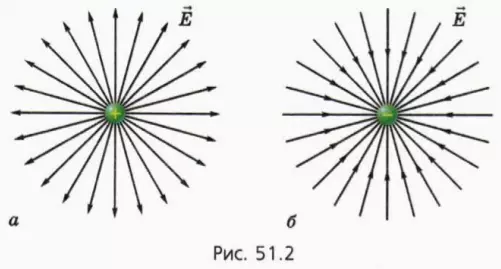
? 6. Объясните, почему линии напряженности электрического поля положительного и отрицательного точечных зарядов имеют вид, изображенный на рисунках 51.2, а и 51.2, б.

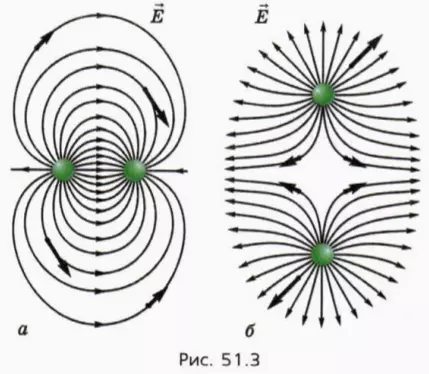
? 7. На рисунке 51.3 изображены линии напряженности поля, созданного одинаковыми по модулю зарядами (разноименными и одноименными). В некоторых точках для наглядности изображены векторы напряженности поля.

а) Перенесите рисунки в тетрадь и обозначьте на них знаки зарядов.
б) Изобразите в тетради линии напряженности поля, созданного двумя одноименными зарядами, которое не совпадает ни с одним из приведенных рисунков.
в) Чему равна напряженность поля в центральной точке рисунка 51.3, б (в середине отрезка, соединяющего заряды? Поясните ваш ответ с помощью закона Кулона.

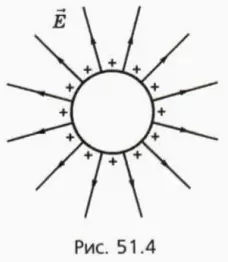
Поле равномерно заряженной сферы

На рисунке 51.4 изображены линии напряженности электрического поля равномерно заряженной сферы.

Мы видим, что вне сферы зто поле совпадает с полем точечного заряда, ровного суммарному заряду сферы и расположенного в центре сферы.
Можно доказать, что внутри заряженной сферы напряженность поля ровна нулю. (Доказательство этого факта выходит за рамки нашего круга.)

? 8. На сфере радиусом 5 см находится заряд 6 нКл. Чему равна напряженность поля этого заряда:
а) в центре сферы?
б) на расстоянии 4 см от центра сферы?
в) на расстоянии 10 см от центра сферы?
г) вне сферы на расстоянии 1 см от ближайшей к этой точке поверхности сферы?

Однако напряженность электрического поля внутри заряженной сферы не обязательно равна нулю! Если внутри этой сферы находится заряженное тело, то согласно принципу суперпозиции напряженность электрического поля равна векторной сумме напряженности поля, создаваемого зарядом этого тела, и напряженности поля, создаваемого зарядом сферы.

Внутри сферы поле создается только заряженным телом, находящимся внутри сферы, потому что напряженность поля, созданного заряженной сферой, внутри сферы равна нулю. А в любой точке вне сферы напряженность поля можно найти, складывая векторы напряженности поля, создаваемого телом, расположенным внутри сферы, и поля, создаваемого зарядом сферы.

? 9. Имеются две концентрические (имеющие общий центр) сферы радиусом 5 см и 10 см. Заряд внутренней сферы равен 6 нКл, а заряд внешней сферы равен –9 нКл. Чему равен модуль напряженности поля в точке, находящейся от общего центра сфер на расстоянии, равном:
а) 3 см; б) 6 см; в) 8 см; г) 12 см; д) 20 см?

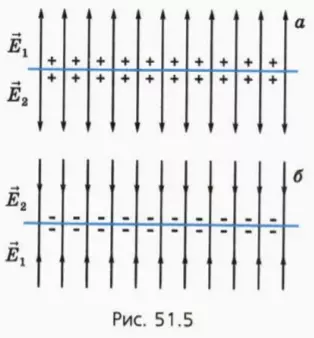
Поле равномерно заряженной плоскости

На рисунке 51.5 изображены линии напряженности электрического поля вблизи равномерно заряженной плоской пластины.

Будем считать, что размеры пластины намного больше расстояний от нее до тех точек пространства, в которых мы рассматриваем напряженность поля. В таких случаях говорят о поле равномерно заряженной плоскости.

Напряженность поля равномерно заряженной плоскости практически одинакова (по модулю и по направлению) во всех точках пространства по одну сторону от плоскости. Линии напряженности этого поля представляют собой параллельные прямые, перпендикулярные плоскости и расположенные на равных расстояниях друг от друга. Такое электрическое поле называют однородным.

По другую сторону плоскости изменяется только направление напряженности поля, а ее модуль остается таким же.

? 10. Напряженность электрического поля, создаваемого большой однородно заряженной пластиной, равна 900 Н/Кл. На расстоянии 40 см от пластины находится точечный заряд, равный по модулю 1 нКл.
а) На каком расстоянии от точечного заряда модуль напряженности его поля равен модулю напряженности поля пластины?
б) На каком расстоянии от плоскости результирующая напряженность поля плоскости и точечного заряда равна нулю, если знак точечного заряда совпадает со знаком заряда плоскости? Если знак точечного заряда противоположен знаку заряда плоскости?

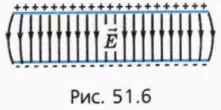
Поле двух разноименно заряженных плоских пластин

Возьмем две одинаковые равномерно заряженные пластины, заряды которых равны по модулю, но противоположны по знаку. Расположим пластины параллельно друг друту на малом расстоянии друг от друга (рис. 51.6).

? 11. Объясните, почему в пространстве между пластинами напряженность поля в 2 раза больше, чем напряженность поля, создаваемого каждой из пластин, а вне пластин практически равна нулю.
Подсказка. Воспользуйтесь принципом суперпозиции электрических полей.

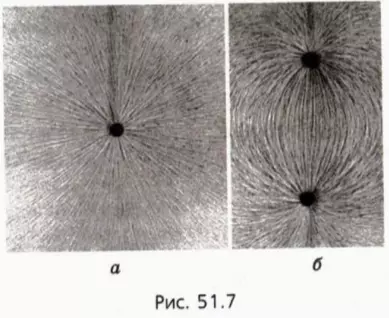
Как увидеть линии напряженности?

Поставим опыт
Поместим в электрическое поле состоящие из диэлектрика мелкие тела продолговатой формы – кристаллики, частицы манной крупы, мелко настриженные волосы и т. п. В электрическом поле они поворачиваются так, чтобы их более длинная сторона была направлена вдоль вектора напряженности поля. В результате эти тела выстраиваются вдоль линий напряженности, делая их форму видимой. На рисунке 51.7 приведены полученные таким образом «картины» электрических полей, создаваемых заряженным шариком (рис. 51.7, а) и двумя разноименно заряженными шариками (рис. 51.7, б).

Дополнительные вопросы и задания

12. Небольшой заряженный шарик массой 0,2 г подвешен на нити в однородном электрическом поле, напряженность которого направлена горизонтально и равна по модулю 50 кН/Кл.
а) Изобразите на чертеже положение равновесия шарика и силы, действующие на него.
б) Чему равен заряд шарика, если нить отклонена от вертикали на угол 30º?

13. Какова должна быть напряженность поля, чтобы капелька воды радиусом 0,01 мм находилась в этом поле в равновесии, потеряв 10³ электронов? Как должна быть направлена напряженность поля?

Рис. 3.1

Пример
1.
Два точечных электрических заряда Q₁
=
1нКл
и Q₂
=
-2 нКл
находятся
в воздухе на рас­стоянии d
= 10 см друг
от друга. Определить напря­женность
Е
и потенциал φ
поля, создаваемого этими зарядами в
точке А,
удаленной от заряда Q₁
на расстоя­ние r₁=
9 см и от
заряда Q₂
на r₂
= 7 см.
Определить также
силу F,
действующую в точке
А
на точечный заряд
Q
=10
нКл.

Решение.
Согласно принципу суперпозиции
элек­трических полей, каждый заряд
создает поле независимо от присутствия
в пространстве других зарядов. Поэтому
напряженность
электрического поля в искомой точке
может быть найдена как геометрическая
сумма напряженностей₁
и
₂
полей, создаваемых каждым зарядом в
отдельности:
.
Напряженности электриче­ского поля,
создаваемого в воздухе (ε=1)
зарядами Q₁
и Q₂,

;
.
(3.1)

Вектор
₁
(см. рис. 3.1) направлен по силовой линии
от заряда Q₁,
так как этот заряд положителен; вектор
₂
направлен также по силовой линии, но к
заряду Q₂,
так как этот заряд отрицателен.

Модуль
вектора
найдем по теореме косинусов:

,
(3.2)

где
– угол между векторами₁
и
₂,
,который
может
быть  найден  из  треугольника  со  сторонамиr₁,  r₂  и  d:

.
В данном случае во избежание громоздких
записей удобно значение cos α
вычислить отдельно:

.

Подставляя
выражение Е₁
и E₂
из (3.1) в (3.2) и вынося общий множитель
1/(4πε₀)
за знак корня, полу­чаем

. (3.3)

В
соответствии с принципом суперпозиции
электриче­ских полей, потенциал φ
результирующего
поля, созда­ваемого двумя зарядами
Q₁
и Q₂,
равен алгебраической сумме потенциалов:

φ=φ₁+φ₂. (3.4)

Потенциал
электрического поля, создаваемого в
ва­кууме точечным зарядом Q
на расстоянии r
от него, выра­жается формулой

. (3.5)

В нашем случае
согласно формулам (3.4) и (3.5) получим

,

или

.

Сила,
действующая на точечный заряд, находящийся
в электрическом поле в точке А

,

где напряженность
находится из выражения (3.3).

Произведем
вычисления:

;

.

П

Рис. 3.2.

ример 2. Три точечных
заряда Q₁=1
нКл, Q₂=
2 нКл и Q₃=
3 нКл расположены в вершинах
равностороннего треугольника, длина
стороны которого а= 5 см.
Определить напряженность поля в точке
А, находящейся
на пересечении биссектрис треугольника.

Решение.
Согласно принципу суперпозиции
элек­трических полей, каждый заряд
создает поле независимо от присутствия
в пространстве других зарядов. Поэтому
напряженность
электрического поля в искомой точке
может быть найдена как геометрическая
сумма напряженностей₁
и
₂
и
полей,
создаваемых каждым зарядом в отдельности:.
Напряженности электриче­ского поля,
создаваемого в воздухе (ε=1)
зарядами Q₁
и Q₂
и
Q₃:

; ;;.
(3.6)

Вектор
₁
(см. рис. 3.2) направлен по силовой линии
от заряда Q₁,
вектор
₂
направлен по силовой линии от заряда
Q₂
и вектор

₃
направлен
по силовой линии от заряда Q₃,
так как все заряды положительны.

Модуль
вектора
найдем из соотношения

,
(3.7)

где
и– проекции векторов_1
,2
и₃
на
координатные оси x
и y
(рис. 3.2).

,

.(3.8)

Подставляя
выражение Е₁
, Е₂
и E₃
из (3.6) в (3.8), получаем:

.
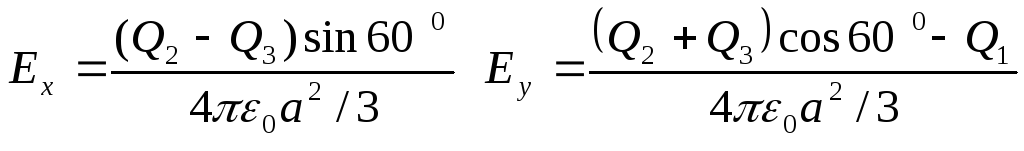
(3.9)

Модуль
вектора
находим, подставляя (3.9) в (3.7):.

Произведем
вычисления:

.

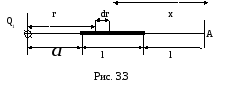
Пример
3. На тонком
стержне длиной l
= 10 см
нахо­дится равномерно распределенный
электрический заряд. На продолжении
оси стержня на расстоянии а
= 5 см от
ближайшего конца находится точечный
заряд Q₁=40
нКл, который
взаимодействует со стержнем с си­лой
F = 6 мкН.
Определить линейную плотность τ
заряда на стержне. Найти потенциал φ
в точке А,
расположенной на оси стержня и удаленной
от

его
ближайшего конца на расстояние l.

Решение.
Сила взаимодействия F
заряженного стержня с точечным зарядом
Q₁
зависит от линейной плотности τ
заряда на стержне. Зная эту зависимость,
можно определить τ.
При вычислении силы F
следует иметь в виду, что заряд на стержне
не является точеч­ным, поэтому закон
Кулона непосредственно применить
нельзя. В этом случае можно поступить
следующим образом. Выделим из стержня
(рис. 3.3) малый участок dr
с зарядом dQ
= τdr.
Этот заряд можно рассматривать как
точечный. Тогда, согласно закону Кулона:

.

Интегрируя
это выражение в пределах от а
до а+l,
получаем:

,

откуда

.

Проверим,
дает ли рас­четная формула единицу
линейной плотности электрического
заряда. Для этого в правую часть формулы
вместо символов величин подста­вим
их единицы:

Найденная единица
является единицей линейной плот­ности
заряда.

Произведем
вычисления:

.

Потенциал
dφ,
создаваемый точечным зарядом
в точке А (рис. 3.3), можно определить по
формуле

.

Согласно
принципу суперпозиции электрических
полей, потенциал электрического поля,
создаваемого заряженным стержнем в
точ­ке А, найдем интегрирова­нием
этого выражения:

.

Выполним
интегрирование:

.
(3.10)

Потенциал
в точке А по принципу суперпозиции
является суммой потенциалов, созданных
точечным зарядом
и стержнем с распределенным зарядом:,
где– потенциал в точке,
созданный зарядом;
а– потенциал в точке,
созданный стержнем и определяемый
выражением (3.10). Откуда

.

Подставим  числовые  значе­ния  физических  величин  в  СИ
(1/(4πε₀)=9^.10⁹
м/Ф,
Q₁=4^.
10^-8 Кл,
l=10^-1м,
а= 5^.10^-2
м, τ=10
^.10^-9
Кл/м)
и произведем вычис­ления:

φ=9
^.10⁹
(⁺1,25
^.10^-9
.0,693)=7,8
В.

Рис. 3.4

Рис.
3.4

Пример
4. По тонкой
нити, изогнутой по дуге окруж­ности,
равномерно распределен заряд с линейной
плот­ностью τ
= 10 нКл/м.
Определить напряженность
и потенциалφ
электрического поля, созда-ваемого
таким распределенным зарядом в точке,
совпадающей с цент­ром кривизны дуги.
Длина l
нити составляет ⅓ длины окружности и
равна 15 см.

Решение.
Выберем оси координат так, чтобы на­чало
координат совпадало с центром кривизны
дуги, а ось Оу была бы симметрично
расположена относительно концов дуги
(рис. 3.4). На нити выделим элемент длины
dl.
Заряд dQ=rdl,
находящийся на выделенном участке,
можно считать точечным.

Определим
напряженность электрического поля в
точке О. Для этого найдем сначала
напряженность dE
поля, создаваемого зарядом dQ:

,

где
– радиус-вектор, на­правленный от
элементаdl
к точке, в которой вычисляется
напряженность.

Выразим
вектор
через проекцииdE_x
и dE_y
на оси координат:

,

где
и– единичные векторы направлений (орты).
Напряженностьнайдем интегрированием:

.

Интегрирование
ведется вдоль дуги длиной l.
В силу симметрии
.
Тогда

, (3.11)

где
dE_y=dEcosθ=τdlcosθ/(4πε₀r²).
Так как r=R=const,
dl=Rdθ,
то

.

Подставим
выражение dE_y
в (3.11) и, приняв во внима­ние симметричное
расположение дуги относительно оси Оу,
пределы интегрирования возьмем от 0 до
π/3, а результат удвоим:

.

Выразив
радиус R
через длину l
нити (3l=2πR),
получим:

. (3.12)

Из
этой формулы видно, что напряженность
поля по направлению совпадает с осью
Оу.

Найдем
потенциал электрического поля в точке
О. Сначала найдем потенциал dφ,
создаваемый точечным зарядом dQ
в точке О:

.

Заменим
r
на R
и проведем интегрирование:

.

Так
как l
=
πR,
то
. (3.13)

Произведем
вычисления по формулам (3.12) и (3.13):

=2,17
кВ/м,

=188
В.

Рис. 3.5

Пример
5. По тон­кому
кольцу равномерно распределен заряд Q
= 50 нКл с
ли­нейной плотностью τ
= 40 нКл/м.
Опреде­лить напряженность Е
электрического поля, создаваемого этим
за­рядом в точке А, лежа­щей на оси
кольца и удаленной от его цен­тра на
расстояние, рав­ное половине радиуса.

Решение.
Совместим координатную плоскость хОу
с плоскостью коль­ца, а ось Oz – с осью
кольца (рис. 3.5). На кольце выделим малый
участок длиной dl.
Так как заряд dQ
= τ
dl, находящийся
на этом участке, можно считать точечным,
то напряженность

электрического поля, создаваемого этим
зарядом, может быть записана в виде

,

где
–
радиус-вектор, направленный от элементаdl
к точке А.

Разложим
вектор
на две
составляющие:
₁,
пер­пенди-кулярно плоскости кольца
(сонаправленную с осью Oz), и₂,
параллельную плоскости кольца (плос­кости
хОу), т.е.

=₁+₂.

Напряженность


электрического поля в точке А найдем
интегрированием:

,

где
интегрирование ведется по всем элементам
заряженно­го кольца. Заметим, что для
каждой пары зарядов dQ
и dQ’ (dQ=dQ’),
расположенных симметрично относительно
центра кольца, векторы dE₂
и dE₂’
в точке А равны по модулю и противоположны
по направлению:
₂=
—.
Поэтому векторная сумма (интеграл)
.
Состав­ляющиеdE₁
для всех элементов кольца сонаправлены
с осью Oz (единичным вектором
),
т.е.
₁=.
Тогда

.

Так
как
,и,
то

.

Таким образом,

.

Из
соотношения Q=2πRτ
определим радиус кольца:
.
Тогда

.

Модуль
напряженности
. (3.14)

Проверим,
дает ли правая часть полученного
равен­ства единицу напряженности,
В/м:

.

Выразим
физические величины, входящие в формулу
(3.14), в единицах СИ (τ=5^.10^-8
Кл/м,
Q=4^.10^-8Кл,
ε₀=8,85^.10^-12Ф/м)
и произведем вычисления:

.

Пример
6. Две
концентрические проводящие сферы
радиусами R₁=5
см и R₂
= 10 см
несут соответственно заряды Q₁
= 10 нКл
и Q ₂=-5
нКл. Найти
напряжен­ность Е
поля в точках, отстоящих от центра сфер
на рас­стояниях r₁
= 4 см,
r₂
= 8 см,
r₃
= 15 см.
Построить график Е(r).

Решение.
Заметим, что точки, в которых требуется
найти напряженности электрического
поля, лежат в трех областях (рис. 3.6):
обла­сти /(r₁<R₁),
области //(R₁<r₂<R₂),
области /// (r₃>R₂).

1. Для
определения на­пряженности Е₁
в области / проведем гауссову повер­хность
S₁
радиусом r₁
и воспользуемся теоремой Остроградского
– Гаусса:

(так
как суммарный заряд, находящийся внутри
гауссо­вой поверхности, равен нулю).
Из соображений симметрии E_n=E₁=const.
Следовательно,
иЕ₁
(напря­женность поля в области /) во
всех точках, удовлетворяю­щих условию
r₁<R₁,
будет равна нулю.

Рис. 3.6

2.
В области // гауссову поверхность проведем
радиу­сом r₂.
В этом случае диэлектрическую проницаемость
среды будем считать равной единице
(вакуум) и воспользуемся теоремой
Остроградского– Гаусса:

(так
как внутри гауссовой поверхности
находится только заряд Q₁).

Так
как Е_n=Е₂=const,
то Е можно
вынести за знак интеграла:

,
или
;

,

где
S₂=4πr₂²
– площадь гауссовой поверхности. Тогда

.
(3.15)

3.
В области /// гауссова поверхность
проводится ра­диусом r₃.
Обозначим напряженность E
области /// через Е₃
и учтем, что в этом случае гауссова
поверхность охватывает обе сферы и,
следовательно, суммарный заряд бу­дет
равен Q₁+Q₂.
Тогда

.

Заметив,
что Q₂<0,
это выражение можно переписать в виде

. (3.16)

Убедимся
в том, что правая часть равенств (3.15) и
(3.16) дает единицу напряженности:

. Выразим все величины в единицах СИ (Q₁
= 10^-8
Кл, Q₂
= —
5^.10^-9
Кл, r₁
= 0,08 м,
r₃
= 0,15 м,
1/(4πε₀)
= 9^.10⁹
м/Ф)
и произведем вычисления:

;

.

Построим
график Е(r).
В области / (r₁<R₁)
Е=0.
В области // (R₁≤r₂<R₂)
E₂(r)
изменяется по закону
.
В точкеr=R₁
напряженность E₂(R₁)
=

=36 кВ/м. В
точке r=R₂
(r стремится к R₂
слева) E₂(R₂)==
9 кВ/м.
В области /// (r>R₂)
E₃(r)
изменяется по закону
,
причем в точкеr=R₂
(r стре­мится к R₂
справа) E₃(R₂)
=

= 4,5 кВ/м.
Таким образом, функция Е(r)
в точках r=R₁
и r=R₂
терпит раз­рыв. График зависимости
E(r)
представлен на рис. 3.7.

Пример
7. В вакууме
имеется скопление зарядов в форме
длинного цилиндра радиуса R₀
= 2 cм.
Объемная
плотность зарядов
постоянна и равна2
мкКл/м³.
Найти напряженность поля в точках 1 и
2, лежащих на расстояниях r₁
= 1 cм,
r₂
= 3 cм
от оси цилиндра, и разность потенциалов
между этими точками. Построить графики
и.

Поле
создано зарядом, р

РРРИ

Рис.
3.8.

Рис.
3.8

авно-мерно распределенным по объему.
Конфигурация зарядов позволяет считать,
что поле обладает осевой симметрией:
силовые линии – прямые и в любой
плоскости, перпендикулярной оси цилиндра,радиальны
(рис. 3.8).

Вспомогательной
поверхности следует придать форму
цилиндрической поверхности, коаксиальной
заряду. Длина этого цилиндра может быть
произвольной, но заведомо много меньше,
чем длина заряженного цилиндра. Характер
функциональной зависимости
для точек, лежащих внутри и вне объемного
заряда, различен. Поэтому следует
провести две вспомогательные цилиндрические
поверхностиS₁
и S₂
с радиусами
и.

Определим
проекцию вектора E
на нормаль выбранной поверхности
Е_n1=E=const
и E_n2=0.
Поток через выбранную поверхность
цилиндра равен

(3.17)

где
h
– высота цилиндра.

Определим
заряд, попадающий внутрь выделенной
поверхности: при r<R₀

,
а приr>R₀

.
(3.18)

Применим
теорему Гаусса
,
используя выражение (3.17) и (3.18),
откуда

–напряженность
внутри цилиндра (3.19)

,
откуда

–напряженность
вне цилиндра. (3.20)

Для
определения разности потенциалов между
точками 1
и 2
разобьем 
на два интеграла: в пределах от точки 1
до поверхности, ограничивающей объемный
заряд, и от этой поверхности до точки
2:.
В первый интеграл следует подставлять
выражение  (3.19),  во  второй  выражение
(3.20):.
(3.21)

Подставляя
в (3.19) r=r₁
и в (3.20) r=r₂,
находим:

;

.

Вычислим численное
значение выражения (3.21):

.

Для
построения графика E_r(r)
на основании выражений (3.19) и (3.20)
целесообразно сначала рассчитать E_r
при r=R₀:

В/м.

Графическая
зависимость E_r(r)
показана на рис. 3.9.

График
зависимостиможно построить из анализа графикаE_r(r),
учитывая, что
.
Выберем начало отсчета на оси объемного
заряда:(0)=0.
Так как во всей области E_r>0,
т.е. (d/dr)<0,
то потенциал непрерывно убывает. В
области r<R₀
E_r
возрас-

тает

,
соответственно
и график(r)
обращен вогнутостью вниз. При
r>R₀
E_r
убывает
, соответственно

и график(r)
обращен вогнутостью вверх.

При
r=R₀
кривая (r)
имеет точку перегиба (вторая производная
изменяет знак). График (r)
изображен на рис. 3.10. Если изменить
начало отсчета потенциала, то характер
графика не изменяется, например, при
выборе начала отсчета на поверхности
объемного заряда
график примет вид, изображенный на рис.
3.10 пунктиром.

Пример
8. Электрическое
поле создается двумя зарядами Q₁
=2 мкКл
и Q₂
= -4 мкКл,
находящимися на расстоянии а=
0,2 м друг от
друга. Определить ра­боту A_1,2
сил поля по перемещению заряда Q=50
нКл из точки
1 в точку 2
(рис. 3.11).

Решение.
Для определения работы A_1,2
сил поля воспользуемся соотношением
A_1,2
=
Q(φ₁—φ₂).

Рис. 3.11

Применяя
принцип суперпозиции электрических
полей, определим по­тенциалы φ₁
и φ₂
точек 1 и
2 поля:

;

.

Тогда

,

или

.

Проверим, дает ли
правая часть равенства единицу работы
(Дж):

.

Подставим
числовые значения физических величин
в СИ:

(Q=50
^.10^-9Кл,
Q₁=2^.10^-6Кл,
Q₂=
4^.10^-6Кл,
a= 0,2 м,
)
и произведем вычис­ления:

.

Пример
9. Определить
ускоряющую разность потен­циалов U,
которую должен пройти в электрическом
поле электрон, обладающий скоростью
v₁=3^,10⁶м/с,
что­бы скорость его возросла в n
= 3 раза.

Решение.
Ускоряющую разность потенциалов можно
найти, вычислив работу А
сил электростатиче­ского поля. Эта
работа определяется произведением
эле­ментарного заряда е
на разность потенциалов U:

A=eU. (3.22)

Работа
сил электростатического поля в данном
слу­чае равна изменению кинетической
энергии электрона:

, (3.23)

где
Т₁
и Т₂
– кинетическая энергия электрона до и
после прохождения ускоряющего поля; m
– масса элект­рона; v₁
и v₂
– начальная и конечная скорости его.

Приравняв
правые части равенств (3.22) и (3.23), получим:

,
где
.

Отсюда
искомая разность потенциалов
.

Произведем
вычисления:

=
204,7 В.

Рис. 3.12

Пример
10.
С поверхности бесконечного равномерно
заряженного
(τ = 50 нКл/м)
прямого цилиндра вылетает α-частица
(v₀
= 0).
Определить кинетическую энергию T₂
α-частицы (кэВ)
в точке 2 на расстоянии 8R
от поверх­ности цилиндра (рис. 3.12).

Решение.
Так как силы электростатического поля
являются консервативными, то для
определения кинети­ческой энергии
α-частицы в точке 2 воспользуемся зако­ном
сохранения энергии, записанном в виде
W₁=W₂,
где W₁
и W₂
– полные
энергии α-частицы в точках 1 и 2.

Так
как W₁=T₁+U₁
и W₂=T₂+U₂
(T₁
и Т₂
– кине­тические энергии α-частицы;
U₁
и U₂
– потенциальные) , то, учитывая, что Т₁=0
(v₀=0),
можно записать U₁=T₂+U₂,
откуда Т₂=U₁-U₂=Q(φ₁-φ₂)
(Q
– заряд α-частицы; φ₁
и φ₂
– потенциалы точек 1 и 2).

Для
определения разности потенциалов
воспользуемся соотношением между
напряженностью по­ля и изменением
потенциала: Е=-gradφ.
Для поля с осевой симметрией, каким
является поле цилиндра, это соотношение
можно записать в виде

,
или dφ=-Edr.

Интегрируя
это выражение, найдем разность
потен­циалов двух точек, отстоящих
на расстояниях r₁
и r₂
оси цилиндра:

. (3.24)

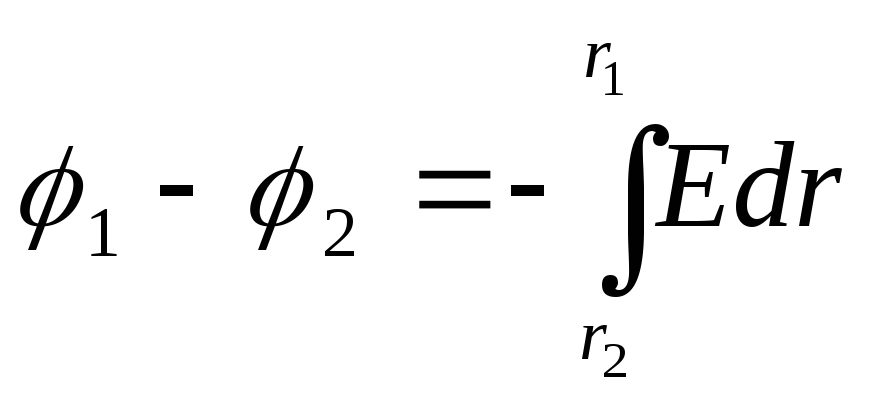
Так как цилиндр
длинный и точки взяты вблизи его средней
части, то для выражения напряженности
поля можно воспользоваться формулой
напряженности поля, создаваемого
бесконечно длинным цилиндром:

.

Подставив
это выражение в (3.24), получим:

.

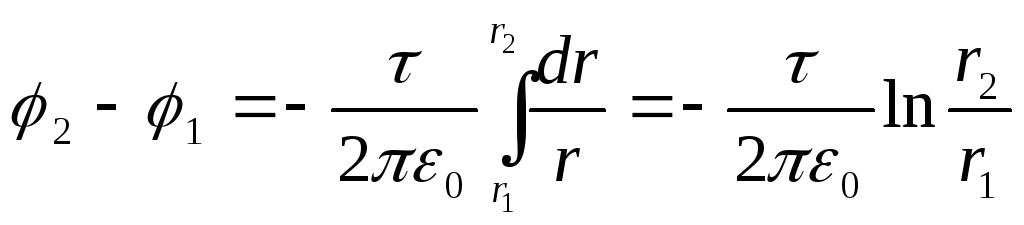
Учитывая,
что,
а,
запишем

.

Тогда

.

Выразим
все величины в единицах СИ (Q= 2^.1,60^.10^-19
Кл, τ= 50^.10^-9
Кл/м,
)
и произведем вычисления (—
коэффициент перевода из Дж
в эВ):

= = 3,96 кэВ.

Пример
11. Конденсатор
емкостью С₁=6
мкФ был
заряжен до разности потенциалов U₁=20
В. После
отключения от источника тока конденсатор
соединили параллельно с другим
незаряженным конденсатором емкостью
С₂=10
мкФ. Какая
энергия W’
израсходуется на образование искры в
момент присоединения второго конденсатора?

Решение.
Энергия, израсходованная на образо­вание
искры:

W’=W₁—W₂, (3.25)

где
W₁
– энергия, которой обладал первый
конденсатор до присоединения к нему
второго конденсатора; W₂
– энергия, которую имеет батарея,
составленная из двух конденсаторов.

Энергия заряженного
конденсатора определяется по формуле

W=½CU², (3.26)

где
С – емкость
конденсатора или батареи конденса­торов.

Выразив
в формуле (3.25) энергии W₁
и W₂
по фор­муле (3.26) и приняв во внимание,
что общая емкость параллельно соединенных
конденсаторов равна сумме емкостей
отдельных конденсаторов, получим

W’=½C₁U₁²-½(C₁+C₂)U₂², (3.27)

где
U₂
– разность потенциалов на зажимах
батареи конденсаторов.

Учитывая,
что заряд после присоединения второго
конденсатора остался прежним, выразим
разность потен­циалов U₂
следующим образом:

.

Подставив
выражение U₂
в (3.27)), найдем

,

или

.

Произведем
вычисления:

Дж=750
мкДж.

Пример
12. Потенциометр
сопро­тивлением R=150
Ом подключен к батарее с ЭДС
=300
В и внутрен­ним
сопротивлением R_i
= 50
Ом. Определить:
1) показание вольтметра сопротивлением
R_V
= 500 Ом,
соединенного с одной из клемм потенциомет­ра
и подвижным контактом, установленным
посередине потенциометра; 2) разность
потенциалов между теми же точками
потенциометра при отключении вольтметра.

Решение.
1. Показание вольтметра, подключенно­го
к точкам A
и В (рис. 3.13), определим по формуле

U₁=I₁R_1,

гдеR₁
– сопротивление параллельно соединенных
вольт­метра и половины потенциометра;
I₁
– суммарная сила тока в ветвях этого
соединения (она равна силе тока в
неразветвленной части цепи).

Силу
тока I₁
найдем по закону Ома для полной цепи:

I₁=/(R_e+R_i), (3.28)

где
R_e
– сопротивление внешней цепи. Это
сопротивле­ние есть сумма двух
сопротивлений:

R_e=R/2+R₁. (3.29)

Сопротивление
R₁
найдем по формуле параллельного
соединения проводников
,
откуда

Подставив
в (3.28) выражение R_e
по (3.29), найдем

.

В
данном случае решение задачи в общем
виде было бы громоздким. Поэтому удобно
вычисление величин провести раздельно:

=
65,22 Ом;

=
1,58 A;

U₁=1,58
^.65,22
= 103,04 B.

2.
Разность потенциалов между точками А
и В при отключенном вольтметре равна
произведению силы тока I₂
на половину сопротивления потенциометра:

,
(3.30)

где
I₂
– сила тока в цепи при отключенном
вольтметре. Ее определим по формуле

.

Подставив
выражение I₂
в (3.30), найдем

.

Произведем
вычисления:

=
112,5 В.

П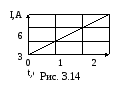ример
13. Сила тока
в проводнике сопротивлением R=20
Ом нарастает
в течение времени Δt
=2 с по
линей­ному закону от I₀=0
до I=6
А (рис. 3.14). Определить теплоту Q₁,
выделившуюся в этом проводнике за первую
секунду, и Q₂
– за вторую, а также найти отношение
.

Решение.
Закон Джоуля–Ленца в виде Q=I²Rt
справедлив для постоянного тока
(I=const).
Если же сила тока в проводнике изменяется,
то указанный закон справедлив для
бесконечно малого интервала времени и
записывается в виде

dQ=I²Rdt. (3.31)

Здесь
сила тока I
является некоторой функцией вре­мени.
В данном случае

I=kt,
(3.32)

где
k
— коэффициент про­порциональности,
характе­ризующий скорость измене­ния
силы тока:

.

С
учетом (3.32) формула (3.31) примет вид

dQ=k²Rt²dt. (3.33)

Для
определения теплоты, выделившейся за
конечный интервал времени Δt,
выражение (3.33) надо проинтегриро­вать
в пределах от t₁
до t₂:

.

Произведем
вычисления:

Q₁=^.
3^2
.20(1-0)=60
Дж;

Q₂=^.3^2.20(8-1)=420
Дж.

Следовательно,

,

т.е.
за вторую секунду выделится теплоты в
семь раз больше, чем за первую.