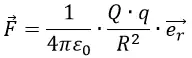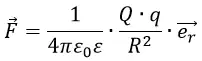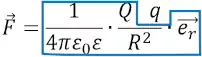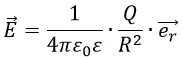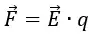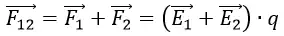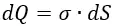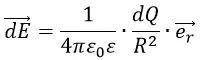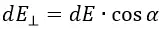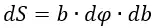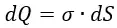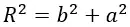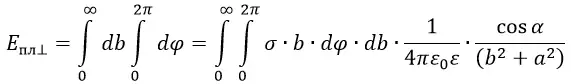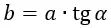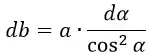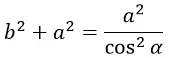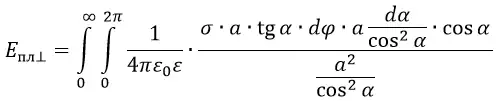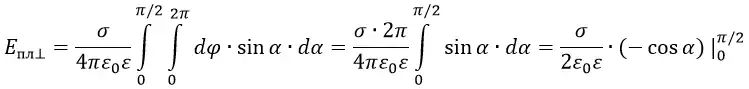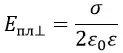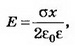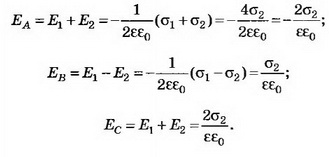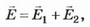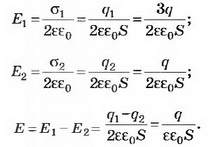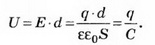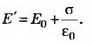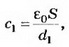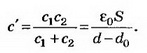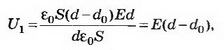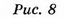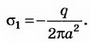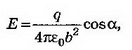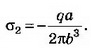Как найти напряженность поля внутри пластины

Выполним расчёт электрического поля плоской пластины бесконечных размеров, которая заряжена с постоянной плотностью. В основу положим закон Кулона для взаимодействия 2-х точечных электрических зарядов в вакууме. Если в какой-то точке пространства находится заряд Q, а на удалении R от него расположен некий пробный заряд q, то на данный пробный заряд в соответствии с формулой действует сила F.

Где ε₀ – диэлектрическая проницаемость вакуума;
R – расстояние между двумя зарядами Q и q;
Q и q – величины электрических зарядов;
e_r – единичный вектор, направленный по линии зарядов.

Если два электрических заряда Q и q помещены не в вакуум, в пространство с веществом, то к формуле добавляется относительная диэлектрическая проницаемость ε, которая отличает проводящие свойства какого-либо вещества от вакуума. ε является безразмерной константой.

В данной формуле можно выделить часть, которая не зависит от пробного заряда q:

Обозначим её буквой E:

Она носит название «напряжённость электрического поля». Из определения следует, что напряжённость поля не зависит от величины пробного заряда q, помещённого в точку. Напряжённость электрического поля определяется однозначно исходным зарядом Q, а также расстоянием R до точки, то есть геометрией пространства.

В таком случае сила кулона F будет равна:

Эта формула применима для любого точечного заряда.

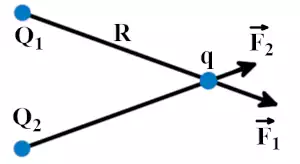
Электрическое поле обладает свойством суперпозиции. Если есть несколько электрических зарядов Q₁ и Q₂, то каждый заряд взаимодействует с точечными силами F₁ и F₂, и общая сила складывается по правилу сложения векторов.

В такой ситуации можно написать:

F₁₂ – суммарная сила.

Из формулы можно увидеть, что напряжённость электрического поля складывается. Этот факт называется принципом суперпозиции электрического поля, и он будет использован для расчёта сложной системы электрических зарядов, то есть зарядов, распределённых по плоскости.

Расчёт напряжённости электрического поля плоской пластины

Постановка задачи: имеется бесконечная плоская пластина с определённой плотностью заряда σ. Выделим на ней площадку dS. Заряд dQ площадки dS будет равен:

Будем считать, что плоская пластина равномерно заряжена и σ не зависит от координат.

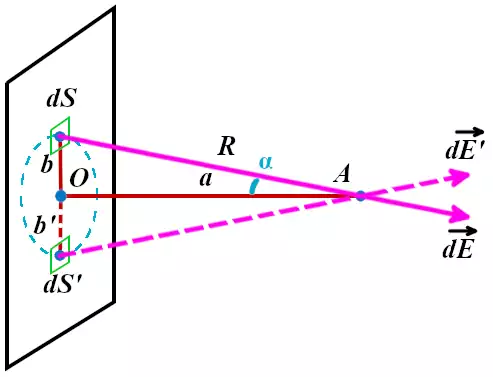
Посчитаем напряжённость электрического поля всей плоской пластины в точке A, находящейся на удалении a от этой пластины: E(A)=?

Для примера возьмём на плоской пластине небольшую площадку площадью dS на удалении b от центра. Обладая электрическим зарядом dQ, эта площадка создаёт электрическое поле с напряжённостью dE в точке A по закону Кулона.

На расстоянии b‘, равному расстоянию b, будет находится площадка dS‘, которая будет создавать электрическое поле с напряжённостью dE‘, равное по величине напряжённости поля dE, но направленное под другим углом. При сложении двух этих полей сумма расположенных параллельно пластине составляющих их векторов будет равны нулю. В связи с этим нам нужно учитывать только составляющую, расположенную перпендикулярно поверхности плоской пластины.

Обозначим угол между напряжённостью поля dE и перпендикуляром к пластине через α. Тогда интересующая нас составляющая dE_⊥ будет равна:

Точно такую же составляющую будут создавать все точки на плоской пластине, находящиеся на удалении b от точки O. Это связано с тем, что расстояния от них до точки A, а также углы между перпендикуляром и напряжённостями электрического поля будут такими же.

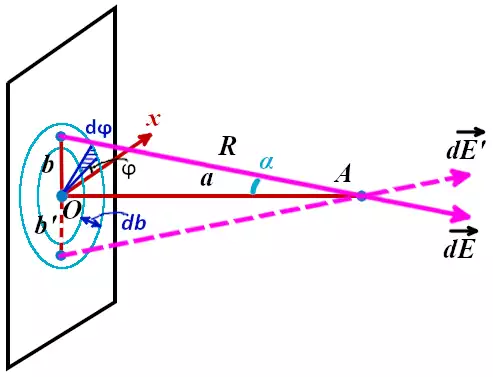
Выделим окружность радиусом b и толщиной db на плоской пластине. В полученном кольце рассмотрим элемент, расположенный под углом ϕ к оси x. Элемент вырезается из кольца в виде сегмента с размером dϕ. При малости dϕ и при малости db этот участок плоской пластины можно считать квадратом. В таком случае площадь dS будет равна:

Заряд dQ равен:

Полную напряжённость электрического поля кольца можно посчитать путём интегрирования по ϕ. А полное поле всей пластины можно посчитать путём интегрирования всех колец по b от 0 до ∞.

Для вычисления интеграла сделаем замену переменных и выразим всё через угол α. В этом случае получим:

В данной формуле сокращаем cos²α и a. Интеграл от 0 до ∞ выразится в интеграл от 0 до π/2.

Физический смысл этой формулы состоит в том, что напряжённость электрического поля около равномерно заряженной плоской пластины не зависит от расстояния до этой пластины.

Рнс. 33.

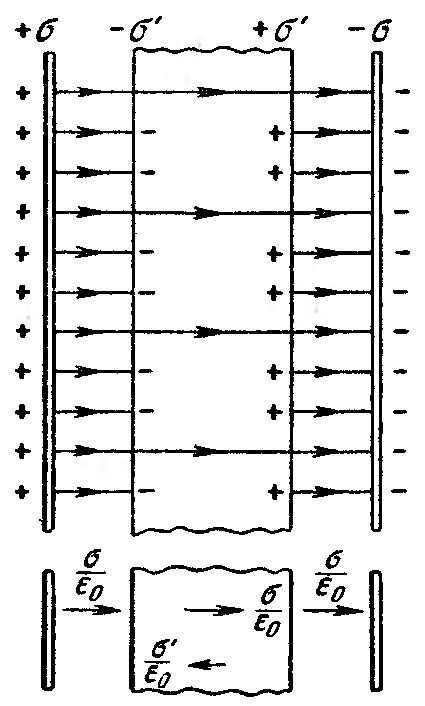
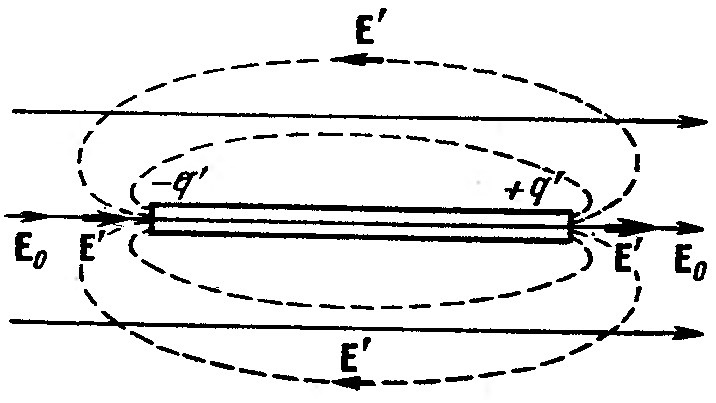
Рассмотрим поле, создаваемое в
вакууме двумя бесконечными разноименно
заряженными плоскостями. Обозначим
напряженность поля Е₀, а
электрическое смещение D
=  ₀
Е₀.

Внесем в это поле пластину из однородного
диэлектрика и расположим ее так, как
показано на рис. 33. Под действием поля
диэлектрик поляризуется и на его
поверхностях появятся связанные заряды
плотности  ’.
Эти заряды создадут внутри пластины
однородное поле, напряженность которого
равна Е‘ =  ’/ ₀.
Вне диэлектрика в данном случае Е‘
= 0. Напряженность поля Е₀ равна
 / ₀.
Оба поля направлены навстречу друг
другу, следовательно, внутри диэлектрика

(16.17)

Вне диэлектрика Е = Е₀.

Поляризация диэлектрика обусловлена
полем (16.17). Поскольку оно перпендикулярно
к поверхности пластины, Е_n
= Е. Кроме того, в соответствии с
(15.12) ’
= k₀E.
Подставляя это значение в формулу
(16.17), получаем E =
E₀ – kE
откуда

(16.18)

Итак, в рассматриваемом случае
относительная диэлектрическая
проницаемость 
показывает, во сколько раз ослабляется
поле за счет диэлектрика.

Умножив (16.18) на ₀,
получим электрическое смещение внутри
пластины

D = ₀
E = ₀E₀.
(16.19)

Таким образом, внутри пластины
электрическое смещение равно напряженности
поля свободных зарядов, умноженной на
₀,
т. е. совпадает с электрическим смещением
внешнего поля D₀.
Вне пластины 
= 1 и D также равно
₀E₀.

Чтобы найти ’,
выразим в (16.18) Е и Е₀
через плотности зарядов

Отсюда

(16.20)

Рис. 33 выполнен в предположении, что 
= 3. В соответствии с этим густота линий
Е в диэлектрике в три раза меньше,
.чем вне пластины. Линии проведены на
одинаковых расстояниях друг от. друга,
поскольку поле однородно. В данном
случае ’
можно найти, не прибегая к формуле
(16.20). Действительно, раз напряженность
поля внутри пластины в три раза меньше,
чем вне ее, то из трех линий напряженности,
начинающихся (или заканчивающихся) на
свободных зарядах, две должны заканчиваться
(соответственно, начинаться) на связанных
зарядах. Отсюда вытекает, что плотность
связанных зарядов должна быть равной
2/3 плотности свободных зарядов.

Пример характерен тем, что диэлектрик
был однородным и ограничивающие его
поверхности совпадали с эквипотенциальными
поверхностями. Полученный нами в этих
случаях результат является общим. Если
однородный диэлектрик полностью
заполняет объем, ограниченный
эквипотенциальными поверхностями, то
вектор электрического смещения совпадает
с вектором напряженности поля свободных
зарядов, умноженным на ₀
и, следовательно, напряженность поля
внутри диэлектрика в е раз меньше, чем
напряженность поля свободных зарядов.

Рис. 35.

Рис. 36.

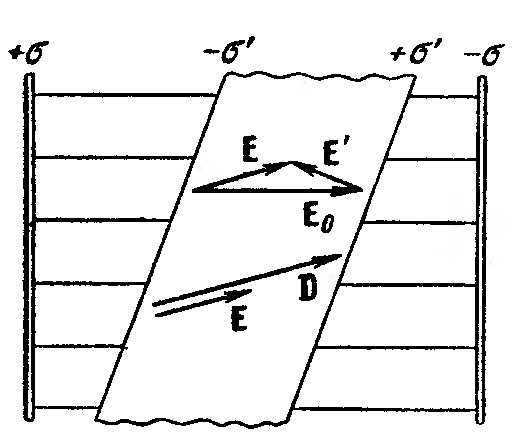
Если упомянутые условия не
соблюдаются, векторы D
и ₀Е₀
не совпадают. На рис. 35 показано поле в
пластине диэлектрика, перекошенной
относительно плоскостей, несущих
свободные заряды. Вектор Е‘
перпендикулярен к граням пластины,
поэтому Е и Е₀
неколлинеарны. Вектор D
направлен так же, как Е,
следовательно, D
и ₀Е₀
не совпадают по направлению. Можно
показать, что они не совпадают и по
величине.

Во всех рассмотренных выше примерах
из-за специально выбранной формы
диэлектрика поле Е‘ было отлично
от нуля только внутри диэлектрика. В
общем случае Е‘ может быть отлично
от нуля и за пределами диэлектрика.
Поместим в первоначально однородное
поле стержень из диэлектрика (рие. 36).
Вследствие поляризации на концах стержня
образуются связанные заряды противоположных
знаков. Их поле вне стержня эквивалентно
полю диполя (линии Е‘ показаны
на рисунке пунктиром). Легко видеть, что
результирующее поле Е вблизи
концов стержня больше Е₀.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Задачи по электростатике можно разделить на две группы: задачи о точечных зарядах и задачи о заряженных телах, размеры которых нельзя не учитывать [1—5].

Решение задач по расчёту электрических полей и взаимодействий точечных зарядов основано на применении закона Кулона и не вызывает особых затруднений. Более сложным является определение напряжённости поля и взаимодействия заряженных тел конечных размеров: сферы, цилиндра, плоскости. При вычислении напряжённости электростатических полей различной конфигурации следует подчеркнуть важность принципа суперпозиции и использовать его при рассмотрении полей, созданных не только точечными зарядами, но и зарядами, распределёнными по поверхности и объёму. При рассмотрении действия поля на заряд формула F=qE в общем случае справедлива для точечных заряженных тел и только в однородном поле применима для тел любых размеров и формы, несущих заряд q.

Электрическое поле конденсатора получается в результате наложения двух полей, созданных каждой пластиной.

В плоском конденсаторе можно рассматривать одну пластину как тело с зарядом q₁ помещённое в электрическое поле напряжённостью Е₂, созданное другой пластиной.

Рассмотрим несколько задач.

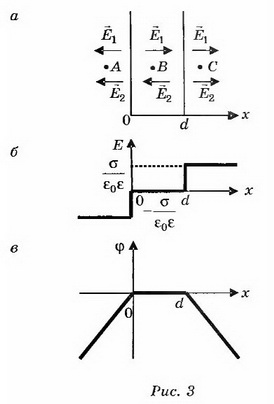
1. Бесконечная плоскость заряжена с поверхностной плотностью σ>0. Найдите напряжённость поля Е и потенциал ϕ по обе стороны плоскости, считая потенциал плоскости равным нулю. Постройте графики зависимостей Е(х), ϕ(х). Ось х перпендикулярна плоскости, точка х=0 лежит на плоскости.

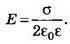
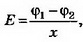
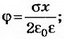
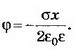
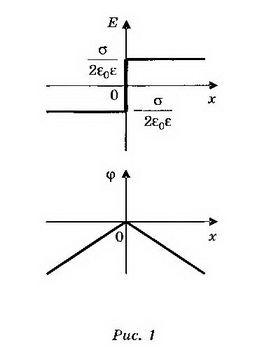
Решение. Электрическое поле бесконечной плоскости является однородным и симметричным относительно плоскости. Его напряжённостьСвязь между напряжённостью и разностью потенциалов между двумя точками однородного электростатического поля выражается формулойгде х — расстояние между точками, измеренное вдоль силовой линии. Тогда  ϕ₂=ϕ₁-Eх. При х<0 при х>0  Зависимости Е(х) и ϕ(х) представлены на рисунке 1.

2. Две плоскопараллельные тонкие пластины, расположенные на малом расстоянии d друг от друга, равномерно заряжены зарядом поверхностной плотностью σ₁ и σ₂. Найдите напряжённости поля в точках, лежащих между пластинами и с внешней стороны. Постройте график зависимости напряжённости Е(х) и потенциала ϕ(х), считая ϕ(0)=0. Рассмотрите случаи, когда: a) σ₁=-σ₂; б) σ₁= σ₂; в) σ₁=3σ₂—

Решение. Так как расстояние между пластинами мало, то их можно рассматривать как бесконечные плоскости.

Напряжённость поля положительно заряженной плоскости равна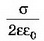и направлена от неё; напряжённость поля отрицательно заряженной плоскости направлена к ней.

Согласно принципу суперпозиции поле в любой рассматриваемой точке будет создаваться каждым из зарядов в отдельности.

а) Поля двух плоскостей, заряженных равными и противоположными по знаку зарядами (плоский конденсатор), складываются в области между плоскостями и взаимно уничтожаются во внешних областях (рис. 2, а).

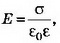
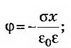
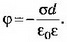
При х<0 Е=0, ϕ=0; при 0<x<d при x>d Е=0,Графики зависимости напряжённости и потенциала от расстояния х приведены на рисунке 2, б, в.

Если плоскости конечных размеров, то поле между плоскостями не будет строго однородным, а поле вне плоскостей не будет точно равно нулю.

б) Поля плоскостей, заряженных равными по величине и знаку зарядами (σ₁=σ₂), компенсируют друг друга в пространстве между плоскостями и складываются во внешних областях (рис. 3, а). При х<0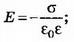при 0<x<d E=0; при х>d 

Воспользовавшись графиком Е(х) (рис. 3, б), построим качественно график зависимости ϕ(х) (рис. 3, в).

в) Если σ₁= σ₂, то, учитывая направления полей и выбирая направление направо за положительное, находим:

Зависимость напряжённости Е от расстояния показана на рисунке 4.

3. На одной из пластин плоского конденсатора ёмкостью С находится заряд q₁=+3q, а на другой q₂=+q. Определите разность потенциалов между пластинами конденсатора.

Решение. 1-й способ. Пусть площадь пластины конденсатора S, а расстояние между ними d. Поле внутри конденсатора однородное, поэтому разность потенциалов (напряжение) на конденсаторе можно определить по формуле U=E*d, где Е — напряжённость поля внутри конденсатора.

где Е₁, Е₂ — напряжённости поля, создаваемого пластинами конденсатора.

Тогда

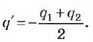
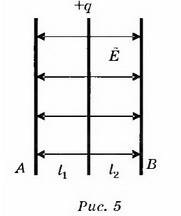
2-й способ. Добавим на каждую пластину зарядТогда пластины конденсатора будут иметь заряды +q и -q. Поля одинаковых зарядов пластин внутри конденсатора компенсируют друг друга. Добавленные заряды не изменили поле между пластинами, а значит, и разность потенциалов на конденсаторе. U=q/C.

4. В пространство между обкладками незаряженного плоского конденсатора вносят тонкую металлическую пластину, имеющую заряд +q. Определите разность потенциалов между обкладками конденсатора.

Решение. Так как конденсатор не заряжен, то электрическое поле создаётся только пластиной, имеющей заряд q (рис. 5). Это поле однородное, симметричное относительно пластины, и его напряжённость 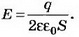Пусть потенциал металлической пластины равен  ϕ. Тогда потенциалы обкладок А и В конденсатора будут равны ϕ-ϕ_А=ϕEl₁; ϕ_А=ϕ-El₁; ϕ-ϕ_B=ϕ-El₂; ϕ_B=ϕ-El₂.

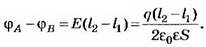
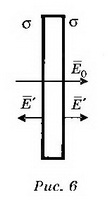
Разность потенциалов между обкладками конденсатора Если пластина находится на одинаковом расстоянии от обкладок конденсатора, то разность потенциалов между обкладками равна нулю.

5. В однородное электрическое поле напряжённостью Е₀ перпендикулярно силовым линиям помещают заряженную металлическую пластину с плотностью заряда на поверхности каждой стороны пластины σ (рис. 6). Определите напряжённость поля Е’ внутри и снаружи пластины и поверхностную плотность зарядов σ₁и σ₂, которая возникнет на левой и правой сторонах пластины.

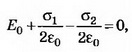
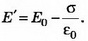
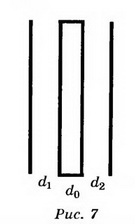
Решение. Поле внутри пластины равно нулю и является суперпозицией трёх полей: внешнего поля Е₀, поля, создаваемого зарядами левой стороны пластины, и поля, создаваемого зарядами правой стороны пластины. Следовательно,где σ₁ и σ₂ — поверхностная плотность заряда на левой и правой сторонах пластины, которая возникает после внесения пластины в поле Е₀. Суммарный заряд пластины не изменится, поэтому σ₁+σ₂=2σ, откуда σ₁=σ-ε₀E₀, σ₂=σ+ε₀E₀. Поле снаружи пластины является суперпозицией поля Е₀ и поля заряженной пластины Е. Слева от пластиныСправа от пластины 

6. В плоском воздушном конденсаторе напряжённость поля Е= 10⁴ В/м. Расстояние между обкладками d=2 см. Чему будет равна разность потенциалов, если между пластинами параллельно им поместить металлический лист толщиной d₀=0,5 см (рис. 7)?

Решение. Поскольку электрическое поле между пластинами однородное, то U=Ed, U=200 В.

Если между пластинами пометить металлический лист, то получается система из двух последовательно соединённых конденсаторов с расстоянием между пластинами d₁ и d₂. Ёмкости этих конденсаторов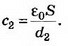Их общая ёмкость

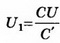
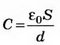
Так как конденсатор отключён от источника тока, то заряд конденсатора при внесении металлического листа не меняется: q’=CU=С’U₁;где  емкость конденсатора до внесения в него металлического листа. Получаем:

U₁=150 В.

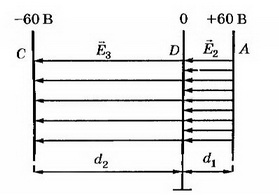
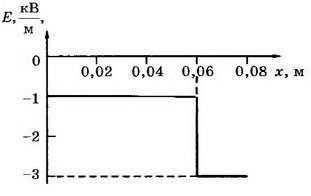
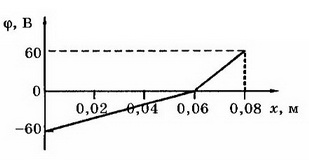
7. На пластинах А и С, расположенных параллельно на расстоянии d=8 см друг от друга, поддерживаются потенциалы ϕ₁= 60 В и ϕ₂=-60 В соответственно. Между ними поместили заземлённую пластину D на расстоянии d₁=2 см от пластины А. На сколько изменилась напряжённость поля на участках AD и CD? Постройте графики зависимостей ϕ(x) и Е(х).

Решение. Первоначальная напряжённость поля между пластинами А и С:

E₁=1,5 кВ/м.

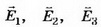
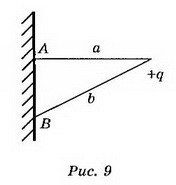
Напряжённость поля на участке AD: Е₂= ϕ₁/d₁, Е₂=3 кВ/м, т. е. увеличилась на 1,5 кВ/м. Напряжённость поля на участке CD  Е₃= ϕ₂/d₂, т.е. уменьшилась на Е₃=0,5 кВ/м.  Поскольку векторы направлены противоположно положительному направлению оси Ох, то Е_г, Е₂, Е₃<0 (рис. 8).

8. Точечный заряд q=5*10^-9 Кл находится на расстоянии 3 см от проводящей заземлённой стенки. Найдите поверхностную плотность заряда, индуцированного на стенке в точке А, ближайшей к заряду, и в точке В, находящейся на расстоянии 5 см от заряда.

Решение. В точках А, В, расположенных в непосредственной близости к поверхности проводника (рис. 9), поле создаётся точечным зарядом q и зарядом q’, индуцированным на стенке:

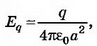
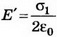
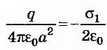
В точке Агде а — расстояние от заряда до стенки,. Но поле внутри проводника равно нулю; следовательно,. Отсюда  

В точке В величина нормальной составляющей напряжённости поля точечного заряда

где b — расстояние от заряда до точки, cosα=a/b,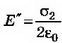— напряжённость поля плоскости.

Следовательно,

Список использованной литературы

1. Балаш, В. А. Задачи по физике и методы их решения / В. А. Балаш. — 4-е изд. — М. : Просвещение, 1983. — 432 с.

2. Бутиков, Е. И. Физика в примерах и задачах / Е. И. Бутиков, А. А. Быков, А. С. Кондратьев. — 3-е изд. — М. : Наука, 1989. — 462 с.

3. Зилъберман, Г. Е. Электричество и магнетизм / Г. Е. Зильберман. — М. : Наука, 1990. — 384 с.

4. Меледин, Г. В. Физика в задачах / Г. В. Меледин. — 2-е изд. — М. : Наука, 1990. — 270 с.

5. Сборник задач по физике / Л. П. Баканина [и др.]; под ред. С. М. Козела. — М. : Наука, 1990. — 347 с.

Прежде чем смотреть решения задач, изучите теорию и постарайтесь решить сами. Потому что в этой теме главное — набить руку.

Задача 1.

Используя теорему Гаусса, определите напряжённость электрического поля:

-внутри и вне равномерно заряженной сферы, если полный заряд сферы ;

-равномерно заряженной бесконечной нити, если заряд единицы длины нити ;

-равномерно заряженной бесконечной плоскости, если поверхностная плотность заряда плоскости ;

-внутри и вне равномерно заряженного шара радиуса , если объёмная плотность заряда ; нарисуйте график зависимости напряжённости электрического поля от расстояния до центра шара;

-внутри и вне равномерно заряженного бесконечного цилиндра радиуса , если объёмная плотность заряда внутри цилиндра равна ; нарисуйте график зависимости напряжённости электрического поля от расстояния до оси цилиндра;

-вне и внутри равномерно заряженной бесконечной пластины толщины , если объёмная плотность заряда в пластине равна ; нарисуйте график зависимости напряжённости электрического поля от расстояния до центральной плоскости пластины.

Решение. Равномерно заряженная сфера.

Поток вектора напряженности через поверхность сферы равен

Где — площадь сферы.

По теореме Гаусса поток равен

Причем — заряд внутри гауссовой поверхности. Для сферы наиболее удобно взять в качестве гауссовой поверхности также сферу. Если ее радиус больше радиуса (), то все заряды оказываются внутри гауссовой поверхности и

То есть поле аналогично точечному заряду.

Если радиус гауссовой сферы меньше , то заряды оказываются все снаружи, поэтому заряд внутри – нулевой.

Бесконечная нить. Охватим нить гауссовой поверхностью в виде цилиндра. Причем поток будет проходить только через боковую поверхность цилиндра, а через торцы поток будет нулевым.

Поток вектора напряженности через боковую поверхность цилиндра равен

Где — площадь боковой поверхности цилиндра.

По теореме Гаусса поток равен

Причем .

Таким образом,

Равномерно заряженная бесконечная плоскость. Вектор напряженности направлен от плоскости перпендикулярно ей. Выделим элемент плоскости. Если этот элемент двигать по плоскости вправо-влево, поток не изменится. Поэтому поток не зависит от расположения выделенного элемента. Значит, в качестве гауссовой поверхности возьмем цилиндр, ось которого совпадает с направлением вектора напряженности – то есть перпендикулярна плоскости. Поток через боковую поверхность цилиндра в данном случае равен нулю, то есть

Где — площадь основания цилиндра.

По теореме Гаусса поток равен

Причем .

Равномерно заряженный шар. Он будет иметь заряд

Поток вектора напряженности

Охватим шар гауссовой сферой, где — площадь ее поверхности .

Если ее радиус больше радиуса шара (), то весь заряд шара внутри этой поверхности и

Если радиус гауссовой сферы меньше радиуса шара (), то внутри гауссовой сферы оказывается не весь заряд шара, а лишь его часть, пропорциональная объему:

Тогда

Бесконечный заряженный цилиндр. Охватим его гауссовой поверхностью в виде цилиндра. Через торцы цилиндра поток будет нулевым – они параллельны вектору напряженности. Через боковую поверхность радиуса

По теореме Гаусса

Где — заряд внутри.

Получаем

Это снаружи цилиндра. А внутри? Там мы  тоже можем охватить какой-то объем гауссовым цилиндром, и заряд, который окажется внутри, будет пропорционален объему.

Тогда

Осталась бесконечная пластина толщиной . Понятно, что снаружи, при , поле пластины будет совпадать с полем заряженной плоскости:

Теперь определим поле внутри. Расстояние будем отсчитывать от центра, так что нам понадобится плоскость, разбивающая пластину на две толщиной . Гауссовой поверхностью будет цилиндр, поток через его боковые стенки равен нулю – они параллельны вектору напряженности. А поток через основания равен

С другой стороны,

Где — заряд внутри. Поскольку мы находимся на расстоянии от центра пластины, заряд, оказавшийся внутри нашей гауссовой поверхности, может быть найден как

Таким образом,

Задача 2.

Точечный заряд находится в центре куба. Найти поток вектора напряженности электростатического поля через любую грань куба.

Решение. Полный поток будет равен

А так как это поток через все шесть граней, то через одну

Ответ:

Задача 3.

Точечный заряд находится в вершине куба. Найти поток вектора напряженности электростатического поля через грань куба, не проходящую через заряд.

Окружим данный куб еще семью, так, чтобы заряд оказался в самом центре конструкции:

Тогда поток, создаваемый зарядом через один из восьми кубов, равен

А так как у каждого из восьми кубов конструкции только три грани обращены наружу, то через каждую грань поток будет равен

Ответ:

Задача 4.

В равномерно заряженной бесконечной пластине вырезали сферическую полость так, как показано на рисунке. Толщина пластины , объёмная плотность заряда . Чему равна напряжённость электрического поля в точке А? в точке В? Найдите зависимость напряжённости электрического поля вдоль прямой ОА от расстояния до точки .

Решение. Рассмотрим пластину (сплошную) и шар с объемной плотностью заряда . Мы уже находили поле заряженной пластины – см. задачу 1. Внутри пластины при напряженность поля будет равна нулю. Поэтому в точке напряженность будет создавать только шар. Снова обращаемся к задаче 1 и пишем напряженность поля на границе шара:

Подставляя , имеем

В точке произойдет суммирование векторов напряженностей, созданных плоскостью и шаром, а на деле они будут вычитаться:

Ответ: ; .

Спрятать решение

Источник: Са­вчен­ко О. Я. За­да­чи по фи­зи­ке, М.: «Наука», 1988 (№ 6.2.6 (е))