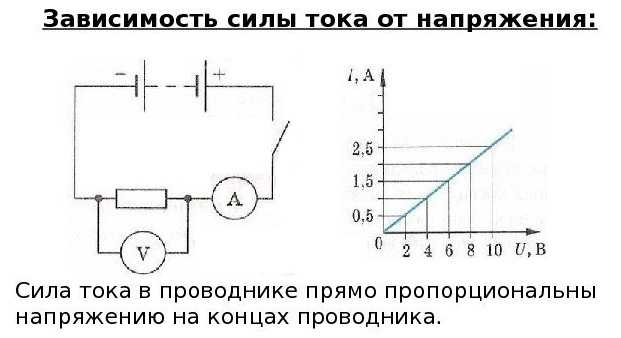
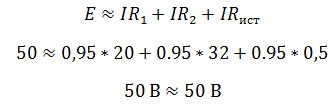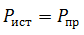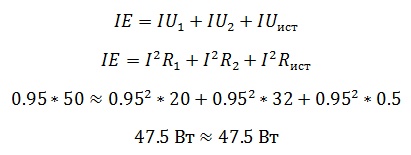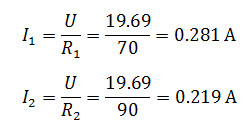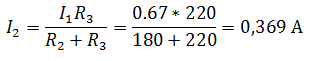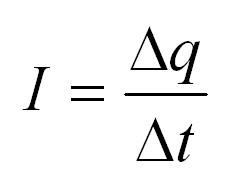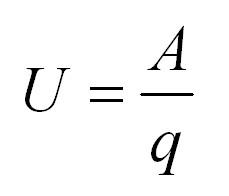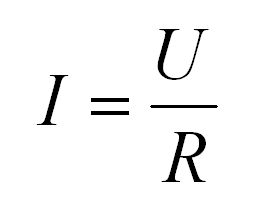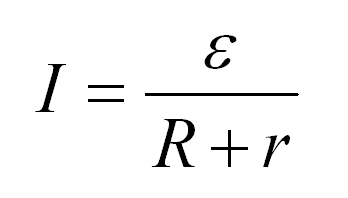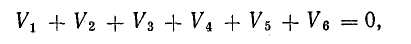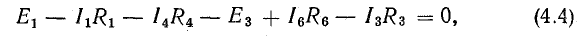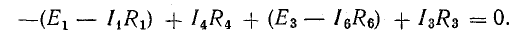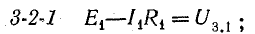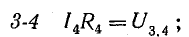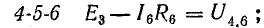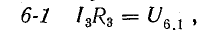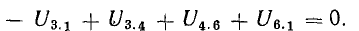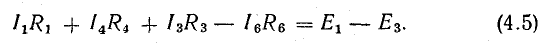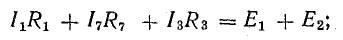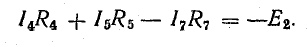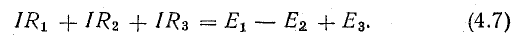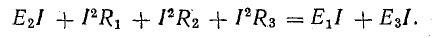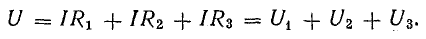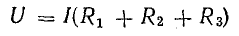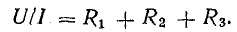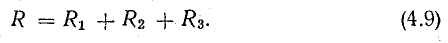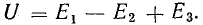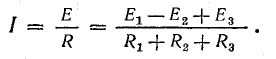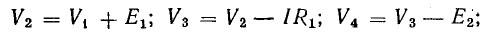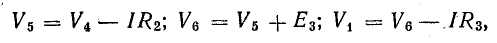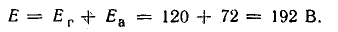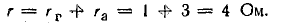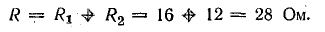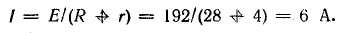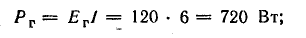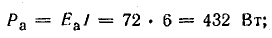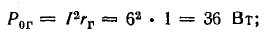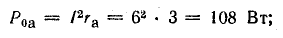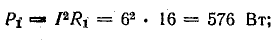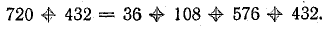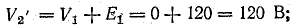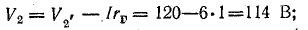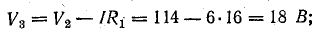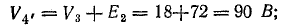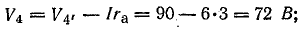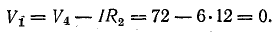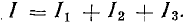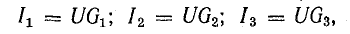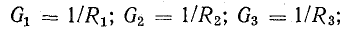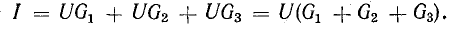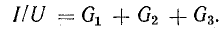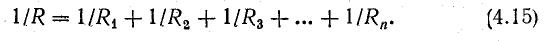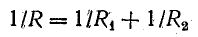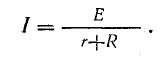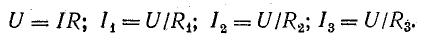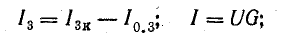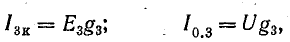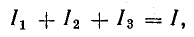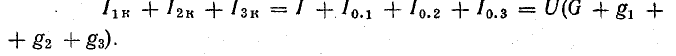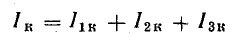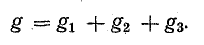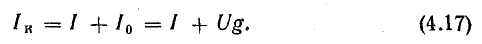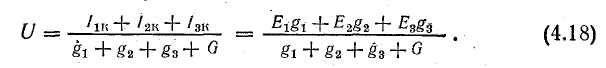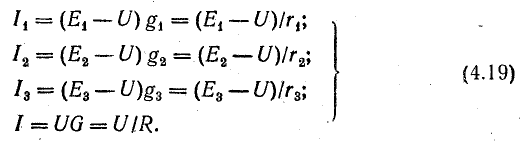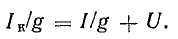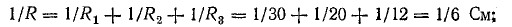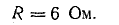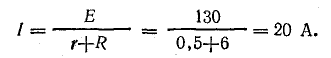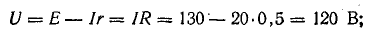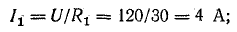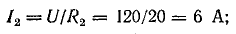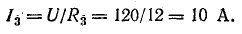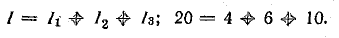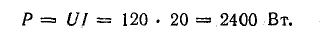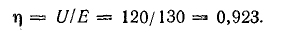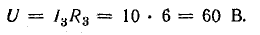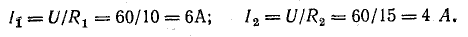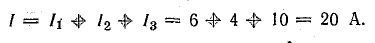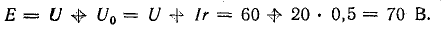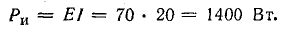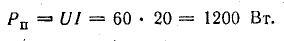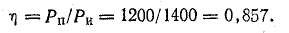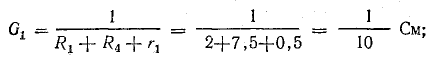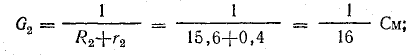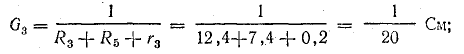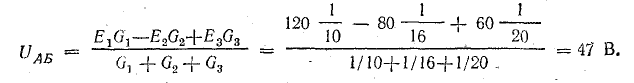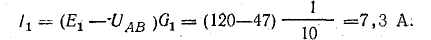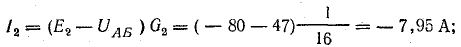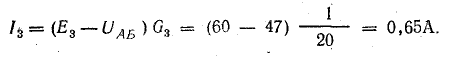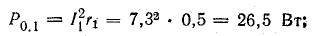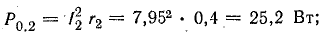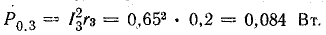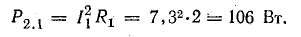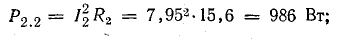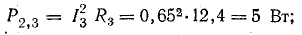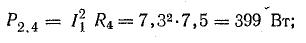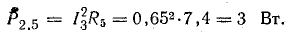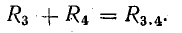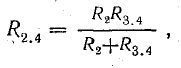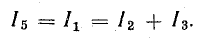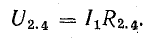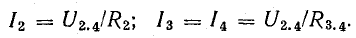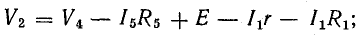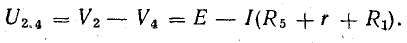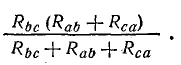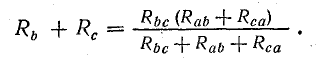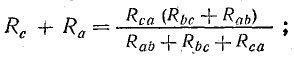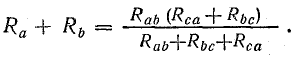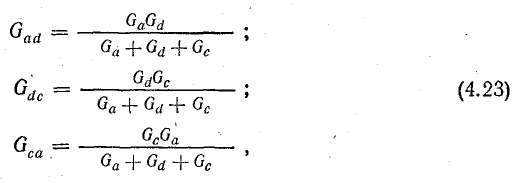Расчет простых цепей постоянного тока
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1
Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2
Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.
Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.
Если у вас возникли затруднения, прочтите статью законы Кирхгофа.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи
А затем напряжение
Зная напряжения, найдем токи, протекающие через резисторы
Как видите, токи получились теми же.
Пример 3
В электрической цепи, изображенной на схеме R1=50 Ом, R2=180 Ом, R3=220 Ом. Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.
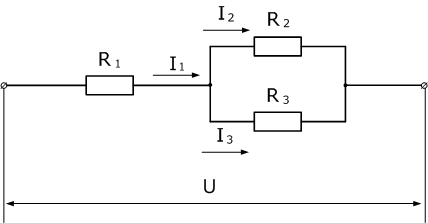
Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R1, необходимо определить ток I1, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.
Эквивалентное сопротивление и ток в цепи

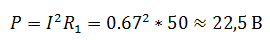
Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U3, как напряжение на резисторе R2
Таким образом производится расчет простых цепей постоянного тока.
Одним из самых фундаментальных терминов в электротехнике является термин «электрическое напряжение». В этой статье мы объясним, что это такое и как его рассчитать.
Объяснение простыми словами
Электрическое напряжение U является той самой причиной, которая «заставляет» протекать электрический ток I. Электрическое напряжение всегда возникает, когда заряды разделены друг от друга, то есть все отрицательные заряды на одной стороне, а все положительные — на другой. Если соединить эти две стороны электропроводящим материалом, потечет электрический ток.
Общепринятое определение термина «электрическое напряжение».
Электрическое напряжение (или просто напряжение) — это разность потенциалов между двумя точками в электрическом поле. Это движущая сила для электрического заряда.
Потенциал в электрическом поле — это энергия заряженного тела, не зависящая от его электрического заряда. Для пояснения вы можете посмотреть на сравнение с водяным контуром чуть ниже в статье.
Есть другое определение (из учебника по физике 8 класса):
Напряжение — это физическая велuчuна, характеризующая электрическое поле. Электрическое напряжение между двумя точками электрического поля численно равно работе, совершенной при переносе между ними заряда 1 Кл силами электрического поля.
Сравнение с использованием модели протекания воды.
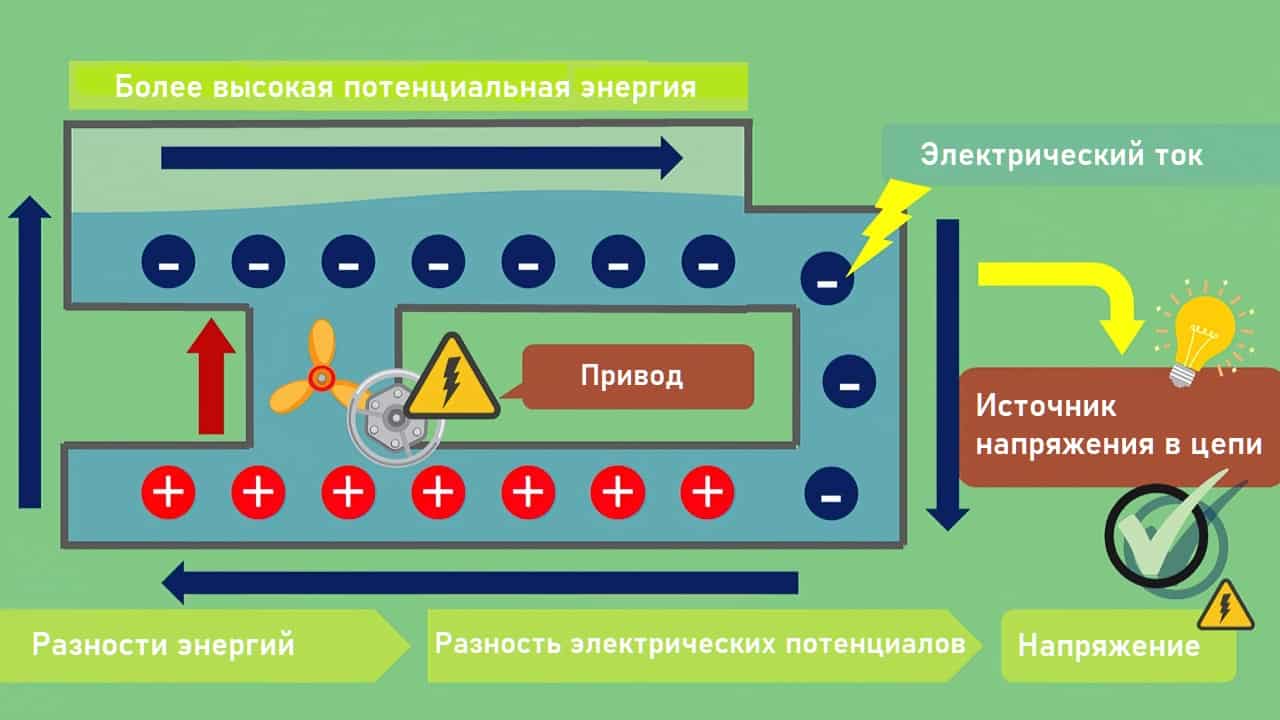
Хорошей аналогией, которая поможет вам представить себе электрическое напряжение и потенциал, является водяной контур. В этой схеме у вас есть два бассейна на разной высоте, которые соединены трубой. В этой трубе вода может перетекать из верхнего бассейна в нижний. Затем вода перекачивается обратно в верхний бассейн с помощью насоса, как показано на рисунке ниже.
В своих размышлениях вы теперь легко можете сравнить насос с источником электрического напряжения. Кроме того, поток воды можно сравнить с электрическим током. Насос транспортирует воду из нижнего бассейна в верхний. Оттуда она самостоятельно течет обратно в нижний бассейн. В данном примере насос является приводом для потока. Чем больше разница в высоте, тем сильнее поток. Решающим фактором является потенциальная энергия верхнего бассейна. Вы можете сравнить разность энергий двух бассейнов с разностью электрических потенциалов. Проще говоря, большая разница в высоте соответствует большему электрическому напряжению.
Формула
Формула для электрического напряжения U, согласно закона Ома для участка цепи, имеет вид
U = R * I .
Как видно из этой формулы, если электрическое напряжение остается неизменным, то чем больше электрическое сопротивление (R), тем меньше сила тока (I).
Другая формула для расчета электрического напряжения такова:
U = P / I .
То есть электрическое напряжение U равно мощности деленной на силу тока I.
Единица измерения электрического напряжения
Единицей измерения электрического напряжения в СИ является Вольт, сокращенно В (в честь итальянского учёного А. Вольта).
1 вольт (1 В) — это напряжение между двумя точками электрического поля, при переносе между которыми заряда 1 Кл совершается работа 1 Дж.
[U] = 1 В
Теперь вы можете объяснить смысл надписи 4,5 В или 9 В на круглой или плоской батарейке. Смысл в том, что при переносе с одного полюса источника на другой (через спираль лампочки или другой проводник) заряда 1 Кл силами электрического поля может быть совершена работа соответственно 4,5 Дж или 9 Дж.
В электротехнике напряжение может варьироваться от микровольт (1 мкВ = 1 * 10-6 В) и миливольт (1 мВ = 10-3 В), до киловольт (1 кВ = 1 * 103 В) и мегавольт (1 МВ = 106 В)
Вы можете преобразовать отдельные единицы измерения следующим образом:
1 В = 1000 мВ, 1 мВ = 1000 мкВ, 1 МВ = 1000 кВ, 1 кВ = 1000 В.
Электрическое напряжение в цепи
Для источников напряжения в схемах обычно используется один из следующих символов.
Источник напряжения всегда имеет два соединения/полюса. Полюс «плюс» и полюс «минус». Само напряжение обозначено стрелкой напряжения (UQ). Для источников оно всегда отображается от плюса к минусу.
Электрическое напряжение, падающее на резисторе, также можно обозначить стрелкой напряжения (на схеме обозначена как красная стрелка UR ). Это указывает на техническое направление электрического тока.
Также часто можно услышать термин «напряжение холостого хода» или «напряжение источника». Это выходное напряжение ненагруженного источника, т.е. источника, к которому ничего не подключено. Если цепь замкнута с нагрузкой, то можно измерить только напряжение на полюсах источника.
Электрические напряжения при последовательном и параллельном соединении
У нас уже есть статья о последовательном и параллельном соединении проводников, в котором мы обсуждаем эту тему более подробно. Поэтому здесь мы рассмотрим лишь некоторые основы.
При последовательном соединении компоненты подключаются в ряд.
Здесь электрическое напряжение источника делится на резисторы. Этот момент также описывается вторым правилом Кирхгофа. Здесь применимо следующее:
UQ = U1 + U2 + U3
то есть напряжение источника равно сумме электрических напряжений на отдельных резисторах. Напряжение источника по-разному распределяется по разным резисторам.
В электрической цепи с параллельным соединением компоненты расположены, соответственно, параллельно друг относительно друга. Это можно увидеть на следующей схеме.
Здесь гораздо проще определить электрические напряжения на резисторах, так как при параллельном соединении:
UQ = U1 = U2 = U3
Поэтому электрическое напряжение на резисторах такое же высокое, как и электрическое напряжение источника.
Измерение электрического напряжения
Приборы для измерения напряжения, также называемые вольтметрами, всегда подключаются параллельно потребителю, на котором необходимо измерить электрическое напряжение.
Одним из наиболее часто используемых вольтметров является цифровой мультиметр (DMM), поэтому мы покажем вам процедуру измерения напряжения с помощью DMM. Сначала необходимо установить тип электрического напряжения (DC — постоянный ток или AC — переменный ток).
Для постоянного тока необходимо обратить внимание на правильную полярность, т.е. подключить плюс к положительному полюсу. На следующем этапе необходимо выбрать правильный диапазон измерения. Если вы не можете оценить, насколько велика измеряемая величина, установите наибольший возможный диапазон и двигайтесь от него вниз, пока не найдете нужный. Наконец, вам нужно только «считать» электрическое напряжение прибором.
Примеры типовых значений электрического напряжения
Для некоторых применений соответствующее электрическое напряжение можно найти в таблице ниже.
| Светодиод | 1,2 — 1,5 В |
| Зарядное устройство USB | 5 В |
| Напряжение автомобильного аккумулятора | 12, 4 — 12,8 В |
| Напряжение в розетке (среднеквадратичное или действующее значение) | 230 В |
| Высоковольтные линии электропередач (ЛЭП) | 60 кВ — 1 МВ |
Вы можете видеть, что на высоковольтных линиях присутствует напряжение до мегавольт. Такие большие электрические напряжения используются для того, чтобы уменьшить потери в длинных линиях.
Решающим фактором для потребителя является мощность P, которую можно рассчитать для постоянного напряжения с помощью формулы:
P = U * I
Это означает, что электрический ток I так же важен для потребителя, как и электрическое напряжение. Согласно закону Ома, зависимость между током и напряжением имеет вид:
U = R * I .
Если напряжение остается неизменным, сопротивление определяет величину тока. Чтобы проиллюстрировать это, представьте следующее. У вас есть три разных бассейна, которые заполнены одинаковым количеством воды. Каждый бассейн имеет слив, который различается по сечению, т.е. в одном бассейне сливная труба очень маленькая, а в другом — очень большая.
Постоянное электрическое напряжение можно определить по тому, что все емкости заполнены на одинаковую высоту. Если слив узкий в нижней части, он представляет собой большое сопротивление. Ток здесь может течь только медленно. Если сечение сливной трубы больше, то сопротивление меньше и, соответственно, может протекать больший ток.
Чтобы хоть немного разбираться в электрике, необходимо знать основополагающие законы. Один из них — закон Ома. С него начинают изучение электрики и не зря. Он иллюстрирует зависимость параметров электрической цепи друг от друга.
Содержание статьи
- 1 Как звучит закон Ома для участка цепи
- 2 Разбираемся что такое ток и сопротивление
- 3 Говорим о напряжении
- 4 Что изменится для полной цепи
- 5 Как найти сопротивление, напряжение
- 6 Параллельное и последовательное соединение
- 6.1 Последовательное соединение
- 6.2 Параллельное соединение
- 6.3 Что нам дает параллельное и последовательное соединение?
Как звучит закон Ома для участка цепи
Есть говорить об официальной формулировке, то закон Ома можно озвучить так:
Сила тока имеет прямую зависимость от напряжения и обратную от сопротивления. Это высказывание справедливо для участка цепи с каким-то определенным и стабильным сопротивлением.
Формула этой зависимости на рисунке. Тут I — это сила тока, U — напряжение, R — сопротивление.
Формула закона Ома
- Чем больше напряжение, тем больше ток.
- Чем больше сопротивление, тем ток меньше.
Не так легко представить себе смысл этого выражения. Ведь электричество нельзя увидеть. Мы только приблизительно знаем что это такое. Попытаемся уяснить себе смысл этого закона при помощи аналогий.
Разбираемся что такое ток и сопротивление
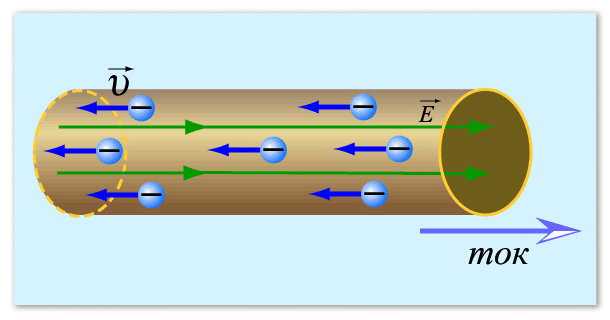
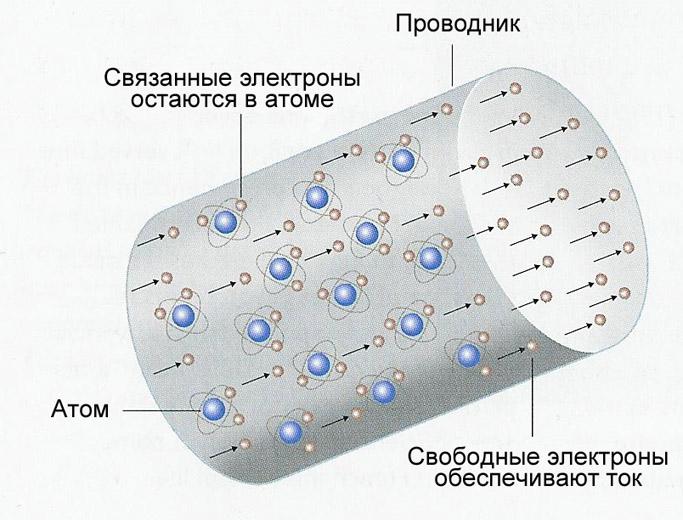
Начнем с понятия электрического тока. Если говорить коротко, электрический ток применительно к металлам — это направленное движение электронов — отрицательно заряженных частиц. Их обычно представляют в виде небольших кружочков. В спокойном состоянии они передвигаются хаотически, постоянно меняя свое направление. При определенных условиях — возникновении разницы потенциалов — эти частицы начинают определенное движение в какую-то сторону. Вот это движение и есть электрический ток.
Чтобы было понятнее, можно сравнить электроны с водой, разлитой на какой-то плоскости. Пока плоскость неподвижна, вода не движется. Но, как только появился наклон (возникла разница потенциалов), вода пришла в движение. С электронами примерно так же.
Примерно так можно себе представить электрический ток
Теперь надо понять, что такое сопротивление и почему с силой тока у них обратная связь: чем выше сопротивление, тем меньше ток. Как известно, электроны движутся по проводнику. Обычно это металлические провода, так как металлы обладают хорошей способностью проводить электрический ток. Мы знаем, что металл имеет плотную кристаллическую решетку: много частиц, которые расположены близко и связаны между собой. Электроны, пробираясь между атомами металла, на них наталкиваются, что затрудняет их движение. Это помогает проиллюстрировать сопротивление, которое оказывает проводник. Вот теперь становится понятным, почему, чем выше сопротивление, тем меньше сила тока — чем больше частиц, тем электронам сложнее преодолевать путь, делают они это медленнее. С этим, вроде, разобрались.
Если у вас есть желание проверить эту зависимость опытным путем, найдите переменный резистор, соедините последовательно резистор — амперметр — источник тока (батарейка). Еще желательно в цепь вставить выключатель — обычный тумблер.
Цепь для проверки зависимости силы тока от сопротивления
Крутя ручку резистора вы изменяете сопротивление. При этом показания на амперметре, который измеряет силу тока, тоже меняются. Причем чем больше сопротивление, тем меньше отклоняется стрелка — меньше ток. Чем сопротивление меньше — тем сильнее отклоняется стрелка — ток больше.
Вместо стрелочного прибора можно использовать цифровой мультиметр в режиме измерения постоянного тока. В этом случае отслеживаются показания на жидкокристаллическом цифровом табло.
Зависимость тока от сопротивления почти линейная, то есть на графике отражается почти прямой линией. Почему почти — об этом надо говорить отдельно, но это другая история.
Говорим о напряжении
Не менее важно понять что такое напряжение. Давайте сразу начнем с аналогии и снова используем воду. Пусть в воронке находится вода. Она просачивается через узкое горлышко, которое создает сопротивление. Если представить, что на воду уложили груз, движение воды ускорится. Этот груз — и есть напряжение. И теперь тоже понятно, почему чем выше напряжение, тем сильнее ток — чем сильнее давление, тем быстрее будет двигаться вода. То есть, зависимость прямая: больше напряжение — больше ток. И именно это положение отражает закон Ома — «давление» стоит в числителе (в верхней части дроби).
Можно попробовать представить напряжение по-другому. Есть все те же электроны, которые скопились на одном краю источника питания. На втором краю их мало. Так как каждый из электронов имеет какой-то заряд, там, где их много, суммарный заряд больше, где мало — меньше. Разница между зарядами и есть напряжение. Это тоже несложно представить. С точки зрения электричества — это более корректное представление, хоть и не точное.
На тему закона Ома есть немало забавных картинок, позволяющих чуть лучше понять все эти явления. Одна из них перед вами и иллюстрирует, как ток зависит от напряжения и сопротивления. Смотрите что получается: сопротивление старается уменьшить ток (обратная зависимость), а с ростом напряжения он увеличивается (прямая зависимость). Это и есть закон Ома, но переданный простыми словами.
Благодаря картинке просто понять зависимость тока от напряжения и сопротивления
Если вы хотите убедиться и в этой зависимости, тоже надо создать простенькую цепь. Но нужен будет либо регулируемый источник питания, либо несколько батареек, которые выдают разное напряжение. Или можно последовательно включать несколько батареек — тоже вариант. Но менять/подпаивать батарейки надо при разорванной цепи (выключенном тумблере).
В этой схеме используются два измерительных прибора: амперметр включается последовательно с нагрузкой (резистор на схеме ниже), вольтметр параллельно нагрузке.
Схема для иллюстрации закона Ома
Так как другие параметры цепи остаются в норме, при увеличении напряжения мы увидим увеличение силы тока. Чем больше напряжение подаем, тем больше отклоняются стрелки вольтметра и амперметра. Если задаться целью построить график, он будет в виде прямой. Если поставить другое сопротивление, график также будет в виде прямой, но угол наклона ее изменится.
Что изменится для полной цепи
В ситуации выше рассмотрен только некоторый участок цепи, обладающий каким-то фиксированным сопротивлением. Мы предполагаем, что при определенных условиях электроны начнут движение. Причина этого движения — тот самый груз на картинке. В реальных условиях это — источник тока. Это может быть батарейка, генератор постоянного тока, подключенный шнур блока питания и т.д. При подключении источника питания к проводнику в нем начинает протекать ток. Это мы тоже знаем и наблюдаем, когда включаем лампу в сеть, ставим заряжаться мобильный телефон и т.д.
Полная цепь включает в себя источник питания
Участок цепи имеет какое-то сопротивление. Это понятно. Но источник питания тоже имеет сопротивление. Его обычно обозначают маленько буквой r. Так как ток бежит по кругу, ему приходится преодолевать сопротивление провода и сопротивление источника тока. Вот это суммарное сопротивление цепи и источника питания — называют импеданс. Говорят еще что это комплексное сопротивление. В формуле Ома для полной цепи его отображают при помощи суммы. В знаменателе стоит сумма сопротивлений цепи и внутреннего сопротивления источника тока (R + r).
Всем, наверное, понятно, что именно источник тока создает нужные условия для движения электронов. Все благодаря тому, что он обладает ЭДС — электродвижущей силой. Эта величина обозначается обычно E. Чем больше эта сила, тем больше ток. Это тоже, вроде, понятно. Поэтому обозначение ЭДС — латинскую букву E — ставят в числитель. Таким образом, формулировка закона Ома для полной цепи звучит так:
Сила тока прямо пропорциональна ЭДС источника тока и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника тока.
Вроде не слишком сложно, но можно попробовать еще проще:
- Чем выше ЭДС источника тока, тем больше ток.
- Чем больше суммарное сопротивление, тем ток меньше.
Как найти сопротивление, напряжение
Зная формулу закона Ома для участка цепи, мы можем рассчитать напряжение и сопротивление. Напряжение находится как произведение силы тока и сопротивления.
Формула напряжения и сопротивления по закону Ома
Сопротивление можно найти, разделив напряжение на ток. Все действительно несложно. Если мы знаем, что к участку цепи было проложено определенное напряжение и знаем какой при этом был ток, мы можем рассчитать сопротивление. Для этого напряжение делим на ток. Получаем как раз величину сопротивления этого куска цепи.
С другой стороны, если мы знаем сопротивление и силу тока, которая должна быть, мы сможем рассчитать напряжение. Надо всего лишь перемножить силу тока и сопротивление. Это даст напряжение, которое необходимо подать на этот участок цепи чтобы получить требуемый ток.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.
Закон Ома для параллельного и последовательного соединения
Последовательное соединение
Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.
Последовательное соединение и параметры этого участка цепи
При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.
Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.
Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
- Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
- Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга. Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя. Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.
Практическое применение закона Ома: можно создавать источники питания с нужным напряжением и силой тока
В общем, это наиболее распространенные варианты использования этих соединений.
Говорят: «не знаешь закон Ома – сиди дома». Так давайте же узнаем (вспомним), что это за закон, и смело пойдем гулять.
Основные понятия закона Ома
Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления.
Сила тока I
Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10-19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.
Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в Амперах.
Напряжение U, или разность потенциалов
Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.
Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах. Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль.
Сопротивление R
Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в Омах.
Формулировка и объяснение закона Ома
Закон немецкого учителя Георга Ома очень прост. Он гласит:
Сила тока на участке цепи прямо пропорционально напряжению и обратно пропорциональна сопротивлению.
Георг Ом вывел этот закон экспериментально (эмпирически) в 1826 году. Естественно, чем больше сопротивление участка цепи, тем меньше будет сила тока. Соответственно, чем больше напряжение, тем и ток будет больше.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Данная формулировка закона Ома – самая простая и подходит для участка цепи. Говоря «участок цепи» мы подразумеваем, что это однородный участок, на котором нет источников тока с ЭДС. Говоря проще, этот участок содержит какое-то сопротивление, но на нем нет батарейки, обеспечивающей сам ток.
Если рассматривать закон Ома для полной цепи, формулировка его будет немного иной.
Пусть у нас есть цепь, в ней есть источник тока, создающий напряжение, и какое-то сопротивление.
Закон запишется в следующем виде:
Объяснение закона Ома для полой цепи принципиально не отличается от объяснения для участка цепи. Как видим, сопротивление складывается из собственно сопротивления и внутреннего сопротивления источника тока, а вместо напряжения в формуле фигурирует электродвижущая сила источника.
Кстати, о том, что такое что такое ЭДС, читайте в нашей отдельной статье.
Как понять закон Ома?
Чтобы интуитивно понять закон Ома, обратимся к аналогии представления тока в виде жидкости. Именно так думал Георг Ом, когда проводил опыты, благодаря которым был открыт закон, названный его именем.
Представим, что ток – это не движение частиц-носителей заряда в проводнике, а движение потока воды в трубе. Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.
Отсюда следует вывод, что скорость потока воды (сила тока в проводе) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов)
Сила тока прямо пропорциональна напряжению.
Теперь обратимся к сопротивлению. Гидравлическое сопротивление – это сопротивление трубы, обусловленное ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.
Сила тока обратно пропорциональна сопротивлению.
Такую аналогию можно проводить лишь для принципиального понимания закона Ома, так как его первозданный вид – на самом деле довольно грубое приближение, которое, тем не менее, находит отличное применение на практике.
В действительности, сопротивление вещества обусловлено колебанием атомов кристаллической решетки, а ток – движением свободных носителей заряда. В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.
В данной статье мы постарались дать простое объяснение закона Ома. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Конечно, мы привели его простейшую формулировку закона Ома и не будем сейчас лезть в дебри высшей физики, разбираясь с активным и реактивным сопротивлениями и прочими тонкостями.
Если у Вас возникнет такая необходимость, Вам с удовольствием помогут сотрудники нашего студенческого сервиса. А напоследок предлагаем Вам посмотреть интересное видео про закон Ома. Это действительно познавательно!
Содержание:
Расчет электрических цепей постоянного тока:
Основная цель расчета электрической цепи заключается в определении токов в ее ветвях. Зная токи, нетрудно найти напряжения и мощности ветвей и отдельных элементов цепи.
Величины токов, напряжений, мощностей дают возможность оценить условия и эффективность работы электротехнического оборудования и приборов во всех участках электрической цепи.
Связь между э.д.с., напряжениями и токами линейных электрических цепей выражается линейными уравнениями, т. е. уравнениями первой степени, поэтому для расчета их применяются аналитические методы с обычными алгебраическими преобразованиями.
Законы Кирхгофа
Для расчета электрических цепей наряду с законом Ома применяются два закона Кирхгофа, являющиеся следствиями закона сохранения энергии.
Первый закон Кирхгофа
Первый закон Кирхгофа применяется к узлам электрических цепей:
в ветвях, образующих узел электрической цепи, алгебраическая сумма токов равна нулю:
В эту сумму токи входят с разными знаками в зависимости от направления их по отношению к узлу. На основании первого закона Кирхгофа для каждого узла можно составить уравнение токов. Например, для точки 3 схемы рис. 3.16 такое уравнение имеет вид
I1 + I2 — I4 — I7 = 0.
В этом уравнении токи, направленные к узлу, условно взяты положительными, а токи, направленные от узла, — отрицательными:
I1 + I2 = I4 + I7. (4.2)
Уравнение (4.2) позволяет дать другую формулировку первого закона Кирхгофа:
сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла.
Этот закон следует из принципа непрерывности тока. Если допустить преобладание в узле токов одного направления, то заряд одного знака должен накапливаться, а потенциал узловой точки непрерывно изменяться, что в реальных цепях не наблюдается.
Второй закон Кирхгофа
Второй закон Кирхгофа применяется к контурам электрических цепей:
в контуре электрической цепи алгебраическая сумма напряжений на его ветвях равна нулю:
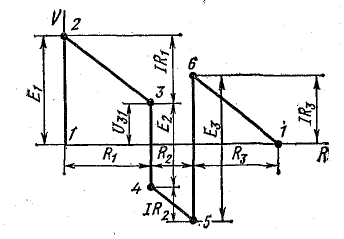
Для доказательства второго закона Кирхгофа обойдем контур 1-2-3-4-5-6-1 в схеме рис. 3.16 по часовой стрелке и запишем выражения потенциалов точек контура при указанных направлениях токов в ветвях (выбраны произвольно). Обход начнем от точки 1, потенциал которой V1. Потенциал каждой последующей точки выразим относительно точки предыдущей: V2 = V1 + Е1; V3 = V2 — I1R1; V4 = V3 — I4R4; V5 = V4 — E3; V6 = V5 + I6R6; V1 = V6 — I3R3.
Изменение потенциала по выбранному контуру должно быть равно нулю, так как оно выражает работу, затраченную на перемещение частиц, обладающих вместе единицей заряда, по замкнутому пути в электрических полях источников и приемников энергии. Таким образом, в замкнутом контуре
или
В этом уравнении напряжения ветвей
поэтому
В уравнении (4.4) напряжения, направленные по обходу контура, считаются положительными, а направленные против обхода — отрицательными.
Уравнение (4.4) перепишем в следующем виде:
Уравнение (4.5) позволяет дать другую формулировку второго закона Кирхгофа:
в контуре электрической цепи алгебраическая сумма падений напряжения на пассивных элементах равна алгебраической сумме э. д. с. этого контура:
Другим контурам соответствуют другие уравнения, которые нетрудно написать, не прибегая к выражениям потенциалов точек контура.
Для этого можно пользоваться следующим правилом. В левую часть уравнения следует записать алгебраическую сумму падений напряжения в пассивных элементах контура, а в правую—алгебраическую сумму э.д.с., встречающихся при обходе контура.
При этом положительными считаются токи и э. д. с., направление которых совпадает с направлением обхода.
Согласно этому правилу, запишем уравнения для двух других контуров схемы, представленной на рис. 3.16:
для 1-2-3-6-1
для 3-4-6-3
Неразветвленная электрическая цепь
Элементы неразветвленной электрической цепи соединены между собой последовательно.
Отличительной особенностью последовательного соединения является то, что электрический ток во всех участках цепи один и тот же.
Общий случай последовательного соединения
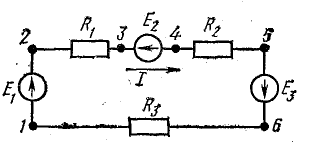
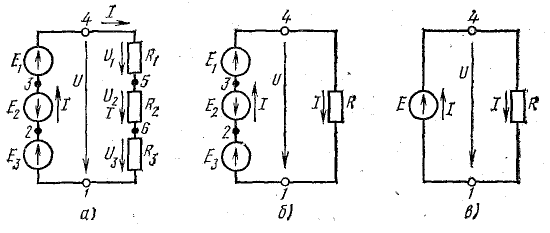
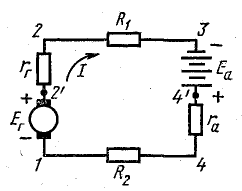
Рассмотрим общий случай последовательного соединения источников и приемников электрической энергии (рис. 4.1), пренебрегая внутренними сопротивлениями источников. Составим уравнение по второму закону Кирхгофа, произвольно задавшись направлением тока в цепи и направлением обхода контура (например, по часовой стрелке):
Ток в цепи
При обходе контура видно, что относительно направления обхода э. д. с. Е1 и Е3 направлены одинаково, т. е. согласно, а э. д. с. Е2 — им навстречу.
Ток в цепи определяется действием всех трех э.д.с., и при заданных направлениях э. д. с. и тока нетрудно установить, что элементы с э. д. с. E1 и Е3 вырабатывают электрическую энергию, а элемент с э. д. с. Е2 ее потребляет. Если в качестве источников э. д. с. в данном случае предположить аккумуляторы, то источники Е1 и Е3 разряжаются, а источник Е2 заряжается.
В элементах цепи, характеризующихся сопротивлениями R1, R2 и R3, электрическая энергия преобразуется в тепловую. Рассматривая в качестве примера схему рис. 4.1, нетрудно убедиться в том, что второй закон Кирхгофа является следствием закона сохранения энергии в применении его к контуру электрической цепи.
Рис. 4.1. Схема неразветвленной электрической цепи
Для этого достаточно умножить уравнение (4.7) на I, перенеся предварительно Е2 в левую часть:
Получим уравнение баланса мощности — для рассматриваемой цепи: сумма мощностей источников электрической энергии равна сумме мощностей приемников.
Ток в цепи с последовательным соединением элементов (рис. 4.1) не изменится и баланс мощностей сохранится, если произвести перестановку элементов цепи, сгруппировав э. д. с. и сопротивления, как показано на рис. 4.2, а.
Рис. 4.2. Преобразование схемы неразветвленной электрической цепи
Последовательное соединение пассивных элементов
Участок цепи 4-5-6-1 представляет собой последовательное соединение резисторов. На рассматриваемом участке действует напряжение U, равное алгебраической сумме э. д. с. левой части схемы [см. правую часть уравнения (4.7)]. Это напряжение равно также сумме падений напряжения в правой части схемы [см. левую часть уравнения (4.7)].
Вынеся I за скобку, получим
или
Отношение U/I = R есть некоторое сопротивление, эквивалентное по своему действию всем трем сопротивлениям:
Это равенство позволяет на участке 4-5-6-1 три сопротивления заменить одним (эквивалентным) и получить более простую схему (рис. 4.2, б) при условии неизменности тока в цепи и сохранении того же баланса мощностей. Этот вывод можно распространить на любое число последовательно включенных пассивных элементов:
т. е. общее сопротивление неразветвленной цепи равно сумме сопротивлений ее участков.
Последовательное соединение источников э.д.с.
Участок 1-2-3-4 цепи на рис. 4.2, а представляет собой последовательное соединение источников э. д. с. Напряжение между точками 4-1
Последнее равенство позволяет на участке 1-2-3-4 три э. д. с. заменить одной (эквивалентной)
и получить более простую схему (рис. 4.2, в), в которой только одна (эквивалентная) э. д. с. Е.
Этот вывод можно распространить на любое число последовательно включенных источников. Если э. д. с. всех источников равны и направлены согласно, как это имеет место при включении аккумуляторных элементов в батарее, то общая э. д. с. может быть определена по формуле
где Еn — э. д. с. одного элемента; n — число элементов в батарее.
Согласно составленной эквивалентной схеме (рис. 4.2, в),
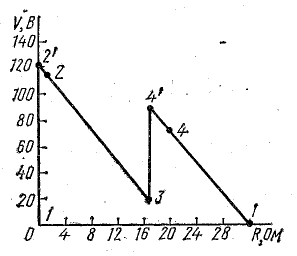
Потенциальная диаграмма
В схеме, представленной на рис. 4.1, при переходе от точки 1 к точке 2 потенциал повышается на величину Е1, а при переходе от точки 2 к точке 3 — снижается на величину U2.3 = IR1. При переходе от точки 3 к точке 4 потенциал понижается на величину U3.4 = —E2.
Рис. 4.3. Потенциальная диаграмма электрической цепи
Изменение потенциалов в электрической цепи можно наглядно изобразить графически в виде потенциальной диаграммы.
Потенциальная диаграмма представляет собой график изменения потенциала при обходе цепи, построенный в прямоугольной системе координат, в которой по оси абсцисс откладываются в определенном масштабе сопротивления участков цепи, а по оси ординат — потенциалы соответствующих точек. Потенциальная диаграмма цепи, изображенной на рис. 4.1, показана на рис. 4.3.
Потенциалы точек цепи найдены согласно равенствам
причем потенциал точки 1 принят равным нулю.
Поскольку внутренние сопротивления источников э. д. с. приняты равными нулю, при переходе через эти элементы потенциалы изменяются скачком.
Задача 4.3.
Генератор постоянного тока, аккумуляторная батарея и два резистора с постоянным сопротивлением составляют неразветвленную цепь Э. д. с. генератора Eг = 120 В; внутреннее сопротивление rг = 1,0 Ом, э. д. с. батареи Еа = 72 В, внутреннее сопротивление rа = 3 Ом, R1 = 16 Ом, R2 = 12 Ом.
Определить ток в цепи, составить баланс мощностей и построить потенциальную диаграмму цепи.
Решение. По условию задачи составлена схема (рис 4.4), из которой видно, что генератор и аккумуляторная батарея включены согласно: относительно произвольно выбранного направления обхода цепи обе э. д. с. направлены одинаково.
Рис. 4.4. К задаче 4.3
Эквивалентная э. д. с. цепи
Эквивалентное внутреннее сопротивление
Эквивалентное сопротивление нагрузки
Ток в цепи
Для составления баланса мощностей найдем мощность каждого элемента цепи:
генератора
аккумуляторной батареи
потерь внутри генератора
потерь внутри аккумуляторной батареи
потребления в резисторе R1
потребления в резисторе R2
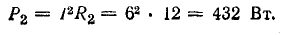
Баланс мощностей (общая мощность источников энергии равна суммарной мощности потребления)
Для построения потенциальной диаграммы найдем потенциалы точек цепи, полагая потенциал точки 1 V1 = 0:
Потенциальная диаграмма показана на рис. 4.5.
Рис. 4.5. Потенциальная диаграмма.
Разветвленная электрическая цепь с двумя узлами
Разветвленная электрическая цепь, как видно из названия, состоит из нескольких ветвей.
Ветви, присоединенные к одной паре узлов, включены параллельно (рис. 4.7, а). Отличительной особенностью параллельного соединения является то, что ко всем ветвям приложено одно и то же напряжение.
Рис. 4.7. Преобразование схемы с параллельным соединением приемников
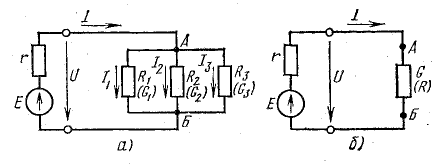
Параллельное соединение пассивных элементов
Приемники электрической энергии, представленные на схеме рис.4. 7, а сопротивлениями R1, R2, R3 и источник электрической энергии Е с внутренним сопротивлением r подключены к одной паре узлов (точки А и Б). Составим уравнение токов для узла А в соответствии с первым законом Кирхгофа:
Токи приемников можно выразить, используя напряжение между узлами и проводимости ветвей:
где
Разделим это уравнение на U:
Отношение UU есть проводимость G, соответствующая общему току цепи и общему напряжению:
Этот вывод можно распространить на любое число n параллельно соединенных приемников:
При параллельном соединении пассивных ветвей общая проводимость между двумя узлами равна сумме проводимостей всех ветвей.
Исходя из формул (4.13) и (4.14), можно заменить три проводимости (в общем случае n проводимостей) одной (эквивалентной) проводимостью GО и получить более простую схему (рис. 4.7, б).
Эквивалентное сопротивление при параллельном соединении нескольких ветвей определяется из равенства
Очень часто встречается параллельное соединение двух ветвей. В этом случае эквивалентное сопротивление определяется по формуле
или
Схема на рис. 4.7, б, полученная после замены трех проводимостей одной (эквивалентной), представляет собой простейшую схему электрической цепи.
Ток в этой схеме, равный току в неразветвленной части (рис. 4.7,а), определяется по формуле
Целью расчета электрической цепи является не только определение общего тока, но и тока в каждой ветви.
Если заданы э.д.с. и все сопротивления, то после определения общего тока по формуле (3.15) нужно определить напряжение между узловыми точками и токи в ветвях по закону Ома:
Параллельное соединение источников энергии
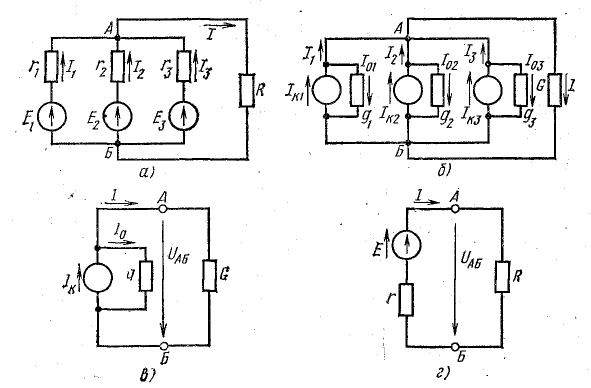
В практике часто встречаются случаи параллельного включения источников электрической энергии, работающих совместно на один или несколько приемников (рис. 4.8).
Рис. 4.8. Преобразование схемы с параллельным соединением источников
В таких случаях определением токов в источниках решается важная задача распределения нагрузки между ними.
Представим источники энергии в схеме рис. 4.8, а эквивалентными схемами источников тока, а сопротивление приемника заменим проводимостью G (рис. 4.8, б):
где U = Uаб — напряжение между узловыми точками А и Б.
По первому закону Кирхгофа, для узла А
или
Это равенство дает основание три источника тока заменить одним (эквивалентным), а схему рис. 4.8, б заменить более простой (рис. 4.8, в). Эквивалентный источник тока характеризуется током короткого замыкания
и внутренней проводимостью
Для схемы рис. 4.8, в
Напряжение между узлами
Токи в ветвях можно определить по следующим формулам:
Из этих выражений следует, что источники с относительно большей э. д. с. и меньшим внутренним сопротивлением имеют больший ток, т. е. принимают на себя большую нагрузку. Если э. д. с. и внутренние сопротивления источников одинаковы, нагрузка между ними распределяется поровну.
Общий ток в этом случае определяется произведением тока одного источника In на число параллельно включенных источников:
Величина тока каждого источника ограничена его номинальным значением Iном, сверх которого нагружать источник нельзя. Параллельное соединение источников применяется для увеличения общего тока, благодаря чему достигается увеличение мощности потребления энергии без изменения напряжения.
От схемы с эквивалентным источником тока можно перейти к схеме с эквивалентным источником э. д. с. (рис. 4.8, г), разделив уравнение (4.17) на g:
Так как l/g = r — внутреннее сопротивление эквивалентного источника э. д. с., то Iкr = Ir + U.
Но Iкr — Е — э. д. с. эквивалентного источника; Ir — падение напряжения во внутреннем сопротивлении, поэтому Е = U + Ir.
Рассматривается метод расчета разветвленных электрических цепей, предусматривающий замену всех источников э.д.с. одним (эквивалентным), который принято называть эквивалентным генератором.
Общий случай параллельного соединения источников и приемников электрической энергии
Выводы и формулы, полученные ранее, могут быть применены для расчета электрических цепей с двумя узловыми точками, между которыми содержится любое число параллельных ветвей с источниками и приемниками энергии, в том числе и такие ветви, которые имеют несколько элементов, соединенных последовательно (например, схема рис. 4.9).
Порядок расчета таких цепей, предусматривающий предварительное определение напряжения между узловыми точками, называется методом узлового напряжения.
Для применения этого метода должны быть заданы э.д.с. источников и проводимости ветвей (последние можно определить, если заданы сопротивления элементов каждой ветви).
Рис. 4.9. Схема с двумя узлами
В общем случае токи в ветвях и э. д. с. могут иметь различное направление, поэтому при определении узлового напряжения нужно взять алгебраическую сумму произведений ЕG и формула (4.18) примет вид
Знак э. д. с. устанавливается в соответствии с положительным направлением токов в ветвях, которое выбирается произвольно, но одинаково для всех ветвей (например, от Б к А).
Э. д. с. ветви считается положительной, если ее направление совпадает с положительным направлением тока. В противном случае э. д. с. подставляют со знаком минус в формулу (4.21) и также при определении токов по формулам (4.19).
Задача 4.8.
Для схемы, изображенной на рис. 4.7, а, известны: Е = 130 В, r = 0,5 Ом, R1 = 30 Ом, R2 = 20 Ом, R3 = 12 Ом. Определить токи в схеме, мощность передачи энергии приемникам и к. п. д. источника.
Решение. Вначале определим эквивалентное сопротивление между точками А и Б:
Ток в неразветвленной части цепи
Для определения токов в параллельных ветвях между узловыми точками определим напряжение на зажимах источника, которое в данном случае равно напряжению на приемниках:
Проверим правильность определения токов по уравнению (4.1):
Мощность передачи энергии приемникам
К. п. д. источника
Задача 4.10.
Для схемы, изображенной на рис. 4.7, а, известны: R1 = 10 Ом; R2 = 15 Ом; R3 = 6 Ом, r = 0,5 Ом, l3 = 10 А. Определить токи в схеме, мощность и к. п. д. источника.
Решение. Используя данные условия, относящиеся к третьей ветви, определим напряжение между узлами А и Б по закону Ома:
Напряжение U является общим для всех ветвей, присоединенных к точкам А и Б. Это дает возможность использовать ту же формулу для определения токов в двух ветвях:
Ток в неразветвленной части цепи
Э. д. с. источника
Мощность источника
Мощность потребления энергии приемниками
К. п. д. источника
Задача 4.12.
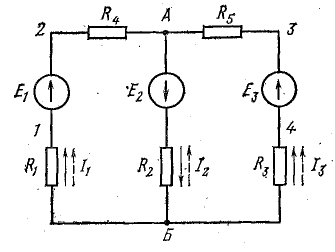
Определить токи и составить баланс мощностей для схемы, изображенной на рис. 4.9, если известны: E1 = 120 В; E2 = 80 В; E3 = 60 В; r1 = 0,5 Ом; r2 = 0,4 Ом; r3 = 0,2 Ом; R1 = 2 Ом; R2 = 15,6 Ом; R3 = 12,4 Ом; R4 = 7,5 Ом; R5 = 7,4 Ом.
Решение. Применяя метод узлового напряжения, найдем UАБ по формуле (4.21). Предварительно зададим положительное направление токов от Б к А и подсчитаем проводимости ветвей:
Токи в ветвях:
Токи l1 и l3 положительны. Их направление совпадает с выбранным ранее условно-положительным направлением от узла Б к узлу А. Направление тока l2 противоположно положительному направлению; в результате расчета этот ток получился отрицательным. На схеме рис. 4.9 пунктиром показано положительное направление токов в ветвях, а сплошной стрелкой — их действительное направление.
Для составления баланса мощностей необходимо подсчитать мощность каждого элемента схемы, в том числе и мощность потерь внутри источников. Заметим, что направления э. д. с. и токов во всех ветвях совпадают — источники Э. д. с. являются источниками энергии.
Мощности источников: P1.1 = E1I1 = 120 • 7,3 = 876 Вт; P1.2 = Е2I2 = 80 • 7,95 = 636 Вт; Р1.3 = E3I3 = 60 • 0,65 = 39 Вт.
Общая мощность источников 1551 Вт.
При определении мощности источников можно не задумываться над тем, в каком режиме работает тот или другой источник. Ответ на этот вопрос дает знак полученной мощности, если токи и э. д. с. подставлять с теми знаками, какие были приняты или получены в расчете. Например, мощность второго источника положительна: P1.2 = —80 • (—7,95) = 636 Вт. Это указывает на то, что в данной ветви работает источник энергии. Раньше Е2 и I2 сразу были взяты положительными, так как отмечено совпадение направлений напряжения и тока.
Мощность потерь внутри источников:
Общая мощность потерь внутри источников приблизительно 52 Вт. Мощность приемников:
Общая мощность приемников 1499 Вт.
Баланс мощностей (мощность источников равна мощности приемников плюс мощность потерь внутри источников) 1551 Вт = 1499 + 52 Вт.
Расчет электрических цепей методом эквивалентных сопротивлений (метод «свертывания» цепи)
Метод эквивалентных сопротивлений применяется для расчета таких электрических цепей, в которых имеются пассивные элементы, включенные между собой последовательно, параллельно или по смешанной схеме.
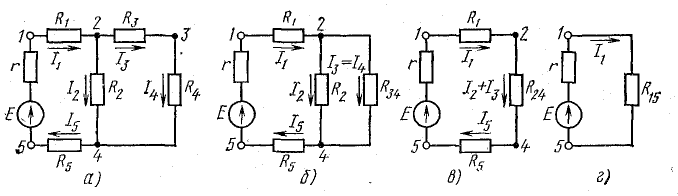
Определение эквивалентных сопротивлений
На схеме рис. 4.10, а сопротивления R3 и R4 включены последовательно: между ними (в точке 3) нет ответвления с током, поэтому I3 = I4. Эти два сопротивления можно заменить одним (эквивалентным), определив его как сумму
После такой замены получается более простая схема (рис. 4.10, б). Сопротивления R2 и R3.4 соединены параллельно, их можно заменить одним (эквивалентным), определив его по формуле (4.16):
и получить более простую схему (рис. 4.10, в).
Рис. 4.10. К методу эквивалентных сопротивлений
В схеме рис. 4.10, в сопротивления R1, К2.4, К5 соединены последовательно. Заменив эти сопротивления одним (эквивалентным) сопротивлением между точками 1 и 5, получим простейшую схему (рис. 4.10, г).
Подобными преобразованиями схему смешанного соединения пассивных элементов с одним источником энергии в большинстве случаев можно привести к простейшей схеме. В более сложных схемах методом эквивалентных сопротивлений достигается упрощение, которое значительно облегчает расчет.
Определение токов
В простейшей схеме (рис. 4.10, г) ток I определяется по закону Ома с использованием формулы (3.15). Токи в других ветвях первоначальной схемы определяют, переходя от схемы к схеме в обратном порядке.
Из схемы рис. 4.10, в видно, что
Кроме того, напряжение между точками 2 и 4
Зная это напряжение, легко определить токи I2 и I3 = I4:
После определения токов I1 и I5 напряжение U2.4 можно найти как разность потенциалов между точками 2 и 4. Для этого положим V4 известным (например, равным нулю), а V2 найдем так же, как при построении потенциальной диаграммы, обойдя от точки 4 неразветвленный участок цепи с током I1 =I5:
Метод преобразования треугольника и звезды сопротивлений
Пассивные элементы в электрических цепях соединяются не только последовательно или параллельно. Во многих схемах можно выделить группы из трех элементов, образующих треугольник или звезду сопротивлений.
При расчете подобных цепей упрощение схем выполняют известным методом эквивалентных сопротивлений, но предварительно проводят преобразование треугольника сопротивлений в эквивалентную звезду или наоборот.
Треугольник и звезда сопротивлений
Рассмотрим в качестве примера схему рис. 4 .11, а, которая применяется для измерения сопротивлений (схема моста Уитстона).
В этой схеме нет элементов, соединенных последовательно или параллельно, но имеются замкнутые контуры из трех сопротивлений (треугольники сопротивлений), причем точки, разделяющие каждую пару смежных сопротивлений, являются узловыми.
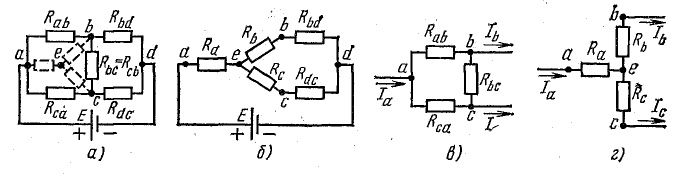
К узловым точкам a, b, c присоединен треугольник сопротивлений Rab, Rbc, Rca. Его можно заменить эквивалентной трехлучевой звездой сопротивлений Ra, Rb, Rc (на рисунке изображены штриховыми линиями), присоединенных с одной стороны к тем же точкам a, b, c, а с другой — в общей (узловой) точке e.
Рис. 4.11. Преобразование треугольника сопротивлений в эквивалентную звезду
Смысл замены становится понятным при рассмотрении эквивалентной схемы 4.11, б, где сопротивления Rb и Rbd соединены между собой последовательно, так же как b сопротивления Rc и Rdc.
Две ветви между узловыми точками e и d с этими парами сопротивлений соединены параллельно. Соответствующими преобразованиями схему можно привести к простейшему виду.
Преобразование треугольника сопротивлений в эквивалентную звезду
Замена треугольника сопротивлений эквивалентной звездой и наоборот осуществляется при условии, что такая замена не изменяет потенциалов узловых точек a, b, c, являющихся вершинами треугольника и эквивалентной звезды.
Одновременно предполагают, что в остальной части схемы, не затронутой преобразованием, режим работы не изменяется (не меняются токи, напряжения, мощности). Для доказательства возможности перехода от треугольника к звезде и наоборот рассмотрим схемы рис. 4.11, в, г.
Эти схемы остаются эквивалентными для всех режимов, в том числе и для режима, при котором Ia = 0, что соответствует обрыву общего провода, ведущего к точке а. В этом случае в схеме треугольника между точками b и c включены параллельно две ветви с сопротивлениями Rbc и Rab + Rca
Общее сопротивление между этими точками
В схеме звезды между точками b и c включены последовательно сопротивления Rb и Rc. Общее сопротивление между этими точками Rb + Rc.
По условиям эквивалентности напряжение между точками b и c и токи Ib и Ic в обеих схемах должны быть одинаковыми. Следовательно, и сопротивления между точками b и c в обеих схемах одинаковы, т. е.
Полагая Ib =0, а затем Ic = 0, получим:
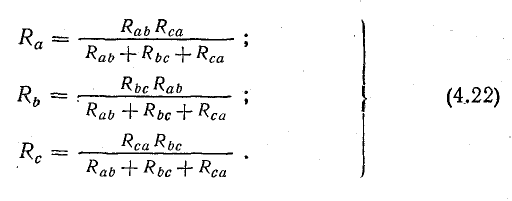
Совместное решение трех полученных уравнений приводит к следующим выражениям, которые служат для определения сопротивлений трехлучевой звезды по известным сопротивлениям эквивалентного треугольника:
Преобразование звезды сопротивлений в эквивалентный треугольник
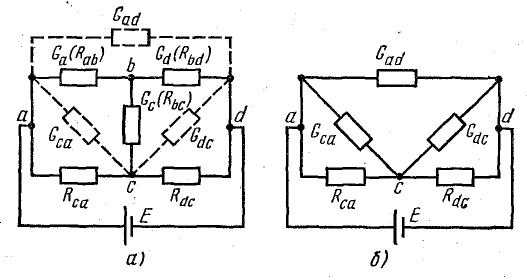
Для расчета некоторых схем применяется преобразование трехлучевой звезды в эквивалентный треугольник, которое показано на рис. 4.12, а, где схема взята такой же, как на рис. 4.11, а.
При этом для определения параметров треугольника по заданным параметрам звезды пользуются формулами, которые записаны применительно к схемам рис. 4.12, а, б:
где Gad; Gdc; Gca — проводимости сторон треугольника; Ga; Gd; Gc — проводимости лучей звезды.
Зная проводимости, нетрудно определить сопротивления треугольника, если это необходимо.
Рис. 4.12. Преобразование трехлучевой звезды в эквивалентный треугольник
- Методы анализа сложных электрических цепей
- Метод узловых напряжений
- Метод узловых потенциалов
- Принцип и метод наложения
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Электрическая цепь
- Электрический ток