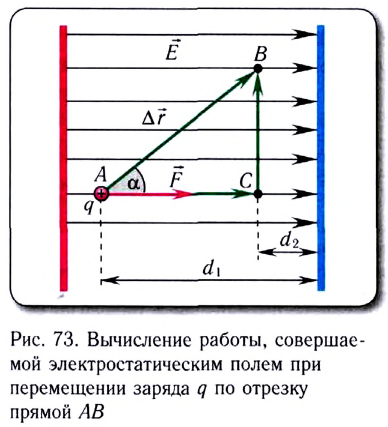
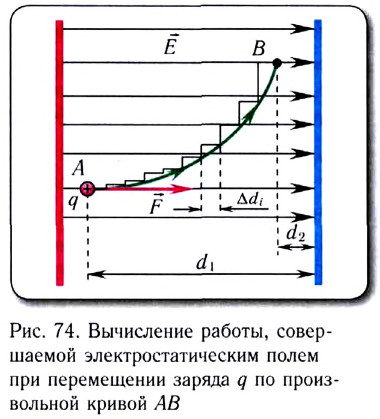
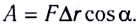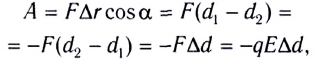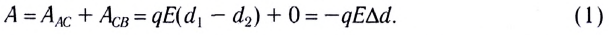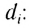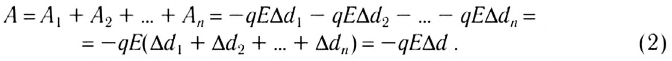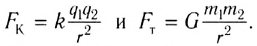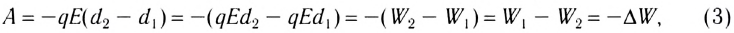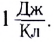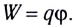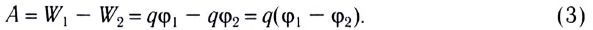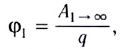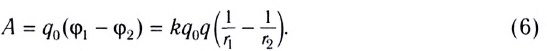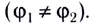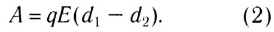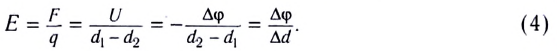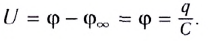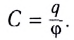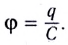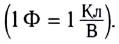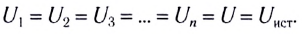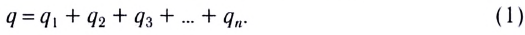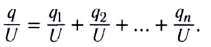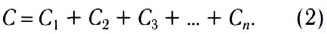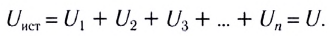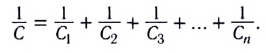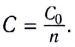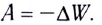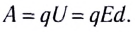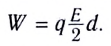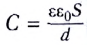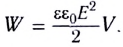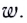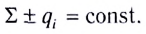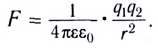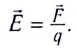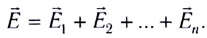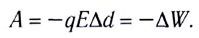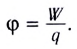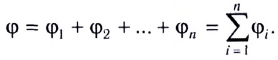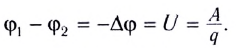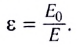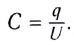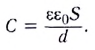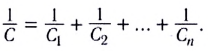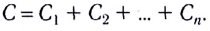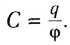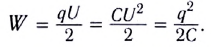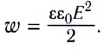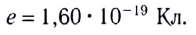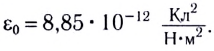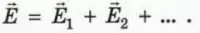Электростатика: элементы учебной физики
Лекция 5. Напряжённость электрического поля
Продолжение. См. № 17,
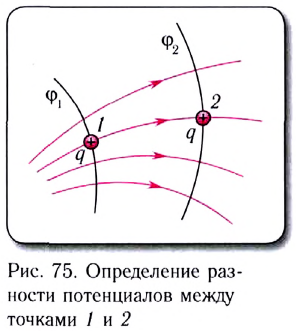
18, 19, 20/07
В.В.МАЙЕР,
ГОУ ВПО ГГПИ им. В.Г.Короленко, г. Глазов,
Республика Удмуртия
varaksina_ei@list.ru
Электростатика: элементы учебной
физики
Понятие электрического поля оказалось
плодотворным потому, что удалось ввести
количественные характеристики, которые
позволяют решать конкретные физические задачи. К
ним в первую очередь относятся напряжённость и
потенциал электрического поля.
Экспериментальные исследования
учащихся должны показать, что напряжённость
реально может быть измерена и что эта величина
действительно характеризует электрическое поле.
Относительно новое для школьников – один и тот
же прибор, электростатический динамометр, при
соответствующей градуировке может быть
использован в качестве измерителя и силы, и
напряжённости. Однако это вовсе не значит, что
этим прибором можно измерить любую
электростатическую величину: ни при какой
градуировке электростатического динамометра не
удастся получить прибор, измеряющий, скажем,
потенциал электрического поля.
Принципиально важно
экспериментальное обоснование принципа
суперпозиции электрических полей. Такое
обоснование можно было бы осуществить уже при
введении понятия электрического поля, но
предпочтительнее сделать это, когда учащиеся
будут ознакомлены с понятием напряжённости.
5.1. Напряжённость электрического
поля. Силовой характеристикой
электрического поля является вектор
напряжённости электрического поля E,
равный отношению вектора силы, действующей в
данной точке поля на пробный положительный
заряд, к величине этого заряда:
( 5.1)
Напряжённость в системе единиц СИ
выражается в ньютонах на кулон (Н/Кл).
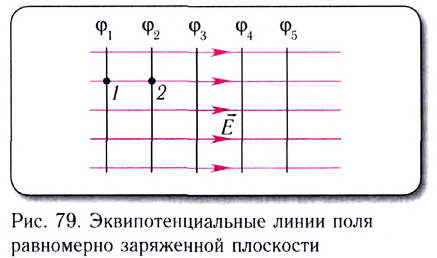
5.2. Напряжённость электрического
поля точечного заряда. Во многих задачах
электростатики размерами заряженных тел по
сравнению с расстояниями до точек наблюдения
можно пренебречь. В таких случаях говорят о
точечных зарядах. Понятно, что на самом деле
никаких точечных зарядов или заряженных точек в
природе не существует, — это просто удобная
абстракция.
Закон Кулона, как вы знаете, справедлив
именно для точечных зарядов. Непосредственно из
закона Кулона следует, что модуль вектора
напряжённости электрического поля точечного
заряда Q:
(5.2)
где R – расстояние до точки
наблюдения, q – пробный положительный заряд.
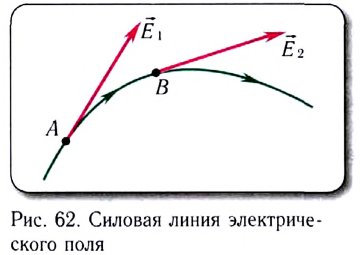
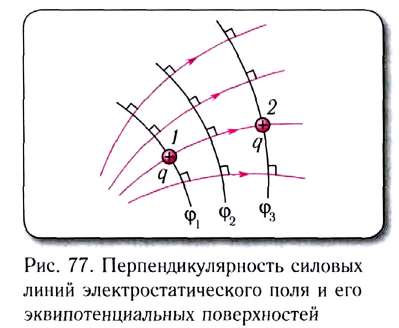
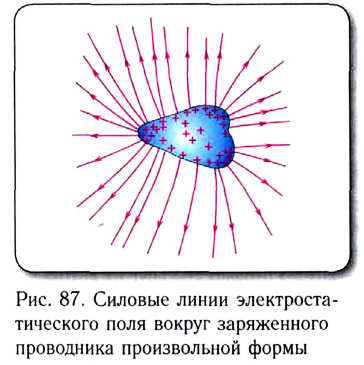
5.3. Силовые линии
электростатического поля. Фарадей, который
ввёл понятие электрического поля, внутренним
взором видел заряды, окружённые полями.
Изображать их он стал линиями, вдоль которых на
пробный заряд со стороны поля действуют силы. Силовые
линии электростатического поля часто
называют линиями напряжённости, т.к. вектор
напряжённости электрического поля в любой точке
такой линии касателен к ней. Вместо пробного
заряда для построения силовых линий удобнее
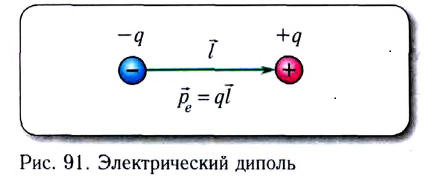
использовать электрический диполь.
Введя в электрическое поле
положительный пробный заряд на нити, по его
отклонению от положения равновесия определим
направление напряжённости поля. Уберём заряд и
вместо него в ту же точку внесём диполь. При
этом обнаружим, что он повернулся своим
положительным полюсом в направлении вектора
напряжённости электрического поля. Используя
диполь, нетрудно экспериментально доказать, что
электрическое поле можно характеризовать
силовыми линиями, т.е. такими линиями, в каждой
точке которых напряжённость поля является
касательной к ним.
Для этого создадим произвольное
электрическое поле, введём в него диполь и
отметим положение его положительного и
отрицательного полюсов. Переместим диполь так,
чтобы его, например, отрицательный полюс совпал с
точкой, в которой находился положительный.
Многократно повторяя эту операцию, получим
совокупность точек. Соединив эти точки плавной
линией, получим силовую линию исследуемого
электростатического поля.
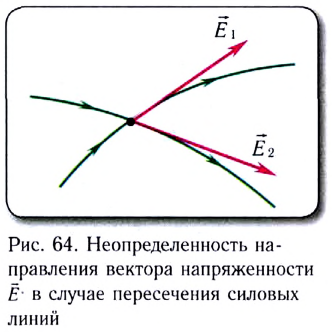
Опыт показывает, что через каждую
точку поля проходит только одна силовая линия.
Если бы было не так, то в точке пересечения двух
силовых линий одного поля на заряд действовали
бы разные силы.
Повторяя описанные выше действия,
построим семейство силовых линий так, чтобы их
начальные точки находились на поверхности
заряженного тела на равных расстояниях друг от
друга. Обнаружим, что силовые линии
располагаются с различной густотой. Внесём в
поле пробный заряд на нити в области с
максимальной и минимальной густотой силовых
линий и обнаружим, что в этих областях
напряжённость электрического поля
соответственно максимальна и минимальна.
Силовые линии сгущаются возле зарядов,
т.е. там, где модуль вектора напряжённости
электрического поля больше. Значит, густота
силовых линий определяется напряжённостью поля.
Семейство силовых линий в принципе может
полностью охарактеризовать электрическое поле.
Проделанные опыты показывают, что
силовые линии начинаются или заканчиваются на
зарядах, идут в бесконечность или выходят из неё.
В электростатическом поле замкнутых силовых
линий нет.
5.4. Принцип суперпозиции
напряжённостей электростатических полей.
Из принципа суперпозиции полей следует, что сила,
действующая на пробный заряд со стороны других
зарядов, равна геометрической сумме всех
действующих на заряд сил по отдельности. Но если
это так, то напряжённости электрических полей,
равные отношениям сил к величине пробного
заряда, складываются подобно силам.
Таким образом, для электрических полей
справедлив принцип суперпозиции в
следующей формулировке: напряжённость
результирующего электрического поля есть
геометрическая (векторная) сумма напряжённостей
полей, создаваемых отдельными зарядами:
E = E1 + E2 + E3 + …
(5.3)
Применение принципа суперпозиции для
напряжённостей позволяет существенно облегчить
решение многих задач электростатики.
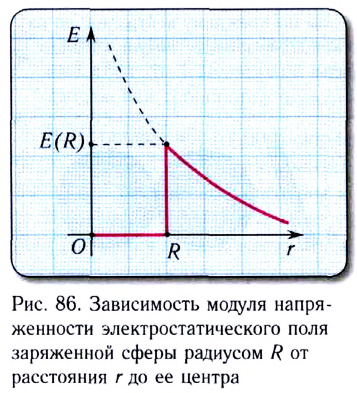
5.5. Поток вектора напряжённости
электрического поля. Представим себе
точечный положительный заряд Q, находящийся
в центре сферической поверхности 1 радиусом r.
В точках этой поверхности напряжённость
электрического поля 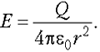
поверхности сферы S = 4r2, то её
произведение на напряжённость электрического
поля не зависит ни от чего, кроме заряда:
(5.4)
поэтому характеризует электрическое
поле в целом. Эта величина получила название потока
вектора напряжённости электрического поля.
Поток напряжённости через
концентрические сферические поверхности 1 и
2 одинаков. Так как он характеризует поле
заряда в целом, нужно, чтобы он оставался тем же и
для произвольной замкнутой поверхности 3. Но
для неё вектор напряжённости уже не является
нормалью к элементу поверхности. Поэтому для
определения потока вектора E через
элемент поверхности вместо площади этого
элемента следует брать площадь его проекции на
плоскость, перпендикулярную вектору E.
Условимся поток считать положительным, если
вектор напряжённости выходит из замкнутой
поверхности, и отрицательным, если он входит в
неё. Если заряд находится вне замкнутой
поверхности 4, то поток напряжённости через
неё равен нулю. Дело в том, что входящий внутрь
области поток по модулю равен выходящему.
5.6. Теорема Гаусса. Мысленно
переместим заряд из центра сферической
поверхности в любую точку внутри неё. Очевидно,
поток вектора напряжённости электрического поля
от этого не изменится, т.к., по самому определению,
он один и тот же для любой замкнутой поверхности,
окружающей заряд. Разместим внутри этой
поверхности не один, а несколько в общем случае
различных зарядов. По принципу суперпозиции
электрические поля этих зарядов не влияют друг
на друга, значит, потоки, созданные каждым
зарядом по отдельности, остаются неизменными.
Результирующий поток, очевидно, равен сумме
потоков от всех зарядов.
Это и есть теорема Гаусса: поток
вектора напряжённости через произвольную
замкнутую поверхность равен алгебраической
сумме зарядов, расположенных внутри этой
поверхности, делённой на электрическую
постоянную:
(5.5)
Если алгебраическая сумма зарядов
внутри замкнутой поверхности равна нулю, то
поток напряжённости электрического поля через
эту поверхность также равен нулю. Это понятно,
поскольку положительные заряды внутри
поверхности создают положительный поток, а
отрицательные – равный ему по модулю
отрицательный.
5.7. Поверхностная плотность
заряда. Если проводящему телу сообщить
заряд, то он будет распределён по его
поверхности. В общем случае на участках
поверхности одинаковой площади окажутся разные
заряды. Отношение заряда Q к площади поверхности
S, на которой
он распределён, называется поверхностной
плотностью заряда
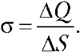
(5.6)
Поверхностная плотность заряда
выражается в кулонах на квадратный метр (Кл/м2).
5.8. Напряжённость электрического
поля заряженного шара. Используя теорему
Гаусса, нетрудно определить напряжённость
электрического поля, созданного заряженным
проводящим шаром. Действительно, если на
поверхности сферы радиусом r > R, центр
которой совпадает с центром шара, равномерно
распределён заряд Q, то поток вектора E
через сферическую поверхность радиусом r,
согласно теореме Гаусса, равен:
Отсюда напряжённость электрического
поля на расстоянии r от центра заряженной сферы
равна
(5.7)
Сравнивая (5.7) с (5.2), приходим к выводу,
что напряжённость электрического поля
заряженного шара равна напряжённости такого же
точечного заряда, расположенного в центре шара.
5.9. Напряжённость электрического поля
заряженной плоскости. Рассмотрим
бесконечную плоскость, заряженную равномерно с
поверхностной плотностью заряда . Электрическое поле такой
поверхности однородно, причём силовые линии
перпендикулярны поверхности. Чтобы найти
напряжённость поля, воспользуемся теоремой
Гаусса. Для этого построим замкнутую
цилиндрическую поверхность, ось которой
параллельна силовым линиям поля, а основания
площадью S находятся по разные стороны от
поверхности. Поток напряжённости через боковую
поверхность цилиндра равен нулю, т.к. силовые
линии её не пересекают. Поэтому полный поток
напряжённости через выбранную поверхность равен
сумме потоков через основания цилиндра: N = 2 • ЕS.
Полный заряд внутри цилиндра равен Q = S. Согласно
теореме Гаусса,
Отсюда напряжённость электрического поля
(5.8)
Итак, напряжённость электрического
поля заряженной плоскости равна поверхностной
плотности заряда, делённой на удвоенное значение
электрической постоянной.
5.10. Напряжённость электрического
поля разноимённо заряженных параллельных
плоскостей. Пусть некоторая плоскость
заряжена равномерно с плотностью заряда . Параллельно этой
плоскости расположим вторую, с такой же
плотностью заряда противоположного знака.
Найдём напряжённость электрического поля в этом
случае.
Каждая плоскость создаёт поле
напряжённостью E’ = /(2
0).
Согласно принципу суперпозиции, напряжённость
результирующего электрического поля равна сумме
напряжённостей этих полей. Так как между
плоскостями напряжённости полей имеют
одинаковое направление, то результирующая
напряжённость Е = 2E’:
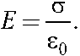
Следовательно, напряжённость
электрического поля между параллельными
плоскостями, несущими равные по модулю
разноимённые заряды, равна поверхностной
плотности заряда одной из плоскостей, делённой
на электрическую постоянную. Вне плоскостей
векторы напряжённостей направлены
противоположно и, поскольку их модули равны, поле
вообще отсутствует. Обратите внимание, что не
важно, проводят плоскости электричество или нет.
Исследование 5.1. Напряжённость
электрического поля
Проблема. Возможна ли в доступном
учебном эксперименте количественная оценка
напряжённости электрического поля, создаваемого
зарядами на наэлектризованных телах?
Задание. Используя
электростатический динамометр, разработайте
методику введения понятия напряжённости
электрического поля и предложите прибор для
измерения напряжённостей.
Вариант выполнения. Проводящему
шару сообщите заряд, для определённости
положительный. На пробный шарик
электростатического динамометра (см.
исследование 3.4) также нанесите некоторый заряд.
Введите динамометр в электрическое поле
заряженного шара и разверните так, чтобы его
показания стали максимальны. Это означает, что
пробный шарик электростатического динамометра
отклоняется в ту же сторону, куда направлена
сила, действующая на него со стороны
электрического поля.
Прикоснитесь к пробному шарику таким
же незаряженным шариком и уберите его: пробный
заряд уменьшится в два раза, показания
динамометра для того же расстояния до точки
наблюдения тоже уменьшаются в два раза.
Повторяя опыт с разными зарядами,
убедитесь, что отношение силы f, действующей
на пробный заряд q, к величине этого заряда в
данной точке поля остаётся постоянным, а при
переходе от одной точки к другой, вообще говоря,
меняется. Значит, это отношение может
характеризовать электрическое поле. Оно и
получило название напряжённости
электрического поля. Шкалу
электростатического динамометра, которым вы
пользовались для измерения силы
электростатического взаимодействия, можно
отградуировать в единицах напряжённости. Тогда
допустимо считать этот прибор измерителем
напряжённости электрического поля.
Градуировку нетрудно осуществить в единицах
Н/Кл, если предварительно измерить величину
пробного заряда (см. исследование 3.6).
Учащиеся должны понять, каким образом
один и тот же прибор превратился из измерителя
силы в измеритель напряжённости.
Исследование 5.2. Зависимость
напряжённости электрического поля от радиуса
заряженного шара
Задание. Разработайте
демонстрационный эксперимент, который может
служить обоснованием справедливости теоремы
Гаусса для электростатических полей.
Вариант выполнения.
Зарядите стоящий на диэлектрической
подставке небольшой проводящий шар. К нему
подведите измеритель напряжённости
электрического поля, пробный шарик которого
несёт такой же по знаку заряд, как заряд,
создающий исследуемое поле. Запомните
отклонение стрелки измерителя.
Первый шар с зарядом опустите в
полость второго проводящего шара значительно
большего диаметра, установленного на
диэлектрической подставке. Приближайте этот
второй шар к пробному шарику измерителя
напряжённости. Оказывается, когда центр второго
шара совпадает с точкой, в которой находился
центр первого шара, стрелка измерителя
отклоняется на первоначальное число делений.
Отсюда следует, что независимо от
радиуса заряженного шара на одном и том же
расстоянии от его центра напряжённость
электрического поля одна и та же. Тем самым
теорема Гаусса получила подтверждение в
демонстрационном эксперименте.
Понятно, что теорема Гаусса носит
общий характер и, строго говоря, не нуждается в
обоснованиях, подобных здесь рассмотренному. Но
в дидактических целях такое обоснование
совершенно необходимо, поскольку оно
способствует укреплению в сознании учащихся
неразрывной связи физической теории с
объективной реальностью.
Исследование 5.3. Суперпозиция
электрических полей
Информация. Чтобы убедиться в
справедливости принципа суперпозиции
электрических полей, нужно уметь определять не
только модули сил, действующих на заряды, но и их
направления. Делать это с помощью
электростатического динамометра неудобно. Кроме
того, он не позволяет графически изображать
векторы сил. Если на нити подвесить лёгкое
заряженное тело, то силу, действующую на него в
электрическом поле, можно оценить по отклонению
тела из положения равновесия. Но для измерения
этого отклонения воспользоваться линейкой не
удастся: приближение её к заряженному телу
вызывает изменение его положения. Чтобы
устранить эту трудность, можно спроецировать
заряженное тело на горизонтальную плоскость.
Задание. Разработайте и выполните
эксперимент, доказывающий справедливость
принципа суперпозиции электрических полей.
Вариант выполнения. К стеклянному
баллону маленькой лампочки приклейте тонкую
нить с лёгким проводящим шариком небольшого
радиуса на конце. Нанесите на шарик пробный
заряд. Лампочку закрепите над листом бумаги и
включите её. На листе бумаги цифрой 0
отметьте положение тени от шарика, находящегося
в положении равновесия. Приблизьте к пробному
заряду заряд Q1 и цифрой 1 отметьте
на листе положение тени отклонившегося шарика.
Уберите заряд Q1 и вместо него вблизи
пробного шарика расположите заряд Q2.
При этом тень от шарика займёт новое положение 2.
Верните заряд Q1 в
первоначальное положение. Теперь пробный шарик
находится в поле сразу двух зарядов и
отклоняется от положения равновесия так, что его
тень занимает положение 3. Проанализируйте
результат эксперимента. Очевидно, при смещении
шарика из положения равновесия его тень
смещается на величину, пропорциональную силе,
действующей на шарик в новом положении
равновесия (см. исследование 3.5). При малых
отклонениях пробного шарика эту силу
приближённо можно считать равной силе,
действующей на шарик в исходном положении. Длины
отрезков, соединяющих точку 0 с точками 1,
2 и 3, пропорциональны модулям
соответствующих сил. Соединив указанные точки
векторами, вы обнаружите, что вектор
результирующей силы, действующей на пробный
заряд, примерно равен сумме векторов сил,
действующих на него со стороны каждого заряда по
отдельности. Понятно, что точные измерения,
выполненные с более совершенными приборами,
вместо приближённого дадут точное равенство.
Поразительно единство природы: силы,
созданные электрическими полями, складываются
так же, как механические! Но если это так, то
напряжённости электрических полей, равные
отношениям сил к величине пробного заряда,
складываются подобно силам. Оставив шары
неподвижными, изменяйте их заряды в одинаковое
число раз (см. п. 2.6). При этом вы обнаружите, что
направление напряжённости результирующего поля
остаётся неизменным.
Таким образом, принцип суперпозиции
электростатических полей экспериментально
обоснован.
Исследование 5.4. Демонстрация
принципа суперпозиции напряжённостей
Проблема. Индивидуальный опыт,
выполненный в результате предыдущего
исследования, не позволяет убедиться в
справедливости принципа суперпозиции
напряжённостей электростатических полей всему
классу непосредственно на уроке. Как решить эту
проблему?
Задание. Учитывая возможности
кодоскопа, разработайте демонстрационный
вариант эксперимента, обосновывающего
справедливость принципа суперпозиции, и
методику проведения его на уроке.
Вариант выполнения. Из толстой
алюминиевой проволоки в изоляции выгните
специальный штатив высотой примерно 30 см и
поставьте его на конденсор кодоскопа. К верхнему
концу штатива привяжите конец тонкой нейлоновой
нити длиной примерно 20 см. На нижнем конце нити
закрепите шарик диаметром около 3 мм из тонкой
алюминиевой фольги. На конденсор кодоскопа на
стойках высотой 10 см, изготовленных из
полиэтиленовых трубок, поставьте пенопластовые
шары диаметром 15–20 мм, обёрнутые тонкой фольгой.
Основания стоек лучше сделать из прозрачного
оргстекла.
Уберите с конденсора стойки с шарами,
включите осветитель кодоскопа и на классной
доске получите изображение висящего на нити
пробного шарика. Одноимёнными зарядами зарядите
пробный шарик и два шара на стойках. На доске
мелом отметьте положение пробного шарика.
Поставьте на конденсор один из заряженных шаров,
отметьте его положение и положение пробного
шарика. Уберите первый заряженный шар и в
произвольное место поставьте второй, отметив на
доске новое положение пробного шарика. Верните в
первоначальное положение первый шар, обозначьте
результирующее положение пробного шарика, мелом
на доске нарисуйте соответствующие векторы сил и
предложите учащимся сделать вывод из
продемонстрированного опыта.
Исследование 5.5. Плотность заряда
на поверхности проводника
Задание. Докажите, что плотность
заряда на поверхности проводника, вообще говоря,
различна.
Вариант выполнения. Зарядите
расположенный на изолирующей подставке
проводник цилиндрической формы с остриём и
коническим углублением. Пробным шариком на
изолирующей ручке, предварительно заземлённым,
коснитесь цилиндрической поверхности
проводника и поместите его внутрь полого шара,
соединённого с электрометром. Если угол
отклонения стрелки мал, повторите перенос заряда
несколько раз. Запомните показания электрометра,
разрядите его и пробный шарик. Попробуйте снять
заряд из конического углубления в поверхности
проводника, и вы убедитесь, что там он
практически отсутствует. Повторите опыт, касаясь
пробным шариком теперь уже точки поверхности,
расположенной на острие проводника. В этом
случае угол отклонения стрелки электрометра
будет значительно больше, чем в первом опыте. Так
как вблизи острия пробный шарик заряжается до
большей величины, то в этой области плотность
распределения заряда по поверхности проводника
больше.
Зарядите металлический диск,
закреплённый за изолирующую ручку в штативе.
Проведя опыты, аналогичные описанным, покажите,
что плотность заряда во всех точках плоской
поверхности диска вдали от его края одинакова, а
на краю возрастает.
Исследование 5.6. Напряжённость
электрического поля вблизи заряженного
проводника
Задание. Поставьте опыт,
показывающий, что напряжённость электрического
поля вблизи заряженного проводника определяется
поверхностной плотностью заряда.
Вариант выполнения. Вблизи
проводника сложной формы расположите
электростатический динамометр и перемещайте его
так, чтобы расстояние до поверхности проводника
оставалось постоянным, а сила действовала на
шарик динамометра по нормали к поверхности. Опыт
должен показать, что там, где на поверхности
проводника плотность заряда больше, вблизи этой
поверхности больше и напряжённость
электрического поля (см. исследование 5.5).
Проанализируйте полученные результаты и
сделайте соответствующие выводы.
Исследование 5.7. Электрическое
поле вблизи заряженных плоскостей
Задание. Прямым экспериментом
подтвердите, что равномерно заряженная
плоскость даёт электрическое поле по обе стороны
от неё, а две параллельно установленные
плоскости, несущие равные заряды
противоположных знаков, создают электрическое
поле только в области между ними.
Вариант выполнения. На нитях
подвесьте два одинаковых обёрнутых алюминиевой
фольгой пенопластовых шарика так, чтобы они
касались металлического диска с противоположных
сторон. Зарядите диск от пьезоэлектрического или
иного источника. При этом шарики отойдут от диска
на равные расстояния, свидетельствуя о том, что
электрическое поле существует по обе стороны от
заряженного диска.
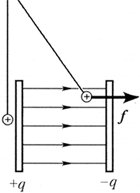
модулю и противоположным по знаку зарядом.
Постепенно приближайте второй диск к первому
так, чтобы они оставались параллельными. Вы
заметите, что отклонение шарика, находящегося
вне дисков, уменьшается, а находящегося между
дисками – увеличивается. Наконец, первый шарик
касается диска, показывая, что поле вне дисков
практически исчезло, а второй шарик отклоняется
на угол, примерно в два раза превышающий
первоначальный.
Исследование 5.8. Точное
подтверждение закона Кулона
Информация.
На диэлектрической стойке закрепите
металлический шар и заключите его между двумя
проводящими полусферами, одна из которых имеет
отверстие. Через отверстие проводником на
изолированной нити соедините шар с полусферами.
Зарядите полусферы. За нить удалите проводник.
Разомкнув шар и полусферы, разведите полусферы в
стороны, разрядите их, а к шару подсоедините
чувствительный электрометр: никакого заряда на
шаре вы не обнаружите. Значит, эксперимент ещё
раз показывает, что на проводнике, находящемся
внутри другого проводника, заряда нет.
Это справедливо потому, что справедлив
закон Кулона. Действительно, внутри проводящей
равномерно заряженной сферы выберем
произвольную точку А и вертикальными
конусами вырежем на сфере площадки S1 и
S2. Из геометрии
известно, что Но
эти площадки имеют заряды, пропорциональные их
величинам:
Небольшие площадки создают в точке А поля
напряжённостями
и отношение
которых
Значит, поскольку напряжённости полей,
созданных любыми подобными парами площадок на
сфере, равны по модулю и противоположно
направлены, результирующая напряжённость поля,
созданного в точке А всей заряженной сферой,
должна быть равна нулю.
Это и показывает эксперимент. Если бы
на опыте был обнаружен хотя бы слабый заряд на
внутреннем шаре, то оказалась бы неверной
формула для напряжённости поля точечного заряда
(5.2) и, следовательно, в законе Кулона (3.1) сила
взаимодействия между зарядами не была бы обратно
пропорциональна квадрату расстояния между ними.
Так как заряд можно измерить с гораздо более
высокой точностью, чем силу взаимодействия между
зарядами, а из закона Кулона следует, что поле
внутри тела отсутствует независимо от его формы,
то рассмотренный эксперимент корректнее
доказывает справедливость закона Кулона, чем
ранее описанные опыты.
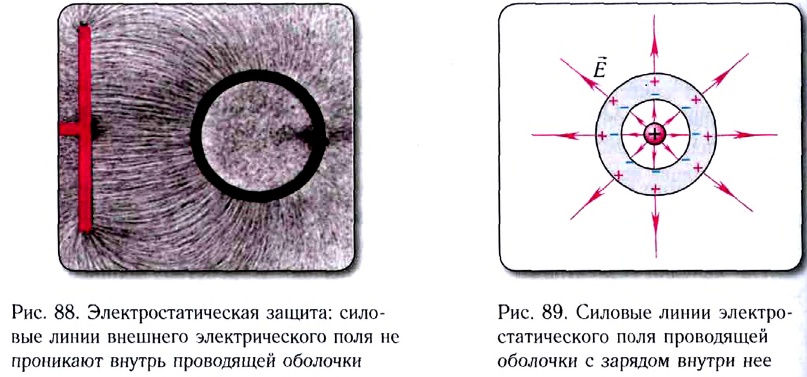
Задание. Разработайте и поставьте
доступный вариант рассмотренного эксперимента,
с максимальной убедительностью показывающий,
что внутри заряженного полого проводника
электрическое поле отсутствует.
Вариант выполнения. Чтобы
обнаружить электрическое поле, можно
воспользоваться явлением электростатической
индукции. Внесём в поле два соприкасающихся
проводящих тела на изолированных ручках. В них
произойдёт перераспределение зарядов. Не удаляя
из поля, разъединим эти тела – на них останутся
заряды противоположных знаков. Эти заряды можно
измерить электрометром, находящимся вне
исследуемого поля.
Эксперимент можно поставить так. На
подставке из диэлектрика закрепите полый
металлический шар. Проводником в хорошей
изоляции соедините его с одним из кондукторов
электрофорной машины. К шару приблизьте второй
кондуктор и приведите машину в действие. При этом
возникнут мощные искровые разряды длиной до 10 см.
Аккуратно введите внутрь шара одинаковые
металлические пластинки на ручках из оргстекла.
Приведите пластинки в соприкосновение, затем
разъедините, аккуратно достаньте из полости шара
и по очереди введите в шар электрометра. Вы
обнаружите, что никакого заряда на пластинках
нет! Значит, внутри проводящего шара
электрическое поле отсутствует, несмотря на то,
что шар в целом несёт значительный заряд,
сообщаемый ему работающей электрофорной
машиной. Повторите опыт, прикоснувшись пробным
шариком изнутри к металлу заряженного шара, – вы
вновь не обнаружите никакого заряда. Таким
образом, весь электрический заряд сосредоточен
на поверхности проводящего тела. Объясняется
этот результат тем, что справедлив закон Кулона.
В свою очередь, этот экспериментальный факт с
высокой точностью подтверждает справедливость
закона Кулона.
Вопросы для самоконтроля
1. В чём суть методики введения и
формирования понятия напряжённости
электрического поля?
2. Сравните метод построения силовых
линий посредством диполя с методом визуализации
электростатического поля мелким порошком,
взвешенным в жидком диэлектрике.
3. Изложите методику демонстрации на
уроке принципа суперпозиции электростатических
полей.
4. Каким экспериментом можно
подтвердить справедливость теоремы Гаусса?
5. Как зависят плотность заряда и
напряжённость электрического поля от формы
проводника?
6. Предложите демонстрационный опыт,
прямо показывающий зависимость плотности заряда
от площади проводника.
7. В чём дидактическая ценность
опыта с обнаружением электрического поля вблизи
одной и двух параллельных заряженных проводящих
пластин?
8. Нужно ли в школе рассматривать
метод точного подтверждения закона Кулона?
Литература
Бутиков Е.И., Кондратьев А.С.
Физика: Учеб. пособие: В 3-х кн. Кн. 2.
Электродинамика. Оптика. – М.: Физматлит, 2004.
Демонстрационный эксперимент по
физике в старших классах средней школы: Т. 2.
Электричество. Оптика. Физика атома: Под ред.
А.А.Покровского. – М.: Просвещение, 1972.
Кабардин О.Ф., Орлов В.А., Эвенчик
Э.Е. Физика: Учеб. для 10 кл. шк. и кл. с углубл.
изуч. физики: Под ред. А.А.Пинского. – М.:
Просвещение, 1997.
Учебное оборудование для кабинетов физики
общеобразовательных учреждений: Под ред.
Г.Г.Никифорова. — М.: Дрофа, 2005. (Cм. также «Физика»
(«ПС») № 10/2005; № 4/2007.)
Продолжение см. в № 22/07
§ 14. НАПРЯЖЕННОСТЬ
ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
ЭЛЕКТРИЧЕСКОЕ
СМЕЩЕНИЕ
Основные
формулы
Напряженность
электрического поля
E=F/Q,
где F — сила,
действующая на точечный положительный
заряд Q, помещенный в данную точку
поля.
Сила, действующая
на точечный заряд Q, помещенный в
электрическое поле,
F=QE.
Поток вектора
напряженности Е электрического
поля:
а) через произвольную
поверхность S,
помещенную в неоднородное поле,
или
,
где
— угол между вектором напряженности Е
и нормалью n к элементу поверхности;
dS — площадь элемента поверхности;
En — проекция вектора
напряженности на нормаль;
б) через плоскую
поверхность, помещенную в однородное
электрическое поле,
ФE=ЕScos.
Поток вектора
напряженности Е через замкнутую
поверхность
,
где
интегрирование ведется по всей
поверхности.
Теорема Остроградского
— Гаусса. Поток вектора напряженности
Е
через любую замкнутую поверхность,
охватывающую заряды
Ql,
Q2,
. . .,
Qn,
,
где
— алгебраическая
сумма зарядов, заключенных внутри
замкнутой поверхности; п — число
зарядов.
Напряженность
электрического поля, создаваемого
точечным зарядом Q
на расстоянии r от
заряда,
.
Напряженность
электрического поля, создаваемого
металлической сферой радиусом
R, несущей заряд
Q,
на расстоянии r от
центра сферы:
а) внутри сферы
(r<.R)
E=0;
б) на поверхности
сферы (r=R)
;
в) вне сферы
(r>R)
.
Принцип
суперпозиции (наложения) электрических
полей, согласно которому напряженность
Е результирующего поля, созданного
двумя (и более) точечными зарядами, равна
векторной (геометрической) сумме
напряженностей складываемых полей:
Е=E1+Е2+…+Еn.
В
случае двух электрических полей с
напряженностями Е1
и Е2
модуль вектора напряженности
,
где
— угол между векторами E1
и E2.
Напряженность
поля, создаваемого бесконечно длинной
равномерно заряженной нитью (или
цилиндром) на расстоянии r
от ее оси,
,
где — линейная
плотность заряда.
Линейная плотность
заряда есть величина, равная отношению
заряда, распределенного по нити, к длине
нити (цилиндра):
Напряженность
поля, создаваемого бесконечной равномерно
заряженной плоскостью,
где
— поверхностная плотность заряда.
Поверхностная
плотность заряда есть величина, равная
отношению заряда, распределенного по
поверхности, к площади этой поверхности:
.
Напряженность
поля, создаваемого двумя параллельными
бесконечными равномерно и разноименно
заряженными плоскостями, с одинаковой
по модулю поверхностной плотностью о
заряда (поле плоского конденсатора)
.
Приведенная формула
справедлива для вычисления напряженности
поля между пластинами плоского
конденсатора (в средней части его)
только в том случае, если расстояние
между пластинами много меньше линейных
размеров пластин конденсатора.
Электрическое
смещение D
связано с напряженностью E
электрического поля соотношением
D=0E.
Это соотношение
справедливо только для изотропных
диэлектриков.
Поток вектора
электрического смещения выражается
аналогично потоку вектора напряженности
электрического поля:
а) в случае
однородного поля поток сквозь плоскую
поверхность
;
б) в случае
неоднородного поля и произвольной
поверхности
,
где Dn
— проекция вектора D на направление
нормали к элементу поверхности, площадь
которой равна dS.
Теорема
Остроградского — Гаусса. Поток вектора
электрического смещения сквозь любую
замкнутую поверхность, охватывающую
заряды Q1,Q2,
…,Qn,
,
где п—число
зарядов (со своим знаком), заключенных
внутри замкнутой поверхности.
Циркуляция
вектора напряженности электрического
поля есть величина, численно равная
работе по перемещению единичного
точечного положительного заряда вдоль
замкнутого контура. Циркуляция выражается
интегралом по замкнутому контуру
,
где El—проекция
вектора напряженности Е в данной точке
контура на направление касательной к
контуру в той же точке.
В случае
электростатического поля циркуляция
вектора напряженности равна нулю:
.
Примеры
решения задач
П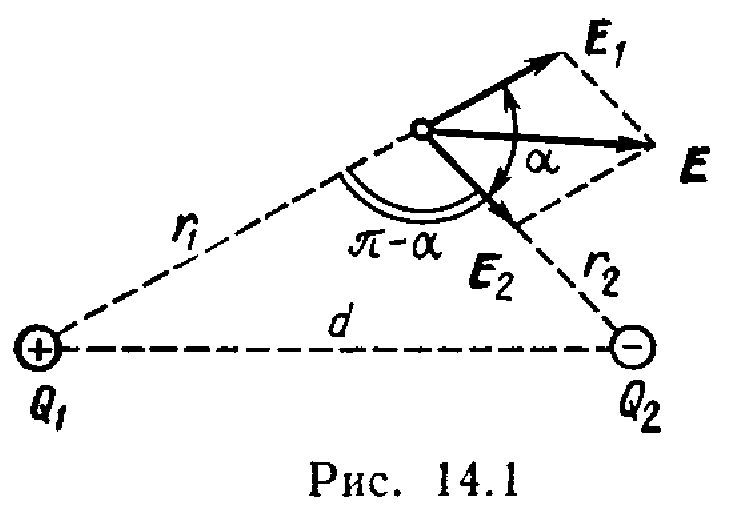
1. Электрическое поле создано двумя
точечными зарядами: Q1=30
нКл и Q2=
–10 нКл. Расстояние d
между зарядами равно 20 см. Определить
напряженность электрического поля в
точке, находящейся на расстоянии r1=15
см от первого и на расстоянии r2=10
см от второго зарядов.
Решение.
Согласно принципу суперпозиции
электрических полей, каждый заряд
создает поле независимо от присутствия
в пространстве других зарядов. Поэтому
напряженность Е электрического
поля в искомой точке может быть найдена
как векторная сумма
напряженностей E1 и Е2
полей, создаваемых каждым зарядом в
отдельности: E=E1+E2.
Напряженности
электрического поля, создаваемого в
вакууме первым и вторым зарядами,
соответственно равны
(1)
Вектор E1
(рис. 14.1) направлен по силовой линии от
заряда Q1,
так как заряд Q1>0;
вектор Е2 направлен также
по силовой линии, но к заряду
Q2,
так как Q2<0.
Модуль вектора Е
найдем по теореме косинусов:
, (2)
где угол
может быть найден из треугольника со
сторонами r1,
r2
и d:
.
В данном случае
во избежание громоздких записей вычислим
отдельно значение cos.
По этой формуле найдем
cos
=0,25.
Подставляя выражения
E1
и E2
а по формулам (1) в равенство (2) и вынося
общий множитель 1/(40)
за знак корня, получаем
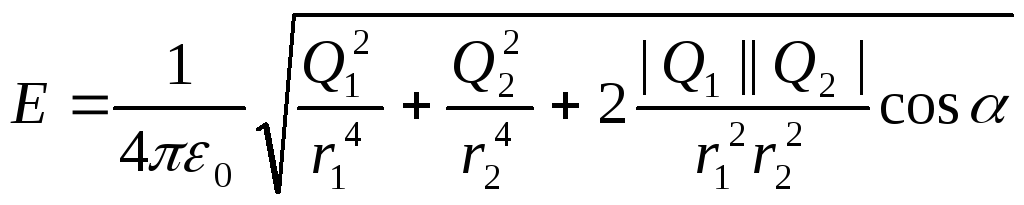
Подставив значения
величин ,
0,
Q1,
Q2,
r1-,
r2
и в последнюю
формулу и произведя вычисления, найдем
Пример 2.
Электрическое поле создано двумя
параллельными бесконечными заряженными
плоскостями с поверхностными плотностями
заряда 1=0,4
мкКл/м2 и 2=0,1
мкКл/м2. Определить напряженность
электрического поля, созданного этими
заряженными плоскостями.
Р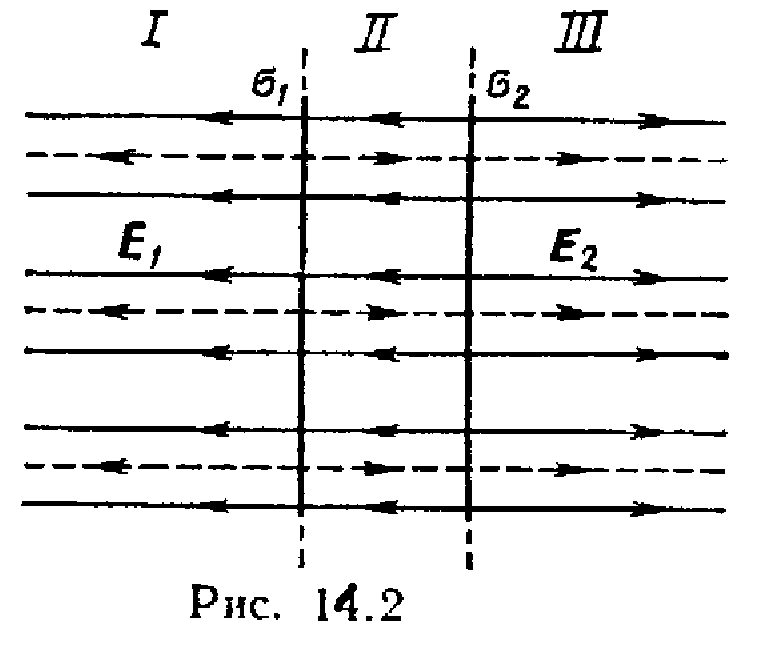
Согласно принципу суперпозиции, поля,
создаваемые каждой заряженной плоскостью
в отдельности, накладываются друг на
друга, причем каждая заряженная плоскость
создает электрическое поле независимо
от присутствия другой заряженной
плоскости (рис. 14.2).
Напряженности
однородных электрических полей,
создаваемых первой и второй плоскостями,
соответственно равны:
;
.
Плоскости делят
все пространство на три области: I,
II и III.
Как вид но из рисунка, в первой и
третьей областях электрические силовые
линии обоих полей направлены в одну
сторону и, следовательно, напряженности
суммарных полей Е(I)
и E(III)
в первой и третьей областях равны между
собой и равны сумме напряженностей
полей, создаваемых первой и второй
плоскостями: Е(I)=
E(III)=E1+E2,
или
Е(I)=
E(III)=.
Во второй области
(между плоскостями) электрические
силовые линии полей направлены в
противоположные стороны и, следовательно,
напряженность поля E(II)
равна разности напряженностей полей,
создаваемых первой и второй плоскостями:
E(II)=|E1-E2|,
или
.
Подставив данные
и произведя вычисления, получим
E(I)=E(III)=28,3кВ/м=17
кВ/м.
Картина
распределения силовых линий суммарного
поля представлена на рис. 14.3.
Пример 3. На
пластинах плоского воздушного конденсатора
находится заряд Q=10
нКл. Площадь S
каждой пластины конденсатора равна 100
см2 Определить силу F,
с которой притягиваются пластины. Поле
между пластинами считать однородным.
Решение. Заряд
Q одной пластины
находится в поле, созданном зарядом
другой пластины конденсатора.
Следовательно, на первый заряд действует
сила (рис. 14.4)
F=E1Q,, (1)
где E1
— напряженность поля, создаваемого
зарядом одной пластины. Но
где
– поверхностная
плотность заряда пластины.
Формула (1) с учетом
выражения для E1
примет вид
F=Q2/(20S).
Подставив значения
величин Q, 0
и S в эту формулу и
произведя вычисления, получим
F=565
мкН.
Пример 4.
Электрическое поле создано, бесконечной
плоскостью, заряженной с поверхностной
плотностью =400
нКл/м2, и бесконечной прямой
нитью, заряженной с линейной плотностью
=100 нКл/м. На расстоянии
r=10 см от нити находится
точечный заряд Q=10
нКл. Определить силу, действующую на
заряд, ее направление, если заряд и нить
лежат в одной плоскости, параллельной
заряженной плоскости.
Решение. Сила,
действующая на заряд, помещённый в поле,
F=EQ, (1)
где Е —
напряженность поля в точке, в которой
находится заряд Q.
Определим
напряженность Е поля, создаваемого,
по условию задачи, бесконечной заряженной
плоскостью и бесконечной заряженной
нитью. Поле, создаваемое бесконечной
заряженной плоскостью, однородно, и его
напряженность в любой точке
. (2)
Поле, создаваемое
бесконечной заряженной линией,
неоднородно. Его напряженность зависит
от расстояния и определяется по формуле
. (3)
Согласно принципу
суперпозиции электрических полей,
напряженность поля в точке, где находится
заряд Q,
равна векторной сумме напряженностей
E1
и Е2 (рис. 14.5):
E=E1+E2.
Так как векторы E1
и Е2 взаимно
перпендикулярны, то
.
Подставляя выражения
E1
и E2 по
формулам (2) и (3) в это
равенство, получим
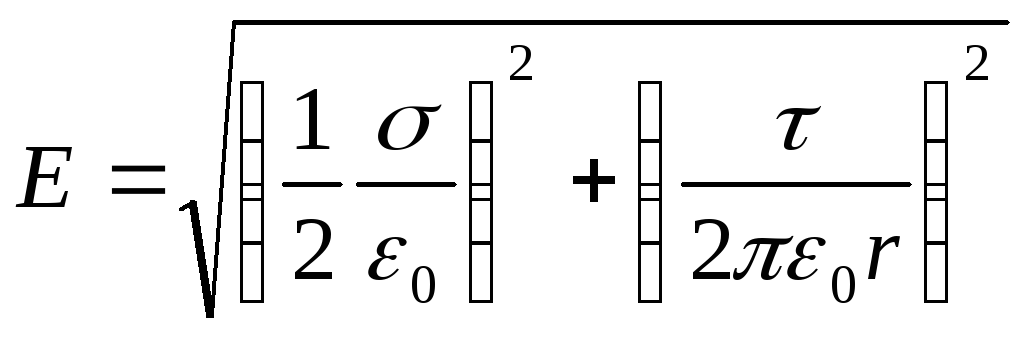
или
.
Теперь найдем силу
F, действующую на
заряд, подставив выражение Е в
формулу (1):
. (4)
Подставив значения
величин Q, 0,
, ,
и r
в формулу (4) и сделав вычисления, найдем
F=289
мкН.
Направление силы
F, действующей на положительный
заряд Q, совпадает с направлением
вектора напряженности Е поля.
Направление же вектора Е задается
углом к заряженной
плоскости. Из рис. 14.5 следует, что
,
откуда
.
Подставив значения
величин , r,
и
в это выражение и вычислив, получим
=51°3
Пример 5.
Точечный заряд Q=25
нКл находится в ноле, созданном прямым
бесконечным цилиндром радиусом
R=1
см, равномерно заряженным с поверхностной
плотностью =2 мкКл/м2.
Определить силу, действующую на заряд,
помещенный от оси цилиндра на расстоянии
r=10 см.
Решение. Сила,
действующая на заряд Q, находящийся
в поле,
F=QE, (1)
где Е —
напряженность поля в точке, в которой
находится заряд Q.
Как известно,
напряженность поля бесконечно длинного
равномерно заряженного цилиндра
E=/(20r), (2)
где
— линейная плотность
заряда.
Выразим линейную
плотность через
поверхностную плотность .
Для этого выделим элемент цилиндра
длиной l и выразим
находящийся на нем заряд Q1
двумя, способами:
Q1=S=2Rl
и Q1=l.
Приравняв правые
части этих равенств, получим l=2Rl.
После сокращения на l
найдем =2R.
С учетом этого формула (2) примет вид
E=R/(0r).
Подставив это выражение Е в формулу
(1), найдем искомую силу:
F=QR/(0r). (3)
Так как
R и r
входят в формулу в виде отношения, то
они могут быть выражены в любых, но
только одинаковых единицах.
Выполнив вычисления
по формуле (3), найдем
F=2510-9210-610-2/(8,8510-121010-2)H==56510-6H=565мкH.
Направление силы
F совпадает с
направлением вектора напряженности
Е, а последний в силу симметрии (цилиндр
бесконечно длинный) направлен
перпендикулярно цилиндру.
Пример 6.
Электрическое поле создано тонкой
бесконечно длинной нитью, равномерно
заряженной с линейной плотностью =30
нКл/м. На расстоянии а=20 см от нити
находится плоская круглая площадка
радиусом r=1 см.
Определить поток вектора напряженности
через эту площадку, если плоскость ее
составляет угол =30°
с линией напряженности, проходящей
через середину площадки.
Решение. Поле,
создаваемое бесконечно равномерно,
заряженной нитью, является неоднородным.
Поток вектора напряженности в этом
случае выражается интегралом
, (1)
где En
— проекция вектора Е на нормаль
n к поверхности площадки
dS. Интегрирование
выполняется по всей поверхности площадки,
которую пронизывают линии напряженности.
П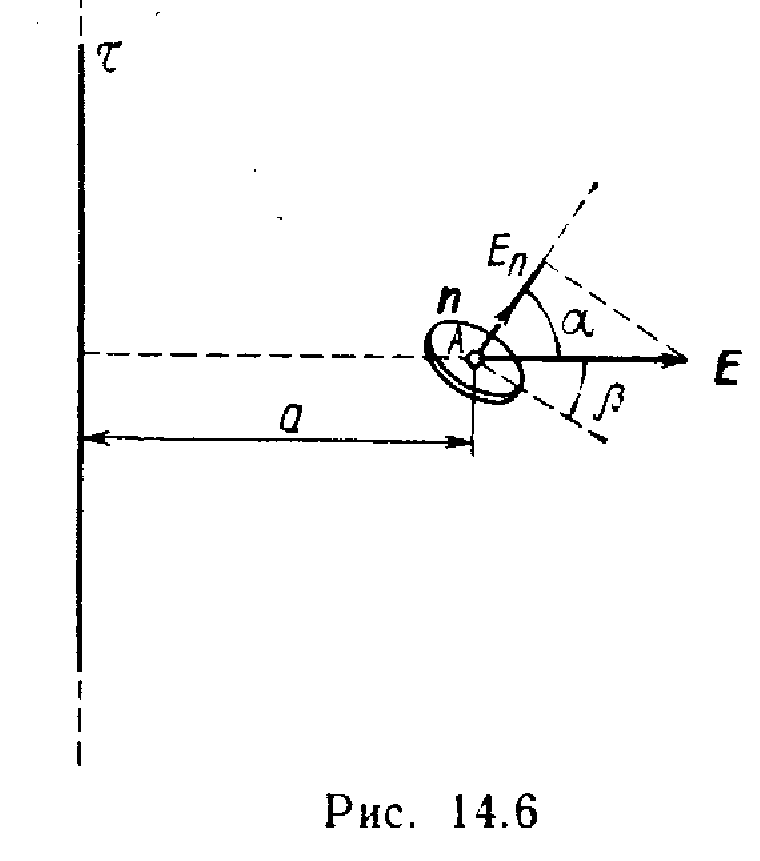
Еп вектора напряженности
равна, как видно из рис. 14.6,
Еп=Еcos,
где
— угол между направлением вектора и
нормалью n. С учетом этого формула
(1) примет вид
.
Так как размеры
поверхности площадки малы по сравнению
с расстоянием до нити (r<<a),
то электрическое поле в пределах площадки
можно считать практически однородными.
Следовательно, вектор напряженности Е
очень мало. меняется по модулю и
направлению в пределах площадки, что
позволяет заменить под знаком интеграла
значения Е и cos
их средними значениями <E>
и <cos>
и вынести их за знак интеграла:
Выполняя
интегрирование и заменяя <E>
и <cos>
их приближенными значениями ЕA
и cosA,
вычисленными для средней точки площадки,
получим
ФE=ЕAcosAS=r2ЕAcosA. (2)
Напряженность ЕA
вычисляется по формуле EA=/(20a).
Из
рис. 14.6 следует
cosA=cos(/2—)=sin.
С учетом выражения
ЕA и
cosA
равенство (2.) примет вид
.
Подставив в
последнюю формулу данные и произведя
вычисления, найдем
ФE=424
мВ.м.
Пример 7.
Две концентрические проводящие сферы
радиусами R1=6
см и R2=10
см несут соответственно заряды
Q1=l
нКл и Q2=
–0,5 нКл. Найти напряженность
Е поля в точках, отстоящих от центра
сфер на расстояниях r1=5
см, r2=9
см r3=15см.
Построить график Е(r).
Р
Заметим, что точки, в которых требуется
найти напряженности электрического
поля, лежат в трех областях (рис. 14.7):
область I (r<R1),
область II (R1<r2<R2),
область III (r3>R2).
1. Для определения
напряженности E1
в области I проведем
сферическую поверхность
S1
радиусом r1
и воспользуемся теоремой Остроградского—Гаусса.
Так как внутри области I
зарядов нет, то согласно указанной
теореме получим равенство
, (1)
где En
— нормальная составляющая напряженности
электрического поля.
Из соображений
симметрии нормальная составляющая En
должна быть равна самой напряженности
и постоянна для всех точек сферы, т. е.
En=E1=const.
Поэтому ее можно вынести за знак
интеграла. Равенство (1) примет вид
.
Так как площадь
сферы не равна нулю, то
E1=0,
т. е. напряженность
поля во всех точках, удовлетворяющих
условию r1<.R1,
будет равна нулю.
2. В области II
сферическую поверхность проведем
радиусом r2.
Так как внутри этой поверхности находится,
заряд Q1,
то для нее, согласно теореме
Остроградского—Гаусса, можно
записать равенство
. (2)
Так как
En=E2=const,
то из условий симметрии следует
,
или ES2=Q1/0,
откуда
E2=Q1/(0S2).
Подставив сюда
выражение площади сферы, получим
E2=Q/(4). (3)
3. В области III
сферическую поверхность проведем
радиусом r3.
Эта поверхность охватывает
суммарный заряд Q1+Q2.
Следовательно, для нее уравнение,
записанное на основе теоремы
Остроградского — Гаусса, будет иметь
вид
.
Отсюда, использовав
положения, примененные в первых двух
случаях, найдем
. (4)
Убедимся в том,
что правые части равенств (3) и (4) дают
единицу напряженности электрического
поля;
Выразим все величины
в единицах СИ (Q1=10-9
Кл, Q2=
–0,510-9
Кл, r1=0,09
м, r2=15
м, l/(40)=9109
м/Ф) и произведем вычисления:
4. Построим график
E(r).В
области I (r1<R1)
напряженность E=0. В
области II (R1r<.R2)
напряженность E2(r)
изменяется по закону l/r2.
В точке r=R1
напряженность E2(R1)=Q1/(40R)=2500
В/м.В точке r=R1
(r стремится к
R1
слева) E2(R2)=Q1/(40R)=900В/м.
В области III (r>R2)E3(r)
изменяется по закону 1/r2,
причем в точке r=R2
(r стремится к R2
справа) Е3(R2)=(Q1–|Q2|)/(40R)=450
В/м. Таким образом, функция Е(r)
в точках r=R1
и r=R2
терпит разрыв. График зависимости Е(r)
представлен на рис. 14.8.
Задачи
Напряженность
поля точечных зарядов
14.1. Определить
напряженность Е электрического
поля, создаваемого точечным зарядом
Q=10
нКл на расстоянии r=10
см от него. Диэлектрик —
масло.
14.2. Расстояние
d между двумя
точечными зарядами Q1=+8
нКл и Q2=
–5,3 нКл равно 40 см. Вычислить
напряженность Е поля в точке, лежащей
посередине между зарядами. Чему равна
напряженность, если второй заряд будет
положительным?
14.3. Электрическое
поле создано двумя точечными зарядами
Q1=10
нКл и Q2=
–20 нКл, находящимися на расстоянии
d=20
см друг от друга. Определить напряженность
E поля в точке, удаленной
от первого заряда на r1=30
см и от второго на r2=50
см.
14.4. Расстояние
d между двумя точечными положительными
зарядами Q1=9Q
и Q2=Q
равно 8 см. На каком расстоянии г от
первого заряда находится точка, в которой
напряженность Е поля зарядов равна
нулю? Где находилась бы эта точка, если
бы второй заряд был отрицательным?
14.5. Два точечных
заряда Q1=2Q
и Q2=
–Q находятся на
расстоянии d друг от друга. Найти
положение точки на прямой, проходящей
через эти заряды, напряженность Е
поля в которой равна нулю,
14.6. Электрическое
поле создано двумя точечными зарядами
Q1=40
нКл и Q2=
–10 нКл, находящимися на расстоянии
d=10 см друг от друга.
Определить напряженность Е поля в
точке, удаленной от первого заряда на
r1=12
см и от второго на r2=6
см.
Напряженность
поля заряда, распределенного по кольцу
и сфере
14.7. Тонкое
кольцо радиусом R=8 см
несет заряд, равномерно распределенный
с линейной плотностью =10
нКл/м. Какова напряженность Е
электрического поля в точке, равноудаленной
от всех точек кольца на расстояние r=10
см?
14.8. Полусфера
несет заряд, равномерно распределенный
с поверхностной плотностью =1,нКл/м2.
Найти напряженность Е электрического
поля в геометрическом центре полусферы.
14.9. На
металлической сфере радиусом R=10
см находится заряд Q=l
нКл. Определить напряженность Е
электрического поля в
следующих точках: 1) на расстоянии r1=8
см от центра сферы; 2) на
ее поверхности; 3) на расстоянии r2=15
см от центра сферы. Построить график
зависимости E от r.
14.10. Две
концентрические металлические заряженные
сферы радиусами R1=6cм
и R2=10
см несут соответственно заряды
Q1=1
нКл и Q2=
–0,5 нКл. Найти
напряженности Е поля в точках.
отстоящих от центра сфер на расстояниях
r1=5 см, r2=9
см, r3=15
см. Построить график зависимости Е(r).
Напряженность
поля заряженной линии
14.11. Очень
длинная тонкая прямая проволока несет
заряд, равномерно распределенный по
всей ее длине. Вычислить линейную
плотность заряда,
если напряженность E
поля на расстоянии а=0,5 м от проволоки
против ее середины равна 200 В/м.
14.12. Расстояние
d между двумя длинными
тонкими проволоками, расположенными
параллельно друг другу, равно 16 см.
Проволоки равномерно заряжены
разноименными зарядами с линейной
плотностью ||=^150.
мкКл/м. Какова напряженность Е поля
в точке, удаленной на r=10
см как от первой, так и от второй проволоки?
14.13. Прямой
металлический стержень диаметром d=5
см и длиной l=4 м несет
равномерно распределенный по его
поверхности заряд Q=500
нКл. Определить напряженность Е
поля в точке, находящейся против середины
стержня на расстоянии а=1 см от его
поверхности.
14.14. Бесконечно
длинная тонкостенная металлическая
трубка радиусом R=2
см несет равномерно распределенный по
поверхности заряд (=1
нКл/м2). Определить напряженность
Е поля в точках, отстоящих от оси
трубки на расстояниях r1=l
см, r2=3
см. Построить график зависимости Е(r).
Содержание:
По современным представлениям основой всего многообразия явлений природы являются четыре фундаментальных взаимодействия между частицами микромира (электрон, протон и др.) — сильное, слабое, электромагнитное и гравитационное. Каждый вид взаимодействия связан с определённой характеристикой частицы. Например, гравитационное взаимодействие зависит от масс частиц, электромагнитное — от электрических зарядов.
Электромагнитное взаимодействие лежит в основе всех электрических, магнитных и оптических явлений. Этим же взаимодействием обусловлены силы упругости и силы трения, известные вам из механики. Взаимодействие атомов и молекул, которое мы рассматривали при изучении молекулярно-кинетической теории, также является электромагнитным. Электромагнитное взаимодействие определяет свойства веществ в различных агрегатных состояниях и их химические превращения. Поскольку молекулярные силы имеют электромагнитную природу, то практически все биологические явления обусловлены электромагнетизмом.
Электродинамика — раздел физики, в котором изучают закономерности физических явлений, обусловленных электрическими и магнитными взаимодействиями, материальным носителем которых является электромагнитное поле. Термин «электродинамика» ввёл в физику французский учёный Андре Мари Ампер (1775—1836) в 1822 г.
При изучении электродинамики вы познакомитесь с законами взаимодействия тел (частиц), обладающих электрическим зарядом, особенностями упорядоченного движения заряженных частиц, физическими величинами, характеризующими электрические и магнитные явления.
В 10 классе вам предстоит изучить следующие разделы электродинамики: электростатика, постоянный электрический ток, ток в различных средах и электромагнитные явления.
Электростатика — раздел электродинамики, в котором изучают свойства, взаимодействие и условия равновесия неподвижных в некоторой инерциальной системе отсчёта электрически заряженных тел, распределение заряда на которых не изменяется со временем, а также электростатические поля, создаваемые зарядами таких тел. Термин «электростатика» введён Ампером в 1822 г. Фундамент электростатики составляют экспериментальные научные факты, отражающие поведение заряженных тел при их электрическом взаимодействии. Ядро электростатики составляют закон сохранения электрического заряда, опытным путём установленный в 1759 г. петербургским академиком Францем Эпинусом (1724—1802), и закон взаимодействия покоящихся точечных зарядов, экспериментально открытый в 1785 г. французским учёным Шарлем Кулоном (1736—1806).
Электростатика
На уроках физики в 8 классе при проведении опытов вы наблюдали притяжение крошек пенопласта, небольших кусочков бумаги (рис. 76), лёгкой станиолевой гильзы (рис. 77) к потёртой о сухую бумагу пластмассовой линейке или стеклянной палочке. Во всех перечисленных случаях имело место явление электризации тел. Оно заключается в возникновении противоположных по знаку электрических зарядов, модули которых равны, на первоначально электрически нейтральных телах. А что означает, что тело или частица обладает электрическим зарядом? Как взаимодействуют электрически заряженные тела?
Электрический заряд
Электрический заряд частицы является источником электромагнитного поля, связанного с материальным носителем. Электрический заряд, или количество электричества (обозначают буквой q или Q), — физическая скалярная величина, характеризующая интенсивность электромагнитного взаимодействия тел (частиц). Электрическому заряду присущи следующие фундаментальные свойства:
- электрический заряд существует в двух видах, которые названы положительным и отрицательным зарядом (существование двух видов заряда установил Шарль Дюфэ (1698—1739) в 1733 г., а в 1747 г. Бенджамин Франклин (1706—1790) приписал им знаки « + » и « —»);
- в любой электрически изолированной системе алгебраическая сумма зарядов тел (частиц) не изменяется;
- значение электрического заряда тела (частицы) не зависит от выбора системы отсчёта, а значит, не зависит от того, движется оно (она) или покоится;
- электрический заряд тела (частицы) не зависит ни от его (её) механического состояния, ни от каких-либо действующих на него (неё) сил.
Носителем заряда может быть как элементарная частица, так и макроскопическое тело.
В одном моле вещества
Как вы знаете, электрическое взаимодействие проявляется в том, что одноимённо заряженные тела (частицы) отталкивают друг друга (рис. 78, а), а разноимённо заряженные — притягивают друг друга (рис. 78, б). Если в электрически нейтральном теле заряды распределены неравномерно и вследствие этого возникли противоположно заряженные части, то такие тела тоже электрически взаимодействуют (см. рис. 76 и 77).
Заряды разных тел (частиц) могут отличаться не только знаком, но и числовым значением.
За единицу электрического заряда в СИ принят кулон (Кл). Эта единица названа в честь Ш. Кулона. 1 Кл — электрический заряд, проходящий через поперечное сечение проводника за промежуток времени 1 с при силе постоянного тока 1 А.
Один кулон — очень большая единица заряда. Расчёты показывают, что диаметр удалённого от всех остальных тел металлического шара, находящегося в сухом воздухе, должен быть равен примерно 110 м, чтобы на нём мог находиться избыточный заряд 1 Кл. Вместе с тем при включении автомобильных фар сила тока в цепи приблизительно 10 А, т. е. ежесекундно через поперечное сечение проводников, подсоединённых к фарам, проходит заряд приблизительно 10 Кл.
На рубеже XIX и XX столетий учёные экспериментально установили, что в природе существует электрический заряд, модуль которого минимален, называемый элементарным. Ядра всех атомов содержат протоны, которые являются носителями положительного элементарного заряда, а сами атомы содержат электроны, являющиеся носителями отрицательного элементарного заряда. Равенство модулей зарядов электрона и протона установлено с точностью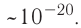
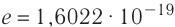
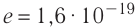
Электроны, протоны и нейтроны входят в состав всех тел, так как из них состоят атомы и молекулы любого вещества. В электрически нейтральном теле алгебраическая сумма зарядов всех частиц равна нулю. Если каким-нибудь образом создать в таком теле избыток зарядов одного знака, то оно окажется заряженным. Заряд q тела образуется совокупностью элементарных зарядов и всегда кратен элементарному заряду е (электрический заряд дискретен):
где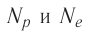
Например, тело, заряд которого q = 7e, отличается от нейтрального тела потерей семи электронов.
Закон сохранения электрического заряда
Модули противоположных по знаку зарядов, возникших в результате электризации на находившихся в контакте телах, равны. В этом можно убедиться на опыте. Возьмём эбонитовую палочку и кусочек меха. При трении друг о друга тела электризуются. Поместим поочерёдно внутрь металлической сферы, укреплённой на стержне электрометра, эбонитовую палочку (рис. 79, а) и кусочек меха (рис. 79, б). Стрелка электрометра отклонится, причём как в первом, так и во втором случаях на один и тот же угол. Если одновременно опустить внутрь сферы эбонитовую палочку и кусочек меха (рис. 79, в), то стрелка электрометра останется на месте. Следовательно, модули зарядов обоих тел равны, а их знаки противоположны.
Результаты многочисленных экспериментов позволили сформулировать утверждение, которое является фундаментальным законом природы — законом сохранения электрического заряда: в электрически изолированной системе при любых взаимодействиях алгебраическая сумма электрических зарядов остаётся постоянной:
где n — число зарядов в системе. Систему тел (частиц) называют электрически изолированной, если между ней и внешними телами нет обмена электрически заряженными частицами.
- Электрический заряд — физическая скалярная величина, характеризующая интенсивность электромагнитного взаимодействия тел (частиц). Электрический заряд существует в двух видах: положительный и отрицательный. Одноимённые заряды отталкиваются, а разноимённые — притягиваются.
- Существует заряд, модуль которого минимален, называемый элементарным:
- Электрический заряд дискретен, т. е. электрический заряд любой частицы или тела является кратным элементарному электрическому заряду.
- Закон сохранения электрического заряда: в электрически изолированной системе при любых взаимодействиях алгебраическая сумма электрических зарядов остаётся постоянной:
- Значение электрического заряда не зависит от того, движется он или покоится.
Взаимодействие точечных зарядов
Обсуждая электризацию как электростатическое явление, мы не задавали вопрос: «А как определить силу, с которой одно заряженное тело притягивает или отталкивает другое?». Ответ на этот вопрос был найден в конце XVIII столетия независимо друг от друга двумя учёными: Г. Кавендишем в 1774 г. и Ш. Кулоном в 1785 г. Однако современникам стали известны только результаты опытов Кулона.
Закон Кулона
Вы уже встречались с физическими моделями при изучении механики (материальная точка) и молекулярной физики (идеальный газ). В электростатике при изучении взаимодействия электрически заряженных тел эффективной оказывается модель «точечный заряд». Точечный заряд — заряд такого заряженного тела, размеры которого значительно меньше расстояния от этого тела до точки наблюдения и до других тел (т. е. размерами заряженного тела в условиях данной задачи можно пренебречь).
Кулон первым опубликовал результаты своих исследований по взаимодействию неподвижных точечных зарядов.
Он на опыте изучил зависимость сил электрического взаимодействия тел от модулей зарядов этих тел и расстояния между ними. Полученное им соотношение является одним из основных законов электростатики.
В своих опытах Кулон использовал специальный прибор — крутильные весы (рис. 80). Крутильные весы представляют собой два стеклянных цилиндра, внутри которых на тонкой серебряной нити подвешено лёгкое непроводящее коромысло. На одном конце коромысла закреплён проводящий шар 1, а на другом — бумажный противовес 3. Шар 1 можно заряжать с помощью такого же проводящего шара 2, находящегося на изолирующем стержне, который крепится на крышке нижнего цилиндра. При соприкосновении шара 1 с заряженным шаром 2 заряд распределяется между ними поровну, и шары отталкиваются. По углу закручивания нити, отсчитываемому по шкале, можно определить силу, с которой заряд шара 2 действует на заряд шара 1. Проведя большое количество опытов, Кулон установил, что модуль сил взаимодействия двух заряженных шаров 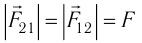
Разряжая шар 2 прикосновением руки, а затем касаясь им уже заряженного шара 1, Кулон смог получить на нём заряды, модуль которых в 2, 4, 8 и т. д. раз меньше первоначального. Он выяснил, что при неизменном расстоянии модуль сил взаимодействия двух неподвижных небольших заряженных тел прямо пропорционален произведению модулей электрических зарядов каждого из них:
Обобщив экспериментальные данные, Кулон сформулировал закон, получивший его имя.
Модули сил взаимодействия двух неподвижных точечных заряженных тел в вакууме прямо пропорциональны произведению модулей зарядов этих тел, обратно пропорциональны квадрату расстояния между ними, а сами силы направлены вдоль прямой, соединяющей эти тела, являясь силами отталкивания для одноимённых зарядов и силами притяжения для разноимённых.
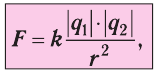
где k — коэффициент пропорциональности, зависящий от выбора единиц физических величин, 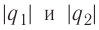
Силы взаимодействия неподвижных точечных зарядов называют кулоновскими силами. В соответствии с третьим законом Ньютона эти силы противоположно направлены 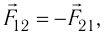
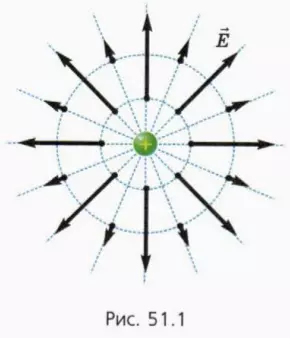
В СИ коэффициент пропорциональности
где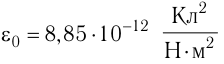
Опытным путём установили, что силы взаимодействия двух точечных зарядов не изменяются при появлении третьего точечного заряда или любого числа точечных зарядов. В этом случае силы воздействия
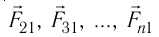
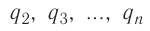
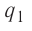
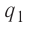
Используя принцип суперпозиции и закон Кулона, можно описать электростатическое взаимодействие любой системы зарядов. На рисунке 82 показаны три взаимодействующих между собой точечных электрических заряда: 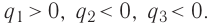
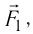
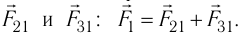
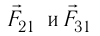
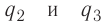
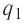
Закон Кулона, описывающий электростатическое взаимодействие, формально похож на закон всемирного тяготения Ньютона, определяющий силы гравитационного взаимодействия двух тел:
В обоих случаях модуль сил взаимодействия:
- — обратно пропорционален квадрату расстояния между материальными точками;
- — прямо пропорционален величинам, характеризующим те свойства тел (материальных точек), которые определяют взаимодействия, — массам в одном случае и электрическим зарядам — в другом.
Для измерения сил электрического и гравитационного взаимодействий учёные использовали похожие по устройству экспериментальные установки.
Однако между силами гравитационного и электростатического взаимодействий существует и важное различие. Ньютоновские силы тяготения — это всегда силы притяжения. Кулоновские же силы взаимодействия зарядов могут быть как силами притяжения (между разноимёнными зарядами), так и силами отталкивания (между одноимёнными зарядами).
Закон Кулона в виде (14.1) справедлив не только для точечных зарядов, но и для заряженных тел сферической формы, заряды которых распределены равномерно по всему объёму или по поверхности этих тел (при этом r — расстояние между центрами сферических тел).
Как показывают опыты, взаимодействие электрически заряженных тел в вакууме практически не отличается от их взаимодействия в воздухе. Поэтому формулу (14.1) применяют, описывая взаимодействие заряженных тел как в вакууме, так и в воздухе. Если заряженное тело находится в воде, керосине, масле или какой-нибудь другой непроводящей среде, то модуль сил взаимодействия будет меньше, чем в вакууме.
Экспериментальные факты свидетельствуют о том, что воздействие неподвижного в данной инерциальной системе отсчёта точечного заряда на движущийся точечный заряд может быть описано законом Кулона с приемлемой точностью. Так, описание рассеяния а-частиц на ядрах атомов золота в опытах Резерфорда с помощью модели точечного заряда, на который действует кулоновская сила со стороны неподвижного ядра, согласуется с экспериментальными данными в пределах точности последних 
Два и более движущихся в данной инерциальной системе заряда не могут характеризоваться только кулоновским взаимодействием, так как каждый из них создаёт в окружающем пространстве магнитное поле, которое действует магнитной силой на остальные заряды, движущиеся в нём.
- Точечный заряд — заряд такого заряженного тела, размеры которого значительно меньше расстояния от этого тела до точки наблюдения и до других тел (т. е. размерами заряженного тела в условиях данной задачи можно пренебречь).
- Закон Кулона: модули сил взаимодействия двух неподвижных точечных заряженных тел в вакууме прямо пропорциональны произведению модулей зарядов этих тел, обратно пропорциональны квадрату расстояния между ними, а сами силы направлены вдоль прямой, соединяющей эти тела, являясь силами отталкивания для одноимённых зарядов и силами притяжения для разноимённых:
- Силы взаимодействия двух точечных зарядов не изменяются при появлении других точечных зарядов. Силы воздействия
каждого из зарядов
на заряд
определяют по закону Кулона, а результирующую силу, действующую на заряд
находят как векторную сумму сил, с которыми каждый из этих зарядов в отдельности воздействует на заряд
(принцип суперпозиции).
- Закон Кулона справедлив для неподвижных точечных зарядов и сферических тел с равномерным распределением заряда по поверхности или объёму.
Пример №1
Две бусинки, электрические заряды которых 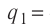
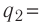
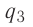
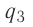
Дано:
r= 40 см = 0,40 м
x-?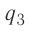
Решение, а) Третья бусинка, имеющая заряд 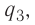
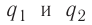
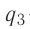
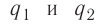
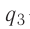
Согласно второму закону Ньютона эта бусинка будет покоиться, если модули сил 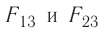
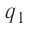
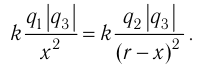
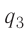
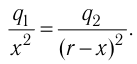
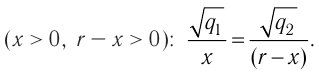
Такое же значение х мы получим, если примем заряд 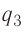
б) Сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равна нулю, если, например, третья бусинка притягивает вторую с силой, модуль 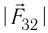
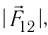
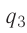
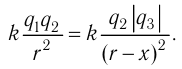
Ответ: х=16 см, расстояние до бусинки с зарядом 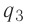
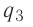
Пример №2
Два одинаковых маленьких проводящих шарика массой m = 20мг каждый подвешены в воздухе на лёгких нерастяжимых нитях длиной l = 0,20 м, закреплённых в одной точке подвеса. Один из шариков отвели в сторону, сообщили ему заряд q < 0 и отпустили. После столкновения шарики разошлись так, что угол между нитями составил 2а = 60° (рис. 85). Определите значение заряда, который был сообщён первому шарику, а также количество избыточных электронов на каждом из шариков после их столкновения.
Дано:
l=0,20 м
2а = 60°
q — ? N — ?
Решение. Воспользуемся законом сохранения электрического заряда. При столкновении двух одинаковых проводящих шариков сообщённый одному из них заряд разделился поровну и на каждом шарике оказался избыточный отрицательный заряд 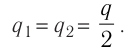
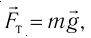
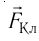
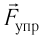
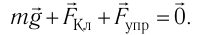
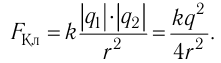
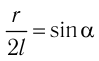
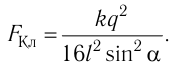
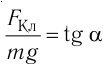
Количество избыточных электронов на каждом шарике
Электростатическое поле
Заряженные тела и частицы, которые кратко называют зарядами, взаимодействуют друг с другом. Это подтверждают многочисленные опыты, а закон Кулона позволяет определить силы взаимодействия неподвижных точечных зарядов. Но что является причиной подобного взаимодействия, каков его механизм?
Первым, кто догадался, что «тела действуют друг на друга на расстоянии посредством обращения окружающей среды в состояние напряжения», был выдающийся английский учёный Майкл Фарадей (1791 —1867). Обобщая результаты собственных исследований, проведённых с 1832 г. по 1852 г., Фарадей ввёл в физику новое понятие — поле. Математическую завершённость идее Фарадея об изменении состояния пространства вблизи заряженных тел (частиц) и возникновении новой сущности, впоследствии названной электромагнитным полем, придал его гениальный соотечественник и преемник Джемс Клерк Максвелл (1831 —1879).
Электрический заряд, создающий в окружающем пространстве электрическое поле, называют источником поля и часто обозначают символом Q. Электрическое поле оказывает силовое действие на любой другой заряд q, помещённый в него.
Самая существенная особенность электрического поля — его материальность, т. е. электрическое поле — вид материи. В реальности существования электрического поля можно убедиться по его проявлениям: поле, созданное зарядом, действует с определённой силой на другие заряды, которые в него вносят.
Поле, создаваемое неподвижными относительно используемой инерциальной системы отсчёта электрическими зарядами, называют электростатическим полем.
Чтобы исследовать электростатическое поле, создаваемое зарядом Q, поместим в это поле заряд q$, называемый пробным. Под пробным зарядом
понимают заряд, модуль которого достаточно мал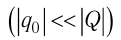
Отметим, что свойство электрического поля, обусловленное присутствием тела с зарядом-источником поля Q, воздействовать некоторой силой проявляется не только в точке, в которой находится пробный заряд д0. Это свойство присуще всем точкам поля, создаваемого зарядом Q.
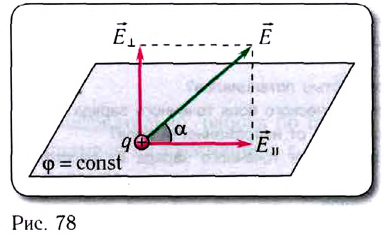
Используя пробный заряд q0, можно количественно охарактеризовать электростатическое поле, создаваемое любым заряженным телом, указав модуль и направление силы, действующей на этот заряд д0. Удобно пользоваться такой характеристикой электростатического поля, которая не зависит от числового значения пробного заряда. Ею является напряжённость.
Напряжённость электростатического поля
Если в произвольно выбранную точку А электростатического поля, созданного зарядом Q, внести пробный заряд 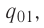
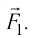
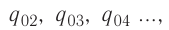
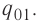
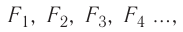
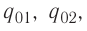
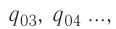
Таким образом, отношение силы, действующей на помещённый в некоторую точку поля пробный заряд, к значению этого заряда для данной точки поля остаётся неизменным. Это отношение является силовой характеристикой электростатического поля, получившей название напряжённость.
Напряжённостью 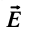
с которой поле действует на пробный заряд 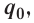
Из выражения (15.1) следует, что единицей напряжённости электростатического поля в СИ является ньютон на кулон 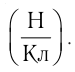
Выражение (15.1) позволяет определить силу, действующую на точечный заряд q, помещённый в электростатическое поле напряжённостью 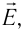
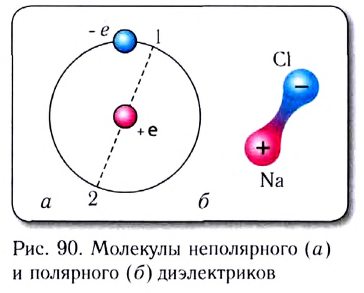
Напряжённость поля, как и сила, величина векторная. Направление напряжённости поля совпадает с направлением силы, действующей на положительный пробный электрический заряд. Напряжённость в любой точке электростатического поля направлена вдоль прямой, соединяющей эту точку и точечный заряд, создающий поле. Напряжённость поля, созданного точечным положительным зарядом Q > 0, направлена от заряда, а напряжённость поля, созданного точечным отрицательным зарядом Q < 0, —к заряду (рис. 87).
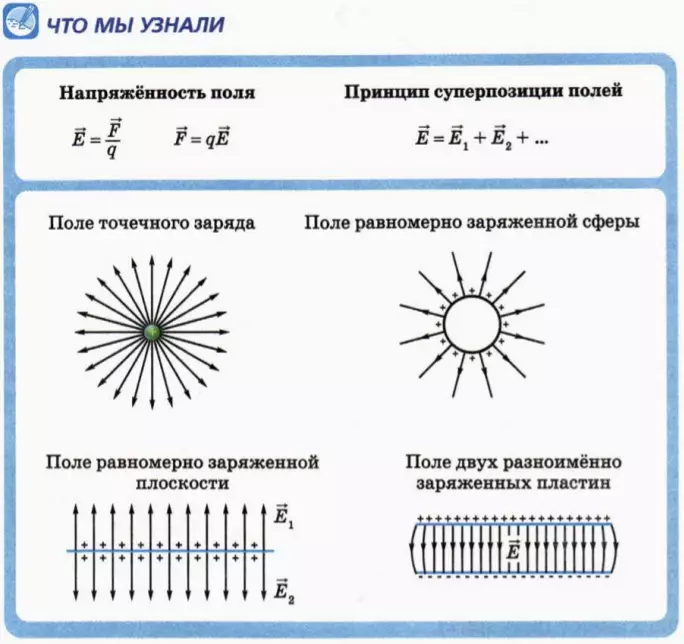
Напряжённость поля, создаваемое точечным зарядом
Найдём напряжённость электростатического поля, созданного точечным зарядом, модуль которого |Q|. Поместим в некоторую точку поля положительный пробный заряд 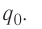
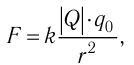
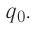
Модуль напряжённости поля, создаваемого равномерно заряженной сферой, заряд которой Q, в точках на её поверхности и вне сферы на расстоянии r от её центра определяют по формуле 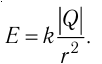
внутри сферы, как мы увидим дальше,
Напряжённость электростатического поля, создаваемого равномерно заряженной бесконечной плоскостью, одинакова во всех точках полупространства с каждой стороны от плоскости (при этом 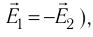
где S — площадь некоторого участка плоскости, q — заряд этого участка.
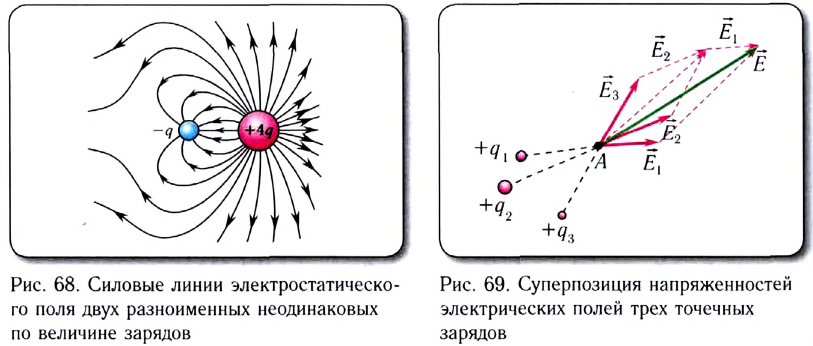
Принцип суперпозиции электрических полей
Если заряженные тела, создающие электростатические поля, не меняют своего состояния (распределения электрических зарядов) в зависимости от присутствия или отсутствия других тел, то напряжённость 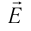
где 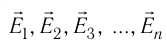
Самым простым примером проявления принципа суперпозиции являются электростатические поля, созданные разными точечными зарядами: если в определённой точке пространства электростатические поля создаются системой точечных зарядов, напряжённости которых в указанной точке 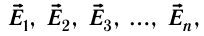
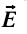
На рисунке 88 показано, как можно определить напряжённость результирующего поля, созданного двумя точечными электрическими зарядами противоположных знаков 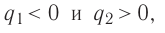
Напряжённости 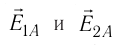
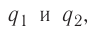
прямой, соединяющей заряды, в противоположные стороны. Напряжённость 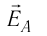
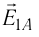
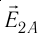
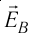
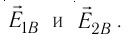
Аналогично определяют напряжённость и для электростатического поля системы проводящих концентрических заряженных сфер.
Линии напряжённости электростатического поля
Чтобы наглядно отображать распределение поля в пространстве, Фарадеем в 1845 г. был предложен способ изображения электрических полей в виде воображаемых линий, называемых линиями напряжённости (силовыми линиями).
Линии напряжённости — воображаемые направленные линии, касательные к которым в каждой точке поля совпадают по направлению с напряжённостью электростатического поля в той же точке (т. е. с направлением электростатической силы, действующей на положительный заряд) (рис. 89).
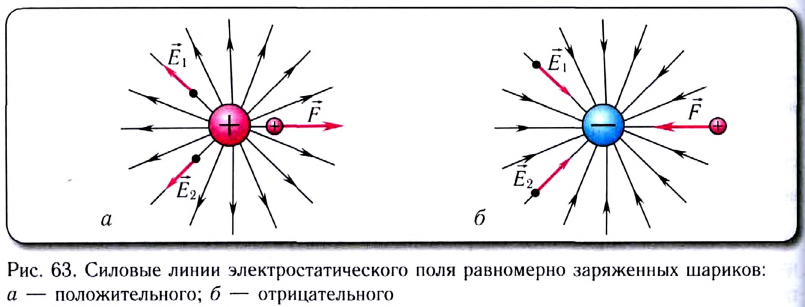
Очевидно, что через любую точку поля, в которой 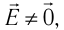
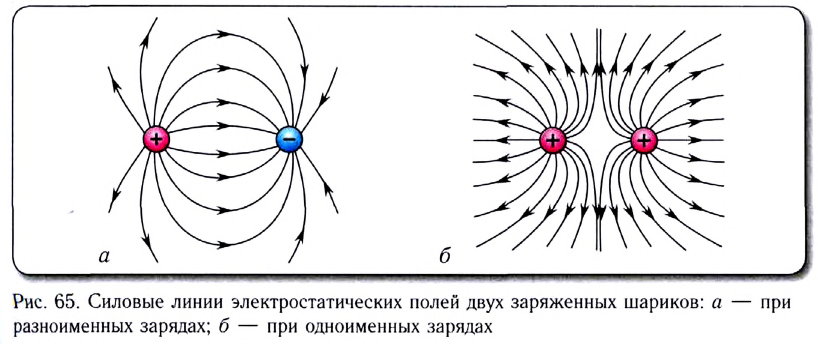
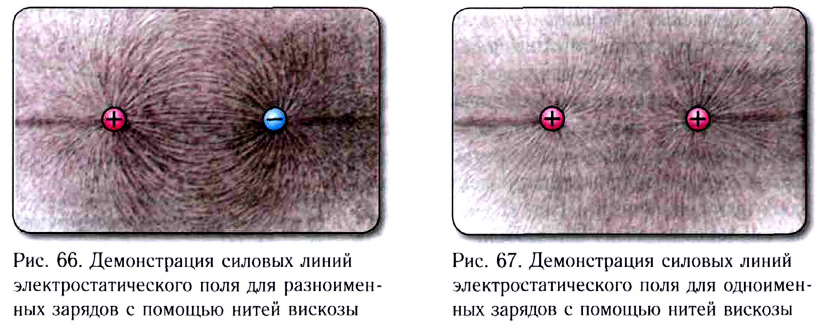
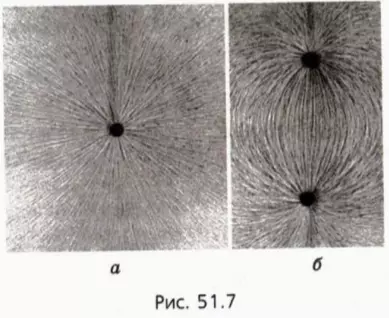
На рисунке 90, а показаны линии напряжённости полей, образованных зарядами, равномерно распределёнными по поверхности уединённых проводящих шариков. Направление каждой стрелки на рисунке 90, а совпадает с направлением напряжённости поля. Линии напряжённости в первом случае направлены от положительного заряда в бесконечность, а во втором — из бесконечности к отрицательному заряду и оканчиваются на нём.
В электростатическом поле линии напряжённости начинаются и оканчиваются на электрических зарядах даже тогда, когда одним своим концом уходят в бесконечность, где и находятся недостающие на рисунке заряды.
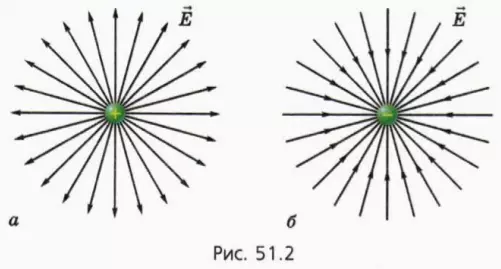
На рисунке 90, б показаны линии напряжённости электростатического поля, образованного двумя разноимёнными зарядами, модули которых одинаковые, находящимися на проводящих шариках. Стрелки показывают направления напряжённости поля в различных его точках.
На рисунке 90, в приведены линии напряжённости электростатического поля двух одинаково заряженных шариков.
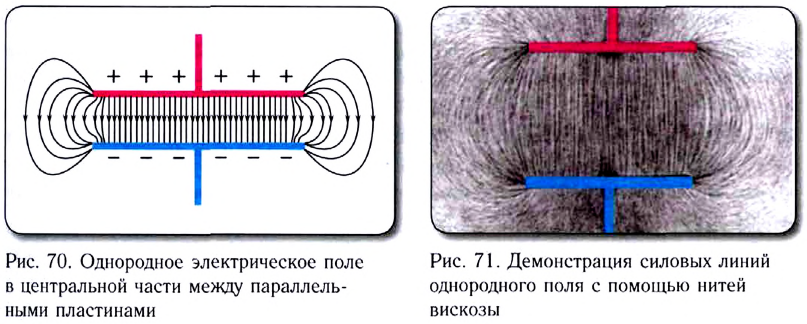
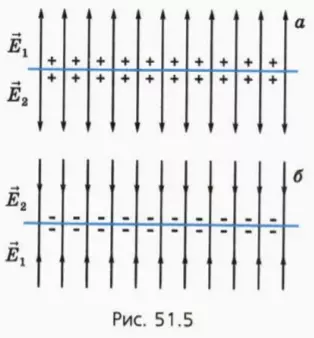
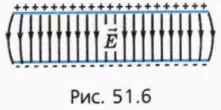
На рисунке 90, г изображено поле, созданное зарядами противоположных знаков, модули которых одинаковые, находящимися на двух плоских металлических пластинах, длина которых много больше расстояния между ними. Линии напряжённости такого поля параллельны друг другу за исключением пространства вблизи краёв пластин и вне области их перекрытия. Электростатическое поле в центральной области между разноимённо заряженными металлическими пластинами является примером однородного поля. Электростатические поля, изображённые на рисунке 90, а, б, в, являются неоднородными, так как или модуль, или направление (или и то и другое) напряжённости в разных точках поля отличаются.
Электростатическое поле, напряжённость которого в любой его точке одинакова, называют однородным электростатическим полем.
Линии напряжённости электростатического поля не прерываются в пространстве (при отсутствии в нём других зарядов), никогда не пересекаются и не касаются друг друга.
Чтобы линии напряжённости отображали не только направление, но и модуль напряжённости поля, на рисунках их условились проводить с определённой густотой. Густота линий напряжённости в пространстве зависит от модуля напряжённости поля: линии напряжённости идут гуще там, где модуль напряжённости поля больше, и реже там, где он меньше. В однородном электростатическом поле густота линий напряжённости не меняется. Картину линий напряжённости принято строить так, чтобы она по возможности отображала симметрию изображаемого электростатического поля. Количество линий напряжённости, началом или концом которых служит данный заряд, пропорционально значению этого заряда (рис. 91)
- Поле, создаваемое неподвижными относительно используемой инерциальной системы отсчёта электрическими зарядами, называют электростатическим полем.
- Напряжённостью электростатического поля в любой его точке называют физическую векторную величину, характеризующую силовое действие поля на вносимые в него заряды и равную отношению силы, с которой поле действует на пробный заряд, находящийся в выбранной точке, к значению этого заряда:
- Модуль напряжённости поля, создаваемого в вакууме или воздухе точечным зарядом, прямо пропорционален модулю этого заряда и обратно пропорционален квадрату расстояния между зарядом и точкой, в которой определяют значение напряжённости:
- Линии напряжённости — воображаемые направленные линии, касательные к которым в каждой точке поля совпадают по направлению с напряжённостью электростатического поля. Линии напряжённости начинаются на положительных зарядах и оканчиваются на отрицательных, нигде не прерываются в пространстве, не содержащем других зарядов, не пересекаются и не касаются друг друга.
- Электростатическое поле, напряжённость которого в любой его точке одинакова, называют однородным электростатическим полем.
Пример №3
Два неподвижных точечных заряда 
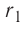
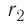
Дано:
Решение. Согласно принципу суперпозиции напряжённость результирующего поля 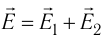
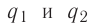
теореме Пифагора, следует, что угол между 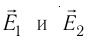
поля найдём по теореме Пифагора:
как заряды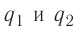
С учётом этого
Пример №4
Первоначально неподвижный шарик массой m = 10 г и зарядом q = 10 нКл начинает падать с ускорением, модуль которого 
Дано:
Решение. В начальный момент на шарик действуют сила тяжести 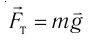
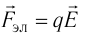
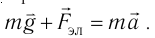
Ответ: напряжённость электростатического поля направлена вертикально вверх и её модуль
Потенциальность электростатического поля
Электростатическое поле, действуя на находящиеся в нём заряды с определённой силой, может их перемещать. Из механики вы знаете, что при перемещении тела действующая на него сила совершает работу. Выясним, от чего зависит работа силы по перемещению электрического заряда в электростатическом поле.
Работа силы однородного электростатического поля по перемещению электрического заряда. В общем случае работа сил электрического поля при перемещении заряда зависит как от его начального и конечного положений, так и от вида траектории, по которой движется заряд.
Однако электростатическое поле имеет важную особенность. Работа сил этого поля при перемещении заряда между двумя точками зависит только от положения этих точек и не зависит от вида траектории. Такой же особенностью обладает и гравитационное поле. Физические поля, работа сил которых не зависит от формы траектории, называют потенциальными (или консервативными). Покажем, что электростатическое поле потенциально.
Пусть положительный пробный заряд 
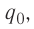
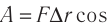
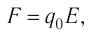
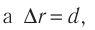
Если заряд перемещают по прямой из точки В в точку D под углом a к направлению напряжённости поля 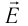
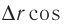
Очевидно, что для перемещения заряда в обратном направлении (из точки D в точку В) внешней силе требуется, преодолевая силу поля, совершить
работу, минимальное значение которой будет таким же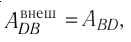
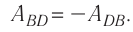
Предположим, что перемещение заряда 
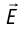
где 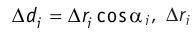
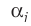
Таким образом, работа силы однородного электростатического поля по перемещению заряда из одной точки поля в другую не зависит от формы траектории, т. е. однородное электростатическое поле потенциально.
Воспользовавшись законом сохранения энергии, можно показать, что любое электростатическое поле является потенциальным. Это означает, что электростатическое и гравитационное поля имеют похожие свойства, определяемые их потенциальным характером. Применительно к электростатическому полю эти свойства выражаются в следующем:
а) Точечный электрический заряд, находящийся в любой точке электростатического поля, обладает потенциальной энергией взаимодействия с этим полем, значение которой определяют относительно произвольно выбираемой нулевой точки. В нулевой точке потенциальную энергию заряда в поле принимают равной нулю. Потенциальная энергия взаимодействия точечного заряда с электростатическим полем равна работе, которую совершили бы силы поля при перемещении данного заряда из указанной точки поля в нулевую точку.
б) Работа сил электростатического поля по перемещению электрического заряда из начальной точки 1 в конечную точку 2 равна приращению (изменению) потенциальной энергии заряда в поле, взятому со знаком минус, или же убыли потенциальной энергии:
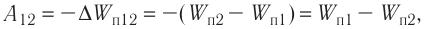
где 
Следует подчеркнуть, что потенциальная энергия — это энергия взаимодействия, и её необходимо относить не к заряженной частице или телу, а к системе в целом. В частности, для заряженной частицы (тела), находящейся в электростатическом поле, это потенциальная энергия взаимодействия заряженной частицы с полем, т. е. с другими заряженными частицами и (или) телами, являющимися источниками этого поля. Кратко это принято формулировать так: потенциальная энергия заряда в поле.
Знак «минус» в выражении (16.2) означает, что если сила электростатического поля совершает положительную работу (подобно силе гравитационного поля Земли при падении камня), то потенциальная энергия заряженного тела в поле уменьшается: 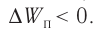
отсутствуют) увеличивается кинетическая энергия тела:
На этом основано ускорение заряженных частиц электростатическим полем. Если работа сил электростатического поля отрицательна (подобно работе силы гравитационного поля при движении камня, брошенного вверх), то потенциальная энергия заряда в поле увеличивается: 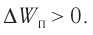
Потенциал электростатического поля как его энергетическая характеристика
Из выражений (16.1) и (16.2) следует, что приращение (изменение) потенциальной энергии заряда в однородном электростатическом поле при его перемещении из точки / в точку 2 поля пропорционально значению этого заряда. Как свидетельствуют результаты многочисленных экспериментов, эта пропорциональность сохраняется и для неоднородного электростатического поля. После выбора точки поля, в которой потенциальная энергия заряда принята равной нулю, значения потенциальной энергии заряда во всех остальных точках поля становятся однозначно определяемыми формулой (16.2). Если в произвольно выбранную точку электростатического поля поочерёдно вносить пробные заряды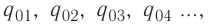
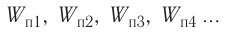
Таким образом, отношение потенциальной энергии пробного заряда в поле к значению этого заряда для данной точки поля остаётся неизменным. Это отношение является энергетической характеристикой электростатического поля, получившей название потенциал.
Потенциалом 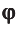
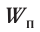
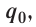
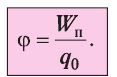
Поскольку потенциальная энергия заряда в электростатическом поле зависит от выбора нулевой точки, то эта зависимость сохраняется и для потенциала. Если принять, что на бесконечно большом расстоянии от источника поле отсутствует, т. е. потенциальная энергия системы «заряд — электростатическое поле» на бесконечности равна нулю, то потенциал поля в данной точке можно определить следующим образом:
Потенциал электростатического поля в данной точке численно равен работе, которую совершают силы поля при перемещении единичного положительного заряда из данной точки в бесконечность.
За единицу потенциала в СИ принят вольт (В). Единица названа в честь итальянского учёного Алессандро Вольта (1745—1827), внёсшего большой вклад в изучение электрических явлений. 1 В — потенциал такой точки электростатического поля, в которой заряд 1 Кл обладал бы потенциальной энергией 1 Дж.
Потенциал 
(16.4)
Знак заряда-источника поля определяет знак потенциала этого поля. Потенциал поля, создаваемого равномерно заряженной сферой радиусом R, заряд которой q, в вакууме или в воздухе в точках вне сферы на расстоянии r > R от её центра определяют по формуле 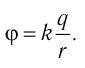
Для потенциала выполняется принцип суперпозиции: если поле создано системой n точечных зарядов, то потенциал 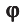
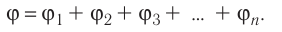
Геометрическое место точек в электростатическом поле, потенциалы которых одинаковы, называют эквипотенциальной поверхностью.
Используя эквипотенциальные поверхности, можно представлять графически электростатические поля. Через каждую точку поля проходят только одна линия напряжённости и одна эквипотенциальная поверхность. В каждой точке электростатического поля линия напряжённости и эквипотенциальная поверхность взаимно перпендикулярны (рис. 97). Представление электростатического поля с помощью эквипотенциальных поверхностей, как и термин «потенциал», ввёл немецкий учёный К. Ф. Гаусс в 1840 г.
- Работа сил электростатического поля по перемещению заряда из начальной точки 1 в конечную точку 2 равна приращению (изменению) потенциальной энергии заряда в этом поле, взятому со знаком минус, или же убыли потенциальной энергии:
- Работа силы однородного электростатического поля по перемещению заряда
- Работа сил электростатического поля по перемещению заряда из начальной точки 1 в конечную точку 2 равна приращению (изменению) потенциальной энергии заряда в этом поле, взятому со знаком минус, или же убыли потенциальной энергии:
- Потенциалом электростатического поля в данной точке пространства называют физическую скалярную величину, характеризующую энергетическое состояние поля в данной точке пространства и равную отношению потенциальной энергии точечного (пробного) заряда, помещённого в данную точку поля, к значению этого заряда:
- Если иоле создано системой точечных зарядов, то его потенциал в данной точке пространства равен алгебраической сумме потенциалов полей в этой точке, создаваемых каждым из точечных зарядов системы в отдельности:
Пример №5
Электрон, двигаясь со скоростью, модуль которой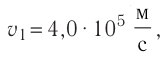
Дано:
Решение. До изменения направления движения сила однородного электростатического поля совершает отрицательную работу по торможению электрона:
Эту работу также можно определить по формуле А = eEd.
Значит, —
Согласно закону сохранения энергии полная энергия системы «электрон— поле» остаётся неизменной, т. е. 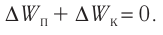
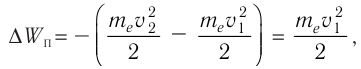
поле возрастает на величину
Разность потенциалов электростатического поля
Напряжение. Связь между напряжением и напряжённостью однородного электростатического поля
Поскольку потенциальная энергия любой системы тел, взаимодействующих посредством потенциальных сил, зависит от выбора нулевой точки (нулевого уровня), то до осуществления такого выбора потенциальная энергия системы может быть определена только с точностью до некоторой постоянной величины. Но изменение потенциальной энергии не зависит от значения этой постоянной величины и однозначно характеризует процесс перехода системы из одного состояния в другое. Это относится и к изменению потенциальной энергии заряженной частицы (заряда) в электростатическом поле.
Понятие потенциала существенно для количественного описания электростатического поля наряду с его напряжённостью. Перемещение заряженных частиц в электростатическом поле, сопровождаемое изменением их потенциальной энергии, характеризуют, используя понятие «разность потенциалов». Как и приращение (изменение) потенциальной энергии, разность потенциалов не зависит от выбора нулевой точки.
Разностью потенциалов 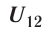
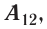
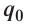
Разность потенциалов определяется убылью потенциальной энергии перемещаемого в поле единичного положительного заряда.
Противоположную по знаку разности потенциалов величину называют приращением (изменением) потенциала:
За единицу разности потенциалов в СИ принимают вольт (В). 1 В — разность потенциалов 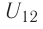
Потенциал проводника можно измерить электрометром. Для этого проводник соединяют со стрелкой электрометра, корпус которого заземляют. Отклонение стрелки электрометра покажет наличие разности потенциалов между проводником и Землёй. Приняв потенциал Земли равным нулю, можно считать, что электрометр измеряет потенциал проводника.
Если имеются два заряженных проводника, то, соединив один из них со стрелкой, а другой с корпусом электрометра, измеряют разность потенциалов между заряженными проводниками.
Связь между напряжением и напряжённостью однородного электростатического поля
Термин «напряжение» ввёл в 1792 г. Вольта. Для электростатических полей понятия «электрическое напряжение» и «разность потенциалов» тождественны.
Работа, совершаемая силами однородного электростатического поля напряжённостью 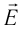
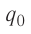
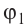
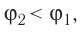
а в соответствии с выражением (16.1)
где d — модуль перемещения заряда вдоль линии напряжённости электростатического поля.
Приравнивая соответствующие части равенств, найдём выражение, устанавливающее связь между модулем напряжённости однородного электростатического поля и разностью потенциалов, т. е. между двумя характеристиками электростатического поля: 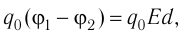
Принимая во внимание, что 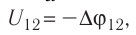
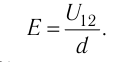
На основании формулы (17.2) вводят единицу напряжённости СИ вольт
на метр 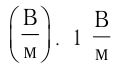
Используя термин «напряжение», на практике точки / и 2 поля выбирают так, чтобы
- Работа, совершаемая силами электростатического поля мри перемещении пробного заряда из начальной точки 1 в конечную точку 2, равна произведению значения заряда и разности потенциалов (напряжения) между этими двумя точками поля:
- Модуль напряжённости однородного электростатического поля и разность потенциалов (напряжение) при условии, что
связаны между собой соотношением
Пример №6
В центре сферы с равномерно распределённым положительным зарядом 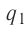
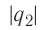
Дано:
Решение. Потенциал в искомой точке определим по принципу суперпозиции: 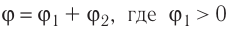
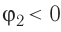
Поскольку:
Ответ:
Пример №7
Электрон, движущийся вдоль линии напряжённости электростатического поля, в точке поля с потенциалом 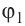
дуль которой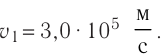
электрон начинает двигаться в обратном направлении. Масса электрона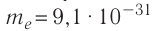
Дано:
Решение. При движении электрона силы поля совершают работу 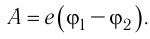
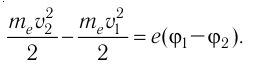
движения электрона уменьшилась до нуля, получим:
откуда
Проводники в электростатическом поле
Мы уже обсуждали сходство и различие гравитационного и электростатического взаимодействий. Следует отметить ещё одно их существенное различие. От сил тяготения нельзя защититься. Нет такого убежища, в котором бы силы тяготения не действовали. А вот получить надёжную защиту от электростатических сил вполне возможно. Такую защиту может обеспечить любой проводник. Так какие же свойства проводников позволяют использовать их для электростатической защиты?
В металлах свободными заряженными частицами являются электроны. Это происходит потому, что электроны, находящиеся на внешних оболочках атомов, утрачивают связи со своими атомами и могут относительно свободно передвигаться по всему объёму металла.
Выясним, что происходит в однородном металлическом проводнике, если его внести в электростатическое поле. Для этого поместим металлический проводник А в электростатическое поле, созданное двумя заряженными пластинами В и С (рис. 99). Напряжённость 
Под действием электрических сил свободные электроны наряду с непрекращающимся тепловым движением начнут двигаться упорядоченно. Они будут накапливаться слева у поверхности проводника А, создавая там избыточный отрицательный заряд. Недостаток электронов на правой стороне проводника приведёт к возникновению на ней избыточного положительного заряда.
Перераспределившиеся заряды создают собственное электрическое поле 
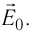
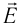
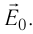
Следовательно, электростатическое поле внутри проводника отсутствует. Суммарный заряд любой внутренней области проводника равен нулю и не влияет на распределение зарядов на его поверхности и на напряжённость поля внутри проводника. На этом свойстве проводников основана электростатическая защита. Чтобы защитить чувствительные к электрическому полю приборы, их помещают внутрь заземлённых полых проводников со сплошными или сетчатыми стенками. Чаще, однако, экранируют не приборы, а сам источник электрического поля, от нежелательного воздействия которого необходимо защитить расположенные поблизости устройства.
Следствием того, что напряжённость электростатического поля внутри однородного проводника равна нулю, является то, что потенциал всех точек проводника одинаков. В самом деле, если напряжённость поля равна нулю, то разность потенциалов между любыми двумя точками проводника равна нулю. Поэтому можно говорить о потенциале проводника, не указывая конкретную точку, в которой он определён.
Электростатическая индукция
В соответствии с законом сохранения электрического заряда модули избыточных зарядов, возникающих на противоположных поверхностях первоначально незаряженного проводника при внесении его в электростатическое поле, должны быть равными. Проверим это на опыте.
Закрепим на непроводящих стержнях два плотно соприкасающихся металлических цилиндра А и В с прикреплёнными к ним листочками тонкой бумаги. Внесём их в электростатическое поле положительно заряженного шара (рис. 100, а). Листочки бумаги разойдутся, что свидетельствует о появлении зарядов на цилиндрах. Свободные электроны под действием поля, создаваемого зарядом шара, переместятся с цилиндра В на цилиндр А, зарядив его отрицательно. Цилиндр В из-за недостатка электронов станет положительно заряженным.
Явление, при котором на поверхности проводника (в данном случае на поверхности соединённых цилиндров), помещённого в электростатическое поле, появляются электрические заряды, называют электростатической индукцией или электризацией через влияние. Электрические заряды, возникающие в результате электростатической индукции, называют индуцированными.
Если заряженный шар убрать, то угол расхождения листочков бумаги уменьшится до нуля. Это объясняется тем, что в отсутствие электростатического поля, создаваемого зарядом шара, электроны равномерно распределяются по всему объёму обоих цилиндров.
При разъединении цилиндров в поле заряженного шара на них окажутся противоположные по знаку заряды (рис. 100, б), модули которых равны. Эти заряды сохранятся и в том случае, если заряженный шар, создающий поле, убрать (рис. 100, в). Только в этом случае заряды будут у соседних оснований цилиндров. В том, что модули зарядов обоих цилиндров равны, можно убедиться, соединив их (рис. 100, г): угол между листочками равен нулю.
Распределение зарядов в проводнике
Выясним, как распределяются заряды в наэлектризованном проводнике. Проведём опыт. Сообщим проводнику электрический заряд. Маленьким шариком на изолирующей ручке будем касаться различных точек на внешней поверхности заряженного полого металлического шара, а затем электрометра (рис. 101, а). Отмечая каждый раз угол отклонения стрелки электрометра, можно убедиться, что на внешней поверхности шара заряд распределяется равномерно. Если же коснуться маленьким шариком внутренней поверхности заряженного полого шара, а затем электрометра, то стрелка электрометра не отклонится (рис. 101, б). Следовательно, на внутренней поверхности шара избыточного заряда нет, т. е. заряды, сообщённые проводнику, располагаются на его внешней поверхности.
Зарядим проводник стреловидной формы положительным зарядом. Наибольший заряд, приходящийся на < небольшие одинаковой площади участки поверхности, находится на выпуклостях проводника, особенно на остриях. На рисунке 102 штриховой линией для наглядности показано распределение модуля напряжённости
поля у поверхности заряженного проводника стреловидной формы. Напряжённость электростатического поля вблизи острых выступов заряженного проводника может оказаться настолько большой, что начнётся ионизация молекул газов, входящих в
состав воздуха, в результате которой появятся положительные и отрицательные ионы и электроны. Заряженные частицы с тем же знаком заряда, что и на острие, движутся от него, увлекая нейтральные молекулы. Вследствие этого возникает направленное движение воздуха у острия, или, как говорят, «электрический ветер». Его можно обнаружить, если поднести к острию зажжённую свечу: её пламя отклонится в сторону от острия и может быть даже погашено.
Явление стекания зарядов с заострённых проводников приходится учитывать в технике. Для предотвращения стекания зарядов у всех приборов и механизмов, используемых в высоковольтных системах, металлические части делают закруглёнными, а концы металлических стержней снабжают гладкими наконечниками.
- Проводник — одна из моделей, используемых в электростатике, описывающая однородное тело, внутри которого напряжённость электростатического поля везде равна нулю.
- Явление, при котором на поверхности проводника, помещённого в электростатическое поле, появляются электрические заряды, называют электростатической индукцией или электризацией через влияние.
- Потенциалы всех точек на поверхности и внутри однородного проводника, помещённого в электростатическое поле, одинаковы.
- Заряды, сообщённые проводнику, располагаются на его внешней поверхности.
Диэлектрики в электростатическом поле
Исследуя явление электризации через влияние, английский физик Стефан Грей (1670—1736) установил в 1729 г., что вещества можно разделить на два класса: способные переносить электрические заряды и этим свойством не обладающие. Соответствующие термины «проводник» и «изолятор» были введены в 1742 г. англичанином Жаном Теофилом Дезагюлье (1683 —1744). Примерами хороших диэлектриков являются янтарь, стекло, эбонит, резина, шёлк, пластмасса, слюда, фарфор. Что происходит в диэлектрике, помещённом в электростатическое поле?
Диэлектрики
Термин «диэлектрик» ввёл Фарадей в 1838 г. для обозначения вещества, в которое проникает электростатическое поле («диэлектрик» от греч. dia — через, сквозь и англ, electric — электрический). В диэлектрике все электроны связаны с ядрами атомов. Электрическое поле не «отрывает» их от атомов, а лишь слегка смещает по отношению к положительно заряженным ядрам. Диэлектрик содержит только связанные заряды, т. е. заряды, входящие в состав атомов (молекул) диэлектрика и лишённые возможности свободно перемещаться под действием электрического поля.
Выясним, что происходит в диэлектрике, помещённом в электростатическое поле.
Проведём опыт. Длинную деревянную линейку установим на подставке так, чтобы она могла свободно вращаться (рис. 103). Наэлектризуем стеклянную (или эбонитовую) палочку и поднесём её к одному из концов линейки. Линейка начнёт поворачиваться. Следовательно, незаряженный диэлектрик, каким является деревянная линейка, притягивается к заряженному телу. Подобное поведение диэлектрика возможно только при условии появления на его концах избыточных зарядов, противоположных по знаку.
Поляризация диэлектрика
Каков же механизм перераспределения зарядов по поверхности диэлектрика? Действие электростатического поля с напряжённостью 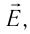
Если диэлектрики состоят из молекул, являющихся электрическими диполями в отсутствие внешнего поля, то их называют полярными (вода, аммиак, эфир, ацетон и др.). У полярных диэлектриков в отсутствие внешнего электростатического поля молекулы-диполи, совершая тепловое движение, располагаются хаотически (рис. 105, а). Результирующее электрическое поле, создаваемое молекулами-диполями, практически равно нулю.
Под действием внешнего электростатического поля молекулы-диполи стремятся повернуться так, чтобы их оси совпали с направлением напряжённости внешнего поля (рис. 105, б). Если направление напряжённости поля перпендикулярно поверхностям, ограничивающим диэлектрик, то одна из этих поверхностей оказывается заряженной отрицательно, а другая — положительно.
У неполярных диэлектриков (парафин, бензол, азот и др.) молекулы со сферически симметричным распределением зарядов в отсутствие внешнего электрического поля не создают и собственного поля (рис. 105, в). Под влиянием электростатического поля, как уже было сказано, положительные и отрицательные заряды в пределах молекулы несколько смещаются один относительно другого, образуя диполь. Поэтому, как и в случае с полярными диэлектриками, в неполярных диэлектриках на одной поверхности появляется положительный поляризационный заряд, на другой — отрицательный (рис. 105, г).
В отличие от свободных зарядов проводника поляризационные заряды в диэлектрике не перемещаются, поэтому их и называют связанными. Эти заряды нельзя отделить один от другого. Так, если поляризованный диэлектрик разрезать пополам во внешнем электрическом поле, то на одной стороне каждой половинки будет нескомпенсированный положительный заряд, а на другой — отрицательный.
Электрическое поле внутри диэлектрика
Поляризационные заряды (см. рис. 105, б, г) создают собственное электростатическое поле, напряжённость 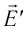
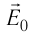
Согласно принципу суперпозиции модуль напряжённости Е результирующего электростатического поля внутри диэлектрика
Для характеристики электрических свойств диэлектриков вводят физическую величину, называемую диэлектрической проницаемостью вещества.
Диэлектрическая проницаемость вещества 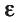
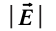
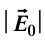
Если точечные неподвижные заряды 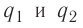
Различные диэлектрики поляризуются внешним полем по-разному и имеют разную диэлектрическую проницаемость. Так, диэлектрическая проницаемость дистиллированной воды при температуре 25 °С равна 78,54, льда при температуре —10 °С — 95, а стекла — от 4 до 16 в зависимости от его сорта. Диэлектрическую проницаемость воздуха, равную 1,0006, при решении задач округляют до 1.
Поляризацию частиц в сильном электростатическом поле используют в электрических фильтрах для очистки дыма от твёрдых продуктов сгорания топлива, загрязняющих территорию вокруг тепловых электростанций и крупных предприятий (рис. 106). Для этого в дымоходах устанавливают проводники специальной формы, которым сообщают определённый электрический заряд
Электрофильтры устанавливают на химических заводах, в цехах, производящих цемент, и других аналогичных производствах. Поляризованные частицы всевозможной пыли притягиваются к вертикальным электродам (рис. 107). Когда модуль силы тяжести, действующей на частицы, задерживаемые фильтром, достигает определённого значения, пыль оседает на дно фильтра. Для очистки фильтра пыль из него периодически удаляют.
- Диэлектрик — одна из моделей, используемых в электростатике, описывающая такое вещество, что внутри тел, состоящих из этого вещества, напряжённость электростатического поля может быть отлична от нуля.
- Явление перераспределения электрических зарядов в диэлектрике при внесении его в электростатическое поле называют поляризацией.
- Диэлектрическая проницаемость вещества — физическая скалярная величина, показывающая, во сколько раз модуль напряжённости электростатического поля внутри однородного диэлектрика меньше модуля напряжённости поля в вакууме:
Электроёмкость
Проводники и системы, состоящие из нескольких проводников, обладают свойством накапливать электрический заряд. Во многих электротехнических и радиотехнических приборах используют устройства, способные при малых размерах накапливать достаточно большой по абсолютной величине электрический заряд. Выясним, как это можно осуществить.
Электрическая ёмкость
Для характеристики свойства проводника накапливать электрический заряд ввели физическую величину — электрическую ёмкость. Для объяснения физического смысла этой величины рассмотрим следующий опыт: присоединим тонким длинным проводником к стержню электрометра с заземлённым корпусом уединённый полый металлический шар.
Проводник считают уединённым, если он расположен вдали от возможных источников электрического поля как проводящих, так и непроводящих тел. Если вблизи заряженного проводника находятся другие тела, то вследствие явления электростатической индукции в проводниках происходит перераспределение свободных электрических зарядов, а в диэлектриках — смещение в противоположные стороны разноимённых зарядов, входящих в состав атомов и молекул вещества, приводящее к возникновению поляризационных зарядов. Поляризационные заряды, возникающие в диэлектриках, и заряды, индуцируемые на проводниках, создают дополнительное электростатическое поле, изменяющее потенциал заряженного проводника.
Касаясь наэлектризованным проводящим шариком, закреплённым на изолирующей ручке, внутренней поверхности полого металлического шара, будем последовательно сообщать ему одинаковые положительные электрические заряды, увеличивая его суммарный заряд в 2, 3 и т. д. раз (рис. 108). Чем больше сообщённый шару электрический заряд, тем больше его потенциал, так как 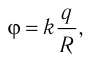
Значит, во сколько раз увеличился заряд шара, соответственно во столько же раз увеличился и его потенциал, т. е. отношение электрического заряда к потенциалу остаётся величиной постоянной для данного шара:
Прямая пропорциональная зависимость между потенциалом и электрическим зарядом справедлива не только для шарообразных проводников, но и для любого уединённого проводника произвольной формы. Необходимо только, чтобы форма и размеры проводника, а также диэлектрические свойства среды, в которой он находится, оставались неизменными.
Электрическая ёмкость С уединённого проводника — физическая скалярная величина, количественно характеризующая способность проводника накапливать электрический заряд и равная отношению заряда q проводника к его потенциалу
Обращаем ваше внимание, что электрическая ёмкость является характеристикой проводника и не зависит ни от его заряда, ни от потенциала. Поскольку заряды располагаются только на внешней поверхности проводника, то ни от вещества, из которого он изготовлен, ни от его массы электроёмкость проводника также не зависит. Она зависит только от формы и размеров проводника, а также от диэлектрической проницаемости среды, в которой этот проводник находится.
Единицу электрической ёмкости в СИ называют фарад (Ф).
1 Ф — электроёмкость такого уединённого проводника, которому для повышения потенциала на 1 В необходимо сообщить заряд 1 Кд:
1 Ф — очень большая электроёмкость. Например, в вакууме электроёмкостью С — 1 Ф обладал бы уединённый шар радиусом 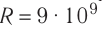
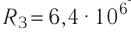
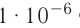
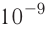

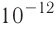
Например, электроёмкость такого огромного проводника, как земной шар, С = 0,71 мФ, а электроёмкость человеческого тела примерно С= 50 пФ.
Электроёмкость уединённого проводящего шара радиусом R, находящегося в безграничной среде с диэлектрической проницаемостью 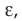
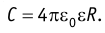
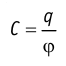
Конденсаторы
Для получения нужных значений электроёмкости используют конденсатор — систему, состоящую из двух или более проводников и способную накапливать и отдавать (перераспределять) электрические заряды. Конденсатор — от лат. condensare — уплотнять, сгущать.
Чтобы на электроёмкость конденсатора не оказывали влияние окружающие тела, проводникам, образующим конденсатор, придают такую форму, при которой поле, создаваемое зарядами этих проводников, сосредоточено между ними. Этому условию удовлетворяют две близко расположенные пластины (плоский конденсатор) (рис. 109, а), два коаксиальных цилиндра (цилиндрический конденсатор) (рис. 109, б), две концентрические сферы (сферический конденсатор) (рис. 109, в).
Широко распространенный тип конденсаторов представляет собой две ленты металлической фольги, разделённые тонкой парафинированной бумагой, полистиролом, слюдой или другим диэлектриком, которые свёрнуты в тугую спираль и запаяны (рис. 110).
Используют и так называемые воздушные конденсаторы, в которых изолирующим слоем, отделяющим проводники, является воздух.
Простейший конденсатор — система, состоящая из двух проводников, разделённых слоем диэлектрика, толщина d которого мала по сравнению с размерами проводников (рис. 111). Проводники, образующие конденсатор, называют его обкладками.
На обкладках конденсатора накапливаются противоположные по знаку электрические заряды, модули которых равны. Процесс накопления зарядов на обкладках называют зарядкой конденсатора. Процесс нейтрализации зарядов при соединении обкладок конденсатора проводником называют разрядкой конденсатора. Модуль заряда, находящегося на одной из обкладок конденсатора, называют зарядом конденсатора.
Свойство конденсатора накапливать и сохранять в течение длительного промежутка времени электрические заряды характеризуют его электрической ёмкостью.
Электрической ёмкостью С конденсатора называют физическую скалярную величину, количественно характеризующую способность конденсатора накапливать электрические заряды и равную отношению заряда q конденсатора к напряжению U между его обкладками:
Электроёмкость плоского конденсатора
Если обкладками конденсатора являются две одинаковые параллельные друг другу пластины, то конденсатор называют плоским. Электростатическое поле заряженного плоского конденсатора в основном сосредоточено между его обкладками и является практически однородным (рис. 112, а). Вблизи краёв пластин однородность поля нарушается, однако этим часто пренебрегают, когда расстояние между пластинами значительно меньше их размеров (рис. 112, б).
Чтобы установить, от чего зависит электроёмкость плоского конденсатора, проведём несколько опытов. В качестве обкладок конденсатора используем две металлические пластины, расположенные в воздухе на некотором расстоянии параллельно друг другу.
Соединим стержень электрометра с одной из пластин, а его корпус с другой (рис. 113). Зарядим конденсатор, подключив его к батарее элементов (источнику тока) на некоторый промежуток времени. Когда между пластинами конденсатора возникнет напряжение (стрелка электрометра отклонится), отключим его от источника тока.
Если перемещать пластины относительно друг друга, уменьшая площадь их взаимного перекрытия при неизменном расстоянии между ними, то показания электрометра при этом увеличиваются, хотя сообщённый пластинам при зарядке конденсатора заряд не изменяется. Так как напряжение между пластинами увеличивается при уменьшении площади перекрытия пластин конденсатора, то его электроёмкость должна уменьшаться
Увеличивая расстояние между пластинами конденсатора, не меняя площади их перекрытия, будем наблюдать возрастание показаний электрометра, т. е. увеличение напряжения между пластинами конденсатора, что возможно при уменьшении его электроёмкости. Значит, чем больше расстояние между пластинами конденсатора, тем меньше его электроёмкость
Если между обкладками конденсатора поместить пластину из диэлектрика, например, из стекла, то показания электрометра уменьшатся. Напряжение между обкладками в этом случае уменьшается, следовательно, электроёмкость конденсатора увеличивается
В СИ коэффициентом пропорциональности между электроёмкостью конденсатора и определяющими её величинами (S, d, 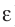
постоянная
Результаты экспериментов позволяют записать формулу для определения электроёмкости плоского конденсатора:
где S — площадь одной из обкладок конденсатора, d — расстояние между обкладками, 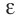
Зависимость электроёмкости конденсатора от расстояния между его пластинами используют в схемах кодирования клавиатуры персонального компьютера. Под каждой клавишей находится конденсатор, электроёмкость которого изменяется при нажатии на клавишу. Микросхема, подключённая к каждой клавише, при изменении электроёмкости выдаёт кодированный сигнал, соответствующий данной букве (рис. 114).
Условное изображение конденсатора постоянной электроёмкости на электрических схемах представлено на рисунке 115.
На схемах номинальную электроёмкость конденсаторов обычно указывают в микрофарадах и пикофарадах. Однако реальная электроёмкость конденсатора может значительно меняться в зависимости от многих факторов. Другой, не менее важной характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором его можно использовать в заданных условиях в течение срока службы. Это напряжение может находиться в пределах от нескольких вольт до нескольких сотен киловольт. Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. Для многих типов конденсаторов с увеличением температуры допустимое напряжение уменьшается.
Для получения нужной электроёмкости конденсаторы соединяют в батареи, используя их параллельное и последовательное соединение. При параллельном соединении (рис. 116) положительно заряженные обкладки конденсаторов соединяют в одну группу, а отрицательно заряженные — в другую. При таком соединении напряжение на всех конденсаторах одинаковое, но их заряды могут быть разными.
При параллельном соединении конденсаторов:
1) напряжение на полюсах батареи конденсаторов равно напряжению на каждом конденсаторе:
2) полный заряд батареи конденсаторов равен сумме зарядов отдельных конденсаторов
3) электроёмкость батареи конденсаторов равна сумме электроёмкостей отдельных конденсаторов:
Параллельное соединение конденсаторов применяют для получения большой электроёмкости.
При последовательном соединении (рис. 117) положительно заряженная обкладка предыдущего конденсатора соединена с отрицательно заряженной обкладкой последующего. При таком соединении модули зарядов на всех обкладках равны, а суммарный заряд соединённых друг с другом обкладок равен нулю.
При последовательном соединении конденсаторов:
1) напряжение на полюсах батареи конденсаторов равно сумме напряжений на отдельных конденсаторах:
2) заряд батареи конденсаторов равен заряду каждого конденсатора:
3) величина, обратная электроёмкости батареи, равна сумме величин, обратных электроёмкостям отдельных конденсаторов:
1. Электрическая ёмкость уединённого проводника — физическая скалярная величина, количественно характеризующая способность проводника накапливать электрический заряд и равная отношению заряда проводника к его потенциалу:
2. Электроёмкость проводника зависит только от его формы и размеров, а также от диэлектрической проницаемости среды, в которой этот проводник находится.
3. Электрической ёмкостью конденсатора называют физическую скалярную величину, количественно характеризующую способность
конденсатора накапливать электрические заряды и равную отношению заряда конденсатора к напряжению между его обкладками:
4. Электроёмкость плоского конденсатора зависит от площади обкладок, расстояния между ними и диэлектрической проницаемости среды, находящейся между обкладками:
Пример №8
Плоскому конденсатору электроёмкостью С = 0,4 мкФ сообщён электрический заряд q = 2 нКд. Определите модуль напряжённости электростатического поля между обкладками конденсатора, если расстояние между ними d- 5 мм.
Дано:
Решение. Модуль напряжённости однородного электростатического поля определим по формуле 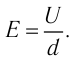
Ответ:
Пример №9
Пространство между обкладками плоского конденсатора заполнено диэлектриком. Конденсатор зарядили до напряжения 
Дано:
Решение.
В обоих случаях заряд конденсатора будет одинаковым 
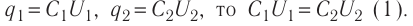
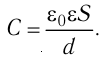
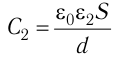
Ответ:
Энергия электростатического поля конденсатора
В процессе электризации тел внешние силы совершают работу по перераспределению зарядов между телами, преодолевая силы кулоновского притяжения при разделении отрицательных и положительных зарядов. Но всякое разделение зарядов приводит к возникновению электростатического поля. Это означает, что для создания электростатического поля системы заряженных тел необходимо совершить работу по перемещению зарядов между этими телами. Если в качестве таких тел рассматривать обкладки конденсатора, то процесс его зарядки можно представить как перенос заряда q с одной обкладки на другую, в результате чего одна из них приобретает заряд —q, а другая — +q. Работа, совершённая при этом внешними силами, равна энергии электростатического поля заряженного конденсатора.
Убедиться в том, что заряженный конденсатор обладает энергией, можно на опыте. Соберём электрическую цепь, состоящую из источника тока, конденсатора и электрической лампы (рис. 118). Зарядим конденсатор, подсоединив его к источнику тока. Затем, отключив конденсатор от источника тока, подсоединим его к лампе. При этом наблюдаем кратковременную вспышку света. В данном случае во время разрядки конденсатора его энергия превращается во внутреннюю энергию спирали лампы, часть этой энергии расходуется на излучение света.
При прохождении электрического тока по цепи конденсатор заряжался, т. е. на его обкладках накапливались электрические заряды. При этом в окружающем конденсатор пространстве возникло электростатическое поле. Суммарный электрический заряд обеих обкладок конденсатора до зарядки, во время зарядки и после разрядки равен нулю. Единственное изменение, которое произошло при разрядке конденсатора, заключается в том, что исчезло электростатическое поле, которое создавалось зарядами на обкладках конденсатора. Следовательно, энергией обладало электростатическое поле, образованное зарядами на обкладках заряженного конденсатора.
Если форма и размеры обкладок конденсатора, а также расстояние между ними и диэлектрические свойства среды, заполняющей пространство между обкладками, остаются неизменными, то напряжение на конденсаторе прямо пропорционально модулю
заряда его обкладок 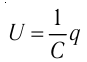
увеличить модуль заряда на обкладках от 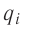
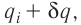
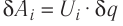
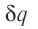
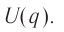
Приращение энергии электростатического поля заряженного конденсатора равно работе, совершённой внешней силой при его зарядке:
Учитывая, что q-CU, формулу для определения энергии электростатического поля заряженного конденсатора можно записать в виде
Энергию электростатического поля заряженного конденсатора можно выразить через напряжённость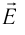
Электроёмкость плоского конденсатора 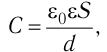
где V-Sd — объём пространства между обкладками конденсатора.
Применение конденсаторов
Конденсаторы находят широкое применение в электротехнике, радиотехнической и телевизионной аппаратуре, радиолокационной технике, телефонии, технике счётно-решающих устройств, лазерной технике, электроэнергетике (например, для улучшения коэффициента мощности промышленных установок, регулирования напряжения в распределительных сетях, в устройствах освещения люминесцентными лампами), металлопромышленности (например, для плавки и термической обработки металлов), добывающей промышленности (например, в электровзрывных устройствах), медицинской технике (например, в рентгеновской аппаратуре, приборах электротерапии), фототехнике (для получения вспышки света при фотографировании).
В связи с этим наряду с миниатюрными конденсаторами, имеющими массу менее грамма и размеры порядка нескольких миллиметров, существуют конденсаторы с массой в несколько тонн (рис. 121).
Энергию электростатического поля любого конденсатора можно определить но формулам
Пример №10
Плоский воздушный конденсатор, состоящий из двух обкладок площадью 5= 100 
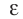
Дано:
Решение. Модуль заряда каждой из обкладок
конденсатора 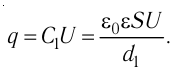
После отключения конденсатора от источника тока заряды на его обкладках не изменяются.
Энергию электростатического поля конденсатора после увеличения расстояния между его обкладками определим следующим образом:
Работа, которую необходимо совершить, чтобы увеличить расстояние между обкладками конденсатора, равна приращению энергии электростатического поля конденсатора:
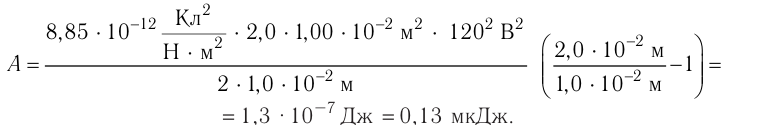
Электрический заряд и электрическое поле
Перераспределение зарядов в теле, вызываемое воздействием другого заряженного тела, называется электризацией через влияние или электростатической индукцией.
Существуют заряды двух видов: положительные и отрицательные. Элементарный заряд
Электрические явления известны с древних времен. Но только XX в. можно назвать «веком электричества». Вряд ли можно представить себе нашу жизнь без компьютеров, телевизоров, телефонов, светильников и различной бытовой техники.
Само слово «электричество» происходит от греческого названия янтаря 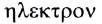
И янтарь, и линейка приобретают электрический заряд благодаря трению, т. е. происходит электризация трением. Но для электризации существенным является не столько трение, сколько контакт (соприкосновение) тел. Трение играет лишь вспомогательную роль. Благодаря ему достигается более тесный контакт, что приводит к более сильной электризации. Простейшим способом электризации является контактный, при котором заряженное и незаряженное тела приводят в соприкосновение. В результате часть заряда с заряженного тела переходит на незаряженное.
Следовательно, электрический заряд — это физическая скалярная величина, определяющая способность тел участвовать в электромагнитных взаимодействиях и их интенсивность.
Существующие два вида электрических зарядов в 1733 г. французский физик Шарль Франсуа Дюфе (1698 — 1739) назвал смоляным и стеклянным. «Я не сомневаюсь, что стекло и горный хрусталь ведут себя совершенно противоположно копаловой смоле, янтарю или испанскому воску» — писал он в мемуарах Парижской академии наук. Он отметил также, что «наэлектризованные тела отталкиваются теми телами, которые сообщили им электричество, но притягиваются некоторыми другими наэлектризованными телами». Это доказывают и эксперименты, которые Вы можете проделать сами. Если подвесить наэлектризованную линейку на нити и поднести к ней такую же наэлектризованную линейку, то они оттолкнутся (рис. 57, а, б). Если же заряды линеек различны, то они притягиваются друг к другу (рис. 57, в).
В 1750 г. американский ученый Бенджамин Франклин (1706—1790) разработал теорию электрических явлений. Основная идея этой теории: существует универсальная электрическая материя (субстанция), которая не наблюдается в нормальном состоянии тел. По терминологии Франклина тело, получившее избыток такой материи, например, в результате трения, оказывается заряженным положительно, а тело, потерявшее часть материи, — отрицательно. Он предложил считать заряды, возникающие на стекле, потертом о шелк, — положительными, а заряды, возникающие на поверхности эбонита, потертого о мех, — отрицательными. Одноименные заряды отталкиваются, а разноименные — притягиваются.
В обычных условиях тела содержат одинаковое количество положительных и отрицательных зарядов, т. е. они не заряжены, или электрически нейтральны. Тело можно наэлектризовать, т. е. создать на нем избыток или недостаток зарядов. Явление перераспределения зарядов между телами, называется электризацией, а тело, обладающее избытком или недостатком зарядов какого-либо знака, — наэлектризованным телом. Простейший способ электризации тел — электризация трением, при котором электризуются оба тела и притом разноименно. Например, при натирании янтаря тканью происходит разделение зарядов между ними, но сумма разделившихся зарядов равна нулю. Поэтому названия «положительный» и «отрицательный» следует понимать как знаки перед абсолютной величиной электрического заряда.
Явление электризации иллюстрирует один из фундаментальных законов природы — закон сохранения электрического заряда:
в любой замкнутой (электрически изолированной) системе алгебраическая сумма электрических зарядов остается постоянной при любых взаимодействиях внутри нее.
Этот закон справедлив как в макромире, например при зарядке конденсаторов, так и в микромире, например в ядерных реакциях и процессах взаимодействия элементарных частиц. Поэтому подобные законы называются фундаментальными.
Положительно и отрицательно заряженные частицы входят в состав всех атомов. Полный электрический заряд q системы равен алгебраической сумме ее положительных и отрицательных зарядов:
Для исследования заряженных тел используют модель точечного заряда. По аналогии с понятием материальной точки в механике точечным зарядом называется заряженное тело, размерами которого в условиях данной задачи можно пренебречь. Модель точечного заряда применима, если сила, действующая на заряженное тело, не зависит от его ориентации. Это условие выполняется, когда расстояние между заряженными телами велико по сравнению с их размерами и их формой и взаимной ориентацией можно пренебречь.
Эксперименты показывают, что ни у одного из заряженных тел не встречается заряд, который был бы по абсолютной величине меньше, чем заряд электрона. Поэтому абсолютное значение заряда электрона называют элементарным зарядом.
Носителями элементарных зарядов являются элементарные частицы: электроны (—е) и протоны (+е), которые входят в состав всех тел.
В СИ основной единицей заряда является кулон (1 Кл).
Один кулон — заряд, проходящий за одну секунду через поперечное сечение проводника, в котором проходит постоянный ток силой один ампер (1 Кл = 1 А • с).
1 Кл — очень большой заряд. Он в 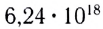
Название «протон» от греческого слова 
Для обнаружения электрического заряда используется электроскоп (рис. 58).
Он состоит из корпуса, внутри которого находятся два (или один) подвижных листочка. Листочки укреплены на металлическом стержне, который изолирован от корпуса и заканчивается металлическим шариком. Если поднести заряженный предмет близко к шарику, то листочки окажутся одноименно заряженными и оттолкнутся друг от друга. Чем больше заряд, тем больше расходятся листочки. Знак заряда таким образом определить невозможно.
Электроскоп можно использовать для определения знака заряда, предварительно сообщив ему какой-либо заряд известного знака, например отрицательный. Поднеся к шарику электроскопа отрицательно заряженное тело, мы увидим, что листочки раздвинутся больше. В случае положительно заряженного тела листочки электроскопа
сблизятся. В настоящее время для измерения величины электрического заряда используются чувствительные приборы — электрометры.
Если в каждой точке исследуемого пространства обнаруживается действие некоторой силы, причем это действие изменяется закономерно при переходе от одной точки к другой, то говорят, что в пространстве существует поле сил,
В случае, когда поле характеризуется векторными величинами (т. е. не только их модулями, по и направлениями), оно называется векторным.
Электрическим полем называют вид материи, посредством которого происходит взаимодействие электрических зарядов, т. с. поле играет роль передатчика взаимодействий между заряженными телами.
Понятие электрического поля было введено Майклом Фарадеем (1791 — 1867) в 30-х гг. XIX в. Согласно Фарадею, каждый заряд создает в окружающем пространстве электрическое поле. Поле одного заряда действует на другой заряд, и наоборот. Так осуществляется взаимодействие зарядов.
Свойства электрического поля:
- является материальным (обладает импульсом, энергией);
- порождается электрическим зарядом;
- обнаруживается по действию на заряд (действует на заряды с некоторой силой).
Поле, создаваемое неподвижными электрическими зарядами, называется электростатическим.
Раздел физики, в котором изучают свойства и взаимодействие неподвижных электрических зарядов и создаваемых ими электрических полей, называется электростатикой.
Классическая механика исходила из принципа дальнодействия. В соответствии с ним силу создает одно тело, которое мгновенно действует на другое удаленное тело.
В случае электромагнитного взаимодействия, как показало развитие науки, необходимо исходить из принципа близкодействия, при котором воздействие передается от одной точки к другой в окружающем пространстве. При этом необходимо учитывать конечную скорость передачи действия.
Электрическое иоле не является абстрактным понятием, введенным для удобства описания электрических взаимодействий. Оно представляет собой объективную реальность, особую форму материи, обладающую определенными физическими свойствами. При наличии в электрическом поле других зарядов оно взаимодействует с ними.
Электростатическое поле можно описать различными способами, например с помощью формул (аналитически), в виде таблиц, графически.
Помимо электростатического поля, порождаемого неподвижными зарядами, существует электрическое поле, порождаемое иными источниками, о которых речь пойдет в дальнейшем.
При изучении общих свойств этих нолей мы будем говорить об электрическом поле.
Любой технологический процесс, связанный с распылением, разделением, дроблением, смешиванием, перемещением ио трубам и т. п. различных диэлектрических материалов, сопровождается электризацией. В результате этого ежегодно в мире происходят сотни взрывов и пожаров на нефтяных базах, бензохранилищах, танкерах, самолетах, причиной которых является статическое электричество. Так, при заправке самолетов горючим разность потенциалов между Землей и горючим в топливных баках может достигать
160 000 В.
Закон Кулона
Радиус-вектор 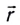
Закон всемирного тяготения: две материальные точки притягиваются друг к другу с силой, прямо пропорциональной произведению их масс, обратно пропорциональной квадрату расстояния между ними и направленной по прямой соединяющей эти точки:
Единицы в СИ: силы тока — ампер (1 А); силы — ньютон (1 Н). Масса электрона
В 1785 г. появились первые мемуары Шарля Огюстена Кулона (17.36—1806), в которых описывалось экспериментальное определение закона взаимодействия наэлектризованных тел. Прибор, которым пользовался Кулон для своих опытов, назывался крутильными весами (рис. 59).
Он состоял из подвижного коромысла ас длиной 21,7 см, подвешенного на тонкой серебряной нити диаметром 40 мкм длиной 75,8 см. На одном конце коромысла крепился шарик а диаметром 4,5—6 мм, а на втором — противовес с. Второй шарик b находился на неподвижном стержне, прикрепленном к крышке весов. В опытах измерялась сила отталкивания между одноименно заряженными шариками при различных расстояниях между ними.
На поверхность цилиндра, защищавшего всю систему от внешних воздействий, была нанесена шкала, позволявшая определять расстояние между шариками при их различных положениях. При зарядке шариков коромысло под действием силы отталкивания поворачивалось.
Для его возвращения в исходное положение необходимо было закрутить упругую нить в противоположную сторону на некоторый угол. По углу закручивания нити определялась сила взаимодействия заряженных шариков. Таким образом, удалось измерить силу отталкивания между одноименно заряженными шариками при различных расстояниях между ними.
При помощи крутильных весов Кулон установил количественный закон электростатического взаимодействия, называемый в настоящее время законом Кулона:
силы взаимодействия F двух точечных электрических зарядов в вакууме, покоящихся в данной инерциальной системе отсчета, прямо пропорциональны их величинам 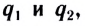
Здесь k — коэффициент пропорциональности (как видно из формулы,
в СИ 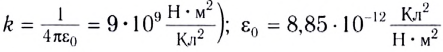
Формула (1) определяет модули сил, с которыми взаимодействуют заряды. Силы направлены по прямой линии, соединяющей заряды. Заряд 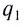
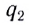
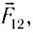
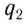
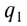
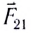
В соответствии с третьим законом Ньютона 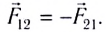
В векторном виде закон Кулона записывается так: 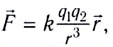
В аналогичном виде можно записать и закон всемирного тяготения с учетом того, что радиус-вектор 
Модуль силы взаимодействия F уменьшается, если заряды взаимодействуют не в вакууме, а в веществе (это изменение будет обсуждаться позже).
Наиболее простой вид законы взаимодействия заряженных тел имеют в случае точечных зарядов. Подчеркнем, что закон Кулона применим не только к взаимодействию точечных зарядов, но и к равномерно заряженным телам сферической формы независимо от величины расстояния между центрами сфер.
Справедливость закона Кулона подтверждена тщательными многочисленными экспериментами, и в настоящее время показатель степени при 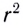
Первым закон взаимодействия неподвижных зарядов сформулировал английский физик Генри Кавендиш (1731 —1810) в 1773 г., но он редко публиковал свои исследования, поэтому большая часть его трудов осталась неопубликованной. Только в 1879 г. английский физик Дж. К. Максвелл, ознакомившись с хранившимися в Кембриджском университете неизданными рукописями Кавендиша, опубликовал его работы.
Напряженность электрического поля. Принцип суперпозиции электрических полей
Для количественной характеристики электрического поля вводят физическую векторную величину — напряженность электрического поля.
Исследуют электростатическое поле с помощью пробного заряда, который условились считать положительным. Под пробным понимается точечный заряд, собственное поле которого не изменяет механического состояния и распределения остальных зарядов, создающих исследуемое поле.
Внесем в электрическое иоле неподвижного точечного электрического заряда q пробный заряд 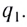
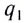
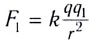
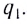
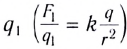
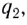
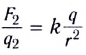
Эта величина обозначается буквой Е и называется модулем напряженности электрического поля. Напряженность поля является величиной векторной, так как получается посредством деления векторной величины — силы Кулона на скалярную величину — заряд. Поэтому можно дать следующее определение:
- напряженность электрического поля
векторная физическая величина, являющаяся силовой характеристикой электрического поля, определяется отношением силы, действующей со стороны поля на положительный точечный электрический заряд, находящийся в данной точке поля, к величине этого заряда:
В случае положительного заряда направления вектора напряженности электростатического поля и вектора силы совпадают, а в случае отрицательного заряда — противоположны.
Единицей напряженности электрического поля в СИ является ньютон на
кулон
Модуль напряженности Е электрического поля в данной точке пространства, находящейся на расстоянии r от точечного заряда q, может быть вычислен по
формуле
В векторном виде напряженность электростатического поля можно определить следующим образом:
где 
Таким образом, вектор напряженности определяется во всех точках пространства и зависит только от положения точки наблюдения, задаваемой радиус-вектором 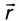
А можно ли определить напряженность электрического поля в точке, где находится сам заряд, т. е. при r = 0? Оказывается, напряженность поля в этой точке для точечного заряда не определена. Но в этом случае модель точечного
заряда не применима. Реальное заряженное тело обладает определенными размерами и формой, которые необходимо учитывать при нахождении напряженности электростатического поля. Если форма проводящего тела сферическая, то напряженность поля достаточно просто определяется везде.
Зная вектор 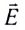
Часто в экспериментальных задачах напряженность электрического поля измеряется в большом числе точек, и результаты записываются в виде таблицы. Это еще один способ задания поля — табличный.
Гораздо нагляднее представлять поля графически. Этот способ придумал Майкл Фарадей в 1845 г. Он изображал электрическое поле с помощью силовых линий и получал своеобразные карты, или диаграммы, поля. Силовая линия — воображаемая направленная линия в пространстве, касательная к которой в каледой точке направлена вдоль вектора напряженности поля 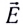
Условились считать, что силовые линии начинаются на положительных и оканчиваются на отрицательных зарядах (это следует из выбора знака пробного заряда). Линии могут начинаться на положительных зарядах и уходить в бесконечность (рис. 63, а) или приходить из бесконечности к отрицательному заряду (рис. 63, б).
Графическое изображение поля с помощью силовых линий наглядно показывает направление сил Кулона в каждой точке поля.
Кроме того, силовые линии проводят таким образом, чтобы их густота была пропорциональна модулю напряженности поля. А поскольку модуль напряженности электрического поля пропорционален заряду (E~q), то число линий, выходящих из заряда или входящих в него, пропорционально величине заряда. Там, где силовые линии расположены гуще, напряженность поля больше, и наоборот.
Силовые линии поля не могут пересекаться (рис. 64), так как в этом случае вектор напряженности поля в точке пересечения имел бы несколько различных направлений.
Силовые линии двух точечных разноименных и одноименных зарядов приведены на рисунках 65 а, б, 66 и 67 соответственно.
Подчеркнем, что если в случае одинаковых по модулю зарядов силовые линии симметричны (см. рис. 65), то при различных значениях зарядов это не так (рис. 68).
Эксперименты показывают, что напряженности электрических полей подчиняются принципу суперпозиции:
напряженность 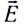
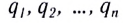
Рис. 65. Силовые линии электростатических нолей двух заряженных шариков: а — при разноименных зарядах; б — при одноименных зарядах
Принципы суперпозиции (от латинского слова superposition — добавление) устанавливают правила сложения физических величин одинаковой природы.
Принцип суперпозиции означает, что присутствие других точечных зарядов никак не сказывается на поле, создаваемом данным точечным зарядом, т. е. поля существуют независимо друг от друга.
Электрическое поле называется однородным, если в каждой его точке вектор напряженности 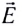
Примерами однородного электростатического поля являются:
- поле между двумя пластинами, заряды которых равны по модулю и противоположны по знаку (рис. 70, 71);
- поле равномерно заряженной бесконечной плоскости в вакууме (рис. 72).
Отметим, что у краев пластин существуют области краевых эффектов, в которых поля являются неоднородными.
Работа электростатического поля при перемещении заряда
Работа силы — это физическая скалярная величина, равная произведению модулей силы, перемещения и косинуса угла между направлениями силы и перемещения;
Единица работы в СИ — джоуль (1 Дж).
Внешние силы — это силы, действующие на тела системы со стороны тел, не входящих в исследуемую систему.
Внутренние силы в любой механической системе — это силы взаимодействия между телами, входящими в исследуемую систему.
Силы, работа которых не зависит от траектории, а определяется только начальным и конечным положениями тела в пространстве, называются потенциальными или консервативными.
Потенциальная энергия — это энергия взаимодействия тел. В поле силы тяжести для тела массой m, находящегося на высоте h над уровнем, выбранным за нулевой, она определяется по формуле 
Работа консервативных сил равна приращению потенциальной энергии, взятому с обратным знаком, или ее убыли:
На заряд q, помещенный в однородное электростатическое поле напряженностью 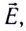
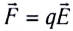
Поэтому при перемещении заряда вдоль отрезка АВ электростатическим полем будет совершена работа
где 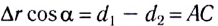
Рассмотрим теперь перемещение заряда по траектории АСВ. В этом случае работа однородного поля может быть вычислена как сумма работ по двум прямолинейным взаимно перпендикулярным участкам траектории:
Как видно, работа поля такая же, как и при перемещении заряда по отрезку АВ.
Наконец рассмотрим перемещение заряда между точками А и В по кривой АВ (рис. 74).
Его можно представить как совокупность n малых перемещений в виде ступенек. На этих малых участках кривой АВ работа совершается только
на участках, параллельных напряженности 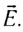
Если работа сил электростатического поля не зависит от траектории, то такое поле является потенциальным, или консервативным.
Следовательно, сила Кулона является консервативной, так же как и сила тяжести. Это следует и из сравнения формул закона Кулона и закона всемирного
тяготения:
Работу консервативных сил системы «заряд — поле» можно представить как разность потенциальных энергий в начале и в конце траектории:
где 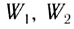
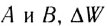
Напомним, что убыль физической величины 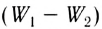
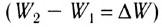
Как мы показали, потенциальная энергия заряда q в однородном электростатическом поле напряженностью 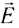
где d — расстояние от заряда до отрицательно заряженной пластины.
Таким образом, во всех разобранных примерах работа сил электростатического поля по перемещению заряда не зависит от траектории и равна изменению потенциальной энергии заряда в поле, взятому с противоположным знаком.
Аналогичное свойство имеет сила тяжести, работа которой также не зависит от траектории движения тела, а определяется только его начальным и конечным положениями.
Потенциал. Разность потенциалов. Напряжение. Принцип суперпозиции потенциалов
Электростатическое поле в каждой точке пространства можно описывать не только векторной силовой характеристикой — напряженностью 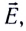
Потенциал электростатического поля 
Единицей потенциала в СИ является вольт: 1 В =
Один вольт — потенциал, создаваемый электростатическим полем в точке, в которой потенциальная энергия пробного заряда величиной один кулон равна одному джоулю.
Из определения потенциала 
Как было показано в предыдущем параграфе, работу сил электростатического поля по перемещению заряда q из произвольной точки 1 пространства в произвольную точку 2 (рис. 75) можно вычислить как
Если потенциал, создаваемый электростатическим полем в точке 1, равен 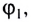
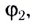
Таким образом, дня расчета работы сил электростатического поля по перемещению заряда q достаточно знать только разность потенциалов 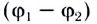
В электростатическом поле разность потенциалов называют еще электрическим напряжением и обозначают U.
Таким образом, под разностью потенциалов (электрическим напряжением) между двумя точками в пространстве понимают отношение работы сил электростатического поля по перемещению точечного заряда q из точки 1 в точку 2 к величине этого заряда:
Поскольку при вычислении работы сил поля необходимо знать только разность потенциалов, то выбирать нулевой уровень отсчета потенциала можно произвольно. Для удобства проведения расчетов часто за нулевой потенциал (уровень) выбирают потенциал поверхности Земли или проводника, соединенного с Землей. Такой проводник называют заземленным.
Заметим, что под действием сил электростатического поля свободный положительный точечный заряд будет перемещаться из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательный — наоборот.
Это различие объясняется тем, что силы, действующие со стороны поля на заряды различных знаков, имеют различные направления. В качестве механической аналогии движения положительного заряда в сторону убывания потенциала можно привести пример со скатывающимся с горы мячиком, который также движется в направлении «убывания» высоты горки (потенциальной энергии).
Если полагать, что в бесконечности поле отсутствует, т. е. потенциальная энергия находящегося там заряда равна нулю, то выражение для потенциала принимает вид
где 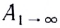
Таким образом, потенциал электростатического поля в данной точке пространства численно равен работе, которую совершают силы поля при перемещении единичного положительного точечного заряда из данной точки пространства в бесконечность.
Можно показать, что потенциал поля, создаваемого точечным зарядом q, в точке, находящейся в вакууме на расстоянии r от заряда, определяется по формуле
Следовательно, работа по перемещению заряда 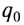
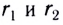
Рассмотрим систему, состоящую из n точечных зарядов, произвольным образом расположенных в пространстве. Для вычисления потенциала электростатического поля, создаваемого данной системой, в некоторой точке пространства используется принцип суперпозиции потенциалов:
потенциал 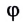
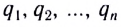
Знак потенциала 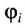
Потенциал любого изолированного проводника можно измерить, отсчитывая его от потенциала Земли. Сделать это можно с помощью прибора, называемого электрометром или электростатическим вольтметром.
Один из простейших электрометров — электрометр Брауна (рис. 76) — аналогичен по устройству обычному электроскопу. Для определения потенциала заряженного проводника необходимо соединить его со стержнем электрометра, а металлический корпус электрометра соединить с Землей.
Часть заряда перейдет на стержень электрометра и подвижную легкую стрелку, которая, отталкиваясь от стержня, отклонится на некоторый угол и укажет на шкале значение потенциала проводника относительно Земли.
Электрометр Брауна пригоден для измерения разностей потенциалов от 1 кВ до 10 кВ. Существуют более чувствительные электрометры (статические вольтметры), позволяющие измерять напряжения от 0,01 В до 0,1 В.
Эквипотенциальные поверхности. Связь между напряжением и напряженностью для однородного поля
Для графического изображения полей, кроме силовых линий электрического поля, удобно использовать эквипотенциальные поверхности, или поверхности равного потенциала:
Пересекаясь с плоскостью чертежа, эквипотенциальные поверхности дают эквипотенциальные линии.
Через каждую точку поля проходит только одна силовая линия и одна эквипотенциальная поверхность, причем в каждой точке поля силовая линия и
соответствующая эквипотенциальная поверхность взаимно перпендикулярны (рис. 77).
Докажем свойство перпендикулярности силовых линий и эквипотенциальных поверхностей методом «от противного». Для этого предположим, что справедливо обратное утверждение — перпендикулярность отсутствует. Тогда должен существовать компонент вектора напряженности 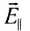
Следовательно, при перемещении заряда по эквипотенциальной поверхности эта сила будет совершать отличную от нуля работу. Но тогда согласно определению разности потенциалов 
Таким образом, применив метод «от противного», мы пришли к противоречию. Это значит, что истинно утверждение: при 
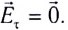
Начертив эквипотенциальные линии, соответствующие различным значениям потенциала, можно получить наглядное представление о том, как изменяется потенциал в данном поле (рис. 79, 80, 81).
В тех областях поля, где потенциал быстрее изменяется от точки к точке, эквипотенциальные поверхности расположены гуще. Модуль напряженности электростатического поля больше в точках, расположенных в таких областях.
Найдем связь между напряженностью 
Для этого вычислим работу сил поля двумя различными способами.
С одной стороны, при перемещении заряда q из точки 1 в точку 2 электрическим полем будет совершена работа
С учетом определения напряженности поля 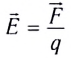
С другой стороны, работу сил поля можно определить через электрическое напряжение:
Приравнивая правые части соотношений (2) и (3), получим
Из соотношения (4) видно, что напряженность электрического поля можно измерять как в вольтах на метр, так и в ньютонах на кулон 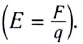
Поскольку двум соседним эквипотенциальным поверхностям соответствует одна и та же разность потенциалов 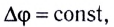
можно сделать вывод о том, что эквипотенциальные поверхности гуще там 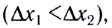
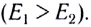
Во многих электрических установках используются очень высокие разности потенциалов — порядка 10—100 кВ (например, в кинескопе телевизора ~25 кВ).
При таких разностях потенциалов поля могут ионизировать воздух, т. е. поле «вырывает» электроны из атомов. Образуется большое число свободных заряженных частиц, и воздух становится проводником. Электрический пробой (искрение) сухого воздуха происходит при напряженности поля 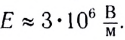
Формулы для напряжения позволяют также выражать работу и энергию во внесистемных энергетических величинах — электрон-вольтах, которые часто применяются при исследовании элементарных частиц, движущихся в электрических и магнитных полях.
Электрон-вольт — энергия, которую приобретет частица с зарядом, равным по модулю заряду электрона 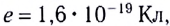
Проводники в электростатическом поле. Электростатическая защита
Электролиты — вещества, растворы или расплавы которых проводят электрический ток (кислоты, основания, соли); плазма — четвертое состояние вещества с высокой степенью ионизации его частиц; ион — атом (или группа атомов), потерявший или приобретший один или несколько электронов.
Проводники — вещества, по которым могут свободно перемещаться электрические заряды.
Проводниками являются металлы, электролиты, а также вещества, находящиеся в плазменном состоянии.
Термин «проводник» является переводом английского слова conductor, который ввел Ж-Т. Дезагюлье в 1739 г. для обозначения «тел, действующих как каналы для транспорта электрической силы».
В металлах носителями заряда являются свободные электроны (электроны проводимости), в электролитах — положительные и отрицательные ионы, в плазме — свободные электроны и ионы.
В отсутствие внешнего электростатического поля носители зарядов в проводнике находятся в равновесии. Если бы это условие не выполнялось, то свободные легкоподвижные заряженные частицы, имеющиеся в достаточном количестве во всяком проводнике, под действием сил поля пришли бы в движение, и равновесие было бы нарушено. Они двигались бы до тех пор, пока действующая на них сила не обратилась бы в нуль. Следовательно, напряженность электростатического поля в любой точке внутри проводника равна нулю. Это означает также, что потенциал проводника одинаков во всех его точках.
Незаряженный проводник содержит в себе в равных количествах положительные и отрицательные заряды. Во внешнем электростатическом поле в первоначально незаряженном проводнике происходит движение свободных зарядов; положительных по направлению приложенного поля, отрицательных — в противоположном направлении.
Полный заряд проводника в соответствии с законом сохранения электрического заряда, остается равным нулю, хотя на одной части поверхности проводника накапливаются положительные, а на другой — отрицательные заряды (рис. 83).
Такие заряды называют индуцированными.
Явление разделения разноименных зарядов в проводнике, помещенном в электрическое поле, называется электростатической индукцией. Возникшее разделение зарядов исчезает при отключении внешнего поля.
Явление электростатической индукции доказывает факт существования разноименных электрических зарядов в любом незаряженном проводнике.
В незаряженном проводнике, помещенном во внешнее электростатическое поле (создаваемое зарядами на других телах), происходит перераспределение свободных зарядов до тех пор, пока напряженность поля во всех точках внутри проводника не станет равной нулю.
Таким образом, условие 
Явление электростатической индукции позволяет осуществлять бесконтактное разделение зарядов (рис. 84) и получение заряда необходимого знака с помощью заземления (рис. 85).
Значок 
Рассмотрим проводник сферической формы. Будем считать, что он достаточно удален от других тел и от поверхности Земли. Его избыточный заряд будет распределяться по поверхности равномерно. Если заряд сферы q, а площадь поверхности S, то величина 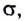
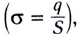
Модуль напряженности электростатического поля в вакууме у поверхности сферы радиусом R, равномерно заряженной с поверхностной плотностью 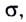
Внутри сферы E = 0, поскольку поля, создаваемые различными ее участками, компенсируют друг друга (рис. 86).
Когда форма проводника отличается от сферической, то распределение силовых линий вокруг него неравномерно (рис. 87).
Как показывают эксперименты, наибольшая плотность силовых линий (поверхностная плотность заряда) возникает на острых частях проводника, которые имеют наибольшую кривизну (наименьший радиус кривизны).
Если проводник имеет острие, то поверхностная плотность заряда на конце такого острия будет настолько велика, что под действием сильного электрического поля воздух вблизи острия будет ионизироваться. При этом молекулы воздуха «отнимают» заряды от острия и, зарядившись, устремляются от него вдоль силовых линий поля (если пренебречь массой молекул). Заряд проводника как бы «стекает» с острия по силовым линиям, образуя так называемый «электрический ветер».
Открытие разряжающих свойств металлического острия принадлежит Б. Франклину. Он же предложил использовать свойства острия для молниеотвода (громоотвода).
В силу этого обстоятельства проводник, имеющий острие, быстро теряет заряд. Для того чтобы заряд на изолированном проводнике мог достаточно долго сохраняться, проводник должен иметь «плавные» формы.
На явлении «электрического ветра» основано устройство молниеотвода. Во время грозы вблизи концов проводников возникает электрическое поле такой напряженности, что оно ионизирует окружающий воздух. Возникает «электрический ветер», «дующий» с острия молниеотвода навстречу заряженному грозовому облаку. Этот «ветер» разряжает облако и предотвращает попадание молнии в защищаемый объект. Иными словами, молниеотвод предотвращает разряд атмосферного электричества, а не «вызывает» его на себя. «Электрический ветер» используется в медицине для лечения кожи и внутренних органов.
По словам Б. Франклина, молниеотвод «…либо предотвращает удар молнии из ” облака, либо уже при ударе отводит его в землю без ущерба для здания».
На бюсте Б. Франклина вырезана надпись «Он отнял молнию у небес и власть у тиранов».
Первый молниеотвод в Европе в 1754 г. создал чешский ученый Прокопий Дивиш (1698— 1756).
Установлено, что наибольшая напряженность электрического поля в сухом воздухе при нормальном атмосферном давлении достигает 
Поле внутри проводника равно нулю. Так, например, если проводник заряжен отрицательно, то отрицательные заряды внутри проводника будут стремиться к его поверхности, чтобы расположиться как можно дальше друг от друга. Параллельная поверхности проводника составляющая вектора напряженности электрического поля отсутствует, иначе в проводнике возник бы электрический ток. Это означает, что внешнее электростатическое поле никаких «действий» во внутренних частях проводника произвести не может. Следовательно, замкнутая проводящая оболочка защищает все, что находится внутри нее, от действия внешнего электростатического поля (рис. 88).
Силовые линии внешнего электростатического поля заканчиваются на индуцированных зарядах, располагающихся только на поверхности проводника. Кроме того, у поверхности проводника силовые линии должны быть направлены перпендикулярно поверхности вследствие отсутствия составляющей вектора напряженности электрического поля, параллельной поверхности.
В этом и заключается принцип электростатической защиты: чувствительные приборы помещают внутрь проводящей оболочки, например металлической сетки, предотвращая таким образом влияние на них внешних электростатических полей.
Отметим, что проводящая оболочка экранирует только поле внешних зарядов. Если заряды находятся внутри оболочки, индуцированные заряды возникают и на ее внутренней поверхности. Поэтому замкнутая проводящая оболочка не экранирует поле электрических зарядов, помещенных внутри нее (рис. 89).
Диэлектрики в электрическом поле. Диэлектрическая проницаемость вещества
Вещество называется изотропным, если его свойства во всех направлениях одинаковы.
Диэлектрики (изоляторы) — вещества, в которых практически отсутствуют свободные носители зарядов. В таких веществах не может проходить электрический ток.
Диэлектриками являются все газы (неионизированные), ряд жидкостей (дистиллированная вода, спирт и др.) и твердых веществ (стекло, эбонит, фарфор, слюда, шелк и др.).
Термин «диэлектрик» происходит от греческого слова 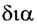
Этот термин введен М. Фарадеем в 1838 г. для обозначения веществ, в которые проникает электрическое поле.
Термин «изолятор» происходит от французского слова isoler — разобщать.
В диэлектриках, в отличие от проводников, свободные электрические заряды практически отсутствуют. Заряженные частицы внутри диэлектрика могут только незначительно смещаться относительно своих равновесных положений, что объясняет плохую электропроводность диэлектриков.
Диэлектрики все же незначительно проводят электрический ток, поскольку в них есть свободные носители тока, но их в 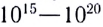
Существуют полярные и неполярные диэлектрики.
Неполярный диэлектрик состоит из атомов или молекул, у которых центры
распределения положительных и отрицательных зарядов совпадают. К таким диэлектрикам относятся, например, инертные газы, кислород, водород, бензол (рис. 90, а).
Полярный диэлектрик состоит из молекул, у которых центры распределения положительных и отрицательных зарядов не совпадают (рис. 90, б). Такие молекулы можно рассматривать как электрические диполи. Слово «диполь» происходит от двух греческих слов: 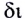
Векторная физическая величина, обозначаемая 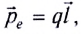
Полярными диэлектриками являются спирты, вода. Взаимодействие молекул полярного диэлектрика с заряженной палочкой представлено на рисунке 92.
Любой диэлектрик, как и проводник, электризуется при внесении его во внешнее электрическое поле. В неполярных диэлектриках центры разноименных зарядов молекул под действием внешнего электрического поля смещаются в противоположные стороны и молекулы превращаются в диполи (рис. 93).
В полярных диэлектриках на диполи будет действовать пара сил (например, 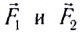
Вследствие того что заряды в атомах и молекулах связаны силами притяжения, во много раз большими, чем силы, действующие на эти же заряды во внешнем поле, они могут только немного сместиться под действием поля на расстояния порядка размеров самого атома. На поверхности диэлектрика возникают заряды. Их называют, в отличие от свободных, поляризационными или связанными. На ближайшей к заряженному телу части возникают заряды, разноименные с зарядом влияющего тела, а на удаленной части диэлектрика — одноименные. Явление смещения разноименных связанных зарядов в противоположные стороны под действием приложенного внешнего электростатического поля называется поляризацией.
Смещение поляризационных зарядов в диэлектрике приводит к возникновению дополнительного электрического поля 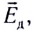
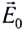
Напряженность результирующего поля 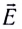
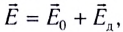
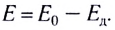
Уменьшение внешнего поля определяется способностью диэлектрика поляризоваться, и оно тем сильнее, чем больше поляризационных зарядов появится на поверхности диэлектрика.
Диэлектрическая проницаемость 
Попытка разделить диэлектрик на две части во внешнем поле не приводит к появлению разноименно заряженных тел, как это происходит с проводником. Особенности поляризации диэлектрика проявляются в том, что на противоположных сторонах каждой из частей появляются разноименные заряды.
После извлечения обеих частей диэлектрика из внешнего поля индуцированные связанные заряды исчезают.
Безразмерная физическая величина, равная отношению модуля напряженности 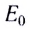
Диэлектрическая проницаемость показывает, во сколько раз напряженность электрического поля внутри однородного изотропного диэлектрика меньше, чем в вакууме. Диэлектрические проницаемости веществ приведены в таблице 2.
Таблица 2.
Диэлектрическая проницаемость некоторых веществ
При графическом изображении полей вне и внутри диэлектрика густота силовых линий внутри должна быть в 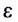
При расчете модулей кулоновской силы взаимодействия, напряженности поля и потенциала точечных зарядов необходимо учитывать ослабление электрического поля внутри диэлектрика и руководствоваться формулами, содержащими диэлектрическую проницаемость данной среды:
Сегнетоэлектрики — вещества, имеющие очень большую диэлектрическую проницаемость. Например, диэлектрическая проницаемость 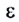
Сегнетоэлектрики широко используются в детекторах электромагнитных волн.
Электроемкость
Еще в середине XVIII в. считалось, что электричество — это особая жидкость, содержащаяся в любом заряженном теле. Наблюдавшееся с течением времени уменьшение заряда на телах трактовалось как «испарение» такой «электрической жидкости». Поэтому для уменьшения «испарения» (сохранения заряда) вполне естественно было поместить заряженное тело в какую-нибудь емкость. Как отголосок тех наивных представлений об электричестве в физике осталось слово электроемкость.
Чтобы разобраться со значением этого понятия, рассмотрим два проводника произвольной формы, находящиеся в однородном изотропном диэлектрике. Зарядим их равными разноименными зарядами +q и — q. При этом между проводниками установится некоторая разность потенциалов (напряжение):
Эксперимент показывает, что увеличение заряда каждого проводника, например, в 2 раза приводит к увеличению напряжения между ними также в 2 раза, т. е. отношение 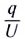
Физическую скалярную величину, определяемую данным отношением, обозначают С и называют электроемкостью. Она характеризует способность системы проводников накапливать электрический заряд.
Понятием электроемкости можно охарактеризовать и уединенный проводник, считая, что заряды противоположного знака при этом находятся в бесконечности. Рассмотрим уединенный заряженный проводник, находящийся в однородном изотропном диэлектрике в отсутствие внешних полей. Его потенциал (относительно бесконечности) пропорционален заряду:
Электроемкость уединенного проводника равна отношению заряда проводника к его потенциалу и является для данного проводника величиной постоянной:
Электроемкость определяется геометрической формой, размерами проводника и диэлектрической проницаемостью среды, в которой он находится. Она не зависит от вещества проводника, находящегося на нем заряда и его потенциала.
Определим электроемкость уединенного шара. При сообщении шару заряда q вокруг него возникает электрическое поле, такое же, как поле точечного заряда q. Поэтому потенциал шара относительно бесконечности будет
С другой стороны,
Получаем электроемкость уединенного шара радиусом /? в однородном ди-
электрике:
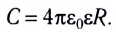
В СИ единицей электроемкости является фарад — это электроемкость уединенного проводника, потенциал которого увеличивается на один вольт при сообщении ему заряда один кулон
1Ф — это очень большая величина. Такой емкостью обладает в вакууме уединенный шар радиусом 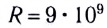
Конденсаторы
Для практического использования электрической энергии необходимо уметь ее накапливать. Эта задача решается с помощью конденсатора — специального электрического устройства. Конденсатор — устройство, состоящее из изолированных друг от друга проводников, предназначенное для накопления (аккумуляции) электрического заряда и энергии.
Проводники, образующие конденсатор, называются его обкладками. Как правило, при зарядке конденсатора заряды его обкладок равны по величине и противоположны по знаку. Под зарядом конденсатора понимают значение заряда положительно заряженной обкладки.
Термин «конденсатор» от латинского слова condensate — сгущать ввел A. Вольта в 1782 г.
Первые электрические конденсаторы были изготовлены Э. Клейстом и П. Ван Мушенбреком в 1745 г. По имени города Лейдена, где работал Мушенбрек, французский физик Жан Нолле назвал их лейденскими банками (рис. 96).
Плоским называется конденсатор, состоящий из двух параллельных металлических пластин (обкладок), расположенных на небольшом расстоянии друг от друга и разделенных слоем диэлектрика (рис. 97).
Электроемкостью (емкостью) конденсатора называется физическая скаляр
ная величина, равная отношению заряда конденсатора к разности потенциалов 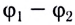
При использовании этой формулы предполагается, что расстояние ме>клу обкладками плоского конденсатора намного меньше их собственных размеров. Тогда внутри конденсатора электрическое поле однородное, а вне его равно нулю.
Электроемкость конденсатора зависит от его размеров и формы, а также свойств заполняющего его диэлектрика.
Найдем электроемкость плоского конденсатора. Внутри него электрическое поле складывается из полей положительно и отрицательно заряженных обкладок. Вследствие того что расстояние между обкладками намного меньше их размеров, поле внутри конденсатора можно найти согласно принципу суперпозиции полей, создаваемых равномерно заряженными бесконечными плоскостями, с учетом диэлектрической проницаемости заполняющего его вещества:
Исходя из определения поверхностной плотности заряда
находим
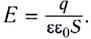
Искомое напряжение между обкладками
Следовательно,
где 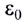
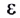
Емкость плоского конденсатора прямо пропорциональна площади его обкладок, диэлектрической проницаемости заполняющего его вещества и обратно пропорциональна расстоянию между пластинами.
Разность потенциалов между обкладками конденсатора нельзя повышать беспредельно, так как увеличиваются электрические силы, стремящиеся оторвать друг от друга разноименно заряженные части молекул диэлектрика. При некотором предельном для данного конденсатора значении разности потенциалов происходит разрушение диэлектрика. Заряды обкладок практически мгновенно нейтрализуются, т. е. происходит пробой конденсатора. Конденсатор при этом выходит из строя. Внешне пробой конденсатора часто проявляется в виде электрических искр, проходящих через диэлектрик. Таким образом, каждый конденсатор характеризуется максимальным рабочим напряжением, при превышении которого происходит его пробой.
В зависимости от используемого диэлектрика различают бумажные, воздушные, электролитические (рис. 98), керамические, слюдяные, полистирольные конденсаторы.
Кроме того, по используемому рабочему напряжению конденсаторы подразделяются на низковольтные и высоковольтные.
К низковольтным относятся электролитические и слюдяные конденсаторы с напряжением пробоя 100 В. Если напряжение пробоя превышает 100 В, то конденсаторы относятся к высоковольтным. Примером высоковольтного конденсатора, разность потенциалов в котором может быть доведена до 100 кВ, является лейденская банка.
На электрических схемах конденсатор обозначается символом
Соединения конденсаторов
В настоящее время практически ни одно электронное или радиотехническое устройство не обходится без конденсаторов.
Конденсаторы соединяют в батареи, чтобы обеспечить требуемую электроемкость при заданном напряжении. Соединение конденсаторов в батарее может быть параллельным, последовательным или смешанным.
При параллельном соединении конденсаторов (рис. 99) и подключении его к источнику напряжением 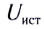
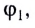
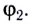
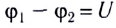
Напряжение U на обкладках всех конденсаторов одно и то же, т. е. U= 
Кроме того, знаки зарядов нижних обкладок конденсаторов одинаковы и противоположны знакам зарядов верхних обкладок, а суммарный заряд батареи q равен сумме зарядов на каждом из конденсаторов (см. рис. 99):
Разделив это выражение на U, получим
Следовательно, электроемкость батареи при параллельном соединении конденсаторов определяется по формуле
В случае, когда 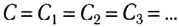
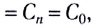
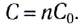
Параллельное соединение конденсаторов применяется для увеличения емкости системы, при этом
При последовательном соединении конденсаторов (рис. 100) и подключении его к источнику напряжением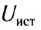
Если участок между конденсаторами 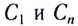
В результате одинаковым является заряд q каждого конденсатора, равный полному заряду батареи:
а напряжение батареи последовательно соединенных конденсаторов равно сумме напряжений на всех конденсаторах:
Если учесть, что 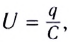
В случае, когда 
Таким образом, при последовательном соединении емкость батареи всегда не превышает наименьшую из емкостей конденсаторов, составляющих ее.
Последовательное соединение конденсаторов применяется для увеличения
предельного рабочего напряжения батареи, так как 
Энергия заряженного конденсатора. Энергия электрического поля
Работа, совершаемая внешними силами над системой, идет на увеличение ее энергии: 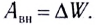
Заряженный конденсатор обладает энергией, которую можно рассматривать либо как потенциальную энергию взаимодействия зарядов, сосредоточенных на обкладках, либо как энергию создаваемого этими зарядами электрического поля, заключенного между обкладками конденсатора.
При зарядке конденсатора в нем создается электростатическое поле, при разрядке оно исчезает. Работа, совершенная внешним источником для зарядки конденсатора, идет на увеличение энергии поля, а работа при разрядке конденсатора совершается за счет уменьшения энергии поля. Можем сделать вывод, что электростатическое поле обладает определенным количеством потенциальной энергии.
Энергия заряженного конденсатора определяется работой, совершенной для его зарядки (способ зарядки на величину энергии не влияет), т. е. на перемещение заряда с одной обкладки на другую для создания заданного напряжения U на обкладках:
Работа А, совершаемая электрическим полем при разрядке конденсатора.
определяется площадью S треугольника ОАВ в предположении, что напряжение U па конденсаторе равномерно уменьшалось до нуля в процессе разрядки
(рис. 102):
Здесь 
Изменение энергии электрического поля равно работе, совершенной при разрядке конденсатора:
С учетом определения электроемкости 
Получим формулу для энергии плоского конденсатора аналитически, исходя из того, что для полной разрядки конденсатора необходимо совершить работу А, чтобы переместить электроны, создающие отрицательный заряд — q обкладки, на положительно заряженную обкладку. В результате электрическое поле исчезнет.
С одной стороны, если U — напряжение на обкладках конденсатора, 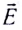
С другой стороны, работа электростатических сил совершается за счет убыли потенциальной энергии конденсатора:
В конденсаторе, напряженность поля внутри которого Е, заряд одной обкладки создает поле, модуль напряженности которого 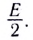
Потенциальная энергия этого заряда в поле конденсатора будет
Здесь d — расстояние между обкладками.
Вследствие того что напряжение U на обкладках конденсатора и модуль напряженности поля в нем связаны соотношением Е — Ud, энергия конденсатора определяется полученным ранее графически соотношением
С учетом выражения для электроемкости плоского конденсатора
и напряжения U = Ed получим 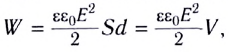
Таким образом, энергию плоского конденсатора можно рассчитать по формуле
Поле плоского конденсатора существует практически только внутри него — между обкладками. Тогда энергию заряженного конденсатора можно представить также как энергию поля, локализованного в пространстве между обкладками с плотностью энергии
Плотность энергии поля численно равна энергии поля, находящейся в единичном объеме:
Она пропорциональна квадрату напряженности электрического поля в этой
области. Это выражение справедливо не только для однородных полей, но и для электростатических полей любой конфигурации в случае, когда вещество, заполняющее пространство, изотропное.
Впервые понятие плотности энергии электрического поля ввел Дж. Максвелл. Он полагал, что энергия электрического поля рассредоточена по всему объему с плотностью 
Основные формулы электростатики
Закон сохранения электрического заряда:
Закон Кулона:
Напряженность электрического поля:
Принцип суперпозиции:
Работа сил электростатического поля:
Потенциал 
Потенциал 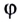
Разность потенциалов:
Диэлектрическая проницаемость вещества:
Электроемкость конденсатора:
Электроемкость плоского конденсатора:
Последовательное соединение конденсаторов:
Параллельное соединение конденсаторов:
Электроемкость уединенного проводника:
Энергия заряженного конденсатора:
Плотность энергии электростатического поля:
Элементарный заряд:
Электрическая постоянная:
Единицы измерения основных величин, встречающихся в электростатике
- Закон сохранения заряда в физике
- Электрическое поле заряженного шара
- Электрические явления в физике
- Потенциал поля точечного заряда в физике
- Тепловые двигатели и их КПД
- Тепловое состояние тел
- Изменение агрегатного состояния вещества
- Электродинамика
Задача. Два противоположных по знаку точечных заряда, модули которых равны, находятся в воздухе. В точке на прямой, соединяющей заряды, отстоящей на расстояния мм и
мм от зарядов, потенциал электростатического поля
мВ. Определите модуль напряжённости поля в этой точке.
Решение
Думаем: источником электростатического поля в задаче являются точечные заряды, тогда:
- для модуля напряжённости точечного заряда:
(1)
- для потенциала точечного заряда:
(2)
Т.к. зарядов несколько,, то для поиска общих параметров системы будем использовать принцип суперпозиции:
- для вектора напряжённости (вектор полной напряжённости равен векторной сумме напряжённостей, создаваемых каждым из зарядов):
(3)
- для потенциала (полный потенциал, создаваемый в точке равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в этой точке):
(4)
Решаем: для (1) и (2) нам необходимо визуализировать систему (рис. 1).
Рис. 1. Система зарядов
Для поиска полной напряжённости, создаваемой системой зарядов нам нужно визуализировать напряжённости, создаваемые каждым из зарядов, воспользоваться (3) и спроецировать результат на выбранную ось (рис. 2). Помним, что от положительного заряда линии напряжённости «уходят», к отрицательному «приходят».
Рис. 2. Напряжённости от каждого из зарядов
где — напряжённости, создаваемые положительным и отрицательным зарядами соответственно. Спроецируем вектора на выбранную ось OX:
(5)
Недостающие напряжённости можно найти исходя из (1):
(6)
(7)
Подставим (6) и (7) в (5):
(8)
Неизвестные значения зарядов можно получить исходя из последнего неиспользованного дано — общего потенциала (). Для поиск общего потенциала в точке воспользуемся (4):
(9)
где и
— потенциалы, создаваемые обоими зарядами в искомой точке. Найдём значение этих потенциалов исходя из (2):
(10)
(11)
Подставим (10) И (11) в (9):
(12)
Выразим недостающее из (12):
(13)
Подставим (13) в (8):
(14)
Считаем: не забываем перевести всё параметры в единицы СИ.
Н/м.
Ответ: Н/м.
Ещё задачи на тему «Потенциал электростатического поля»
1. Определение напряженности
Как вы уже знаете из курса физики основной школы, электрическое взаимодействие заряженных тел осуществляется посредством электрического поля: каждое заряженное тело создает вокруг себя электрическое поле, которое действует на другие заряженные тела. Представление об электрическом поле ввел английский ученый Майкл Фарадей в первой половине 19-го века.
Электрическое поле в данной точке пространства можно охарактеризовать с помощью силы, действующей со стороны этого поля на точечный заряд, помещенный в данную точку. (Этот заряд должен быть достаточно мал, чтобы создаваемое им поле не изменяло распределения зарядов, которые создают данное поле.)
Как показывает опыт, сила 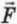
Напряженностью 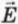
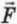
Напряженность поля – векторная величина. Ее направление в каждой точке совпадает с направлением силы, действующей на положительный заряд, помещенный в эту точку.
Единицей напряженности поля является 1 Н/Кл. 1 Н/Кл – небольшая напряженность. Например, напряженность электрического поля вблизи поверхности Земли, обусловленная электрическим зарядом Земли, составляет примерно 130 Н/Кл.
Если известна напряженность поля 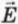
Из формул (1) и (2) следует, что направление напряженности поля в данной точке совпадает с направлением силы, действующей на положительный заряд, помещенный в эту точку.
Напряженность поля точечного заряда
Если внести в поле положительного точечного заряда Q другой положительный заряд, он будет отталкиваться от заряда Q.
Следовательно, напряженность поля положительного точечного заряда во всех точках пространства направлена от этого заряда. На рисунке 51.1 изображены векторы напряженности поля точечного заряда в некоторых точках. Видно, что при удалении от заряда модуль напряженности поля уменьшается.
? 1. Объясните, почему модуль напряженности поля точечного заряда Q на расстоянии r от заряда выражается формулой
Подсказка. Воспользуйтесь законом Кулона и определением напряженности поля.
? 2. Чему равна напряженность поля точечного заряда 2 нКл на расстоянии 2 м от него?
? 3. Модуль напряженности поля точечного заряда на расстоянии 0,5 м от него равен 90 Н/Кл. Чему может быть равен этот заряд?
Принцип суперпозиции полей
Если заряд находится в поле, созданном несколькими зарядами, то каждый из этих зарядов действует на данный заряд независимо от других.
Отсюда следует, что равнодействующая сил, действующих на данный заряд со стороны других зарядов, равна векторной сумме сил, действующих на данный заряд со стороны каждого из остальных зарядов.
Это означает, что справедлив принцип суперпозиции полей:
напряженность поля, созданного несколькими зарядами, равна векторной сумме напряженностей полей, созданных каждым из зарядов:
Используя принцип суперпозиции, можно найти напряженность поля, создаваемого несколькими зарядами.
? 4. Два точечных заряда расположены на расстоянии 60 см друг от друга. Модуль каждого заряда равен 8 нКл. Чему равен модуль напряженности поля, создаваемого этими зарядами:
а) в точке, расположенной на середине отрезка, соединяющего заряды, если заряды одноименные? разноименные?
б) в точке, находящейся на расстоянии 60 см от каждого заряда, если заряды одноименные? разноименные?
Для каждого из этих случаев сделайте в тетради чертеж, поясняющий решение.
2. Линии напряженности
На примере поля точечного заряда (рис. 51.1) можно заметить, что векторы напряженности электрического поля в разных точках пространства выстраиваются вдоль некоторых линий.
В случае точечного заряда эти линии представляют собой прямые лучи, проведенные из точки, в которой находится заряд. В поле, созданном несколькими зарядами, зти линии будут некоторыми кривыми, причем напряженность поля в каждой точке будет направлена по касательной к одной из таких линий.
Воображаемые линии, касательные к которым в каждой точке совпадают с направлением напряженности электрического поля, называют линиями напряженности электрического поля.
Линии напряженности начинаются на положительных зарядах и заканчиваются на отрицательных. Густота линий напряженности пропорциональна модулю напряженности.
? 5. Объясните, почему линии напряженности электрического поля не могут пересекаться.
Поля точечных зарядов
? 6. Объясните, почему линии напряженности электрического поля положительного и отрицательного точечных зарядов имеют вид, изображенный на рисунках 51.2, а и 51.2, б.
? 7. На рисунке 51.3 изображены линии напряженности поля, созданного одинаковыми по модулю зарядами (разноименными и одноименными). В некоторых точках для наглядности изображены векторы напряженности поля.
а) Перенесите рисунки в тетрадь и обозначьте на них знаки зарядов.
б) Изобразите в тетради линии напряженности поля, созданного двумя одноименными зарядами, которое не совпадает ни с одним из приведенных рисунков.
в) Чему равна напряженность поля в центральной точке рисунка 51.3, б (в середине отрезка, соединяющего заряды? Поясните ваш ответ с помощью закона Кулона.
Поле равномерно заряженной сферы
На рисунке 51.4 изображены линии напряженности электрического поля равномерно заряженной сферы.
Мы видим, что вне сферы зто поле совпадает с полем точечного заряда, ровного суммарному заряду сферы и расположенного в центре сферы.
Можно доказать, что внутри заряженной сферы напряженность поля ровна нулю. (Доказательство этого факта выходит за рамки нашего круга.)
? 8. На сфере радиусом 5 см находится заряд 6 нКл. Чему равна напряженность поля этого заряда:
а) в центре сферы?
б) на расстоянии 4 см от центра сферы?
в) на расстоянии 10 см от центра сферы?
г) вне сферы на расстоянии 1 см от ближайшей к этой точке поверхности сферы?
Однако напряженность электрического поля внутри заряженной сферы не обязательно равна нулю! Если внутри этой сферы находится заряженное тело, то согласно принципу суперпозиции напряженность электрического поля равна векторной сумме напряженности поля, создаваемого зарядом этого тела, и напряженности поля, создаваемого зарядом сферы.
Внутри сферы поле создается только заряженным телом, находящимся внутри сферы, потому что напряженность поля, созданного заряженной сферой, внутри сферы равна нулю. А в любой точке вне сферы напряженность поля можно найти, складывая векторы напряженности поля, создаваемого телом, расположенным внутри сферы, и поля, создаваемого зарядом сферы.
? 9. Имеются две концентрические (имеющие общий центр) сферы радиусом 5 см и 10 см. Заряд внутренней сферы равен 6 нКл, а заряд внешней сферы равен –9 нКл. Чему равен модуль напряженности поля в точке, находящейся от общего центра сфер на расстоянии, равном:
а) 3 см; б) 6 см; в) 8 см; г) 12 см; д) 20 см?
Поле равномерно заряженной плоскости
На рисунке 51.5 изображены линии напряженности электрического поля вблизи равномерно заряженной плоской пластины.
Будем считать, что размеры пластины намного больше расстояний от нее до тех точек пространства, в которых мы рассматриваем напряженность поля. В таких случаях говорят о поле равномерно заряженной плоскости.
Напряженность поля равномерно заряженной плоскости практически одинакова (по модулю и по направлению) во всех точках пространства по одну сторону от плоскости. Линии напряженности этого поля представляют собой параллельные прямые, перпендикулярные плоскости и расположенные на равных расстояниях друг от друга. Такое электрическое поле называют однородным.
По другую сторону плоскости изменяется только направление напряженности поля, а ее модуль остается таким же.
? 10. Напряженность электрического поля, создаваемого большой однородно заряженной пластиной, равна 900 Н/Кл. На расстоянии 40 см от пластины находится точечный заряд, равный по модулю 1 нКл.
а) На каком расстоянии от точечного заряда модуль напряженности его поля равен модулю напряженности поля пластины?
б) На каком расстоянии от плоскости результирующая напряженность поля плоскости и точечного заряда равна нулю, если знак точечного заряда совпадает со знаком заряда плоскости? Если знак точечного заряда противоположен знаку заряда плоскости?
Поле двух разноименно заряженных плоских пластин
Возьмем две одинаковые равномерно заряженные пластины, заряды которых равны по модулю, но противоположны по знаку. Расположим пластины параллельно друг друту на малом расстоянии друг от друга (рис. 51.6).
? 11. Объясните, почему в пространстве между пластинами напряженность поля в 2 раза больше, чем напряженность поля, создаваемого каждой из пластин, а вне пластин практически равна нулю.
Подсказка. Воспользуйтесь принципом суперпозиции электрических полей.
Как увидеть линии напряженности?
Поставим опыт
Поместим в электрическое поле состоящие из диэлектрика мелкие тела продолговатой формы – кристаллики, частицы манной крупы, мелко настриженные волосы и т. п. В электрическом поле они поворачиваются так, чтобы их более длинная сторона была направлена вдоль вектора напряженности поля. В результате эти тела выстраиваются вдоль линий напряженности, делая их форму видимой. На рисунке 51.7 приведены полученные таким образом «картины» электрических полей, создаваемых заряженным шариком (рис. 51.7, а) и двумя разноименно заряженными шариками (рис. 51.7, б).
Дополнительные вопросы и задания
12. Небольшой заряженный шарик массой 0,2 г подвешен на нити в однородном электрическом поле, напряженность которого направлена горизонтально и равна по модулю 50 кН/Кл.
а) Изобразите на чертеже положение равновесия шарика и силы, действующие на него.
б) Чему равен заряд шарика, если нить отклонена от вертикали на угол 30º?
13. Какова должна быть напряженность поля, чтобы капелька воды радиусом 0,01 мм находилась в этом поле в равновесии, потеряв 103 электронов? Как должна быть направлена напряженность поля?

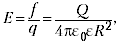
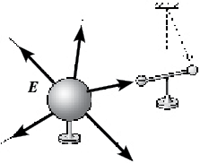
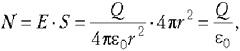
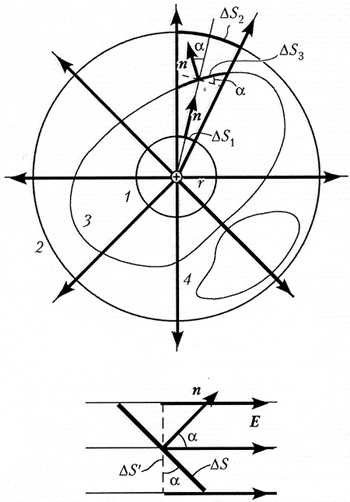
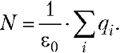
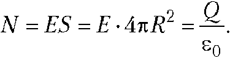
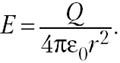
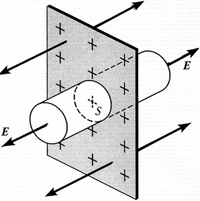
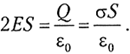
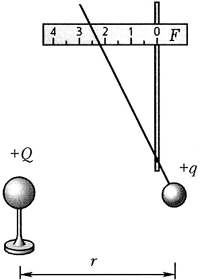
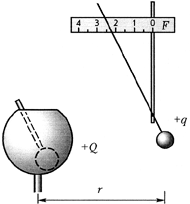
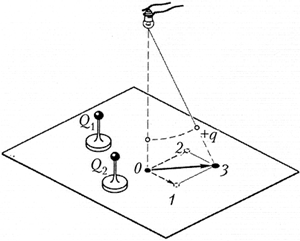


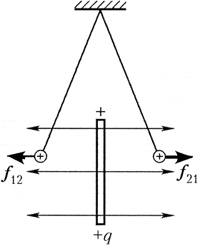
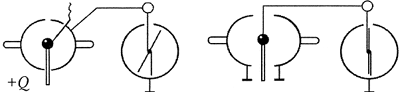
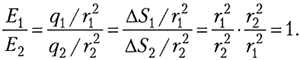
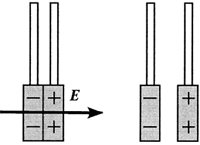
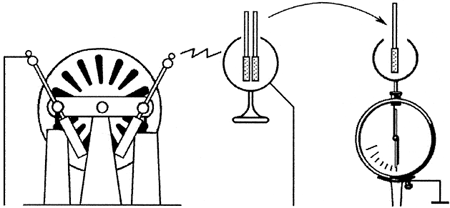
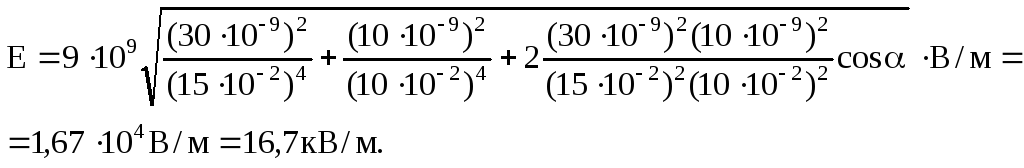
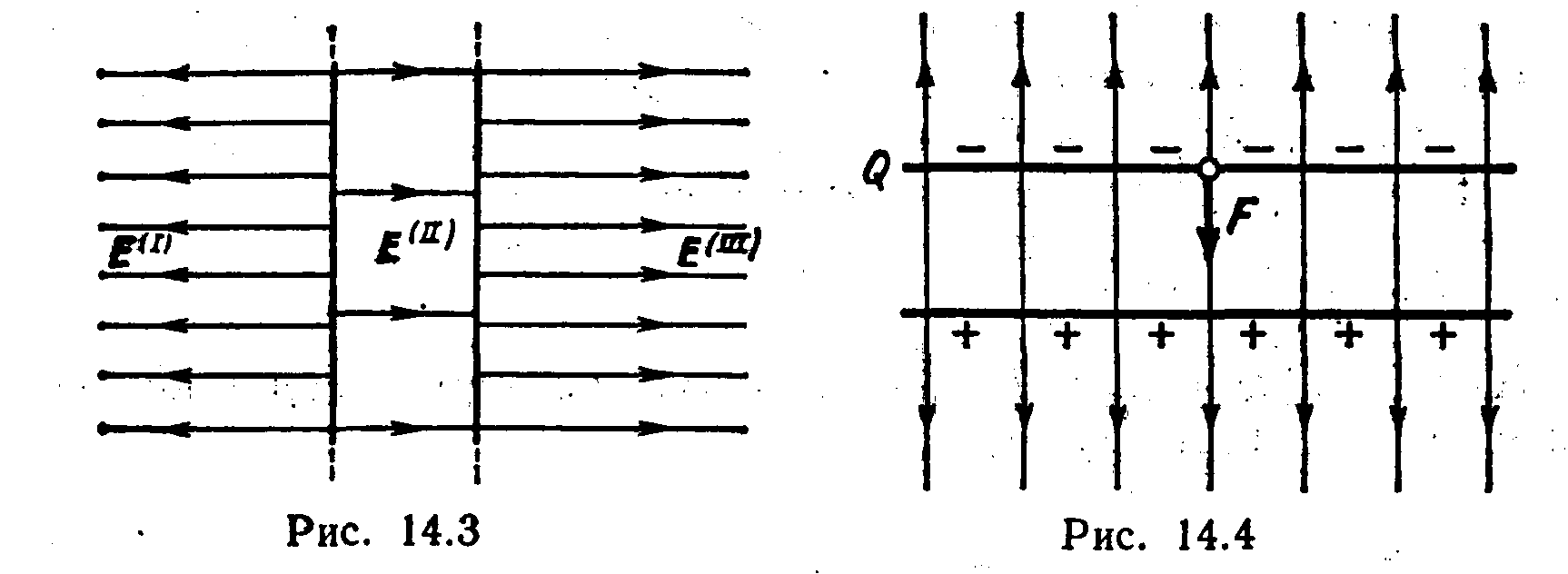
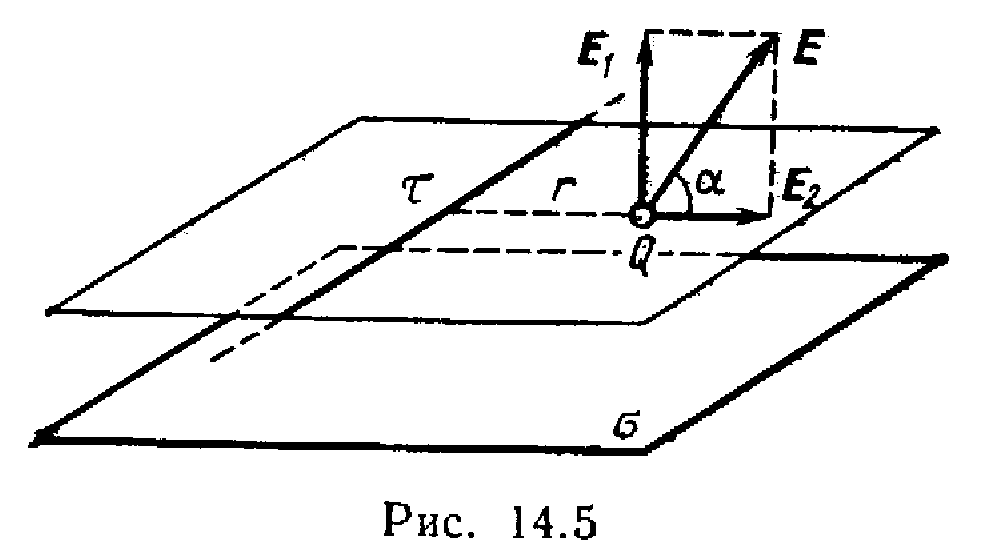
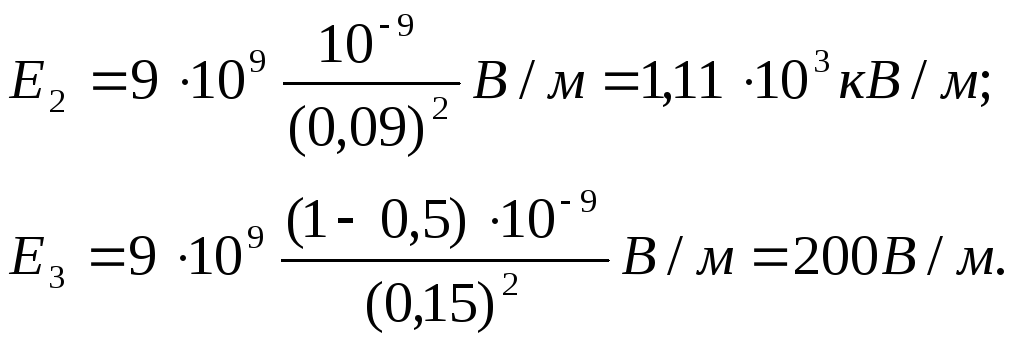
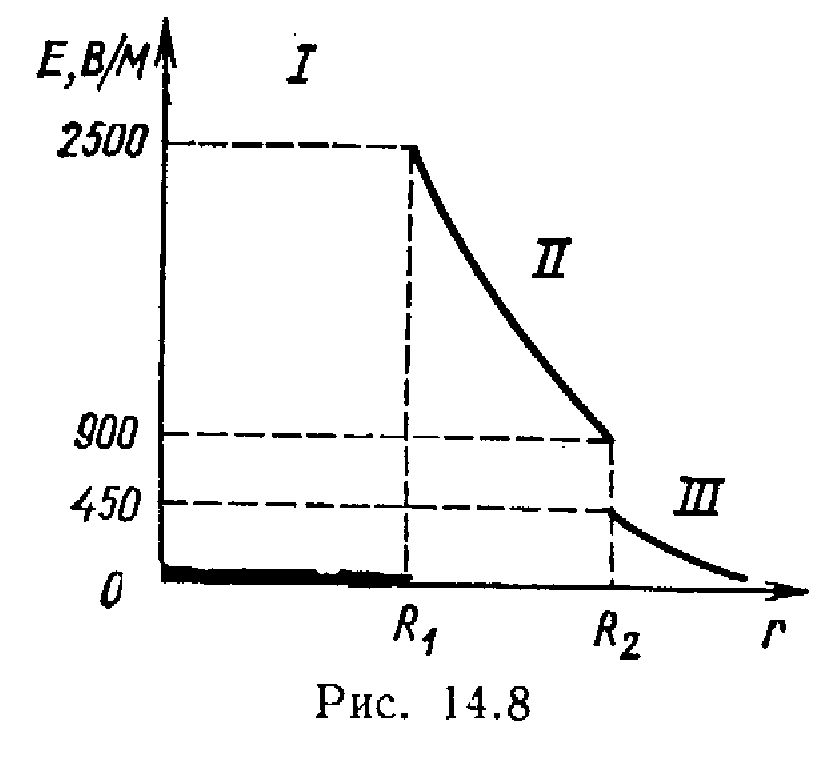
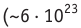
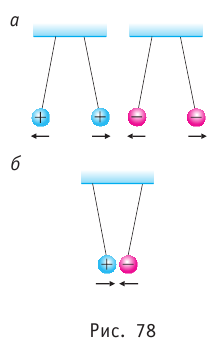
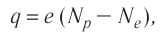
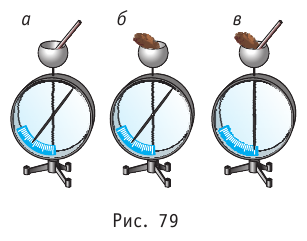

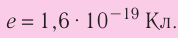

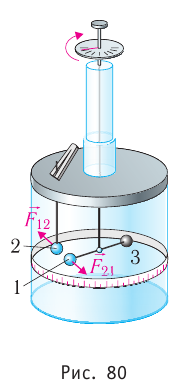
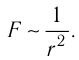
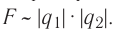
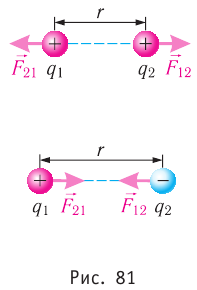
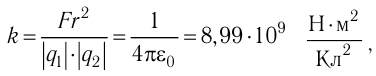
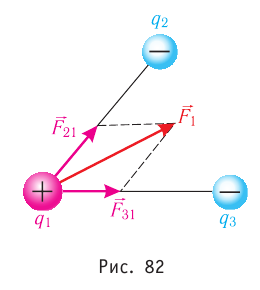
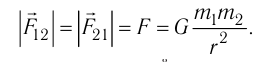
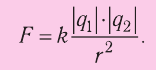
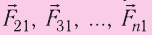 каждого из зарядов
каждого из зарядов 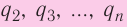 на заряд
на заряд 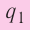 определяют по закону Кулона, а результирующую силу, действующую на заряд
определяют по закону Кулона, а результирующую силу, действующую на заряд 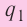 находят как векторную сумму сил, с которыми каждый из этих зарядов в отдельности воздействует на заряд
находят как векторную сумму сил, с которыми каждый из этих зарядов в отдельности воздействует на заряд 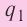 (принцип суперпозиции).
(принцип суперпозиции).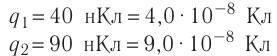

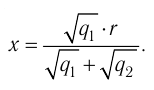
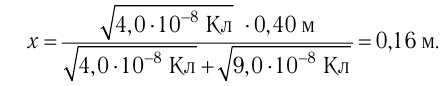
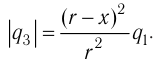
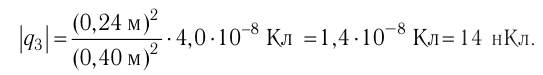
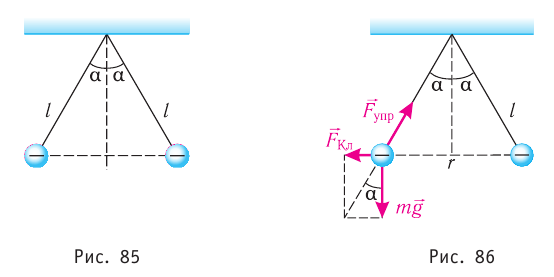
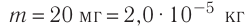

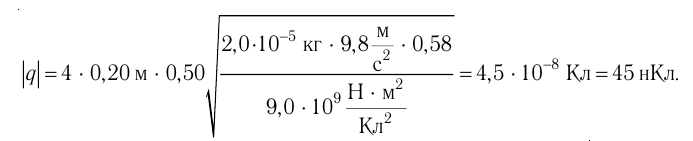
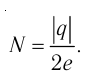
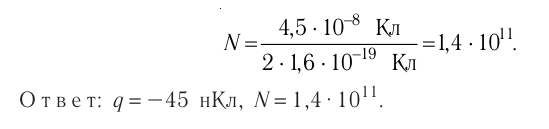
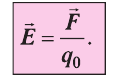
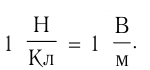
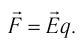
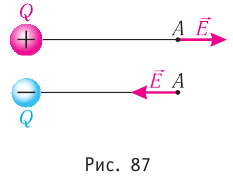
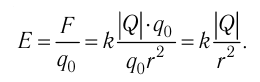
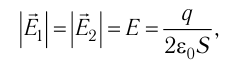
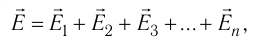
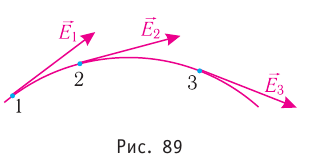
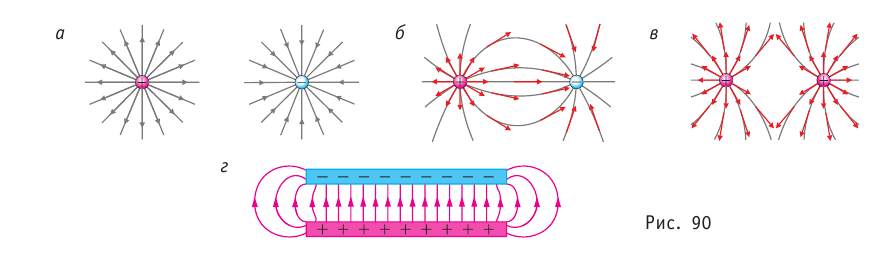
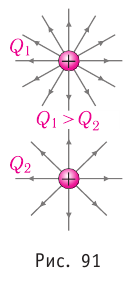
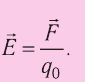
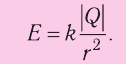
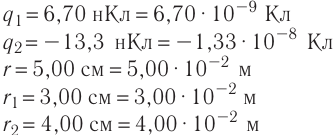

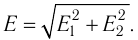
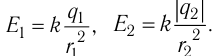
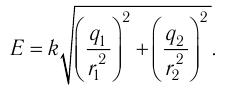
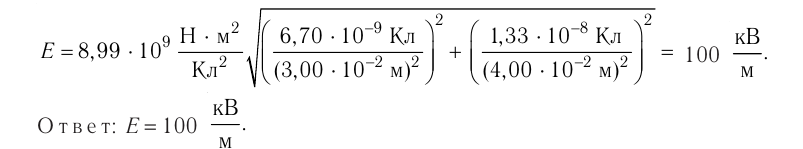
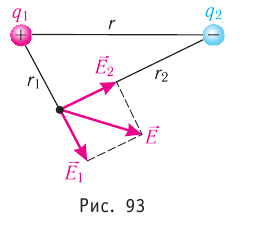
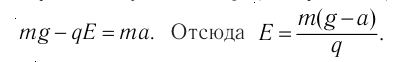
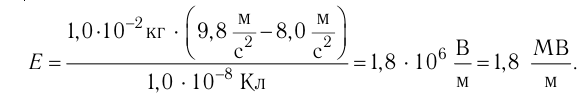
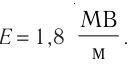
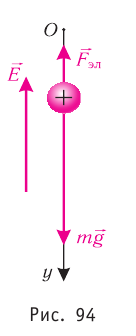

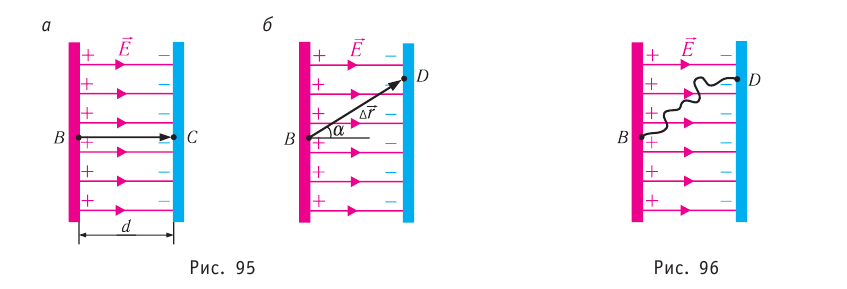
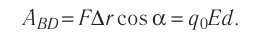
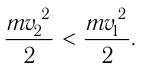
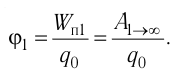
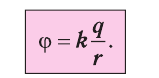
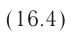
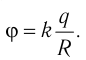
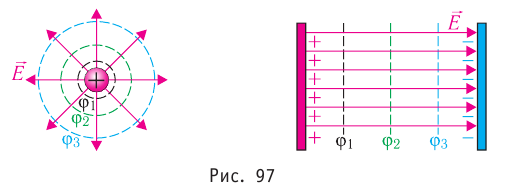
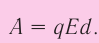
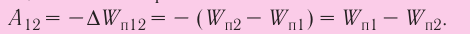
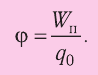
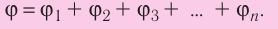
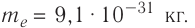
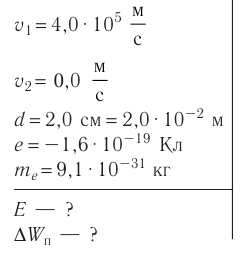
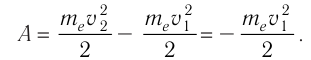



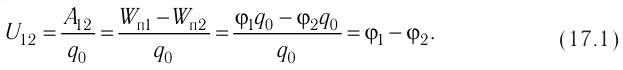
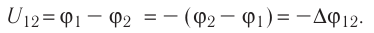
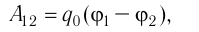
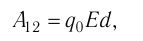
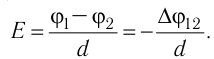
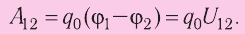
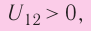 связаны между собой соотношением
связаны между собой соотношением 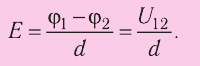
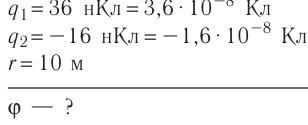
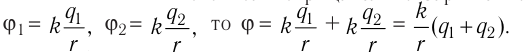
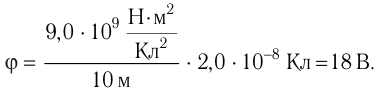
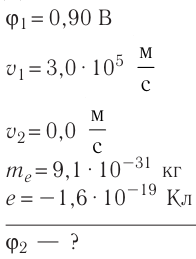

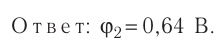
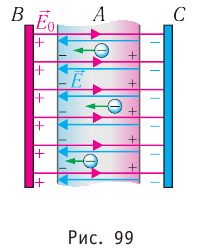
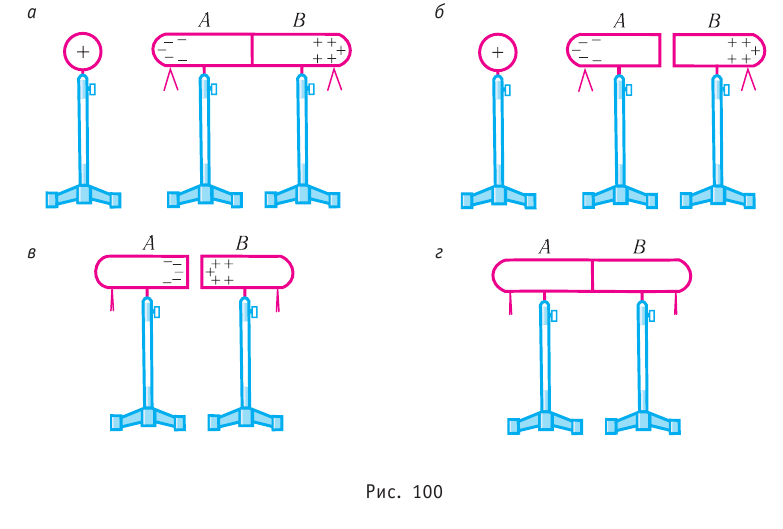
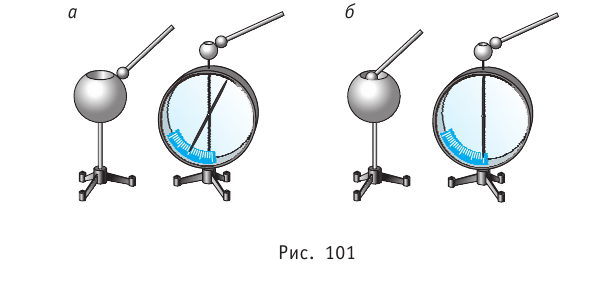
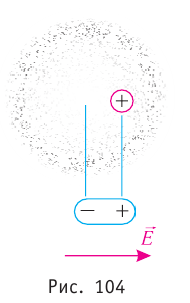
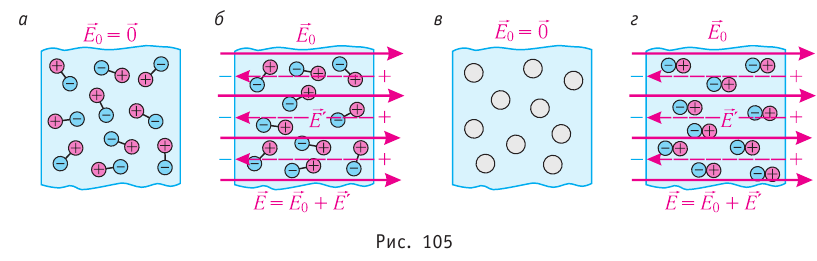
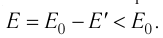
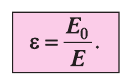
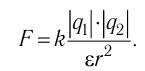

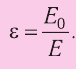
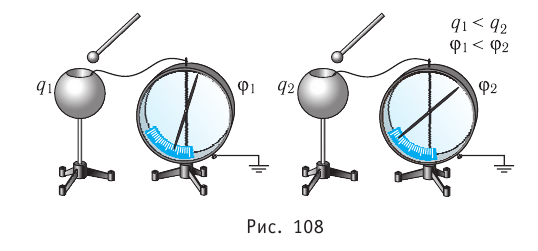
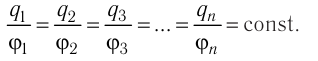
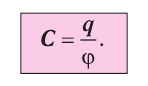
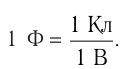
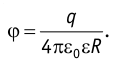
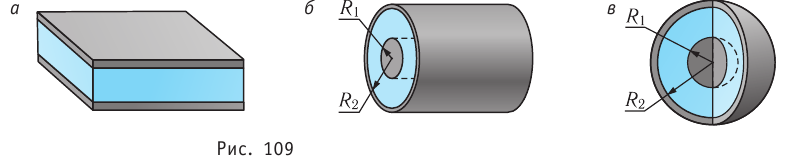
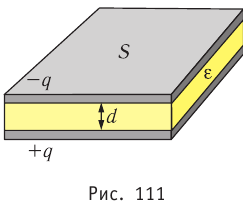
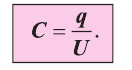
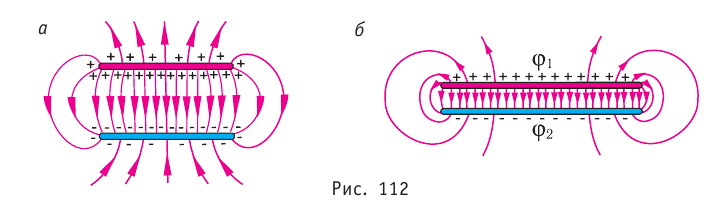
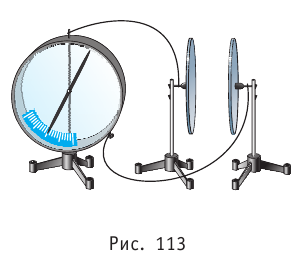
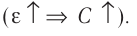
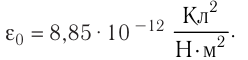
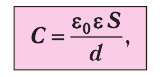
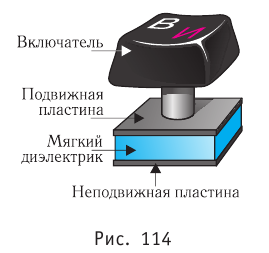
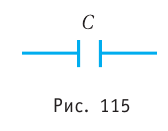
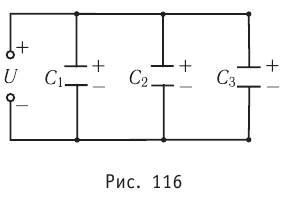
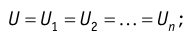
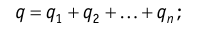
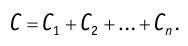
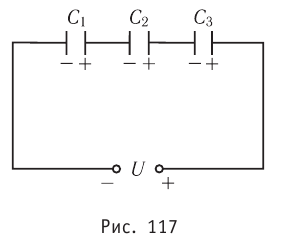
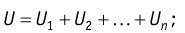
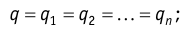
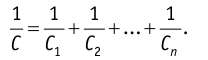
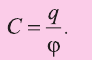
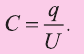
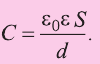
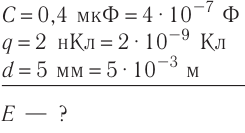
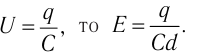
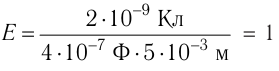
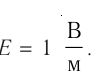
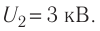
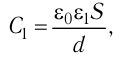
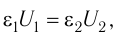
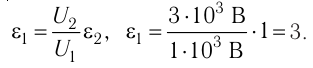
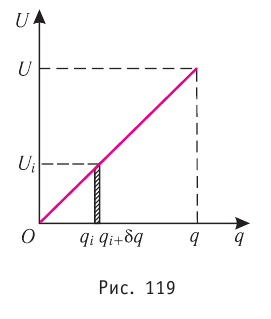
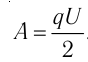
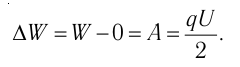
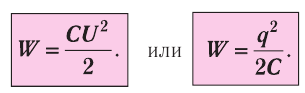
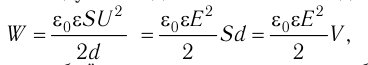
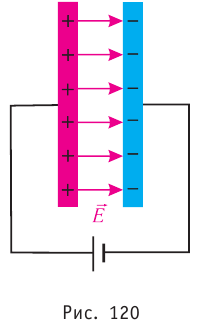

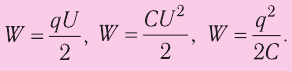
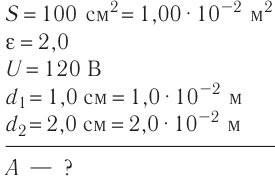
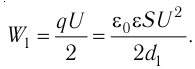
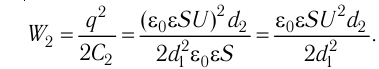
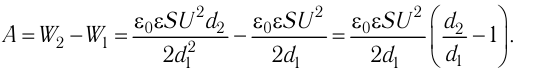
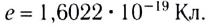
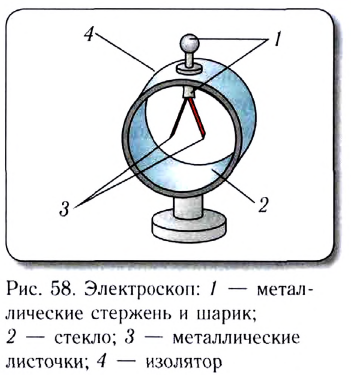
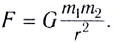
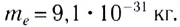
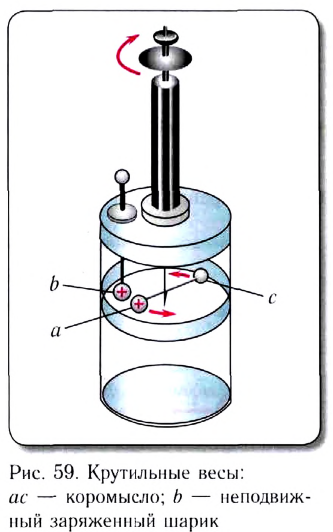

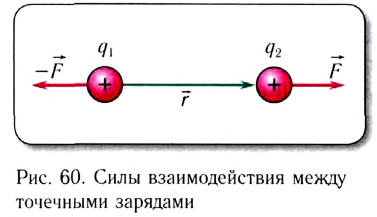
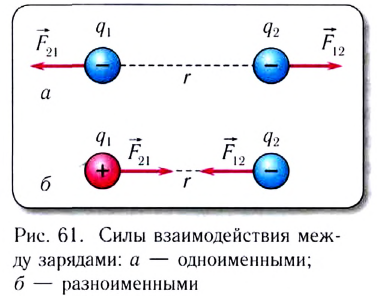
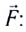
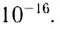
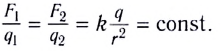
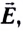 векторная физическая величина, являющаяся силовой характеристикой электрического поля, определяется отношением силы, действующей со стороны поля на положительный точечный электрический заряд, находящийся в данной точке поля, к величине этого заряда:
векторная физическая величина, являющаяся силовой характеристикой электрического поля, определяется отношением силы, действующей со стороны поля на положительный точечный электрический заряд, находящийся в данной точке поля, к величине этого заряда: