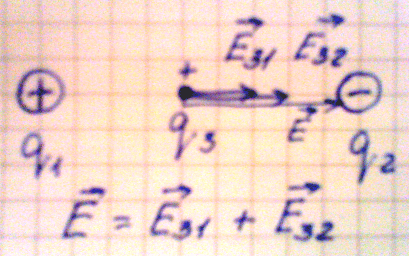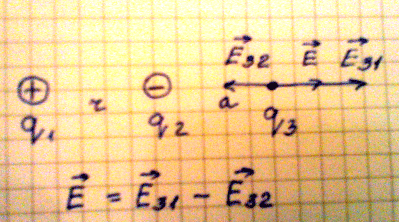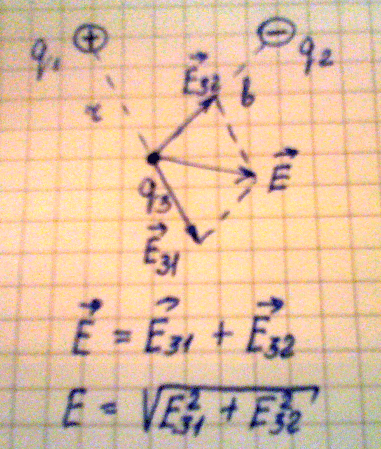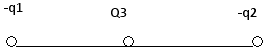Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.
Задачи урока:
- формирование понятия напряжённости электрического поля; дать понятие о
линиях напряжённости и графическое представление электрического поля; - научить учащихся применять формулу E=kq/r2 в решении
несложных задач на расчёт напряжённости.
Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.
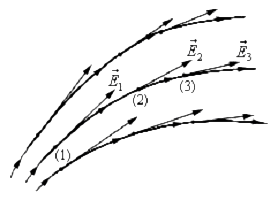
Графически изображая поле, следует помнить, что линии напряженности
электрического поля:
- нигде не пересекаются друг с другом;
- имеют начало на положительном заряде (или в бесконечности) и конец на
отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями; - между зарядами нигде не прерываются.
Рис.1
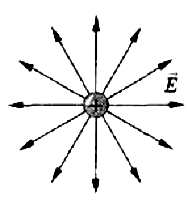
Силовые линии положительного заряда:
Рис.2
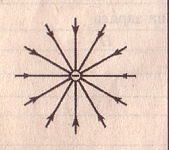
Силовые линии отрицательного заряда:
Рис.3
Силовые линии одноименных взаимодействующих зарядов:
Рис.4
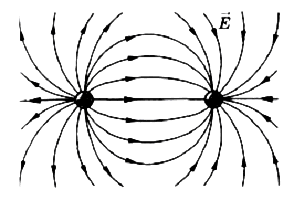
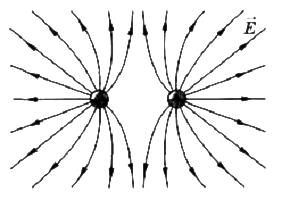
Силовые линии разноименных взаимодействующих зарядов:
Рис.5
Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
или
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда
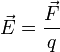
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда
где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.
В системе СИ
Н·м2/Кл2,
где ε0 – электрическая
постоянная, равная 8,85·10-12 Кл2/Н·м2;
q – электрический заряд (Кл);
r – расстояние от заряда до точки в которой определяется напряженность.
Направление вектора напряженности совпадает с направлением силы Кулона.
Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.
Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:
Рассмотрим несколько случаев определения напряженности.
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:
Е31 – напряженность точечного заряда 3 со стороны заряда 1;
Е32 – напряженность точечного заряда 3 со стороны заряда 2.
Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е31 и Е32.
Напряженность в данной точке определяется по формуле:
Е = kq1/x2 + kq2/(r – x)2
где: r – расстояние между первым и вторым зарядом;
х – расстояние между первым и точечным зарядом.
Рис.6
2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е31 и Е32.
Формула напряженности в данной точке равна:
Е = kq1/(r + a)2 – kq2/a2
Где: r – расстояние между взаимодействующими зарядами;
а – расстояние между вторым и точечным зарядом.
Рис.7
3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:
Е = (Е312 +Е322)1/2
Следовательно:
Е = ((kq1/r2 )2 + (kq2/b2)2)1/2
Рис.8
Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.
4. Закрепление темы.
Проверочная работа.
Вариант № 1.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: электрическое поле – это ….
3. Как направлены силовые линии напряженности данного заряда?
4. Определить знаки зарядов:
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Вариант № 2.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: напряженностью называется …
3. Как направлены силовые линии напряженности данного заряда?
4. Определить заряды.
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Задачи на дом:
1. Два заряда q1 = +3·10-7 Кл и q2 = −2·10-7
Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите
напряженность поля в точке С, расположенной на линии, соединяющей заряды, на
расстоянии 0,05 м вправо от заряда q2.
2. В некоторой точке поля на заряд 5·10-9 Кл действует сила 3·10-4
Н. Найти напряженность поля в этой точке и определите величину заряда,
создающего поле, если точка удалена от него на 0,1 м.
Краткая теория
Поле точечного заряда (закон Кулона)
$$
vec{E}(vec{r}) =qfrac{vec{r}-vec{r}_q}{|vec{r}-vec{r}_q|^3},
$$
где $q$ – заряд,
$vec{r}_q$ – радиус-вектор точки, в которой находится заряд,
$vec{r}$ – радиус-вектор точки, в которой вычисляется поле (точки наблюдения).
Если ввести обозначение $vec{R}=vec{r}-vec{r}_q$, то закон Кулона принимает вид
$$
vec{E}(vec{r}) =frac{q}{R^2}vec{e}_R.
$$
Потенциал поля точечного заряда
$$
varphi(vec{r}) =frac{q}{R}+rm{const}.
$$
Если система включает в себя несколько точечных зарядов, то поле в точке $vec{r}$ равно
$$
vec{E}(vec{r})=sum_i vec{E}_i(vec{r})=sum_i frac{q_i}{R^2_i}vec{e}_{Ri}; (принцип; суперпозиции),
$$
где $R_i=|vec{r}-vec{r}_{qi}|$.
В случае распределенной плотности заряда заряженную область можно мысленно разбить на малые части,
так что каждая малая часть будет рассматриваться как точечный заряд. Тогда, в соответствии с принципом суперпозиции,
потенциал в точке $vec{r}$ равен
begin{equation}label{Q_eq1}
varphi(vec{r})=intlimits_V frac{rho(vec{r}’)dV’}{left|vec{r}-vec{r}’right|}+
intlimits_S frac{sigma(vec{r}’)dS’}{left|vec{r}-vec{r}’right|}+
intlimits_{ell} frac{varkappa(vec{r}’)dell’}{left|vec{r}-vec{r}’right|},
end{equation}
где слагаемые отвечают зарядам, распределенным по объему, поверхности и линии соответственно.
В формуле eqref{Q_eq1} предполагается, что потенциал на бесконечности можно положить равным нулю.
Если это не так (например, в случае равномерно заряженной прямой), то формула eqref{Q_eq1} неприменима, поскольку
интеграл расходится. В этом случае потенциал рассчитывается решением уравнения Пуассона или интегрированием
напряженности $vec{E}(vec{r})$, которую можно найти каким-нибудь методом.
Пусть область $V$, ограниченная замкнутой поверхностью $S$, содержит полный заряд $Q$.
Тогда поток поля $vec{E}$ через поверхность $S$ описывается формулой, выражающей теорему Гаусса:
begin{equation}label{Q_eq2}
oiintlimits_S (vec{E}cdot dvec{S})=4pi Q,
end{equation}
где $dvec{S}$ – вектор, модуль которого равен площади элемента поверхности $dS$, а направление совпадает с направлением внешней нормали. Отметим, что заряд $Q$ предполагается распределенным внутри поверхности $S$. Если сама граница $S$ содержит поверхностный заряд и этот заряд включен в $Q$, то в качестве поверхности, через которую рассчитывается поток, следует выбрать такую, которая охватывает область $V$ вместе с $S$.
Если система обладает определенной симметрией, то в ряде случаев входящий в eqref{Q_eq2} интеграл переходит
в произведение поля $E_S$ в точках границы на площадь части поверхности $S$, откуда можно найти значение поля на границе области $V$.
Теорема Гаусса позволяет в случае симметричных заряженных систем легко, т. е. минуя интегрирование, находить величину поля в произвольной точке $vec{r}$. Для этого
нужно в качестве области $V$ выбрать подходящую пространственную фигуру. В случае сферической симметрии удобно
выбрать шар с центром в центре симметрии, в случае аксиальной симметрии – цилиндр с осью на оси симметрии.
Если система симметрична относительно плоскости, то в качестве $V$ удобно выбрать цилиндр, высота которого
перпендикулярна этой плоскости и делится ею пополам. Конкретные примеры разобраны в решении типовой задачи
Р9(а-в) из задачника [1].
Задача №586
| Найти электрическое поле $vec{E}(vec{r})$ внутри и снаружи заряженного шара радиуса $a$ с объёмной плотностью заряда $rho(r)=rho_0frac{r^3}{a^3}$. |
Показать решение
Задача №585
| Найти электрическое поле $vec{E}(vec{r})$ внутри и снаружи заряженного шара радиуса $a$ с объёмной плотностью заряда $rho(r)=rho_0frac{r^2}{a^2}$. |
Показать решение
Задача №584
| Отрезок длиной $a$ заряжен с линейной плотностью $varkappa(x)=frac{x}{a}varkappa_0$. Найти потенциал в точке O (см. рисунок). | |
Показать решение
Задача №583
| Тонкое кольцо радиуса $a$ заряжено с линейной плотностью $varkappa(alpha)=frac{alpha}{2pi}varkappa_0$. Найти потенциал на оси кольца как функцию $z$ (см. рисунок). | |
Показать решение
Задача №545
| Изолированная проводящая незаряженная сферическая оболочка радиуса $R_1$ помещена во внешнее, исходно однородное, электрическое поле $vec{E}_0$. В центре оболочки находится проводящий шар радиуса $R_2$ с зарядом $Q$. Найти распределение электрического потенциала $varphi$ во всем пространстве и распределение плотности заряда на внешней поверхности оболочки. |
|
Показать решение
Задача №544
| Изолированная проводящая незаряженная сферическая оболочка радиуса $R_1$ помещена во внешнее, исходно однородное, электрическое поле $vec{E}_0$. В центре оболочки находится непроводящий шар радиуса $R_2$, равномерно заряженный с объемной плотностью заряда $rho$. Найти распределение электрического потенциала $varphi$ во всем пространстве и распределение плотности заряда на внутренней поверхности оболочки. |
|
Показать решение
Задача №541
| На оси равномерно заряженного с поверхностной плотностью $sigma$ бесконечно длинного полуцилиндра расположена длинная нить, равномерно заряженная с линейной плотностью $varkappa$. Найти силу, действующую на единицу длины нити. |
|
Показать решение
Задача №540
| Найти силу, действующую на точечный заряд $q$, расположенный в центре полусферы, равномерно заряженной с поверхностной плотностью $sigma$. |
|
Показать решение
Задача №539
| На расстоянии $l$ от центра проводящей незаряженной сферы радиуса $R<l$ расположен точечный диполь с дипольным моментом $vec{d}$, ориентированным под углом $alpha$ к прямой OC (см. рис.). Найти потенциал в точке A, если потенциал на бесконечности равен нулю. |
|
Показать решение
Задача №538
| На расстоянии $l$ от центра проводящей незаряженной сферы радиуса $R<l$ расположен точечный диполь с дипольным моментом $vec{d}$, ориентированным под углом $alpha$ к прямой OC (см. рис.). Найти потенциал в точке A, если потенциал на бесконечности равен нулю. |
|
Показать решение
Задача №537
| В центре проводящей изолированной сферы радиуса $R$, несущей на себе полный заряд $Q$, находится точечный диполь с электрическим дипольным моментом $vec{d}$. Найти поле во всем пространстве и плотность заряда на внешней и внутренней границах сферы. | |
Показать решение
Задача №521
| Цилиндрический конденсатор с обкладками радиуса $a$ и $b$ заполнен диэлектриком, проницаемость которого меняется по закону $varepsilon(alpha)=varepsilon_0 (1+sin^2alpha)$. Найти емкость на единицу длины конденсатора. |
Показать решение
Задача №520
| Сферический конденсатор с обкладками радиуса $a$ и $b$ заполнен диэлектриком, проницаемость которого меняется по закону $varepsilon(theta)=varepsilon_0 (1+sin^2theta)$. Найти емкость конденсатора. |
Показать решение
Задача №492
| Четыре электрода расположены на горизонтальной границе проводящего полупространства с удельной проводимостью $sigma$ и диэлектрической проницаемостью $varepsilon$. В точках А и В подключён источник тока, а в точках М и N измеряется напряжение. Найти «кажущееся» сопротивление $R^*=U_{MN} /I_{AB}$, если AM=MN=NB=$l$ и лежат на одной прямой (схема Веннера, левый рис.). Что будет, если проводящее полупространство разделено вертикальной границей на две области с удельной проводимостью $sigma_1$ и $sigma_2$, диэлектрической проницаемостью $varepsilon_1$ и $varepsilon_2$ так, что электроды расположены вдоль границы раздела (правый рис)? Проверить ответ при $sigma_1=sigma_2=sigma$. |
|
Показать решение
Задача №487
| Бесконечная по координате y полоса $(z=0,, -bleqslant xleqslant b)$ однородно заряжена с поверхностной плотностью заряда $sigma$. Найти напряжённость электрического поля $vec{E}$ в точке $(0;0;a)$. |
|
Показать решение
Задача №486
| Бесконечная по координате $y$ полоса $(z=0,,, 0leqslant xleqslant b)$ однородно заряжена с поверхностной плотностью заряда $sigma$. Найти напряжённость электрического поля $vec{E}$ в точке $(-a;0;0)$. |
|
Показать решение
Задача №485
| Точечный заряд $q$ расположен внутри сферической полости в незаряженном проводящем шаре радиуса $a$. Найти плотность зарядов на внешней поверхности шара. |
|
Показать решение
Задача №484
| Бесконечно длинная тонкая нить, равномерно заряженная с линейной плотностью $varkappa$, протянута внутри цилиндрической полости в незаряженном проводящем бесконечно длинном цилиндре радиуса $a$. Оси нити, полости и цилиндра параллельны. Найти плотность зарядов на внешней поверхности цилиндра. |
|
Показать решение
Задача №472
| Кабель с постоянным напряжением на конце упал на землю. Электрик хочет определить место падения. Для этого в своей системе координат на поверхности земли он измеряет напряжение между точками O(0,0), A($a$,0) и B(0,$a$), которые равны соответственно $U_1 =varphi(A) — varphi(O)$, $U_2 =varphi(B) — varphi(O)$. Найти расстояние $r$ до точки падения кабеля и направление (угол $alpha$ от оси $x$), в системе координат электрика, если $аll r$, общий ток утечки $I$, а проводимость почвы в этой местности постоянна и равна $sigma$. Толщину проводящего слоя считать бесконечной. |
|
Показать решение
Задача №465
| На некотором расстоянии от плоской границы раздела двух диэлектриков с диэлектрическими проницаемостями $varepsilon_1$ и $varepsilon_2$ находится точечный заряд $q$ (в среде с проницаемостью $varepsilon_1$). Найти поток $Phi$ напряженности электрического поля $vec{E}$ через область границы (включая границу), имеющую форму круга с осью, проходящей через источник, и угловой радиус, видимый из источника, равный $theta$. |
|
Показать решение
Задача №458
| Шар радиуса $a$ заряжен с объёмной плотностью $rho(theta) = rho_0 cos theta$, где $theta$ – угол с осью $Oz$, проходящей через центр O шара. Найти электрическое поле $vec{E}(vec{r})$ во всём пространстве. |
Показать решение
Задача №457
| Двугранный угол образован проводящими плоскостями $y = 0,,x > 0$ и $x = 0,, y > 0$. Плоскости электрически изолированы вдоль соединяющего ребра, а между ними приложена разность потенциалов $U$. Внешняя часть двугранного угла заполнена средой с диэлектрической проницаемостью $varepsilon$. Найти поверхностную плотность свободного заряда $sigma (x), (x > 0)$ в плоскости $y = 0$. |
|
Показать решение
Задача №455
| Однородно заряженная с линейной плотностью заряда $varkappa$ нить согнута, как показано на рисунке (её изгиб образует четверть окружности радиуса $R$). Найти значение вектора напряженности электрического поля $vec{E}$ в центре этой дуги. |
|
Показать решение
Задача №454
| Однородно заряженная с линейной плотностью заряда $varkappa$ нить согнута, как показано на рисунке (её изгиб образует четверть окружности радиуса $R$). Найти значение вектора напряженности электрического поля $vec{E}$ в центре этой дуги. |
|
Показать решение
Задача №453
| Бесконечный плоский слой толщины $2a,, (-aleqslant zleqslant a)$ заряжен с объёмной плотностью заряда $rho(z)=rho_0sin (pi z/a)$. Найти напряжённость электрического поля $vec{E}(z)$ внутри и вне слоя. |
Показать решение
Задача №452
| Бесконечный плоский слой толщины $2a,, (-aleqslant zleqslant a)$ заряжен с объёмной плотностью заряда $rho(z)=rho_0frac{z}{a}$. Найти напряжённость электрического поля $vec{E}(z)$ внутри и вне слоя. |
Показать решение
Задача №422
| Оголенный конец изолированного провода, по которому течет ток $I$, погружен в проводящую жидкость, занимающую все пространство. Ток из провода растекается на бесконечность. На расстоянии $l$ от конца провода находится идеально проводящий $(sigma = infty)$ шар радиуса $R$ $(R < l)$. Найти объемную плотность тока $vec{j}(vec{r})$ в жидкости. |
|
Показать решение
Задача №421
| Найти плотность заряда $rho(z)$ в плоском конденсаторе с квадратными электродами размером $a times a$, расстоянием между пластинами $d ll a$, (см. рис.), разностью потенциала между пластинами $U$. Удельная проводимость материала между пластинами зависит от $z$ как $sigma(z)=sigma_0 e^{-alpha z}$. |
|
Показать решение
Задача №420
| Оголенный конец изолированного провода, по которому течет ток $I$, погружен в проводящую жидкость, занимающую сферическую полость радиуса $R$ внутри идеального проводника, и находится на расстоянии $l$ от центра сферической полости $(l < R)$. Ток из провода растекается на бесконечность. Найти объемную плотность тока $vec{j}(vec{r})$ во всем пространстве. |
|
Показать решение
Задача №415
| Определить емкость на единицу длины (погонную емкость) цилиндрического конденсатора, радиусы обкладок которого равны $a$ и $b$, соответственно $(a < b)$, а диэлектрическая проницаемость диэлектрика между ними зависит от расстояния до оси как $varepsilon(r)=frac{b}{r}tgfrac{r}{a}$. |
Показать решение
Задача №414
| В цилиндрической системе координат плотность заряда зависит от расстояния до оси координат как $$ left{ begin{array}{l} rho(r)=frac{a}{r}rho_0cosfrac{2pi r}{a},, при,, 0leqslant rleqslant a,\\ rho(r)=0,, при ,,r>a. end{array} right. $$ Найти напряженность электрического поля $vec{E}(r)$. |
Показать решение
Задача №413
| В сферической системе координат плотность заряда зависит от расстояния до центра координат как $$ left{ begin{array}{l} rho(r)=frac{a^2}{r^2}rho_0sinfrac{2pi r}{a}, при, 0leqslant rleqslant a,\\ rho(r)=0, при, r>a. end{array} right. $$ Найти напряженность электрического поля $vec{E}(r)$. |
Показать решение
Задача №412
| Кольцо радиуса $a$ заряжено с неоднородной линейной плотностью $varkappa = varkappa_0 |sin alpha|$, где $alpha$ – угол с осью Ox, проходящей по диаметру кольца. Найти электрическое поле E(x) на оси Ox. |
|
Показать решение
Задача №380
| Конец провода, по которому течет ток $I_0$, касается тонкой однородной проводящей поверхности, занимающей область $z = 0$, $xgeq 0$, $y geq 0$ в точке, равноудаленной на расстояние $a$ от ее краев. Найти распределение поверхностных токов $vec{i}(vec{r})$. |
|
Показать решение
Задача №379
| Конец провода, по которому течет ток $I_0$, касается полубесконечной тонкой однородной проводящей поверхности в точке, удаленной на расстояние $a$ от ее края. Найти распределение поверхностных токов $vec{i}(vec{r})$. | |
Показать решение
Задача №374
| Внутри проводящей заземленной сферы радиуса $R$ расположена дуга радиуса $a$ и углового размера $alpha$, заряженная с плотностью $varkappa$. Сфера и дуга имеют общий центр. Найти потенциал в центре сферы. |
|
Показать решение
Задача №373
| Снаружи от проводящей заземленной сферы радиуса $R$ расположена дуга радиуса $a$ с зарядом $Q$. Сфера и дуга имеют общий центр. Найти заряд, индуцированный на сфере. | |
Показать решение
Задача №368
| Непроводящая сфера радиуса $R$ заряжена поверхностным зарядом, распределенным по закону $sigma = sigma_0cdot cos theta$ (угол $theta$ отсчитывается от оси $z$). Центр сферы находится в начале координат – точке $O$. Найти поток электрического поля внутри сферы через плоскость $z = 0$. |
|
Показать решение
Задача №367
| Вычислить поток поля $vec{E}$ от точечного заряда $q$ через боковую поверхность конуса, показанного на рисунке. | |
Показать решение
Задача №366
| Дуга радиуса $R$ с угловым размером, показанным на рисунке ($alpha=60^{circ}$), равномерно заряжена с линейной плотностью заряда $varkappa$. Найти электрическое поле в центре координат (в точке O). | |
Показать решение
Задача №365
| Дуга радиуса $R$ с угловым размером, показанным на рисунке ($alpha=60^{circ}$), равномерно заряжена с линейной плотностью заряда $varkappa$. Найти электрическое поле в центре координат (в точке O). | |
Показать решение
Задача №331
| Тонкое круговое кольцо радиуса $a$ расположено в плоскости $xy$ и заряжено с линейной плотностью $varkappa(alpha)=varkappa_0+varkappa_1cosalpha$ (см. рис.). Найти первые два неисчезающих члена разложения потенциала $varphi(vec{r})$ вблизи начала координат $(rll a)$. Константу в выражении потенциала выбрать из условия $varphi(infty)=0$. |
|
Показать решение
Задача №321
| Точечный электрический диполь находится между двумя точечными зарядами $q_1$ и $q_2$ на расстоянии $r$ от каждого. Дипольный момент $vec{d}$ ориентирован вдоль прямой, соединяющей точечные заряды. Найти силу, действующую на диполь. | |
Показать решение
Задача №319
| Четыре одинаковых заряда $q$ размещены в углах квадрата со стороной $l$. Найти изменение потенциала $delta varphi(vec{r})$ на больших расстояниях, если в центр квадрата на одинаковом удалении от каждого из зарядов поместить незаряженную металлическую сферу радиуса $a$ $(rgg l>asqrt{2})$. |
|
Показать решение
Задача №318
| В углах квадрата со стороной $l$ находятся четыре заряда $q$, $-q$, $q$, и $-q$. В центр квадрата на одинаковом удалении от каждого из зарядов помещена незаряженная металлическая сфера радиуса $a$. Найти потенциал $varphi(vec{r})$ на больших расстояниях от этой системы ($rgg l>asqrt{2}$). | |
Показать решение
Задача №315
| Два заряда $q_1$ и $q_2$ расположены в точках с декартовыми координатами $(x_1,0,0)$ и $(0,y_2,0)$ соответственно. Найти величину заряда $q$ и декартовые координаты точки, в которую его нужно поместить, чтобы величина электрического поля на больших расстояниях от системы зарядов была как можно меньше. |
Показать решение
Задача №314
| Два заряда $q_1$ и $q_2$ расположены в точках с декартовыми координатами $(0,y_1,0)$ и $(x_2,0,0)$ соответственно. Найти величину заряда $q$ и декартовые координаты точки, в которую его нужно поместить, чтобы величина электрического поля на больших расстояниях от системы зарядов была как можно меньше. |
Показать решение
Задача №313
| Область шара, ограниченная телесным углом $Omega$ и радиусами $a$ и $b$ (см. рисунок), равномерно заряжена с объемной плотностью $rho$. Найти потенциал в точке O. Константу в выражении потенциала выбрать из условия $varphi(infty)=0$. |
|
Показать решение
Задача №312
| Сектор кольца углового размера $alpha$ и толщины $w$ (см. рисунок) равномерно заряжен с поверхностной плотностью $sigma$. Найти потенциал в точке O. Константу в выражении потенциала выбрать из условия $varphi(infty)=0$. |
|
Показать решение
Задача №309
| Точечные разноименные заряды $q_1$ и $-q_2$ разделены некоторым расстоянием. Найти потоки электрического поля, силовые линии которого (а) уходят на бесконечность и (б) замыкаются между двумя зарядами. |
Показать решение
Задача №265
| Точечные заряды $q_1$ и $q_2$ находятся на расстояниях $r_1$ и $r_2$ от центра заземленного металлического шара радиуса $a$. Какой заряд $Delta Q$ протечет через заземление на шар, если точечные заряды поменять местами? |
|
Показать решение
Задача №264
| Точечные заряды $q_1$ и $q_2$ находятся на расстояниях $r_1$ и $r_2$ от центра заземленного металлического шара радиуса $a$. Какой заряд $Delta Q$ стечет через заземление с шара, если точечные заряды поменять местами? |
|
Показать решение
Задача №261
| В центр бесконечного диэлектрического цилиндра радиуса $R$ с диэлектрической проницаемостью $varepsilon$ поместили бесконечную однородно заряженную нить с линейной плотностью заряда $varkappa$. Найти электрическое поле во всем пространстве и связанный заряд на единицу длины на границе цилиндра. |
Показать решение
Задача №260
| В центр диэлектрического шара радиуса $R$ с диэлектрической проницаемостью $varepsilon$ поместили точечный заряд $q$. Найти электрическое поле во всем пространстве и связанный заряд на границе шара. |
Показать решение
Задача №230
| Поток частиц зарядом $e$ с концентрацией $n$ падает со скоростью $v$ перпендикулярно бесконечной проводящей плоскости, покрывая круг радиуса $a$. Ток отводится по тонкому проводу, присоединенному на расстоянии $l$ от центра круга. Найти распределение поверхностных токов $vec{J}(vec{r})$ на плоскости. | |
Показать решение
Задача №222
| Две взаимно перпендикулярные нити расположены на расстоянии $a$ друг от друга (см. рис.) и заряжены равномерно с линейной плотностью $varkappa$. Определить силу кулоновского взаимодействия между ними. | |
Показать решение
Задача №220
| Проводник $A$ находится внутри замкнутой проводящей оболочки $B$. Прослойка такого конденсатора состоит из двух областей c границей раздела, образующей замкнутую поверхность (показана на рисунке пунктиром). Форма электродов и границы раздела произвольные. Диэлектрическая проницаемость и проводимость областей равны $varepsilon_1,, sigma_1$ и $varepsilon_2,, sigma_2$ соответственно. К электродам подано напряжение, такое, что от $A$ к $B$ течет постоянный ток $I$. Какой свободный заряд $Q$ накапливается при этом на границе раздела? |
|
Показать решение
Задача №216
| Пространство с $x<0,, y<0,, z<0$ заполнено диэлектриком с диэлектрической проницаемостью $varepsilon_1$. Остальное пространство заполнено диэлектриком с диэлектрической проницаемостью $varepsilon_2$. В начало координат поместили точечный заряд $q$. Найти потенциал и напряженность электрического поля во всем пространстве. |
Показать решение
Задача №215
| Концентрические сферы радиусов $a$ и $b$ заряжены равномерно по поверхности суммарными зарядами $q_a$ и $q_b$ соответственно. Найти поле $vec{E}(vec{r})$ и потенциал $varphi(vec{r})$ во всем пространстве. |
|
Показать решение
Задача №214
| Два соосных цилиндра с радиусами $a$ и $b$ заряжены равномерно по поверхности с погонной плотностью заряда $varkappa_a$ и $varkappa_b$ соответственно. Считая длины цилиндров бесконечными, найти распределение поля $vec{E}$ и потенциала $varphi$ во всем пространстве. Потенциал поверхности $r=b$ принять равным нулю. |
|
Показать решение
Задача №211
| Бесконечная вдоль оси $y$ полоса шириной $d, (-dleqslant xleqslant 0)$ (см. рис.) однородно заряжена с поверхностной плотностью заряда $sigma$. Найти напряженность электрического поля в точке с координатами $(a,0,0)$. |
|
Показать решение
Задача №210
| В вершине бесконечного конуса с углом раствора $2theta_0$ расположен заряд $q$. Внутренняя часть конуса заполнена диэлектриком с диэлектрической проницаемостью $varepsilon_1$, остальная часть пространства заполнена диэлектриком с проницаемостью $varepsilon_2$. Найти потенциал и электрическое поле во всем пространстве. |
|
Показать решение
Задача №180
| Точечный заряд $q$ помещен на плоскую границу полупространств с диэлектрической проницаемостью $varepsilon_1$ и $varepsilon_1$ и проводимостью $sigma_1$ и $sigma_2$ соответственно. Пренебрегая влиянием магнитного поля, найти зависимость заряда от времени $q(t)$, если $q(0)=q_0$. |
|
Показать решение
Задача №177
| Тонкий прямой очень длинный стержень заряжен однородно с линейной плотностью $varkappa$. Стержень лежит на оси $z$ и занимает отрицательную ее часть. Определить вектор напряженности электрического поля на расстоянии $R$ от стержня в плоскости $z=0$ (2 б). Вычислить поток электрического поля через полусферу радиуса $R$ с центром на конце стержня (см. рисунок) (2 б). |
|
Показать решение
Задача №157
| Два проводящих тела произвольной формы, одно из которых находится в полости другого, заряжены зарядами $q_1$ и $q_2$, при этом их потенциалы равны $V_1$ и $V_2$ соответственно. Найти потенциал тел $V$ после их соединения проводящим стержнем. (3 б) |
|
Показать решение
Задача №153
| Оголенный конец изолированного провода оказался в морской воде (то есть проводящей среде) на глубине $h$ от поверхности моря, как показано на рисунке. В результате из провода в воду потек ток $I$. Проводимость верхнего полупространства (воздуха) считать равной нулю. Найти объемную плотность тока в воде вблизи поверхности, т.е. $vec{j}(r)$ при $z=0$, $r$ – расстояние до оси $z$. (Подсказка — воспользуйтесь методом изображения). |
|
Показать решение
Задача №152
| Найти сопротивление цилиндрического конденсатора. Радиусы внутренней и внешней обкладок $a$ и $b$, длина $lgg a,b$. Краевыми эффектами можно пренебречь. Конденсатор заполнен проводниками с проводимостями $sigma_1$ и $sigma_2$, как показано на рисунке. |
|
Показать решение
Задача №148
| Заряд $q$ расположен в вершине куба, как показано на рисунке. Найти поток вектора напряженности электрического поля через заштрихованную грань куба. |
|
Показать решение
Задача №147
| Найти силу, с которой точечный заряд $q$ действует на полубесконечную проволочку, равномерно заряженную с линейной плотностью заряда $varkappa$. Заряд расположен на расстоянии $a$ от конца проволочки на линии, которая является ее продолжением (как показано на рисунке). |
|
Показать решение
Задача №144
| В шаре радиуса $R$ заряд распределен так, что электрическое поле внутри шара имеет только радиальную компоненту: $vec{E}=E_0frac{r}{R}vec{e}_r$. Поверхностных зарядов на сфере $r=R$ нет. Вне шара зарядов нет. Найти электрическое поле вне шара. |
Показать решение
Задача №143
| Найти электрическое поле в точке с координатами $x=0$, $y=h$, создаваемое зарядом $q$, равномерно распределенным на стержне длины $a$, изображенном на рисунке. |
|
Показать решение
Задача №132
| Три одинаковых идеально проводящих шарика расположены на прямой AC в точках ABC. Расстояние $AB$=$BC$=$L$. Радиусы шариков $all L$. Вначале первому шарику, который находится в точке $A$, сообщили заряд $Q$. Затем этот шарик соединили идеальным проводником со вторым шариком, находящимся в точке $B$. После того, как заряд перераспределился между первым и вторым шариком, проводник, соединяющий эти шарики, убрали, а затем соединили проводником второй шарик и третий шарик, находящийся в точке $C$. Какие будут заряды на шариках после окончания переходных процессов (с точностью до членов $a/L$)? |
|
Показать решение
Задача №131
| Три одинаковых идеально проводящих шарика расположены в вершинах равнобедренного прямоугольного треугольника $ABC$, длина катета у которого $AB$=$BC$=$L$. Угол $ABC$ прямой, радиусы шариков $all L$. Вначале первому шарику, который находится в точке $A$, сообщили заряд $Q$. Затем этот шарик соединили идеальным проводником со вторым шариком, находящимся в точке $B$ (в вершине прямого угла). После того, как заряд перераспределился между первым и вторым шариком, проводник, соединяющий эти шарики, убрали, а затем соединили проводником второй шарик и третий шарик, находящийся в точке $C$. Какие будут заряды на шариках после окончания переходных процессов (с точностью до членов $a/L$)? |
|
Показать решение
Задача №128
| Заряд $q$ равномерно распределен по боковой поверхности цилиндра радиуса $a$ с высотой $h$. Найти потенциал в центре основания цилиндра. |
Показать решение
Задача №127
| Тонкое полукольцо радиуса $a$, равномерно заряженное зарядом $q$, расположено в плоскости (x,y), как показано на рисунке. Найти напряженность поля $vec{E}$ в точке с координатами (0,0,$z_0$). |
|
Показать решение
Задача №12
| Однородно заряженный с объемной плотностью заряда $rho$ бесконечный цилиндр радиуса $a$ вращается вокруг своей оси с равномерно возрастающей угловой скоростью $omega=kt$. Найти электрическое и магнитное поле во всем пространстве в зависимости от времени |
Показать решение
Задача №11
| Найти емкость длинного ($lgg b,a$) цилиндрического конденсатора (сечение показано на рисунке), верхняя и нижняя половины которого заполнены диэлектриком с проницаемостью $varepsilon_1$, $varepsilon_2$ соответственно. Найти силу, действующую на внутреннюю обкладку, если разность потенциалов между обкладками равна $U$. |
|
Показать решение
Задача №10
| Заземление представляет собой идеально проводящий шар радиуса $a$, помещенный в бесконечную среду с проводимостью $sigma$. 1. Найти сопротивление заземления. 2. Найти сопротивление заземления, если в среде образовалась сферическая полость радиуса $b$, заполненная идеальным проводником (внутри полости $sigma_{in}=infty$), расстояние между центрами заземляющего шара и полости равно $l$. 3. Найти сопротивление заземления, если полость не проводит ток (внутри полости $sigma_{in}=0$). Качественно нарисовать линии тока во всех случаях, $l>a+b$, $all b,l-b$. |
Показать решение
Задача №9
| Длинный цилиндрический конденсатор (радиусы обкладок $a$ и $c$, длина $L$) имеет заполнение в виде двух концентрических слоев с различными проводимостями ($sigma_1$ и $sigma_2$) и диэлектрическими проницаемостями ($varepsilon_1$ и $varepsilon_2$), причем $sigma_1/varepsilon_1=sigma_2/varepsilon_2$. Радиус границы раздела слоев – $b$. Внутренняя обкладка конденсатора заземлена, к внешней приложено постоянное напряжение $U$. В некоторый момент времени $t = t_0$ внешнюю обкладку мгновенно отключают от источника напряжения и соединяют с землей через сопротивление $R$. Найти ток через сопротивление $I_R(t)$ |
|
Показать решение
Задача №8
| Два тонких кольца радиусами $a$ и $b$, расположенные соосно в плоскостях $z=0$ и $z=h$, равномерно заряжены зарядами $q$ и $-q$. Найти два первых ненулевых члена разложения потенциала на больших расстояниях $r$ |
|
Показать решение
Задача №6
| Две концентрические тонкостенные проводящие сферы с радиусами $a$ и $b$ заряжены зарядами $q_1$ и $q_2$ соответственно. 1. Найти потенциал внутренней сферы $varphi_1$ (потенциал на бесконечности равен нулю). 2. Чему равен этот потенциал, если пространство между сферами – однородный диэлектрик с проницаемостью $varepsilon$? |
|
Показать решение
Задача №5
| Два отрезка длиной $a$, заряженные равномерно по длине зарядом $q$ каждый, лежат на одной прямой. Найти силу взаимодействия между отрезками, если расстояние между их центрами равно $l$ ($l>a$) |
|
Показать решение
Задача №4
| Плоская спираль, описываемая уравнением $r=a exp(balpha)$, имеет $N$ полных оборотов (см. рисунок, где для примера показана спираль при $N = 2$) и равномерно заряжена с линейной плотностью $varkappa$. Найти электрический потенциал в центре $O$ спирали. |
|
Показать решение
Задача №3
| Проводящий шар радиуса $a$, находящийся в центре проводящей заземленной сферы радиуса $b>a$, имеет потенциал $varphi_{0}$. Найти заряд на шаре. |
Показать решение
Задача №2
| Участки $AB$ и $CD$ тонкого непроводящего кольца радиуса $R$ равномерно (с постоянной линейной плотностью) заряжены зарядом $+q$ и $-q$ соответственно. Точки $ABCD$ образуют вершины квадрата. Найти электрическое поле в центре кольца. |
|
Показать решение
Задача №1
| Полусфера радиуса $R$ заряжена с поверхностной плотностью $sigma(theta) =sigma_0 sintheta$. Найти электрическое поле в точке O |
|
Показать решение
Рис. 3.1
Пример
1.
Два точечных электрических заряда Q1
=
1нКл
и Q2
=
-2 нКл
находятся
в воздухе на расстоянии d
= 10 см друг
от друга. Определить напряженность
Е
и потенциал φ
поля, создаваемого этими зарядами в
точке А,
удаленной от заряда Q1
на расстояние r1=
9 см и от
заряда Q2
на r2
= 7 см.
Определить также
силу F,
действующую в точке
А
на точечный заряд
Q
=10
нКл.
Решение.
Согласно принципу суперпозиции
электрических полей, каждый заряд
создает поле независимо от присутствия
в пространстве других зарядов. Поэтому
напряженность
электрического поля в искомой точке
может быть найдена как геометрическая
сумма напряженностей1
и
2
полей, создаваемых каждым зарядом в
отдельности:
.
Напряженности электрического поля,
создаваемого в воздухе (ε=1)
зарядами Q1
и Q2,
;
.
(3.1)
Вектор
1
(см. рис. 3.1) направлен по силовой линии
от заряда Q1,
так как этот заряд положителен; вектор
2
направлен также по силовой линии, но к
заряду Q2,
так как этот заряд отрицателен.
Модуль
вектора
найдем по теореме косинусов:
,
(3.2)
где
– угол между векторами
1
и
2,
,
который
может
быть найден из треугольника со сторонамиr1, r2 и d:
.
В данном случае во избежание громоздких
записей удобно значение cos α
вычислить отдельно:
.
Подставляя
выражение Е1
и E2
из (3.1) в (3.2) и вынося общий множитель
1/(4πε0)
за знак корня, получаем

В
соответствии с принципом суперпозиции
электрических полей, потенциал φ
результирующего
поля, создаваемого двумя зарядами
Q1
и Q2,
равен алгебраической сумме потенциалов:
φ=φ1+φ2. (3.4)
Потенциал
электрического поля, создаваемого в
вакууме точечным зарядом Q
на расстоянии r
от него, выражается формулой
. (3.5)
В нашем случае
согласно формулам (3.4) и (3.5) получим
,
или
.
Сила,
действующая на точечный заряд, находящийся
в электрическом поле в точке А
,
где напряженность
находится из выражения (3.3).
Произведем
вычисления:
;

П
Рис. 3.2.
ример 2. Три точечных
заряда Q1=1
нКл, Q2=
2 нКл и Q3=
3 нКл расположены в вершинах
равностороннего треугольника, длина
стороны которого а= 5 см.
Определить напряженность поля в точке
А, находящейся
на пересечении биссектрис треугольника.
Решение.
Согласно принципу суперпозиции
электрических полей, каждый заряд
создает поле независимо от присутствия
в пространстве других зарядов. Поэтому
напряженность
электрического поля в искомой точке
может быть найдена как геометрическая
сумма напряженностей1
и
2
и
полей,
создаваемых каждым зарядом в отдельности:.
Напряженности электрического поля,
создаваемого в воздухе (ε=1)
зарядами Q1
и Q2
и
Q3:
;
;
;
.
(3.6)
Вектор
1
(см. рис. 3.2) направлен по силовой линии
от заряда Q1,
вектор
2
направлен по силовой линии от заряда
Q2
и вектор
3
направлен
по силовой линии от заряда Q3,
так как все заряды положительны.
Модуль
вектора
найдем из соотношения
,
(3.7)
где
и
– проекции векторов
1
,2
и3
на
координатные оси x
и y
(рис. 3.2).
,
.(3.8)
Подставляя
выражение Е1
, Е2
и E3
из (3.6) в (3.8), получаем:
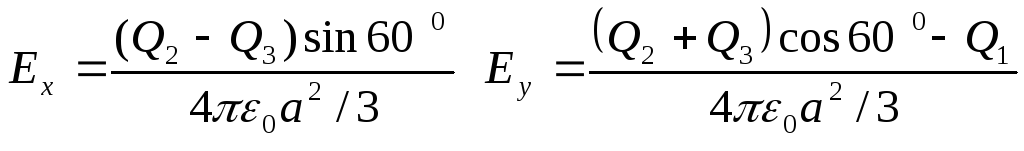
(3.9)
Модуль
вектора
находим, подставляя (3.9) в (3.7):

Произведем
вычисления:

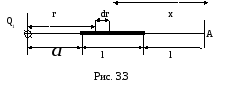
Пример
3. На тонком
стержне длиной l
= 10 см
находится равномерно распределенный
электрический заряд. На продолжении
оси стержня на расстоянии а
= 5 см от
ближайшего конца находится точечный
заряд Q1=40
нКл, который
взаимодействует со стержнем с силой
F = 6 мкН.
Определить линейную плотность τ
заряда на стержне. Найти потенциал φ
в точке А,
расположенной на оси стержня и удаленной
от
его
ближайшего конца на расстояние l.
Решение.
Сила взаимодействия F
заряженного стержня с точечным зарядом
Q1
зависит от линейной плотности τ
заряда на стержне. Зная эту зависимость,
можно определить τ.
При вычислении силы F
следует иметь в виду, что заряд на стержне
не является точечным, поэтому закон
Кулона непосредственно применить
нельзя. В этом случае можно поступить
следующим образом. Выделим из стержня
(рис. 3.3) малый участок dr
с зарядом dQ
= τdr.
Этот заряд можно рассматривать как
точечный. Тогда, согласно закону Кулона:
.
Интегрируя
это выражение в пределах от а
до а+l,
получаем:
,
откуда
.
Проверим,
дает ли расчетная формула единицу
линейной плотности электрического
заряда. Для этого в правую часть формулы
вместо символов величин подставим
их единицы:
Найденная единица
является единицей линейной плотности
заряда.
Произведем
вычисления:
.
Потенциал
dφ,
создаваемый точечным зарядом
в точке А (рис. 3.3), можно определить по
формуле
.
Согласно
принципу суперпозиции электрических
полей, потенциал электрического поля,
создаваемого заряженным стержнем в
точке А, найдем интегрированием
этого выражения:
.
Выполним
интегрирование:
.
(3.10)
Потенциал
в точке А по принципу суперпозиции
является суммой потенциалов, созданных
точечным зарядом
и стержнем с распределенным зарядом:
,
где– потенциал в точке
,
созданный зарядом;
а– потенциал в точке
,
созданный стержнем и определяемый
выражением (3.10). Откуда
.
Подставим числовые значения физических величин в СИ
(1/(4πε0)=9.109
м/Ф,
Q1=4.
10-8 Кл,
l=10-1м,
а= 5.10-2
м, τ=10
.10-9
Кл/м)
и произведем вычисления:
φ=9
.109
(+1,25
.10-9
.0,693)=7,8
В.
Рис. 3.4
Рис.
3.4
Пример
4. По тонкой
нити, изогнутой по дуге окружности,
равномерно распределен заряд с линейной
плотностью τ
= 10 нКл/м.
Определить напряженность
и потенциалφ
электрического поля, созда-ваемого
таким распределенным зарядом в точке,
совпадающей с центром кривизны дуги.
Длина l
нити составляет ⅓ длины окружности и
равна 15 см.
Решение.
Выберем оси координат так, чтобы начало
координат совпадало с центром кривизны
дуги, а ось Оу была бы симметрично
расположена относительно концов дуги
(рис. 3.4). На нити выделим элемент длины
dl.
Заряд dQ=rdl,
находящийся на выделенном участке,
можно считать точечным.
Определим
напряженность электрического поля в
точке О. Для этого найдем сначала
напряженность dE
поля, создаваемого зарядом dQ:
,
где
– радиус-вектор, направленный от
элементаdl
к точке, в которой вычисляется
напряженность.
Выразим
вектор
через проекцииdEx
и dEy
на оси координат:
,
где
и
– единичные векторы направлений (орты).
Напряженностьнайдем интегрированием:
.
Интегрирование
ведется вдоль дуги длиной l.
В силу симметрии
.
Тогда
, (3.11)
где
dEy=dEcosθ=τdlcosθ/(4πε0r2).
Так как r=R=const,
dl=Rdθ,
то
.
Подставим
выражение dEy
в (3.11) и, приняв во внимание симметричное
расположение дуги относительно оси Оу,
пределы интегрирования возьмем от 0 до
π/3, а результат удвоим:
.
Выразив
радиус R
через длину l
нити (3l=2πR),
получим:
. (3.12)
Из
этой формулы видно, что напряженность
поля по направлению совпадает с осью
Оу.
Найдем
потенциал электрического поля в точке
О. Сначала найдем потенциал dφ,
создаваемый точечным зарядом dQ
в точке О:
.
Заменим
r
на R
и проведем интегрирование:
.
Так
как l
=
πR,
то
. (3.13)
Произведем
вычисления по формулам (3.12) и (3.13):
=2,17
кВ/м,
=188
В.
Рис. 3.5
Пример
5. По тонкому
кольцу равномерно распределен заряд Q
= 50 нКл с
линейной плотностью τ
= 40 нКл/м.
Определить напряженность Е
электрического поля, создаваемого этим
зарядом в точке А, лежащей на оси
кольца и удаленной от его центра на
расстояние, равное половине радиуса.
Решение.
Совместим координатную плоскость хОу
с плоскостью кольца, а ось Oz – с осью
кольца (рис. 3.5). На кольце выделим малый
участок длиной dl.
Так как заряд dQ
= τ
dl, находящийся
на этом участке, можно считать точечным,
то напряженность
электрического поля, создаваемого этим
зарядом, может быть записана в виде
,
где
–
радиус-вектор, направленный от элементаdl
к точке А.
Разложим
вектор
на две
составляющие:
1,
перпенди-кулярно плоскости кольца
(сонаправленную с осью Oz), и2,
параллельную плоскости кольца (плоскости
хОу), т.е.
=
1+
2.
Напряженность
электрического поля в точке А найдем
интегрированием:
,
где
интегрирование ведется по всем элементам
заряженного кольца. Заметим, что для
каждой пары зарядов dQ
и dQ’ (dQ=dQ’),
расположенных симметрично относительно
центра кольца, векторы dE2
и dE2’
в точке А равны по модулю и противоположны
по направлению:
2=
—.
Поэтому векторная сумма (интеграл)
.
СоставляющиеdE1
для всех элементов кольца сонаправлены
с осью Oz (единичным вектором
),
т.е.
1=
.
Тогда
.
Так
как
,
и
,
то
.
Таким образом,
.
Из
соотношения Q=2πRτ
определим радиус кольца:
.
Тогда
.
Модуль
напряженности
. (3.14)
Проверим,
дает ли правая часть полученного
равенства единицу напряженности,
В/м:
.
Выразим
физические величины, входящие в формулу
(3.14), в единицах СИ (τ=5.10-8
Кл/м,
Q=4.10-8Кл,
ε0=8,85.10-12Ф/м)
и произведем вычисления:
.
Пример
6. Две
концентрические проводящие сферы
радиусами R1=5
см и R2
= 10 см
несут соответственно заряды Q1
= 10 нКл
и Q 2=-5
нКл. Найти
напряженность Е
поля в точках, отстоящих от центра сфер
на расстояниях r1
= 4 см,
r2
= 8 см,
r3
= 15 см.
Построить график Е(r).
Решение.
Заметим, что точки, в которых требуется
найти напряженности электрического
поля, лежат в трех областях (рис. 3.6):
области /(r1<R1),
области //(R1<r2<R2),
области /// (r3>R2).
1. Для
определения напряженности Е1
в области / проведем гауссову поверхность
S1
радиусом r1
и воспользуемся теоремой Остроградского
– Гаусса:
(так
как суммарный заряд, находящийся внутри
гауссовой поверхности, равен нулю).
Из соображений симметрии En=E1=const.
Следовательно,
иЕ1
(напряженность поля в области /) во
всех точках, удовлетворяющих условию
r1<R1,
будет равна нулю.
Рис. 3.6
2.
В области // гауссову поверхность проведем
радиусом r2.
В этом случае диэлектрическую проницаемость
среды будем считать равной единице
(вакуум) и воспользуемся теоремой
Остроградского– Гаусса:
(так
как внутри гауссовой поверхности
находится только заряд Q1).
Так
как Еn=Е2=const,
то Е можно
вынести за знак интеграла:
,
или
;
,
где
S2=4πr22
– площадь гауссовой поверхности. Тогда
.
(3.15)
3.
В области /// гауссова поверхность
проводится радиусом r3.
Обозначим напряженность E
области /// через Е3
и учтем, что в этом случае гауссова
поверхность охватывает обе сферы и,
следовательно, суммарный заряд будет
равен Q1+Q2.
Тогда
.
Заметив,
что Q2<0,
это выражение можно переписать в виде
. (3.16)
Убедимся
в том, что правая часть равенств (3.15) и
(3.16) дает единицу напряженности:
. Выразим все величины в единицах СИ (Q1
= 10-8
Кл, Q2
= —
5.10-9
Кл, r1
= 0,08 м,
r3
= 0,15 м,
1/(4πε0)
= 9.109
м/Ф)
и произведем вычисления:
;
.
Построим
график Е(r).
В области / (r1<R1)
Е=0.
В области // (R1≤r2<R2)
E2(r)
изменяется по закону
.
В точкеr=R1
напряженность E2(R1)
=
=36 кВ/м. В
точке r=R2
(r стремится к R2
слева) E2(R2)==
9 кВ/м.
В области /// (r>R2)
E3(r)
изменяется по закону
,
причем в точкеr=R2
(r стремится к R2
справа) E3(R2)
=
= 4,5 кВ/м.
Таким образом, функция Е(r)
в точках r=R1
и r=R2
терпит разрыв. График зависимости
E(r)
представлен на рис. 3.7.
Пример
7. В вакууме
имеется скопление зарядов в форме
длинного цилиндра радиуса R0
= 2 cм.
Объемная
плотность зарядов
постоянна и равна2
мкКл/м3.
Найти напряженность поля в точках 1 и
2, лежащих на расстояниях r1
= 1 cм,
r2
= 3 cм
от оси цилиндра, и разность потенциалов
между этими точками. Построить графики
и
.
Поле
создано зарядом, р
РРРИ
Рис.
3.8.
Рис.
3.8
авно-мерно распределенным по объему.
Конфигурация зарядов позволяет считать,
что поле обладает осевой симметрией:
силовые линии – прямые и в любой
плоскости, перпендикулярной оси цилиндра,радиальны
(рис. 3.8).
Вспомогательной
поверхности следует придать форму
цилиндрической поверхности, коаксиальной
заряду. Длина этого цилиндра может быть
произвольной, но заведомо много меньше,
чем длина заряженного цилиндра. Характер
функциональной зависимости
для точек, лежащих внутри и вне объемного
заряда, различен. Поэтому следует
провести две вспомогательные цилиндрические
поверхностиS1
и S2
с радиусами
и
.
Определим
проекцию вектора E
на нормаль выбранной поверхности
Еn1=E=const
и En2=0.
Поток через выбранную поверхность
цилиндра равен
(3.17)
где
h
– высота цилиндра.
Определим
заряд, попадающий внутрь выделенной
поверхности: при r<R0
,
а приr>R0
.
(3.18)
Применим
теорему Гаусса
,
используя выражение (3.17) и (3.18),
откуда
–напряженность
внутри цилиндра (3.19)
,
откуда
–напряженность
вне цилиндра. (3.20)
Для
определения разности потенциалов между
точками 1
и 2
разобьем
на два интеграла: в пределах от точки 1
до поверхности, ограничивающей объемный
заряд, и от этой поверхности до точки
2:
В первый интеграл следует подставлять
выражение (3.19), во второй выражение
(3.20):
(3.21)
Подставляя
в (3.19) r=r1
и в (3.20) r=r2,
находим:
;
.
Вычислим численное
значение выражения (3.21):
.
Для
построения графика Er(r)
на основании выражений (3.19) и (3.20)
целесообразно сначала рассчитать Er
при r=R0:
В/м.
Графическая
зависимость Er(r)
показана на рис. 3.9.
Г
зависимостиможно построить из анализа графикаEr(r),
учитывая, что
.
Выберем начало отсчета на оси объемного
заряда:(0)=0.
Так как во всей области Er>0,
т.е. (d/dr)<0,
то потенциал непрерывно убывает. В
области r<R0
Er
возрас-

,
соответственно
и график(r)
обращен вогнутостью вниз. При
r>R0
Er
убывает
, соответственно
и график(r)
обращен вогнутостью вверх.
При
r=R0
кривая (r)
имеет точку перегиба (вторая производная
изменяет знак). График (r)
изображен на рис. 3.10. Если изменить
начало отсчета потенциала, то характер
графика не изменяется, например, при
выборе начала отсчета на поверхности
объемного заряда
график примет вид, изображенный на рис.
3.10 пунктиром.
Пример
8. Электрическое
поле создается двумя зарядами Q1
=2 мкКл
и Q2
= -4 мкКл,
находящимися на расстоянии а=
0,2 м друг от
друга. Определить работу A1,2
сил поля по перемещению заряда Q=50
нКл из точки
1 в точку 2
(рис. 3.11).
Решение.
Для определения работы A1,2
сил поля воспользуемся соотношением
A1,2
=
Q(φ1—φ2).
Рис. 3.11
Применяя
принцип суперпозиции электрических
полей, определим потенциалы φ1
и φ2
точек 1 и
2 поля:
;
.
Тогда
,
или
.
Проверим, дает ли
правая часть равенства единицу работы
(Дж):
.
Подставим
числовые значения физических величин
в СИ:
(Q=50
.10-9Кл,
Q1=2.10-6Кл,
Q2=
4.10-6Кл,
a= 0,2 м,
)
и произведем вычисления:
.
Пример
9. Определить
ускоряющую разность потенциалов U,
которую должен пройти в электрическом
поле электрон, обладающий скоростью
v1=3,106м/с,
чтобы скорость его возросла в n
= 3 раза.
Решение.
Ускоряющую разность потенциалов можно
найти, вычислив работу А
сил электростатического поля. Эта
работа определяется произведением
элементарного заряда е
на разность потенциалов U:
A=eU. (3.22)
Работа
сил электростатического поля в данном
случае равна изменению кинетической
энергии электрона:
, (3.23)
где
Т1
и Т2
– кинетическая энергия электрона до и
после прохождения ускоряющего поля; m
– масса электрона; v1
и v2
– начальная и конечная скорости его.
Приравняв
правые части равенств (3.22) и (3.23), получим:
,
где
.
Отсюда
искомая разность потенциалов
.
Произведем
вычисления:
=
204,7 В.
Рис. 3.12
Пример
10.
С поверхности бесконечного равномерно
заряженного
(τ = 50 нКл/м)
прямого цилиндра вылетает α-частица
(v0
= 0).
Определить кинетическую энергию T2
α-частицы (кэВ)
в точке 2 на расстоянии 8R
от поверхности цилиндра (рис. 3.12).
Решение.
Так как силы электростатического поля
являются консервативными, то для
определения кинетической энергии
α-частицы в точке 2 воспользуемся законом
сохранения энергии, записанном в виде
W1=W2,
где W1
и W2
– полные
энергии α-частицы в точках 1 и 2.
Так
как W1=T1+U1
и W2=T2+U2
(T1
и Т2
– кинетические энергии α-частицы;
U1
и U2
– потенциальные) , то, учитывая, что Т1=0
(v0=0),
можно записать U1=T2+U2,
откуда Т2=U1-U2=Q(φ1-φ2)
(Q
– заряд α-частицы; φ1
и φ2
– потенциалы точек 1 и 2).
Для
определения разности потенциалов
воспользуемся соотношением между
напряженностью поля и изменением
потенциала: Е=-gradφ.
Для поля с осевой симметрией, каким
является поле цилиндра, это соотношение
можно записать в виде
,
или dφ=-Edr.
Интегрируя
это выражение, найдем разность
потенциалов двух точек, отстоящих
на расстояниях r1
и r2
оси цилиндра:
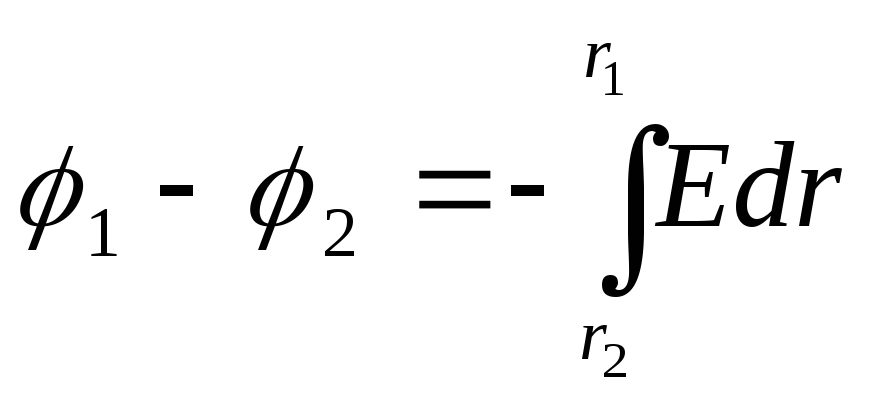
Так как цилиндр
длинный и точки взяты вблизи его средней
части, то для выражения напряженности
поля можно воспользоваться формулой
напряженности поля, создаваемого
бесконечно длинным цилиндром:
.
Подставив
это выражение в (3.24), получим:
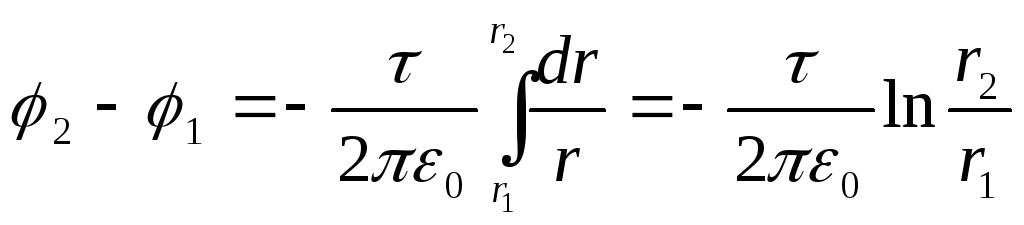
Учитывая,
что,
а,
запишем
.
Тогда
.
Выразим
все величины в единицах СИ (Q= 2.1,60.10-19
Кл, τ= 50.10-9
Кл/м,
)
и произведем вычисления (—
коэффициент перевода из Дж
в эВ):
= = 3,96 кэВ.
Пример
11. Конденсатор
емкостью С1=6
мкФ был
заряжен до разности потенциалов U1=20
В. После
отключения от источника тока конденсатор
соединили параллельно с другим
незаряженным конденсатором емкостью
С2=10
мкФ. Какая
энергия W’
израсходуется на образование искры в
момент присоединения второго конденсатора?
Решение.
Энергия, израсходованная на образование
искры:
W’=W1—W2, (3.25)
где
W1
– энергия, которой обладал первый
конденсатор до присоединения к нему
второго конденсатора; W2
– энергия, которую имеет батарея,
составленная из двух конденсаторов.
Энергия заряженного
конденсатора определяется по формуле
W=½CU2, (3.26)
где
С – емкость
конденсатора или батареи конденсаторов.
Выразив
в формуле (3.25) энергии W1
и W2
по формуле (3.26) и приняв во внимание,
что общая емкость параллельно соединенных
конденсаторов равна сумме емкостей
отдельных конденсаторов, получим
W’=½C1U12-½(C1+C2)U22, (3.27)
где
U2
– разность потенциалов на зажимах
батареи конденсаторов.
Учитывая,
что заряд после присоединения второго
конденсатора остался прежним, выразим
разность потенциалов U2
следующим образом:
.
Подставив
выражение U2
в (3.27)), найдем

или
.
Произведем
вычисления:
Дж=750
мкДж.
Пример
12. Потенциометр
сопротивлением R=150
Ом подключен к батарее с ЭДС
=300
В и внутренним
сопротивлением Ri
= 50
Ом. Определить:
1) показание вольтметра сопротивлением
RV
= 500 Ом,
соединенного с одной из клемм потенциометра
и подвижным контактом, установленным
посередине потенциометра; 2) разность
потенциалов между теми же точками
потенциометра при отключении вольтметра.
Решение.
1. Показание вольтметра, подключенного
к точкам A
и В (рис. 3.13), определим по формуле
U1=I1R1,
г
– сопротивление параллельно соединенных
вольтметра и половины потенциометра;
I1
– суммарная сила тока в ветвях этого
соединения (она равна силе тока в
неразветвленной части цепи).
Силу
тока I1
найдем по закону Ома для полной цепи:
I1=/(Re+Ri), (3.28)
где
Re
– сопротивление внешней цепи. Это
сопротивление есть сумма двух
сопротивлений:
Re=R/2+R1. (3.29)
Сопротивление
R1
найдем по формуле параллельного
соединения проводников
,
откуда
Подставив
в (3.28) выражение Re
по (3.29), найдем
.
В
данном случае решение задачи в общем
виде было бы громоздким. Поэтому удобно
вычисление величин провести раздельно:
=
65,22 Ом;
=
1,58 A;
U1=1,58
.65,22
= 103,04 B.
2.
Разность потенциалов между точками А
и В при отключенном вольтметре равна
произведению силы тока I2
на половину сопротивления потенциометра:
,
(3.30)
где
I2
– сила тока в цепи при отключенном
вольтметре. Ее определим по формуле
.
Подставив
выражение I2
в (3.30), найдем
.
Произведем
вычисления:
=
112,5 В.
П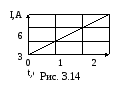
13. Сила тока
в проводнике сопротивлением R=20
Ом нарастает
в течение времени Δt
=2 с по
линейному закону от I0=0
до I=6
А (рис. 3.14). Определить теплоту Q1,
выделившуюся в этом проводнике за первую
секунду, и Q2
– за вторую, а также найти отношение
.
Решение.
Закон Джоуля–Ленца в виде Q=I2Rt
справедлив для постоянного тока
(I=const).
Если же сила тока в проводнике изменяется,
то указанный закон справедлив для
бесконечно малого интервала времени и
записывается в виде
dQ=I2Rdt. (3.31)
Здесь
сила тока I
является некоторой функцией времени.
В данном случае
I=kt,
(3.32)
где
k
— коэффициент пропорциональности,
характеризующий скорость изменения
силы тока:
.
С
учетом (3.32) формула (3.31) примет вид
dQ=k2Rt2dt. (3.33)
Для
определения теплоты, выделившейся за
конечный интервал времени Δt,
выражение (3.33) надо проинтегрировать
в пределах от t1
до t2:

Произведем
вычисления:
Q1=.
32
.20(1-0)=60
Дж;
Q2=.32.20(8-1)=420
Дж.
Следовательно,
,
т.е.
за вторую секунду выделится теплоты в
семь раз больше, чем за первую.
Теорема Гаусса и постулат Максвелла, представленные в интегральной форме, дают возможность решить ряд задач в тех случаях, когда условия симметрии таковы, что в каждой точке замкнутой поверхности интегрирования (поверхности симметрии), охватывающей заряды, вектор напряженности поля (или электрического смещения
)
имеет одно и то же значение и может быть вынесен из-под интеграла.
Пример 1. Точечный заряд q = 10-9 Кл помещен в начале сферической системы координат. Определить напряжение между точками а (Ra = 4см, qа = 45°, jа = 0°) и b (Rb = 8см, , qb = 180°, jb = 90°) и напряженность в тех же точках, если окружающей средой является воздух.
Решение.
Решение будем проводить с помощью теоремы Гаусса (1.9), так как среда однородна.
Поскольку поле точечного заряда характеризуется сферической симметрией, то, если в качестве поверхности интегрирования взять поверхность сферы с центром в точке, где расположен заряд (в нашем случае это начало системы координат), то в любой точке на поверхности этой сферы напряженность поля будет иметь одно и то же значение. Направление же вектора будет совпадать с направлением радиуса, то есть перпендикулярно к поверхности сферы. В связи с этим, интеграл по этой поверхности, составленный по теореме Гаусса, можно преобразовать следующим образом:
.
Поскольку данный интеграл (согласно теореме Гаусса) равен отношению заряда, помещенного внутри сферы, к диэлектрической проницаемости среды, то напряженность поля будет определяться соотношением
Еr = q/(4pe0r2).
Здесь индекс r у напряженности проставлен для того, чтобы показать, что напряженность поля имеет одну составляющую, направленную по радиусу.
Отметим, что данная формула полностью соответствует выражению (1.1), полученному из закона Кулона.
Поскольку напряженность электрического поля в данном случае имеет только радиальную составляющую, величина которой является функцией радиуса и не зависит от угловой координаты, то в указанных в исходном задании точках она будет равна:
E(ra)=q/(4pe0ra2)=10-9/(4p?8.85·10-12·0.042)=5.62кВ/м.
E(rв)=q/(4pe0rв2)=10-9/(4p8.85·10-12·0.082)=1.405кВ/м.
Разность потенциалов между точками а и в определяется при помощи выражения (1.6). Эта разность в потенциальном поле не зависит от пути интегрирования. Поэтому, если разбить путь интегрирования на две части и сначала проводить интегрирование вдоль радиуса от точки а до точки, которая является точкой пересечения продолжения этого радиуса с поверхностью воображаемой сферы с центром в начале координат и радиусом rв, а затем проводить интегрирование по любой линии, лежащей на поверхности этой серы от данной точки до точки в, то интеграл вдоль этой линии будет равен нулю, поскольку вектор напряженности поля имеет одну составляющую, направленную вдоль радиуса, а подинтегральным выражением в формуле (1.6) является скалярное произведение вектора напряженности поля и вектора dl, который совпадает с касательной к поверхности сферы.
Таким образом, разность потенциалов между точками а и в будет равна

Пример 2. Уединенный проводящий шар радиусом R0 = 6 см, поверхностная плотность заряда которого s = 0,1*10-6 Кл/м2, помещен в диэлектрик (er = 3).
Определить закон изменения напряженности поля и потенциала в функции расстояния r от центра шара, приняв потенциал равным нулю в бесконечности. Рассчитать напряжение между точками, одна из которых лежит на поверхности шара, а другая – на расстоянии 20 см от его поверхности. Вычислить емкость шара.
Решение.
Поле внутри проводящего шара отсутствует. Поле вне шара обладает сферической симметрией, поэтому рассчитывается с помощью теоремы Гаусса точно так же как и для точечного заряда.
Здесь в качестве поверхности интегрирования взята поверхность сферы радиуса r ?
R0 с центром, совпадающим с центром шара.
Заряд шара определяется через поверхностную плотность
q = s·4p·R02.
Таким образом, напряженность поля вне шара имеет только одну радиальную составляющую и равна
Еr = s·R02/(ere0r2) =
0,1·10-6·0,062/(3·8,85·10-12r2).
Потенциал в любой точке вне шара, находящейся на расстоянии r от его центра, определяется с помощью выражения (1.5), которое с учетом того, что напряженность поля направлена вдоль радиуса, будет иметь следующий вид:
Потенциал шара равен потенциалу любой точки, лежащей на поверхности шара (r = R0) U =
13,56/0,06 = 173,8 В.
Разность потенциалов между любыми точками А (r = RA) и В (r = RВ) определяется с помощью следующей формулы:
UA – UВ = 13,56· (1/RA – 1/RВ).
Таким образом, разность потенциалов между точкой, лежащей на поверхности шара, и точкой, отстоящей от поверхности на расстоянии 20 см, равна
UAВ = 13,56· (1/0,06 – 1/0,26) = 173,8 В.
Емкость шара можно определяется выражением (1.19)
С = 4·p·ere0·R0 = 4·p·3·8,85·10-12·0,06 = 2·10-11 Ф.
Пример 3.
Шар из диэлектрика (er = 4) заряжен и расположен в воздухе. Объемная плотность заряда является функцией расстояния r от центра шара: r = k*r,
где k = 0,05p [Кл/м4].
Радиус шара R = 2см. Рассчитать и построить графики изменения потенциала и напряженности поля вдоль радиуса.
Решение. В
данном случае поле также обладает сферической симметрией, но область не однородна. Поэтому здесь удобнее применять постулат Максвелла (1.10).
Так, при 0 ? r ? R где s – сферическая поверхность радиусом r с
центром, совпадающим с центром шара; v – объем, заключенный внутри этой поверхности.
Перепишем уравнение с учетом симметрии поля
Отсюда находим радиальную составляющую вектора электрического смещения:
Dr = 0,25·k·r2.
Напряженность электрического поля, которая также как и вектор электрического смещения направлена по радиусу, внутри шара будет равна
(1.8):
E1r = Dr/ere0 = 0,25·k·r2/ere0.
Вне шара (r ? R) электрическое смещение, исходя из постулата Максвелла, определяется следующим образом:
Следовательно, электрическое смещение и напряженность поля будут равны:
Dr = 0,25·k·R4/r2; Er = Dr/e0.
Графики изменения напряженности поля и вектора электрического смещения представлены на рис.1.4. Значения напряженности поля и вектора электрического смещения даны в относительных единицах. За базисные значения приняты значения этих величин на поверхности шара, которые для заданных исходных данных соответственно равны Erb = 4,435·105В/м; Drb = 1,571·10-5Кл/м2.
Потенциал поля внутри шара можно определить по формуле
,
где С1 – постоянная интегрирования.
Принимая потенциал бесконечно удаленной точки равным нулю, определим потенциал любой произвольной точки в области вне шара.

Постоянную интегрирования С1 можно определить из условия равенства потенциалов U1 и U2 на поверхности шара (при r = R)

Отсюда

График изменения потенциала вдоль радиуса также в относительных единицах показан на рис.1.4. За базисное значение потенциала принято значение потенциала на поверхности шара Ub = 35.5кВ.
Отметим, что если бы объемная плотность заряда r оставалась постоянной, то напряженность поля и потенциалы поля в соответствующих подобластях определялись бы следующими выражениями:
E1 = r·r/(3·ere0); U1 = – r·r2/(6·ere0) + C1;
E2 = r·R3/(3·e0·r2);
U2 = r·R3/(3·e0·r).
Постоянная С1 в этом случае определяется также из условия равенства потенциалов U1 и U2 на поверхности шара
С1 = r·R3· (1+2·er)/(6·e0·er).
Пример 4. Сферический конденсатор с двухслойным диэлектриком имеет радиус внутренней сферы r1=12 мм, внутренний радиус наружной сферы – r3=22 мм и радиус поверхности раздела диэлектриков – r2=16 мм.
Относительное значение диэлектрической проницаемости внутреннего слоя диэлектрика er1=5, наружного слоя – er2=3. Разрез конденсатора показан на рис.1.5. Заряд конденсатора q = 10-8Кл.
Определить и построить график изменения напряженности поля вдоль радиуса. Найти разность потенциалов между электродами. Вычислить емкость конденсатора. Изменяя радиус поверхности раздела диэлектриков r2 и значение диэлектрической проницаемости наружного слоя er2 получить конденсатор с наилучшим использованием двухслойного диэлектрика. Рассчитать емкость данного конденсатора и сопоставить ее с емкостью исходного конденсатора.
Решение. Используя постулат Максвелла для любой сферической поверхности радиусом r, построенной внутри k-го слоя (k=1,2) диэлектрика с диэлектрической проницаемостью erk, получим выражение для вектора электрического смещения и напряженности электрического поля
Dk = q/(4pr2); Ek = Dk/(erk·e0) = q/(4pr2·erk·e0).
Максимальное значение напряженности поля в первом слое, очевидно, будет на поверхности внутреннего электрода
E1max = q/(4p·r12·er1e0)=10-8/(4p·122·10-6·5·8,85·10-12) = 1,249·105 В/м.
Максимальное значение напряженности поля во втором слое на сферической поверхности раздела диэлектриков
E2max = q/(4pr22·er2·e0)=10-8/(4p162·10-6·3·8,85·10-12) =1,171*105 В/м.
Графики изменения напряженности поля в диэлектрике вдоль радиуса представлены на рис.1.6. Значения напряженности на графиках приведены в относительных единицах. За базисное значение принято максимальное значение напряженности в первом слое Eb= E2max.
Разность потенциалов между электродами определяется при помощи следующего выражения:
Емкость конденсатора равна (1.15)
C=q/U12 = 10-8/885,6 = 1,129·10-11Ф.
Отметим, что емкость сферического конденсатора с двухслойным диэлектриком можно определить и по такой формуле
С=С1С2/(С1+С2),
где С1 – емкость сферического конденсатора с однослойным диэлектриком с радиусами обкладок r1 и r2 и диэлектрической проницаемостью диэлектрика, равной диэлектрической проницаемости первого слоя; С2 – емкость сферического конденсатора с однослойным диэлектриком с радиусами обкладок r2 и r3 и диэлектрической проницаемостью диэлектрика, равной диэлектрической проницаемости второго слоя.
Поскольку емкость сферического конденсатора с однослойным диэлектриком определяется с помощью выражения (1.18), то емкости С1, С2 и С будут равны:
С1 = 4·p·8,85·10-12·5·0,012·0,016/(0,016-0,012) = 2,669·10-11Ф;
С2=4·p·8,85·10-12·3·0,016·0,022/(0,022-0,016) = 1,957·10-11Ф;
С=2,669·1,957·10-11(2,669+1,957) = 1,129·10-11Ф.
Для наилучшего использования диэлектриков в конденсаторе необходимо так подобрать толщину слоев, чтобы максимальное значение напряженности поля было одинаковым. Поскольку напряженность поля имеет максимальное значение у внутренней поверхности слоя, то для выполнения этого условия, необходимо, чтобы произведение квадрата внутреннего радиуса слоя на его диэлектрическую проницаемость было постоянным, то есть r12e1= r22e2=const.
Если значение диэлектрической проницаемости оставлять неизменным, а изменять толщину слоев, то с помощью данного выражения можно определить радиус поверхности раздела диэлектриков.
м.
Разность потенциалов U12 и емкость такого конденсатора будут равны: U12=910,13В; C=1,099*10-11Ф.
Пример 5.
Бесконечно длинная тонкая заряженная нить расположена в воздухе вдоль оси z цилиндрической системы координат (рис. 1.7). Линейная плотность заряда t=10-9Кл/м. Рассчитать и построить график изменения напряженности поля вдоль радиуса. Определить разность потенциалов между точками
m (rm=10cм; qm=270°) и n (rn=40cм; qn=180°).
Решение. В этом случае поле характеризуется цилиндрической симметрией, то есть во всех точках цилиндрической поверхности, охватывающей заряженную нить, произвольного радиуса r напряженность поля имеет одно и то же значение и направлена перпендикулярно к поверхности. Поэтому, если окружить нить цилиндрической поверхностью длиной l и радиусом r и использовать теорему Гаусса, то можно получить выражение для напряженности поля Е.
График изменения напряженности поля вдоль радиуса представлен на рис. 1.8.
Значение напряженности поля на графике даны в относительных единицах. За базисное значение принято значение напряженности на расстоянии одного миллиметра от начала координат (Еb=1,798·104 В/м).
Потенциал поля в любой точке m, расположенной на расстоянии rm от оси провода, равен:

Здесь rp – расстояние от оси провода до некоторой фиксированной точки пространства р, в которой потенциал принимается равным нулю.
Если за такую точку принять точку, расположенную на расстоянии одного метра от оси провода, то потенциал точки m будет равен:
.
Изменение потенциала вдоль радиуса представлено на рис. 1.8. Значения потенциала даны также в относительных единицах. За базисное значение потенциала принято значение потенциала в той же точке, что и базисное значение напряженности поля (Ub=124,226 В).
Разность потенциалов между точками, указанными в условии задачи, равна 24,931 В.
Пример 6.
Бесконечно длинный цилиндрический конденсатор с двухслойным диэлектриком имеет радиус внутреннего электрода r1=1 мм , внутренний радиус внешнего электрода – r3=4 мм и радиус поверхности раздела диэлектриков – r2=2 мм.
Относительное значение диэлектрической проницаемости внутреннего слоя диэлектрика er1=5, наружного слоя – er2=2,5. Поперечное сечение конденсатора показано на рис.1.9. Линейная плотность заряда конденсатора t = 10-8 Кл/м.
Определить и построить график изменения напряженности поля вдоль радиуса. Найти разность потенциалов между электродами.
Вычислить емкость конденсатора на единицу длины.
Решение. Для решения задачи используем обобщенную теорему Гаусса. В качестве поверхности интегрирования возьмем замкнутую цилиндрическую поверхность длиной l и радиусом r (r1?r?r3).
.
Ввиду цилиндрической симметрии (вектор электрического смещения на этой поверхности не изменяется по величине и направлен по радиусу) последнее уравнение можно переписать следующим образом:
D·2·p·r·l = t·l,
откуда
D = Dr = t/(2·p·r).
Напряженность поля в первом слое диэлектрика (r1 ?r ? r2) будет при этом равна:
E1 = D/(er1e0) = t/(2·p·er1e0·r).
Во втором слое (r2 ?r ? r3) –
E2 = D/(er2e0) = t/(2·p·er2e0·r).
График изменения напряженности поля представлен на рис.1.10. На графике значения напряженности поля представлены в относительных единицах. За базисное значение принято значение напряженности в первом слое при r = r1, ( Eb = 35,970 кВ/м).
Как видно из рис. 1.10, напряженность поля на границе раздела диэлектриков испытывает скачек. Для лучшего использования изоляции стараются подобрать толщину слоев диэлектрика и их диэлектрическую проницаемость таким образом, чтобы максимальное значение напряженности поля в обоих слоях было одинаково. Это будет соблюдаться при условии r1e1 = r2e2, как в данном примере.
Разность потенциалов между электродами определяется при помощи выражения (1.6), которое для цилиндрического конденсатора можно переписать в следующем виде:
74,792В.
Емкость конденсатора на единицу его длины будет равна:
С = t/U = 10-8/74,792 = 0,1337 нФ/м.
Отметим, что емкость цилиндрического конденсатора с двухслойным диэлектриком можно определить и по такой формуле
С=С1С2/(С1+С2),
где С1 – емкость цилиндрического конденсатора с однослойным диэлектриком с радиусами обкладок r1 и r2 и диэлектрической проницаемостью диэлектрика, равной диэлектрической проницаемости первого слоя; С2 – емкость цилиндрического конденсатора с однослойным диэлектриком с радиусами обкладок r2 и r3 и диэлектрической проницаемостью диэлектрика, равной диэлектрическойпроницаемости второго слоя.
Поскольку емкость цилиндрического конденсатора с однослойным диэлектриком определяется с помощью выражения (1.23), то емкости С1, С2 и С будут равны:
С = С1·С2/(С1 + С2) = 0,1337 нФ/м.
Пример 7.
Бесконечно длинный цилиндр, выполненный из диэлектрика, относительное значение диэлектрической проницаемости которого er1 = 4, заряжен и находится в минеральном масле (er2 = 2,5).
Радиус цилиндра r0 = 5мм (рис. 1.11). Объемная плотность заряда является функцией расстояния от оси цилиндра r = r/10.

Решение. В
качестве поверхности интегрирования выбирается боковая поверхность цилиндра длиной один метр, радиусом r и с осью, совпадающей с осью исходного цилиндра. При 0 ? r ? r0 внутри этой поверхности будет находиться заряд, величина которого может быть определена с помощью следующего выражения:
Таким образом, с учетом цилиндрической симметрии поля,
получим
Отсюда
где А1=9.416·108 В/м3.
В области вне цилиндра (r0?r??)
Из этого выражения легко определяется напряженность поля вне цилиндра
где А2=183.432 В.
Потенциал электрического поля внутри цилиндра (при условии, что точка, в которой потенциал поля принимается равным нулю, лежит на оси цилиндра) можно определить следующим образом:
Потенциал поля в области вне цилиндра равен
Здесь В2 – постоянная интегрирования, которую можно найти из условия равенства потенциалов на поверхности цилиндра.
В.
Распределение напряженности электрического поля и потенциала представлено в относительных единицах на рис. 1.12. За базисные значения напряженности поля и потенциала приняты максимальное значение напряженности на границе раздела сред (Еmax=3.669·104 В/м) и значение потенциала при r=0.019 м (jв=-284 В).
В частном случае, когда объемная плотность заряда r является постоянной величиной, решение упрощается, и выражения для функции напряженности поля и потенциала будут иметь вид:
где

Рассчитать электростатическое поле, создаваемое зарядом, который равномерно распределен между двумя цилиндрическими бесконечно длинными поверхностями.
Объемная плотность заряда r=10-6 Кл/м3.
Радиус внешнего цилиндра R1=20 см, внутреннего – R2 =4 см, расстояние между осями цилиндров – а=10 см. Относительное значение диэлектрической проницаемости окружающей среды и обоих цилиндров равно er1=1.
Определить распределение составляющих напряженности электрического поля и потенциала вдоль осей Х и Y (рис. 1.13).
Решение.
Данная задача решается методом наложения. Сначала рассчитывается поле в любой точке М от заряда с объемной плотностью +r, равномерно распределенного по объему всего большого цилиндра. Затем в этой же точке рассчитывается поле от заряда, объемная плотность которого равна -r, равномерно распределенного по объему малого цилиндра. Результирующая напряженность поля Е в любой точке М определяется как векторная сумма напряженности Е1 и Е2. Потенциал любой точки определяется также как сумма потенциалов U1 и U2.
Так, в точке М, которая находится на расстоянии r1 от оси большого цилиндра и r2 от оси малого цилиндра и имеет координаты r1 и a (рис. 1.14) модули напряженности поля от соответствующих зарядов определяются согласно теореме Гаусса по следующим формулам:
Вектор напряженности Е1 направлен по радиусу r1 от оси О большого цилиндра, а вектор Е2 – по радиусу r2 к оси О1 малого цилиндра (рис. 1.14).
Потенциалы поля при этом будут равны:
Здесь С1 и С2 – постоянные интегрирования.
Потенциал поля в области между цилиндрами определяется следующим выражением:
Принимая потенциал равным нулю на оси большого цилиндра (r1=0; r2=a), найдем постоянную интегрирования С.
С учетом этого, выражение для потенциала в области между цилиндрами окончательно можно записать в следующем виде:
Если поле определяется в области, лежащей внутри малого цилиндра, то напряженность поля в произвольной точке этой области будет определяться при помощи следующего выражения:
Здесь i – единичный орт, направленный вдоль оси Х.
Таким образом, внутри малого цилиндра напряженность поля будет иметь только одну составляющую, направленную вдоль оси Х и являющуюся постоянной величиной.
Потенциал поля при этом будет равен
где В – постоянная интегрирования.
Эта постоянная определяется исходя из равенства потенциалов для точки, лежащей на поверхности малого цилиндра, один из которых рассчитывается по последнему уравнению, а второй – по выражению, справедливому для точек, находящихся в области между цилиндрами.
Определяя с помощью теоремы косинусов r2 через r1, выражения для потенциала и напряженности поля можно преобразовать.
.
Если точка, в которой определяется поле, лежит в области вне цилиндров (r1?R1), то модули напряженности поля будут определяться при помощи следующих выражений:
где t1 и t2 – линейная плотность зарядов большого и малого цилиндров.
Направление векторов напряженности поля определяется так же, как и для области, лежащей между цилиндрами.
Потенциал поля для области вне цилиндров будет равен
Постоянная интегрирования В1 определяется из условия равенства потенциалов на поверхности большого цилиндра (r1=R1, r2=R1-a), один из которых рассчитывается по последнему уравнению, а второй – по выражению, справедливому для точек, находящихся в области между цилиндрами.
Следовательно, окончательно можно записать следующее выражение для определения потенциала в данной области:
Построим графики изменения модуля напряженности поля и потенциала вдоль оси Y при х=0, для чего положим r1=y; r2=(y2+a2)0,5.
При этом выражения для напряженности поля и потенциала можно несколько преобразовать. Так, при 0?y?R1 они будут иметь следующий вид:
В области вне цилиндров (у?R1) эти выражения можно записать следующим образом:
Графики изменения данных функций представлены на рис. 1.15.
На графиках все величины даны в относительных величинах. За базисные значения потенциала и напряженности поля приняты значения соответствующих функций на поверхности цилиндра радиусом R1 (x=0; y=R1), которые оказались равными Uб=-1057 В,
Еб=10,94 кВ/м.
На рис. 1.16 представлены графики распределения потенциала и напряженности поля (в относительных единицах) вдоль оси Х (при Y=0).
Пример 9.
Рассчитать электростатическое поле от двух бесконечно длинных, равномерно заряженных, параллельных, тонких проводников, расположенных в воздухе на расстоянии 2d=6 м друг от друга. Проводники имеют одинаковые по величине, но противоположные по знаку заряды, линейная плотность которых равна t=4*10-9 Кл/м.
Построить график изменения напряженности поля вдоль оси Y (при х=0) и вывести уравнения для построения эквипотенциальных линий и линий поля.
Решение.
Поскольку среда линейна, то данную задачу можно решить методом наложения.
Вначале рассчитываем напряженность поля в любой точке М от правого провода (рис. 1.17), а затем в этой же точке от левого провода. Задача по расчету поля от бесконечно длинного заряженного провода решена в примере 5. Поэтому сразу запишем выражения для определения напряженности поля от правого и левого провода
Направление векторов напряженности поля показано на рис. 1.17. Результирующая напряженность поля определяется как векторная сумма этих векторов
Модуль данной результирующей напряженности поля рассчитывается по формуле
где
E1x, E2x,
E1y, E2y—
проекции векторов напряженности поля на соответствующие декартовы оси координат.
Здесь yм и xм – координаты произвольной точки М.
В частности, если точка М лежит на оси Y, то (r1=r2) результирующая напряженность поля будет направлена вдоль оси Х (Е=Ех). График распределения данной величины вдоль оси Y представлен на рис. 1.18. Значения напряженности поля на графике даны в относительных единицах, при этом за базисное значение принято значение напряженности в начале координат (x=0, y=0), которое оказалось равным 47,956 В/м.
Потенциал поля в любой точке М определяется также, как сумма потенциалов поля от одного и другого провода
Здесь С – постоянная интегрирования. Эта постоянная будет равна нулю, если принять потенциал точки, которая находится в начале координат, равным нулю.
В этом случае ось OY будет являться эквипотенциальной линией нулевого потенциала.
Все остальные линии равного потенциала являются окружностями с центрами, лежащими на оси ОХ. Координаты этих центров и радиусы окружностей определяются с помощью следующих формул:
Таким образом, если необходимо провести линию равного потенциала через точку, потенциал которой задан (например, 100 В), то надо определить k, используя формулу для потенциала
При построении картины поля, для того чтобы приращение потенциала при переходе от любой линии равного потенциала к соседней оставалось постоянным, должно соблюдаться условие
Здесь В – постоянная; n – порядковый номер линии равного потенциала.
Таким образом, число k при возрастании порядкового номера линии равного потенциала n должно изменяться в геометрической прогрессии.
Линиями поля данной системы заряженных проводников являются дуги окружностей, пересекающихся с проводниками. При этом, центры этих дуг лежат на оси OY и имеют координаты, которые определяются при помощи следующей формулы:
Чтобы при построении картины поля подразделить поле на трубки равного потенциала, необходимо при переходе от любой линии напряженности поля к соседней изменять угол J на постоянную величину.
Пример 10.
Два одинаковых бесконечно длинных проводящих цилиндра расположены в воздухе. Радиус цилиндров R=0.04 м, расстояние между геометрическими осями 2h=0.12 м (рис.1.19).
Напряжение, приложенное к цилиндрам U12=100 В.
Рассчитать электростатическое поле, построить графики изменения напряженности поля и потенциала вдоль оси х.
Найти емкость системы проводов на единицу длины.
Решение.
Поле внутри проводящих проводов отсутствует. Поле же в воздухе будет точно таким, как и поле от двух бесконечно тонких линейных проводников, проходящих через электрические оси данных проводов.
Таким образом, задача по расчету поля двух проводов круглого сечения сводится к нахождению электрических осей проводов, поскольку в дальнейшем расчет поля в воздухе будет аналогичным расчету поля, проведенному в предыдущем примере.
Поскольку поверхность проводящих проводов является поверхностью равного потенциала, то, используя выражения для координаты центра и радиуса линий равного потенциала, которые приведены в примере 9, можно получить формулу для определения координат центра электрических осей проводов b.
В условии задачи задана не линейная плотность зарядов, а разность потенциалов между проводами (разность потенциалов между точками m и n).
Поэтому, прежде всего, следует определить линейную плотность зарядов t. Для этого используем выражение для потенциалов, которое также приведено в предыдущем примере
Здесь r1 и r2 – расстояние от электрической оси первого (левого) и второго провода, соответственно, до точки m, которая находится на поверхности первого провода, а r1/ и r2/ – расстояние от электрической оси первого и второго провода, соответственно, до точки n, которая находится на поверхности второго провода.
С учетом последних соотношений, можно записать выражение для определения линейной плотности зарядов
После определения линейной плотности зарядов и расположения электрических осей проводов, выражения для расчета напряженности поля и потенциала в области вне проводов полностью аналогичны тем, которые приведены в примере 9.
Графики распределения напряженности поля и потенциала вдоль оси ОХ (при y=0) приведены на рис. 1.20. Все значения на графике даны в относительных единицах, причем, за базисные значения приняты значения напряженности поля и потенциала на поверхности правого провода, которые оказались равными Еб=2904 В/м, jб=-50 В.
С учетом того, что ось OY является осью симметрии для напряженности поля и осью антисимметрии для потенциала, графики построены только для положительных значений х.
Емкость между двумя проводниками на единицу их длины определяется при помощи следующего выражения:
Пример 11. Рассчитать
электростатическое поле от двух параллельных бесконечно длинных заряженных несоосных проводящих цилиндров, расположенных в воздухе. Радиусы цилиндров R1=0.02 м и R2=0.04 м. Расстояние между геометрическими осями D=0.08 м (рис. 1.21). Цилиндры имеют одинаковый по величине, но противоположный по знаку заряд, линейная плотность которого t1=-t2=t=10-8 Кл/м.
Определить разность потенциалов между цилиндрами, емкость системы на единицу длины.
Построить график изменения потенциала поля вдоль оси ОХ (при y=0).
Решение.
Расположим оси цилиндров (О1 и О2) так, чтобы их поверхности совпали с поверхностями равного потенциала. Обозначим через h1 и h2 расстояние от геометрических осей первого и второго цилиндра до плоскости постоянного (нулевого) потенциала, а через b – расстояние от электрических осей-до этой плоскости. После определения данных величин задача по расчету поля в области вне цилиндров сводится к расчету электростатического поля от двух заряженных бесконечно длинных линейных проводов, проходящих через центры зарядов, и оказывается, таким образом, полностью аналогичной задачам, рассмотренным в предыдущих примерах.
Используя выражение для определения координат центров зарядов, справедливое как для одного, так и для второго провода, составим следующее уравнение:
или
При заданном расположении цилиндров (рис. 1.21) имеем
h1+h2=D
и, следовательно,
.
В этом случае
Разность потенциалов между двумя цилиндрами можно определить по следующей формуле (как и в примере 10):
Здесь r1/ и r2/ – расстояние от центра электрических осей первого и второго цилиндра, соответственно, до точки n, лежащей на поверхности первого цилиндра; r1// и r2// – расстояние от центра электрических осей первого и второго цилиндра, соответственно, до точки m, лежащей на поверхности второго цилиндра
r1/ = (R1 + b – h1) = 0.0131м; r2/ = 2b – r1/ = 0.0381м;
r2// = (R2 + b – h2) = 0.0181м; r1// = 2b – r2// = 0.0331м.
Потенциал любой произвольной точки d будет равен
где r1 и r2 – расстояние от электрических осей первого и второго провода до точки d.
Если точка d лежит на оси ОХ между цилиндрами, то
r2 = b – x; r1 = b + x;
График изменения потенциала вдоль оси ОХ (при (R1 – h1) < x < (h2 – – R2)) показан на рис. 1.22.
Емкость системы цилиндров на единицу длины определяется по следующей формуле:
Построение линий равного потенциала и линий поля в области вне цилиндров проводится таким же образом, как и для линейных проводов, которые совпадают с электрическими осями (см. пример 9).
Пример 12. Бесконечно длинный проводящий цилиндр радиусом R1=2см расположен внутри другого бесконечно длинного проводящего цилиндра радиусом R2=6см.
Расстояние между геометрическими осями цилиндров D=3см (рис. 1.23). Область между цилиндрами заполнена диэлектриком с относительным значением диэлектрической проницаемости er=2.
Цилиндры имеют одинаковый по величине, но противоположный по знаку заряд, линейная плотность которого t1=-t2=t=10-8Кл/м.
Определить разность потенциалов между цилиндрами, емкость системы на единицу длины. Построить график изменения напряженности поля вдоль оси Х (при Y=0) между цилиндрами.
Решение.
Решение данной задачи, как и в предыдущих примерах, сводится к отысканию положения электрических осей.
Полагая, что оси проводов расположены так, что их поверхности совпадают с эквипотенциальными поверхностями электростатического поля, будем иметь:
где h1 и h2 – расстояние от геометрических осей цилиндров до плоскости постоянного (нулевого) потенциала; b – расстояние от электрических осей до этой же плоскости.
Последнее выражение можно переписать следующим образом:
Но, поскольку при расположении цилиндров один внутри другого, выполняется равенство
то
Таким образом, выражения для определения h1, h2, и b будут иметь следующий вид:
После нахождения положения электрических осей задача по расчету поля в диэлектрике между цилиндрами становится полностью аналогичной задаче по расчету поля от линейных проводов, совпадающих с электрическими осями цилиндров.
Так, потенциал любой точки М, находящейся в области между цилиндрами, будет равен
где r1 и r2 – расстояние от электрических осей первого и второго цилиндров соответственно до точки М.
Разность потенциалов между цилиндрами (между точками m и n) при этом будет равна
Здесь r1/ и r2/ – расстояние от электрических осей первого и второго цилиндров соответственно до точки m, а r1// и r2// – расстояние от электрических осей этих цилиндров до точки n.
При заданном расположении цилиндров указанные расстояния будут равны
Таким образом, разность потенциалов между цилиндрами Umn будет составлять величину, равную 67.1В.
Напряженность электрического поля в любой точке, лежащей на оси ОХ между цилиндрами (между точками m и n), находится методом наложения
График изменения данной величины вдоль оси ОХ представлен на рис. 1.24.
Для удобства изображения все величины на рисунке представлены в относительных единицах. За базисное значение напряженности поля принято значение напряженности поля на поверхности малого цилиндра в точке m (Eb =Еm=8020 В/м), а за базисное значение переменной х – абсолютное значение координаты этой же точки (хb=|хm|= 0.0183 м).
Емкость системы проводов на единицу их длины определяется с помощью следующей формулы:
Зная разность потенциалов между цилиндрами и линейную плотность зарядов t емкость С, согласно определению, можно найти и как отношение линейной плотности зарядов к разности потенциалов
Для построения силовых линий и линий равного потенциала можно воспользоваться рекомендациями, данными в предыдущих примерах.