Что такое вихревое электрическое поле
В электростатике источником поля являются положительно или отрицательно заряженные неподвижные частицы.
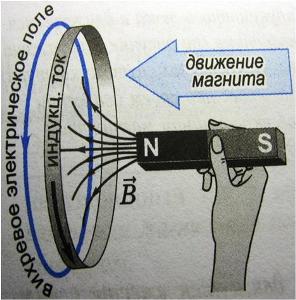
Возьмем замкнутый проводник. В проводнике имеются свободные электроны, движение которых без воздействия электрического поля носит хаотичный характер. Поместим проводник в магнитное поле. По закону электромагнитной индукции, открытому М. Фарадеем, при изменении магнитного потока, пронизывающего виток, в витке появляется электродвижущая сила (ЭДС).
ЭДС действует на свободные электроны проводника, в результате заряды начинают двигаться упорядоченно. Так возникает индукционный ток, который вместе с ЭДС является индикатором вихревого поля.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Вихревое поле в физике — это электрическое поле, появляющееся в результате взаимодействия переменного магнитного поля и проводящего контура. Силовые линии вихревого поля всегда замкнуты.
Особенности, что является причиной возникновения
Магнитное поле само по себе не является источником зарядов, оно порождает ЭДС.
Примечание 1
Сделаем следующий вывод: главное отличие вихревого поля от электростатического заключается в том, что условие существования первого — наличие изменяющегося во времени магнитного потока, а второго — наличие электрического заряда или зарядов.
Из указанного свойства следует, что вихревое поле может существовать даже при отсутствии проводника. Благодаря этой особенности явление электромагнитной индукции и электрические вихревые поля находят применение в ускорителях частиц.
Магнитное поле также можно считать вихревым, поскольку его силовые линии замкнуты и поле существует без «магнитных» зарядов. Тогда аналогично электрическому вихревое магнитное поле возникает при:
- наличии тока проводимости, то есть при движении заряженных частиц;
- изменении во времени электрического поля.
Изменяющееся во времени электрическое поле, порождающее магнитное, называют током смещения.
Примечание 2
Ток смещения не является током в общепринятом понимании. Токи смещения — это не движущийся поток частиц-зарядов, а скорее физическое явление.
Явление, при котором под действием электрического образуется магнитное поле, называют магнитоэлектрической индукцией.
Взаимодействие электрического и магнитного полей приводит к появлению электромагнитных волн. При этом напряженность электрического поля и индукция магнитного совершают колебания в перпендикулярных плоскостях.
Скорость распространения электромагнитных волн, как и любых других волн, будет зависеть от свойств среды.
Работа вихревого электрического поля
В электростатическом поле работа по перемещению заряда зависит от величины этого перемещения. Когда заряженная частица, находясь в электростатическом поле, перемещается по замкнутому контуру, работа равна нулю.
Это утверждение нельзя применить к полю, имеющему вихревой характер. В этом случае, на всей траектории движения векторы силы и перемещения направлены в одну строну, и циркуляция векторного поля (работа сил поля) будет равна ЭДС.
Вихревое электрическое поле является не потенциальным, так как работа сил не зависит от величины перемещения.
Потенциальными называют поля, работа сил которых не зависит от траектории движения объекта, а определяется величиной перемещения — разностью конечных и начальных координат объекта. Силовые линии таких полей всегда разомкнуты.
Пример
Примерами потенциальных полей являются электростатическое, гравитационное поля.
Напряженность вихревого электрического поля, формула
Электрическое поле в данной точке характеризуется величиной напряженности.
Линии напряженности вихревого электрического поля представляют собой замкнутые витки. Направление вектора напряженности совпадает с направлением индукционного тока и определяется по правилу Ленца.
Правило
Индукционный ток в витке направлен так, чтобы противодействовать внешнему магнитному полю, приведшему к появлению этого тока.
На практике часто используют правило правой руки. Для этого правой рукой охватывают проводник так, чтобы отогнутый большой палец совпадал с направлением силовых линий магнитного поля. Четыре пальца при этом укажут направление вектора напряженности. При уменьшении магнитного поля вектор напряженности будет направлен в противоположную сторону.
Сила, с которой поле воздействует на единичный заряд q, определяется по формуле:
Формула 1
(overrightarrow F=qcdotoverrightarrow E)
Отсюда получим выражение для напряженности:
Формула 2
(overrightarrow E=frac{overrightarrow F}q)
ЭДС представляет собой работу сил поля, отнесенную к величине заряда, то есть:
Формула 3
(ЭДС=frac Aq=frac{Fcdot S}q)
где S — величина перемещения, м.
Вихревое поле возникает в замкнутом проводнике, перемещение равно длине окружности. Тогда подставив в выражении для ЭДС формулу силы, получим:
Формула 4
(ЭДС=frac{Ecdot qcdot2cdotpicdot r}q=2mathrmpicdotmathrm rcdotmathrm E)
где r — радиус проводника, м.
Тогда формула для напряженности будет иметь вид:
Формула 5
(mathrm E=frac{mathrm{ЭДС}}{2mathrmpicdotmathrm r})
Вихревое электрическое поле — это электрическое поле, которое порождается переменным магнитным полем и линии напряженности которго замкнуты.
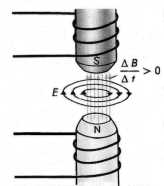
Переменное магнитное поле порождает индуцированное электрическое поле. Если магнитное поле постоянно, то индуцированного электрического поля не возникнет. Следовательно, индуцированное электрическое поле не связано с зарядами, как это имеет место в случае электростатического поля; его силовые линии не начинаются и не заканчиваются на зарядах, а замкнуты сами на себя, подобно силовым линиям магнитного поля. Это означает, что индуцированное электрическое поле, подобно магнитному, является вихревым.
Если неподвижный проводник поместить в переменное магнитное поле, то в нем индуцируется э. д. с. Электроны приводятся в направленное движение электрическим полем, индуцированным переменным магнитном полем; возникает индуцированный электрический ток. В этом случае проводник является лишь индикатором индуцированного электрического поля. Поле приводит в движение свободные электроны в проводнике и тем самым обнаруживает себя. Теперь можно утверждать, что и без проводника это поле существует, обладая запасом энергии.
Сущность явления электромагнитной индукции заключается не столько в появлении индуцированного тока, сколько в возникновении вихревого электрического поля.
Это фундаментальное положение электродинамики установлено Максвеллом как обобщение закона электромагнитной индукции Фарадея.
В отличие от электростатического поля индуцированное электрическое поле является непотенциальным, так как работа, совершаемая в индуцированном электрическом поле, при перемещении единичного положительного заряда по замкнутому контуру равна э. д. с. индукции, а не нулю.
Направление вектора напряженности вихревого электрического поля устанавливается в соответствии с законом электромагнитной индукции Фарадея и правилом Ленца. Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока.
Так как вихревое электрическое поле существует и в отсутствие проводника, то его можно применять для ускорения заряженных частиц до скоростей, соизмеримых со скоростью света. Именно на использовании этого принципа основано действие ускорителей электронов — бетатронов.
Индукционное электрическое поле имеет совершенно другие свойства в отличии от электростатического поля.
Отличие вихревого электрического поля от электростатического
1) Оно не связано с электрическими зарядами;
2) Силовые линии этого поля всегда замкнуты;
3) Работа сил вихревого поля по перемещению зарядов на замкнутой траектории не равна нулю.
|
электростатическое поле |
индукционное электрическое поле |
| 1. создается неподвижными электр. зарядами | 1. вызывается изменениями магнитного поля |
| 2. силовые линии поля разомкнуты — потенциальное поле | 2. силовые линии замкнуты — вихревое поле |
| 3. источниками поля являются электр. заряды | 3. источники поля указать нельзя |
| 4. работа сил поля по перемещению пробного заряда по замкнутому пути = 0. | 4. работа сил поля по перемещению пробного заряда по замкнутому пути = ЭДС индукции |
Вихревое электрическое поле
Из закона
электромагнитной индукции следует, что
любое изменение сцепленного с контуром
магнитного потока Ф приводит к
возникновению ЭДС индукции εi
и появлению
индукционного тока i
Возникновение ЭДС
индукции возможно и в неподвижном
контуре при условии, что существует
переменное магнитное поле. Известно,
что ЭДС в цепи возникает тогда, когда в
ней на носители тока действуют сторонние
силы. При электромагнитной индукции
эти силы не связаны ни с тепловыми,
химическими и другими процессами в
контуре. Они не являются силами Лоренца,
т.к. на неподвижные заряды сила Лоренца
не действует, Для объяснения ЭДС индукции
в неподвижных проводниках Максвелл
высказал гипотезу, что всякое
переменное поле (магнитное), возбуждает
в окружающем пространстве электрическое
поле, которое и является причиной
возникновения индукционного тока в
проводнике. При этом контур, в котором
возникает ЭДС, играет второстепенную
роль инструмента для обнаружения
возникающего электрического поля.
Циркуляция вектора ЕВ
напряженности этого поля по любому
замкнутому контуру L
представляет собой ЭДС индукции
εi
=
= —.
Учитывая, что dФ
= ВdS,
можно записать
=
и тогда
= —
.
Поля, для которых
циркуляция вектора по замкнутому контуру
не равна нулю, называются вихревыми.
Таким образом, электрическое поле
напряженностью ЕВ,
возбуждаемое переменным магнитным
полем, является вихревым, как и само
магнитное поле. Напомним, что циркуляция
вектора Еq
электростатического поля равна нулю,
т.к. электростатическое поле является
не вихревым, а потенциальным.
Ток смещения
По гипотезе
Максвелла всякое переменное магнитное
поле возбуждает в окружающем пространстве
вихревое электрическое поле. Основная
же идея Максвелла заключается в том,
что между электрическим и магнитным
полями существует и обратное соотношение,
т.е. изменяющееся во времени э
поле должно приводить к появлению
переменного магнитного поля. Для
установления количественных соотношений
между изменяющимся электрическим и
возникающим магнитным полями Максвелл
ввел в рассмотрение так называемыйток
смещения,
плотность которого обозначим jсм.
Рассмотрим участок цепи переменного
тока, содержащего конденсатор.
Движение
свободных носителей заряда имеет место
во всей цепи, кроме зазора между обкладками
конденсатора. При зарядке конденсатора
(рис. 131а) ток течет в направлении к
положительно заряженной обкладке,
поверхностная плотность заряда на
которой +σ. Между обкладками будет
существовать электрическое поле с
напряженностью Е
и индукцией D.
D
= ε ε0E;
D
= σ.
При
зарядке индукция D
в зазоре возрастает, т.е.
и по направлению совпадает с направлением
jпр
плотности
тока проводимости в обкладке конденсатора.
Величина jпр
тока проводимости в обкладке площадью
S
можно выразить так
.
По
Максвеллу переменное электрическое
поле в конденсаторе создает такое
магнитное поле, как если бы между
обкладками конденсатора существовал
ток проводимости плотностью такой же,
как в обкладке конденсатора, т.е.
jпр
= jсм.
Из
этого следует, что
При
разрядке конденсатора (рис. 131б) изменяется
во времени поверхностная плотность
заряда σ на обкладках, а значит, изменяется
и индукция D
в зазоре. Индукция D
убывает,
Это значит, чтоjсм
=совпадает по направлению и по величине
сjпр
как и при
зарядке конденсатора. Из сказанного
можно заключить, что ток проводимости
и ток смещения равны по величине и
одинаковы по направлению.
Ток
смещения следует понимать в том смысле,
что переменное электрическое поле
в конденсаторе в любой момент времени
создает такое же магнитное поле, как
если бы между обкладками существовал
ток проводимости, имеющий силу, равную
силе тока в подводящих проводниках. Из
всех физических свойств, присущих току
проводимости, Максвелл приписал току
смещения лишь одно – способность
создавать в окружающем пространства
магнитное поле, т.е. ток смещения
эквивалентен току проводимости только
по способности создавать магнитное
поле.
Если
в проводнике течет переменный ток, то
внутри проводника существует
переменное электрическое поле, а значит,
имеются ток проводимости и ток
смещения. Магнитное поле в нем определяется
суммой токов, т.е. полным током. При
расчетах магнитных полей в формулы
нужно подставлять полную плотность
тока jполн
= jпр
+ jсм
= jпр
+
В зависимости от электропроводности
среды и быстроты изменения поля (частоты
тока) оба слагаемых играют разную роль.
В хорошо проводящих веществах плотность
тока смещения мала и им можно пренебречь.
В плохо проводящих средах и при высоких
частотах ток смещения играет основную
роль.
Уравнения
Максвелла.
Теория
электромагнитного поля Максвелла
основана на двух основных положениях:
-
всякое изменение
магнитного поля вызывает появление
вихревого магнитного поля; -
всякое изменение
электрического поля вызывает появление
вихревого электрического поля.
Эта
теория в строгой форме выражена в виде
уравнений Максвелла. В учении об
электричестве и магнетизме эти уравнения
играют такую же роль, как законы Ньютона
в механике или основные законы в
термодинамике.
Полная система
уравнений Максвелла в интегральной
форме:
1.
3.
2.
4.
.
-
Электрическое
поле может быть потенциальным ( ЕQ
) и вихревым
( ЕВ
), поэтому
напряженность суммарного поля Е равна
Е
= ЕQ
+ ЕВ.
Циркуляция вектора ЕQ
равна нулю, а циркуляция вектора ЕВ
отражает закон электромагнитной
индукции
.
Из этого уравнения
следует, что электрические поля
создаются электрическими зарядами и
изменяющимися во времени магнитными
полями.
-
Это уравнение —
закон полного тока в обобщенном виде
и показывает, что магнитные поля
создаются движущимися зарядами (токами)
либо (и) переменными электрическими
полями. -
Это уравнение –
есть выражение теоремы Остроградского-Гаусса
для электростатического поля в
диэлектрике, где ρ – объемная
плотность заряда в рассматриваемом
объеме V. -
Теорема
Остроградского-Гаусса для потока
магнитной индукции означает, что линии
магнитной индукции замкнуты.
Для решения этих
уравнений необходимо знать связь между
вхоящими в них величинами
D
= εε0E
; B
= μμ0H
; j
=
γE.
Для стационарных
полей ( E
= const,
B
= const
) Уравнения Максвелла примут вид:
.
В
этом случае электрические и магнитные
поля независимы друг от друга и могут
изучаться отдельно друг от друга.
Уравнения Максвелла
в дифференциальной форме имеют вид:
.
Контрольные
вопросы.
-
Магнитное поле.
Индукция магнитного поля. Сила Лоренца.
Движение заряженной частицы в
магнитном поле. -
Сила Ампера.
Работа, совершаемая при перемещении
проводника с током в магнитном поле. -
Контур с током в
магнитном поле. Момент сил, действующих
на контур. Магнитный момент. Энергия
контура с током в магнитном поле. -
Закон Био-Савара-Лапласа
и его применение к расчёту магнитного
поля. -
Теорема Гаусса и
теорема о циркуляции (закон полного
тока) для магнитного поля. Применение
закона полного тока к расчёту магнитного
поля. -
Магнитное поле
длинного соленоида. Потокосцепление.
Индуктивность, Индуктивность длинного
соленоида. -
Индукция токов в
движущихся проводниках. Электродвижущая
сила индукции. Вращение рамки в магнитном
поле. Генераторы переменного тока. -
Явление
электромагнитной индукции. Закон
электромагнитной индукции. Правило
Ленца. Вихревое электрическое поле. -
Явление самоиндукции.
Электродвижущая сила самоиндукции.
Магнитная энергия тока. Объёмная
плотность энергии магнитного поля. -
Магнитные моменты
атомов. Диа- и парамагнетизм.
Намагниченность. Закон полного тока
для магнитного поля в веществе.
Напряжённость магнитного поля. Магнитная
восприимчивость и магнитная проницаемость. -
Ферромагнетики.
Кривая намагничивания. Магнитный
гистерезис,
Остаточное намагничивание.
Коэрцитивная сила. Магнитная проницаемость
ферромагнетика. -
Ток
смещения. Система уравнений Максвелла
в интегральной форме. Физический смысл
уравнений Максвелла. Дифференциальные
уравнения.
Соседние файлы в папке Физика
- #
- #
- #
- #
- #
- #