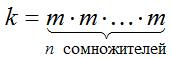Натуральные числа — одно из старейших
математических понятий.
В далёком прошлом люди не знали чисел и,
когда им требовалось пересчитать предметы
(животных, рыбу и т.д.), они делали это не так, как
мы сейчас.
Количество предметов сравнивали с частями тела, например, с
пальцами на руке и говорили: «У меня столько же орехов, сколько пальцев на руке».
Со временем люди поняли, что пять орехов, пять коз и пять зайцев обладают
общим свойством — их количество равно пяти.
Запомните!
Натуральные числа — это числа, начиная с 1, получаемые
при счете предметов.
1, 2, 3, 4, 5…
Наименьшее натуральное число — 1.
Наибольшего натурального числа не существует.
При счёте число ноль не используется. Поэтому ноль не
считается натуральным числом.
Записывать числа люди научились гораздо позже, чем считать. Раньше
всего они стали изображать единицу одной палочкой, потом
двумя палочками — число 2, тремя — число 3.
| — 1, || — 2, ||| — 3, ||||| — 5 …
Затем появились и особые знаки для обозначения чисел — предшественники современных
цифр. Цифры, которыми мы пользуемся для записи чисел, родились в Индии примерно 1 500
лет назад. В Европу их привезли арабы, поэтому их называют
арабскими цифрами.
Всего цифр десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С помощью этих
цифр можно записать любое натуральное число.
Запомните!
Натуральный ряд — это последовательность всех натуральных чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …
В натуральном ряду каждое число больше предыдущего на 1.
Натуральный ряд бесконечен, наибольшего натурального числа в нём не существует.
Систему счёта (счисления), который мы пользуемся,
называют десятичной позиционной.
Десятичной потому, что 10 единиц каждого разряда образуют
1 единицу старшего разряда. Позиционной потому, что значение цифры
зависит от её места в записи числа, то есть от
разряда, в котором
она записана.
Важно!
Разряды и классы
(включая класс миллионов) подробно разобраны
на нашем сайте в материалах для начальной школы.
Класс миллиардов
Если взять десять сотен миллионов, то получим новую разрядную единицу —
один миллиард или в записи цифрами.
1 000 миллионов = 1 000 000 000 = 1 млрд
Десять таких единиц — десять миллиардов, десять десятков миллиардов образуют
следующую единицу — сто миллиардов.
Запомните!
Миллиарды, десятки миллиардов и сотни миллиардов образуют четвёртый
класс — класс миллиардов.
Разряды и классы натурального числа
Рассмотрим натуральное число 783 502 197 048
| Название класса |
Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) |
7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
| Название класса |
Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) |
7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
C помощью таблицы разрядов прочитаем это число. Для этого надо слева направо по очереди
называть количество единиц каждого класса и добавлять название класса.
Название класса
единиц не произносят, также не произносят название класса, если все три
цифры в его разрядах — нули.
Теперь прочтем число 783 502 197 048 из таблицы:
783 миллиарда 502 миллиона 197 тысяч
48.
Числа 1, 10, 100, 1000… называются разрядными единицами. С их помощью натуральное число
записывается в виде разрядных слагаемых. Так, например, число 307 898 будет выглядеть
в виде разрядных слагаемых.
307 898 = 300 000 + 7 000 + 800 + 90 + 8
Проверить свои вычисления
вы можете с помощью нашего
калькулятора разложения числа на разряды онлайн.
Следующие за миллиардом классы названы в соответствии с латинскими
наименованиями чисел. Каждая следующая единица содержит тысячу предыдущих.
- 1 000 миллиардов = 1 000 000 000 000 = 1 триллион («три» — по латыни «три»)
- 1 000 триллионов = 1 000 000 000 000 000 = 1 квадриллион («квадра» — по латыни «четыре»)
- 1 000 квадриллионов = 1 000 000 000 000 000 000 = 1 квинтиллион («квинта» — по латыни «пять»)
Все числа пересчитать невозможно, поскольку за каждым числом следует число на единицу большее,
но очень большие числа в повседневной жизни не нужны.
Однако, физики нашли число, которое превосходит количество всех атомов (мельчайших частиц вещества)
во всей Вселенной.
Это число получило специальное название — гугол. Гугол — число, у которого
100 нулей.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
7 сентября 2021 в 6:39
Анастасия Орнацкая
Профиль
Благодарили: 0
Сообщений: 1
Анастасия Орнацкая
Профиль
Благодарили: 0
Сообщений: 1
Рассмотрим частное от делений всевозможных двузначных натуральных чисел на суммы их цифр. Какое из частных окажется наибольшим?
0
Спасибо
Ответить
8 сентября 2021 в 3:32
Ответ для Анастасия Орнацкая
Александр Войтов
Профиль
Благодарили: 0
Сообщений: 1
Александр Войтов
Профиль
Благодарили: 0
Сообщений: 1
10
0
Спасибо
Ответить
7 октября 2020 в 10:53
Екатерина Шабан
Профиль
Благодарили: 0
Сообщений: 1
Екатерина Шабан
Профиль
Благодарили: 0
Сообщений: 1
Добрый день. Помогите с заданием: Найти все возможные значения натуральные числа x,y,z, таких, что произведение любых двух увеличеное на 1 будет делится на третье.
0
Спасибо
Ответить
10 октября 2020 в 1:07
Ответ для Екатерина Шабан
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Пусть x ≤ y ≤ z. Тогда xy + 1 = kz ≥ ky.
Откуда y(k — x) ≤ 1.
Тогда x = y = 1; k = 2; z=1;
Или x = y = 1; k = 1; z=2.
0
Спасибо
Ответить
4 декабря 2019 в 19:33
Иван Федянин
Профиль
Благодарили: 0
Сообщений: 1
Иван Федянин
Профиль
Благодарили: 0
Сообщений: 1
Известно, что c и d натуральные числа и 5c+d=33
Каким может быть число c?
Помогите решить и расписать решение.
0
Спасибо
Ответить
18 декабря 2019 в 12:03
Ответ для Иван Федянин
Эмма Аддамс
Профиль
Благодарили: 0
Сообщений: 2
Эмма Аддамс
Профиль
Благодарили: 0
Сообщений: 2
1. Натуральное число может быть только положительным и оно всегда отлично от нуля.
2. Таким образом, если 5с-d=33, то с= и это целое(!) число.
3. Значит, 33-d деится на 5 нацело.
4. Вспоминаем, что на пять делятся числа: 5, 10, 15, 20, 25, 30,…
5.Теперь находим значения d, а потом выражаем через них значения с.
33-d=5, d=28. c==1
33-d=10. d=23. c=2
………………………………….
и так далее до 33-d=30. d=3
Числа больше 35 мы не берем, поскольку тогда мы получим отрицательные значения чисел с и d, а это противоречит условию натуральности этих чисел
6. Ответ: с=1, 2, 3, 4, 5, 6.
Задача решена:)
А вот здесь онлайн занятия по математике
https://www.youtube.com/channel/UChuPWiMp13sUQ6G6oPTjzag
0
Спасибо
Ответить
13 февраля 2019 в 23:06
Mamikon Papikyan
Профиль
Благодарили: 0
Сообщений: 1
Mamikon Papikyan
Профиль
Благодарили: 0
Сообщений: 1
Здравствуйте. Помогите пожалуйста решить этот вопрос!!!как узнать сколько чисел заключенных между 1000 и 9999 содержат цифру 1?
0
Спасибо
Ответить
15 февраля 2019 в 23:26
Ответ для Mamikon Papikyan
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Всего чисел от 1000 до 9999 − 9000.
Чисел без 1 − 8 · 93.
Значит, остальные 9000 − 8 · 93 с единицей.
0
Спасибо
Ответить
15 ноября 2016 в 0:26
Злата Крамаренко
Профиль
Благодарили: 0
Сообщений: 3
Злата Крамаренко
Профиль
Благодарили: 0
Сообщений: 3
Найдите все пары натуральных чисел а и b, таких, что а ? b и выполнено равенство:
+
=
Я привела к дроби левой части к общему знаменателю, сделала правилом пропорции, получила: 10(а+в)=ав. После я предположила, что 10 — это как 5*2, 2*5, 10*1 и 1*10, натуральные числа. но если делать так, то получается, что во всех случаях одно из чисел отрицательное, т.е не натуральное. Пыталась как-то выделить одну переменную через другую, но не пришла ни к чему. И в конце я просто нашла методом подбора и логически это пары (например, 20 и 20, 15 и 30, 14 и 35), но методом подбора это задание решить нельзя, ведь натуральные числа это от 1 и до бесконечности. Что делать? Заранее спасибо.
0
Спасибо
Ответить
18 ноября 2016 в 2:07
Ответ для Злата Крамаренко
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
(11; 110); (12; 60); (14; 35); (15; 30); (20; 20).
b = 10 + .
0
Спасибо
Ответить
26 апреля 2016 в 18:35
Вика Вдовина
Профиль
Благодарили: 0
Сообщений: 1
Вика Вдовина
Профиль
Благодарили: 0
Сообщений: 1
Даны 10 натуральных чисел по порядку, когда убрали одно число, то сумма оставшихся чисел стала 961. Найдите это число?
0
Спасибо
Ответить
1 мая 2016 в 17:16
Ответ для Вика Вдовина
Миха Подписчик
Профиль
Благодарили: 0
Сообщений: 2
Миха Подписчик
Профиль
Благодарили: 0
Сообщений: 2
Пусть х — первое наименьшее число из 10 порядковых натуральных чисел.
Найдем сумму арифметической прогрессии этих чисел:
Сумма чисел без первого числа будет равна:
10х + 45 — х = 9х + 45
Если убрали не первое число, то полученная сумма больше, чем 961.
Составим неравенство и решим его:
9х + 45 > 961
9х > 961 — 45
9х > 916
х > 916: 9
x > 101,777777778
Допустим, что первое наименьшее число х = 102,
тогда сумма всех 10 чисел равна:
1065 — 961 = 104 — число, которое убрали.
Ответ: 104.
Надеюсь помог
0
Спасибо
Ответить
8 июня 2016 в 13:00
Ответ для Вика Вдовина
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Ответ: 104.
Пусть убрали число (k + p).
(k + 1) + (k + 2) +… + (k + 10) = 10k + 55 = 961 + (k + p)
=> p = 9k — 906.
Значит р равно 3 или 6.
p = 3 => k = 101;
p = 6 => 3k = 304, ?.
0
Спасибо
Ответить
11 декабря 2015 в 16:46
Вика Богатырёва
Профиль
Благодарили: 0
Сообщений: 1
Вика Богатырёва
Профиль
Благодарили: 0
Сообщений: 1
верно ли утверждение? а) 3,5 пренадлежит множеству натуральных чисел? б) 7 пренадлежит множеству дествительных чисел? в) 5,4 пренадлежит множеству рациональных чисел?
0
Спасибо
Ответить
14 декабря 2015 в 21:47
Ответ для Вика Богатырёва
Юрий Деченко
Профиль
Благодарили: 0
Сообщений: 4
Юрий Деченко
Профиль
Благодарили: 0
Сообщений: 4
а ложное, б)верно в)тоже верно
0
Спасибо
Ответить
Натуральные числа
Математика начинается с натуральных чисел. Мы оперируем ими ежедневно: складываем, вычитаем, умножаем. Это лишь верхушка айсберга. Мы попросили учителя математики рассказать, что такое натуральные числа и каковы их особенности
Натуральные числа применялись человеком всегда. Даже в древности, используя для счета пальцы или палочки, люди обращались к натуральным числам. Считали, по порядку на единицу увеличивая исходное значение. Ловили рыбу — один карась, второй, третий. Продавали зерно — один мешок, второй, третий. Делали пряжу — один клубок, второй, третий.
Дальше числа оформили графически, а сейчас с их помощью выполняют любые математические действия.
Определение натуральных чисел
Натуральное — это число, которое применяется при счете. С его помощью можно определить количество любых предметов, их осязаемую последовательность. Например, подсчитать, сколько денег в кошельке, ворон на ветке, долек в апельсине, цветов в радуге.
Ряд натуральных чисел открывает единица. А замыкающего у него нет — он бесконечен. При этом в натуральном ряду каждый следующий символ на единицу больше предшественника — 10, 11, 12… Только так и никак иначе.
К натуральным не относятся отрицательные числа, дроби и ноль. С их помощью мы не можем посчитать конкретные, осязаемые предметы.

Натуральными не являются числа, которые не применяются для счета предметов, например отрицательные числа и дроби
Натуральные числа классифицируются по разрядам. Разряд зависит от количества знаков в числе. Как правило, в повседневной жизни используются первые пятнадцать разрядов натуральных чисел: единицы (1, 2, 3), десятки (10, 20, 30), сотни (100, 200, 300) и далее вплоть до сотен триллионов (пятнадцатый разряд).
В каждом разряде натуральные числа различаются по классам, чтобы с помощью них было удобнее считать. Например, в числе 238 672 последние три цифры представляют класс единицы, а первые три — класс тысячи. При этом внутри класса каждое число занимает свое место — сотни, десятки, единицы (238, 672).
Получается, что четкая иерархия и понятная последовательность — главные принципы натуральных чисел. Простота, удобство и универсальность — их основной конек. Поэтому каждый человек в любой точке земного шара, знакомый с десятичной системой исчисления, знает, как прочитать любое число и как с ним работать.
Свойства натуральных чисел
Считать, считать и еще раз считать. Это их прямое и самое важное назначение. С их помощью выполняются самые популярные математические расчеты. Они помогают сложить и умножить числа, вычесть из одного другое, разделить и возвести в степень.
При этом отдельные свойства натуральных чисел упрощают их использование, делая счет простым и понятным. Например, перемена мест слагаемых или множителей при неизменном итоговом результате.
Число ПИ
Что это такое, для чего оно нужно и чему равно
Подробнее
Примеры натуральных чисел
100, 5769, 13, 48221, 487654321 — любое целое положительное число будет натуральным.
Популярные вопросы и ответы
Отвечает Наталия Черняк, учитель математики; профессиональный стаж работы — 11 лет.
Какие числа не являются натуральными?
Натуральными не являются числа, которые не применяются для счета предметов. В математике это отрицательные и нецелые числа. Вот простой пример. Зимой столбик термометра опускается ниже ноля градусов, показывая значения: -3, -10, -25. Эти числа отрицательные. Они натуральными не являются. Что касается нецелых чисел, то здесь приведу такой пример. В корзине лежало пять целых яблок и еще одна половинка. Половинка – это нецелое яблоко, ее нельзя представить целым числом. Ее записывают с помощью дробей: 0,5 или ½. Дроби также не относятся к натуральным числам.
Что такое наименьшее натуральное число?
Применительно к нашей корзинке с яблоками это минимальное количество фруктов, которое может в ней лежать. Наименьшим натуральным числом принято считать единицу. Именно с нее начинается счет предметов.
Относится ли ноль к натуральным числам?
Ноль означает некое отсутствие чего-либо, счет предметов с него не начинается. Соответственно, к натуральным числам он не относится.
История натуральных чисел началась ещё в первобытные времена. Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.
Натуральные числа – это числа которые мы используем при счете предметов.
Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….
Нуль не относится к натуральным числам.
Все натуральные числа или назовем множество натуральных чисел обозначается символом N.
Таблица натуральных чисел.
Натуральный ряд.
Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.
Свойства натурального ряда:
- Наименьшее натуральное число – единица.
- У натурального ряда следующее число больше предыдущего на единицу. (1, 2, 3, …) Три точки или троеточие ставятся в том случае, если закончить последовательность чисел невозможно.
- Натуральный ряд не имеет наибольшего числа, он бесконечен.
Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5
Пример №2:
Нуль является натуральным числом?
Ответ: нет.
Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.
Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.
Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.
Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.
Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.
Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.
Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.
Содержание:
- Определение натурального числа
- Сложение натуральных чисел
- Умножение натуральных чисел
Определение натурального числа
Определение
Натуральными числами называются числа, которые используются при счете или для указания
порядкового номера предмета среди однородных предметов.
Например. Натуральными будут такие числа: $2,37,145,1059,24411$
Натуральные числа, записанные в порядке возрастания, образуют числовой ряд. Он начинается с наименьшего натурально числа 1.
Множество всех натуральных чисел обозначают $N={1,2,3, dots n, ldots}$. Оно бесконечно,
так как не существует наибольшего натурального числа. Если к любому натуральному числу прибавить единицу, то получаем натуральное число,
следующее за данным числом.
Пример
Задание. Какие из следующих чисел являются натуральными?
$$-89 ; 7 ; frac{4}{3} ; 34 ; 2 ; 11 ; 3,2 ; sqrt[3]{129} ; sqrt{5}$$
Ответ. $7 ; 34 ; 2 ; 11$
На множестве натуральных чисел вводится две основные арифметические операции —
сложение и
умножение.
Для обозначения этих операций используются соответственно символы » + « и
» • « (или » × «).
Сложение натуральных чисел
Каждой паре натуральных чисел $n$ и $m$ ставится в соответствие натуральное число $s$, называемое суммой. Сумма
$s$ состоит из стольких единиц, сколько их содержится в числах $n$ и $m$. О числе
$s$ говорят, что оно получено в результате сложения чисел $n$ и $m$, и пишут
$$n+m=s$$
Числа $n$ и $m$ называются при этом слагаемыми. Операция сложения натуральных чисел обладает следующими свойствами:
- Коммутативность: $n+m=m+n$
- Ассоциативность: $(n+m)+k=n+(m+k)$
Подробнее о сложении чисел читайте по ссылке.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти сумму чисел:
$13+9 quad$ и $ quad 27+(3+72)$
Решение. $13+9=22$
Для вычисления
второй суммы, для упрощения вычислений, применим к ней вначале свойство ассоциативности сложения:
$$27+(3+72)=(27+3)+72=30+72=102$$
Ответ. $13+9=22 quad;quad 27+(3+72)=102$
Умножение натуральных чисел
Каждой упорядоченной паре натуральных чисел $n$ и $m$ ставится в соответствие натуральное число
$r$, называемое их произведением. Произведение $r$ содержит стольких единиц, сколько их содержится в числе
$n$, взятых столько раз, сколько единиц содержится в числе $m$. О числе
$r$ говорят, что оно получено в результате умножения чисел $n$ и $m$, и пишут
$n cdot m=r quad $ или $ quad n times m=r$
Числа $n$ и
$m$ называются множителями или сомножителями.
Операция умножения натуральных чисел обладает следующими свойствами:
- Коммутативность: $n cdot m=m cdot n$
- Ассоциативность: $(n cdot m) cdot k=n cdot(m cdot k)$
Подробнее о умножении чисел читайте по ссылке.
Пример
Задание. Найти произведение чисел:
12$cdot 3 quad $ и $ quad 7 cdot 25 cdot 4$
Решение. По определению операции умножения:
$$12 cdot 3=12+12+12=36$$
Ко второму произведению применим свойство ассоциативности умножения:
$$7 cdot 25 cdot 4=7 cdot(25 cdot 4)=7 cdot 100=700$$
Ответ. $12 cdot 3=36 quad;quad 7 cdot 25 cdot 4=700$
Операция сложения и умножения натуральных чисел связаны законом дистрибутивности умножения относительно сложения:
$$(n+m) cdot k=n cdot k+m cdot k$$
Сумма и произведение любых двух натуральных чисел всегда есть число натуральное, поэтому множество всех натуральных чисел
замкнуто относительно операций сложения и умножения.
Так же на множестве натуральных чисел можно ввести операции
вычитания и
деления, как операции обратные к операциям
сложения и умножения соответственно. Но эти операции не будут однозначно определенны для любой пары натуральных чисел.
Свойство ассоциативности умножения натуральных чисел позволяет ввести понятие натуральной степени натурального числа:
$n$-й степенью натурального числа $m$ называется натуральное число
$k$, полученное в результате умножения числа $m$ самого на себя $n$ раз:
Для обозначения $n$-й степени числа $m$ обычно используется запись: $m^{n}$, в котором число
$m$ называется lt strong>основанием степени lt /strong>, а число $n$ — показателем степени.
Пример
Задание. Найти значение выражения $2^{5}$
Решение. По определению натуральной степени натурального числа это выражение можно записать следующим образом
$$2^{5}=2 cdot 2 cdot 2 cdot 2 cdot 2=32$$
Ответ. $2^{5}=32$
Читать дальше: что такое рациональное число.
Понятие
Данное понятие появилось в математике одним из первых. В древности люди перечисляли предметы на пальцах, и им вполне этого хватало. Но с бурным развитием торговли и ростом количества продукции на рынках одних пальцев для счета стало не хватать. Поэтому древние люди придумали символы, обозначающие количество чего-либо, которые они использовали для перечисления скота, различных вещей и т.д. Чуть позже числа вошли в науку математику, где стали активно применяться в качестве материала для многочисленных алгебраических преобразований. Натуральные числа — все символы, используемые при счете каких-либо предметов, тем самым вычисляя их последовательность и количество. Все отрицательные и дробные числа не являются натуральными.
Важно! Нуль не входит в натуральное множество, то есть не является одним из них, потому мы и не применяем его при счете.
Соответственно — наименьшей является единица. Наибольшего натурального числа не существует, так как счет можно продолжать до бесконечности.
Вернемся в древние времена. Тогда числа записывали чаще с помощью палочек или любых других примитивных знаков:
- 1 = I;
- 2 = II;
- 3 = III.
Но когда палочек приходилось писать слишком много (100, 1000), люди задумались над более емкой системой записи количества предметов. Так, арабы придумали и завезли в Европу свои цифры, которые на континенте назвали арабскими. Мы прекрасно знаем все эти цифры:
0 1 2 3 4 5 6 7 8 9 (10 штук).
Из данных цифр можно составить абсолютно все натуральные числа. Их множество обозначается знаком N.
Натуральный ряд
Разберем еще одно понятие, связанное с главной темой. Натуральный ряд — последовательная запись всех натуральных символов. Как мы уже выяснили, высшего натурального числа не существует, поэтому данный ряд представляет собой последовательность, которая не заканчивается. Каждый последующий символ натурального ряда больше предыдущего ровно на единицу. Пример: Указать наименьший натуральный знак на отрезке от -7 до 27. Ответ: единица.
Разряды и классы
Для начала скажем, что при счете мы обычно применяем десятичную систему исчисления. Она подразумевает то, что 10 единиц низшего разряда образуют 1 единицу более старшего, и данная закономерность сохраняется до конца счета. Разрядные единицы — это такие символы, которые обозначают начало определенного разряда. Пример: 1, 10, 100 и т.д. Благодаря разрядным единицам, можно сделать запись менее длинной и более упрощенной. Пример: Записать 298 481 в виде суммы разрядных слагаемых. Решение: 200 000 + 90 000 + 8 000 + 400 + 80 + 1.
Важно! 12-ти разрядные числа называются большими и редко употребляются в алгебраических вычислениях.
Если число состоит из одного знака, то оно называется однозначным. Соответственно — различают двузначные, трехзначные, четырехзначные и т.д. Теперь стоит немного рассказать и о натуральных классах. При чтении определенного числа его разделяют на классы, включающие по три разряда. Первые три единицы представляют собой класс единиц, следующие три — класс тысяч. Далее идут довольно крупные группы — классы миллионов, миллиардов и другие. Помните, что каждая цифра любого класса является разрядом, то есть классы состоят из разрядов. Сравнивать их можно через классы или разряды. Соответственно — то число, где количество старших разрядов преобладает, является более крупным по значению.
Главные свойства
Рассмотрим основные свойства, которые характерны для всех натуральных чисел. Они применимы всегда и везде, так как способствуют упрощению некоторых выражений различных типов. Их используют при различных вычислениях и преобразованиях.
Свойство 1
От перемены места слагаемых сумма не меняется. Пример: 2 + 1 = 1 + 2 = 3. Как бы мы не переставляли слагаемые, сумма все равно останется такой же.
Свойство 2
От перемены места множителей произведение не меняется. Пример: 2 х 1 = 1 х 2 = 2. Аналогичное правило есть и в умножении. Значение произведения в итоге остается тем же.
Свойство 3
Чтобы прибавить к числу сумму двух других чисел, можно сначала произвести сложение одного числа, а затем — второго. Пример : 2 + (3 + 10) = 3 + (2 + 10) = 15. Данное правило еще называется сочетательным свойством.
Свойство 4
Чтобы умножить на число произведение двух других чисел, можно сначала произвести умножение одного числа, а затем — второго. Пример: 5 х (6 х 4) = (5 х 6) х 4 = 120. Правило, аналогичное предыдущему, только здесь используется другой вид арифметических действий. Принцип остается тем же.
Свойство 5
Для того, чтобы умножить сумму натуральных чисел на другое число, нужно умножить это число на каждую из представленных слагаемых, а затем сложить полученные произведения чисел. Пример: 5 х (4 + 3) = 5 х 4 + 5 х 3 = 35. Это правило умножения числа относительно сложения двух других. Часто применяется в решении заданий по преобразованию каких-либо выражений. Мы выяснили и разобрали на примерах самые главные свойства натуральных чисел. Если вы их не знали раньше, то советуем вам обратить на них особое внимание. А теперь перейдем к изучению наиболее распространенных и часто используемых операций.
Характерные операции и взаимодействия
Конечно, с данным видом чисел можно выполнять очень много различных действий. Однако мы разберем те основные операции, которые не выводят конечный результат из натурального множества.
Сложение
Один из наиболее простейших видов взаимодействий. Здесь мы берем две части (два слагаемых) и соединяем (складываем) их, образуя конечный результат — сумму. Пример: 6 + 2 = 8. Восемь в данном случае будет являться суммой двух слагаемых — шести и двух.
Вычитание
Вид операций, противоположный предыдущему. В данном случае имеем уже три составляющих. То выражение, из которого мы вычитаем определенное количество, называется уменьшаемым. Количество. которое уже отделено от первоначального, называется вычитаемым. А конечный результат, соответственно, именуется разностью, то есть подразумевается разность между двумя количествами. Пример: 8 — 2 = 6. Восемь — уменьшаемое, два — вычитаемое, шесть — разность.
Умножение
Вид операций, при которой одно число берется такое количество раз, которое равно второму. Оба исходных числа называются множителями. Результат взаимодействия именуется произведением. Пример: 6 х 5 = 30. Шесть и пять — множители, тридцать — произведение чисел.
Деление
Вид операций, противоположный умножению. Число, подвергаемое делению, носит название делимого, а то, на которое делят именуется делителем. Результат деления называется частным. Существует деление с остатком. После такого деления остается небольшой остаток, который уже не делится на исходный делитель. Так как мы разбираем натуральный вид, то и ответ должен получиться натуральным, поэтому в данном случае мы лишь приписываем остаток к ответу. Пример: 6 : 2 = 3. Шесть — делимое, 2 — делитель, 3 — частное. Пример деления с остатком: 7 : 3 = 2 (1) — ответ записываем в виде натурального числа. Один — остаток. Остальное по аналогии с предыдущим примером.
Возведение в степень
Такой вид арифметических операций, при котором число умножается на себя количество раз, равное указанной степени. Здесь мы имеем три элемента: исходное число, степень и ответ. Пример: 63 = 6 х 6 х 6 = 216.
Порядок решения — пример
Итак, после подробного разбора основных арифметических операций рассмотрим алгоритм выполнения всех указанных действий в одном равенстве. Возьмем какой-нибудь пример, включающий в себя большинство всех представленных выше взаимодействий. (36 + 76) х (85 — 80) + 96 ÷ 3 = Сначала необходимо выполнить те действия, которые расположены в скобках, то есть требуется раскрыть скобки слева направо. Раскроем скобки в нашем примере и получим следующее выражение: 112 х 5 + 96 ÷ 3 = Далее также слева направо выполняем все действия умножения и деления, соответственно — мы получим следующую сумму: 560 + 32 = Наконец, производим финальное действие — сложение: 592 — конечный результат. Таким образом, мы узнали, что натуральные числа — это все целые и положительные числа, нуль не является таковым. Вникли в небольшую предысторию данных символов и поняли их важное значение в математике. Произвели разбор основных свойств и арифметических действий, производимых с ними. Также рассмотрели алгоритм действий, необходимых для вычисления ответа. Чтобы проверить свои знания по изученной теме, рекомендуем вам пройти тест, представленный ниже, а также посмотреть видео, где вы найдете еще больше примеров решения различных уравнений с натуральными числами.
Еще статьи по математике:
- Дружественные числа