Как найти натуральную величину сечения цилиндра - Исправление недочетов и поиск решений вместе с Examum.ru

7.1. Общие понятия и определения. 7.2. Сечения многогранников и тел вращения плоскостями частного положения. Определение натуральной величины сечения. 7.3. Сечения многогранников и тел вращения плоскостями общего положения. Определение натуральной величины сечения

7.1. Общие понятия и определения

Сечением называется плоская фигура, полученная в результате пересечения геометрического тела секущей плоскостью и содержащая точки, принадлежащие поверхности тела и плоскости.

Сечение ограничивается замкнутой ломаной линией, если плоскостью пересекается гранная поверхность, и замкнутой кривой линией, если плоскостью пересекается кривая поверхность.

Построение линии сечения в общем случае сводится к определению точек пересечения ребер многогранника или образующих кривой поверхности с секущей плоскостью. Следовательно, построение линии сечения сводится к множественной задаче определения точек пересечения прямой с плоскостью.

7.2. Сечения многогранников и тел вращения плоскостями частного положения. Определение натуральной величины сечения

Сечение поверхностей гранных геометрических тел плоскостями частного положения. Сечением многогранника плоскостью является плоский многоугольник, вершины которого принадлежат ребрам, а стороны — граням многогранника. В зависимости от вида гранной поверхности и положения секущей плоскости сечение может принимать различные геометрические фигуры. Например, при пересечении поверхностей прямых правильных призмы и пирамиды плоскостями возможно образование геометрическихфигур, показанныхнарис. 88 и89.

Рис. 88. Сечение прямой призмы плоскостями частного положения

101

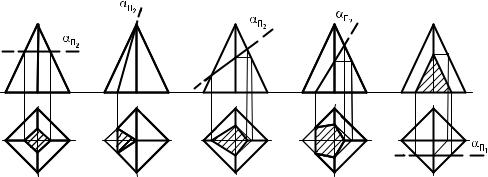
Рис. 89. Сечение прямой пирамиды плоскостями частного положения

Построение линии пересечения многогранника плоскостью сводится к многократному решению задачи на определение точек пересечения ребер многогранника с секущей плоскостью. Определение натуральной величины сечения гранной поверхности плоскостью определяют любым известным способом, например, способом совмещения секущей плоскости с плоскостью проекций, способом вращения, способом замены плоскостей проекций и т. д.

Рассмотрим некоторые примеры.

З а д а ч а 19

Дано: прямая шестигранная пирамида ABCDEFS с вершиной в точке S и фронтально-проецирующая плоскость α (рис. 90).

Выполнить: 1) построить линию пересечения пирамиды плоскостью; 2) определить натуральную величину сечения пирамиды плоскостью.

Порядок выполнения:

1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α

обладает собирательным свойством (любой геометрический элемент, принадлежащий фронтально-проецирующей плоскости, в т. ч. и линия пересечения пирамиды плоскостью, будет проецироваться в ее фронтальный след). Следовательно, пересечение фронтального следа αΠ2 с ребрами пирамиды образует фронтальную проекцию сечения

геометрического тела плоскостью 122232425262.

2.Горизонтальную проекцию сечения геометрического тела плос-

костью 112131415161 определяют из условия принадлежности точки прямой.

3.Натуральную величину сечения пирамиды плоскостью в данной задаче определяют способом вращения, совмещая секущую плоскость

сгоризонтальной плоскостью проекций, однако допустимо применение и любого другого способа.

102

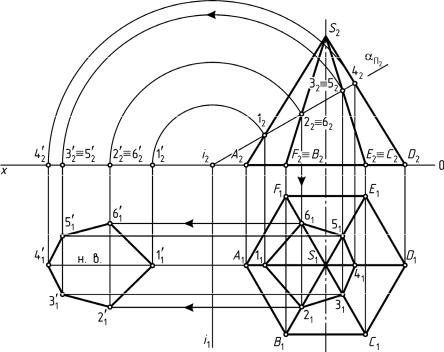
Рис. 90. Пересечение прямой пирамиды плоскостью частного положения

З а д а ч а 20 Дано: прямая шестигранная призма и фронтально-проецирующая

плоскость α (рис. 91).

Выполнить: 1) построить линию пересечения призмы плоскостью; 2) определить натуральную величину сечения призмы плоскостью.

Порядок выполнения:

1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α

обладает собирательным свойством (любой геометрический элемент, принадлежащий фронтально-проецирующей плоскости, будет проецироваться в ее фронтальный след). Следовательно, пересечение фронтального следа αΠ2 с ребрами призмы образует фронтальную проек-

цию сечения геометрического тела плоскостью 122232425262.

2.Призматическая поверхность является горизонтально-проеци- рующей, поэтому горизонтальную проекцию сечения геометрического

тела плоскостью 112131415161 определяют из этого условия и условия принадлежности точки прямой.

3.Натуральную величину сечения призмы плоскостью в данной задаче определяют способом вращения, совмещая секущую плоскость

сгоризонтальной плоскостью проекций, однако допустимо применение и любого другого способа.

103

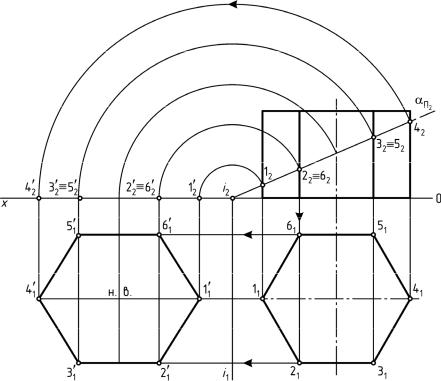
Рис. 91. Пересечение прямой призмы плоскостью частного положения

З а д а ч а 21

Дано: наклонная пирамида ABCDS с вершиной в точке S и горизон- тально-проецирующая плоскость α (рис. 92).

Порядок выполнения:

1. Горизонтальный след αΠ1 горизонтально-проецирующей плос-

кости α обладает собирательным свойством (любой геометрический элемент, принадлежащий горизонтально-проецирующей плоскости, в т. ч. и линия пересечения пирамиды плоскостью, будет проецироваться в ее горизонтальный след). Следовательно, пересечение следа αΠ1 с поверхностью наклонной пирамиды образует горизонтальную

проекциюсечениягеометрическоготелаплоскостью11213141.

2.Фронтальную проекцию сечения геометрического тела плоскостью 12223242 определяют из условия принадлежности точки прямой.

3.Натуральная величина сечения пирамиды плоскостью в данной задаче определена способом плоскопараллельного перемещения и вынесена за пределы графических построений.

104

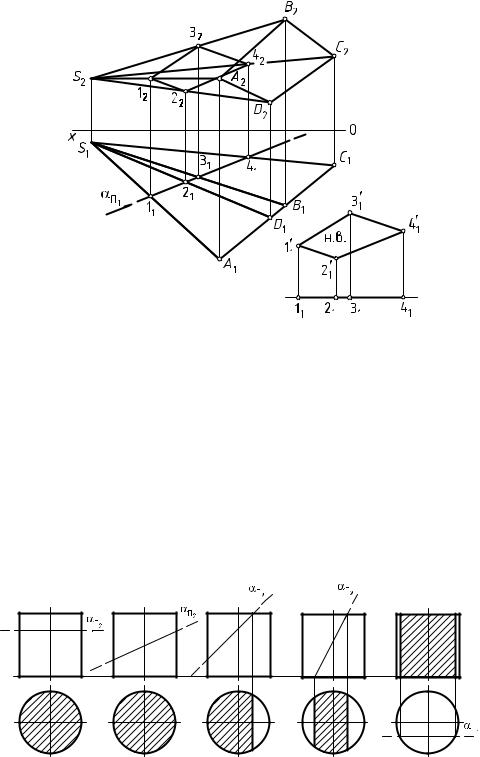
Рис. 92. Пересечение наклонной пирамиды плоскостью частного положения

Сечение поверхностей геометрических тел вращения плоско-

стями частного положения. Сечением тел вращения плоскостью является плоская кривая линия. В зависимости от вида поверхности вращения и положения секущей плоскости сечение может принимать различные геометрические фигуры. Так, при пересечении поверхности прямого кругового цилиндра плоскостью возможно образование следующих геометрических фигур:

окружности, если секущая плоскость перпендикулярна оси цилиндра, такое сечение называют нормальным (рис. 93, а);

эллипса, если секущая плоскость наклонена к оси цилиндра и пересекает все его образующие (рис. 93, б);

а	б	в	г	д
Рис. 93. Пересечение прямого цилиндра плоскостями частного положения

105

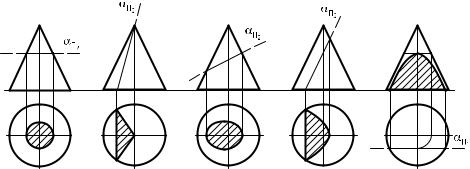
усеченного эллипса, если секущая плоскость наклонена к оси цилиндра и пересекает одно или оба его основания (рис. 93, в и г);

прямоугольника, если секущая плоскость параллельна оси цилинд-

ра (рис. 93, д).

При пересечении поверхности прямого кругового конуса плоскостью возможно образование следующих геометрических фигур:

окружности, если секущая плоскость перпендикулярна оси конуса

(рис. 94, а);

треугольника, если секущая плоскость пересекает конус через его вершину по двум образующим (рис. 94, б);

эллипса, если секущая плоскость наклонена к оси конуса и пересекает все его образующие (рис. 94, в).

параболы, если секущая плоскость параллельна одной из образующих конуса (рис. 94, г);

гиперболы, если секущая плоскость параллельна оси конуса или параллельна двум его образующим (рис. 94, д).

а б в г д

Рис. 94. Пересечение прямого конуса плоскостями частного положения

Построение линии пересечения тел вращения плоскостью сводится к многократному решению задачи на определение точек пересечения образующих кривой поверхности с секущей плоскостью.

Рассмотрим некоторые примеры. З а д а ч а 22

Дано: прямой круговой цилиндр и фронтально-проецирующая плоскость α (рис. 95, а).

Выполнить: 1) построить линию пересечения цилиндра плоскостью; 2) определить натуральную величину сечения цилиндра плоскостью.

Порядок выполнения:

1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α

обладает собирательным свойством. Следовательно, пересечение фронтального следа αΠ2 с поверхностью цилиндра образует фрон-

106

тальную проекцию сечения геометрического тела плоскостью

А21222D23242B25262C27282.

2.Цилиндрическая поверхность является горизонтально-проецирую- щей, поэтому горизонтальную проекцию сечения геометрического тела плоскостью А11121D13141B15161C17181 определяют из этого условия

иусловия принадлежности точки прямой.

3.Натуральную величину сечения цилиндра плоскостью в данной задаче определяют способом замены плоскостей проекций.

Рис. 95. Пересечение геометрических тел плоскостью частного положения

З а д а ч а 23 Дано: сфера и фронтально-проецирующая плоскость α (рис. 95, б).

Выполнить: 1) построить линию пересечения сферы плоскостью; 2) определить натуральную величину сечения сферы плоскостью.

Порядок выполнения:

1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α

обладает собирательным свойством. Следовательно, пересечение фронтального следа αΠ2 с поверхностью сферы образует фронтальную про-

екцию сечения геометрического тела плоскостью 1222426282725232.

107

2.Горизонтальную проекцию сечения геометрического тела

плоскостью 1121416181715131 определяют из условия принадлежности точки прямой.

3.Натуральную величину сечения сферы плоскостью в данной задаче определяют способом замены плоскостей проекций, однако допустимо применение и любого другого способа.

З а д а ч а 24 Дано: прямой круговой конус и фронтально-проецирующая плос-

костьα (рис. 96).

Выполнить: 1) построить линию пересечения конуса плоскостью; 2) определить натуральную величину сечения конуса плоскостью.

Рис. 96. Пересечение прямого конуса плоскостью частного положения

Порядок выполнения:

1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α

обладает собирательным свойством. Следовательно, пересечение фронтального следа αΠ2 с поверхностью конуса образует фронталь-

ную проекцию сечения геометрического тела плоскостью

128242621022292523272.

2. Горизонтальную проекцию сечения геометрического тела плоскостью 118141611012191513171 определяют из условия принадлежности точки прямой.

108

3. Натуральную величину сечения конуса плоскостью в данной задаче определяют способом вращения, совмещая секущую плоскость с горизонтальной плоскостью проекций, однако допустимо применение и любого другого способа.

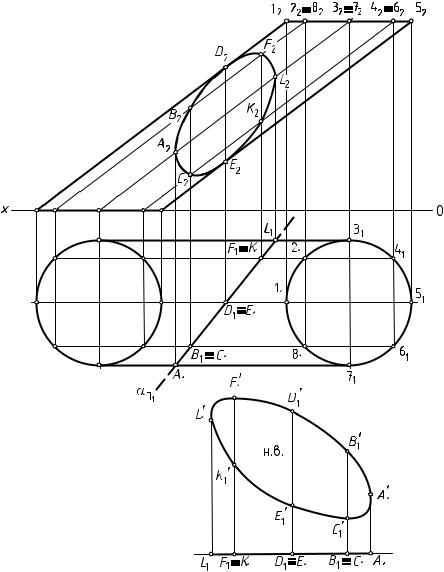
З а д а ч а 25 Дано: наклонный цилиндр и горизонтально-проецирующая плос-

кость α (рис. 97).

Рис. 97. Пересечение наклонного цилиндра плоскостью частного положения

109

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Способ замены (перемены) плоскостей проекций для нахождения натуральной величины сечения цилиндра

Способ замены (перемены) плоскостей проекций

Цель видеоурока Автокад/НГ: Обучение Автокад 2D на практике и закрепление пройденного материала раздела «Теоретические и практические видеоуроки Автокад». Закрепление знаний по решению задач на построение натуральной величины отрезка, треугольника, сечения и т.д. используя для этого любой способ преобразования чертежа.

Чертеж Автокад Сечение цилиндра плоскостью содержит практически все данные для построения развертки усеченного цилиндра. Осталось только найти натуральную величину сечения цилиндра.
Натуральную величину сечения цилиндра найдем способом замены (перемены) плоскостей проекций.

Алгоритм решения задачи с использованием способа замены (перемены) плоскостей проекции.

Вводим новую плоскость S, которая будет располагаться параллельно отрезка, в который проецируется сечение цилиндра на фронтальной плоскости проекции.
Строим линии связи.
На линиях проекционной связи откладываем координаты Y точек сечения цилиндра.

Более подробно смотрите в видеоуроке по начертательной геометрии в Автокад.

Видео «Способ замены (перемены) плоскостей проекций»

Источник

Как построить сечение цилиндра

Линия пересечения поверхности с плоскостью принадлежит одновременно поверхности и секущей плоскости. Линия пересечения цилиндрической поверхности секущей плоскостью, параллельной прямой образующей – прямая линия. Если секущая плоскость перпендикулярна к оси поверхности вращения – в сечении будет окружность. В общем случае линия пересечения цилиндрической поверхности с секущей плоскостью – кривая линия.

Вам понадобится

Карандаш, линейка, треугольник, лекала, циркуль, измеритель.

Инструкция

Пример: построить сечение цилиндра фронтально-проектирующей плоскостью Σ(Σ₂). В данном примере линия сечения строится по точкам пересечения образующих цилиндра с секущей плоскостью Σ.

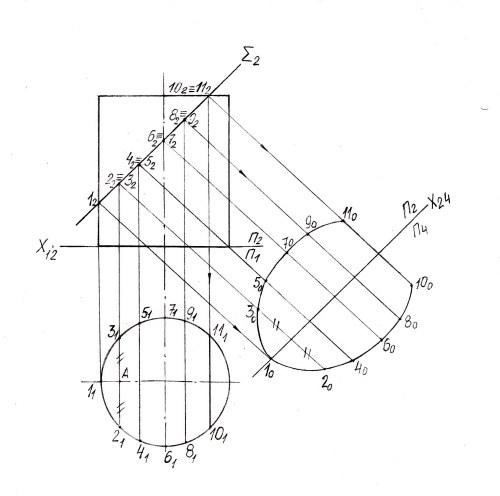
На фронтальной плоскости проекций П₂ линия сечения совпадает с проекцией секущей плоскости Σ₂ в виде прямой.
Обозначьте точки пересечения образующих цилиндра с проекцией Σ₂ 1₂, 2₂ и т.д. до точек 10₂ и 11₂.

На плоскости П₁ проекция цилиндра – это окружность. Отмеченные на плоскости сечения Σ₂ точки 1₂ , 2₂ и т.д. с помощью линии проекционной связи спроектируются на очерке этой окружности. Обозначьте их горизонтальные проекции симметрично относительно горизонтальной оси окружности.

Таким образом, проекции искомого сечения определены: на плоскости П₂ – прямая (точки 1₂, 2₂…10₂); на плоскости П₁ – окружность (точки 1₁, 2₁…10₁).

По двум проекциям постройте натуральную величину сечения данного цилиндра фронтально-проектирующей плоскостью Σ. Для этого используйте способ замены плоскостей проекций.

Проведите новую плоскость П₄ параллельно проекции плоскости Σ₂. На этой новой оси x₂₄ отметьте точку 1₀. Расстояния между точками 1₂ – 2₂, 2₂ – 4₂ и т.д. с фронтальной проекции сечения отложите на оси x₂₄, проведите тонкие линии проекционной связи перпендикулярно оси x₂₄.

В данном способе плоскостью П₄ заменяется плоскость П₁, поэтому с горизонтальной проекции размеры от оси до точек перенесите на ось плоскости П₄.

Например, на П₁ для точек 2 и 3 это будет расстояние от 2₁ и 3₁ до оси(точка А) и т.д.

При построении сечения необходимо особо отмечать положение так называемых опорных точек. К ним относятся точки, лежащие на контуре проекции (точки 1, 10, 11), на проекции крайних образующих поверхности (точки 6 и 7), точки видимости и т.д.

Отложив с горизонтальной проекции указанные расстояния, получите точки 2₀, 3₀, 6₀, 7₀, 10₀, 11₀. Затем для большей точности построения, определяются остальные, промежуточные, точки.

Соединив лекальной кривой все точки, получите искомую натуральную величину сечения цилиндра фронтально-проектирующей плоскостью.

Источники:

как заменить плоскость

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Разделы

Уроки по теме

Сечение цилиндра наклонной плоскостью

Автор: Moroz

Дата: 2012-03-01

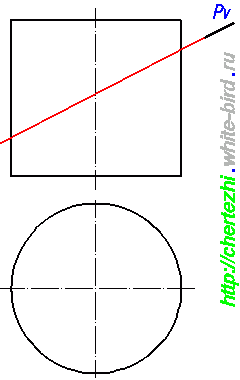
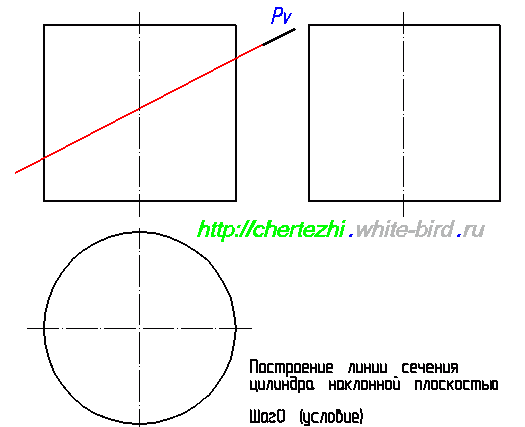
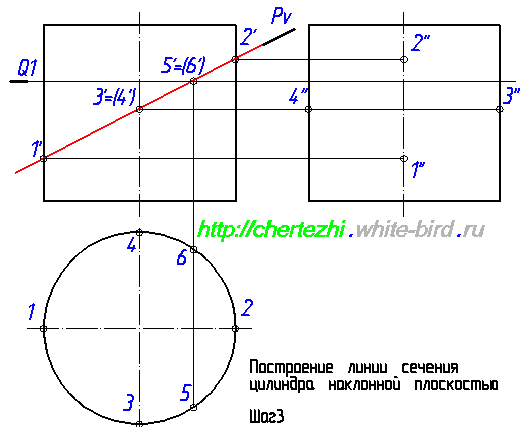
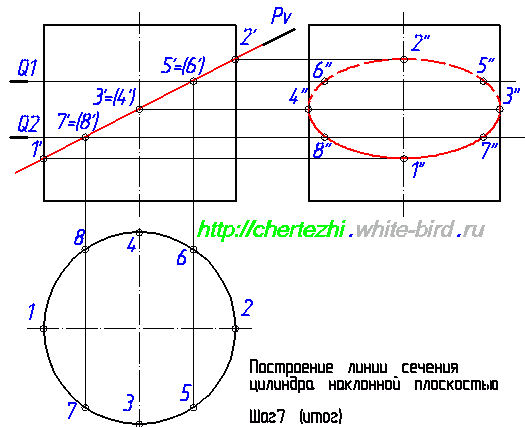
    Этим уроком я открываю серию статей, посвященных построению линий пересечения простых тел вращения с наклонной плоскостью. Умение выполнять эти действия вам поможет не только решить одноименные задачи, но и будет серьезным подспорьем при нахождении натурального вида фигуры сечения сложных деталей. Ведь детали состоят из кусочков простых тел: конусов, цилиндров, параллелепипедов, сфер. Сегодня я научу вас строить линию пересечения плоскости с цилиндром. Исходное задание как правило имеет вид как на картинке слева от этого абзаца. Изображены два вида, дающие нам представление о том, что фигура является цилиндром вращения, а так же задается секущая плоскость, в моем случае это плоскость Pv.
    Давайте попробуем предположить, что мы получим на каждом из трех видов? Определенно можно сказать, что вся линия пересечения на фронтальном виде сольется с прямой обозначающей секущую плоскость, а на горизонтальном виде, все точки пересечения будут лежать на окружности, которой задан цилиндр. Главный интерес данной задачи заключается в нахождении линии пересечения на третьем виде(на профильной проекции цилиндра). Вероятнее всего вы уже догадываетесь, что на третьем виде линия пересечения будет представлять собой эллипс. В частном случае, если секущая плоскость наклонена к цилиндру вращения под углом ровно 45 градусов, то в проекция сечения на третьем виде будет являться эллипсом с равными осями, т.е. эллипс выродится в окружность. Это был маленький кусочек теории, сейчас же предлагаю перейти к практическим построениям.
    Итак, перед нами цилиндр с заданной фронтально-проецирующей секущей плоскостью. Начнем с подготовки третьего вида. Он будет точно такой же как и главный вид:

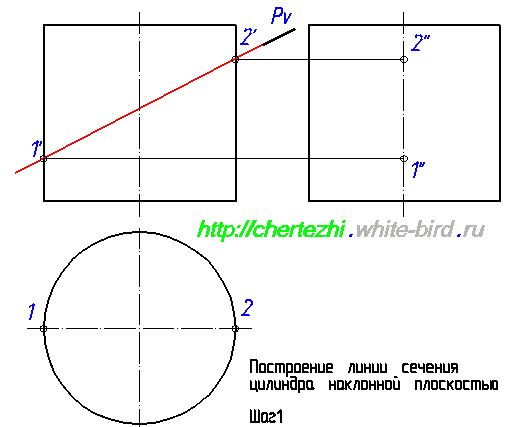
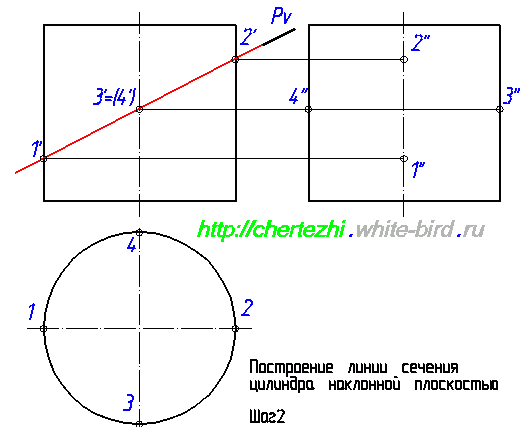
Первым делом давайте обозначим определяющие точки, которые можно найти сразу, без дополнительных построений. Определим точки 1′ и 2′. Горизонтальные проекции 1 и 2 лежат на пересечении образующей окружности с осью, а проекции 1» и 2» лежат на оси цилиндра. Это нужно либо понимать, либо поверить мне

Еще одна пара определяющих точек — точки 3 и 4. Определим их фронтальную проекцию, а потом найдем горизонтальную и профильную. Это не сложно:

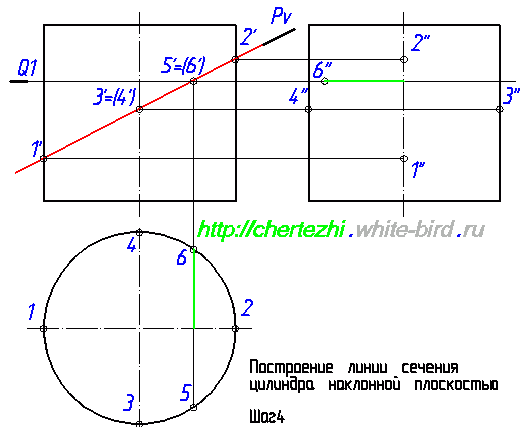
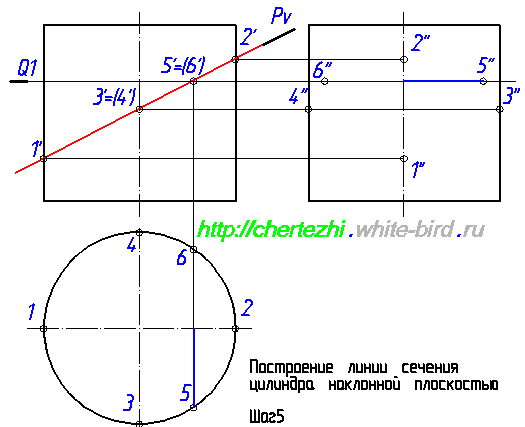
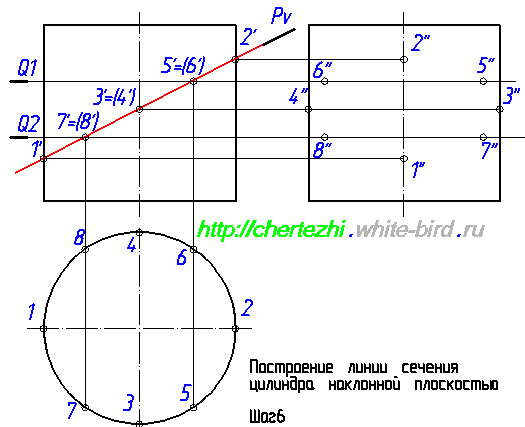
Если бы наша задача была построить сечение в AutoCad, то на этом можно было бы остановиться, поскольку мы уже имеем 4 точки, определяющие оси эллипса. Но так как мы учимся чертить руками, то мы должны построить дополнительные точки, которые бы позволили нам с вами, не обладая точностью компьютера, максимально точно начертить линию пересечения.
Проведем вспомогательную секущую плоскость Q1. На фронтальной проекции в точке пересечения Q1 и Pv отметим точки 5′ и 6′. Снесем их по линии связи на горизонтальную проекцию, отметим там точки 5 и 6:

Теперь нужно построить профильные проекции 5» и 6». Отложим на фронтальной проекции влево от оси точку 6» на расстоянии равном удалению точки 6 от оси окружности на горизонтальной проекции. Эти соответствующие расстояния на рисунке ниже отмечены зелеными отрезками:

Чтобы построить точку 5» нужно выполнить ровно такие же действия. Нужно отложить аналогичное расстояние вправо от оси цилиндра. Соответствие размеров на профильной и горизонтальной проекции на рисунке ниже обозначено синими отрезками:

Проведем еще одну вспомогательную секущую плоскость — Q2. Мне нравится проводить вспомогательные плоскости симметрично относительно середины сечения — так во многих случаях удается сделать менее загруженный линиями чертеж. Т.е. я провел Q2 симметрично Q1 относительно точек 3′,4′. Полученные с ее помощью проекции точек 7 и 8 строим по аналогии с построениями проекций точек 5 и 6:

Мы ограничимся построением двух вспомогательных плоскостей и проведем эллипс по имеющимся точкам. Но на практике имеет смысл провести еще хотя бы по одной вспомогательной плоскости выше и ниже точки пересечения Pv с осью цилиндра. Особенно если вы не считаете себя мастером построения эллипса «от руки». Итак, завершающий этап: построение линии пересечения плоскости с цилиндром. Она имеет форму эллипса, строим его аккуратно соединяя точки. И последний штрих — на профильной проекции верхняя половина линии пересечения будет проходить за цилиндром, соответственно будет невидима. Что мы и обозначим штриховой линией.

В следующем уроке мы рассмотрим один из случаев построения линии пересечения конуса с плоскостью.

Вы можете сказать «спасибо!» автору статьи:

пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»

или

или запишите наш телефон и расскажите о нас своим друзьям — кто-то наверняка ищет способ выполнить чертежи

или создайте у себя на страничке или в блоге заметку про наши уроки — и кто-то еще сможет освоить черчение.

А вот это — не реклама. Это напоминание, что каждый из нас может сделать. Если хотите — это просьба. Мы действительно им нужны:

Комментарии:

Мне нужно вырезать эллипс в крыше для вывода металлической трубы, поэтому мне важнее начертить проекцию цилиндра на самой крыше.
Спасибо.

Михаил!
Ваша задача сводится к продолжению задачи о сечении цилиндра плоскостью. Необходимо найти натуральную величину получившегося сечения. Имея его на руках — распечатываем на формате соответствующего размера, вырезаем трафарет и накладываем в нужном месте на крышу. Останется обвести и произвести вырезание по полученной линии.
На сайте есть урок, связанный с нахождением натуральной величины сечений, но там не разобрано построение сечений циллиндрических поверхностей.
Ну а в целом — спасибо за доброе слово!

Вопрос к практическому применению, понятно как изготовить шаблон верхней проекции сечения, но мне, как сварщику, непонятно как изготовить шаблон для торцовки труб. Объясните, пожалуйста. Спасибо.

    Сергей, попробую предложить вам способ. Сразу оговорюсь, что вряд ли он наиболее удобный, но зато качество разметки должно получиться хорошим.
Метод потребует выполнить построение развертки цилиндра с нанесением на него линии пересечения с плоскостью. Т.е. я предлагаю вам на чем либо (рубероид, упаковочная бумага, лист обоев и т.д.) построить развертку цилиндра, нанести на нее линию пересечения цилиндра с наклонной плоскостью, отрезать лишнюю часть и, приложив ее к трубе, обвести по краю. Получиться должно просто замечательно.
    Думаю, идею вы поняли. Ну а реализация построения линии пересечения на развертке цилиндра — либо найдете, либо дождетесь — планирую написать соответствующую статью.
    Всего наилучшего!

линия пунктир(пункт по немецки точка)не показывает невидимую линию. Линия невидимого контура называется штриховая. ГОСТ 2.303

Вот! Всегда есть шанс, что кто-то не поленится найти неточность и поправит! Спасибо за замечание, исправляю!

Спасибо, это понятно по начерт.геометрии, но хотелось бы сделать построение математическим путём, т.к. шаблон, плаз, очень большой. Если дадите буду благодарен.

спасибо огромноое
очень помогло
вспомнил

Извиняюсь, Вы нарисовали бред, попробуйте построить по Вашему методу сечение цилиндра плоскостью с наклоном 45 и получите круг, а не эллипс ))))

Приветствую Злого Енота! Зачем строить? Это и так известно, будет круг. У меня написано: эллипс с равными осями. Частный случай. Эллипс выродится в круг. Возможно, нужно было прочитать еще пару строк? Или попробовать построить эллипс с равными осями?

спасибо очень пригодилось!

Здравствуйте! Подскажите как выполните такое же задание при условии что цилиндр проецируется в виде круга на профильную плоскость? Зарание спасибо.

Благлдарю!Много перелопатил информации,и в основном построенной на рекламе,а толком ничего путного,все вокруг да около,а вот зашел на Ваш сайт,сразу все стало на свои места.Ведь я где-то далеко помню,это было еще в школьные годы,и кого не спрашивал,никто дать толковую информацию так и не смог.С помощью Ваших уроков я вышел из положения,и теперь рекомендую Ваш сайт своим друзьям,знакомым.Ведь много людей занимаются строительством,и часто и густо выходят из того или иного положения методом втыка.Благодарю еще раз.

Добавьте свой комментарий:

Последние уроки

Как построить диметрию детали?

Построение наклонного сечения, заданного на виде слева

Определение линии пересечения двух плоскостей. Метод вспомогательных секущих плоскостей.

Наша почта:

zakaz@trivida.ru

Наша страница в ВК:

Случайный комментарий

Николай:

Не являюсь Вашим заказчиком, поскольку сам неплохо разбираюсь в предмете, да и принцип у меня есть — за весь период учебы не купил ни одной работы, всё делал сам. Кроме того, пока учился почти каждую ночь выполнял работы по НГ и ИГ. Я отошел от дел, так что рекламой этот пост не является
Видимо я сильно продешевил в свое время, раз уж Ваши работы покупают за столь серьёзные по моим тогдашним меркам суммы. Залез к Вам на страницу, и кусаю локти теперь
С уважением к Вам, коллеги
Николай, ПГУПС

Николай, спасибо за ваше мнение! И я рад, что в результате нашей с вами переписки я получил эти строки: «Спасибо за реакцию, — признаться, приятно иметь дело с адекватным человеком. Надеюсь, не подпортил Вам репутации.»

Источник

Как найти натуральную величину цилиндра

Увы, но найти натуральную величину цилиндра методами начертательной геометрии не представляется возможным. Универсальная
характеристика цилиндра — это его объём, а он, в общем случае не находится по причинам геометрического мироустройства.
Вероятно, вам требуется найти сечение цилиндра плоскостью и натуральную величину.

Построение сечения цилиндра можно найти на плоскости проекции относительно которой секущая занимает
проецирующее положение. Замена плоскостей проекций П₁/П₂→П₁/П₄, П₄⊥h0α
1 находит очевидную проекцию сечения определённую прямым отрезком.

Для построения горизонтальной проекции линии сечения используют образующие, которые можно определять начиная с любой проекции.
По пересечению образующих с основанием цилиндра на П₄, найдены горизонтальные проекции пересечений.
Горизонтальные проекции образующих построены с условием параллельности к оси цилиндра. Горизонтальная проекция точек сечения
найдена по проекционным связям от П₄ с условием принадлежности точек образующим цилиндра.

Замена проекций П₁/П₄→П₅/П₄, П₅║α и
построение точек сечения цилиндра, определяет натуральную величину.

Найти натуральную величину фигуры методом вращения.
Определить натуральную величину четырехугольника abcd.

Определение натуральной величины.

Решение задач по начертательной геометрии.

Источник