Как найти натуральную величину сечения конуса - Исправление недочетов и поиск решений вместе с Examum.ru

Наверх

В статье рассмотрим вопрос: «Как чертится натуральная величина сечения конуса»

Первоначально необходимо начертить сечение конуса, полученное в результате секущей плоскости, и отобразить на трех видовых проекциях.

Определение точек сечения определяется с помощью секущих плоскостей.

1.) Отмеряем размер от оси Х до осевой линии вида сверху и откладывается от точки до оси строящегося сечения;

2.) Также как и в 1 пункте отмеряем длину от оси Х до оси вида сверху;

3.) Чертим центральную ось сечения под углом 90⁰;

4.) Отмеряют расстояние согласно рисунку;

5.) Подобным образом переносятся остальные точки;

6.) Соединяем и обводим полученное сечение.

Вы также можете ознакомиться с построение в видео.

Просмотрели 631

Источник

Сечение поверхности конуса плоскостью общего положения

При пересечении прямого кругового конуса с плоскостью могут образовываться следующие кривые второго порядка: окружность, эллипс, гипербола и парабола. Вид этих кривых зависит от угла наклона секущей плоскости к оси конической поверхности.

Ниже мы рассмотрим задачу, в которой требуется построить проекции и натуральную величину сечения конуса ω плоскостью α . Начальные данные представлены на рисунке ниже.

Содержание

Определение высшей и низшей точки сечения. Границы видимости
Построение промежуточных точек и проекций эллипса
Построение натуральной величины сечения методом совмещения

Определение высшей и низшей точки сечения. Границы видимости

Построение линии пересечения следует начинать с нахождения её характерных точек. Они определяют границы сечения и его видимость по отношению к наблюдателю.

Через ось конической поверхности проведем вспомогательную плоскость γ, параллельную П₂. Она пересекает конус ω по двум образующим, а плоскость α по фронтали f_γ. Точки 1 и 2 пересечения f_γ с образующими являются граничными точками. Они делят сечение на видимую и невидимую части.

Определим высшую и низшую точки линии пересечения. Для этого через ось конуса перпендикулярно h₀_α введем дополнительную секущую плоскость β. Она пересекает коническую поверхность по образующим SL и SK, а плоскость α по прямой MN. Искомые точки 3 = SL ∩ MN и 4 = SK ∩ MN определяют большую ось эллипса. Его центр находится в точке O, которая делит отрезок 3–4 пополам.

Определение промежуточных точек и построение проекций эллипса

Чтобы построить проекции сечения наиболее точно, найдем ряд дополнительных точек. В случае с эллипсом целесообразно определить величину его малого диаметра. Для этого через центр O проводим вспомогательную горизонтальную плоскость δ. Она пересекает коническую поверхность по окружности диаметром AB, а плоскость α – по горизонтали h_δ. Строим горизонтальные проекции окружности и прямой h_δ. Их пересечение определяет точки 5′ и 6′ малого диаметра эллипса.

Для построения промежуточных точек 7 и 8 вводим вспомогательную горизонтальную плоскость ε. Проекции 7′ и 8′ определяются аналогично 5′ и 6′, как это показано на рисунке.

Соединив найденные точки плавной кривой, мы получили контур эллиптического сечения. На рисунке он обозначен красным цветом. Фронтальная проекция контура меняет свою видимость в точках 1 и 2, как это было отмечено выше.

Построение натуральной величины сечения методом совмещения

Чтобы найти натуральную величину сечения, повернем плоскость α до совмещения её с горизонтальной плоскостью. В качестве оси вращения будем использовать след h₀_α. Его положение в процессе преобразований останется неизменным.

Построение начинается с определения направления фронтального следа f₁_α. На прямой f₀_α возьмем произвольную точку E и определим её проекцию E’. Из E’ опустим перпендикуляр к h₀_α. Пересечение данного перпендикуляра с окружностью радиусом X_αE» определяет положение точки E’₁. Через X_α и E’₁ проводим f₁_α.

Строим проекцию горизонтали h’₁_δ ∥ h₀_α, как это показано на рисунке. Точки O’₁ и 5′₁, 6′₁ лежат на пересечении h’₁_δ с прямыми, проведенными перпендикулярно h₀_α из O’ и 5′, 6′. Аналогично на горизонтали h’₁_ε находим 7′₁ и 8′₁.

Строим проекции фронталей f’₁_γ ∥ f₁_α, f’₃ ∥ f₁_α и f’₄ ∥ f₁_α. Точки 1′₁, 2′₁, 3′₁ и 4′₁ лежат на пересечении этих фронталей с перпендикулярами, восстановленными к h_0α из 1′, 2′, 3′ и 4′ соответственно.

Источник

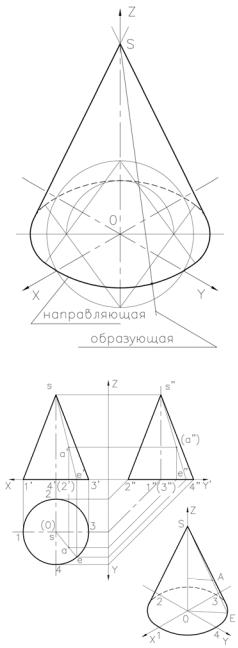
Лекция 16. ПРОЕКЦИИ КОНУСА

Конус – тело вращения.

Прямой круговой конус относится к одному из видов тел вращения.

Коническая поверхность образуется прямой линией, проходящей через некоторую неподвижную точку и последовательно через все точки некото-

рой кривой направляющей линии. Неподвижная точка S называется вершиной. Основанием конуса служит поверхность образованная замкнутой направляющей.

Конус, основанием которого является окружность, а вершина S находится на оси

перпендикулярной основанию, проходящей через его середину, называется прямым кру-

говым конусом. Рис. 1.

Построение ортогональных проекций конуса, приведено на рис. 2.

Горизонтальная проекция конуса представляет собой окружность, равную основанию конуса, а вершина конуса S совпадает с ее центром. На фронтальную и профильную проекции конус проецируется в виде треугольни-

ка, ширина основания которого равна диаметру основания. А высота равна высоте конуса. Наклонные стороны треугольника – проекции крайних (очерковых) образующих конуса.

		Построение конуса в прямоуголь-
		ной изометрии приведено на рис. 2.
	Рис. 1	Построение начинаем с расположе-
	ния аксонометрических осей OX, OY, OZ,

		проведя их под углом 1200 друг к другу. Ось
		конуса направим по оси OZ, и отложим на
		ней высоту конуса, получив точку S. Прини-
		мая точку O за центр основания конуса,
		строим овал, представляющий основание
		конуса. Затем проводим две наклонные ка-
		сательные из т. S к овалу, которые будут
		крайними (очерковыми) образующими кону-
		са. Невидимую часть нижнего основания ко-
		нуса выполним штриховой линией.

Построение точек на поверхности конуса в ортогональных и аксонометриче-

ской проекциях показано на рис. 2, 3.

Если на фронтальной проекции конуса Рис. 2 заданы точки А и В, то недостающие проек-

ции этих точек можно построить двумя способами.

Первый способ: с помощью проекций вспомогательной образующей проходящей через заданную точку.

Дано: фронтальная проекция точки А – точка (а’), расположенная в пределах видимой части конуса.

Через вершину конуса и заданную точку (a’) проводим прямую линию до основания конуса и получаем точку (e’) – основание образующей s’e’.

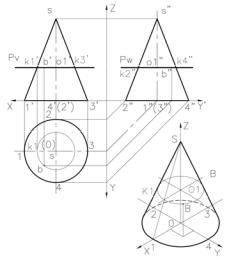
Далее строим горизонтальную проекцию этой образующей на плоскости

H. Найдем горизонтальную проекцию т. e в пределах видимой части окружности основания конуса, проведя проецирующую прямую e’e, и соединим полученную т. е с горизонтальной проекцией вер-

шины конуса s.

Так как искомая т. А принадлежит обра-

зующей s’e’ то она должна лежать на ее горизонтальной проекции. Поэтому с помощью линии связи мы переносим ее на линию se и по-

лучаем горизонтальную проекцию т. a. Профильная проекция a” т. А определя-

ется пересечением той же образующей s”e” на профильной проекции с линиями связи, переносящими т. а с горизонтальной и фронталь-

ной проекций.

Профильная проекция a” т. А в данном

случае невидимая, т. к. находится за проекцией крайней образующей s”4” и обозначается в круглых скобках.

Рис. 3 Второй способ: с помощью построения проекций сечения конической поверхности горизонтальной плоскостью Pv па-

раллельной основанию конуса и проходящей через заданную точку В. Рис. 3. Дано: фронтальная проекция точки В – т. b’, расположенная в пределах

видимой части конуса.

Через т. b’ проводим прямую, Pv параллельную основанию конуса, кото-

рая является фронтальной проекцией секущей плоскости P. Эта линия пересе-

кает ось конуса в т. 01’ и крайние образующие в т. k1’ и k3’. Отрезок прямой k1’k3’ является фронтальной проекцией сечения конуса через т. b’.

Горизонтальной проекцией этого сечения будет окружность, радиус которой определяется на фронтальной проекции как расстояние 01’k1’ от оси ко-

нуса до крайней образующей.

Так как точка b’ лежит в плоскости сечения, то с помощью линии связи переносим ее на горизонтальную проекцию сечения в пределах видимой части конуса.

Профильная проекция т. b” определяется как пересечение профильной

проекции сечения k2”k4” с линией связи, переносящей положение т. b с гори-

зонтальной проекции.

Построение точек на поверхности конуса в аксонометрии.

Строим конус в прямоугольной изометрии. Построение окружности основания конуса в аксонометрии повторяет построение основания цилиндра. (См. раздел 8.2.1.). Отложив на вертикальной оси высоту конуса, проводим две образующие – касательные к овалу основания.

Первый способ. Рис. 2.

Строим образующую SE: на оси X или Y откладываем координаты Х или

Y соответствующие т. Е на горизонтальной проекции и проведем через них линии параллельные оси Y или X соответственно. Пересечение их дает положение точки Е на основании конуса.

Соединим т. Е с вершиной конуса S и с центром основания т. 0. Рассмотрим полученный треугольник S0E: сторона 0S – ось симметрии конуса совпадающая с осью Z. Сторона SE – образующая конуса, на которой находится т. А. Сторона 0E — основание треугольника составляющая с осью Z угол 900.

Рис. 4

Высоту т. А берем на фронтальной проекции по перпендикуляру от ос-

нования конуса до т. a’ и откладываем ее в аксонометрии на оси Z, то есть на стороне 0S.

Через полученную засечку проводим прямую в плоскости треугольника

параллельно основанию треугольника до пересечения с образующей SE. Таким образом, переносим высоту положения т. А на поверхность кону-

са.

Второй способ. Рис. 3.

Строим сечение конуса плоскостью параллельной основанию и проходящей через т. В. Такое сечение конуса есть окружность с радиусом равным

отрезку ОК расположенной на высоте равной высоте т. В. В аксонометрии эта окружность строиться в виде эллипса (или заменяющего его овала).

Затем, на осях X и Y в основании конуса откладываем соответствующие

координаты X и Y т. В взятые с горизонтальной проекции и из точки их пересечения восстанавливаем перпендикуляр до пересечения с эллипсом сечения,

что определит положение т. В.

Сечения конуса.

Взависимости от направления в пространстве секущей плоскости, проходящей через конус, в сечении прямого кругового конуса могут получаться

различные плоские фигуры:

А – прямые (образующие) Б – гипербола

В– окружность

Г – парабола

Д – эллипс Конические сечения – эллипс, парабола и гипербола являются лекаль-

ными кривыми, которые строятся по точкам принадлежащим кривой сечения.

А. Сечение конуса вертикальной плоскостью проходящей через его вершину представляет собой прямые. Рис. 4.

На горизонтальной проекции конуса через точку S проводим линию Ph под произвольным углом к осям X и Y, которая является горизонтальной проекцией секу-

щей вертикальной плоскости. Эта линия

пересекает окружность основания конуса в двух точках a и b, а отрезок aob является горизонтальной проекцией сечения конуса.

Мысленно отбросим левую часть конуса от линии Ph и справа от нее получим горизонтальную проекцию усеченного ко-

нуса.

Отрезки SA и SB — горизонтальные

проекции образующих конуса, по которым и проходит секущая плоскость Ph.

Строим образующие SA и SB на

фронтальной проекции, перенеся на нее точки A и B и соединив полученные точки a’ и b’ с вершиной s’. Треугольник a’s’b’ и будет фронтальной проекцией сечения

конуса, а линия s’3’ – крайней образующей конуса.

Рис. 5

Аналогично строим профильную проекцию сечения конуса, перенеся

точки a и b с горизонтальной проекции на профильную и соединив полученные точки a” и b” с вершиной конуса s”. Треугольник a”s”b” является профильной проекцией сечения конуса, а линия s”2” есть крайняя образующая конуса.

Построение аксонометрии. Рис. 4.

Строим конус в аксонометрии, как описано выше.

Далее с горизонтальной проекции конуса берем координаты по оси X или Y для точек A и B и переносим их на аксонометрические оси X или Y. Через полученные точки проводим вспомогательные линии параллельные осям Y

или X соответственно. Их пересечение с линией основания конуса позволяет получить точки A и B на аксонометрии. Соединив их между собой, и каждую из

них с вершиной конуса S, получим треугольник ABS являющийся сечением конуса вертикальной плоскостью P.

Б. Сечение конуса вертикальной плоскостью, не проходящей через его вершину, представляет собой гиперболу. Рис. 5.

Строим три проекции конуса — горизонтальную, фронтальную и про-

фильную.

Если вертикальная секущая плоскость P не проходит через вершину конуса, то она уже не совпадает с образующими его боковой поверхности, а наоборот – пересекает

их.

На горизонтальной проекции конуса проводим секущую плоскость Ph на произвольном расстоянии от вершины S и парал-

лельную оси Y. В общем случае положение

секущей плоскости относительно осей X и Y может быть любое.

Линия Ph пересекает окружность основания конуса в двух точках a и b. Отрезок ab этой прямой есть горизонтальная проек-

ция сечения конуса. Часть окружности слева от линии Ph делим на произвольное коли-

чество равных частей, в донном случае на 12 и, затем каждую полученную точ-

ку на окружности соединяем с вершиной конуса s. Эти образующие пересека-

ются секущей плоскостью Ph и мы получаем ряд точек, которые принадлежат образующим и проекции сечения конуса ab одновременно.

Строим полученные образующие на фронтальной проекции конуса

.Переносим с горизонтальной проекции все точки на основании конуса (a, 1, …,

5, b) и на фронтальной проекции получаем точки (a’, 1’, …, 5’, a’) и соединяем из с вершиной конуса s’. Проводим на фронтальной проекции через точку b’ секущую плоскость Pv перпендикулярно основанию конуса. Линия Pv пересекает

все образующие, и точки их пересечения принадлежат проекции сечения конуса.

Повторим построение всех образующих на профильной проекции конуса, перенеся на нее точки (a, 1, …, 5, b) с горизонтальной проекции. Полученные точки (a”, 1”, …, 5”, b”) соединим с вершиной s”.

На полученные образующие перенесем с фронтальной проекции точки пересечения соответствующих образующих с секущей плоскостью Pv. Полученные точки соединим кривой линией, которая представляет собой лекальную

кривую – гиперболу.

Построение аксонометрии. Рис. 5.

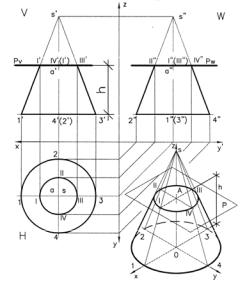
Рис. 6

Строим конус в аксонометрии, как описано выше.

Далее с горизонтальной проекции конуса берем координаты по оси X или Y для всех точек a, 1, …, 5, b и переносим их на аксонометрические оси X или Y находим их положение на основании конуса в аксонометрии. Соединяем

их последовательно с вершиной конуса S и получаем ряд образующих на поверхности конуса соответствующих образующим на ортогональных проекциях.

На каждой образующей найдем точку ее пересечения с секущей плоскостью P аналогично тому, как это было описано выше (см. построение точек на поверхности конуса, первый способ).

Соединив полученные на образующих точки лекальной кривой, а также точки A и B получим аксонометрическую проекцию усеченного конуса.

В Сечение конуса горизонтальной плоскостью. Рис. 6.

Сечение прямого кругового конуса горизонтальной плоскостью параллельной основанию – есть окружность.

Если рассечь конус на произвольной высоте h от основания конуса через точку a’

лежащую на его оси o’s’ плоскостью параллельной его основанию, то на фронтальной проекции мы увидим горизонтальную линию Pv являющуюся фронтальной проекцией секущей плоскости, которая образует сечение

конуса I’, II’, III’, IV’. На профильной проекции

W вид секущей плоскости и сечение конуса аналогичен и соответствует линии Pw.

На горизонтальной проекции сечение

конуса представляет собой круг в натураль-

ную величину, радиус окружности которого проецируется с фронтальной проекции как расстояние от оси конуса в точке a’ до точки I’, лежащей на крайней образующей 1’s’.

Построение аксонометрии. Рис. 6.

Строим конус в аксонометрии, как опи-

сано выше.

Затем на оси Z откладываем высоту h точки А от основания конуса. Через точку А проводим линии параллельные осям X и Y и строим окружность в

аксонометрии радиусом R=a’I’ взятым с фронтальной проекции.

Г Сечение конуса наклонной плоскостью, параллельной образующей. Рис. 7.

Строим три проекции конуса — горизонтальную, фронтальную и профильную. (см. выше).

На фронтальной проекции конуса проводим секущую плоскость Pv параллельно очерковой образующей s’6’на произвольном расстоянии от ее нача-

ла на основании конуса через т. a’(b’). Отрезок a’c’ есть фронтальная проекция сечения конуса.

На горизонтальной проекции строим проекцию основания секущей плоскости Р через точки a, b. Отрезок ab – есть проекция основания сечения конуса.

Далее окружность основания конуса делим на произвольное количество частей и полученные точки соединяем с вершиной конуса s. Получаем ряд образующих конуса, которые последовательно переносим на фронтальную и профильную проекции. (см. пункт Б).

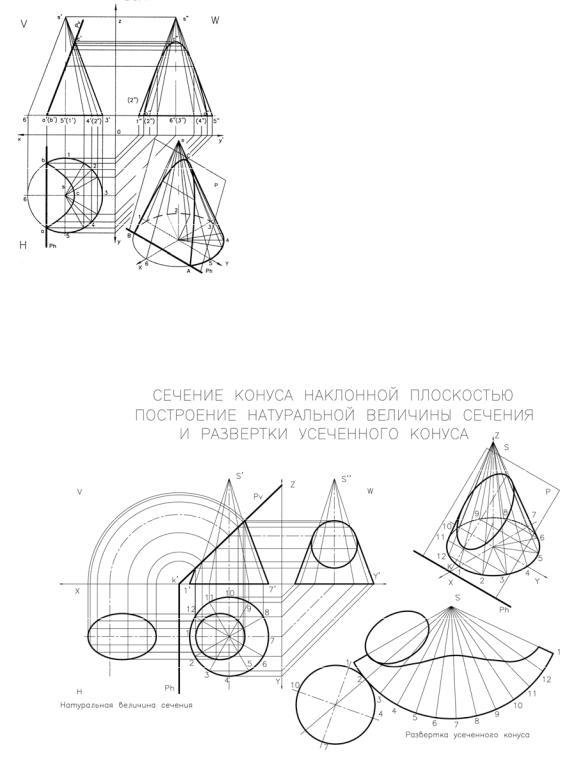
На фронтальной проекции след секущей плоскости Pv пересекает обра-

зующие и в пересечении дает ряд точек, которые принадлежат как секущей плоскости, так и образующим конуса одновременно.

Переносим линиями связи эти точки на проекции образующих на гори-

зонтальную и профильную проекции.

Полученные точки соединим кривой линией, которая представляет собой

лекальную кривую — параболу.

Построение аксонометрии. Рис. 7.

Строим аксонометрическую проекцию конуса, как описано выше.

Далее с горизонтальной проекции конуса берем координаты по оси X или Y для

всех точек (a, b, 1, …, 6) и переносим их на аксонометрические оси X или Y соответственно, определив, таким образом их поло-

жение на основании конуса в аксонометрии. Соединяем их последовательно с вершиной

конуса S и получаем ряд образующих на поверхности конуса, соответствующих образующим на ортогональных проекциях.

На каждой образующей найдем точку ее пересечения с секущей плоскостью P

аналогично тому, как это было описано выше (см. построение точек на поверхности конуса).

		Соединив полученные на образующих
	Рис. 7
	точки лекальной кривой, а также точки A и B

		получим сечение конуса в виде параболы.

Д. Сечение конуса наклонной плоскостью, расположенной под произвольным углом к основанию конуса представляет собой эллипс. Рис. 8.

Рис. 8

Строим три проекции конуса — горизонтальную, фронтальную и про-

фильную. (см. выше).

На фронтальной проекции конуса проводим линию секущей плоскости Pv под произвольным углом к основанию конуса.

На горизонтальной проекции, окружность основания конуса делим на произвольное количество равных частей ( в данном случае на 12) и получен-

ные точки соединяем с вершиной конуса S. Получаем ряд образующих, которые с помощью линий связи, последовательно переносим на фронтальную и профильную проекции.

На фронтальной проекции секущая плоскость Pv пересекает все образующие, и полученные точки их пересечения принадлежат одновременно и се-

кущей плоскости и боковой поверхности конуса, являясь фронтальной проекцией искомого сечения.

Переносим эти точки на горизонтальную проекцию конуса.

Затем строим и профильную проекцию сечения конуса (см. выше), соединяя полученные точки лекальной кривой, которая представляет собой эл-

липс.

Построение натуральной величины сечения.

Лекальные кривые (эллипсы) на горизонтальной и профильной проекции представляют собой искаженные изображения сечения конуса.

Истинная (натуральная) величина сечения получается путем совмеще-

ния секущей плоскости P с горизонтальной плоскостью проекций H. Все точки сечения конуса на фронтальной проекции переносим на ось X при помощи циркуля, поворачивая их вокруг точки k’. Далее, на горизонтальной проекции, линиями связи, параллельными оси Y продолжаем их до пересечения их с ли-

ниями связи, взятыми с горизонтальной проекции соответствующих точек. Пе-

ресечение горизонтальных и вертикальных линий связи соответствующих точек позволяет получить точки, принадлежащие натуральной величине сечения. Соединив их лекальной кривой, мы получим эллипс натуральной величины сечения конуса.

Построение аксонометрии усеченного конуса. Рис. 8.

Построение аксонометрии усеченного конуса выполняется путем нахождения точек принадлежащих сечению конуса любым из описанных выше способов (см. выше).

Построение развертки поверхности усеченного конуса. Рис. 8.

Предварительно построим развертку боковой поверхности не усеченного

конуса. Задаемся положением т. S на листе и проводим из нее дугу радиусом равным натуральной величине длины образующей конуса (например, s’1’или s’7’). Задаемся положением т. 1 на этой дуге. Последовательно откладываем от нее столько одинаковых отрезков (хорд) на сколько частей разделена окружность основания конуса. Полученные на дуге точки 1, 2, …, 12, 1 соединяем с т. S. Сектор 1S1 представляет собой развертку боковой поверхности не усе-

ченного конуса. Пристроив к ней в нижней части (например, к т. 2) натуральную величину основания конуса в виде круга взятого с горизонтальной проекции мы

получим полную развертку не усеченного конуса.

Для построения развертки боковой поверхности усеченного конуса необходимо определить натуральную величину всех усеченных образующих. На

фронтальной проекции все точки сечения перенесем на очерковую образующую s’7’ линиями параллельными основанию конуса. Затем каждый отрезок образующей от т. 7’ до соответствующей точки сечения переносим на соответствующую образующую на развертке. Соединив эти точки на развертке, получим кривую линию, соответствующую линии сечения боковой поверхности ко-

нуса.

Затем к линии сечения на развертке (например, к образующей S1) при-

страиваем эллипс натуральной величины сечения полученный на горизонтальной проецирующей плоскости Н.

Развертки поверхности геометрических тел представляют собой чертежи

– выкройки из бумаги и служат для выполнения макета фигуры.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Построение натуральной величины сечения конуса

Построение сечения конуса плоскостью выполняется на проекции, относительно которой секущая занимает проецирующее
положение. В этом положении, пересечение любой линии (образующей) поверхности конуса и секущей определяется пересечением
проекции образующей и секущей, которая выражена прямой линией.

Так как сечение конуса плоскостью является плоской фигурой уложенной в секущую, то построение натуральной величины сечения
можно выполнить при выполнении условия проецирования фигуры в натуральную величину —
параллельности секущей и плоскости проекций. Для этого можно выполнить замену проекции на плоскость параллельную
секущей конуса.

Как найти натуральную величину высоты пирамиды.
Угол равный натуральной величине.

Определение натуральной величины.

Решение задач по начертательной геометрии.

Источник

10 дек2018

10 декабря 2018. Категория: #СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА/НАХОЖДЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ

Определение натуральной величины сечения

Цель видеоурока Автокад/НГ: Обучение Автокад 2D на практике и закрепление пройденного материала раздела «Теоретические и практические видеоуроки Автокад». Закрепление знаний по решению задач на построение натуральной величины отрезка, треугольника, сечения и т.д. используя для этого любой способ преобразования чертежа.

Дано: чертеж «Сечение комбинированной поверхности плоскостью».

Задание: Построить натуральную величину сечения, применив для этого любой способ преобразования чертежа.

Читать статью…

11 дек2018

11 декабря 2018. Автор статьи: Евгений Курицин. Категория: #СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА/НАХОЖДЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ

Натуральная величина сечения комбинированной поверхности

В предыдущем видеоуроке Пересечение поверхности плоскостью мы построили 3 проекции сечения. В этом видеоуроке мы построим натуральную величину сечения.

При использовании способа совмещения будет наложение изображений, поэтому фронталь плоскости сечения разместим на свободном поле чертежа. Радиус вращения каждой точки сечения возьмем с горизонтальной проекции и он будет соответствовать расстоянию от точки до продольной оси симметрии (оси вращения).

Читать статью…

10 дек2018

10 декабря 2018. Автор статьи: Евгений Курицин. Категория: #СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА/НАХОЖДЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ

Построение натуральной величины сечения

Дано: Пересечение многогранников (пирамиды и призмы)

Необходимо произвести построение натуральной величины сечения призмы, образованного гранью ACNM фронтально-проецирующей призмы.

Читать статью…

10 дек2018

Натуральная величина треугольника

Задание: Определить натуральную величину треугольника ABC.

Дано: Таблица значения координат.

Читать статью…

10 дек2018

Определение натуральной величины треугольника

Найти натуральную величину треугольника общего положения можно следующими действиями:

- Плоскопараллельным перемещением треугольник ABC приводится в положение проецирующией плоскости
- Вращением вокруг проецирующей прямой в пложение когда плоскость заданная треугольником будет параллельна плоскости проекций

В треугольнике ABC построим линию пересечения его с треугльником EDK.

Читать статью…

10 дек2018

Способ совмещения как частный случай вращения

В предыдущем видеоуроке Автокад мы произвели сечение конуса плоскостью частного положения. В этом уроке мы найдем натуральную величину сечения конуса способом совмещения.

Дано: Сечение конуса плоскостью
Необходимо: Найти натуральную величину сечения конуса способом (методом) совмещения.

Способ совмещения в начертательной геометрии мы уже использовали в видеоуроке Автокад Построение натуральной величины сечения.

Читать статью…

10 дек2018

Способ замены (перемены) плоскостей проекций

Чертеж Автокад Сечение цилиндра плоскостью содержит практически все данные для построения развертки усеченного цилиндра. Осталось только найти натуральную величину сечения цилиндра.
Натуральную величину сечения цилиндра найдем способом замены (перемены) плоскостей проекций.

Алгоритм решения задачи с использованием способа замены (перемены) плоскостей проекции.

Читать статью…

Источник