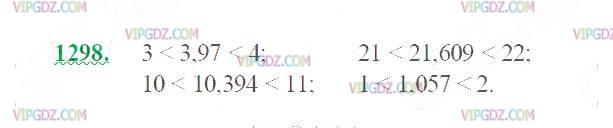ГДЗ и решебники
вип уровня
- ГДЗ
- 5 класс
- Математика
- Виленкин
- Задание 1298
Условие
Для каждого из чисел найдите натуральные приближённые значения с недостатком и с избытком: 3,97; 21,609; 10,394; 1,057.
Решение 1
Решение 2
Решение 3
Популярные решебники
Человеку постоянно приходится сталкиваться с решением различных практических и теоретических задач, которые чаще всего связаны с нахождением числовых значений величин.
Измерить какую-либо величину- это значит сравнить ее с однородной величиной, принятой за единицу измерения.
В большинстве случаев полученные значения в результате вычислений и измерений получаются неточными, приближенными: немного больше или меньше истинного значения.
Точность- это степень приближения результата измерения (вычисления) к реальному значению.
Чем меньше точность, тем больше погрешность (расхождение истинного и полученного значения) и, соответственно, чем меньше погрешность, тем выше точность.
Точные измерения проблематичны в реальности по ряду причин:
Эта информация доступна зарегистрированным пользователям
- Несовершенство органов чувств человека.
- Неточность и несовершенство измерительных приборов.
- Характеристики самого измеряемого объекта, не позволяющие выполнить точные измерения и вычисления.
Так, например, невозможно точно до метра определить протяженность рек, гор, расстояние от Земли до Луны, с точностью до грамма проблематично определить массу грузовика и т.д.
Сегодня на уроке мы научимся находить приближенные значения с избытком и недостатком.
Эта информация доступна зарегистрированным пользователям
Познакомимся с правилом округления чисел до заданного разряда.
Рассмотрим несколько примеров округления чисел.
В настоящее время в различные сферы жизни человека все больше внедряются современные высокоточные устройства, которые позволяют быстро и точно производить измерения и вычисления.
Однако, порой нам даже нет необходимости знать точное значение величины.
Не раз нам приходилось встречать такие фразы: «около одного часа», «примерно один килограмм» или «приблизительно двадцать тысяч рублей» и т.п.
В подобных фразах синонимы: «около», «примерно», «приблизительно» и т.д. указывают на приближенность значений величины, на чуть большее или меньшее значение относительно реального.
Например, говоря о своем возрасте, мы чаще всего называем количество лет и месяцев, не упоминая о прожитых днях и часах.
На вопрос «который час?» мы скорее всего назовем сколько часов и минут в данный промежуток времени, не указывая секунды.
Числа, с которыми нам приходится встречаться и использовать в действительности, бывают двух типов:
- Точные (в истинности которых мы не сомневаемся).
Например, говоря о том, что у треугольника 3 стороны, число 3 представляет собой точным числом.
Эта информация доступна зарегистрированным пользователям
В утверждении о том, что стул имеет 4 ножки, число 4 так же является точным.
Эта информация доступна зарегистрированным пользователям
- Приближенные (близкие к истинному значению).
На практике, измеряя расстояние, массу, температуру, объем, площадь и другие величины, мы не можем определить их точные значения, а порой эти точные значения вовсе не требуется находить.
Эта информация доступна зарегистрированным пользователям
Поэтому важно знать (заранее установить) с какой точностью необходимо выполнить измерения и вычисления, т.е. необходимо выяснить какие доли единицы измерения необходимо принять во внимание, а какими можно пренебречь.
Приближенные значения делят на:
- Приближенные значения с недостатком.
- Приближенные значения с избытком.
Рассмотрим поясняющий пример.
Обратите внимание на рисунок.
Эта информация доступна зарегистрированным пользователям
Улитка проползла некоторое расстояние и остановилась, данное расстояние обозначим как х (см).
Заметим, что улитка смогла преодолеть больше 7 см, но не смогла доползти до отметки 8 см.
Получается, что расстояние, которое проползла улитка больше 7 см, но меньше 8 см:
7 < x < 8
В данном случае число 7, 8— это приближенные значения числа х.
Путь, который проползла улитка, изображен в виде отрезка МN.
Конец отрезка MN заключен между отметками 7 см и 8 см.
Если А< x < В (число х больше числа А, но меньше числа В), то А называют приближенным значением числа х с недостатком, а число В— приближенным значением числа х с избытком.
Получаем в нашем случае 7 см- это приближенное значение длины отрезка MN с недостатком, а 8 см- это приближенное значение длины отрезка MN с избытком.
Так, если бы улитка проползла х = 6,3 см, то 6 см являлось бы приближенным значением пути улитки с недостатком, а значение 7 см было бы приближенным значением пути с избытком.
Рассмотрим пару заданий, в которых необходимо произвести оценку величины.
Задание №1.
Из предложенных чисел 2,1; 2,7; 4,1; 3,2; 2,4; 3,5 выберите те, для которых 2,3 является приближенным значением числа с недостатком, а число 3,7 является приближенным значением числа с избытком.
Для искомых чисел должно выполняться условие 2,3 < x < 3,7.
Такому условию удовлетворяют следующие десятичные дроби:
2,4 так как 2,3 < 2,4 < 3,7
2,7 так как 2,3 < 2,7 < 3,7
3,2 так как 2,3 < 3,2 < 3,7
3,5 так как 2,3 < 3,5 < 3,7
Задание №2.
Определите между какими двумя ближайшими натуральными числами расположена дробь 2,4.
К какому натуральному числу ближе заданная десятичная дробь 2,4?
С помощью координатного луча мы можем оценить расположение десятичной дроби.
Отметим на координатном луче число 2,4 (две целых четыре десятых).
Разложим заданное число по разрядам.
2,4 = 2 + 0,4
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Эта информация доступна зарегистрированным пользователям
Отложим два целых единичных отрезка от начала координат, получим две целых единицы.
Чтобы отметить дробь 0,4, третий единичный отрезок разделим на десять долей, каждая такая доля будет равна (mathbf{frac{1}{10} = 0,1}).
От точки с координатой 2 отложим вправо четыре доли единичного отрезка ОЕ, получим точку 2,4.
Если мы посмотрим на координатный луч, то заметим, что десятичная дробь 2,4 находится между натуральными числами 2 и 3, причем десятичная дробь 2,4 удалена от точки 2 всего на четыре доли единичного отрезка, а точка 3 удалена от точки 2,4 на шесть таких долей, следовательно, десятичная дробь 2,4 расположена ближе к натуральному числу 2.
2 < 2,4 < 3
Эта информация доступна зарегистрированным пользователям
Чтобы найти приближенное значение числа, используют математическое действие- округление чисел (замена числа его ближайшим «круглым» числом).
«Круглым» числом называют число, оканчивающееся одним или несколькими нулями.
Округление- это математическая операция, с помощью которой можно уменьшить количество знаков в числе за счет замены этого числа его близким значением с определенной точностью.
Суть операции округления заключается в нахождении числа ближайшего по своему значению к истинному.
Округлить можно любое число до любого разряда.
Важно знать и помнить правильное название и расположение разрядов в числе.
Вспомним разряды десятичных дробей.
Эта информация доступна зарегистрированным пользователям
Замену числа ближайшим к нему натуральным числом или нулем называют округлением этого числа до целых.
Десятичные дроби возможно округлять так же как натуральные числа до единиц, десятков, сотен, тысяч и т.д.
При округлении числа до десятков число заменяют «круглым» числом, которое должно состоять из целых десятков, а вместо разряда единиц должен быть нуль.
Если необходимо округлить число, например, до сотен, это число заменяют «круглым» числом, в котором остается разряд сотен, а в разряде десятков и единиц должны стоять нули.
Пример.
Округлим 1,7 до целого.
Рассмотрим процесс округления десятичной дроби с помощью координатного луча.
Разложим заданное число по разрядам.
1,7 = 1 + 0,7
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Эта информация доступна зарегистрированным пользователям
Отметим на координатном луче точку с координатой 1,7.
Отложим один целый единичный отрезок от начала координат, получим одну целую единицу.
Чтобы отметить дробь 0,7, второй единичный отрезок разделим на десять долей, каждая такая доля будет равна (mathbf{frac{1}{10} = 0,1}).
От точки с координатой 1 отложим вправо семь долей единичного отрезка ОЕ, получим точку с координатой 1,7.
Обратим внимание, что точка 1,7 находится между натуральными числами 1 и 2.
Точка с координатой 1,7 удалена от точки Е(1) на семь долей единичного отрезка ОЕ, а от точки с координатой 2— всего на три доли единичного отрезка ОЕ.
Таким образом, можно утверждать, что точка с координатой 1,7 расположена ближе к точке с координатой 2.
Значит, при округлении числа 1,7 до целых получается число 2 (1,7 приближенно равно 2).
1,7 ≈ 2
Десятичные дроби так же можно округлять до определенного разряда, стоящего после десятичной запятой: до десятых, сотых, тысячных и т.д.
При округлении до какого-либо разряда все последующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их просто отбрасывают.
Округление чисел происходит по определенному правилу, рассмотрим его.
Чтобы округлить число до какого-либо разряда нужно:
Эта информация доступна зарегистрированным пользователям
Поясним на примерах.
Пример №1.
Округлим 83421 до сотен.
Решение:
Подчеркнем в числе цифру 4, так как она стоит в разряде сотен.
83421
За подчеркнутой цифрой стоит цифра 2, следовательно, необходимо действовать согласно Правила №1: оставить цифру 4 без изменения.
Все цифры, стоящие после разряда сотен (цифры 2 и 1), заменим нулями.
Эта информация доступна зарегистрированным пользователям
В итоге получим округление числа 83421 до 83400.
Результат запишем следующим образом: 83421 ≈ 83400.
Пример №2.
Округлим до разряда единиц число 316,52.
Решение:
Число 316,52 будем округлять до целых.
Известно, что десятичная дробь состоит из целой части (находящейся до десятичной запятой) и дробной части (находящейся после десятичной запятой).
В заданной десятичной дроби 316,52 в разряде единиц стоит цифра 6.
Подчеркнем цифру 6.
316,52
Цифра, стоящая справа от подчеркнутой цифры- это цифра 5, следовательно, необходимо действовать согласно Правила №2: к подчеркнутой цифре 6 прибавить единицу.
Получим в разряде единиц цифру 7, все цифры, стоящие следом за округляемым разрядом (стоящие после десятичной запятой), отбрасываем.
Эта информация доступна зарегистрированным пользователям
В итоге получим округление числа 316,52 до 317.
Результат запишем следующим образом: 316,52 ≈ 317.
Пример №2.
Округлим число 27,819 до разряда сотых.
Решение:
В заданной десятичной дроби 27,819 в разряде сотых стоит цифра 1, подчеркнем ее.
27,819
За подчеркнутым разрядом стоит цифра 9, следовательно, необходимо действовать согласно Правила №2: к подчеркнутой цифре 1 прибавить единицу.
Получим в разряде сотых цифру 2, все цифры, следующие за разрядом сотых, просто отбрасываем.
Эта информация доступна зарегистрированным пользователям
В итоге получим округление числа 27,819 до 27,82.
Результат запишем следующим образом: 27,819 ≈ 27,82.
Эта информация доступна зарегистрированным пользователям
Рассмотрим несколько примеров округления чисел при решении задач.
Задача №1.
Эта информация доступна зарегистрированным пользователям
В первый день продали 20,35 м ткани, во второй день еще 17,8 м ткани.
Сколько метров ткани продали за два дня?
Ответ округлите до десятых.
Решение:
Кратко запишем условие задачи.
Эта информация доступна зарегистрированным пользователям
Схематично изобразим условие задачи.
Эта информация доступна зарегистрированным пользователям
Сложим ткань, которую продали в первый и во второй день, в результате получим сколько метров ткани продали за два дня.
Эта информация доступна зарегистрированным пользователям
20,35 + 17,8 = 38,15 (м) ткани продали за два дня.
Округлим полученное число 38,15 до десятых.
В полученной десятичной дроби 38,15 в разряде десятых стоит цифра 1, подчеркнем ее.
38,15
За подчеркнутым разрядом стоит цифра 5, следовательно, необходимо действовать согласно Правила №2: к подчеркнутой цифре 1 прибавить единицу.
Получим в разряде десятых цифру 2, все цифры, следующие за подчеркнутой цифрой, просто отбрасываем.
Результат запишем следующим образом: 38,15 ≈ 38,2.
Ответ: 38,2 (м).
Задача №2.
Эта информация доступна зарегистрированным пользователям
В первый день автомобиль проехал 124,4 км, а во второй день на 31,2 км меньше.
Какой путь проехал автомобиль за эти два дня?
Ответ округлите до целых.
Решение:
Кратко запишем условие задачи.
Проехал в первый день- 124,4 км
Проехал во второй день- 124,4 – 31,2 км
Чтобы найти путь, который проехал автомобиль, необходимо сложить пройденный путь в первый и во второй день.
Составим выражение.
124,4 + (124,4 – 31,2)
Найдем значение полученного выражения.
Выражение содержит несколько арифметических операций и скобки.
1. Выполним действия в скобках (найдем разность двух десятичных дробей).
Эта информация доступна зарегистрированным пользователям
2. Сложим полученный результат и 124,4.
Эта информация доступна зарегистрированным пользователям
124,4 + 93,2 = 217,6 (км) автомобиль проехал за два дня.
Округлим полученный результат до целых.
В полученной десятичной дроби 217,6 в разряде единиц (в самом младшем разряде целой части десятичной дроби) стоит цифра 7, подчеркнем ее.
217,6
После подчеркнутой цифры стоит цифра 6, следовательно, чтобы верно округлить число, необходимо действовать согласно Правила №2: к подчеркнутой цифре 7 нужно прибавить единицу.
Получим в разряде единиц цифру 8, все цифры, следующие за подчеркнутой цифрой, просто отбрасываем.
Результат запишем следующим образом: 217,6 ≈ 218.
Ответ: 218 (км).
Задача №3.
Эта информация доступна зарегистрированным пользователям
За два дня было продано 45,35 (кг) конфет. В первый день продали 31,20 (кг).
На сколько больше конфет продали в первый день, чем во второй?
Ответ округлите до десятых.
Решение:
Кратко запишем условие задачи.
Эта информация доступна зарегистрированным пользователям
Первым действием найдем сколько конфет продали во второй день, для этого вычтем конфеты, проданные в первый день из общего количества конфет, проданных за два дня.
Эта информация доступна зарегистрированным пользователям
1. 45,35 – 31,20 = 14,15 (кг) конфет продали во второй день.
Следующим действием найдем на сколько килограммов конфет было продано больше в первый день, чем во второй.
Эта информация доступна зарегистрированным пользователям
2. 31,20 – 14,15 = 17,05 (кг)
Округлим полученный результат (десятичную дробь 17,05) до десятых.
В полученной десятичной дроби 17,05 в разряде десятых стоит цифра 0, подчеркнем ее.
17,05
За подчеркнутым разрядом стоит цифра 5, следовательно, необходимо действовать согласно Правила №2: к подчеркнутой цифре 0 прибавить единицу.
Получим в разряде десятых цифру 1, все цифры, следующие за подчеркнутой цифрой, просто отбрасываем.
Результат запишем следующим образом: 17,05 ≈ 17,1.
Ответ: в первый день продали на 17,1 кг конфет больше, чем во второй день.
Эта информация доступна зарегистрированным пользователям
Читайте также
☰
Приближение по недостатку и по избытку
Проводя различные измерения, решая уравнения графическим способом, выполняя арифметические вычисления, часто получают приближенные значения, а не точные. Например, при вычислении корня числа может получиться бесконечная непериодическая дробь (т. е. иррациональное число). Кроме того, существуют бесконечные периодические дроби, использовать которые в вычислениях также неудобно.
Поэтому числа, являющиеся бесконечными десятичными дробями или конечными, но имеющими множество знаков после запятой, принято округлять.
Когда округление выполняется в большую сторону, то говорят о приближении по избытку. Когда округление выполняется в меньшую сторону, то говорят о приближении по недостатку.
Полученное при округлении число называют приближенным по недостатку или избытку с определенной точностью. Рассмотрим несколько примеров приближения.
Число π является бесконечной дробью 3,1415926535… Обычно его округляют с точностью до 0,01. Это значит, что после запятой оставляют только два знака. При приближении по избытку получится 3,15. При приближении по недостатку получится 3,14.
Для числа π обычно используют приближение по недостатку, так как согласно правилу округления положительные числа округляются в большую сторону, если первая отбрасываемая цифра 5 или больше пяти. Так как у числа π третья цифра после запятой — это 1, то округление выполняется в меньшую сторону, то есть для расчетов выполняется приближение по недостатку.
Однако, несмотря на правила округления, имеют право быть приближения как по недостатку, так и по избытку.
Если выполнять приближение числа π с точностью до 0,0001, то по избытку получим π ≈ 3,1416, а по недостатку π ≈ 3,1415.
Рассмотрим иррациональное число √2, которое равно 1,414213… . Вычислим его приближение по недостатку и по избытку с точностью до 0,001. Поскольку приближение выполняется до тысячных долей, то у числа надо оставить три знака после запятой. При приближении по недостатку просто отбрасываются все цифры после третьей после запятой. При приближении по избытку цифры после третьей после запятой отбрасываются, а третья цифра увеличивается на 1. Таким образом, приближение по недостатку будет √2 ≈ 1,414, а по избытку √2 ≈ 1,415.
Но примеры, рассмотренные выше, это положительные числа. А так ли обстоит дело при приближении отрицательных чисел. Если взять число –√2 = –1,414213…, то его приближением по избытку до тысячных долей будет –1,414, так как это число больше, чем –√2. А вот приближением по недостатку будет –1,415, так как это число меньше, чем –√2.
Слайд 2*
Пример. Найти приближенные значения по недостатку и по
избытку с точностью до 0,01 для числа
2,000+2,236=4,236
4,236≈4,23 – приближенное значение с недостатком с точностью до 0,01
4,236≈4,24 приближенное значение с избытком с точностью до 0,01
Слайд 3*
Приближение по недостатку и по избытку называют
округлением числа.
Правило округления: если первая отбрасываемая
цифра меньше 5, то нужно брать приближение по недостатку; если первая отбрасываемая цифра больше или равна 5, то нужно брать приближение по избытку.
Слайд 4*
Задания
1. Найти приближенные значения по недостатку и
по избытку с точностью до 0,0001 для
числа π.
(π = 3,141592…)
2. Округлите число 86,2759 до десятых.
3. Округлите до сотен тысяч число 6 723 401.
4. Округлите дроби:
а) 2,781; 3,1423; 203,962; 80,46 (до десятых);
б) 0,07268; 1,35506; 10,081; 76,544; 4,455 (до сотых);
в) 167,1; 2085,04; 444,4; 300,7; 137 (до десятков).
5. Для каждого из чисел найдите натуральные приближенные значения с недостатком и с избытком: 3,97; 21,609; 10,394; 1,057.
Слайд 5Абсолютная и относительная погрешность
*
Слайд 6
Абсолютной погрешностью приближения называется модуль разности между
истинным значением величины и её приближённым значением.
— истинное значение,
— приближённое.
*
Слайд 7Относительной погрешностью приближения называется отношение абсолютной погрешности
к модулю приближённого значения величины.
—
истинное значение,
— приближённое.
Относительную погрешность обычно выражают в процентах.
*
Слайд 8Пример. Найти абсолютную и относительную погрешность числа
с точностью до единиц.
При округлении числа 24,3
до единиц получается число 24.
Абсолютная погрешность:
Относительная погрешность:
Говорят, что относительная погрешность в этом случае равна 1,25%.
*
Слайд 9Задание 6. Заполните таблицу:
Старинные русские меры массы:
а)
пуд — 16,38 кг (до десятых)
б) лот
-12,797 г (до сотых)
в) золотник — 4,27 г (до целых)
г) доля — 0,044 г (до сотых)
Старинная русская мера длины:
д) верста — 1067м (до сотен)
е) сажень — 2,13м (до десятых)
ж) пядь -17,78 cм (до целых)
з) дюйм — 2,54 см (до десятых)
*
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Приближенные значения действительных чисел
Приближенные значения действительных чисел
И в 7-м и в 8-м классе мы часто решали уравнения графически. Заметили ли вы, что практически во всех таких примерах уравнения имели «хорошие» корни? Это были целые числа, которые без труда отыскивались с помощью графиков, особенно на клетчатой бумаге. Но так бывает далеко не всегда, просто мы до сих пор подбирали «хорошие» примеры.
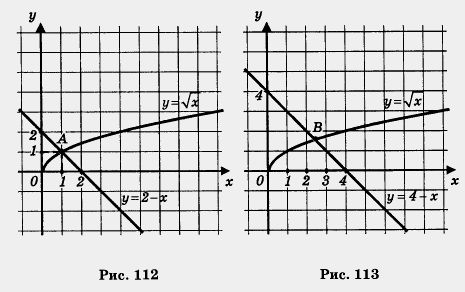
Рассмотрим два уравнения: 
= 2 — х и = 4 — х. Первое уравнение имеет единственный корень х = 1, поскольку графики функций у = и у = 2 — х пересекаются в одной точке А (1; 1) (рис. 112). Во втором случае графики функций — фс и у = 4 — х также пересекаются в одной точке В (рис. 113), но с «плохими» координатами. Пользуясь чертежом, можно сделать вывод, что абсцисса точки В примерно равна 2,5. В подобных случаях говорят не о точном, а о приближенном решении уравнения и пишут так:
Это одна из причин, по которым математики решили ввести понятие приближенного значения действительного числа. Есть и вторая причина, причем, может быть, даже более важная.Что такое действительное число? Это бесконечная десятичная дробь. Но производить вычисления с бесконечными десятичными дробями неудобно, поэтому на практике пользуются приближенными значениями действительных чисел. Например, для числа 
пользуются приближенным равенством 
3,141 или 3,142. Первое называют приближенным значением (или приближением) числа п по недостатку с точностью до 0,001; второе называют приближенным значением (приближением) числа к по избытку с точностью до 0,001. Можно взять более точные приближения: например, 3,1415 — приближение по недостатку с точностью до 0,0001; 3,1416 — приближение по избытку с точностью до 0,0001. Можно взять менее точные приближения, скажем, с точностью до 0,01: по недостатку 3,14, по избытку 3,15.
Знак приближенного равенства » вы использовали и в курсе математики 5—6-го классов и, вероятно, в курсе физики, да и мы пользовались им раньше, например в § 27.
Пример 1. Найти приближенные значения по недостатку и по избытку с точностью до 0,01 для чисел:
Решение,
а) Мы знаем, что 
= 2,236… (см. § 27), следовательно, 
2,23 — это приближение по недостатку с точностью до 0,01; 2,24 — это приближение по избытку с точностью до 0,01.
б) 2 + = 2,000… + 2,236… = 4,236… . Значит, 2 + 4,23 — это приближение по недостатку с точностью до 0,01; 2 + 4,24 — это приближение по избытку с точностью до 0,01.
в) Имеем 
0,31818… (см. § 26). Таким образом, 0,31 — это приближение по недостатку с точностью до 0,01; 0,32 — это приближение по избытку с точностью до 0,01.
Приближение по недостатку и приближение по избытку называют иногда округлением натуральные числа.
Определение.Погрешностью приближения (абсолютной погрешностью) называют модуль разности между точным значением величины х и ее приближенным значением а: погрешность приближения — это | х — а |.
Например, погрешность приближенного равенства 
выражается как 
или соответственно как 
,
Возникает чисто практический вопрос: какое приближение лучше, по недостатку или по избытку, т. е. в каком случае погрешность меньше? Это, конечно, зависит от конкретного числа, для которого составляются приближения. Обычно при округлении положительных чисел пользуются следующим правилом:
Применим это правило ко всем рассмотренным в этом параграфе числам; выберем для рассмотренных чисел те приближения, для которых погрешность окажется наименьшей.
1) 
= 3,141592… . С точностью до 0,001 имеем 3,142; здесь первая отбрасываемая цифра равна 5 (на четвертом месте после запятой), поэтому взяли приближение по избытку.
С точностью до 0,0001 имеем 3,1416 — и здесь взяли приближение по избытку, поскольку первая отбрасываемая цифра (на пятом месте после запятой) равна 9. А вот с точностью до 0,01 надо взять приближение по недостатку: 3,14.
2) = 2,236… . С точностью до 0,01 имеем 2,24 (приближение по избытку).
3) 2 + = 4,236… . С точностью до 0,01 имеем 2 + 4,24 (приближение по избытку).
4) 
= 0,31818… . С точностью до 0,001 имеем 0,318 (приближение по недостатку).
Рассмотрим последний пример подробнее. Возьмем укрупненный фрагмент координатной прямой (рис. 114).
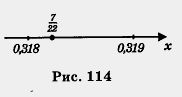
Точка принадлежит отрезку [0,318, 0,319], значит, ее расстояния от концов отрезка не превосходят длины отрезка. Расстояния точки от концов отрезка равны соответственно 
отрезка [0,318, 0,319] равна 0,001. Значит, 
и 
Итак, в обоих случаях (и для приближения числа по недостатку, и для приближения его по избытку) погрешность не превосходит 0,001.
До сих пор мы говорили: приближения с точностью до 0,01, до 0,001 и т. д. Теперь мы можем навести порядок в использовании терминологии.
Если а — приближенное значение числа х и 
, тo говорят, что погрешность приближения не превосходит h или что число х равно числу а с точностью до h.
Почему же важно уметь находить приближенные значения чисел? Дело в том, что практически невозможно оперировать с бесконечными десятичными дробями и использовать их для измерения величин. На практике во многих случаях вместо точных значений берут приближения с заранее заданной точностью (погрешностью). Эта идея заложена и в калькуляторах, на дисплеях которых высвечивается конечная десятичная дробь, т. е. приближение выводимого на экран числа (за редким исключением, когда выводимое число представляет собой конечную десятичную дробь, умещающуюся на экране).
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Сборник конспектов уроков по математике скачать, календарно-тематическое планирование, учебники по всем предметам онлайн
Содержание урокаконспект урока
конспект урока
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 