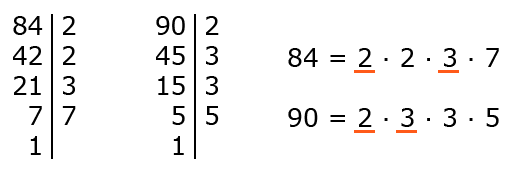Загрузить PDF
Загрузить PDF
Число называется делителем (или множителем) другого числа в том случае, если при делении на него получается целый результат без остатка.[1]
Для малого числа (например, 6) определить количество делителей довольно легко: достаточно выписать все возможные произведения двух целых чисел, которые дают заданное число. При работе с большими числами определить количество делителей становится сложнее. Тем не менее, если вы разложите целое число на простые множители, то легко сможете определить число делителей с помощью простой формулы.
-
1
Запишите заданное целое число вверху страницы. Вам понадобится достаточно места для того, чтобы расположить ниже числа дерево множителей. Для разложения числа на простые множители можно использовать и другие методы, которые вы найдете в статье Как разложить число на множители.
- Например, если вы хотите узнать, сколько делителей, или множителей имеет число 24, запишите
вверху страницы.
- Например, если вы хотите узнать, сколько делителей, или множителей имеет число 24, запишите
-
2
Найдите два числа (помимо 1), при перемножении которых получается заданное число. Таким образом вы найдете два делителя, или множителя данного числа. Проведите от данного числа две ветки вниз и запишите на их концах полученные множители.
-
3
Поищите простые множители. Простым множителем называется такое число, которое делится без остатка лишь на само себя и на 1.[2]
Например, число 7 является простым множителем, так как оно делится без остатка лишь на 1 и 7. Для удобства обводите найденные простые множители кружком.- Например, 2 является простым числом, поэтому обведите
кружком.
- Например, 2 является простым числом, поэтому обведите
-
4
Продолжайте раскладывать составные (не простые) числа на множители. Проводите следующие ветки от составных чисел до тех пор, пока все множители не станут простыми. Не забывайте обводить простые числа кружками.
-
5
Представьте каждый простой множитель в степенной форме. Для этого подсчитайте, сколько раз встречается каждый простой множитель в нарисованном дереве множителей. Это число и будет степенью, в которую необходимо возвести данный простой множитель.[3]
-
6
Запишите разложение числа на простые множители. Первоначально заданное число равно произведению простых множителей в соответствующих степенях.
- В нашем примере
.
Реклама
- В нашем примере
-
1
-
2
Подставьте в формулу величины степеней. Будьте внимательны и используйте степени при простых множителях, а не сами множители.
-
3
Сложите величины в скобках. Просто прибавьте 1 к каждой степени.
-
4
Перемножьте полученные величины. В результате вы определите количество делителей, или множителей данного числа
.
Реклама
Советы
- Если число представляет собой квадрат целого числа (например, 36 является квадратом числа 6), то оно имеет нечетное количество делителей. Если же число не является квадратом другого целого числа, количество его делителей четно.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 121 121 раз.
Была ли эта статья полезной?
Содержание материала
- Как определить количество делителей конкретного числа
- Видео
- Признаки делимости чисел
- Определение [ править
- Как найти число простых делителей числа
- Простые и составные числа
- Чем отличаются друг от друга, как найти
- Тест Миллера Рабина
Как определить количество делителей конкретного числа
Чтобы узнать, сколько положительных делителей у конкретного числа a, каноническое разложение которого выглядит как a = p 1 s 1 · p 2 s 2 · … · p n s n , нужно найти значение выражения ( s 1 + 1 ) · ( s 2 + 1 ) · … · ( s n + 1 ) . О количестве наборов переменных t 1 , t 2 , … , t n мы можем судить по величине записанного выражения.
Покажем на примере, как это вычисляется. Определим, сколько будет натуральных делителей у числа 3 900 , которое мы использовали в предыдущей задаче. Каноническое разложение мы уже записывали: 3 900 = 2 2 · 3 · 5 2 · 13 . Значит, s 1 = 2 , s 2 = 1 , s 3 = 2 , s 4 = 1 . Теперь подставим значения s 1 , s 2 , s 3 и s 4 в выражение ( s 1 + 1 ) · ( s 2 + 1 ) · ( s 3 + 1 ) · ( s 4 + 1 ) и вычислим его значение. Имеем ( 2 + 1 ) · ( 1 + 1 ) · ( 2 + 1 ) · ( 1 + 1 ) = 3 · 2 · 3 · 2 = 36 . Значит, это число имеет всего 36 делителей, являющихся натуральными числами. Пересчитаем то количество, что у нас получилось в предыдущей задаче, и убедимся в правильности решения. Если учесть и отрицательные делители, которых столько же, сколько и положительных, то получится, что у данного числа всего будет 72 делителя.
Условие: определите, сколько делителей имеет 84 .
Решение
Раскладываем число на множители.
84 42 21 7 1 2 2 3 7
Записываем каноническое разложение: 84 = 2 2 · 3 · 7 . Определяем, сколько у нас получится положительных делителей: ( 2 + 1 ) · ( 1 + 1 ) · ( 1 + 1 ) = 12 . Для учета отрицательных нужно умножить это число на 2 : 2 · 12 = 24 .
Ответ: всего у 84 будет 24 делителя – 12 положительных и 12 отрицательных.
Видео
Признаки делимости чисел
Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.
Признак делимости на 10
Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.
Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.
В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.
Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.
Признак делимости на 5 и на 2
Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.
Примеры:
10 : 5 = 2
100 : 5 = 20
100 : 2 = 50
Признак делимости на 5
Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.
Примеры:
355 : 5 = 71
200 : 5 = 40
475 : 5 = 95
Признак делимости на 3
Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:
27 : 3 = 9
Признак делимости на 9
Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9
18 : 9 = 2
Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:
Определение [ править
Функция «сумма положительных делителей »σx(n) для вещественного или комплексного числа x определяется как сумма x-х степеней положительных делителей числа n. Функцию можно выразить формулой
σ x ( n ) = ∑ d | n d x , <displaystyle sigma _(n)=sum _d^,!,>
где d | n <displaystyle > 
Аликвотная сумма s(n) для n — это сумма собственных делителей (то есть делители, за исключением самого n [5] , и равна σ1(n) − n. Аликвотная последовательность для n образуется последовательным вычислением аликвотной суммы, то есть каждое последующее значение в последовательности равно аликвотной сумме предыдущего значения.
Как найти число простых делителей числа
Если речь идет о целом малом числе, то решение такой задачи не представляет никакой сложности. Рассмотрим конкретный пример. Найдем простые делители числа 54.
Для этого:
- 54 делим на «два» и получаем 27;
- 27 нечетное, поэтому разделим его уже не на «два», а на следующее простое число, т. е. «три»;
- заметим, что 27=33;
- таким образом, разложение 54 имеет вид 54 = 21 * 33, т.е. простые делители числа 54 — это «два» и «три».
Однако это не все, что мы хотели знать. Теперь найдем число простых делителей числа 54. Оно равно произведению степеней простых множителей канонического разложения числа n = p1*d1 p2d2*⋅ …⋅*pmdm, увеличенных на 1. Иными словами, в общем случае K = (d1+1)*…* (dm+1).
Тогда для 54 имеем К = 2 * 4 = 8, т. е. общее число делителей равно восьми.
Обратите внимание, что все значительно упростилось, если бы речь шла о 23, 37, 103 и пр., так как каждый знает, сколько делителей у простого числа.
Простые и составные числа
Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:
5 : 1 = 5
5 : 5 = 1
Значит, число 5 является простым числом.
Составным же называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него два и более делителя: 4, 2 и 1
4 : 4 = 1
4 : 2 = 2
4 : 1 = 4
Значит, число 4 является составным числом.
Чем отличаются друг от друга, как найти
Делитель отличается от кратного тем, что:
- делитель — это число, НА которое делится заданное число;
- кратное — это число, которое само ДЕЛИТСЯ НА заданное число.
Чтобы найти делители числа, нужно данное число разложить на множители.
Разложить на множители — представить число в виде произведения целых чисел.
Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.
Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.
Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.
Тест Миллера Рабина
В криптографических целях часто используют именно этот вид определения простоты числа, который имеет несколько модификаций.
Тест Миллера—Рабина основан на проверке ряда условий, выполняемых для чисел, которые делятся только на 1 и на самих себя. Если хотя бы одно из требований нарушено, это «экзаменуемое» число признается составным.
Для данного m находятся целые нечетное число t и s, такие чтобы выполнялось условие m-1=2st.
Затем выбирается случайное число a, такое что 1<a<m. Если a не свидетельствует о простоте числа m, то программа должна выдать ответ «m составное» и завершить свою работу. В противном случае выбирается другое случайное число a и проверка повторяется снова. После того как будут установлены r свидетелей простоты, должен быть выдан ответ «m, вероятно, простое», и алгоритм завершит свою работу.
Следствием теоремы Рабина является тот факт, что если r чисел, которые выбраны случайно, признаны свидетелями для определения простоты числа m, то вероятность того, что оно составное, не может превосходить (4-r).
Теперь вы знаете, сколько делителей имеет простое число и как выяснить наиболее примитивный алгоритм вычисления НПД. Эти знания помогут вам в решении многих практических задач.
Теги
Содержание
- Нахождение всех делителей числа, число делителей числа.
- Все делители числа, их нахождение
- Число делителей числа
- Нахождение всех общих делителей чисел и их количества
- Нахождение всех делителей числа
- Все делители числа
- Калькулятор нахождения всех делителей
- Наибольший общий делитель (НОД), свойства и формулы
- Понятие наибольшего общего делителя
- Свойства наибольшего общего делителя
- Способы нахождения наибольшего общего делителя
- 1. Разложение на множители
- 2. Алгоритм Евклида
Нахождение всех делителей числа, число делителей числа.
Материал этой статьи про нахождение всех делителей числа. Сначала доказана теорема, которая задает вид всех общих делителей данного числа, после чего рассмотрены примеры нахождения всех делителей. Дальше показано, как вычисляется число делителей числа. В заключение подробно разобраны примеры нахождения всех общих делителей нескольких чисел и их количества.
Навигация по странице.
Все делители числа, их нахождение
Дальнейшее изложение подразумевает хорошее владение информацией статьи делители и кратные числа. Мы будем говорить лишь о поиске всех делителей целых положительных чисел (натуральных чисел). Этого вполне достаточно, так как одно из свойств делимости утверждает, что множество делителей целого отрицательного числа −a совпадает со множеством делителей противоположного числа a (которое будет положительным). Напомним также, что число 0 имеет бесконечно много делителей, и нахождение всех делителей нуля не представляет интереса.
положительными делителями простого числа a являются лишь единица и само это число. Следовательно, любое простое число a имеет четыре делителя, среди которых два положительных и два отрицательных: 1 , −1 , a и −a . Например, число 11 – простое, оно имеет всего четыре делителя 1 , −1 , 11 и −11 . Еще пример. Число 367 тоже простое, все его делители – это числа 1 , −1 , 367 и −367 .
Интереснее проходит поиск всех делителей составных чисел. Теоретическая основа этого процесса заключается в следующей теореме.
С одной стороны, по определению делимости число a делится на любое такое число d , так как существует такое целое число q=p1 (s1−t1) ·p2 (s2−t2) ·…·pn (sn−tn) , что a=d·q .
С другой стороны, всякое число d , которое делит a , имеет указанный вид, так как в силу свойств делимости оно не может иметь других простых множителей, кроме p1, p2, …, pn , а показатели этих множителей не могут превышать s1, s2, …, sn соответственно.
Из рассмотренной теоремы следует алгоритм нахождения всех положительных делителей данного числа. Чтобы найти все делители числа a нужно:
- получить его каноническое разложение на простые множители вида a=p1 s1 ·p2 s2 ·…·pn sn ;
- вычислить все значения выражения p1 t1 ·p2 t2 ·…·pn tn , в которых числа t1, t2, …, tn принимают независимо друг от друга каждое из значений t1=0, 1, …, s1 , t2=0, 1, …, s2 , …, tn=0, 1, …, sn .
Обычно наибольшую трудность представляет именно процесс перебора всех возможных комбинаций значений чисел t1, t2, …, tn . Сейчас мы последовательно рассмотрим решения нескольких примеров нахождения всех делителей чисел, откуда будут понятны все тонкости этого процесса.
Найдите все делители числа 8 .
Получить разложение на простые множители числа 8 не составляет труда: 8=2·2·2 . В канонической форме это разложение выглядит так: 8=2 3 . То есть, в нашем случае a=8 , p1=2 , s1=3 .
Тогда все делители числа 8 представляют собой значения выражения p1 t1 =2 t1 , в котором t1 принимает значения 0 , 1 , 2 и 3 ( 3 – последнее значение, так как s1=3 ). Итак, при t1=0 имеем 2 t1 =2 0 =1 , при t1=1 имеем 2 t1 =2 1 =2 , при t1=2 имеем 2 t1 =2 2 =4 , наконец, при t1=3 имеем 2 t1 =2 3 =8 .
Весь процесс нахождения делителей удобно проводить, заполняя таблицу следующего вида:
Таким образом, 1 , 2 , 4 и 8 – это все положительные делители числа 8 . Отрицательными делителями числа 8 являются −1 , −2 , −4 и −8 .
±1 , ±2 , ±4 , ±8 – все делители числа 8 .
Рассмотрим более сложный пример нахождения всех делителей числа a , в нем разложение числа уже будет содержать два простых множителя.
Перечислите все натуральные делители числа 567 .
Сначала разложим на простые множители число 567 :
Каноническое разложение числа 567 на простые множители имеет вид 567=3 4 ·7 . Теперь для нахождения всех натуральных делителей числа 567 заставим t1 и t2 пробегать независимо друг от друга значения 0 , 1 , 2 , 3 , 4 и 0 , 1 соответственно, при этом будем вычислять значения выражения 3 t1 ·7 t2 . Все эти действия удобно поводить, заполняя следующую таблицу:
1 , 3 , 7 , 9 , 21 , 27 , 63 , 81 , 189 и 567 – все натуральные делители числа 567 .
Еще немного усложним пример.
Найдите все положительные делители числа 3 900 .
Разложив число 3 900 на простые множители, получим его каноническое разложение 3 900=2 2 ·3·5 2 ·13 . Все положительные делители найдем, вычисляя значения выражения 2 t1 ·3 t2 ·5 t3 ·13 t4 при t1=0, 1, 2 , t2=0, 1 , t3=0, 1, 2 , t4=0, 1 . 

1 , 2 , 3 , 4 , 5 , 6 , 10 , 12 , 13 , 15 , 20 , 25 , 26 , 30 , 39 , 50 , 52 , 60 , 65 , 75 , 78 , 100 , 130 , 150 , 156 , 195 , 260 , 300 , 325 , 390 , 650 , 780 , 975 , 1 300 , 1 950 , 3 900 — все положительные делители числа 117 000 .
Число делителей числа
Число положительных делителей данного числа a , каноническое разложение которого имеет вид a=p1 s1 ·p2 s2 ·…·pn sn , равно значению выражения (s1+1)·(s2+1)·…·(sn+1) . Величина записанного выражения дает количество всех возможных наборов переменных t1, t2, …, tn , где t1=0, 1, …, s1 , t2=0, 1, …, s2 , …, tn=0, 1, …, sn .
Приведем пример. Вычислим число натуральных делителей числа 3 900 из последнего примера, рассмотренного в предыдущем пункте. Мы выяснили, что 3 900=2 2 ·3·5 2 ·13 , тогда s1=2 , s2=1 , s3=2 , s4=1 . Осталось вычислить значение выражения (s1+1)·(s2+1)·(s3+1)·(s4+1) при данных значениях s1 , s2 , s3 и s4 , которое и даст нам искомое число натуральных делителей. Получаем (2+1)·(1+1)·(2+1)·(1+1)=3·2·3·2=36 . Следовательно, число 3 900 имеет 36 натуральных делителей. Если мы пересчитаем все делители числа 3 900 , полученные в предыдущем примере, то убедимся, что их количество действительно равно 36 . Число всех делителей (и положительных и отрицательных) числа 3 900 равно 36·2=72 , так как число 3 900 имеет 36 положительных делителей, и, следовательно, 36 отрицательных, противоположных каждому из положительных делителей.
Найдите число делителей числа 84 .
Разложим 84 на простые множители:
Таким образом, каноническое разложение имеет вид 84=2 2 ·3·7 . Тогда число положительных делителей равно (2+1)·(1+1)·(1+1)=12 . Следовательно, число всех делителей равно 2·12=24 .
число 84 имеет 24 делителя.
Нахождение всех общих делителей чисел и их количества
Из свойств наибольшего общего делителя следует, что множество делителей данных целых чисел совпадает со множеством делителей НОД этих чисел. Это утверждение относится как к двум числам, так и к трем, и к большему их количеству. Таким образом, чтобы найти все общие делители данных чисел, нужно определить НОД этих чисел и найти все его делители.
Рассмотрим решения примеров, в которых находятся все общие делители некоторых чисел.
Найдите все натуральные общие делители чисел 50 и 140 , а также их количество.
Сначала нам нужно найти наибольший общий делитель чисел 50 и 140 , для этого воспользуемся алгоритмом Евклида: 140=50·2+40 , 50=40·1+10 , 40=10·4 , то есть, НОД(50, 140)=10 .
Теперь определим все положительные делители числа 10 . Его разложение на простые множители имеет вид 10=2·5 . Тогда 2 0 ·5 0 =1 , 2 0 ·5 1 =5 , 2 1 ·5 0 =2 и 2 1 ·5 1 =10 – все делители числа 10 . Следовательно, числа 1 , 2 , 5 и 10 – это все положительные общие делители чисел 50 и 140 , количество этих делителей равно 4 .
1 , 2 , 5 и 10 – это все натуральные делители чисел 50 и 140 , их количество равно 4 .
Определите число всех положительных общих делителей четырех чисел 90 , 45 , 315 и 585 .
Сначала найдем НОД с помощью разложения чисел на простые множители. Так как 90=2·3·3·5 , 45=3·3·5 , 315=3·3·5·7 и 585=3·3·5·13 , то НОД(90, 45, 315, 585)=3·3·5=3 2 ·5 . Количество всех искомых положительных общих делителей исходных четырех чисел равно количеству всех положительных делителей НОД этих чисел. Вычислим количество делителей НОД(90, 45, 315, 585)=3 2 ·5 , оно равно (2+1)·(1+1)=6 .
Источник
Нахождение всех делителей числа
Все делители числа
Все делители, на которые данное число делится нацело, можно получить из разложения числа на простые множители.
Нахождение всех делителей числа выполняется следующим образом:
- Сначала нужно разложить данное число на простые множители.
- Выписываем каждый полученный простой множитель (без повторов, если какой-то множитель повторяется).
- Далее, находим всевозможные произведения всех полученных простых множителей между собой и добавляем их к выписанным простым множителям.
- В конце добавляем в качестве делителя единицу.
Например, найдём все делители числа 40. Раскладываем число 40 на простые множители:
Выписываем (без повторов) каждый полученный простой множитель — это 2 и 5.
Далее находим всевозможные произведения всех полученных простых множителей между собой:
| 2 · 2 = 4, |
| 2 · 2 · 2 = 8, |
| 2 · 5 = 10, |
| 2 · 2 · 5 = 20, |
| 2 · 2 · 2 · 5 = 40. |
Добавляем в качестве делителя 1. В итоге получаем все делители, на которые число 40 делится без остатка:
1, 2, 4, 5, 8, 10, 20, 40.
Других делителей у числа 40 нет.
Калькулятор нахождения всех делителей
Данный калькулятор поможет вам получить все делители числа. Просто введите число и нажмите кнопку «Вычислить».
Источник
Наибольший общий делитель (НОД), свойства и формулы
О чем эта статья:
5 класс, 6 класс
Понятие наибольшего общего делителя
Начнем с самого начала и вспомним, что такое общий делитель. У целого числа может быть несколько делителей. А сейчас нам особенно интересно, как обращаться с делителями сразу нескольких целых чисел.
Делитель натурального числа — это такое натуральное число, которое делит данное число без остатка. Если у натурального числа больше двух делителей, его называют составным.
Общий делитель нескольких целых чисел — это такое число, которое может быть делителем каждого числа из указанного множества. Например, у чисел 12 и 8 общим делителем будет четверка. Чтобы это проверить, напишем верные равенства: 8 = 4 * 2 и 12 = 3 * 4. Но у этой пары чисел есть и другие общие делители: 1, -1 и -4.
Любое число можно разделить на 1, -1 и на само себя. Значит у любого набора целых чисел будет как минимум три общих делителя. Если общий делитель больше 0 — противоположное ему значение со знаком минус также является общим делителем.
Если b — делитель целого числа a, которое не равно нулю, то модуль числа b не может быть больше модуля числа a. Значит любое число, не равное 0, имеет конечное число делителей.
Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать вот так: НОД (a, b).
Например, для 4 и -16 НОД будет 4. Как мы к этому пришли:
Проверить результаты вычислений можно с помощью онлайн-калькулятора НОД и НОК.
- Зафиксируем все делители четырех: ±4, ±2, ±1.
- А теперь все делители шестнадцати: ±16, ±8, ±4, ±3 и ±1.
- Выбираем общие: это -4, -2, -1, 1, 2 и 4. Самое большое общее число: 4. Вот и ответ.
Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.
Найдем наибольший общий делитель нескольких целых чисел: 10, 6, 44, -18. Он будет равен трем. Ответ можно записать так: НОД (12, 6, 42, -18) = 3. А чтобы проверить правильность ответа, нужно записать все делители и выбрать из них самые большие.
Взаимно простые числа — это натуральные числа, у которых только один общий делитель — единица. Их НОД равен 1.
Помимо НОД есть еще и НОК, что расшифровывается, как наименьшее общее кратное и означает наименьшее число, которое делится на каждое из исходных чисел без остатка.
Еще один пример. Рассчитаем НОД для 28 и 64.
- Распишем простые множители для каждого числа и подчеркнем одинаковые
Д (64) = 2 * 2 * 2 * 2 * 2 * 2
Найдем произведение одинаковых простых множителей и запишем ответ
НОД (28; 64) = 2 * 2 = 4
Ответ: НОД (28; 64) = 4
Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.
Свойства наибольшего общего делителя
У наибольшего общего делителя есть ряд определенных свойств. Опишем их в виде теорем и сразу приведем доказательства.
Важно! Все свойства НОД будем формулировать для положительных целых чисел, при этом будем рассматривать делители только больше нуля.
Свойство 1. Наибольший общий делитель чисел а и b равен наибольшему общему делителю чисел b и а, то есть НОД (a, b) = НОД (b, a). Перемена мест чисел не влияет на конечный результат.
Доказывать свойство не имеет смысла, так как оно напрямую исходит из самого определения НОД.
Свойство 2. Если а делится на b, то множество общих делителей чисел а и b совпадает со множеством делителей числа b, поэтому НОД (a, b) = b.
Доказательство
Любой общий делитель чисел а и b является делителем каждого из этих чисел, в том числе и числа b. Так как а кратно b, то любой делитель числа b является делителем и числа а, благодаря свойствам делимости. Из этого следует, что любой делитель числа b является общим делителем чисел а и b.
Значит, если а делится на b, то совокупность делителей чисел а и b совпадает с совокупностью делителей одного числа b. А так как наибольшим делителем числа b является само число b, то наибольший общий делитель чисела и b также равен b, то есть НОД (а, b) = b.
В частности, если a = b, то НОД (a, b) = НОД (a, a) = НОД (b, b) = a = b.
- Например, НОД (25, 25) = 25.
Доказанное свойство наибольшего делителя можно использовать, чтобы найти НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число.
- Например, НОД (4, 40) = 4, так как 40 кратно 4.
Свойство 3. Если a = bq + c, где а, b, с и q — целые числа, то множество общих делителей чисел а и b совпадает со множеством общих делителей чисел b и с. Равенство НОД (a, b) = НОД (b, c) справедливо.
Доказательство
Существует равенство a = bq + c, значит всякий общий делитель чисел а и b делит также и с, исходя из свойств делимости. По этой же причине, всякий общий делитель чисел b и с делит а. Поэтому совокупность общих делителей чисел а и b совпадает с совокупностью общих делителей чисел b и c.
Поэтому должны совпадать и наибольшие из этих общих делителей, и равенство НОД (a, b) = НОД (b, c) можно считать справедливым.
Свойство 4. Если m — любое натуральное число, то НОД (mа, mb) = m * НОД(а, b).
Доказательство
Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД (mа, mb)= mr, где r — это НОД (а, b). На этом свойстве наибольшего общего делителя основан поиск НОД с помощью разложения на простые множители.
Свойство 5. Пусть р — любой общий делитель чисел а и b, тогда НОД (а : p, b : p) = НОД (а, b) : p. А именно, если p = НОД (a, b) имеем НОД (a : НОД (a, b), b: НОД (a, b)) = 1, то есть, числа a : НОД (a, b) и b : НОД (a, b) — взаимно простые.
Так как a = p(a : p) и b = p(b : p), и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД (a, b) = НОД (p(a : p), p(b : p)) = p * НОД (a : p, b : p), откуда и следует доказываемое равенство.
Способы нахождения наибольшего общего делителя
Найти наибольший общий делитель можно двумя способами. Рассмотрим оба, чтобы при решении задач выбирать самую оптимальную последовательность действий.
1. Разложение на множители
Чтобы найти НОД нескольких чисел, достаточно разложить их на простые множители и перемножить между собой общие множители для всех чисел.
Пример 1. Найти НОД (84, 90).
- Разложим числа 84 и 90 на простые множители:
Подчеркнем все общие множители и перемножим их между собой:
Ответ: НОД (84, 90) = 6.
Пример 2. Найти НОД (15, 28).
- Разложим 15 и 28 на простые множители:
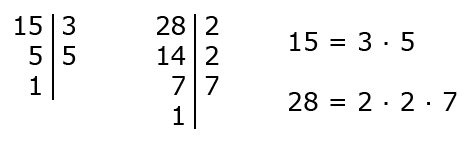
Ответ: НОД (15, 28) = 1.
Пример 3. Найти НОД для 24 и 18.
- Разложим оба числа на простые множители:
Найдем общие множители чисел 24 и 18: 2 и 3. Для удобства общие множители можно подчеркнуть.
Перемножим общие множители:
НОД (24, 18) =2 * 3 = 6
Ответ: НОД (24, 18) = 6
2. Алгоритм Евклида
Способ Евклида помогает найти НОД через последовательное деление. Сначала посмотрим, как работает этот способ с двумя числами, а затем применим его к трем и более.
Алгоритм Евклида заключается в следующем: если большее из двух чисел делится на меньшее — наименьшее число и будет их наибольшим общим делителем. Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя.
Формула НОД: НОД (a, b) = НОД (b, с), где с — остаток от деления a на b.
Пример 1. Найти НОД для 24 и 8.
Так как 24 делится на 8 и 8 тоже делится на 8, значит, 8 — общий делитель этих чисел. Этот делитель является наибольшим, потому что 8 не может делиться ни на какое число, большее его самого. Поэтому: НОД (24, 
В остальных случаях для нахождения наибольшего общего делителя двух чисел нужно соблюдать такой порядок действий:
- Большее число поделить на меньшее.
- Меньшее число поделить на остаток, который получается после деления.
- Первый остаток поделить на второй остаток.
- Второй остаток поделить на третий и т. д.
- Деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель и есть наибольший общий делитель.
Пример 2. Найти наибольший общий делитель чисел 140 и 96:
- 140 : 96 = 1 (остаток 44)
- 96 : 44 = 2 (остаток
- 44 : 8 = 5 (остаток 4)
- 8 : 4 = 2
Последний делитель равен 4 — это значит: НОД (140, 96) = 4.
Ответ: НОД (140, 96) = 4
Пошаговое деление можно записать столбиком:
Чтобы найти наибольший общий делитель трех и более чисел, делаем в такой последовательности:
- Найти наибольший общий делитель любых двух чисел из данных.
- Найти НОД найденного делителя и третьего числа.
- Найти НОД последнего найденного делителя и четвёртого числа и т. д.
Знакомство с темой наибольшего общего делителя начинается в 5 классе с теории и закрепляется в 6 классе на практике. В этой статье мы узнали все основные определения, свойства и их доказательства, а также как найти НОД.
Источник
Содержание
Элементы теории чисел
Литература
Обозначения
$mathbb{N}$ — множество натуральных чисел $1, 2, 3, 4, 5, 6, ldots$
$mathbb{Z}$ — множество целых чисел $0, pm 1, pm 2, pm 3, pm 4, ldots$
$[x]$ — целая часть числа $x$ (наибольшее целое число, не превосходящее $x$)
$sgn(x)$ — знак числа $x$ ($sgn(0)=0$ и $sgn(x)=frac{x}{|x|}$ при $xneq 0$)
Делимость
Определение и свойства делимости
Пусть имеются два целых числа $a$ и $b$. Говорят, что $b$ делит $a$, если существует целое число $b_1$ такое, что $a=bcdot b_1$. Обозначается это так $b|a$. Также в этом случае ещё говорят, что $a$ делится на $b$. Это обозначается $a,vdots, b$.
Рассмотрим некоторые свойства делимости целых чисел:
-
Пусть $c|b$ и $b|a$. Тогда $c|a$.
Действительно, по определению имеются целые числа $b_1$ и $c_1$ такие, что $a=bcdot b_1$ и $b=ccdot c_1$. Но тогда $a=ccdot c_1b_1$, то есть $c|a$. -
Пусть $c|a, c|b$ и $k,linmathbb{Z}$. Тогда $c|(ka+lb)$.
Действительно, по определению имеются целые числа $c_1$ и $c_2$ такие, что $a=ccdot c_1$ и $b=ccdot c_2$. Но тогда $ka+lb=ccdot (kc_1+lc_2)$, что и требуется. Это свойство можно распространить и на произвольное количество чисел. -
Пусть $kinmathbb{Z},kneq 0$. Тогда $b|a$ тогда и только тогда, когда $kb|ka$.
Действительно, если $kinmathbb{Z},kneq 0$, то $a=bcdot b_1$ тогда и только тогда, когда $kcdot a=kcdot bcdot b_1$, где $b_1$ – произвольное целое число.
Определение простых и составных чисел
У числа $1$ есть только один натуральный делитель — оно само. У любого натурального числа $n>1$ имеется как минимум два натуральных делителя – это $1$ и $n$. Если других натуральных делителей у числа $n$ больше нет, то оно называется простым. Примерами простых чисел являются $2,3,5,7,11,13,ldots$
Таким образом, простые числа — это натуральные числа, имеющие ровно два натуральных делителя. Можно ввести специальную функцию $tau(n)$, считающую количество натуральных делителей натурального числа $n$.
$$tau(n)=sumlimits _{d|n};1.$$
Тогда натуральное число $n$ простое тогда и только тогда, когда $tau(n)=2$. Натуральные числа, большие единицы, будем называть составными, если они не являются простыми.
Пример 1. Число $4$ делится на $1,2$ и $4$, а значит $tau(4)=3$ и это число составное. Число $17$ делится только на $1$ и $17$, а значит $tau(17)=2$ и это число простое.
Замечание 1. Согласно определению у составного числа $n$ имеется хотя бы один делитель $d$ с условием $1<d<n$. Например, у числа $4$ таким делителем является $2$.
Замечание 2. Целые числа, делящиеся на $2$, называются чётными, а не делящиеся на $2$ — нечётными. Из этого определения видно, что среди чётных натуральных чисел только число $2$ является простым, а все остальные простые числа являются нечётными.
Наибольший общий делитель
Пусть имеется несколько целых чисел. Их общим делителем называется целое число, делящее каждое из них. Наибольшим общим делителем нескольких целых чисел, не все из которых равны нулю, называется наибольший из их общих делителей. Наибольший общий делитель чисел $a_1,ldots ,a_n$ обозначается $textrm{НОД}(a_1,ldots ,a_n)$ или, чаще всего, просто $(a_1,ldots ,a_n)$. Заметим, что он будет положительным, то есть натуральным числом.
Пример 2. Пусть $p$ – простое число, $a$ – натуральное. Найдём $(a,p)$. Согласно последнему замечанию достаточно найти лишь натуральные общие делители рассматриваемых чисел и среди них выбрать наибольший. Но у числа $p$ лишь два натуральных делителя – это число $1$ (которое также делит и $a$) и само $p$. Поэтому, если $pnmid a$ ($p$ не делит $a$), то есть лишь один общий делитель, и $(a,p)=1$. Если же $p|a$, то общих делителей два – $1$ и $p$. Тогда $(a,p)=p$.
Пример 3. Пусть даны натуральные числа $a$ и $b$ и $b|a$. Тогда $(a,b)=b$. Это следует из того, что $b$ является общим делителем чисел $a$ и $b$, но при этом у $b$ не может быть делителей, больших, чем $b$.
Теорема 1. Наибольший общий делитель целых чисел $a_1,ldots ,a_n$, не все из которых равны нулю, может быть представлен с некоторыми целыми числами $x_1,ldots ,x_n$ в виде $$(a_1,ldots ,a_n)=x_1a_1+ldots +x_na_n.$$
Доказательство. Рассмотрим множество $M={y_1a_1+ldots +y_na_n>0; |; y_1,ldots ,y_ninmathbb{Z}}$. Оно не пусто, поскольку выбор $y_i=a_i, i=1,ldots ,n$ гарантирует, что $y_1a_1+ldots +y_na_n>0$. Так как это множество состоит из натуральных чисел, то в нём есть наименьший элемент. Пусть он равен $x_1a_1+ldots +x_na_n$. Положим $d=(a_1,ldots ,a_n)$. Так как $d|a_1,ldots ,d|a_n$, то $d|(x_1a_1+ldots +x_na_n)$, а значит $x_1a_1+ldots +x_na_ngeqslant d$. Покажем, что $x_1a_1+ldots +x_na_n$ является общим делителем чисел $a_1,ldots ,a_n$, тогда по определению наибольшего общего делителя будем иметь $x_1a_1+ldots +x_na_nleqslant d$, и из сравнения двух полученных неравенств будет следовать $x_1a_1+ldots +x_na_n=d$. Поделим $a_1$ на $x_1a_1+ldots +x_na_n$ с остатком:
$$a_1=q(x_1a_1+ldots +x_na_n)+r,quad 0leqslant r<x_1a_1+ldots +x_na_n.$$
Получаем $r=a_1(1-qx_1)+a_2(-qx_2)+ldots +a_n(-qx_n)$, и если $r>0$, то $rin M$ и при этом $r<x_1a_1+ldots +x_na_n$. Это противоречит выбору $x_1a_1+ldots +x_na_n$ как наименьшего элемента множества $M$. Значит $r=0$, и $a_1$ делится нацело на $x_1a_1+ldots +x_na_n$. Аналогично доказывается, что $x_1a_1+ldots +x_na_n$ делит $a_2,ldots ,a_n$. Теорема 1 доказана.
Следствие 1. Для любого натурального $ngeqslant 2$ множество всех общих делителей целых чисел $a_1,ldots ,a_n$ совпадает с множеством всех делителей числа $textrm{НОД}(a_1,ldots ,a_n)$. В частности, любой общий делитель нескольких целых чисел делит их наибольший общий делитель.
Доказательство. Согласно теореме 1 существуют целые числа $x_1,ldots ,x_n$, такие что $(a_1,ldots ,a_n)=x_1a_1+ldots +x_na_n$. Тогда по второму свойству делимости $(a_1,ldots ,a_n)$ делится на любой общий делитель целых чисел $a_1,ldots ,a_n$. При этом из первого свойства делимости следует, что любой делитель $(a_1,ldots ,a_n)$ будет являться общим делителем чисел $a_1,ldots ,a_n$. Таким образом, множество всех общих делителей нескольких целых чисел совпадает с множеством всех делителей их наибольшего общего делителя. Следствие 1 доказано.
Следствие 2. Имеет место формула
$$(a_1,ldots ,a_{n+1})=( (a_1,ldots ,a_n), a_{n+1}).$$
Доказательство. Множество общих делителей числа $(a_1,ldots ,a_n)$ и числа $a_{n+1}$ по следствию 1 состоит из множества всех общих делителей чисел $a_1,ldots ,a_n$, которые одновременно делят ещё и число $a_{n+1}$. Получается, что это множество состоит из всех общих делителей чисел $a_1,ldots ,a_{n+1}$. Но если два множества совпадают, то и наибольшие элементы этих множеств равны. Получаем $(a_1,ldots ,a_{n+1})=((a_1,ldots ,a_n), a_{n+1})$. Следствие 2 доказано.
Лемма 1. Пусть $a,b,c$ – целые числа, $c|ab$ и $(a,c)=1$. Тогда $c|b$.
Доказательство. По теореме 1 найдутся целые числа $x,y$ такие, что $1=ax+cy$. Домножим обе части этого равенства на $b$, получим $b=abx+bcy$. По условию $c|ab$, а значит и $c|abx$. Очевидно, что также $c|bcy$. Из второго свойства делимости имеем $c|b$. Лемма 1 доказана.
Следствие 3. Пусть $a,b$ – целые числа, $p$ – простое число, $p|ab$ и $pnmid a$. Тогда $p|b$.
Доказательство. Согласно примеру 2, если $pnmid a$, то $(a,p)=1$, так что все условия леммы 1 соблюдены. Следствие 3 доказано.
Наименьшее общее кратное
Далее
Пусть имеется несколько целых чисел. Их общим кратным называется целое число, делящееся на каждое из них. Наименьшим общим кратным нескольких целых чисел называется наименьшее натуральное из их общих кратных. Наименьшее общее кратное чисел $a_1,ldots ,a_n$ обозначается $textrm{НОК}[a_1,ldots ,a_n]$ или, чаще всего, просто $[a_1,ldots ,a_n]$.
Теорема 2. Наименьшее общее кратное целых чисел $a_1,ldots ,a_n$ делит любое общее кратное этих чисел.
Доказательство. Пусть $b=[a_1,ldots ,a_n]$ и $c$ – произвольное общее кратное этих же чисел. Поделим $c$ на $b$ с остатком: $c=qb+r, 0leqslant r<b$. Тогда $r=c-qb$, и, так как $c$ и $b$ делятся на каждое из чисел $a_1,ldots ,a_n$, то по второму свойству делимости $r$ также делится на каждое из них, то есть является их общим кратным. Но если $r>0$, то тогда $r$ – натуральное число, меньшее, чем $b$. Это противоречит тому, что $b$ – наименьшее общее кратное этих чисел. Значит $r=0$ и $c$ делится на $b$. Теорема 2 доказана.
С помощью сравнения совокупностей общих кратных из теоремы 2 легко выводится
Следствие 4. $$[a_1,ldots,a_n, a_{n+1}]=[[a_1,ldots,a_n], a_{n+1}]. $$
Лемма 2. Пусть $a$ и $b$ натуральные числа. Тогда $displaystyleleft(frac{a}{(a,b)},frac{b}{(a,b)}right)=1,quad left[frac{a}{(a,b)},frac{b}{(a,b)}right]=frac{[a,b]}{(a,b)}$.
Доказательство. Пусть $d$ – наибольший общий делитель чисел $displaystyle frac{a}{(a,b)}$ и $displaystyle frac{b}{(a,b)}$. Тогда по третьему свойству делимости число $dcdot(a,b)$ будет делить $a$ и $b$, то есть будет их общим делителем. Но так как $(a,b)$ является наибольшим из их общих делителей, то $d=1$. Пусть теперь $k$ – наименьшее общее кратное чисел $displaystyle frac{a}{(a,b)}$ и $displaystyle frac{b}{(a,b)}$. По третьему свойству делимости число $displaystyle frac{[a,b]}{(a,b)}$ также будет их общим кратным, поэтому $k: | displaystyle frac{[a,b]}{(a,b)}$, а значит $kleqslantdisplaystyle frac{[a,b]}{(a,b)}$. C другой стороны, также по третьему свойству делимости, $kcdot(a,b)$ будет делиться на $a$ и на $b$, то есть будет их общим кратным. Следовательно $[a,b]: |: (kcdot(a,b) )$, и $[a,b]leqslant(kcdot(a,b) )$. Из двух полученных неравенств следует $k=displaystyle frac{[a,b]}{(a,b)}$. Лемма 2 доказана.
Лемма 3. Пусть $a$ и $b$ натуральные числа, $(a,b)=1$. Тогда $[a,b]=ab$.
Доказательство. Так как $[a,b]$ делится на $a$ и на $b$, то существуют натуральные числа $a_1$ и $b_1$ такие, что $$[a,b]=acdot a_1=bcdot b_1.$$ Значит $b|acdot a_1$ и $(a,b)=1$. По лемме 1 имеем $b|a_1$, но тогда $ab|aa_1=[a,b]$ и следовательно $ableqslant [a,b]$. C другой стороны $ab$ является общим кратным чисел $a$ и $b$, и по теореме 2 $[a,b]|(ab)$, откуда $[a,b]leqslant ab$. Из двух полученных неравенств вытекает, что $[a,b]=ab$. Лемма 3 доказана.
Следствие 5. Пусть $a$ и $b$ натуральные числа. Тогда $[a,b](a,b)=ab$.
Доказательство. Из лемм 2 и 3 находим
$$displaystylefrac{[a,b]}{(a,b)}=left[frac{a}{(a,b)},frac{b}{(a,b)}right]=frac{a}{(a,b)}cdotfrac{b}{(a,b)}.$$ Домножим левую и правую части полученного равенства на $(a,b)^2$, получится в точности требуемое равенство. Следствие 5 доказано.
Следствие 6. Пусть $a_1,ldots ,a_n$ натуральные числа, и $(a_i,a_j)=1$ для всех $i,j=1,ldots ,n, ineq j$. Тогда $[a_1,ldots ,a_n]=a_1cdots a_n$.
Доказательство. Проведём индукцию по $n$ (покажем, что утверждение верно при $n=2$, а также, что из справедливости утверждения при произвольном $ngeqslant 2$ вытекает его справедливость и при $n+1$, тогда это будет означать, что утверждение верно при всех $ngeqslant 2$). При $n=2$ утверждение следует из леммы 3. Пусть утверждение верно для некоторого $ngeqslant 2$. По предположению индукции $[a_1,ldots,a_n]=a_1cdots a_n$. Кроме того, из следствия 3 очевидно вытекает, что
$(a_1cdots a_n, a_{n+1})=1$ (если бы нашёлся общий простой делитель, то он делил бы одновременно $a_{n+1}$ и какое-то из $a_i, i=1,ldots ,n$, что противоречило бы условию $(a_i,a_{n+1})=1$). Вновь из леммы 3 следует, что $[[a_1,ldots,a_n], a_{n+1}]=a_1cdots a_ncdot a_{n+1}$. Тогда по следствию 4 получаем
$$[a_1,ldots,a_n, a_{n+1}]=[[a_1,ldots,a_n], a_{n+1}]= a_1cdots a_ncdot a_{n+1}. $$
Следствие 6 доказано.
Алгоритм Евклида
Пусть для двух натуральных чисел $p$ и $q$ необходимо найти их наибольший общий делитель. Для этого применяется следующая процедура. Поделим с остатком $p$ на $q$:
$$p=a_0q+r_1,quad 0leqslant r_1<q.$$
Из этого равенства и второго свойства делимости видно, что множество всех общих делителей $p$ и $q$ совпадает с множеством всех общих делителей $q$ и $r_1$, а значит $(p,q)=(q,r_1)$.
Поделим теперь $q$ на $r_1$ с остатком:
$$q=a_1r_1+r_2,quad 0leqslant r_2<r_1.$$
Затем $r_1$ на $r_2$ и так далее.
Заметим, что последовательность неотрицательных целых чисел $r_1,r_2,r_3,ldots$ строго убывающая, так что при некотором $ngeqslant 0$ будет выполнено $r_{n+1}=0$, то есть
$$r_{n-2}=a_{n-1}r_{n-1}+r_n,quad 0leqslant r_n<r_{n-1}.$$
$$r_{n-1}=a_nr_n.$$
При $n=0$ надо рассматривать лишь последнюю строчку, полагая в ней $r_{-1}=p,r_0=q$.
Из последовательности построенных равенств и второго свойства делимости будет следовать цепочка равенств $$(p,q)=(q,r_1)=(r_1,r_2)=ldots =(r_{n-1},r_n)=r_n.$$
Последнее из этих равенств следует из того, что $r_n|r_{n-1}$ и примера 3.
Таким образом, наибольший общий делитель найден и равен $r_n$.
Теорема 1 утверждает, что с некоторыми целыми $x,y$ можно записать $r_n=(p,q)=px+qy$. Алгоритм Евклида позволяет отыскать эти числа явно. Из первого равенства имеем $r_1=p+q(-a_0)$. Из второго $r_2=q-a_1r_1=p(-a_1)+q(1+a_0a_1)$. И так далее последовательно каждое из чисел $r_1,ldots ,r_n$ выразится в виде линейной комбинации чисел $p$ и $q$ с целыми коэффициентами.
Замечание 3. Из первого в цепочке делений с остатком равенства имеем
$$frac{p}{q}=a_0+frac{r_1}{q}=a_0+frac{1}{frac{q}{r_1}}.$$ Из второго равенства
$$frac{q}{r_1}=a_1+frac{r_2}{r_1}=a_1+frac{1}{frac{r_1}{r_2}}ldots$$
Из последнего равенства будем иметь $$frac{r_{n-1}}{r_n}=a_n.$$
Получается представление $frac{p}{q}$ в виде многоэтажной дроби
$$frac{p}{q}=a_0+frac{1}{a_1+frac{1}{a_2+frac{1}{ldots +frac{1}{a_n}}}}.$$
Такая конструкция называется цепной дробью и обозначается $[a_0;a_1,a_2,ldots ,a_n]$. Подробнее о них речь пойдёт в следующих главах. Упомянем лишь, что числа $x,y$, для которых $r_n=px+qy$, могут быть найдены из равенства
$$-frac{x}{y}=a_0+frac{1}{a_1+frac{1}{ldots +frac{1}{a_{n-1}}}}.$$
Решение в целых числах уравнения $px+qy=r$
Пусть $p,q,r$ – целые числа и требуется найти все целые $x,y$, удовлетворяющие уравнению $px+qy=r$.
Предложение 1. Решение данного уравнения существует тогда и только тогда, когда $(p,q)|r$.
Доказательство. Если какое-либо решение $x,y$ существует, то по второму свойству делимости любой общий делитель чисел $p$ и $q$ делит $r$. В частности $(p,q)|r$. Обратно, если $(p,q)|r$, то найдётся целое число $s$ такое, что $(p,q)s=r$. По теореме 1 найдутся целые числа $x_0,y_0$ с условием $px_0+qy_0=(p,q)$, но тогда $p(x_0s)+q(y_0s)=r$. Предложение 1 доказано.
Итак, если $(p,q)nmid r$, то решений не существует. Если же $(p,q)|r$, то имеется как минимум одно решение, скажем $x_1,y_1$. Чтобы его явно найти, можно с помощью алгоритма Евклида отыскать числа $x_0,y_0$ такие, что $px_0+qy_0=(p,q)$. Тогда, согласно предложению 1, будем иметь
$$x_1=x_0frac{r}{(p,q)},quad y_1= y_0frac{r}{(p,q)}.$$
В некоторых простых случаях частное решение $x_1,y_1$ можно просто подобрать.
Пусть $x,y$ – произвольное решение нашего уравнения. Тогда $px+qy=px_1+qy_1$. Поделим обе части равенства на $(p,q)$ и перегруппируем слагаемые. Получим$$frac{p}{(p,q)}(x-x_1)=-frac{q}{(p,q)}(y-y_1),$$ то есть $frac{p}{(p,q)}$ делит $frac{q}{(p,q)}(y-y_1)$, и по лемме 2 $$left(frac{p}{(p,q)},frac{q}{(p,q)}right)=1.$$ Отсюда по лемме 1 $frac{p}{(p,q)}$ делит $(y-y_1)$, или же $y-y_1=frac{p}{(p,q)}t$ с некоторым целым числом $t$. Но тогда, деля обе части исходного равенства на $frac{p}{(p,q)}$, находим $x-x_1=-frac{q}{(p,q)}t$. Получаем, что произвольное решение должно иметь вид $$x=x_1-frac{q}{(p,q)}t, qquad
y=y_1+frac{p}{(p,q)}t, quad tinmathbb{Z}.$$
Поскольку подстановка такой пары $x,y$ при любом $tinmathbb{Z}$ даёт решение рассматриваемого уравнения, то полученная формула описывает все его решения.
Решение линейного диофантова уравнения от любого числа неизвестных
Диофантовым называют уравнение, которое требуется решить в целых числах. Пусть $a_1,ldots ,a_n$ и $b$ – целые числа и требуется решить диофантово уравнение $a_1x_1+ldots +a_nx_n=b$. Положим $d=(a_1,ldots ,a_n)$, тогда повторение рассуждений, проведённых при доказательстве предложения 1, покажет, что если $dnmid b$, то решений нет, а если $d|b$, то есть. Найти решение можно с помощью следующей процедуры. Необходимо составить матрицу из $n+1$ строки и $n$ столбцов:
$$a_1 a_2 ldots a_{n-1} a_n$$
$$ 1quad 0 ldotsquad 0quad 0$$
$$0quad 1 ldotsquad 0quad 0$$
$$ldots, ldots, ldots, ldots, ldots $$
$$ 0quad 0 ldotsquad 1quad 0$$
$$0quad 0 ldotsquad 0quad 1$$
и с помощью трёх допустимых операций
-
Прибавление к любому столбцу любого другого столбца, умноженного на произвольное целое число (при этом прибавляемый столбец остаётся нетронутым)
-
Замена местами любых двух столбцов
-
Умножение любого столбца на $-1$
привести эту матрицу к виду
$$dhspace{2.8mm} 0hspace{2.8mm} ldots 0$$
$$ c_{11} c_{12} ldots c_{1n}$$
$$c_{21} c_{22} ldots c_{2n}$$
$$ldotsldotsldotsldots $$
$$c_{n1} c_{n2} ldots c_{nn}$$
Добиться этого можно всегда. Например, можно сделать все элементы первой строки неотрицательными (домножая на $-1$ столбцы, в которых первый элемент отрицателен). После этого можно выбрать наименьший ненулевой элемент в первой строке, поделить остальные элементы первой строки на него с остатком и вычесть из всех столбцов столбец, в котором находится этот наименьший элемент, домноженный на подходящее целое число так, чтобы первыми элементами в столбцах оказались уже остатки от деления. В результате наименьший натуральный элемент первой строки будет уменьшаться и, так как процедуру можно продолжать неограниченное число раз, то всё большее количество элементов первой строки будет обнуляться. В итоге станут равны нулю все элементы первой строки, кроме одного, который действительно окажется равен определённому нами выше числу $d$. Это видно из того, что ни одна из трёх допустимых операций со столбцами матрицы не меняет наибольшего общего делителя всех элементов первой строки.
Заметим также следующее свойство столбцов изначально построенной матрицы. Верхний элемент столбца равен результату подстановки стоящих под ним элементов вместо $x_1,ldots , x_n$ в выражение $a_1x_1+ldots +a_nx_n.$ Например, $a_1=a_1cdot 1+a_2cdot 0ldots +a_ncdot 0$. Это свойство также сохраняется при любой из трёх допустимых операций со столбцами матрицы. Таким образом $$a_1cdot c_{11}+a_2cdot c_{21}ldots +a_ncdot c_{n1}=d$$ и
$$a_1cdot c_{1j}+a_2cdot c_{2j}ldots +a_ncdot c_{nj}=0,quad j=2,ldots ,n.$$
Значит при любых $t_2,ldots ,t_n$ вектор
$$x_1hspace{13mm}c_{11}hspace{11mm}c_{12}hspace{24mm}c_{1n}$$
$$x_2hspace{13mm}c_{21}hspace{11mm}c_{22}hspace{24mm}c_{2n}$$
$$cdothspace{3mm} =hspace{.9mm} frac{b}{d}hspace{1.9mm} cdothspace{2.4mm} +hspace{2mm} t_2hspace{1.9mm} cdothspace{2.7mm} +hspace{1.5mm}ldotshspace{.5mm} + t_nhspace{2.3mm} cdot$$
$$cdothspace{15mm}cdothspace{14.5mm}cdothspace{27.2mm}cdot$$
$$x_nhspace{12.9mm}c_{n1}hspace{10.9mm}c_{n2}hspace{23.9mm}c_{nn}$$
будет являться решением уравнения $a_1x_1+ldots +a_nx_n=b$.
Теперь заметим, что мы выразили векторы
$$c_{11}hspace{11mm}c_{12}hspace{24mm}c_{1n}$$
$$c_{21}hspace{11mm}c_{22}hspace{24mm}c_{2n}$$
$$cdothspace{14.5mm}cdothspace{27.2mm}cdot$$
$$cdothspace{14.5mm}cdothspace{10.9mm}ldotshspace{10.4mm}cdot$$
$$c_{n1}hspace{10.9mm}c_{n2}hspace{23.9mm}c_{nn}$$
с помощью трёх допустимых операций в виде линейных комбинаций векторов
$$1hspace{11mm}0hspace{24mm}0$$
$$0hspace{11mm}1hspace{24mm}0$$
$$cdothspace{11.2mm}cdothspace{24mm}cdot$$
$$cdothspace{11.2mm}cdothspace{9.1mm}ldotshspace{9mm}cdot$$
$$0hspace{11mm}0hspace{24mm}1$$
Значит, если последовательно обратить все эти допустимые операции, то уже векторы
$$1hspace{11mm}0hspace{24mm}0$$
$$0hspace{11mm}1hspace{24mm}0$$
$$cdothspace{11.2mm}cdothspace{24mm}cdot$$
$$cdothspace{11.2mm}cdothspace{9.1mm}ldotshspace{9mm}cdot$$
$$0hspace{11mm}0hspace{24mm}1$$
будут выражены в виде линейных комбинаций векторов
$$c_{11}hspace{11mm}c_{12}hspace{24mm}c_{1n}$$
$$c_{21}hspace{11mm}c_{22}hspace{24mm}c_{2n}$$
$$cdothspace{14.5mm}cdothspace{27.2mm}cdot$$
$$cdothspace{14.5mm}cdothspace{10.9mm}ldotshspace{10.4mm}cdot$$
$$c_{n1}hspace{10.9mm}c_{n2}hspace{23.9mm}c_{nn}$$
Тогда, если мы имеем произвольное решение нашего уравнения, скажем вектор
$$x_1hspace{13mm}1hspace{11mm}0hspace{24mm}0$$
$$x_2hspace{13mm}0hspace{11mm}1hspace{24mm}0$$
$$cdothspace{4.5mm} =hspace{0.4mm} x_1hspace{0.2mm} cdothspace{1.4mm} +hspace{1mm} x_2hspace{0.2mm} cdothspace{1.3mm} +hspace{1.0mm}ldotshspace{.5mm} + x_nhspace{0.2mm} cdot$$
$$cdothspace{14.7mm}cdothspace{11.5mm}cdothspace{24mm}cdot$$
$$x_nhspace{13mm}0hspace{11mm}0hspace{23.8mm}1,$$
то он выразится с некоторыми целыми коэффициентами $t_1,t_2,ldots ,t_n$ в виде
$$x_1hspace{13mm}c_{11}hspace{11mm}c_{12}hspace{24mm}c_{1n}$$
$$x_2hspace{13mm}c_{21}hspace{11mm}c_{22}hspace{24mm}c_{2n}$$
$$cdothspace{3mm} =hspace{.9mm} t_1hspace{1.9mm} cdothspace{2.4mm} +hspace{2mm} t_2hspace{1.9mm} cdothspace{2.7mm} +hspace{1.5mm}ldotshspace{.5mm} + t_nhspace{2.3mm} cdot$$
$$cdothspace{15mm}cdothspace{14.5mm}cdothspace{27.2mm}cdot$$
$$x_nhspace{12.9mm}c_{n1}hspace{10.9mm}c_{n2}hspace{23.9mm}c_{nn}$$
Подставив же полученный вектор в уравнение, получим $a_1x_1+ldots +a_nx_n=t_1cdot d=b.$ Откуда $t_1=frac{b}{d}.$
Итак, мы доказали, что все решения нашего уравнения и только они имеют вид
$$x_1hspace{13mm}c_{11}hspace{11mm}c_{12}hspace{24mm}c_{1n}$$
$$x_2hspace{13mm}c_{21}hspace{11mm}c_{22}hspace{24mm}c_{2n}$$
$$cdothspace{3mm} =hspace{.9mm} frac{b}{d}hspace{1.9mm} cdothspace{2.4mm} +hspace{2mm} t_2hspace{1.9mm} cdothspace{2.7mm} +hspace{1.5mm}ldotshspace{.5mm} + t_nhspace{2.3mm} cdot$$
$$cdothspace{15mm}cdothspace{14.5mm}cdothspace{27.2mm}cdot$$
$$x_nhspace{12.9mm}c_{n1}hspace{10.9mm}c_{n2}hspace{23.7mm}c_{nn},$$
где $t_2,ldots ,t_n$ принимают произвольные целые значения.
Простые числа
Бесконечность множества простых чисел
Лемма 4. Пусть $n>1$ натуральное число. Тогда у него есть простой делитель.
Доказательство. Рассмотрим наименьший превышающий единицу делитель числа $n$. Обозначим его через $p$. Если это число составное, то, согласно замечанию 1, существует число $d$ такое, что $d|p$ и $1<d<p$. По первому свойству делимости $d|n$. Но тогда получаем противоречие с тем, что $p$ являлось наименьшим из превышающих единицу делителем числа $n$. Значит $p$ – простое, и лемма 4 доказана.
Следствие 7. Пусть $n>1$ натуральное число. Тогда оно представляется в виде произведения простых чисел (некоторые из которых могут совпадать).
Доказательство. По лемме 4 у числа $n$ есть простой делитель, скажем $p_1$. Если $frac{n}{p_1}>1$, то у этого числа тоже найдётся простой делитель, скажем $p_2$ (при этом допускается и случай $p_2=p_1$). Если и $frac{n}{p_1p_2}>1$, то у этого числа также найдётся простой делитель, скажем $p_3$. Поскольку последовательность натуральных чисел $n,frac{n}{p_1},frac{n}{p_1p_2},frac{n}{p_1p_2p_3},ldots $ строго убывает, то за конечное число шагов (гарантированно не более $n-1$ шага) в этой последовательности возникнет наименьшее натуральное число, то есть $1$. Значит, с некоторым $k$ будем иметь $n=p_1cdot p_2cdots p_k$, что и требовалось. Следствие 7 доказано.
Следствие 8. Пусть $n>1$ натуральное число. Тогда оно является простым, если у него нет простых делителей, не превосходящих $[sqrt{n}]$.
Доказательство. Предположим, что у $n$ нет простых делителей, не превосходящих $[sqrt{n}]$. Покажем, что у него тогда не может быть и простых делителей, больших чем $[sqrt{n}]$, кроме него самого. Пусть $p|n, [sqrt{n}]+1leqslant p<n$. Тогда $1<frac{n}{p}leqslantfrac{n}{[sqrt{n}]+1}< [sqrt{n}]+1$, поскольку $([sqrt{n}]+1)^2>(sqrt{n})^2=n$. А так как $frac{n}{p}$ – число натуральное, то и $frac{n}{p}leqslant [sqrt{n}]$.
Но по лемме 4 у числа $frac{n}{p}$ есть простой делитель $q$. При этом очевидно, что $qleqslantfrac{n}{p}leqslant [sqrt{n}]$ и по первому свойству делимости $q|n$. Противоречие. Следовательно, $n$ не имеет простых делителей, меньших чем $n$. Однако по лемме 4 число $n$ обязано иметь хотя бы один простой делитель. Значит само $n$ необходимо является простым. Следствие 8 доказано.
Теорема 3. Простых чисел бесконечно много.
Доказательство. Предположим, у нас имеется несколько простых чисел $p_1, p_2,ldots ,p_k$. Рассмотрим число $N=p_1cdot p_2cdots p_k+1$. Это число не делится ни на одно из имеющихся простых чисел, так как остаток от деления $N$ на любое из них равен $1$. Вместе с тем, по лемме 4, у числа $N$ должен быть хотя бы один простой делитель. Следовательно, помимо чисел $p_1, p_2,ldots ,p_k$ существуют и другие простые числа. Поскольку по доказанному мы можем к любой совокупности простых чисел всегда добавить ещё хотя бы одно простое число, то простых чисел бесконечно много. Теорема 3 доказана.
Решето Эратосфена
На основе результата леммы 4 возникает следующий алгоритм нахождения всех простых чисел, не превышающих некоторого числа $n$, если известны все простые числа, скажем $p_1,p_2,ldots ,p_k$, не превосходящие $sqrt{n}$. Этот алгоритм именуется решетом Эратосфена. Для осуществления алгоритма нужно выписать все числа от $2$ до $n$ включительно. После этого нужно для каждого $i=1,2,ldots ,k$ вычеркнуть числа $2p_i, 3p_i,ldots ,left[frac{n}{p_i}right] p_i$. Тогда все невычеркнутые числа и составят список всех простых, не превышающих $n$. Действительно, пусть число $mleqslant n$ не вычеркнуто. Тогда либо это одно из простых, не превосходящих $sqrt{n}$, либо оно не делится ни на одно из этих простых. В последнем случае $m$ не делится ни на одно из простых, не превосходящих $sqrt{m}$, так как $sqrt{m}leqslant sqrt{n}$, поэтому по следствию 8 число $m$ – простое. Очевидно, что каждое простое число, не превосходящее $n$, попадёт в список невычеркнутых, так как оно либо не превосходит $sqrt{n}$ и не вычеркнуто по условию алгоритма, либо оно больше $sqrt{n}$ и тогда оно не вычеркнуто, так как по определению не делится на отличные от себя простые числа.
Основная теорема арифметики (единственность разложения на простые)
Теорема 4 (основная теорема арифметики). Пусть $n>1$ натуральное число. Тогда $n$ раскладывается в произведение простых чисел, причём единственным образом с точностью до перестановки сомножителей.
Доказательство. Существование разложения показано в следствии 7. Докажем, что разложение единственно. Пусть $n$ – наименьшее из чисел, которые раскладываются в произведение простых более чем одним способом, и два из его разложений имеют вид
$$p_1cdot p_2cdots p_k=q_1cdot q_2cdots q_l.$$
Ни одно из чисел $p_1, p_2,ldots ,p_k$ не равно ни одному из чисел $q_1, q_2,ldots ,q_l$, так как в противном случае обе части равенства можно было бы сократить на совпадающие простые, и число $n$ было бы не наименьшим из чисел, которые раскладываются в произведение простых более чем одним способом. Поэтому можно считать, что $p_1<q_1$. Рассмотрим число $m=n-p_1cdot q_2cdots q_l$. Оно может быть представлено двумя способами:
$$p_1(p_2cdots p_k — q_2cdots q_l)=(q_1-p_1)cdot q_2cdots q_l.$$ Так как $q_1$ не делится на $p_1$, то по второму свойству делимости и $q_1-p_1$ не делится на $p_1$. Тогда $p_1$ не входит в разложение на простые множители $q_1-p_1=r_1cdots r_i$. Выпишем также разложение на простые множители числа $p_2cdots p_k — q_2cdots q_l=t_1cdots t_j$. Тогда получим, что число $m$, меньшее чем $n$, имеет два разложения на простые множители
$$p_1cdot t_1cdots t_j=r_1cdots r_icdot q_2cdots q_l,$$
в одно из которых входит $p_1$, а в другое – нет. Противоречие с тем, что $n$ – наименьшее из чисел, которые раскладываются в произведение простых более чем одним способом. Следовательно, чисел, раскладывающихся в произведение простых более чем одним способом, не существует. Теорема 4 доказана.
Замечание 4. Разложение числа на простые множители, согласно основной теореме арифметики, единственно с точностью до порядка сомножителей. Один способ упорядочивания сомножителей является общепринятым и называется каноническим. Он подразумевает упорядочивание сомножителей по возрастанию, при этом равные сомножители объединяются в единый множитель в виде простого числа в некоторой степени. В общем виде это выглядит так:
$$n=p_1^{alpha_1}cdot p_2^{alpha_2}cdots p_k^{alpha_k},quad p_1<p_2<ldots <p_k.$$
При этом для каждого простого числа $p$ вводится понятие показателя $nu_p(n)$ – это та степень, в которой $p$ входит в каноническое разложение числа $n$. Например $nu_2(12)=2, nu_3(12)=1, nu_5(12)=0$. Убедитесь, что
-
$nu_p(mcdot n)=nu_p(m)+nu_p(n)$
-
$nu_p(m+n)geqslantmin{nu_p(m),nu_p(n)}$, причём, если $nu_p(m)>nu_p(n)$, то $nu_p(m+n)=nu_p(n)$
Мультипликативные функции
Определение и свойства мультипликативных функций. Свёртка Дирихле
Пусть $f$ – функция натурального аргумента, принимающая действительные (или даже комплексные) значения. Тогда $f$ называется мультипликативной, если
-
$f$ принимает не только нулевые значения;
-
$f(mcdot n)=f(m)cdot f(n)$ при $(m,n)=1$.
Очень важно запомнить, что достаточно, чтобы второе свойство выполнялось только при взаимной простоте чисел $m$ и $n$.
Функция $f$ называется вполне мультипликативной, если
-
$f$ принимает не только нулевые значения;
-
$f(mcdot n)=f(m)cdot f(n)$ при любых $m,n$.
Из определения следует, что если $f$ – мультипликативная функция, то $f(1)=1$. Действительно,
$$f(1)=f(1cdot 1)=f(1)cdot f(1).$$ Отсюда либо $f(1)=0$, либо $f(1)=1$. Но если $f(1)=0$, то для любого натурального $n$ имеем $f(n)=f(ncdot 1)=f(n)cdot f(1)=0$, то есть $f$ принимает только нулевые значения, что противоречит определению мультипликативной функции. Значит, $f(1)=1$.
Предложение 2. Пусть $f,g$ – мультипликативные функции. Тогда для любого натурального числа $n$
$$sum_{d|n}f(d)cdot gleft(frac{n}{d}right)=prod_{p|n}left(f(1)cdot g(p^{nu_p(n)})+f(p)cdot g(p^{nu_p(n)-1})+ldots +f(p^{nu_p(n)-1})cdot g(p)+f(p^{nu_p(n)})cdot g(1)right).$$ Здесь в левой части равенства стоит сумма по всем различным натуральным делителям числа $n$, а справа стоит произведение по всем различным простым делителям числа $n$, $nu_p(n)$ – показатель, определённый после доказательства основной теоремы арифметики. Например, при $n=12$ данное равенство выглядит так:
$$f(1)cdot g(12)+f(2)cdot g(6)+f(3)cdot g(4)+f(4)cdot g(3)+f(6)cdot g(2)+f(12)cdot g(1)=$$
$$=big(f(1)cdot g(4)+f(2)cdot g(2)+f(4)cdot g(1)big)cdotbig(f(1)cdot g(3)+f(3)cdot g(1)big).$$
Доказательство. Пусть $n=p_1^{alpha_1}cdots p_k^{alpha_k}$. Тогда
$$prod_{p|n}left(f(1)cdot g(p^{nu_p(n)})+f(p)cdot g(p^{nu_p(n)-1})+ldots +f(p^{nu_p(n)-1})cdot g(p)+f(p^{nu_p(n)})cdot g(1)right)=$$
$$=prod_{i=1}^kleft(sum_{beta_i=0}^{alpha_i}f(p_i^{beta_i})cdot g(p_i^{alpha_i-beta_i})right)=sum_{beta_1=0}^{alpha_1}ldotssum_{beta_k=0}^{alpha_k}f(p_1^{beta_1})cdot g(p_1^{alpha_1-beta_1})cdots f(p_k^{beta_k})cdot g(p_k^{alpha_k-beta_k}).$$
Воспользуемся мультипликативностью функций $f$ и $g$. Тогда полученное выражение запишется в виде
$$sum_{beta_1=0}^{alpha_1}ldotssum_{beta_k=0}^{alpha_k}f(p_1^{beta_1}cdots p_k^{beta_k})cdot g(p_1^{alpha_1-beta_1}cdots p_k^{alpha_k-beta_k})=sum_{d|n}f(d)cdot gleft(frac{n}{d}right).$$
Последнее равенство выполняется потому, что $d$ является делителем $n$ тогда и только тогда, когда $d=p_1^{beta_1}cdots p_k^{beta_k}$ и $0leqslantbeta_ileqslantalpha_i$ для каждого $i=1,ldots ,k$. Предложение 2 доказано.
По двум заданным функциям $f$ и $g$ натурального аргумента всегда можно построить третью функцию, которую мы будем обозначать $fcirc g$, определяемую для каждого натурального числа $n$ так:
$$fcirc g(n)=sum_{d|n}f(d)cdot gleft(frac{n}{d}right).$$
Эта функция называется свёрткой Дирихле функций $f$ и $g$.
Следствие 9. Если функции $f$ и $g$ мультипликативны, то мультипликативна и их свёртка Дирихле.
Доказательство. Пусть $(m,n)=1$. Это значит, что данные числа раскладываются в произведения простых так, что ни одно простое из разложения одного числа не встречается в разложении другого. Пусть $n=p_1^{alpha_1}cdots p_k^{alpha_k}, m=p_{k+1}^{alpha_{k+1}}cdots p_{k+l}^{alpha_{k+l}}$. Тогда по предложению 2
$$fcirc g(mcdot n)=sum_{d|mcdot n}f(d)cdot gleft(frac{mcdot n}{d}right)=prod_{i=1}^{k+l}left(sum_{beta_i=0}^{alpha_i}f(p_i^{beta_i})cdot g(p_i^{alpha_i-beta_i})right)=$$
$$=prod_{i=1}^{k}left(sum_{beta_i=0}^{alpha_i}f(p_i^{beta_i})cdot g(p_i^{alpha_i-beta_i})right)prod_{i=k+1}^{k+l}left(sum_{beta_i=0}^{alpha_i}f(p_i^{beta_i})cdot g(p_i^{alpha_i-beta_i})right)=$$
$$=sum_{d|n}f(d)cdot gleft(frac{n}{d}right)cdotsum_{d|m}f(d)cdot gleft(frac{m}{d}right)=fcirc g(m)cdot fcirc g(n).$$
Следствие 9 доказано.
Теорема 5. Множество всех мультипликативных функций образует абелеву группу относительно операции свёртки Дирихле.
Доказательство. По следствию 9 свёртка Дирихле двух мультипликативных функций есть также мультипликативная функция. Заметим, что
$$fcirc g(n)=sum_{d|n}f(d)cdot gleft(frac{n}{d}right)=sum_{d_1cdot d_2=n}f(d_1)cdot g(d_2)=sum_{d_2cdot d_1=n}g(d_2)cdot f(d_1)=gcirc f(n),$$
то есть свёртка Дирихле коммутативна.
Аналогично доказывается ассоциативность свёртки Дирихле:
$$fcirc big(gcirc hbig)(n)=sum_{d_1cdot d’=n}f(d_1)cdotbig(gcirc hbig)(d’)=
sum_{d_1cdot d’=n}f(d_1)cdotleft(sum_{d_2cdot d_3=d’}g(d_2)cdot h(d_3)right)=$$
$$=sum_{d_1cdot d_2cdot d_3=n}f(d_1)cdot g(d_2)cdot h(d_3)=sum_{dcdot d_3=n}left(sum_{d_1cdot d_2=d}f(d_1)cdot g(d_2)right)cdot h(d_3)=big(fcirc gbig)circ h(n).$$
Определим функцию $varepsilon(n)$ так, что $varepsilon(1)=1$ и $varepsilon(n)=0$ при всех $n>1$.
Тогда очевидно, что $varepsilon(n)$ мультипликативна, и для любой функции $f$
$$fcircvarepsilon=varepsiloncirc f=f.$$
Осталось показать, что для любой мультипликативной функции $f$ существует мультипликативная функция $f’$ такая, что
$$fcirc f’=varepsilon.$$
Поскольку $fcirc f'(1)=f(1)cdot f'(1)=1cdot 1=1=varepsilon(1)$, то благодаря мультипликативности достаточно, чтобы для любого простого числа $p$ для каждого $i=1,2,ldots$ выполнялось
$$fcirc f'(p^i)=f(1)cdot f'(p^i)+f(p)cdot f'(p^{i-1})+ldots +f(p^{i-1})cdot f'(p)+f(p^i)cdot f'(1)=0=varepsilon(p^i).$$
Ясно как подобрать функцию $f’$. Нужно задать $f'(p)$ так, чтобы выписанное равенство выполнялось при $i=1$. После этого нужно задать $f'(p^2)$ так, чтобы равенство выполнялось при $i=2$. Продолжая эту процедуру, можно задать (причём единственным образом) значение функции $f’$ на $p^i$ при любом $i$. Теорема 5 доказана.
Примеры мультипликативных функций
В доказательстве теоремы 5 уже появился первый пример мультипликативной (и даже вполне мультипликативной) функции — это нейтральный элемент группы мультипликативных функций — функция $varepsilon(n)$.
Функции $textrm{id}(n)=n$ и ${bf 1}(n)=1$, очевидно, тоже (вполне) мультипликативны.
Рассмотрим функцию $tau(n)$, которая подсчитывает количество различных натуральных делителей числа $n$. Имеем
$$tau(n)=sum_{d|n}1=sum_{d|n}{bf 1}(d)cdot {bf 1}left(frac{n}{d}right)={bf 1}circ{bf 1}(n).$$
Теперь по следствию 9 функция $tau(n)$ мультипликативна. Легко увидеть, что
$$tau(p_1^{alpha_1}cdots p_k^{alpha_k})=(alpha_1+1)cdots(alpha_k+1).$$
Для функции $sigma(n)$, которая подсчитывает сумму различных натуральных делителей числа $n$, находим
$$sigma(n)=sum_{d|n}d=sum_{d|n}textrm{id}(d)cdot {bf 1}left(frac{n}{d}right)=textrm{id}circ{bf 1}(n).$$
Отсюда по следствию 9 функция $sigma(n)$ также мультипликативна. При этом
$$sigma(p_1^{alpha_1}cdots p_k^{alpha_k})=(1+p_1+p_1^2+ldots +p_1^{alpha_1})cdots(1+p_k+p_k^2+ldots +p_k^{alpha_k})=frac{p_1^{alpha_1+1}-1}{p_1-1}cdotsfrac{p_k^{alpha_k+1}-1}{p_k-1}.$$
Функция Мёбиуса. Формула обращения Мёбиуса
Функция Мёбиуса $mu(n)$ определяется так:
-
$mu(1)=1$;
-
$mu(n)=0$, если $m^2|n$ при некотором $m>1$;
-
$mu(n)=(-1)^k$, если $n$ есть произведение первых степеней $k$ различных простых чисел.
Её мультипликативность следует из определения. Действительно, пусть $p^2|m$ или $p^2|n$. Тогда $mu(mcdot n)=0=mu(m)cdotmu(n)$. Если же $(m,n)=1, m=q_1cdots q_l, n=p_1cdots p_k$, то
$mu(mcdot n)=(-1)^{l+k}=(-1)^{l}cdot (-1)^{k}=mu(m)cdotmu(n)$. При этом $mu(n)$ не является вполне мультипликативной, так как при простом $p$ имеем $mu (pcdot p)=0$, но $mu(p)cdotmu (p)=(-1)cdot (-1)=1$.
Пользуясь предложением 2, можно заметить, что
$$mucirc {bf 1}(n)=prod_{p|n}(mu(1)+mu(p)+mu(p^2)+ldots+mu(p^{nu_p(n)}) )=prod_{p|n}(1-1+0+ldots +0)=varepsilon(n).$$
Так что функция Мёбиуса является обратной функцией к тождественной единице ${bf 1}(n)$ относительно операции свёртки Дирихле. Также заметим, что
$$mucirctextrm{id}(n)=prod_{p|n}(mu(1)cdot p^{nu_p(n)}+mu(p)cdot p^{nu_p(n)-1}+mu(p^2)cdot p^{nu_p(n)-2}+ldots+mu(p^{nu_p(n)})cdot 1)=prod_{p|n}(p^{nu_p(n)}-p^{nu_p(n)-1}).$$
Из равенства $mucirc {bf 1}=varepsilon$ и ассоциативности свёртки Дирихле вытекает знаменитая формула обращения Мёбиуса:
$$f=gcirc {bf 1}Longleftrightarrow g=fcircmu .$$
Пример 4. Какая функция получится в результате свёртки Дирихле функции Мёбиуса с функцией суммы делителей? Мы уже показали, что $sigma=textrm{id}circ{bf 1}$. По формуле обращения Мёбиуса находим $textrm{id}=sigmacircmu$, то есть $sum_{d|n}sigma(d)cdotmuleft(frac{n}{d}right)=n$. Аналогично из $tau={bf 1}circ{bf 1}$ получаем ${bf 1}=taucircmu$, то есть $sum_{d|n}tau(d)cdotmuleft(frac{n}{d}right)=1$.
Функция Эйлера
Функция Эйлера $varphi (n) $ подсчитывает количество натуральных чисел, не превосходящих $n$ и взаимно простых с $n$. Например, среди чисел от $1$ до $6$ только числа $1$ и $5$ взаимно просты с числом $6$, поэтому $varphi (6)=2$.
Для функции Эйлера можно найти следующее представление.
$$varphi (n) =sum_{1leqslant kleqslant n, (k, n)=1} 1=sum_{k=1}^nvarepsilon ( (k, n) )=sum_{k=1}^nmucirc {bf 1} ( (k, n) )=$$
$$=sum_{k=1}^nsum_{d|(k, n)}mu(d)=sum_{d|n}mu(d)sum_{1leqslant kleqslant n, k,vdots, d}1=sum_{d|n}mu(d)frac {n}{d}=mucirctextrm {id}(n). $$
По предложению 2, таким образом, функция $varphi (n) $ мультипликативна. Здесь при перемене местами двух сумм мы воспользовались следующим соображением: если $d|(k, n)$, то $d|k$ и $d|n$. Так как $k$ меняется от $1$ до $n$, то $d$ пробежит все натуральные делители числа $n $, причём некоторые, возможно, по несколько раз. Каждое конкретное $d$ встречается столько раз, сколько найдётся чисел $k$, делящихся на это $d$. А их будет ровно $frac{n}{d}$.
Из равенства $varphi=mucirctextrm {id} $ по формуле обращения Мёбиуса находим $textrm {id}=varphicirc {bf 1} $, то есть $sum_{d|n}varphi(d)=n$.
Покажем явную формулу для функции Эйлера. Имеем
$$varphi (n) =mucirctextrm {id}(n)=prod_{p|n}(p^{nu_p(n)}-p^{nu_p(n)-1}). $$
Последнее равенство доказано выше в разделе про функцию Мёбиуса.
Поясним отдельно эту формулу в двух простых случаях. Пусть $p$ – простое число. Тогда среди чисел $1,ldots ,p$ с ним взаимно просты все, кроме него самого. Получаем $varphi(p)=p-1$. Среди же чисел $1,ldots ,p^{alpha}$ взаимно просты с $p^{alpha}$ будут все, кроме тех, что делятся на $p$. А таких чисел ровно $p^{alpha-1}$. Следовательно, $varphi(p^{alpha})=p^{alpha}-p^{alpha-1}$.
Иногда в формуле для функции Эйлера избегают использования показателя $nu_p(n)$. Заметим, что
$$varphi (n) =prod_{p|n}(p^{nu_p(n)}-p^{nu_p(n)-1})=prod_{p|n}p^{nu_p(n)}cdotleft(1-frac{1}{p}right)=ncdotprod_{p|n}left(1-frac{1}{p}right).$$
Последнее равенство справедливо, так как $prod_{p|n}p^{nu_p(n)}=n$.
Замечание 5. Равенство $varphicirc {bf 1}=textrm {id} $ можно получить самостоятельно из очень простых соображений, если уже установлена мультипликативность функции Эйлера. Воспользуемся предложением 2:
$$sum_{d|n}varphi(d)=prod_{p|n}(varphi(1)+varphi(p)+varphi(p^2)+ldots +varphi(p^{nu_p(n)}) )
=prod_{p|n}(1+p-1+p^2-p+ldots +p^{nu_p(n)}-p^{nu_p(n)-1})=prod_{p|n}p^{nu_p(n)}=n.$$
Формула включений и исключений
Полученная выше формула для функции Эйлера может быть доказана и с помощью формулы включений и исключений. Сформулируем последнюю.
Пусть имеется $N$ объектов, которые могут обладать (или нет) свойствами $ a_1,ldots , a_k $. Будем обозначать через $N (a_{i_1},ldots ,a_{i_j}) $ количество тех из наших $N $ объектов, что обладают каждым из свойств $a_{i_1},ldots ,a_{i_j}, 1leqslant i_1,ldots , i_jleqslant k$ (но при этом, возможно, и какими-то ещё свойствами). За $ N_0^{(k)}$ обозначим количество тех из наших $N $ объектов, которые не обладают ни одним из свойств $a_1,ldots ,a_k$.
Теорема 6 (формула включений и исключений).
$$N_0^{(k)}=N-N(a_1)-N(a_2)-ldots — N(a_k)+N(a_1,a_2)+N(a_1,a_3)+ldots +N(a_{k-1},a_k)-$$
$$-N(a_1,a_2,a_3)-ldots -N(a_{k-2},a_{k-1},a_k)+ldots +(-1)^kcdot N(a_1,ldots ,a_k).$$
Доказательство. Проведём индукцию по $k$ (если мы покажем, что утверждение верно при $k=1$, а также, что из справедливости утверждения при произвольном натуральном $k$ следует его справедливость и при $k+1$, то утверждение будет справедливо при всех натуральных $k$).
При $k=1$ утверждается, что количество объектов, не обладающих свойством $a_1$, есть количество всех объектов за вычетом количества объектов, которые обладают этим свойством:
$$N_0^{(1)}=N-N(a_1).$$
Это очевидно. Пусть для некоторого $kgeqslant 1$ утверждение теоремы верно и пусть имеется ещё одно свойство $a_{k+1}$. Пусть $M$ – это количество всех тех из наших $N$ объектов, которые обладают свойством $a_{k+1}$. Обозначим через $M (a_{i_1},ldots ,a_{i_j})$ количество тех из только что выделенных $M$ объектов, что обладают каждым из свойств $a_{i_1},ldots ,a_{i_j}, 1leqslant i_1,ldots , i_jleqslant k$. За $M_0$ обозначим количество тех из этих же $M$ объектов, которые не обладают ни одним из свойств $a_1,ldots ,a_k$. Заметим, что, вообще говоря, $M=N(a_{k+1})$ и $M (a_{i_1},ldots ,a_{i_j})=N(a_{i_1},ldots ,a_{i_j},a_{k+1})$.
Запишем формулу включений и исключений для этих выделенных $M$ объектов:
$$M_0=M-M(a_1)-ldots — M(a_k)+M(a_1,a_2)+ldots +M(a_{k-1},a_k)+ldots +(-1)^kcdot M(a_1,ldots ,a_k).$$
Очевидно, что $N_0^{(k+1)}=N_0^{(k)}-M_0$, так как количество чисел, не обладающих ни одним из свойств $a_1,ldots ,a_k,a_{k+1}$ равно количеству чисел, не обладающих ни одним из свойств $a_1,ldots ,a_k$, за вычетом количества тех из них, что обладают свойством $a_{k+1}$.
Имеем
$$N_0^{(k+1)}=N_0^{(k)}-M_0=N-N(a_1)-ldots — N(a_k)+N(a_1,a_2)+ldots +N(a_{k-1},a_k)+ldots +(-1)^kcdot N(a_1,ldots ,a_k)-$$
$$-big(M-M(a_1)-ldots — M(a_k)+M(a_1,a_2)+ldots +M(a_{k-1},a_k)+ldots +(-1)^kcdot M(a_1,ldots ,a_k)big)=$$
$$=N-N(a_1)-ldots — N(a_k)-N(a_{k+1})+N(a_1,a_2)+ldots +N(a_{k-1},a_k)+N(a_1,a_{k+1})+ldots +N(a_k,a_{k+1})+ldots +$$
$$+(-1)^{k+1}cdot N(a_1,ldots ,a_k,a_{k+1}).$$
Теорема 6 доказана.
Пусть теперь у нас есть натуральное число $N=p_1^{alpha_1}cdots p_k^{alpha_k}$. Рассмотрим $N$ объектов, которыми будут числа $1,2,ldots ,N$. Введём свойства $ a_1,ldots , a_k $ так: натуральное число обладает свойством $a_i, i=1,ldots ,k$, если $p_i$ делит данное число. Очень легко сосчитать $N (a_{i_1},ldots ,a_{i_j}) $, ведь некоторое число делится одновременно на $p_{i_1},ldots ,p_{i_j}$ тогда и только тогда, когда оно делится на $p_{i_1}cdots p_{i_j}$, а таких чисел ровно $frac{N}{p_{i_1}cdots p_{i_j}}$. Заметим также, что $N_0^{(k)}=varphi(N)$, поскольку число не делится ни на одно из простых $p_1,ldots ,p_k$ тогда и только тогда, когда это число взаимно просто с $N$. Имеем
$$varphi(N)=N_0^{(k)}=N-N(a_1)-ldots — N(a_k)+N(a_1,a_2)+ldots +N(a_{k-1},a_k)+ldots +(-1)^kcdot N(a_1,ldots ,a_k)=$$
$$=N-frac{N}{p_1}-ldots -frac{N}{p_k}+frac{N}{p_1cdot p_2}+ldots+frac{N}{p_{k-1}cdot p_k}+ldots+(-1)^kfrac{N}{p_1cdots p_k}=$$
$$=NcdotBig(1-frac{1}{p_1}-ldots -frac{1}{p_k}+frac{1}{p_1cdot p_2}+ldots+frac{1}{p_{k-1}cdot p_k}+ldots+(-1)^kfrac{1}{p_1cdots p_k}Big)=$$
$$=Ncdotprod_{i=1}^{k}left(1-frac{1}{p_i}right)=Ncdotprod_{p|N}left(1-frac{1}{p}right).$$
Заметим, что в сумме в предпоследней строчке перед каждым слагаемым вида $frac{1}{p_{i_1}cdots p_{i_j}}$ стоит знак $(-1)^j$, что по определению функции Мёбиуса равно $mu(p_{i_1}cdots p_{i_j})$.
Ещё о мультипликативности функции Эйлера
На самом деле, мультипликативность функции Эйлера можно доказать, пользуясь совсем простыми соображениями. Пусть $m,n$ – натуральные числа и $(m,n)=1$. Тогда натуральное число взаимно просто с $mcdot n$ тогда и только тогда, когда оно взаимно просто как с $m$, так и с $n$.
Запишем числа $1,2,ldots ,mcdot n$ в несколько строк одинаковой длины:
$${}hspace{10mm}1hspace{28mm}2hspace{28mm}3hspace{8mm}ldotshspace{9mm}n$$
$${}hspace{6mm}n+1hspace{20mm}n+2hspace{20mm}n+3hspace{7mm}ldotshspace{7mm}2n$$
$${}hspace{11mm}vdotshspace{29mm}vdotshspace{29mm}vdotshspace{7mm}ldotshspace{10mm}vdots$$
$$(m-1)n+1hspace{5mm}(m-1)n+2hspace{5mm}(m-1)n+3hspace{6mm}ldotshspace{5mm}mcdot n$$
По второму свойству делимости в каждой строке столько же взаимно простых с $n$ чисел, сколько и в первой строке, а именно $varphi(n)$, причём взаимно простые с $n$ числа из каждой строки стоят в одних и тех же столбцах, то есть для каждого столбца либо все элементы взаимно просты с $n$ (и таких столбцов $varphi(n)$), либо все элементы не взаимно просты с $n$. Покажем теперь, что все числа, которые стоят в любом из столбцов, дают различные остатки при делении на $m$. Поскольку в каждом столбце находится $m$ чисел, то это будет означать, что при делении на $m$ они дают все $m$ остатков, какие только бывают. А значит, снова по второму свойству делимости, среди них будет столько же чисел, взаимно простых с $m$, сколько их среди чисел $0,1,2,ldots ,m-1$, а именно $varphi(m)$. Тогда всего в нашей таблице чисел, взаимно простых одновременно с $m$ и с $n$, будет $varphi(m)cdotvarphi(n)$. С другой стороны, это количество чисел среди $1,2,ldots ,mcdot n$, взаимно простых с $mcdot n$, что равно $varphi(mcdot n)$.
Итак, числа в $k$-м столбце имеют вид $acdot n+k, a=0,1,2,ldots ,m-1$. Допустим, у двух из них совпали остатки при делении на $m$. То есть $a_1cdot n+k=q_1cdot m+r$ и $a_2cdot n+k=q_2cdot m+r$, где $0leqslant a_1<a_2<m$. Но тогда $(a_2-a_1)n=(q_2-q_1)m$, и, так как $(m,n)=1$, то $m|(a_2-a_1)$, однако же $0< a_2-a_1<m$. Полученное противоречие показывает, что остатки у всех чисел в столбце различны.
Сравнения
Классы вычетов. Полная и приведённая системы вычетов
Пусть $m$ натуральное число. Произвольное целое число можно поделить на $m$ с остатком, который принимает значения $0,1,2,ldots ,m-1$. Разобьём множество целых чисел на $m$ классов, каждый из которых содержит все целые числа, дающие один и тот же остаток при делении на $m$. Это будут так называемые классы вычетов по модулю числа $m$.
Выберем из каждого класса вычетов ровно по одному представителю, тогда полученное множество называется полной системой вычетов по модулю $m$. Если же из произвольной полной системы вычетов дополнительно выбрать только те числа, которые взаимно просты с $m$, то полученное множество будем называть приведённой системой вычетов по модулю $m$.
Пример 5. Вот некоторые полные системы вычетов по модулю $7$:
$${0,1,2,3,4,5,6},quad{1,2,3,4,5,6,7},quad{-27,-19,-11,-3,5,13,21}.$$
Соответствующие им приведённые системы вычетов по модулю $7$:
$${1,2,3,4,5,6},quad{1,2,3,4,5,6},quad{-27,-19,-11,-3,5,13}.$$
Дадим также некоторые полные системы вычетов по модулю $9$:
$${0,1,2,3,4,5,6,7,8},quad{-4,-3,-2,-1,0,1,2,3,4},quad{100,200,300,400,500,600,700,800,900}.$$
Соответствующие им приведённые системы вычетов по модулю $9$:
$${1,2,4,5,7,8},quad{-4,-2,-1,1,2,4},quad{100,200,400,500,700,800}.$$
Заметим, что если имеются две полные системы вычетов по модулю $m$, то каждый элемент одной из них сравним по модулю $m$ с каким-то одним и только одним элементом другой, просто потому, что каждая полная система вычетов по модулю $m$ содержит ровно по одному представителю из каждого класса вычетов по модулю $m$. То же самое свойство сохранится и если мы рассмотрим две произвольные приведённые системы вычетов по модулю $m$. В частности, поскольку числа $1,2,ldots ,m$ образуют полную систему вычетов по модулю $m$, то соответствующая приведённая система вычетов будет выбираться из этих чисел и по определению функции Эйлера будет состоять из $varphi(m)$ элементов. А следовательно и в любой приведённой системе вычетов по модулю $m$ будет содержаться $varphi(m)$ чисел. Одновременно таково будет количество классов вычетов по модулю $m$, состоящих из взаимно простых с $m$ чисел.
Сравнения и основные их свойства
Если числа $a$ и $b$ содержатся в одном и том же классе вычетов по модулю $m$, то говорят, что они сравнимы по модулю $m$. Обозначается это так:
$$aequiv bpmod{m}.$$
Заметим, что $aequiv bpmod{m}Leftrightarrow m|(b-a)$.
Из этого замечания, самого определения и из свойств делимости вытекают следующие очевидные свойства сравнений:
-
$aequiv apmod{m}$.
-
Если $aequiv bpmod{m}$ и $bequiv cpmod{m}$, то $aequiv cpmod{m}$.
-
Если $aequiv bpmod{m}$ и $cinmathbb{Z}$, то $acdot cequiv bcdot cpmod{m}$.
-
Если $acdot nequiv bcdot npmod{m}$ и $(m,n)=1$, то $aequiv bpmod{m}$.
-
Если $acdot nequiv bcdot npmod{mcdot n}$, то $aequiv bpmod{m}$.
-
Если $aequiv bpmod{m}$ и $cequiv dpmod{m}$, то $apm cequiv bpm dpmod{m}$ и $acdot cequiv bcdot dpmod{m}$.
Прокомментируем лишь последнее свойство. Из третьего свойства получаем $acdot cequiv bcdot cpmod{m}$ и $bcdot cequiv bcdot dpmod{m}$. Теперь по второму свойству находим $acdot cequiv bcdot dpmod{m}$.
Предложение 3. Пусть $a$ пробегает полную систему вычетов по модулю $m$, а также $k,ninmathbb{Z}$ и $(m,n)=1$. Тогда числа вида $acdot n+k$ тоже пробегают полную систему вычетов по модулю $m$.
Доказательство. Достаточно повторить рассуждения последнего абзаца предыдущего доказательства мультипликативности функции Эйлера. Сделаем это. Необходимо показать, что все эти числа $acdot n+k$ лежат в разных классах вычетов по модулю $m$. Допустим, что два из них лежат в одном и том же классе, то есть $a_1cdot n+kequiv a_2cdot n+kpmod{m}$, где $a_1notequiv a_2pmod{m}$. Но тогда из первого и шестого свойств сравнений следует, что $a_1cdot nequiv a_2cdot npmod{m}$, и, так как $(m,n)=1$, то по четвёртому свойству сравнений $a_1equiv a_2pmod{m}$. Противоречие. Предложение 3 доказано.
Следствие 10. Пусть $a$ пробегает приведённую систему вычетов по модулю $m$, а также $ninmathbb{Z}, (m,n)=1$. Тогда числа вида $acdot n$ тоже пробегают приведённую систему вычетов по модулю $m$.
Доказательство. По предложению 3, если $a$ пробегает полную систему вычетов по модулю $m$, то и $acdot n$ тоже. Очевидно, что взаимно просты с $m$ будут те и только те числа $acdot n$, для которых $a$ взаимно просто с $m$. Следствие 10 доказано.
Теорема Эйлера
Теорема Эйлера. Пусть $m$ натуральное число, $binmathbb{Z}, (b,m)=1$. Тогда $b{}^{varphi(m)}equiv 1pmod{m}$.
Доказательство. Пусть $a$ пробегает приведённую систему вычетов по модулю $m$. Тогда по следствию 10 числа вида $acdot b$ тоже пробегают приведённую систему вычетов по модулю $m$. Каждый элемент первой совокупности сравним по модулю $m$ с каким-то одним и только одним элементом второй совокупности. Следовательно произведение элементов первой совокупности сравнимо по модулю $m$ с произведением элементов второй. Если занумеровать элементы первой совокупности $a_1,a_2,ldots ,a_{varphi(m)}$, то можно записать это так:
$$prod_{i=1}^{varphi(m)}a_i equiv prod_{i=1}^{varphi(m)}(a_icdot b) = b{}^{varphi(m)}prod_{i=1}^{varphi(m)}a_ipmod{m}.$$
Так как по определению все элементы приведённой системы вычетов взаимно просты с $m$, то по четвёртому свойству сравнений мы можем сократить левую и правую части сравнения на $displaystyleprod_{i=1}^{varphi(m)}a_i$ и получим, что $b{}^{varphi(m)}equiv 1pmod{m}$. Теорема Эйлера доказана.
Заметим, что если $(b,m)>1$, то сравнение $b{}^{varphi(m)}equiv 1pmod{m}$ не может выполняться, так как из него бы следовало, что с некоторым целым числом $y$ верно $b{}^{varphi(m)}+my= 1$, откуда по второму свойству делимости $(b,m)|1$.
Обратный элемент по модулю $m$
Пусть $(M,m)=1$. Тогда существует бесконечно много решений уравнения $Mx+my=1$. Общее решение имеет вид $x=x_0+mcdot t, y=y_0-Mcdot t, tinmathbb{Z}$. Если перейти на язык сравнений, то получится, что сравнение $Mxequiv 1pmod{m}$ имеет решение $xequiv x_0pmod{m}$. Каждого из представителей класса вычетов по модулю $m$, содержащего $x_0$, будем обозначать $M^{-1}$ и будем говорить, что это обратный к $M$ вычет по модулю $m$. Очевидно, что $(M^{-1},m)=1$ и $(M^{-1})^{-1}equiv Mpmod{m}$. Мы видим, что все вычеты, обратные к данному, содержатся в одном единственном классе по модулю $m$, и для представителей разных классов вычетов по модулю $m$ обратные к ним вычеты будут содержаться также в разных классах по модулю $m$.
Если же $(M,m)>1$, то уравнение $Mx+my=1$ не имеет решений и $M$ не будет иметь обратного элемента по модулю $m$.
Китайская теорема об остатках
Пусть $m_1,ldots ,m_n$ натуральные попарно взаимно простые числа, и требуется решить систему сравнений
$$xequiv a_1pmod{m_1};$$
$$ldots$$
$$xequiv a_npmod{m_n}.$$
Положим $M=m_1cdots m_n$ и $M_i=frac{M}{m_i}, i=1,ldots ,n$. По условию получается, что при всех $i=1,ldots ,n$ будет $(M_i,m_i)=1$ и согласно предыдущему пункту можно найти $M_i^{-1}$ по модулю $m_i$.
Теорема 7. Все решения указанной системы состоят из всех представителей одного единственного класса вычетов по модулю $M$ и удовлетворяют условию
$$xequiv a_1cdot M_1cdot M_1^{-1}+a_2cdot M_2cdot M_2^{-1}+ldots +a_ncdot M_ncdot M_n^{-1}pmod{M}.$$
Доказательство. Пусть $x,y$ два решения нашей системы. Получаем для каждого $i=1,ldots ,n$ выполнено сравнение $xequiv a_iequiv ypmod{m_i}$. Таким образом, $x-y$ делится на каждое $m_i$, а значит является их общим кратным и делится на их наименьшее общее кратное, которое по следствию 6 равняется $M$. Это эквивалентно тому, что $xequiv ypmod{M}$. Обратно, если $y$ является решением системы и $xequiv ypmod{M}$, то $x$ также будет решением системы, так как $x=y+kM$ с некоторым целым числом $k$ и $Mequiv 0pmod{m_i}$ для каждого $i=1,ldots ,n$.
Далее, заметим, что при $jneq i$ имеем $M_jequiv 0pmod {m_i} $. Поэтому при любом $i=1,ldots ,n$ получаем
$$a_1cdot M_1cdot M_1^{-1}+ldots +a_ncdot M_ncdot M_n^{-1}equiv a_icdot M_icdot M_i^{-1}equiv a_ipmod {m_i}, $$
то есть данное число является решением нашей системы сравнений. Теорема 7 доказана.
Замечание 5. Формула, приведённая в условии теоремы 7, устанавливает взаимно однозначное соответствие между совокупностью полных систем вычетов по модулям $m_1,ldots ,m_n$ и полной системой вычетов по модулю $M$. В частности, тот факт, что решение системы единственно по модулю $M$, иногда позволяет на практике угадывать это решение, не прибегая к вычислениям. Например, решением системы
$$xequiv 4pmod{9};$$
$$xequiv 5pmod{8};$$
$$xequiv 6pmod{7}$$
очевидно будет $xequiv 13pmod{504}$.
Теорема Лагранжа
Пусть $p$ простое число, $a,b$ целые и $(a,p)=1$. У сравнения $axequiv bpmod{p}$ существует единственное по модулю $p$ решение, так как все решения уравнения $ax+py=b$ имеют вид $x=x_0+pt, y=y_0-at, tinmathbb{Z}$.
Оказывается, имеет место более общее утверждение, а именно
Теорема 8 (теорема Лагранжа). Пусть $p$ простое число и $f(x)=a_nx^n+a_{n-1}x^{n-1}+ldots +a_1x+a_0$, где $a_n,ldots ,a_0inmathbb{Z}$, причём $a_nnotequiv 0pmod{p}$. Тогда сравнение $f(x)equiv 0pmod{p}$ имеет не более $n$ решений по модулю $p$.
Доказательство. Проведём индукцию по $n$. При $n=1$ справедливость теоремы уже установлена. Пусть утверждение теоремы верно для всех многочленов степени $n-1$. Покажем, что оно справедливо и для многочленов степени $n$. Пусть $f(x)$ – многочлен, описанный в условии теоремы. Если сравнение $f(x)equiv 0pmod{p}$ неразрешимо, то утверждение теоремы выполняется. Допустим указанное сравнение имеет некоторое решение $x_0$, то есть $f(x_0)equiv 0pmod{p}$. Тогда
$$f(x)equiv f(x)-f(x_0)=a_n(x^n-x_0^n)+a_{n-1}(x^{n-1}-x_0^{n-1})+ldots +a_1(x-x_0)=(x-x_0)cdot g(x)pmod{p},$$
где $g(x)=a_nx^{n-1}+ldots$ – многочлен степени $n-1$, и по предположению индукции сравнение $g(x)equiv 0pmod{p}$ имеет не более $n-1$ решения по модулю $p$. При этом из установленного сравнения следует, что $f(x)equiv 0pmod{p}$ тогда и только тогда, когда $g(x)equiv 0pmod{p}$ или $x-x_0equiv 0pmod{p}$. Второе из этих сравнений имеет единственное решение по модулю $p$, а значит сравнение $f(x)equiv 0pmod{p}$ имеет не более $n$ решений. Теорема 8 доказана.
Замечание 6. Если $m$ составное число, то сравнение $f(x)equiv 0pmod{m}$ может иметь более $n$ решений по модулю $m$. Например у сравнения $x^2equiv 4pmod{15}$ имеется $4$ решения: $xequiv pm 2pmod{15}, xequiv pm 7pmod{15}$. Дело в том, что если сравнение выполнено по модулю $15$, то оно также выполняется и по модулям $3$ и $5$. C другой стороны, из любой пары решений сравнения по модулям $3$ и $5$ по китайской теореме об остатках единственным образом можно получить одно из решений сравнения по модулю $15$. То есть решений по модулю $15$ будет ровно столько, сколько можно составить различных пар решений по модулям $3$ и $5$. По модулю $3$, как и по модулю $5$ есть ровно два решения, а именно $xequivpm 2$. Это позволяет составить четыре различные пары, которые и отвечают предъявленным решениям по модулю $15$. В общем случае, если пользоваться обозначениями китайской теоремы об остатках, когда у некоторого сравнения будет $N_1,ldots , N_n$ решений по модулям $m_1,ldots , m_n$, то у этого же сравнения по модулю $M$ будет $N_1cdots N_n$ решений.
Теоремы Ферма и Вильсона, символ Лежандра, критерий Эйлера
Пусть $p$ простое нечётное число, $a,b$ целые и $(a,p)=(b,p)=1$. У сравнения $axequiv bpmod{p}$ существует, как мы видели, единственное по модулю $p$ решение.
Очевидно, что при различных $a$ эти решения тоже будут различны, ведь из сравнений $a_1xequiv a_2xequiv bpmod{p}$ следовало бы $a_1equiv a_2pmod{p}$, так как очевидно $(x,p)=1$.
Заметим также, что если $a_1$ есть решение сравнения $axequiv bpmod{p}$, то, наоборот, $a$ будет решением сравнения $a_1xequiv bpmod{p}$.
При некоторых $b$ возможно, что само $a$ будет решением сравнения $axequiv bpmod{p}$. Это случится тогда и только тогда, когда разрешимо сравнение $x^2equiv bpmod{p}$. Сколько решений может иметь такое сравнение? Пусть $x$ – некоторое решение данного сравнения, тогда $-x$ – тоже его решение. При этом из $(b,p)=1$ следует $xnotequiv 0pmod{p}$, а значит $xnotequiv -xpmod{p}$, поскольку $p$ нечётно. По теореме Лагранжа более двух решений данное сравнение иметь не может. Следовательно $x$ и $-x$ – все решения данного сравнения. Если же $p|b$, то $xequiv 0pmod{p}$, очевидно, является единственным решением.
При $(b,p)=1$ получается, что если сравнение $x^2equiv bpmod{p}$ неразрешимо, то приведённая система вычетов по модулю $p$ разбивается на пары чисел $a,a_1$ таких, что $aa_1equiv bpmod{p}$, а значит произведение всех $p-1$ элементов приведённой системы вычетов будет сравнимо с $b^{frac{p-1}{2}}$ по модулю $p$. Если же сравнение $x^2equiv bpmod{p}$ разрешимо, то приведённая система вычетов по модулю $p$ разбивается на пары чисел $a,a_1$ таких, что $aa_1equiv bpmod{p}$ за исключением двух решений $x$ и $-x$ сравнения $x^2equiv bpmod{p}$, произведение которых сравнимо с $-b$ по модулю $p$. Таким образом, произведение всех $p-1$ элементов приведённой системы вычетов будет сравнимо с $-b^{frac{p-1}{2}}$ по модулю $p$.
Очень удобно рассмотреть следующее обозначение, называемое символом Лежандра:
-
$left(frac{b}{p}right)=1$, если $(b,p)=1$ и сравнение $x^2equiv bpmod{p}$ разрешимо;
-
$left(frac{b}{p}right)=0$, если $(b,p)neq 1$, то есть $p|b$;
-
$left(frac{b}{p}right)=-1$, если сравнение $x^2equiv bpmod{p}$ неразрешимо.
Пример 5. $left(frac{1}{p}right)=1$, так как $(1,p)=1$ и сравнение $x^2equiv 1pmod{p}$ имеет очевидные решения $xequiv 1pmod{p}$ и $xequiv -1pmod{p}$.
Рассмотрим как раз случай $b=1$ в проведённых выше рассуждениях. Так как сравнение $x^2equiv 1pmod{p}$ разрешимо, то произведение всех $p-1$ элементов приведённой системы вычетов будет сравнимо с $-1^{frac{p-1}{2}}$, то есть с $-1$ по модулю $p$. Это позволяет доказать ряд известных теорем.
Теорема Вильсона. Пусть $p$ простое число. Тогда $(p-1)!equiv -1pmod{p}$.
Доказательство. При $p=2$ утверждение теоремы очевидно выполняется. Поскольку числа $1,2,ldots ,p-1$ составляют приведённую систему вычетов по модулю $p$, то их произведение, как раз равное $(p-1)!$, сравнимо с $-1$ по модулю $p$ и в случае любого нечётного простого $p$. Теорема Вильсона доказана.
Критерий Эйлера. Пусть $binmathbb{Z}$. Тогда $left(frac{b}{p}right)equiv b^{frac{p-1}{2}}pmod{p}$.
Доказательство. Пусть $binmathbb{Z}, (b,p)=1$. Мы знаем, что если сравнение $x^2equiv bpmod{p}$ неразрешимо, то $b^{frac{p-1}{2}}$ сравнимо с произведением всех элементов приведённой системы вычетов по модулю $p$, которое, в свою очередь, сравнимо с $-1$. Но и символ Лежандра $left(frac{b}{p}right)$ в этом случае тоже равен $-1$. Если же сравнение $x^2equiv bpmod{p}$ разрешимо, то $-b^{frac{p-1}{2}}$ сравнимо с произведением всех элементов приведённой системы вычетов по модулю $p$, а значит $b^{frac{p-1}{2}}equiv 1pmod{p}$. При этом символ Лежандра $left(frac{b}{p}right)$ в этом случае также равен $1$. Пусть теперь $p|b$. Но тогда $b^{frac{p-1}{2}}equiv 0pmod{p}$, и символ Лежандра $left(frac{b}{p}right)$ тоже равен $0$. Таким образом, во всех случаях критерий Эйлера доказан.
Теорема Ферма. Пусть $binmathbb{Z}, (b,p)=1$. Тогда $b^{p-1}equiv 1pmod{p}$.
Доказательство. Это очевидно следует из критерия Эйлера, поскольку при $(b,p)=1$ будет $b^{frac{p-1}{2}}equivpm 1pmod{p}$, и утверждение теоремы Ферма получится при возведении обеих частей данного сравнения в квадрат. Теорема Ферма доказана.
Второй способ – повторить доказательство теоремы Эйлера, ведь теорема Ферма является её частным случаем при $m=p$.
Заметим, что при $(b,p)neq 1$, то есть когда $p|b$, будет $b^{p-1}equiv 0pmod{p}$. Поэтому, чтобы включить и этот случай в условие теоремы Ферма, используют следующую формулировку: для любого целого числа $b$ выполнено
$$b^pequiv bpmod{p}.$$
Свойства символа Лежандра. Лемма Гаусса. Квадратичный закон взаимности
Пусть $p$ нечётное простое число, $a,binmathbb{Z}$. Тогда
-
Если $aequiv bpmod{p}$, то $left(frac{a}{p}right)=left(frac{b}{p}right)$;
-
$left(frac{acdot b}{p}right)=left(frac{a}{p}right)left(frac{b}{p}right)$;
-
Если $pnmid b$, то $left(frac{b^2}{p}right)=1$, в частности $left(frac{1}{p}right)=1$;
-
-
$left(frac{-1}{p}right)=1$, если $pequiv 1pmod{4}$,
-
$left(frac{-1}{p}right)=-1$, если $pequiv -1pmod{4}$;
-
-
-
$left(frac{2}{p}right)=1$, если $pequivpm 1pmod{8}$,
-
$left(frac{2}{p}right)=-1$, если $pequivpm 3pmod{8}$;
-
-
Квадратичный закон взаимности. Пусть $p,q$ нечётные простые числа, тогда
-
$left(frac{p}{q}right)=-left(frac{q}{p}right)$, если $pequiv qequiv -1pmod{4}$,
-
$left(frac{p}{q}right)=left(frac{q}{p}right)$ иначе.
-
Докажем эти свойства символа Лежандра. Пусть $aequiv bpmod{p}$, тогда, если $pnmid b$, то и $pnmid a$, и сравнение $x^2equiv apmod{p}$ разрешимо тогда и только тогда, когда разрешимо сравнение $x^2equiv bpmod{p}$. Если же $p|b$, то также $p|a$. В обоих случаях по определению символа Лежандра получаем, что $left(frac{a}{p}right)=left(frac{b}{p}right)$. Первое свойство доказано.
По критерию Эйлера имеем
$$left(frac{acdot b}{p}right)equiv (ab)^{frac{p-1}{2}}=a^{frac{p-1}{2}}b^{frac{p-1}{2}}equivleft(frac{a}{p}right)left(frac{b}{p}right)pmod{p}.$$
Поскольку как правая, так и левая часть сравнения есть целое число, не превосходящее $1$ по абсолютной величине, то их разность не превосходит $2$ по абсолютной величине, при этом по определению сравнимости эта разность должна делиться на $p$, которое больше или равно трём, что возможно лишь когда эти два числа равны. Второе свойство доказано.
При $pnmid b$ сравнение $x^2equiv b^2pmod{p}$ имеет два очевидных решения $xequiv bpmod{p}$ и $xequiv -bpmod{p}$, откуда по определению символа Лежандра получаем, что $left(frac{b^2}{p}right)=1$. Третье свойство доказано.
По критерию Эйлера имеем
$$left(frac{-1}{p}right)equiv (-1)^{frac{p-1}{2}}pmod{p}.$$
Опять как правая, так и левая часть сравнения есть целое число, не превосходящее $1$ по абсолютной величине, а модуль по которому эти величины сравнимы, не меньше трёх, а значит эти два числа равны. Но то, что $(-1)^{frac{p-1}{2}}=1$, если $pequiv 1pmod{4}$, и $(-1)^{frac{p-1}{2}}=-1$, если $pequiv -1pmod{4}$, очевидно. Четвёртое свойство доказано.
Пятое свойство можно доказать отдельно, но удобнее воспользоваться следующим результатом:
Лемма Гаусса. Пусть $p$ нечётное простое число, $binmathbb{Z}, pnmid b$. Тогда
$$left(frac{b}{p}right)=(-1)^N,$$
где $N$ – количество отрицательных среди чисел $varepsilon_1,varepsilon_2,ldots ,varepsilon_{frac{p-1}{2}}$, определяемых следующим образом. Поскольку числа $pm 1,pm 2,ldots ,pmfrac{p-1}{2}$ образуют приведённую систему вычетов по модулю $p$, то любое взаимно простое с $p$ число сравнимо по модулю $p$ ровно с одним из этих чисел. Пусть $k=1, 2,ldots ,frac{p-1}{2}$, тогда $bcdot kequivvarepsilon_kr_kpmod{p}$, где $varepsilon_k=pm 1$ и $r_kin{1, 2,ldots ,frac{p-1}{2}}$.
Доказательство. Покажем, что среди чисел $r_1, r_2,ldots ,r_{frac{p-1}{2}}$ нет равных друг другу, то есть они представляют собой перестановку чисел $1, 2,ldots ,frac{p-1}{2}$. От противного, если $i<j$ и $r_i=r_j$, то по определению этих чисел получим, что $bcdot iequivpm bcdot jpmod{p}$, и так как $pnmid b$, то $iequiv pm jpmod{p}$, что невозможно при $1leqslant i<jleqslantfrac{p-1}{2}$. Теперь перемножим левые и правые части сравнений $bcdot kequivvarepsilon_kr_kpmod{p}$ при всех $k=1, 2,ldots ,frac{p-1}{2}$. Получим
$$b^{frac{p-1}{2}}{textstyle frac{p-1}{2}!}equivvarepsilon_1cdotvarepsilon_2cdotsvarepsilon_{frac{p-1}{2}}cdot r_1cdot r_2cdots r_{frac{p-1}{2}}pmod{p}.$$
Так как $r_1, r_2,ldots ,r_{frac{p-1}{2}}$ есть перестановка чисел $1, 2,ldots ,frac{p-1}{2}$, то $r_1cdot r_2cdots r_{frac{p-1}{2}}={textstyle frac{p-1}{2}!}$ и на это взаимно простое с $p$ число обе части полученного сравнения можно сократить. Кроме того, по критерию Эйлера $b^{frac{p-1}{2}}equivleft(frac{b}{p}right)pmod{p}$, а по определению числа $N$ имеем $varepsilon_1cdotvarepsilon_2cdotsvarepsilon_{frac{p-1}{2}}=(-1)^N$. Таким образом, находим $left(frac{b}{p}right)equiv (-1)^Npmod{p}$, откуда уже знакомыми нам из доказательства третьего и четвёртого свойств рассуждениями приходим к требуемому в лемме Гаусса равенству. Лемма Гаусса доказана.
Воспользуемся леммой Гаусса при $b=2$. Поскольку $2cdot kleqslantfrac{p-1}{2}$ при $1leqslant kleqslantleft[frac{p-1}{4}right]$, то $varepsilon_1=ldots =varepsilon_{[frac{p-1}{4}]}=1$, а так как $frac{p-1}{2}<2cdot kleqslant p-1$ при $left[frac{p-1}{4}right]< kleqslant{textstyle frac{p-1}{2}}$, то $varepsilon_{[frac{p-1}{4}]+1}=ldots =varepsilon_{frac{p-1}{2}}=-1$, например $2cdotfrac{p-1}{2}equiv -1pmod{p}$. Отсюда $N=frac{p-1}{2}-left[frac{p-1}{4}right]=left[frac{p+1}{4}right]$. Получаем, что
$left(frac{2}{p}right)=(-1)^{[frac{p+1}{4}]},$ и очевидно, что $(-1)^{[frac{p+1}{4}]}=1$, если $pequivpm 1pmod{8}$, и $(-1)^{[frac{p+1}{4}]}=-1$, если $pequivpm 3pmod{8}$. Пятое свойство доказано.
Если $p=q$, то шестое свойство верно. Пусть теперь $p,q$ различные нечётные простые числа и $b$ произвольное целое число. Будем ассоциировать с ним пару чисел $(b_p,b_q), |b_p|leqslantfrac{p-1}{2}, |b_q|leqslantfrac{q-1}{2}$, где $bequiv b_ppmod{p}$ и $bequiv b_qpmod{q}$. Поскольку $b_p$ и $b_q$ пробегают полные системы вычетов по модулям соответственно $p$ и $q$, то согласно китайской теореме об остатках множество всех пар $(b_p,b_q)$ можно поставить во взаимно однозначное соответствие с произвольной полной системой вычетов по модулю $pq$. Рассмотрим множества
$$P_1=left{1,2,ldots ,frac{pq-1}{2}right},quad P_2=left{-1,-2,ldots ,-frac{pq-1}{2}right}$$
и несколько их подмножеств
$$S_2=left{bin P_1 Big| 1leqslant b_pleqslantfrac{p-1}{2}, -frac{q-1}{2}leqslant b_qleqslant -1right},quad
R_2=left{bin P_2 Big| 1leqslant b_pleqslantfrac{p-1}{2}, -frac{q-1}{2}leqslant b_qleqslant -1right},$$
$$S_3=left{bin P_1 Big| -frac{p-1}{2}leqslant b_pleqslant -1, 1leqslant b_qleqslantfrac{q-1}{2}right},quad
R_3=left{bin P_2 Big| -frac{p-1}{2}leqslant b_pleqslant -1, 1leqslant b_qleqslantfrac{q-1}{2}right},$$
$$S_4=left{bin P_1 Big| -frac{p-1}{2}leqslant b_pleqslant -1, -frac{q-1}{2}leqslant b_qleqslant -1right},quad
R_4=left{bin P_2 Big| -frac{p-1}{2}leqslant b_pleqslant -1, -frac{q-1}{2}leqslant b_qleqslant -1right},$$
$$T_1=left{bin P_1 Big| b_p=0, -frac{q-1}{2}leqslant b_qleqslant -1right},quad
T_2=left{bin P_1 Big| -frac{p-1}{2}leqslant b_pleqslant -1, b_q=0right}.$$
Так как объединение непересекающихся множеств $P_1$ и $P_2$ образует полную систему вычетов по модулю $pq$, то по вышесказанному ему можно поставить в соответствие множество всевозможных пар $(b_p,b_q)$, а значит объединение множеств $S_2$ и $R_2$ будет содержать все числа $b$, удовлетворяющие условиям $1leqslant b_pleqslantfrac{p-1}{2}, -frac{q-1}{2}leqslant b_qleqslant -1$, откуда
$$|S_2|+|R_2|=frac{p-1}{2}cdotfrac{q-1}{2}.$$
Но очевидное сопоставление $xlongleftrightarrow -x$ устанавливает взаимно однозначное соответствие между множествами $R_2$ и $S_3$. Поэтому $|R_2|=|S_3|$ и
$$|S_2|+|S_3|=frac{p-1}{2}cdotfrac{q-1}{2}.$$
Далее, объединение множеств $S_2, S_4$ и $T_1$ содержит все числа из $P_1$ с условием $-frac{q-1}{2}leqslant b_qleqslant -1$. Эти числа можно явно перечислить:
$$frac{q+1}{2},ldots ,q-1,q+frac{q+1}{2},ldots ,2q-1,ldots,frac{p-3}{2}cdot q+frac{q+1}{2},ldots ,frac{p-1}{2}cdot q-1.$$
Их количество равно $frac{p-1}{2}cdotfrac{q-1}{2}$, то есть
$$|S_2|+|S_4|+|T_1|=frac{p-1}{2}cdotfrac{q-1}{2}.$$
Аналогично $$|S_3|+|S_4|+|T_2|=frac{p-1}{2}cdotfrac{q-1}{2}.$$
Комбинируя три полученных равенства, находим
$$2|S_4|+|T_1|+|T_2|=frac{p-1}{2}cdotfrac{q-1}{2}.$$
Откуда $(-1)^{|T_1|+|T_2|}=(-1)^{frac{p-1}{2}cdotfrac{q-1}{2}}$, что равносильно
$$(-1)^{|T_1|}=(-1)^{|T_2|}(-1)^{frac{p-1}{2}cdotfrac{q-1}{2}}.$$
Остаётся заметить, что множество $T_2$ состоит в точности из тех чисел множества $left{q,2q,ldots ,frac{p-1}{2}qright}$, которые по модулю $p$ сравнимы с одним из чисел $-1,-2,ldots ,-frac{p-1}{2}$. Их количество есть в точности число $N$ из леммы Гаусса при $b=q$, так что по этой самой лемме
$$(-1)^{|T_2|}=left(frac{q}{p}right).$$
Аналогично $$(-1)^{|T_1|}=left(frac{p}{q}right).$$
При этом очевидно, что $(-1)^{frac{p-1}{2}cdotfrac{q-1}{2}}=-1$, если $pequiv qequiv -1pmod{4}$, и $(-1)^{frac{p-1}{2}cdotfrac{q-1}{2}}=1$ иначе.
Квадратичный закон взаимности доказан.
Вычисление символа Лежандра. Символ Якоби
Ещё вводя в рассмотрение символ Лежандра $left(frac{b}{p}right)$ мы установили, что он даёт полную информацию о разрешимости сравнения $x^2equiv bpmod{p}$, а именно
-
Если $left(frac{b}{p}right)=1$, то сравнение имеет два решения;
-
Если $left(frac{b}{p}right)=0$, то сравнение имеет одно решение;
-
Если $left(frac{b}{p}right)=-1$, то сравнение не имеет решений.
Это можно резюмировать утверждением, что данное сравнение имеет ровно $left(frac{b}{p}right)+1$ решение. Данное наблюдение можно распространить на произвольное квадратичное сравнение.
Пусть $p$ нечётное простое число и имеется сравнение $ax^2+bx+cequiv 0pmod{p}$, где $a,b,cinmathbb{Z}$ и $pnmid a$ (чтобы сравнение имело именно вторую, а не меньшую степень). Домножим обе части сравнения на взаимно простое с $p$ число $4a$. Это не повлияет на разрешимость и не изменит решения данного сравнения. Получим $4a^2x^2+4abx+4acequiv 0pmod{p}$. Выделяя полный квадрат и производя замену $y=2ax+b$, получаем
$$y^2equiv b^2-4acpmod{p}.$$
Полученное сравнение, как мы видели, имеет в точности $left(frac{b^2-4ac}{p}right)+1$ решений. Столько же решений будет и у исходного сравнения, так как замена $y=2ax+b$ взаимно однозначно отображает полную систему вычетов по модулю $p$ в таковую же.
Следовательно, для подсчёта числа решений квадратичного сравнения по нечётному простому модулю достаточно уметь вычислять символ Лежандра. Доказанных выше свойств этого символа вполне достаточно для эффективного его вычисления, но чтобы делать это максимально быстро удобно ввести также символ Якоби.
Пусть $P>1$ нечётное натуральное число, $P=p_1cdots p_s$ – его разложение на простые множители (возможно совпадающие, но все нечётные) и $Ainmathbb{Z}$. Тогда символ Якоби определяется так:
$$left(frac{A}{P}right)=left(frac{A}{p_1}right)cdots left(frac{A}{p_s}right).$$
Свойства символа Лежандра переносятся и на символ Якоби.
Пусть $P$ нечётное число, $A,Binmathbb{Z}$. Тогда
-
Если $Aequiv Bpmod{P}$, то $left(frac{A}{P}right)=left(frac{B}{P}right)$;
-
$left(frac{Acdot B}{P}right)=left(frac{A}{P}right)left(frac{B}{P}right)$;
-
Если $(P,B)=1$, то $left(frac{B^2}{P}right)=1$, в частности $left(frac{1}{P}right)=1$;
-
-
$left(frac{-1}{P}right)=1$, если $Pequiv 1pmod{4}$,
-
$left(frac{-1}{P}right)=-1$, если $Pequiv -1pmod{4}$;
-
-
-
$left(frac{2}{P}right)=1$, если $Pequivpm 1pmod{8}$,
-
$left(frac{2}{P}right)=-1$, если $Pequivpm 3pmod{8}$;
-
-
Пусть $P,Q$ нечётные числа, большие $1$, тогда
-
$left(frac{P}{Q}right)=-left(frac{Q}{P}right)$, если $Pequiv Qequiv -1pmod{4}$,
-
$left(frac{P}{Q}right)=left(frac{Q}{P}right)$ иначе.
-
Свойства с первого по третье напрямую следуют из определения символа Якоби и аналогичных свойств для символа Лежандра.
Для доказательства четвёртого свойства заметим, что произведение двух чисел, сравнимых с $-1$ по модулю $4$, будет сравнимо с $1$ по модулю $4$. Поэтому, если $Pequiv -1pmod{4}$, то в разложении $P=p_1cdots p_s$ количество простых, сравнимых с $-1$ по модулю $4$, нечётно. Но тогда и в произведении $left(frac{-1}{p_1}right)cdots left(frac{-1}{p_s}right)$ количество символов Лежандра, равных $-1$ будет нечётно, откуда $left(frac{-1}{P}right)=-1$. Если же $Pequiv 1pmod{4}$, то в разложении $P=p_1cdots p_s$ количество простых, сравнимых с $-1$ по модулю $4$, чётно, и $left(frac{-1}{P}right)=1$.
Для доказательства пятого свойства необходимо заметить, что произведение двух чисел, сравнимых с $pm 3$ по модулю $8$, даёт $pm 1$ по модулю $8$. Дальнейшие рассуждения аналогичны предыдущему пункту.
Для доказательства шестого свойства достаточно рассмотреть нетривиальный случай $(P,Q)=1$ и действовать аналогично, исследуя, чётно или нечётно количество простых, сравнимых с $-1$ по модулю $4$, в разложениях $P$ и $Q$.
Замечание 7. Символ Якоби $left(frac{A}{P}right)$ не даёт полной информации о разрешимости сравнения $x^2equiv Apmod{P}$. Разумеется, если $left(frac{A}{P}right)=-1$, то сравнение неразрешимо, но если символ Якоби принимает другие значения, то из этого нельзя сделать определённых выводов. Например, поскольку $15equiv -1pmod{8}$, то $left(frac{2}{15}right)=1$, однако сравнение $x^2equiv 2$ неразрешимо ни по модулю $3$, ни по модулю $5$, а следовательно оно не может быть разрешимо и по модулю $15$.
Поэтому главным предназначением символа Якоби является ускорение процедуры вычисления символа Лежандра. Пусть требуется определить количество решений сравнения
$$x^2-19x+1equiv 0pmod{1013}.$$
Легко убедиться (например с помощью решета Эратосфена), что $1013$ – простое число, а значит данное сравнение будет иметь $1+left(frac{19^2-4}{1013}right)=1+left(frac{357}{1013}right)$ решений. Находим
$$left(frac{357}{1013}right)=left(frac{1013}{357}right)=left(frac{-58}{357}right)=
left(frac{-1}{357}right)left(frac{2}{357}right)left(frac{29}{357}right)=-left(frac{29}{357}right)=-left(frac{357}{29}right)=-left(frac{9}{29}right)=-1.$$
Здесь мы последовательно применили шестое, первое, второе, четвёртое с пятым, снова шестое и, наконец, третье свойства символа Якоби. Мы имели право так действовать, не оглядываясь на то, что число $357$ является составным.
В итоге, получаем, что рассматриваемое сравнение не имеет решений.
Лемма Гензеля
Итак, для того, чтобы всё же определить разрешимость сравнения $x^2equiv Apmod{P}$ необходимо обладать большей информацией, нежели просто значение символа Якоби $left(frac{A}{P}right)$. Чтобы понять, что это за информация для начала рассмотрим сравнения вида $x^2equiv Apmod{p^k}$. Следующий результат описывает даже более полную ситуацию.
Лемма Гензеля. Пусть $p$ простое число, многочлен $f(x)$ имеет целые коэффициенты. Допустим имеется целое число $x_1$ такое, что $f(x_1)equiv 0pmod{p}$ и $f'(x_1)notequiv 0pmod{p}$, где $f'(x)$ – производная многочлена $f(x)$. Тогда для любого натурального числа $k$ в любой полной системе вычетов по модулю $p^k$ найдётся единственный элемент $x_k$ с условиями $x_kequiv x_1pmod{p}$ и $f(x_k)equiv 0pmod{p^k}$.
Прежде чем доказывать лемму Гензеля сформулируем следующий вспомогательный результат.
Лемма 5. Пусть $f(x)$ – многочлен степени $m$. Тогда
$$f(x+a)=f(x)+af'(x)+a^2frac{f»(x)}{2}+ldots +a^mfrac{f^{(m)}(x)}{m!}.$$
Доказательство достаточно провести для многочлена вида $f(x)=x^n$ ввиду линейности. Для такого многочлена необходимое равенство приобретает вид
$$(x+a)^n=x^n+nx^{n-1}a+frac{n(n-1)}{2}x^{n-2}a^2+ldots +frac{n(n-1)cdots 2cdot 1}{n!}a^n,$$
так что оно представляет из себя в точности формулу бинома Ньютона. Лемма 5 доказана.
Доказательство леммы Гензеля проведём индукцией по $k$. При $k=1$ в произвольной полной системе вычетов по модулю $p$ найдётся единственный элемент, сравнимый по этому же модулю с $x_1$, а сравнение $f(x_1)equiv 0pmod{p}$ выполнено по условию. Пусть теперь $k>1$ и для $k-1$ утверждение верно. Мы ищем элемент $x_k$ с условиями $x_kequiv x_1pmod{p}$ и $f(x_k)equiv 0pmod{p^k}$. Но для этого элемента будет тогда также выполнено $f(x_k)equiv 0pmod{p^{k-1}}$. Ввиду единственности решения этого сравнения по модулю $p^{k-1}$ будем иметь $x_kequiv x_{k-1}pmod{p^{k-1}}$. Поэтому $x_k$ следует искать в виде $x_k=x_{k-1}+tcdot p^{k-1}$ с некоторым целым числом $t$. В приведённой системе вычетов по модулю $p^{k}$ найдётся ровно $p$ элементов такого вида, причём соответствующие им значения $t$ составят полную систему вычетов по модулю $p$. Условие $x_kequiv x_1pmod{p}$ будет выполнено автоматически. Для проверки условия $f(x_k)equiv 0pmod{p^k}$ воспользуемся леммой 5 и запишем
$$f(x_k)=f(x_{k-1}+tcdot p^{k-1})=f(x_{k-1})+tcdot p^{k-1}cdot f'(x_{k-1})+ldotsequiv
f(x_{k-1})+tcdot p^{k-1}cdot f'(x_{k-1})pmod{p^k}.$$
Таким образом, должно быть выполнено
$$f(x_{k-1})+tcdot p^{k-1}cdot f'(x_{k-1})equiv 0pmod{p^k}.$$
Так как $f(x_{k-1})equiv 0pmod{p^{k-1}}$, то обе части и модуль этого сравнения можно поделить на $p^{k-1}$. Получим
$$frac{f(x_{k-1})}{p^{k-1}}+tcdot f'(x_{k-1})equiv 0pmod{p}.$$ Поскольку $f'(x_{k-1})equiv f'(x_1)notequiv 0pmod{p}$, полученное сравнение относительно $t$ имеет единственное решение. А следовательно и $x_k$ существует и единственно. Лемма Гензеля доказана.
Применим лемму Гензеля для решения сравнения $x^2equiv Apmod{p^k}$, где $p$ – нечётное простое число.
Если сравнение $x^2equiv Apmod{p}$ неразрешимо, то и наше сравнение не может иметь решений при любом натуральном $k$. Если сравнение $x^2equiv Apmod{p}$ имеет единственное решение, то $Aequiv 0pmod{p}$, а значит и решением будет $x_1equiv 0pmod{p}$. В этом случае лемма Гензеля неприменима, так как при $f(x)=x^2$ будем иметь $f'(x)=2x$, но $2x_1equiv 0pmod{p}$. Однако этот случай достаточно прост, чтобы уделять ему внимание. Пусть теперь сравнение $x^2equiv Apmod{p}$ имеет два различных решения $xequivpm x_1pmod{p}$. Очевидно $2x_1notequiv 0pmod{p}$ и лемма Гензеля может быть применена. Из неё следует, что для каждого натурального $k$ будет иметься ровно два различных решения сравнения $x^2equiv Apmod{p^k}$.
Для полноты картины изучим случай $p=2$, при котором лемма Гензеля для сравнения $x^2equiv Apmod{2^k}$ неприменима, поскольку $2x_1equiv 0pmod{2}$ независимо от значения $x_1$. По модулям $2$ и $4$ ситуация прозрачна.
Предложение 4. Пусть $Ainmathbb{Z}$ нечётно, $kinmathbb{N}, kgeqslant 3$. Тогда сравнение $x^2equiv Apmod{2^k}$ имеет $4$ решения, если $Aequiv 1pmod{8}$, и неразрешимо иначе.
Доказательство. Проведём индукцию по $k$. При $k=3$ четыре числа $pm 1,pm 3$ удовлетворяют сравнению $x^2equiv 1pmod{8}$, а так как они образуют приведённую систему вычетов по модулю $8$, то это все решения данного сравнения. Из этого же следует, что сравнения $x^2equiv Apmod{8}$ неразрешимы при $A=-1,pm 3$.
Пусть теперь для некоторого $kgeqslant 3$ предложение верно. Выберем некоторое $Aequiv 1pmod{8}$. По предположению индукции найдётся некоторое нечётное число $x_k$ такое, что $x_k^2equiv Apmod{2^k}$, то есть $x_k^2=A+ccdot 2^k$. Если теперь $c$ чётно, то $x_k^2equiv Apmod{2^{k+1}}$. Если же $c$ нечётно, то $(x_k+2^{k-1})^2equiv Apmod{2^{k+1}}$, то есть сравнение $x^2equiv Apmod{2^{k+1}}$ будет иметь некоторое решение $x_{k+1}$. Но вместе с ним оно будет иметь по крайней мере четыре решения $pm x_{k+1}pm 2^k$. C другой стороны, поскольку в приведённой системе вычетов по модулю $2^{k+1}$ ровно каждое четвёртое число сравнимо с $1$ по модулю $8$, то, взяв для каждого из этих чисел по четыре решения соответствующего сравнения, мы уже исчерпаем всю приведённую систему вычетов по модулю $2^{k+1}$, а значит более четырёх решений ни у одного из этих сравнений быть не может. Более того, не может быть решений и у сравнений $x^2equiv Apmod{2^{k+1}}$ при $Anotequiv 1pmod{8}$. Предложение 4 доказано.
Замечание 8. Пусть многочлен $f(x)$ имеет целые коэффициенты, и требуется решить сравнение $f(x)equiv 0pmod{p_1^{k_1}cdots p_m^{k_m}}$, где одно из $p_i$ может быть и чётным. Для этого нужно найти решения сравнений $f(x)equiv 0pmod{p_i^{k_i}}$ при всех $i=1,ldots ,m$, и если хотя бы одно из них неразрешимо, то и у исходного сравнения решений нет. Если же каждое из указанных сравнений имеет, скажем, $T_i$ различных решений вида $xequiv x_1pmod{p_1^{k_1}},ldots ,xequiv x_mpmod{p_m^{k_m}}$, то, решая такую систему сравнений (с помощью китайской теоремы об остатках), мы получим решение исходного сравнения по модулю $P$. Всего, действуя таким образом, найдётся $T_1cdots T_m$ решений исходного сравнения.
Из всего вышесказанного видно, что если $P=p_1^{k_1}cdots p_m^{k_m}$, сравнение $x^2equiv Apmod{P}$ будет разрешимо тогда и только тогда, когда разрешимо каждое из сравнений $x^2equiv Apmod{p_i}, i=1,ldots ,s$. При этом, если, скажем, $p_1=2$, то по модулю $p_1^{k_1}$ количество решений определяется с учётом предложения 4, а если $p_i^{k_i}$ – число нечётное, то в соответствии с рассуждениями, идущими после леммы Гензеля. При этом случаи $p_i|A$ нужно аккуратно разбирать индивидуально.
Первообразные корни
Пусть $m$ натуральное число. Если целое число $a$ не взаимно просто с $m$, то сравнение $$a^dequiv 1pmod{m}$$ невозможно ни при каком натуральном $d$, так как левая часть сравнения и модуль будут делиться на одно и то же отличное от $1$ натуральное число. Если же $(a,m)=1$, то натуральное число $d$, с которым это сравнение будет выполняться, обязательно найдётся. Например по теореме Эйлера подойдёт $d=varphi(m)$.
Наименьшее натуральное $d$, с которым выполняется сравнение $a^dequiv 1pmod{m}$, называется показателем числа $a$ по модулю $m$. Из теоремы Эйлера видно, что показатель любого числа не превосходит $varphi(m)$, но он может быть и меньше этого числа. Например, показатель числа $2$ по модулю $7$ равен $3$, поскольку $2^3equiv 1pmod{7}$ и $2^1notequiv 1pmod{7}, 2^2notequiv 1pmod{7}$. При этом $varphi(7)=6$.
Но если всё же показатель числа $a$ оказался равен $varphi(m)$, то это число $a$ называется первообразным корнем по модулю $m$. Например, $3^1notequiv 1pmod{7}, 3^2notequiv 1pmod{7}, 3^3notequiv 1pmod{7}, 3^4notequiv 1pmod{7}, 3^5notequiv 1pmod{7}$. С другой стороны, очевидно, что $3^6equiv 1pmod{7}$, а значит $3$ является первообразным корнем по модулю $7$.
Предложение 5. Пусть $d$ – показатель числа $a$ по модулю $m$ и также с некоторым целым числом $n$ выполняется сравнение $a^nequiv 1pmod{m}$. Тогда $d|n$.
Доказательство. От противного, пусть $n=qd+r, 0<r<d$. Тогда $a^r=a^{n-qd}=a^n(a^d)^{-q}equiv 1pmod{m}$, причём $0<r<d$, но это противоречит тому, что $d$ является показателем числа $a$. Предложение 5 доказано.
Следствие 11. Пусть $d$ – показатель числа $a$ по модулю $m$. Тогда $d|varphi(m)$.
Доказательство. Рассуждения в начале данного параграфа показывают, что наличие у числа $a$ показателя означает, что $(a,m)=1$, а значит применима теорема Эйлера и $a^{varphi(m)}equiv 1pmod{m}$. По предложению 5 теперь $d|varphi(m)$. Следствие 11 доказано.
Следствие 12. Если $(a,m)=1$ и $d$ – показатель числа $a$ по модулю $m$, то $a^kequiv a^npmod{m}$ тогда и только тогда, когда $kequiv npmod{d}$.
Доказательство. Если $kequiv npmod{d}$, то с некоторым $s$ будет $k=n+sd$. Тогда $a^k=a^n(a^d)^sequiv a^npmod{m}$. Обратно, если $a^kequiv a^npmod{m}$, то $a^n(a^{k-n}-1)equiv 0pmod{m}$, и так как $(a,m)=1$, то $a^{k-n}equiv 1pmod{m}$, откуда по предложению 5 $d|k-n$, то есть $kequiv npmod{d}$. Следствие 12 доказано.
Следствие 13. Если $a$ – первообразный корень по модулю $m$, то числа $a^0,a^1,ldots ,a^{varphi(m)-1}$ образуют приведённую систему вычетов по модулю $m$.
Доказательство. По следствию 12, если $a^kequiv a^npmod{m}, 0leqslant n<k<varphi(m)$, то $k-n$ делится на показатель числа $a$, что невозможно, так как по определению первообразного корня показателем числа $a$ является $varphi(m)$, но $0<k-n<varphi(m)$. Значит мы имеем $varphi(m)$ попарно не сравнимых по модулю $m$ чисел, каждое из которых взаимно просто с $m$. Очевидно они образуют приведённую систему вычетов по модулю $m$. Следствие 13 доказано.
Существование первообразных корней по простому модулю
Пусть $p$ простое число. Согласно следствию 13 показателем какого бы то ни было числа может быть только натуральное число $d$, делящее $p-1$. Допустим найдётся какое-то число $a$, имеющее данный показатель $d$. Тогда каждое из чисел $a^0,a^1,ldots ,a^{d-1}$ является решением сравнения $x^d-1equiv 0pmod{p}$, которое не может иметь более $d$ решений по теореме Лагранжа. С другой стороны, по аналогичным с доказательством следствия 13 рассуждениям все эти числа попарно не сравнимы по модулю $p$, а значит это все решения указанного сравнения и только среди них могут присутствовать числа, имеющие показатель $d$. Но если $(k,d)=s$, то $(a^k)^{d/s}equiv 1pmod{p}$, поэтому показатель $d$ могут иметь только такие числа $a^k$, для которых $(k,d)=1$, а таких чисел всего $varphi(d)$. Следовательно, показатель $d$ могут иметь не более чем $varphi(d)$ некоторых чисел. Если мы обозначим за $chi(d)$ количество чисел, имеющих по модулю $p$ показатель $d$, то можно записать $$0leqslantchi(d)leqslantvarphi(d).$$
Поскольку каждое из чисел $1,2,ldots ,p-1$ имеет некоторый показатель, то будем иметь
$$sum_{d|p-1}chi(d)=p-1.$$
Но для функции Эйлера мы также выводили соотношение
$$sum_{d|p-1}varphi(d)=p-1.$$
Из этих двух тождеств и выписанного чуть выше неравенства следует, что для каждого $d$, делящего $p-1$, выполнено $chi(d)=varphi(d)$, в том числе и $chi(p-1)=varphi(p-1)$, то есть существуют числа, имеющие показателем $p-1$. По определению это и означает, что существуют первообразные корни по модулю $p$. Причём их найдётся ровно $varphi(p-1)$ штук (не сравнимых друг с другом по модулю $p$).
Первообразные корни по модулю $2^{k}$
По предыдущему параграфу существует первообразный корень по модулю $2$. Им является, например, число $1$.
По модулю $2^2$ также можно предъявить первообразный корень, скажем $3$.
По модулю же $2^3$ не может существовать первообразный корень, так как мы видели, что любое нечётное число $a$ удовлетворяет сравнению $a^2equiv 1pmod{8}$.
Покажем индукцией по $k$, что для любого $kgeqslant 3$ и нечётного $a$ будет выполнено
$$a^{2^{k-2}}equiv 1pmod{2^k},$$
то есть при таких $k$ по модулю $2^k$ первообразных корней нет.
Действительно, при $k=3$ это верно. Если это верно при некотором $kgeqslant 3$, то можно записать
$$a^{2^{k-1}}-1=(a^{2^{k-2}}-1)(a^{2^{k-2}}+1).$$ По предположению индукции первая из скобок в получившемся произведении делится на $2^k$, а вторая делится на $2$. Тогда всё произведение делится на $2^{k+1}$ и требуемое сравнение выполняется для $k+1$. Доказательство завершено.
Отсутствие первообразных корней по модулям, отличным от $2, 4, p^{k}$ и $2p^{k}$ с нечётным простым $p$
Пусть $m=p_1^{k_1}cdots p_s^{k_s}$. Покажем, что при $N=[varphi(p_1^{k_1}),ldots,varphi(p_s^{k_s})]$ будем иметь $a^Nequiv 1pmod{m}$ для любого взаимно простого с $m$ числа $a$. Действительно, число $a$ будет также взаимно просто с каждым из чисел $p_i^{k_i}$ и по теореме Эйлера будем иметь $a^{varphi(p_i^{k_i})}equiv 1pmod{p_i^{k_i}}$. А так как $varphi(p_i^{k_i})|N$, то для каждого $i=1,ldots,s$ будет выполнено $a^Nequiv 1pmod{p_i^{k_i}}$. По китайской теореме об остатках из этой системы сравнений будет следовать $a^Nequiv 1pmod{p_1^{k_1}cdots p_s^{k_s}}$, что и требовалось.
Заметим, что когда $m=p_1^{k_1}cdots p_s^{k_s}$ не имеет вид $2^k, p^{k}$ или $2p^{k}$ с нечётным простым $p$, то среди чисел, от которых берётся наименьшее общее кратное, обязательно будет несколько чётных чисел, и
$$N=[varphi(p_1^{k_1}),ldots,varphi(p_s^{k_s})]<varphi(p_1^{k_1})cdotsvarphi(p_s^{k_s})=varphi(m),$$
а это означает что по модулю $m$ не может быть первообразных корней.
При этом отсутствие первообразных корней по модулю $2^k$, где $k>2$, уже показано.
Существование первообразных корней по модулям $p^{k}$ и $2p^{k}$ с нечётным простым $p$
При $k=1$ существование первообразного корня нами уже показано.
Теорема 9. Пусть $g$ – первообразный корень по модулю нечётного простого числа $p$. Если $g^{p-1}notequiv 1pmod{p^2}$, то $g$ будет первообразным корнем по модулю $p^k$ при любом натуральном $k$.
Доказательство. Покажем индукцией по $k$, что $g^{p^{k-1}(p-1)}notequiv 1pmod{p^{k+1}}$ и что $g$ будет первообразным корнем по модулю $p^k$. По условию теоремы оба эти утверждения выполняются при $k=1$. Пусть они выполняются для некоторого $k$. Покажем, что будут они выполнены и для $k+1$.
Поскольку $g^{p^{k-1}(p-1)}notequiv 1pmod{p^{k+1}}$, но по теореме Эйлера $g^{p^{k-1}(p-1)}equiv 1pmod{p^{k}}$, то можно записать
$g^{p^{k-1}(p-1)}=1+cp^{k}$, где $c$ не делится на $p$. Возведём обе части полученного равенства в степень $p$ и, применив формулу бинома Ньютона, увидим, что $g^{p^{k}(p-1)}=1+cp^{k+1}+c_1p^{k+2}$, откуда $g^{p^{k}(p-1)}notequiv 1pmod{p^{k+2}}$.
Пусть теперь $g$ не первообразный корень по модулю $p^{k+1}$. Тогда найдётся $d$, меньшее чем $varphi(p^{k+1})$, такое что $g^dequiv 1pmod{p^{k+1}}$. По предложению 5 число $d$ является делителем $varphi(p^{k+1})=p^{k}(p-1)$. Но так как $g$ – первообразный корень по модулю $p^{k}$, то $dgeqslantvarphi(p^{k})=p^{k-1}(p-1)$, а из того, что $g^{p^{k-1}(p-1)}notequiv 1pmod{p^{k+1}}$ следует $dneq p^{k-1}(p-1)$. Значит $d=p^kd’$, где $d’|p-1, d'<p-1$. Так как $g^dequiv 1pmod{p^{k+1}}$, то и $g^dequiv 1pmod{p}$. Получаем
$$g^d=(g^{p^k})^{d’}equiv g^{d’}equiv 1pmod{p}.$$
Это противоречит тому, что $g$ – первообразный корень по модулю $p$, поскольку $d'<p-1$. При этом тот факт, что $g^{p^k}equiv gpmod{p}$ следует из $k$-кратного применения теоремы Ферма. Теорема 9 доказана.
Покажем как найти первообразный корень, удовлетворяющий условию теоремы 9. Если выбрать произвольный первообразный корень $g$ по модулю $p$, то либо $g^{p-1}notequiv 1pmod{p^2}$, и тогда $g$ удовлетворяет всем условиям теоремы, либо $g^{p-1}equiv 1pmod{p^2}$, но тогда рассмотрим число $g_1=g+p$. Очевидно, что это также будет первообразный корень по модулю $p$. Однако по формуле бинома Ньютона $$g_1^{p-1}=(g+p)^{p-1}=g^{p-1}+(p-1)pg^{p-2}+cp^2$$ с некоторым числом $c$. Тогда $g_1^{p-1}equiv 1-pg^{p-2}notequiv 1pmod{p^2}$, так как $p$ не делит первообразный корень $g$. Таким образом, достаточно взять произвольный первообразный корень $g$ по модулю $p$ и если $g^{p-1}notequiv 1pmod{p^2}$, то $g$ удовлетворяет всем условиям теоремы 9, а иначе $g+p$ удовлетворяет всем условиям теоремы 9.
Теорема 10. Пусть $g$ – первообразный корень по модулю $p^k$ для некоторого нечётного простого числа $p$. Если $g$ нечётное число, то $g$ будет первообразным корнем по модулю $2p^k$.
Доказательство. Так как $g$ нечётное число, то оно взаимно просто с $2p^k$. Если оно не первообразный корень по этому модулю, то существует натуральное число $d$, меньшее чем $varphi(2p^{k})=p^{k-1}(p-1)$, такое что $g^dequiv 1pmod{2p^{k}}$. Но тогда и $g^dequiv 1pmod{p^{k}}$. Это противоречит тому, что $g$ – первообразный корень по модулю $p^k$, поскольку $d<p^{k-1}(p-1)=varphi(p^{k})$. Теорема 10 доказана.
Как видно из теорем 9 и 10, если $g$ – первообразный корень по модулю $p^2$, то это же число будет первообразным корнем и по модулю $p^k$ при любом натуральном $k$, а если $g$ нечётно, то и по модулю $2p^k$. При этом, если $g$ – чётное число, то $g+p^2$ будет уже нечётным и при этом останется первообразным корнем по модулю $p^2$.
Таким образом, чтобы для нечётного простого числа $p$ предъявить первообразный корень по модулю $2p^k$, нужно найти первообразный корень $g$ по модулю $p^2$, и если $g$ нечётно, то это и есть искомый первообразный корень, а иначе это будет $g+p^2$.
Нахождение первообразных корней
Теорема 11. Пусть $m$ натуральное число и $g$ целое, взаимно простое с $m$ число. Пусть $varphi(m)=q_1^{k_1}cdots q_s^{k_s}$ – разложение на простые множители. Тогда, если для каждого $i=1,ldots ,s$ выполнено $g^{varphi(m)/q_i}notequiv 1pmod{m}$, то $g$ – первообразный корень по модулю $m$.
Доказательство. Если $g$ – не первообразный корень по модулю $m$, то найдётся натуральное число $d$, меньшее чем $varphi(m)$, такое что $g^dequiv 1pmod{m}$. По предложению 5 $d|varphi(m)$, а значит $d=q_1^{n_1}cdots q_s^{n_s}$, где $0leqslant n_ileqslant k_i$ при всех $i=1,ldots ,s$, причём при некотором $j$ будет $n_jleqslant k_j-1$. Но тогда $d|varphi(m)/q_j$ и $g^{varphi(m)/q_j}equiv 1pmod{m}$. Противоречие. Теорема 11 доказана.
Отыскивать первообразные корни с помощью теоремы 11 рекомендуется только по простому модулю $p$, после чего разумнее находить (если это требуется) первообразные корни по модулям $p^{k}$ и $2p^{k}$, пользуясь процедурами, описанными в предыдущем параграфе.
Итак, требуется
-
разложить на простые множители число $p-1=2^kq_1^{k_1}cdots q_s^{k_s}$
-
выбрать какое-нибудь число $g$ (кандидата в первообразные корни), причём необходимо $pnmid g$
-
убедиться, что символ Лежандра $displaystyleleft(frac{g}{p}right)=-1$
-
проверять, выполняется ли условие $g^{p-1/q_i}notequiv 1pmod{p}$ для каждого $i=1,ldots ,s$
Если все проверки пройдены успешно, то $g$ – первообразный корень по модулю $p$.
Условие $displaystyleleft(frac{g}{p}right)=-1$ является проверкой эквивалентного ему условия $g^{p-1/2}notequiv 1pmod{p}$. Дело в том, что по критерию Эйлера $g^{p-1/2}equiv displaystyleleft(frac{g}{p}right)pmod{p}$, а ненулевой символ Лежандра, если он не сравним с $1$, должен равняться $-1$.
В качестве первого кандидата имеет смысл брать $g=2$. Нет необходимости рассматривать заведомые квадратичные вычеты, например $4$ или вообще какие бы то ни было квадраты. Число $-1$ является первообразным корнем по модулям $2, 3, 4, 6$ и ни по каким другим модулям его рассматривать не нужно, поскольку $(-1)^2equiv 1pmod{m}$ при любом $m$.
Пример 6. Найти первообразный корень по модулю $31$.
Решение. Разложим на простые множители $31-1=2cdot 3cdot 5$. Не будем брать в качестве кандидата число $2$, так как $31equiv -1pmod{8}$ и $displaystyleleft(frac{2}{31}right)=1$. Зато $displaystyleleft(frac{-2}{31}right)=-1$. Но $(-2)^{30/3}=(-2)^{10}=(-32)^2equiv 1pmod{31}$.
Возьмём $3$ в качестве кандидата. Имеем
$$left(frac{3}{31}right)=-left(frac{31}{3}right)=-1.$$ Кроме того
$$3^{30/3}=(3^3)^3cdot 3equiv (-4)^3cdot 3equiv -64cdot 3equiv -6notequiv 1pmod{31}$$
и
$$ 3^{30/5}=(3^3)^2equiv (-4)^2equiv 16notequiv 1pmod{31}.$$
Значит $3$ – первообразный корень по модулю $31$.
Пример 7. Найти первообразный корень по модулю $1637$.
Решение. Разложим на простые множители $1637-1=2^2cdot 409$. Возьмём 2 в качестве кандидата. Так как $1637equiv 5pmod{8}$, то $displaystyleleft(frac{2}{1637}right)=-1$. Кроме того
$2^{1636/409}=16notequiv 1pmod{1637}$. Значит $2$ – первообразный корень по модулю $1637$.
Пример 8. Найти первообразный корень по модулю $2cdot 23^{19}$.
Решение. Достаточно найти нечётный первообразный корень по модулю $23^2$. Для начала найдём первообразный корень по модулю $23$. Разложим на простые множители $23-1=2cdot 11$. Не будем брать в качестве кандидата число $2$, так как $23equiv -1pmod{8}$ и $displaystyleleft(frac{2}{23}right)=1$. Зато $displaystyleleft(frac{-2}{23}right)=-1$. Кроме того
$(-2)^{22/11}=4notequiv 1pmod{23}$. Значит $-2$ – первообразный корень по модулю $23$.
Теперь проверим, что $(-2)^{22}notequiv 1pmod{23^2}$. Это действительно так, поскольку
$$(-2)^{22}-1=2^{22}-1=(2^{11}-1)(2^{11}+1)=2047cdot 2049,$$ но $2047=23cdot 89$, а значит, во-первых, $23$ не делит $2049$, а во-вторых, $23^2$ не делит $(-2)^{22}-1$. Это означает, что $-2$ является первообразным корнем и по модулю $23^2$. Но тогда число $23^2-2=527$ будет нечётным первообразным корнем по модулю $23^2$, а значит и по модулю $2cdot 23^{19}$.
Решение сравнений при помощи первообразных корней
Пользуясь следствием 13 можно решать сравнения некоторого вида. Допустим необходимо найти все решения сравнения
$$x^{17}equiv 5pmod{31}.$$
Мы знаем, что $3$ – первообразный корень по модулю $31$. Все его степени от нулевой до двадцать девятой образуют приведённую систему вычетов по модулю $31$ (всего в ней $varphi(31)=30$ элементов). Находим $3^5=243equiv -5pmod{31}$, следовательно $5equiv 3^{20}pmod{31}$.
Это связано с тем, что для любого первообразного корня $g$ по любому простому модулю $p$ выполнено $-1equiv g^{p-1/2}$. В этом легко убедиться, ведь для первообразного корня всегда выполнено $displaystyleleft(frac{g}{p}right)=-1$, а $displaystyleleft(frac{g}{p}right)equiv g^{p-1/2}pmod{p}$ по критерию Эйлера. При этом ни в какой другой степени от $0$ до $p-2$ первообразный корень не даст $-1$, поскольку по следствию 13 все его степени попарно не сравнимы по модулю $p$.
Положим теперь $xequiv 3^ypmod{31}$. Мы можем это сделать, так как из самого условия задачи очевидно, что $x$ не делится на $31$, а значит сравним с одной (и только одной) из степеней первообразного корня (по следствию 13). Исходное сравнение теперь перепишется в виде
$$ 3^{17y}equiv 3^{20}pmod{31}.$$
По следствию 12 это равносильно сравнению уже по модулю $varphi(31)=30$
$$17yequiv 20pmod{30}.$$ Решая это сравнение, находим $yequiv 10pmod{30}$, откуда $xequiv 3^yequiv -6pmod{31}$.