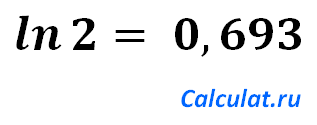Как найти натуральный логарифм онлайн - Исправление недочетов и поиск решений вместе с Examum.ru

Калькулятор натуральных логарифмов поможет найти логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,72.

Обозначение натурального логарифма

Для обозначения натурального логарифма существует несколько способов:

ln
log_e

Так же возможно написание прописными буквами.

Что такое натуральный логарифм

Натуральный логарифм

Понятие натурального логарифма лучше проиллюстрировать примером. Например, натуральный логарифм числа 2 равен 0,693147180 потому, что

e^0,693147180 = 2

Здесь e — основание натурального логарифма.

e =2,718281828

Таким образом натуральный логарифм — это степень, в которую нужно возвести число e для получения исходного числа, логарифм которого мы ищем. Вычисление натурального логарифма несложная задача и наш калькулятор поможет с расчетом.

Натуральный логарифм нуля не существует. Для чисел меньше единицы натуральный логарифм отрицательный.

Таблица натуральных логарифмов некоторых чисел

x	ln x
1	0
2	0,693147
3	1,098612
4	1,386294
5	1,609438
6	1,791759
7	1,94591
8	2,079442
9	2,197225
10	2,302585
100	4,60517
1000	6,907755
10000	9,21034
100000	11,51293

Ваша оценка

[Оценок: 285 Средняя: 2.8]

Калькулятор натуральных логарифмов Автор admin средний рейтинг 2.8/5 — 285 рейтинги пользователей

Источник

Натуральный логарифм

Натуральный логарифм – это логарифм по основанию числа Эйлера e ≐ 2,718282.

График

натуральный логарифм

x
y = ln x

2,72
e1
1

7,39
e 2
2

1,00
e0

$$
begin{aligned}
& e ≐ 2,718282 \ \
& ln x = log_{e} x \ \
& y = ln x Longleftrightarrow x = e^y
end{aligned}
$$

Калькулятор

Формулы

натуральный логарифм

$$
begin{aligned}
& e ≐ 2,718282 \ \
& ln x = log_{e} x
end{aligned}
$$

$$ y = ln x Longleftrightarrow x = e^y $$

$$
begin{aligned}
& ln x = frac{log_a x}{log_a e} = frac{log x}{log e} \ \
& ln x = frac{1}{log_x e}
end{aligned}
$$

$$
begin{aligned}
& lnleft(xcdot zright) = ln x + ln z \ \
& lnleft(frac{x}{z}right) = ln x — ln z
end{aligned}
$$

$$
begin{aligned}
& ln 1 = 0 \ \
& ln e = 1
end{aligned}
$$

$$
begin{aligned}
& ln x^r = rcdotln x \ \
& ln e^r = r \ \
& e^{ln x} = ln e^x = x
end{aligned}
$$

Calculat.org

Если у Вас имеются какие-либо предложения или замечания, мы будем рады узнать о них.

info@calculat.org

На других языках

При предоставлении услуг веб-сайт «Calculat.org» использует файлы куки.

Источник

Существование натурального логарифма обусловлено тем, что он возникает как самостоятельная единица при расчете площади под кривой на графике функции 1/x от 1 до числа a, от которого считается натуральный логарифм, иначе говоря, при возникновении интегралов. Натуральным логарифмом числа называется логарифм этого числа по основанию e, равному приблизительно e≈2,71828182845904523536.
lna=log_ea

AC	7	8	9	←
C	4	5	6	÷
%	1	2	3	×
x^y	.	0	=	—
x²	√	(	)	+

Среди прочего стоит отметить, что натуральный логарифм самого числа e равен единице, поскольку любое число в первой степени равно самому себе, а натуральный логарифм единицы равен нулю.

lne=1
ln1=0

Онлайн калькулятор натурального логарифма считает значения любых натуральных логарифмов от действительных чисел.

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Источник

Натуральный логарифм числа (ln) – это логарифм числа относительно основания экспоненциальной функции e (экспонента). В математике, е-это постоянная, равная 2,71828 и также является основой натурального логарифма. В этой статье мы рассмотрим, что такое натуральный логарифм числа и как он используется в различных областях науки и техники.

Применение натурального логарифма

Натуральный логарифм широко используется в математике, физике, статистике, экономике и инженерии. Он может быть использован для решения различных задач, таких как вычисление процентного изменения, моделирование роста популяции и оценки вероятностей. Кроме того, натуральный логарифм используется в теории вероятностей и статистике для нахождения вероятностей и оценки параметров в распределениях вероятностей.

Свойства натурального логарифма

Натуральный логарифм числа имеет несколько свойств, которые делают его полезным инструментом для решения задач. Одно из самых важных свойств натурального логарифма – это то, что он может быть использован для нахождения процентного изменения. Например, если вам нужно вычислить на сколько процентов увеличится число 50, если к нему добавить 10, то можно использовать формулу: ln(60/50)=0,1823, где 60 – это новое значение числа, 50 – старое значение числа. Таким образом, процентное изменение будет равно 18,23%.

Заключение

Натуральный логарифм числа – это важный инструмент для решения задач в различных областях науки и техники. Он может быть использован для вычисления процентного изменения, моделирования роста популяции и оценки вероятностей. Кроме того, он имеет несколько свойств, которые делают его полезным инструментом для решения задач. Если вы хотите узнать больше о натуральном логарифме числа, обратитесь к учебникам по математике или статистике.

#Калькуляторы #Логарифм #Математика

Источник

Натуральный логарифм

Логарифм, взятый по основанию e, носит название — натуральный логарифм. Часто такие логарифмы называют Неперовыми, что неверно.

Натуральные логарифмы принято обозначать так: lnN. Соответсвенно знак ln есть сокращение слов logarithm natural — натуральный логарифм

[ log_e (N) = ln N ]

Вычислить, найти натуральный логарифм

N (число)

Вычислить

нажмите кнопку для расчета

Натуральный логарифм	стр. 93

Источник