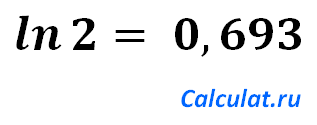Один из способов найти натуральный логарифм дроби — сначала преобразовать дробь в десятичную форму, а затем взять натуральное логарифм. Однако, если дробь содержит переменную, этот метод не будет работать. Когда вы натолкнетесь на натуральный логарифм дроби с х в знаменателе, обратитесь к свойствам логарифмов, чтобы упростить выражение. Используйте свойство, связанное с делением: log (x / y) = log (x) — log (y).
-
Если ваш натуральный логарифм является частью алгебраического уравнения, решите уравнение, используя значение натурального логарифма. Например, если у вас есть уравнение 5 = ln (5 / x), подключите 1.61 — ln (x): 5 = 1.61 — ln (x). Переставьте уравнение, чтобы получить ln (x) = -3, 39. Поднимите е в силу обеих сторон: е ^ = е ^ 3.39. Повышение e до степени ln (x) приводит к x, поэтому x = e ^ 3.39 = 29.7.
Перепишите натуральный логарифм дроби как натуральный логарифм числителя минус натуральный логарифм знаменателя. Если ваша проблема, например, ln (5 / x), перепишите его как ln (5) — ln (x).
Возьмите натуральный логарифм числителя, используя научный калькулятор. Например, ln (5) = 1, 61.
Запишите ответ, используя рассчитанное значение. Например, ln (5 / x) = 1, 61 — ln (x).
подсказки
One way to find the natural logarithm of a fraction is to first convert the fraction to decimal form, then take the natural log. If the fraction includes a variable, however, this method won’t work. When you come across the natural log of a fraction with x in the denominator, turn to the properties of logarithms to simplify the expression. Use the property related to division: log(x/y) = log(x) — log(y).
-
If your natural log is part of an algebraic equation, solve the equation using the value of the natural log. For example, if you have the equation 5 = ln(5/x), plug in 1.61 — ln(x): 5 = 1.61 — ln(x). Rearrange the equation to get ln(x) = -3.39. Raise e to the power of both sides: e^[ln(x)] = e^3.39. Raising e to the power of ln(x) results in x, so x = e^3.39 = 29.7.
Rewrite the natural log of the fraction as the natural log of the numerator minus the natural log of the denominator. If your problem is ln(5/x), for example, rewrite it as ln(5) — ln(x).
Take the natural log of the numerator using a scientific calculator. For example, ln(5) = 1.61.
Record the answer using your calculated value. For example, ln(5/x) = 1.61 — ln(x).
Tips
Логарифмом положительного числа (c) по основанию (a) ((a>0, aneq1)) называется показатель степени (b), в которую надо возвести основание (a), чтобы получить число (c) ((c>0)), т.е.
(a^{b}=c) (Leftrightarrow) (log_{a}{c}=b)
Объясним проще. Например, (log_{2}{8}) равен степени, в которую надо возвести (2), чтоб получить (8). Отсюда понятно, что (log_{2}{8}=3).
|
Примеры: |
(log_{5}{25}=2) |
т.к. (5^{2}=25) |
||
|
(log_{3}{81}=4) |
т.к. (3^{4}=81) |
|||
|
(log_{2})(frac{1}{32})(=-5) |
т.к. (2^{-5}=)(frac{1}{32}) |
Аргумент и основание логарифма
Любой логарифм имеет следующую «анатомию»:

Аргумент логарифма обычно пишется на его уровне, а основание — подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».
Как вычислить логарифм?
Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?
Например, вычислите логарифм: а) (log_{4}{16}) б) (log_{3})(frac{1}{3}) в) (log_{sqrt{5}}{1}) г) (log_{sqrt{7}}{sqrt{7}}) д) (log_{3}{sqrt{3}})
а) В какую степень надо возвести (4), чтобы получить (16)? Очевидно во вторую. Поэтому:
(log_{4}{16}=2)
б) В какую степень надо возвести (3), чтобы получить (frac{1}{3})? В минус первую, так как именно отрицательная степень «переворачивает дробь» (здесь и далее пользуемся свойствами степени).
(log_{3})(frac{1}{3})(=-1)
в) В какую степень надо возвести (sqrt{5}), чтобы получить (1)? А какая степень делает любое число единицей? Ноль, конечно!
(log_{sqrt{5}}{1}=0)
г) В какую степень надо возвести (sqrt{7}), чтобы получить (sqrt{7})? В первую – любое число в первой степени равно самому себе.
(log_{sqrt{7}}{sqrt{7}}=1)
д) В какую степень надо возвести (3), чтобы получить (sqrt{3})? Из свойств степени мы знаем, что корень – это дробная степень, и значит квадратный корень — это степень (frac{1}{2}).
(log_{3}{sqrt{3}}=)(frac{1}{2})
Пример: Вычислить логарифм (log_{4sqrt{2}}{8})
Решение:
|
(log_{4sqrt{2}}{8}=x) |
Нам надо найти значение логарифма, обозначим его за икс. Теперь воспользуемся определением логарифма: |
|
|
((4sqrt{2})^{x}=8) |
Что связывает (4sqrt{2}) и (8)? Двойка, потому что и то, и другое число можно представить степенью двойки: |
|
|
({(2^{2}cdot2^{frac{1}{2}})}^{x}=2^{3}) |
Слева воспользуемся свойствами степени: (a^{m}cdot a^{n}=a^{m+n}) и ((a^{m})^{n}=a^{mcdot n}) |
|
|
(2^{frac{5}{2}x}=2^{3}) |
Основания равны, переходим к равенству показателей |
|
|
(frac{5x}{2})(=3) |
Умножим обе части уравнения на (frac{2}{5}) |
|
|
(x=1,2) |
Получившийся корень и есть значение логарифма |
Ответ: (log_{4sqrt{2}}{8}=1,2)
Зачем придумали логарифм?
Чтобы это понять, давайте решим уравнение: (3^{x}=9). Просто подберите (x), чтобы равенство сработало. Конечно, (x=2).
А теперь решите уравнение: (3^{x}=8).Чему равен икс? Вот в том-то и дело.
Самые догадливые скажут: «икс чуть меньше двух». А как точно записать это число? Для ответа на этот вопрос и придумали логарифм. Благодаря ему, ответ здесь можно записать как (x=log_{3}{8}).
Хочу подчеркнуть, что (log_{3}{8}), как и любой логарифм — это просто число. Да, выглядит непривычно, но зато коротко. Потому что, если бы мы захотели записать его в виде десятичной дроби, то оно выглядело бы вот так: (1,892789260714…..)
Пример: Решите уравнение (4^{5x-4}=10)
Решение:
|
(4^{5x-4}=10) |
(4^{5x-4}) и (10) никак к одному основанию не привести. Значит тут не обойтись без логарифма.
Воспользуемся определением логарифма: |
|
|
(log_{4}{10}=5x-4) |
Зеркально перевернем уравнение, чтобы икс был слева |
|
|
(5x-4=log_{4}{10}) |
Перед нами линейное уравнение. Перенесем (4) вправо. И не пугайтесь логарифма, относитесь к нему как к обычному числу. |
|
|
(5x=log_{4}{10}+4) |
Поделим уравнение на 5 |
|
|
(x=)(frac{log_{4}{10}+4}{5}) |
Вот наш корень. Да, выглядит непривычно, но ответ не выбирают. |
Ответ: (frac{log_{4}{10}+4}{5})
Десятичный и натуральный логарифмы
Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы ((a>0, aneq1)). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:
Натуральный логарифм: логарифм, у которого основание — число Эйлера (e) (равное примерно (2,7182818…)), и записывается такой логарифм как (ln{a}).
То есть, (ln{a}) это то же самое, что и (log_{e}{a}), где (a) — некоторое число.
Десятичный логарифм: логарифм, у которого основание равно 10, записывается (lg{a}).
То есть, (lg{a}) это то же самое, что и (log_{10}{a}), где (a) — некоторое число.
Основное логарифмическое тождество
У логарифмов есть множество свойств. Одно из них носит название «Основное логарифмическое тождество» и выглядит вот так:
Это свойство вытекает напрямую из определения. Посмотрим как именно эта формула появилась.
Вспомним краткую запись определения логарифма:
если (a^{b}=c), то (log_{a}{c}=b)
То есть, (b) – это тоже самое, что (log_{a}{c}). Тогда мы можем в формуле (a^{b}=c) написать (log_{a}{c}) вместо (b). Получилось (a^{log_{a}{c}}=c) – основное логарифмическое тождество.
Остальные свойства логарифмов вы можете найти здесь. С их помощью можно упрощать и вычислять значения выражений с логарифмами, которые «в лоб» посчитать сложно.
Пример: Найдите значение выражения (36^{log_{6}{5}})
Решение:
|
(36^{log_{6}{5}}=) |
Сразу пользоваться свойством (a^{log_{a}{c}}=c) мы не можем, так как в основании степени и в основании логарифма – разные числа. Однако мы знаем, что (36=6^{2}) |
|
|
(=(6^{2})^{log_{6}{5}}=) |
Зная формулу ((a^{m})^{n}=a^{mcdot n}), а так же то, что множители можно менять местами, преобразовываем выражение |
|
|
(=6^{2cdotlog_{6}{5}}=6^{log_{6}{5}cdot2}=(6^{log_{6}{5}})^{2}=) |
Вот теперь спокойно пользуемся основным логарифмическим тождеством. |
|
|
(=5^{2}=25) |
Ответ готов. |
Ответ: (25)
Как число записать в виде логарифма?
Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что (log_{2}{4}) равен двум. Тогда можно вместо двойки писать (log_{2}{4}).
Но (log_{3}{9}) тоже равен (2), значит, также можно записать (2=log_{3}{9}) . Аналогично и с (log_{5}{25}), и с (log_{9}{81}), и т.д. То есть, получается
(2=log_{2}{4}=log_{3}{9}=log_{4}{16}=log_{5}{25}=log_{6}{36}=log_{7}{49}…)
Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.
Точно также и с тройкой – ее можно записать как (log_{2}{8}), или как (log_{3}{27}), или как (log_{4}{64})… Здесь мы как аргумент пишем основание в кубе:
(3=log_{2}{8}=log_{3}{27}=log_{4}{64}=log_{5}{125}=log_{6}{216}=log_{7}{343}…)
И с четверкой:
(4=log_{2}{16}=log_{3}{81}=log_{4}{256}=log_{5}{625}=log_{6}{1296}=log_{7}{2401}…)
И с минус единицей:
(-1=) (log_{2})(frac{1}{2})(=) (log_{3})(frac{1}{3})(=) (log_{4})(frac{1}{4})(=) (log_{5})(frac{1}{5})(=) (log_{6})(frac{1}{6})(=) (log_{7})(frac{1}{7})(…)
И с одной третьей:
(frac{1}{3})(=log_{2}{sqrt[3]{2}}=log_{3}{sqrt[3]{3}}=log_{4}{sqrt[3]{4}}=log_{5}{sqrt[3]{5}}=log_{6}{sqrt[3]{6}}=log_{7}{sqrt[3]{7}}…)
И так далее.
Любое число (a) может быть представлено как логарифм с основанием (b): (a=log_{b}{b^{a}})
Пример: Найдите значение выражения (frac{log_{2}{14}}{1+log_{2}{7}})
Решение:
|
(frac{log_{2}{14}}{1+log_{2}{7}})(=) |
Превращаем единицу в логарифм с основанием (2): (1=log_{2}{2}) |
|
|
(=)(frac{log_{2}{14}}{log_{2}{2}+log_{2}{7}})(=) |
Теперь пользуемся свойством логарифмов: |
|
|
(=)(frac{log_{2}{14}}{log_{2}{(2cdot7)}})(=)(frac{log_{2}{14}}{log_{2}{14}})(=) |
В числителе и знаменателе одинаковые числа – их можно сократить. |
|
|
(=1) |
Ответ готов. |
Ответ: (1)
Смотрите также:
Логарифмические уравнения
Логарифмические неравенства
Калькулятор натуральных логарифмов поможет найти логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,72.
Обозначение натурального логарифма
Для обозначения натурального логарифма существует несколько способов:
- ln
- loge
Так же возможно написание прописными буквами.
Что такое натуральный логарифм
Натуральный логарифм
Понятие натурального логарифма лучше проиллюстрировать примером. Например, натуральный логарифм числа 2 равен 0,693147180 потому, что
e0,693147180 = 2
Здесь e — основание натурального логарифма.
e =2,718281828
Таким образом натуральный логарифм — это степень, в которую нужно возвести число e для получения исходного числа, логарифм которого мы ищем. Вычисление натурального логарифма несложная задача и наш калькулятор поможет с расчетом.
Натуральный логарифм нуля не существует. Для чисел меньше единицы натуральный логарифм отрицательный.
Таблица натуральных логарифмов некоторых чисел
| x | ln x |
| 1 | 0 |
| 2 | 0,693147 |
| 3 | 1,098612 |
| 4 | 1,386294 |
| 5 | 1,609438 |
| 6 | 1,791759 |
| 7 | 1,94591 |
| 8 | 2,079442 |
| 9 | 2,197225 |
| 10 | 2,302585 |
| 100 | 4,60517 |
| 1000 | 6,907755 |
| 10000 | 9,21034 |
| 100000 | 11,51293 |
Ваша оценка
[Оценок: 285 Средняя: 2.8]
Калькулятор натуральных логарифмов Автор admin средний рейтинг 2.8/5 — 285 рейтинги пользователей
Натуральный логарифм — это логарифм по основанию e (математическая константа, приблизительно равная числу 2.718281828459…).
- Определение натурального логарифма
- Связь с экспоненциальной функцией
- Свойства натурального логарифма
- Таблица натуральных логарифмов
- График натурального логарифма
Определение натурального логарифма
Когда e y = x, натуральный логарифм (ln) числа x выглядит следующим образом:
ln(x) = loge(x) = y
Связь с экспоненциальной функцией
Функция логарифма ln(x) является обратной к экспоненциальной функции ex.
Для х > 0,
f (f -1(x)) = eln(x) = x
или
f -1(f (x)) = ln(ex) = x
Свойства натурального логарифма
| Свойство | Формула | Пример |
| Логарифм умножения | ln (x ⋅ y) = ln (x) + ln (y) | ln (3 ⋅ 7) = ln (3) + ln (7) |
| Логарифм деления | ln (x / y) = ln (x) — ln (y) | ln (3 / 7) = ln (3) — ln (7) |
| Логарифм степени | ln (x y) = y ⋅ ln (x) | ln (28) = 8 ⋅ ln (2) |
| Логарифм корня |  |
 |
| Производная логарифма | f (x) = ln (x) ⇒ f ‘ (x) = 1 / x | |
| Интеграл логарифма | ∫ ln (x) dx = x ⋅ (ln (x) — 1) + C | |
| Логарифм отрицательного числа | ln (x) не определен, если x ≤ 0 | |
| Логарифм числа 0 | ln (0) не определен | |
| Логарифм числа 1 | ln (1) = 0 | |
| Логарифм комплексного числа | log z = ln (r) + i (θ + 2nπ) = ln (√(x 2 + y 2)) + i · arctan (y/x)), для комплексного числа z = re iθ = x + iy |
|
| Логарифм бесконечности | lim ln (x) = ∞, если x → ∞ | |
| Тождество Эйлера | ln (-1) = i ⋅ π |
microexcel.ru
Таблица натуральных логарифмов
| x | ln x |
| 0 | не определен |
| 0+ | — ∞ |
| 0.0001 | -9.210340 |
| 0.001 | -6.907755 |
| 0.01 | -4.605170 |
| 0.1 | -2.302585 |
| 1 | 0 |
| 2 | 0.693147 |
| e ≈ 2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
График натурального логарифма
Функция натурального логарифма задается как y = ln x. Существует только при неотрицательных значениях переменной x. График выглядит так: