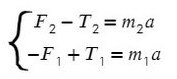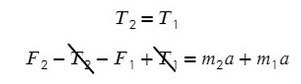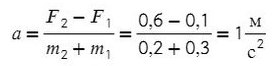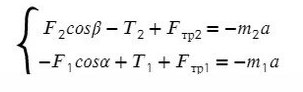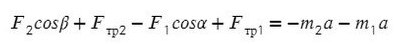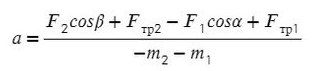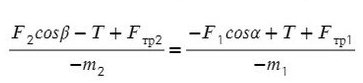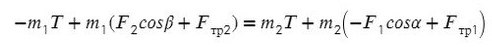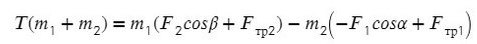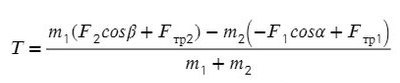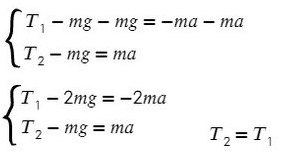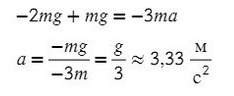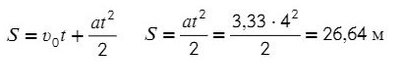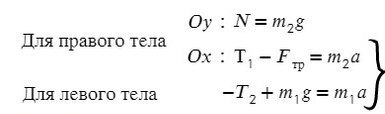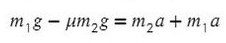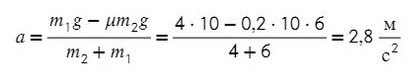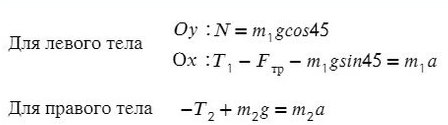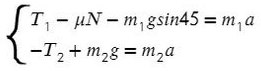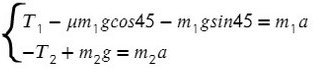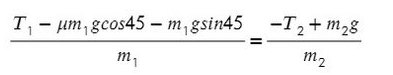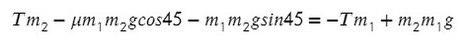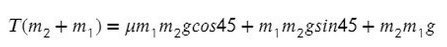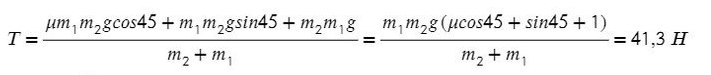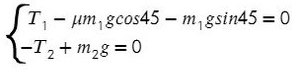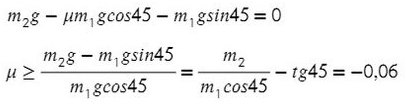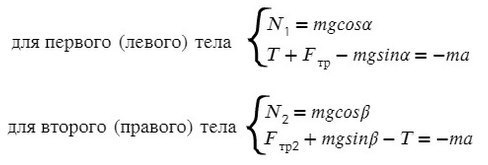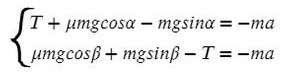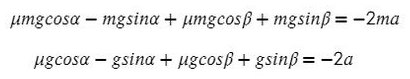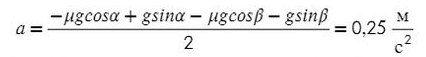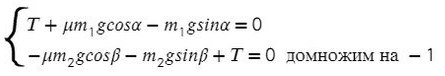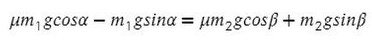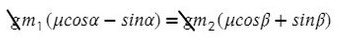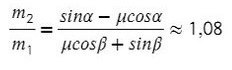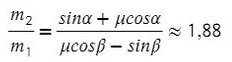Сила натяжения действует на всю струну, веревку или пружину, соответствующую массе объекта, к которому она прикреплена при натяжении.
Сила натяжения, действующая на струну, не одинакова для всех объектов; это зависит от массы, ускорения объекта и силы. Давайте посмотрим, как найти напряжение между двумя блоками.
Как найти напряжение между двумя блоками?
Это сила, определенная для струн, веревки или пружин; ступать как предметы, которые испытывают напряжение при растяжении.
Натяжение между двумя блоками можно найти, зная чистые силы, действующие на два блока, прикрепленных к струне, мы можем рассчитать натяжение, действующее на струну из-за двух блоков.
Подробнее о 15 Список примеров силы натяжения.
Задача: рассмотреть два блока масс m1‘ И м2‘, прикрепленный к веревке и свободно подвешенный в воздухе. Рассчитайте натяжение каната от двух блоков.
Решение: Натяжение, ощущаемое на веревке, связано с висящими на ней блоками и зависит от массы блоков.
Шаг 1: Нарисуйте диаграмму свободного тела для любой задачи.
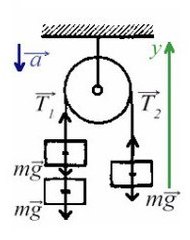
Чтобы рассчитать натяжение веревки, сначала нарисуйте диаграмму свободного тела, понимая проблему, объясняя чистые силы действует на блоки. Вот свободная диаграмма двух блоков для вышеуказанной задачи.
Диаграмма выше дает нам приблизительное представление о натяжении веревки из-за двух блоков. Напряжение Т1 из-за массы m1‘ и напряжение T2 действует из-за массы m2. Натяжение ощущается по всей длине веревки и в обоих направлениях, в положительном направлении оси Y и в отрицательном направлении оси Y. сила тяжести действует вниз из-за того, что оба груза четко обозначены на диаграмме свободного тела.
Шаг 2: Напишите уравнение для чистых сил, действующих на каждый блок.
Суммарная сила, действующая на массу m2‘ — сила натяжения и сила тяжести, действующая вниз в отрицательном направлении y. Итак, у нас есть уравнение, как показано ниже,
Ф=Т2-m2g
m2а=Т2-m2г —(1)
Суммарная сила, действующая на массу m1‘ — сила натяжения и вес, действующие вниз в отрицательном направлении оси Y. Таким образом, мы можем написать уравнение как,
Ф=Т1 — Т2 — M1g
m1а=Т1 — Т2 — M1г — (2)
Шаг 3: Сформулируйте уравнение, чтобы найти чистое ускорение блоков.
масса м2‘ фиксировано и не ускоряется, следовательно, a = 0. Поэтому мы можем записать уравнение (1) как
T2 — M2г=0—(3)
масса м1‘ также зафиксирован в точке и не ускоряется, следовательно, a = 0. Следовательно, из уравнения (2) имеем
T1-T2-m2г=0 —(4)
Это не означает, что если в веревке нет ускорения, то в веревке нет натяжения, из приведенного выше уравнения видно, что в веревке возникает натяжение из-за каждого блока. Посмотрим далее, как найти это натяжение веревки.
Шаг 4: Рассчитайте общее натяжение веревки.
Из уравнения (3) имеем
T2 = м2g
Напряжение Т2 применимо из-за массы m2‘ и ускорение свободного падения, равное весу блока 2.
Из уравнения (4) имеем
T1 = Т2 + м2g
Подстановка значения на T2, теперь у нас есть,
T1 = м1г + м2g
Итак, Т1=г(м2+m1)
Напряжение Т1 обусловлен общей массой, прикрепленной к струне, поскольку веревка оказывает натяжение T1 оказывает вес обоих блоков.
Шаг 5: Найдите чистое натяжение веревки.
Чистое натяжение представляет собой сумму всех натяжений, действующих на веревку. Следовательно, чистое натяжение T равно добавлению T1 и т2,
Т=Т1+T2
Т=г(м2+m1)+м2g
Т = м1г+2м2g
Т=(м1+ 2 млн2)g
Это чистое натяжение веревки за счет двух блоков, подвешенных вертикально над землей.
Напряжение между двумя блоками на склоне
Теперь, когда мы знаем, как рассчитать напряжение между двумя блоками в вертикальном направлении, подумаем также, как измерить натяжение между двумя блоками на наклонном склоне.
Подробнее о Как рассчитать силу натяжения: исчерпывающая информация.
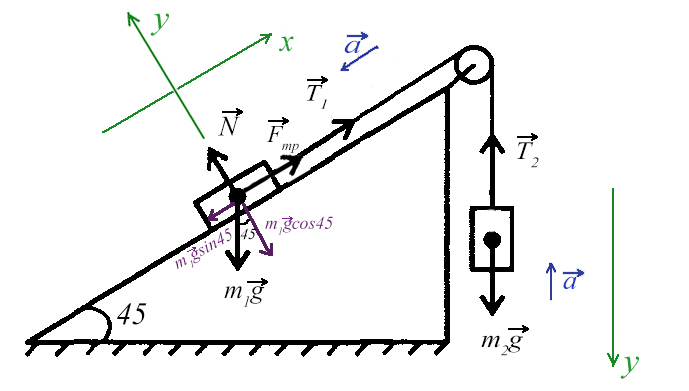
Задача: Рассмотрим два блока массами 30 кг и 45 кг, наклоненные на склоне и прикрепленные к веревке на шкиве. Угол наклона откоса, на котором масса блока m1‘ лежит под углом 300, и наклон, на котором масса m2‘ полагается наклонен под углом 450. Вычислите силу натяжения струны.
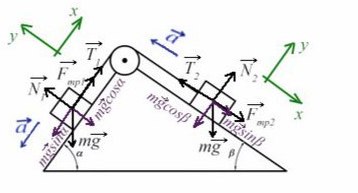
Решение: Сначала нарисуем диаграмму свободного тела двух блоков, наклоненных в плоскости под разными углами.
Теперь напишите уравнение для сил, действующих на блоки. Чистая сила, действующая на каждое тело, представляет собой дополнительные силы из-за веса, силы тяжести, нормальной силы, действующей в направлении, противоположном весу тела, и силы натяжения струны.
Силы, действующие на массу m1 находятся в 2-х направлениях, по оси х, м1а=-м1gSin300+T, знак минус, потому что сила действует в отрицательной оси x; и в y-направлении м1а=-м1gCos300+N.
Силы, действующие на массу m2 по оси х, м2а=м2gSin450-T
Натяжение оказывается в отрицательной оси x.
И в направлении Y m2а=-м2gcos450+ N
Напряжение возникает в направлении х; следовательно, мы будем рассматривать 2 уравнения,
m1а=-м1gSin30°+T
m2а=м2gSin45°-T
Складывая эти два уравнения, мы имеем,
m1а + м2а=м2gSin45°-T – м1gSin30°+T
Рассчитаем ускорение блоков, поэтому подставим заданное значение.
(30+45)a=9.8* (45*1/√2)-30* (1/2)
75a=9.8* (22.5√2-15)
75а=9.8*(31.82-15)
а=9.8*16.82/75
а=2.2 м/с2
Теперь мы знаем ускорение блоков. Подставляя это в любое из приведенных выше уравнений, мы можем найти натяжение веревки из-за двух блоков.
Рассмотрим уравнение, m1а=-м1gSin30°+T
Т = м1а + м1gSin30°
Т = м1(a+gSin30°)
=30* (2.2+9.8*1/2)
=30* (2.2+4.9)
= 30 * 7.1 = 213N
Следовательно, натяжение каната равно 213 Н.
Подробнее о Как рассчитать натяжение в строке: исчерпывающая информация.
Найти напряжение между двумя блоками на горизонтальной поверхности
Натяжение между блоками, расположенными на горизонтальной поверхности, проявляется при приложении к одному из блоков тянущей силы. При подталкивании предмета ближе друг к другу или от другого натяжение нити, соединяющей их, будет отсутствовать.
Подробнее о напряжение Силы.
Задача: рассмотрите два бруска, удерживаемых на плоскости без трения, массой m.1=3кг и м2= 5 кг. Обе эти массы связаны веревкой, и груз массой 5 кг тянется в положительном направлении x с силой 230 Н. Измерьте натяжение струны.
Решение: Давайте нарисуем диаграмму свободного тела, учитывая описанную выше ситуацию,
Напряжение, действующее на блок 1, равно силе ускорения, определяемой уравнением
Т = м1а=3а
Сила, приложенная к блоку 2, равна
Ф=Т+м2a
Напряжение из-за блока 2 составляет
Т=Фм2a
Если известно ускорение бруска, то легко рассчитать силу натяжения.
Суммарная сила, приложенная к блокам, равна
F= (м1+m2)a
Следовательно, а=Ф/м1+m2
Отсюда мы можем записать первое уравнение в виде
Т=3Ф/м1+m2
Следовательно, натяжение нити равно
Т=3* 230/3+5
=3*230/8=86.25 Н
Натяжение 86.25 Н приложено к струне.
Подробнее о Напряжение — это консервативная сила: исчерпывающее понимание.
Часто задаваемые вопросы
К нити прикреплено тело массой 2 кг, которое движется вниз со скоростью 3 м/с. Чему равно натяжение струны?
Данный: м=2кг
а = 3 м / с
Сила, действующая на объект, равна
F=T-мг
Так как ускорение тела направлено вниз F=-ma,
-ma=T-мг
Т=м(га)
=2* (9.8-3)
= 2 * 6.8 = 13.6N
Натяжение струны 13.6 Н.
Что такое сила натяжения?
Сила, действующая на каждый объект, классифицируется в зависимости от формы и размера объекта и направления силы.
Сила натяжения является контактной силой и действует на притягивание объектов. Сила, действующая по всей длине веревки, струн или пружин, называется силой натяжения.
Динамика: движения системы связанных тел.
Проецирование сил нескольких объектов.
Действие второго закона Ньютона на тела, которые скреплены нитью
Если ты, дружок, позабыл, как силушку проецировать, советую мыслишки в своей головушке освежить.
А для тех, кто все помнит, поехали!
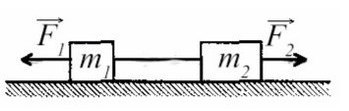
Задача 1. На гладком столе лежат два связанных невесомой и нерастяжимой ниткой бруска с массой 200 г левого и массой правого 300 г. К первому приложена сила 0,1 Н, к левому — в противоположном направлении сила 0,6 Н. С каким ускорением движутся грузы?
Движение происходит только на оси X.
Т.к. к правому грузу приложена большая сила, движение данной системы будет направлено вправо, поэтому направим ось так же. Ускорение у обоих брусков будет направлено в одну сторону — сторону большей силы.
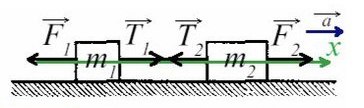
По II з. Ньютона спроецируем силы обоих тел на Ох:
Сложим верхнее и нижнее уравнение. Во всех задачах, если нет каких-то условий сила натяжения у разных тел одинакова T₁ и Т₂.
Выразим ускорение:
Ответ: 1 м/с²
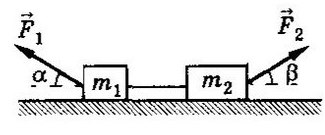
Задача 2. Два бруска, связанные нерастяжимой нитью, находятся на горизонтальной плоскости. К ним приложены силы F₁ и F₂, составляющие с горизонтом углы α и β. Найти ускорение системы и силу натяжения нити. Коэффициенты трения брусков о плоскость одинаковы и равны μ. Силы F₁ и F₂ меньше силы тяжести брусков. Система движется влево.
Cистема движется влево, однако ось можно направить в любую сторону (дело лишь в знаках, можете поэксперментировать на досуге). Для разнообразия направим вправо, против движения всей системы, мы же любим минусы! Спроецируем силы на Ох (если с этим сложности — вам сюда ).
По II з. Ньютона спроецируем силы обоих тел на Ох:
Сложим уравнения и выразим ускорение:
Выразим натяжение нити. Для этого приравняем ускорение из обоих уравнений системы:
Задача 3. Через неподивжный блок перекинуты нить, к которой подвешены три одинаковых груза (два с одной стороны и один с другой) массой 5 кг каждый. Найти ускорение системы. Какой путь пройдут грузы за первые 4 с движения?
В данной задаче можно представить, что два левых груза скреплены вместе без нити, это избавит нас от проецирования взаимно равных сил.
Вычтем из первого уравнения второе:
Зная ускорение и то, что начальная скорость равна нулю, используем формулу пути для равноускоренного движения:
Ответ: 26,64 м
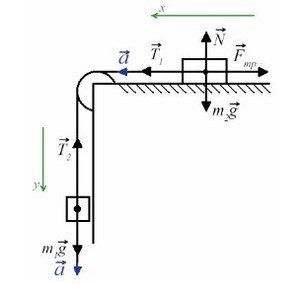
Задача 4. Два груза массами 4 кг и 6 кг соединены легкой нерастяжимой нитью. Коэффициенты трения между грузом и столом μ = 0,2. Определите ускорение, с которым будут двигаться грузы.
Запишем движение тел на оси, из Oy найдем N для силы трения (Fтр = μN):
(Если сложно понять, какие уравнения понадобятся для решения задачи, лучше запишите все)
Сложим два нижних уравнения для того, чтобы T сократилось:
Выразим ускорение:
Ответ: 2,8 м/с²
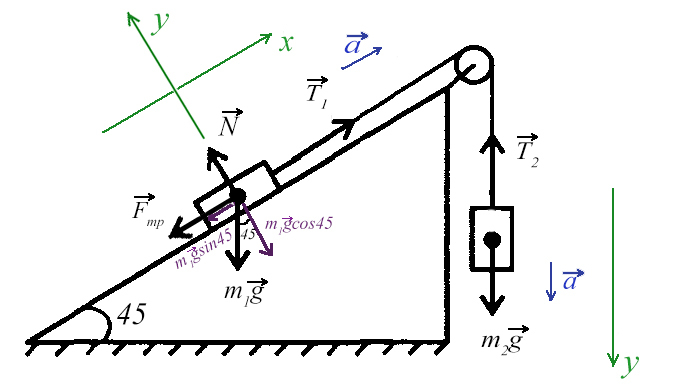
Задача 5. На наклонной поскости с углом наклона 45° лежит брускок массой 6 кг. Груз массой 4 кг присоединен к бруску при помощи нити и перекинут через блок. Определите натяжение нити, если коэффициент трения бруска о плоскость μ = 0,02. При каких значениях μ система будет в равновесии?
Ось направим произвольно и предположим, что правый груз перевешивает левый и поднимает его вверх по наклонной плоскости.
Из уравнения на ось Y выразим N для силы трения на ось Х (Fтр = μN):
Решим систему, взяв уравнение для левого тела по оси Х и для правого тела по оси Y:
Выразим ускорение, чтобы осталась одна неизвестная T, и найдем ее:
Система будет в равновесии. Это означает, что сумма всех сил, действующих на каждое из тел, будет равна нулю:
Получили отрицательный коэффициент трения, значит, движение системы мы выбрали неверно (ускорение, силу трения). Можно это проверить, подставив силу натяжения нити Т в любое уравнение и найдя ускорение. Но ничего страшного, значения остаются теми же по модулю, но противоположными по направлению.
Значит, правильное направление сил должно выглядить так, а коэффициент трения, при котором система будет в равновесии, равен 0,06.
Ответ: 0,06
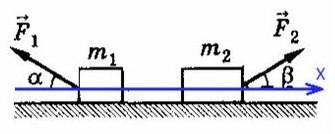
Задача 6. На двух наклонных плоскостях находится по грузу массами 1 кг. Угол между горизонталью и плоскостями равен α = 45° и β = 30°. Коэффициент трения у обеих плоскостей μ = 0,1. Найдите ускорение, с которым движутся грузы, и силу натяжения нити. Каким должно быть отношение масс грузов, чтобы они находились в равновесии.
В данной задаче уже потребуются все уравнения на обе оси для каждого тела:
Найдем N в обоих случаях, подставим их в силу трения и запишем вместе уравнения для оси Х обоих тел:
Сложим уравнения и сократим на массу:
Выразим ускорение:
Подставив в любое уравнение найденное ускорение, найдем Т:
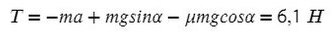
Сложим уравнения
Все, что с одной массой, перенесем в одну часть, все остальное — в другую часть уравнения:
Получили, что отношение масс должно быть таким:
Однако, если мы предположим, что система может двигаться в другом направлении, то есть правый груз будет перевешивать левый, направление ускорения и силы трения изменится. Уравнения останутся такими же, а вот знаки будут другими, и тогда отношение масс получится таким:
Тогда при соотношении масс от 1,08 до 1,88 система будет находиться в покое.
У многих может сложиться впечатление, что соотношение масс должно быть каким-то конкретным значением, а не промежутком. Это правда, если отстутвует сила трения. Чтобы уравновешивать силы тяжести под разными углами, найдется только один варинт, когда система находится в покое.
В данном же случае сила трения дает диапазон, в котором, пока сила трения не будет преодолена, движения не начнется.
Ответ: от 1,08 до 1,88
Задачи для закрепления.
Система связанных тел.
Будь в курсе новых статеек, видео и легкого технического юмора.
Блоки, нити, грузы и перегрузки
Задача 1. К телу массой кг подвешено на веревке тело массой
кг. Масса веревки
кг. Вся система движется ускоренно вверх под действием силы
Н, приложенной к верхнему телу (рис.1). Найти натяжение веревки в ее центре
и в точках крепления тел
и
.
Рисунок 1
Представим всю систему единым телом массой . Будем действовать на эту систему с силой
. Тогда по второму закону Ньютона
Откуда найдем ускорение системы:
Теперь вернемся к первому рисунку и запишем уравнения по второму закону Ньютона для верхнего и нижнего грузов:
Откуда
Очевидно, что посередине веревки сила ее натяжения будет средним арифметическим найденных двух сил:
Ответ: Н,
Н,
Н.
Задача 2. Маляр массой кг работает в подвесном кресле. Ему понадобилось срочно подняться вверх. Он начинает тянуть веревку с такой силой, что сила давления на кресло уменьшается до
Н. Масса кресла
кг. Чему равно ускорение маляра? Чему равна нагрузка на блок?
Рисунок 2
Расставим силы. Отметим все силы, действующие не маляра, и силы, действующие на люльку:
Теперь можно написать уравнения:
Вычитаем уравнения:
Ответ: м/с
.
Задача 3.
Через легкий неподвижный блок перекинута невесомая нерастяжимая нить с двумя грузами на концах, массы которых и
,
. Система приходит в движение, причем нить не проскальзывает относительно блока. Определить ускорение грузов, силу натяжения нити и силу давления на ось блока.
Рисунок 3
Понятно, что больший груз перетянет и начнет двигаться вниз, а меньший – подниматься. Запишем для них уравнение по второму закону:
Сложим уравнения:
Откуда
Теперь можно найти и силу натяжения нити:
Сила давления на блок равна :
Ответ: ,
,
.
Задача 4.
Через блок перекинута нить, на концах которой висят два груза с одинаковыми массами . Одновременно на каждый из грузов кладут по перегрузку: справа массой
, слева
(рис. 2). Определить ускорение системы, силу натяжения нити и силу давления перегрузков на основные грузы.
Рисунок 4
Запишем уравнение по второму закону Ньютона для обоих грузов с учетом массы перегрузков:
Сложение уравнений даст нам
Сила натяжения нити найдется подстановкой найденного ускорения в любое уравнение системы:
Определим силу давления меньшего перегрузка массой на груз
:
Для большего перегрузка
Ответ: ,
,
,
.
Задача 5.
Через неподвижный блок перекинута нить, к которой подвешены три одинаковых груза массой кг каждый (рис. 3). Найти ускорение системы и силу натяжения нити между грузами 1 и 2. Какой путь
пройдут грузы за первые
с движения? Трением пренебречь.
Рисунок 5
Сначала мысленно объединим два груза слева в один и запишем уравнение по второму закону:
Для правого грузика
Складываем уравнения:
Определим силу натяжения нити между грузиками. Обозначим ее . Тогда для самого нижнего грузика слева:
Определяем путь грузиков за 4 с:
Ответ: м/с
,
Н,
м.
Задача 6.
Определить ускорение грузов и силы натяжения всех нитей в системе, изображенной на рисунке. Масса каждого груза , массой блока пренебречь.
Рисунок 6
Сначала определяем ускорение. Для этого записываем уравнение по второму закону для грузиков справа и слева, пока не вспоминая о том, что их там несколько. Для нас сейчас это груз массой справа и
слева. Силу натяжения основной нити обозначим
:
Складываем уравнения:
Тогда
Рассмотрим теперь грузы, висящие справа. Обозначим натяжение нити между ними . Для нижнего груза справа
Осталось определить и
. Для верхнего грузика слева
Откуда
А для нижнего грузика слева
Ответ: ,
,
,
,
.
Задача 7.
Два груза массами г и
г соединены нерастяжимой нитью, перекинутой через невесомый блок (рис.). Грузы прижимаются друг к другу с постоянными силами
Н. Коэффициент трения между ними
. Найти ускорение, с которым движутся грузы.
Рисунок 7
Записываем уравнение по второму закону:
Тогда
Ответ: .
Задача 8.
Невесомая нить, перекинутая через неподвижный блок, пропущена через щель (рис.). При движении нити на нее действует постоянная сила трения . На концах нити подвешены грузы, массы которых
и
. Определить ускорение грузов.
Рисунок 8
Давайте предположим, что . Тогда левый груз начинает движение вверх, правый – вниз. Записываем для них уравнение по второму закону с учетом наличия силы трения:
Складывая уравнения, имеем:
Откуда
Но, если бы , тогда
Тогда, чтобы учесть обе возможности, запишем ответ так:
Ответ: .
Задача 9.
Через невесомый блок перекинута легкая нерастяжимая нить, к одному концу которой привязан груз массой г, а по другому
скользит кольцо массой г (рис.). С каким ускорением движется кольцо, если груз
неподвижен?
Рисунок 9
Сила трения кольца в данном случае и порождает силу натяжения нити, то есть это одна и та же сила. Поэтому для неподвижного груза
А для кольца
Ответ: 6 м/с.
4 комментария
Алексей
✉️
13.08.2020 14:14:09
Задача 6. Определить ускорение грузов и силы натяжения всех нитей в системе, изображенной на рисунке. Масса каждого груза m, массой блока пренебречь. Почему в проекции на ось второй закон ньютона имеет вид ma=T2-T+mg. При чём здесь сила T, если она даже не приложена к грузу.
Анна Валерьевна
✨
14.08.2020 05:46:11
Приложена. Просто, если рисовать ВСЕ силы, рисунок будет очень громоздким. Эта сила (Т2) действует на верхний груз и направлена вниз, а на второй груз — вверх.
Максон
✉️
26.09.2020 13:56:18
Здравствуйте!
Не могли бы вы объяснить, почему в первой задаче при написании второго з-на Ньютона для тела m мы не учли силу F?
Анна
✨
26.09.2020 14:35:07
Очень просто: она к нему не приложена.