Игры с магическими квадратами нравятся всем, кто увлекается головоломками. В поисках магического
числа, заполняя таблицу, ребенок развивает интерес к математике, логику
и наблюдательность.
Как решать магические квадраты?
Разгадывать головоломки легче, когда точно понимаешь что нужно сделать и по каким правилам. Для
начала нужно разобраться, что особенного в этих квадратных таблицах.
Решить магический квадрат — заполнить пустые ячейки так, чтобы сумма чисел по любой
горизонтали, по вертикалям и диагоналям была одинаковой.
Сложите числа в решенной задаче в любой строке, в любом столбце, а также по обеим диагоналям.
Проверь себя

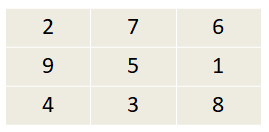
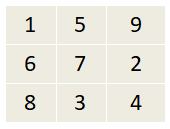
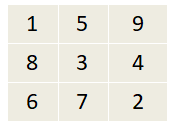
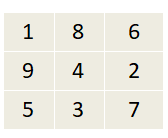
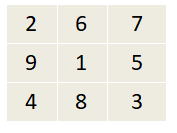
Помоги Клапану узнать, какой из 2 квадратов магический.
Познакомьтесь с примерами головоломок различного уровня сложности. Несколько заданий мы приводим
с ответами и описанием решения.
Магические квадраты для 1-2 класса
Подборка заданий из обучающего курса
ЛогикЛайк
Загрузить PDF
Загрузить PDF
Магические квадраты обрели популярность наряду с появлением математических игр, таких как судоку. Магический квадрат — это таблица, заполненная целыми числами таким образом, чтобы сумма чисел по горизонтали, вертикали и диагонали была одинакова (так называемая магическая константа). Эта статья расскажет вам, как построить квадрат нечетного порядка, квадрат порядка одинарной четности и квадрат порядка двойной четности.
-
1
Вычислите магическую константу.[1]
Это можно сделать при помощи простой математической формулы [n * (n2 + 1)] / 2, где n – количество строк или столбцов в квадрате. Например, в квадрате 3×3 n=3, а его магическая константа:- Магическая константа = [3 * (32 + 1)] / 2
- Магическая константа = [3 * (9 + 1)] / 2
- Магическая константа = (3 * 10) / 2
- Магическая константа = 30/2
- Магическая константа квадрата 3х3 равна 15.
- Сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
-
2
Напишите 1 в центральной ячейке верхней строки. Строить любой нечетный квадрат нужно именно с этой ячейки. Например, в квадрате 3х3 напишите 1 во второй ячейке верхней строки, а в квадрате 15х15 напишите 1 в восьмой ячейке верхней строки.
-
3
Следующие числа (2,3,4 и так далее по возрастанию) записывайте в ячейки по правилу: одна строка — вверх, один столбец — вправо. Но, например, чтобы записать 2, нужно «выйти» за пределы квадрата, поэтому существуют три исключения из данного правила:
- Если вы вылезли за верхний предел квадрата, напишите цифру в самой нижней ячейке соответствующего столбца.
- Если вы вылезли за правый предел квадрата, напишите цифру в самой дальней (левой) ячейке соответствующей строки.
- Если вы попали на ячейку, которая занята другой цифрой, напишите цифру непосредственно под предыдущей записанной цифрой.
Реклама
-
1
Существуют различные методики для построения квадратов порядка одинарной четности и двойной четности.
- Число строк или столбцов в квадрате порядка одинарной четности делится на 2, но не на 4.[2]
- Наименьшим квадратом порядка одинарной четности является квадрат 6х6 (квадрат 2×2 построить нельзя).
- Число строк или столбцов в квадрате порядка одинарной четности делится на 2, но не на 4.[2]
-
2
Вычислите магическую константу. Это можно сделать при помощи простой математической формулы [n * (n2 + 1)] / 2, где n – количество строк или столбцов в квадрате. Например, в квадрате 6×6 n=6, а его магическая константа:
- Магическая константа = [6 * (62 + 1)] / 2
- Магическая константа = [6 * (36 + 1)] / 2
- Магическая константа = (6 * 37) / 2
- Магическая константа = 222/2
- Магическая константа квадрата 6х6 равна 111.
- Сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
-
3
Разделите магический квадрат на четыре квадранта одинакового размера. Обозначьте квадранты через А (сверху слева), C (сверху справа), D (снизу слева) и B (снизу справа). Чтобы выяснить размер каждого квадранта, разделите n на 2.
- Таким образом, в квадрате 6х6 размер каждого квадранта равен 3×3.
-
4
В квадранте А напишите четвертую часть всех чисел; в квадранте В напишите следующую четвертую часть всех чисел; в квадранте С напишите следующую четвертую часть всех чисел; в квадранте D напишите заключительную четвертую часть всех чисел.
- В нашем примере квадрата 6х6 в квадранте А напишите числа 1-9; в квадранте В — числа 10-18; в квадранте С — числа 19-27; в квадранте D — числа 28-36.
-
5
Числа в каждом квадранте записывайте так, как вы строили нечетный квадрат. В нашем примере квадрант А начните заполнять числами с 1, а квадранты С, B, D — с 10, 19, 28, соответственно.
- Число, с которого вы начинаете заполнение каждого квадранта, всегда пишите в центральной ячейке верхней строки определенного квадранта.
- Заполняйте каждый квадрант числами так, как будто это отдельный магический квадрат. Если при заполнении квадранта доступна пустая ячейка из другого квадранта, игнорируйте этот факт и пользуйтесь исключениями из правила заполнения нечетных квадратов.
-
6
Выделите определенные числа в квадрантах А и D.[3]
На данном этапе сумма чисел в столбцах, строках и по диагонали не будет равна магической константе. Поэтому вы должны поменять местами числа в определенных ячейках верхнего левого и нижнего левого квадрантов.- Начиная с первой ячейки верхней строки квадранта А, выделите количество ячеек, равное медиане количества ячеек во всей строке. Таким образом, в квадрате 6×6 выделите только первую ячейку верхней строки квадранта А (в этой ячейке написано число 8); в квадрате 10х10 вам нужно выделить первые две ячейки верхней строки квадранта А (в этих ячейках написаны числа 17 и 24).
- Образуйте промежуточный квадрат из выделенных ячеек. Так как в квадрате 6х6 вы выделили только одну ячейку, то промежуточный квадрат будет состоять из одной ячейки. Назовем этот промежуточный квадрат как A-1.
- В квадрате 10х10 вы выделили две ячейки верхней строки, поэтому необходимо выделить две первые ячейки второй строки, чтобы образовать промежуточный квадрат 2х2, состоящий из четырех ячеек.
- В следующей строке пропустите число в первой ячейке, а затем выделите столько чисел, сколько вы выделили в промежуточном квадрате A-1. Полученный промежуточный квадрат назовем A-2.
- Получение промежуточного квадрата А-3 аналогично получению промежуточного квадрата A-1.
- Промежуточные квадраты А-1, А-2, А-3 образуют выделенную область А.
- Повторите описанный процесс в квадранте D: создайте промежуточные квадраты, которые образуют выделенную область D.
-
7
Поменяйте местами числа из выделенных областей А и D (числа из первой строки квадранта А с числами из первой строки квадранта D и так далее). Теперь сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
Реклама
-
1
Число строк или столбцов в квадрате порядка двойной четности делится на 4.[4]
- Наименьшим квадратом порядка двойной четности является квадрат 4х4.
-
2
Вычислите магическую константу. Это можно сделать при помощи простой математической формулы [n * (n2 + 1)] / 2, где n – количество строк или столбцов в квадрате. Например, в квадрате 4×4 n=4, а его магическая константа:
- Магическая константа = [4 * (42 + 1)] / 2
- Магическая константа = [4 * (16 + 1)] / 2
- Магическая константа = (4 * 17) / 2
- Магическая константа = 68/2
- Магическая константа квадрата 4х4 равна 34.
- Сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
-
3
Создайте промежуточные квадраты А-D. В каждом углу магического квадрата выделите промежуточный квадрат размером n/4, где n – количество строк или столбцов в магическом квадрате.[5]
Обозначьте промежуточные квадраты как A, B, C, D (в направлении против часовой стрелки).- В квадрате 4×4 промежуточные квадраты будут состоять из угловых ячеек (по одной в каждом промежуточном квадрате).
- В квадрате 8х8 промежуточные квадраты будут иметь размер 2×2.
- В квадрате 12х12 промежуточные квадраты будут иметь размер 3×3 (и так далее).
-
4
Создайте центральный промежуточный квадрат. В центре магического квадрата выделите промежуточный квадрат размером n/2, где n – количество строк или столбцов в магическом квадрате. Центральный промежуточный квадрат не должен пересекаться с угловыми промежуточными квадратами, но должен касаться их углов.
- В квадрате 4×4 центральный промежуточный квадрат имеет размер 2×2.
- В квадрате 8×8 центральный промежуточный квадрат имеет размер 4×4 (и так далее).
-
5
Начните строить магический квадрат (слева направо), но числа записывайте только в ячейки, расположенные в выделенных промежуточных квадратах. Например, квадрат 4×4 вы заполните так:
- Напишите 1 в первой строке первом столбце; напишите 4 в первой строке четвертом столбце.
- Напишите 6 и 7 в центре второй строки.
- Напишите 10 и 11 в центре третьей строки.
- Напишите 13 в четвертой строке первого столбца; напишите 16 в четвертой строке четвертого столбца.
-
6
Оставшиеся ячейки квадрата заполняются аналогичным образом (слева направо), но числа нужно записывать в порядке убывания и только в ячейки, расположенные вне выделенных промежуточных квадратов. Например, квадрат 4×4 вы заполните так:
- Напишите 15 и 14 в центре первой строки.
- Напишите 12 во второй строке первого столбца; напишите 9 во второй строке четвертого столбца.
- Напишите 8 в третьей строке первого столбца; напишите 5 в третьей строке четвертого столбца.
- Напишите 3 и 2 в центре четвертой строки.
- Теперь сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
Реклама
Советы
- Воспользуйтесь описанными методами и найдите свой способ решения магических квадратов.
Реклама
Что вам понадобится
- Карандаш
- Бумага
- Ластик
Похожие статьи
Об этой статье
Эту страницу просматривали 352 246 раз.
Была ли эта статья полезной?
A magic square is a puzzle the addition of numbers in every row, column, and diagonal are the same. Every magic square has an order which is nothing but the number of rows x number of columns. Check out the rules to form a magic square and the steps to solve the magic square puzzles in the following sections. You can also find the questions on number patterns on this page.
What is Magic Square?
Magic squares are square grids with a special arrangement of numbers in those grids. The numbers are special because every row, column and the diagonal sum is the same number. No number is repeated in the magic square.
While arranging the numbers in the grids, see the sum of numbers in every row, every column and diagonal are equal. The smallest magic square possible is 3 x 3. The number of elements in the magic square is the multiplication of the square order.
Example:
The sum of numbers in all rows = 15
The sum of numbers in all columns = 15
The sum of numbers in both diagonals = 15
Therefore, it is a 3 x 3 magic square.
More Related Articles:
- Patterns and Mental Mathematics
- Product of The Number
Interesting Facts about Magic Square Puzzles
- We need to have 3² = 9 or 4² = 16 or 5² = 25 different numbers are required to form a magic square.
- We can frame multiple magic squares with the given set of numbers.
- The number of elements in the magic square is its order.
- The order of a magic square N x N means it has N number of rows and N number of columns.
Steps for Forming a Magic Square | Magic Square Rules
Students can get the simple guidelines to form a magic square in the below-mentioned sections.
- Get the set of numbers to be inserted in the magic square.
- Using the trial and error method, place the numbers in the square grids.
- Remember that the sum of numbers in every row, every column, and diagonal are equal.
- At last, check the condition is satisfied or not.
Magic Square Puzzle Examples
Question 1:
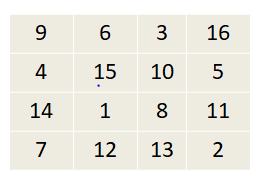
Check whether the following is a magic square or not.
Solution:
The important rule to say a square grid is a magic square is the sum of numbers in every row, column and diagonal is the same number.
The sum of elements in first row = 9 + 6 + 3 + 16 = 34
The sum of elements in second row = 4 + 15 + 10 + 15 = 34
The sum of elements in third row = 14 + 1 + 8 + 11 = 34
The sum of elements in fourth row = 7 + 12 + 13 + 2 = 34
The sum of elements in first column = 9 + 4 + 14 + 7 = 34
The sum of elements in second column = 6 + 15 + 1 + 12 = 34
The sum of elements in third column = 3 + 10 + 8 + 13 = 34
The sum of elements in fourth column =16 + 5 + 11 + 2 = 34
The sum of elements in one diagonal = 9 + 15 + 8 + 2 = 34
The sum of elements in second diagonal = 7 + 1 + 10 + 16 = 34
Therefore, the given is a magic square 4 x 4.
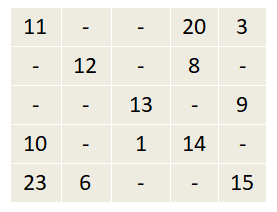
Question 2:
Find the missing numbers in the given 5 x 5 magic square.
Solution:
In the given grid, one diagonal has all the elements. So, find the sum of numbers.
The sum of the numbers of 1st diagonal = 11 + 12 + 13 + 14 + 15 = 65
So, every row, column and diagonal sum should be 65.
The missing number in the 2nd diagonal = 65 – (23 + 13 + 8 + 3)
= 65 – 47 = 18
The missing elements in the 4th row = 65 – (10 + 18 + 1 + 14)
= 65 – 43 = 22
The missing element in 5th column = 65 – (3 + 9 + 22 + 15)
= 65 – 49
The sum of missing elements in the first row = 65 – (11 + 20 + 3)
= 31
Let the missing numbers be 24, 7
The missing number in 2nd column = 65 – (24 + 12 + 18 + 6)
= 5
The missing number in 3rd column = 65 – (7 + 13 + 1 + 19)
= 25
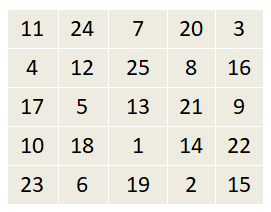
The missing number in 2nd row = 65 – (12 + 25 + 8 + 16) = 4
The missing number in 5th row = 65 – (23 + 6 + 19 + 15) = 2
So, the 5 x 5 magic square puzzle is follows.
Question 3:
Write the number of possible similar magic squares for the numbers from 1 to 9.
Solution:
The list of numbers from 1 to 9 is 1, 2, 3, 4, 5, 6, 7, 8, 9
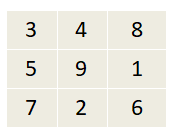
See that the sum of numbers in all rows, columns and diagonals is 15.
The 1st possible arrangement of 3 x 3 magic square is as follows:
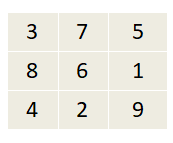
The 2nd possible arrangement is
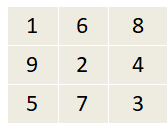
The third possible arrangement of the numbers in the magic square is
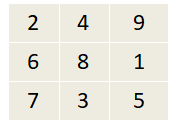
4th Possible arrangement of numbers is
5th possible arrangement of numbers is
6th possible arrangement of numbers is
7th possible arrangement of numbers is
8th possible arrangement of the number is
Формирование логического мышления младших школьников — важная составная часть образовательного процесса. Развивать логическое мышление — это значит учиться сравнивать, находить общие свойства и различия, составные части, соединить эти части в одно целое, выделять существенные свойства предметов, делать правильные выводы из наблюдений или фактов, обобщать, доказывать, излагать мысли последовательно, обоснованно.
В школе главным интеллектообразующим предметом является математика. Знания, умения и навыки, полученные школьниками на уроках математики, развиваются, расширяются, углубляются, находя практическое применение при хорошо организованной внеурочной работе. Для внеурочных занятий наиболее интересными формами работы будут различные дидактические математические игры, логические задачи, викторины, олимпиады разного уровня, материалы по истории математики. Также увлекательным видом является работа с магическими квадратами. В младших классах в учебниках математики встречаются дополнительные задания с магическими квадратами, но только на определение, является ли квадрат магическим (волшебным). А дети могут справиться с заданиями и более повышенного уровня. Например, самим создать магический квадрат. На это отводится 9-10 занятий.
1 занятие. Знакомство с магическими (волшебными) квадратами.
В первом занятии дети знакомятся с квадратом Ло ШУ, определяют, почему квадрат называют магическим (волшебным).
Надо обратить внимание детей не только на то, что сумма чисел по столбцам, строкам и диагоналям равна , но и на то, что данные числа 1 2 3 4 5 6 7 8 9 имеют определенный порядок.
Если сложить все числа магического квадрата, затем разделить эту сумму на 3, то получится сумма квадрата.
На этом занятии можно дать несколько квадратов и попросить определить, являются ли они магическими
2 занятие. На этом занятии дети знакомятся с другим способом определения, является ли квадрат магическим.
| А1 |
А2 |
А3 |
|
А4 |
А5 |
А6 |
|
А7 |
А8 |
А9 |
|
(А4 + А2) : 2 = А9 |
(3 + 1) : 2 = 2 |
|
(А2 +А6) : 2 = А7 |
(1+7) : 2 = 4 |
|
(А6 +А8) : 2 = А1 |
(7 + 9) : 2 = 8 |
|
(А4 + А8) : 2 = А3 |
(9 + 3) : 2 = 6 |
3 занятие. Нахождение недостающих чисел магического квадрата.
Дается всего 4 числа магического квадрата. По трем из них можно найти сумму. Если известна сумма, можно найти и остальные числа.
4 занятие. Среднее числа магического квадрата.
1. На этом занятии дети должны придти к выводу, что среднее число магического квадрата в 3 раза меньше суммы трех чисел.
2. Среднее число магического квадрата стоит в центре ряда данных чисел.
1 2 3 4 5 6 7 8 9
Сумма чисел каждого столбца, строки и диагонали (сумма квадрата) равна 15. Значит, среднее число квадрата должно быть в 3 раза меньше, т.е. равно 5.
5 занятие. Нахождение недостающих чисел магического квадрата по 3 данным числам.
Данные 3 числа должны быть расположены так, чтобы по ним можно было найти среднее число магического квадрата.
Сначала по данным числам находим сумму квадрата, затем по сумме — среднее число квадрата.
6 занятие. Нахождение недостающих чисел магического квадрата по 3 числам. В данном случае, дается среднее число. Сперва находят сумму квадрата, затем другие числа.
7 занятие. Дается только среднее число.
1. Знаем, что среднее число стоит в центре ряда чисел магического квадрата. . . . . 14 . . . .
2. Зная это и то, что числа в ряду имеют определенный порядок, находим остальные числа ряда. Например,
6 8 10 12 14 16 18 20 22
3. Находим сумму квадрата 14 ∙ 3 = 42
6 8 10 12 14 16 18 20 22
4. Создаем тройки связанных между собой чисел
6 . . . 14 . . . 22
8 . . . 14 . . . 20
10 . . .14 . . . 18
12 . . . 14 . . . 16
5. Число 22 не стоит в углу. Можно ставить его в середине первой строки.
6. 22 + 8 + 12 = 42 Из этого следует, что на первой строке вместе с 22 стоят 8 и 12.
6… 14…22
8…14…20
10 …14…18
12…14…16
8 занятие. Дается только сумма магического квадрата.
Дети по данной сумме сперва находят среднее число. Дальше работа ведется как на седьмом занятии.
9 занятие. Дети сами «строят» магический квадрат.
1. Берем ряд девяти чисел по определенному порядку. Например, 2 3 4 5 6 7 8 9 10
2. Находим сумму этих чисел 2+3+4+5+6+7+8+9+1+10= 54
54 : 3 = 18
18 — это сумма квадрата . Значит, среднее число это 6
18 : 3 = 6
Можно и по-другому найти среднее число, затем и сумму.
2 3 4 5 6 7 8 9 10
в центре ряда чисел стоит 6. Это среднее число, умножаем его на 3
6 ∙ 3 = 18 получаем сумму.
3. Находим связанные между собой тройки чисел
2 … 6…10
3…6…9
4…6…8
5…6…7
4. Число 10 не стоит в углу. 10 может стоять в середине первой строки или первого столбца.
5. Рядом с 10 на первом столбце стоят 3 и 5 3+10+5 = 18
6.
18 — 5 — 6 = 7,
18 — 3 — 6 = 9
В младших классах работа ведется с магическими квадратами третьего порядка. Дети с удовольствием, азартом работают над заданиями с магическими квадратами. Они не только доказывают, что квадрат магический, но и сами создают свои магические квадраты.
Секреты магического квадрата:
- Чтобы найти сумму магического квадрата, находим сумму всех его чисел и делим на 3.
- Среднее число магического квадрата меньше суммы в 3 раза.
- Среднее число магического квадрата стоит в центре данного ряда чисел.
- Ряд чисел магического квадрата имеет определенный порядок.
- Если увеличить или умножить числа магического квадрата на одно и то же число, квадрат остается магическим.
- Сумма двух магических квадратов также является магической.
Работу над последними двумя утверждениями можно проводить, исходя из заинтересованности детей.
Среди поклонников логических игр большой популярностью пользуется магический квадрат. Он представляет собой таблицу, заполненную особым образом цифрами. Причём сумма чисел одинакова по всем направлениям. Эту величину принято называть константой. Существует множество вариантов таких головоломок разной степени сложности.

Содержание
- История и современное применение
- Квадрат нечётного порядка
- Одинарная чётность
- Вычисление магической константы
- Дальнейшие действия
- Двойной порядок
История и современное применение
Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.

В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.
В современной общеобразовательной школе разные виды магических квадратов используются на уроках математики. Они способствуют развитию логического мышления и вызывают у детей живой интерес.
С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.
Квадрат нечётного порядка
Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка. Первая группа подразделяется на таблицы одинарной и двойной чётности.
Начальным шагом во всех случаях будет определение магической константы. Делается это с помощью специальной формулы [n * (n2 + 1)] / 2. Разобраться с принципом решения задачи этого класса можно на самом простом примере. Для этого выстраивается таблица из 9 ячеек. В неё нужно расставить цифры от 1 до 9. Дальнейший алгоритм:


Общий алгоритм выполнения задания: каждый следующий знак пишется вверх и правее. Если там нет клетки — дорисовывается ещё один воображаемый квадрат. Если ячейка занята — число записывается ниже предыдущего. Таким способом можно составить любой квадрат нечётного порядка, включая самые сложные, с больши́м числом ячеек.
Одинарная чётность
Магические квадраты могут иметь порядок одинарной или двойной чётности. Для каждого случая предусмотрена отдельная методика вычисления. У таблиц одинарной чётности количество клеток в одной строке или столбце делится пополам, но не делится на четыре. Наименьшим квадратом, отвечающим этому требованию, будет прямоугольник 6х6. Фигуру 2х2 построить и заполнить невозможно.
Вычисление магической константы
Первый этап расчётов проводится по формуле [n * (n2 + 1)] / 2, где символом n обозначено число клеток в одном ряду. Если взять за пример квадрат 6х6, расчёт будет выглядеть следующим образом: [6 х (36 + 1)]: 2 = (6 х 37): 2 = 222:2.

Волшебная постоянная прямоугольника со стороной 6 клеток равна 111. Общая сумма чисел от 1 до 36 в каждой строке и в разных направлениях должна быть равна 111.
Рисунок делится на 4 одинаковые части. В каждой будет по 9 клеток (3х3). Каждую часть обозначают латинскими буквами: А — верхняя левая, С — верхняя правая, D — нижняя левая и В — нижняя правая часть. Если квадрат имеет другой размер, n делится на 2, чтобы узнать точную величину каждой из 4 частей.
Дальнейшие действия
Следующий шаг — вписывание в каждую часть ¼ всех чисел. В квадрант А вносятся числа от 1 до 9, в квадрант В — от 10 до 18, в части С — от 19 до 27, в D — от 28 до 36.
Последовательность вписывания такая же, как при заполнении простейшего нечётного квадрата:

В блоках А и D на этой стадии решения сумма в строках и столбиках будет отличаться от постоянной. Чтобы это исправить, некоторые числа меняют местами между собой.
Алгоритм действий:

Цифры, которые были вписаны в выделенных треугольниках А и D, нужно поменять между собой местами. После этого сумма в каждой строке должна быть одинаковой. Она равняется вычисленной магической константе.
Двойной порядок
Если головоломка имеет порядок двойной чётности, количество окон в каждой горизонтальной строчке или вертикальном столбце должно делиться на 4. Минимальной фигурой с такими свойствами будет таблица 4х4.
Решать магические квадраты двойной чётности следует по тому же алгоритму, что и остальные. Первый шаг при заполнении — вычисление магической константы. Формула применяется та же, что для расчёта других квадратов. Для фигуры со стороной 4 клетки значение константы будет равно 34.

В каждом углу основного поля выделяются промежуточные таблицы. Их размер должен быть равен n/4. Эти области обозначают буквами A, B, C, D, располагая их против хода часовой стрелки. Величина промежуточных фигур зависит от размера исходного квадрата:
Следующий этап — создание центрального промежуточного квадрата. Величина его стороны должна составлять n/2. Эта фигура не должна накладываться на периферические, но при этом соприкасаться с ними углами.
Далее в квадрат вносят цифры слева направо. Их допускается ставить только в свободные ячейки, которые входят в состав промежуточных областей. Например, при заполнении таблицы 4х4 порядок действий будет таким:
По этому же принципу цифрами заполняются оставшиеся клетки. Числа проставляются слева в порядке уменьшения. Если всё сделано верно, сумма всех чисел в любой строчке будет одинаковой.
Предыдущая
МатематикаАлгоритм Евклида — формулы, правила и примеры решения задач
Следующая
МатематикаМинор матрицы — способы, порядок и примеры вычисления