Числовой последовательностью называют ряд чисел, полученных по некоторому правилу или формуле.
Например, правило «все положительные четные числа по возрастанию начиная с двойки» задает последовательность: (2; 4; 6; 8; 10…) А правило «первое число равно (3), а каждое следующее число в два раза больше предыдущего» формирует последовательность: (3; 6; 12; 24; 48….)
Ниже разобраны несколько разных способов задания числовых последовательностей.
Числа, образующие последовательность, называются ее членами
(или элементами). И каждое из этих чисел имеет свой порядковый номер.
Например, в последовательности (3; 6; 12; 24; 48…) тройка является первым членом (порядковый номер – один), шестерка – вторым (ее номер по порядку равен двум), двенадцать – третьим и т.д.
В математике последовательность обозначают маленькой латинской буквой, а каждый отдельный ее элемент – той же буквой с числовым индексом равным порядковому номеру этого элемента.
То есть, если последовательность (3; 6; 12; 24; 48…) обозначить как (a_n), то можно записать, что (a_1=3), (a_2=6), (a_3=12), (a_4=24) и так далее.
Иными словами, для последовательности (a_n={ 3;: 6; :12; : 24; : 48; : 96; : 192; : 384…}).
|
порядковый номер элемента |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
… |
|
обозначение элемента |
(a_1) |
(a_2) |
(a_3) |
(a_4) |
(a_5) |
(a_6) |
(a_7) |
(a_8) |
… |
|
значение элемента |
(3) |
(6) |
(12) |
(24) |
(48) |
(96) |
(192) |
(384) |
… |
Отметим, что членами последовательности необязательно должны быть различные числа. Она может состоять из одних и тех же чисел, например, выглядеть вот так: (1; : 1; : 1; : 1…) .
Способы задания числовых последовательностей
Все способы формирования числовых последовательностей можно разделить на три большие группы:
— I способ: словесный. Здесь все просто – в буквальном смысле словами описывается каким образом можно вычислить элементы искомой последовательности.
Пример: Напишите первые пять членов последовательности квадратов натуральных чисел.
Решение: Натуральными называют числа, возникающие естественным образом при счете количества предметов, то есть: (1; : 2; : 3; : 4; : 5) и т.д. Нашу же последовательность формируют квадраты этих чисел, то есть (1^2;: 2^2; : 3^2; : 4^2; : 5^2…) . Таким образом, имеем ответ: (1; : 4; : 9; : 16; : 25…)
Ответ: (1; : 4; : 9; : 16; : 25…)
Отметим, что последовательности в начале статьи заданы именно словесным способом.
— II способ: аналитический (формулой энного члена). Тут значение каждого элемента последовательности вычисляется по некоторой формуле, в которую подставляется порядковый номер этого элемента.
Пример: Последовательность задана формулой: (b_n=frac{n-1}{n^2}). Вычислите первые пять членов этой последовательности.
Решение: Вычислим (b_1). Это первый член последовательности, то есть его порядковый номер (n) равен единице. Тогда его значение равно (b_1=frac{1-1}{1^2} =frac{0}{1}=0).
У второго члена (n=2), то есть его значение равно (b_2=frac{2-1}{2^2} =frac{1}{4}).
Третий ((n=3)): (b_3=frac{3-1}{3^2} =frac{2}{9}).
Четвертый ((n=4)): (b_4=frac{4-1}{4^2} =frac{3}{16}).
Пятый ((n=5)): (b_5=frac{5-1}{5^2} =frac{4}{25}) .
Готово. Можно писать ответ.
Ответ: (b_n= {0; : frac{1}{4}; : frac{2}{9}; : frac{3}{16}; : frac{4}{25}…}).
Обратите внимание, что при таком задании последовательности, значение каждого элемента зависит только от его порядкового номера. И поэтому, если нам нужно вычислить, например, пятнадцатый элемент, мы можем это сделать сразу, не вычисляя предыдущие четырнадцать.
Пример: Последовательность задана формулой: (a_n=8+5n-n^2). Вычислите (a_9).
Решение: Нужно вычислить значение девятого элемента, то есть порядковый номер (n=9). Подставляем в формулу: (a_9=8+5·9-9^2=8+45-81=-28).
Ответ: (a_9=-28).
III способ: рекуррентное соотношение. Звучит страшно, но суть проста – здесь дается начало последовательности (один или несколько первых элементов) и правило, по которому из предыдущего (или нескольких предыдущих) членов последовательности можно вычислить следующий.
Пример: Последовательность задана условиями: (c_1=4), (c_{n+1}=c_n+3). Вычислите первые пять членов этой последовательности.
Решение: Первый член нам известен: (c_1=4).
Второй мы получим, подставив в формулу вместо (n) единицу: (c_{1+1}=c_1+3)
(c_2=c_1+3=4+3=7)
Третий ((n=2)): (c_{2+1}=c_2+3 )
(c_3=c_2+3=7+3=10).
Четвертый ((n=3)): (c_{3+1}=c_3+3)
(c_4=c_3+3=10+3=13).
Пятый ((n=4)): (c_{4+1}=c_4+3)
(c_5=c_4+3=13+3=16).
Нужные пять элементов вычислены. Теперь можно записывать ответ.
Ответ: (c_n={4; : 7; : 10; : 13; : 16…}).
В этом примере мы по сути получали следующий элемент из предыдущего путем прибавления к предыдущему тройки. Логично, ведь формула (c_{n+1}=c_n+3) требовала именно этого. В ней (c_n) – это предыдущий элемент, а (c_{n+1}) – следующий за ним (ведь его номер на единицу больше).
На практике могут встречаться более сложные формулы, в которых следующий элемент вычисляется из двух, трех или даже большего количества предыдущих.
Пример: У последовательности известны первые два элемента (z_1=2;) (z_2=5). Так же известна формула следующего элемента (z_{n+2}=3z_{n+1}-z_n). Вычислите значения третьего, четвертого и пятого членов.
Решение: Слева будем писать текущую последовательность, а справа вести вычисления очередного элемента.
|
Последовательность на данный момент: |
Вычисления: |
||||||||||||
|
Так как формула дана для элемента с номером (n+2), то чтобы найти (z_3) нужно подставлять вместо (n) единицу:
|
||||||||||||
|
Теперь найдем (z_4), подставив вместо (n) двойку: (z_{2+2}=3z_{2+1}-z_2) (z_4=3z_3-z_2=3·13-5=34) |
||||||||||||
|
Наконец вычисляем (z_5), подставляя вместо (n) тройку: (z_{3+2}=3z_{3+1}-z_3) (z_5=3z_4-z_3=3·34-13=89) |
||||||||||||
|
Готово. Можно писать ответ. |
Ответ: (c_3=13); (c_4=34); (c_5=89).
Важное отличие рекуррентного способа задания последовательности от аналитического – при рекуррентном мы не можем посчитать следующий элемент, не зная предыдущих. То есть, если нам нужно вычислить, например, пятнадцатый элемент, придется сначала вычислить все, что идут до него.
Как определить является ли число элементом последовательности?
Во всех предыдущих примерах мы находили значения элементов последовательности – чему равен третий, пятый или девятый член. Иначе говоря, выясняли какое именно число стоит в последовательности на таком-то месте.
Но в практике встречается также обратная задача – значение известно и надо выяснить, есть ли оно среди элементов некоторой последовательности? А если есть, то на каком месте?
Пример (ОГЭ): Какое из чисел ниже есть среди членов последовательности (a_n=n^2-n):
а) (1) б) (3) в) (6) г) (10) ?
Решение: Из условия задачи понятно, что одно из этих чисел точно является элементом последовательности. Поэтому мы можем просто вычислять элементы по очереди, пока не найдем нужный:
(a_1=1^2-1=0) – мимо.
(a_2=2^2-2=2) – тоже не то.
(a_3=3^2-3=6) – есть!
Нужный элемент найден.
Ответ: (6).
Такой метод решения годится только если заранее известно, что элемент точно в последовательности есть. Потому что если его вдруг там нет – это можно проверять вечность, последовательность ведь бесконечна!
Поэтому в такой ситуации пользуются следующим алгоритмом:
-
Подставляют заданное число в формулу (n) -го члена вместо (a_n);
-
Решая полученное уравнение, находят неизвестное (n);
-
Если (n) – натуральное, то данное число — член последовательности.
Пример: Выяснить, является ли число (3) членом последовательности (a_n=)(frac{51+2n}{n+4}) ?
Решение:
|
(a_n=)(frac{51+2n}{n+4}) |
Если число (3) – член последовательности, то значит при некотором значении (n), формула (frac{51+2n}{n+4}) должна дать нам тройку. Найдем это (n) по алгоритму выше. |
|
(3=)(frac{51+2n}{n+4}) |
Решаем это уравнение. Умножаем левую и правую части на знаменатель ((n+4)). |
|
(3cdot (n+4)=51+2n) |
Получилось линейное уравнение. Раскрываем скобки слева. |
|
(3n+12=51+2n) |
Собираем неизвестные слева, числа справа… |
|
(3n-2n=51-12) |
…и приводим подобные слагаемые. |
|
(n=39) |
Готово. Найденное значение – это то число, которое надо подставить вместо (n) в формулу (frac{51+2n}{n+4}), чтоб получилось тройка (можете проверить это сами). Значит (39)-ый член последовательности равен трем. |
Ответ: Да, число (3) является элементом данной последовательности.
Смотри также:
Арифметическая прогрессия
Геометрическая прогрессия
В курсе высшей математики в теме «Ряды» возникает задача о нахождении общего члена ряда или задача о последующих членах ряда, если задано несколько первых членов. Задача не простая. Особенно, если последовательность хитрая. Решить такую задачу бывает не просто. Вот почему, такие же задачки иногда предлагают в тестах на сообразительность или при проверке коэффициента IQ. Теперь вы сможете и задачи по вышке решать легко и интеллект показать при прохождении тестов. Для этого вам просто надо воспользоваться нашим решателем. Сделать это очень просто. Вводите через запятую известные члены последовательности и добавляете в конце три точки, а затем нажимаете кнопку «решить» и получаете результат, если закономерность существует. В качестве ответа вы получите формулу общего члена ряда и продолжение вашей последовательности. Примеры последовательностей приведены ниже.
1, 4, 9, 16, 25, ...1, -1, 1, -1, 1, ...5, 14, 23, 32, 41, ...А вот пример посерьезнее:
1, 2, 3, 2, 1, 2, 3, 2, 1, ...Или вот такая последовательность — любителям математики:
118, 199, 226, 235, ...И на закуску, совсем жесткая последовательность:
3, 2, 1, 7, 4, 1, 1, 8, ...Наш решатель справляется даже с такой головоломкой.
Правда, с некоторыми головоломками решатель может и не справиться… Пишите в комментариях решенные вами головоломки или те, которые не удалось решить…
Похожие публикации
2015-11-27 • Просмотров [ 30216 ]
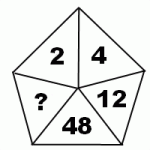
Числа в многоугольнике — один из вариантов оформления заданий из тестов iq. Чтобы найти, какое число следующее в последовательности чисел, заключенных в многоугольник, нужно определить связывающую их закономерность.
Рассмотрим примеры, в которых требуется найти числа в многоугольнике.
Найти пропущенное число
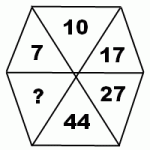
1) Закономерности, связывающие числа в многоугольнике, могут быть самыми разными. Например, это может быть связь последовательно идущих чисел по часовой стрелке или против часовой стрелки, а также чисел, стоящих через одно или два числа, чисел, стоящих напротив друг друга и т.д. Поскольку в данном задании нужно найти всего одно число, можно предположить, что все числа связаны одной закономерностью, а не несколькими. Попробуйте определить, как связаны числа в данном 6-угольнике, и найти, какое число следующее. (Ответ и объяснения скрыты под спойлером).
Показать решение
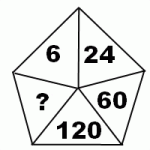
Какое число следующее?
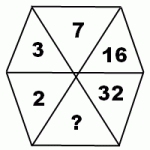
2) Еще одно задание на многоугольник с числами.
Показать решение
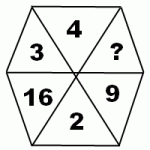
Найти пропущенное число
3)Показать решение
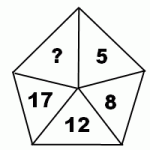
Какое число следующее?
4)Показать решение
Вставьте пропущенное число
5)Показать решение
Какое число следующее?
6)Показать решение
Какое число в многоугольнике пропущено?
7)Показать решение
Как видите, в таких заданиях закономерность, которой связаны числа в многоугольнике, может быть различна. Самый быстрый и эффективный способ научиться решать тестовые задачи — придумывать аналогичные задания самостоятельно. Составляя задачи, подчиненные самым разным закономерностям, вы будете готовы видеть такого рода закономерности и тестах.
Если ваша задача — развитие способностей ребенка, то сначала рассмотрите с ним готовые примеры, обсудите возможные варианты их решения. После этого предложите ему придумать задачи на связь чисел в многоугольнике самому.
Общий член ряда представляе собой рациональную дробь. Выполним разложение дроби на простейшие с помощью метода неопределенных коэффициентов:
$$ frac{1}{(2n+1)(2n+3)} = frac{A}{2n+1} + frac{B}{2n+3} = frac{A(2n+3)+B(2n+1)}{(2n+1)(2n+3)} $$
Приравниваем числитель последней дроби к числителю первой дроби:
$$ A(2n+3)+B(2n+1) = 1 $$
Раскрываем скобки:
$$ 2An + 3A + 2Bn + B = 1 $$
Теперь определяем находим неизвестные коэффициенты:
$$ begin{cases} n^0: &2A+2B=0 \ n^1: &3A+B=1 end{cases}Rightarrow begin{cases} A=frac{1}{2} \ B=-frac{1}{2} end{cases} $$
После разложения общий член ряда записывается следующим образом:
$$ a_n =frac{1}{(2n+1)(2n+3)}=frac{1}{2} frac{1}{2n+1} — frac{1}{2} frac{1}{2n+3} $$
Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$
$$ a_1 = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) $$
$$ a_2 = frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) $$
$$ a_3 = frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) $$
$$ …………………………………. $$
$$ a_{n-1}=frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) $$
$$ a_n = frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) $$
| Замечание |
|
Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $. Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок. |
Итого, получаем:
$$ S_n = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) + frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) + frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) + … $$
$$ … + frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) + frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) = $$
Выносим дробь одну вторую $ frac{1}{2} $ за скобки:
$$ = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9} … + $$
$$ + … frac{1}{2n-1} — frac{1}{2n+1} + frac{1}{2n+1} — frac{1}{2n+3} bigg) = $$
Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:
$$ S_n = frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) $$
Теперь осталось вычислить предел частичной суммы $ S_n $. Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:
$$ S=lim_{ntoinfty} S_n = lim_{ntoinfty} frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = $$
$$ = frac{1}{2} lim_{ntoinfty} bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = frac{1}{2} cdot frac{1}{3} = frac{1}{6} $$
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
- Как называют числа, используемые при счёте предметов? — натуральные числа
- Есть ли среди натуральных чисел наименьшее число? Наибольшее число? В случае утвердительного ответа назовите это число. Наименьшее число натурального ряда — 1. В натуральном ряду нет наибольшего числа — этот ряд бесконечен.
- Опишите ряд натуральных чисел. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, …
- Каждое ли число в ряду натуральных чисел имеет:
- последующее число — да, каждое натуральное число имеет последующие, которое на 1 больше предыдущего. Например, для числа 5 последующим будет 6 (5 + 1 = 6)
- предыдущее число? — предыдущее число имет все натуральные числа кроме 1. Оно будет на 1 меньше исходного. Например для числа предыдущим числом будет 4 (5 — 1 = 4)
Решаем устно
1. Сложите:
- 48 + 7 = 55
- 16 + 9 = 25
- 25 + 34 = 59
- 52 + 49 = 101
2. Вычтите:
- 14 — 6 = 8
- 23 — 7 = 16
- 32 — 8 = 24
- 45 — 19 = 26
3. Умножьте:
- 12 • 4 = 48
- 5 • 20 = 100
- 13 • 6 = 78
- 10 • 100 = 1000
4. Разделите:
- 36 : 12 = 3
- 55 : 11 = 5
- 96 : 8 = 12
- 160 : 20 = 8
5. Около школы растут каштаны и тополя. Каштанов растёт семь, а тополей — в 3 раза больше. Сколько деревьев растёт около школы?
7 + 7 • 3 = 7 + 21 = 28 (деревьев) — растёт около школы.
Ответ: 28 деревьев.
6. В школе учатся 370 учеников. Найдутся ли среди них хотя бы два ученика, которые отмечают день рождения в один и тот же день?
Да, так как в году максимально может быть 366 дней (в високосный год).
370 > 366, значит у нескольких учеников дни рождения будут отмечаться в один и тот же день.
Упражнения
1. Назовите 14 первых натуральных чисел.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14
2. Какого числа не хватает в записи натурального ряда чисел: 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, … ?
В записи натурального ряда не хватает числа 8.
3. Из чисел 5, , 8, 129, 0,
, 4 128,
— выберите натуральные.
5, 8, 129, 4 128
4. Запишите число, которое в натуральном ряду следует за числом: 1) 34; 2) 246; 3) 8 297.
- за числом 34 следует число 35
- за числом 246 следует число 247
- за числом 8 297 следует число 8 298
5. Запишите число, которое в натуральном ряду следует за числом: 1) 72; 2) 121; 3) 6 459.
- за числом 72 следует число 73
- за числом 121 следует число 122
- за числом 6 459 следует число 6 460
6. Запишите число, которое в натуральном ряду является предыдущим числу: 1) 58; 2) 631; 3) 4 500.
- предыдущим к числу 58 является число 57
- предыдущим к числу 631 является число 630
- предыдущим к числу 4 500 является число 4 499
7. Запишите число, которое в натуральном ряду является предыдущим числу: 1) 42; 2) 215; 3) 3 240.
- предыдущим к числу 42 является число 41
- предыдущим к числу 215 является число 214
- предыдущим к числу 3 240 является число 3 239
8. Сколько чисел стоит в натуральном ряду между числами: 1) 6 и 24; 2) 18 и 81?
- между числами 6 и 24 стоит 17 натуральных чисел: 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23.
- между числами 18 и 81 стоит 62 натуральных числа: 19, 20, 21, …, 78, 79, 80.
9. Сколько чисел стоит в натуральном ряду между числами: 1) 13 и 28; 2)29 и 111?
- между числами 13 и 28 стоит 14 натуральных чисел: 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27.
- между числами 29 и 111 стоит 81 натуральное число: 30, 31, 32, …, 108, 109, 110.
10. Некоторое натуральное число, большее 3, обозначили буквой а. Запишите для числа а два предыдущих и три последующих натуральных числа.
Если а — данное натуральное число, большее трёх, то первое предыдущее число для него будет (а — 1), а второе предыдущее — (а — 2). Три последующих числа будут записаны так: (а + 1), (а + 2) и (а + 3).
Проверка: Пусть а = 15. Тогда:
- 15 — 1 = 14 — первое предыдущее число
- 15 — 2 = 13 — второе предыдущее число
- 15 + 1 = 16 — первое последующее число
- 15 + 2 = 17 — второе последующее число
- 15 + 3 = 18 — третье последующее число.
Упражнения для повторения
11. Вычислите:
12. Первое летописное упоминание о Москве встречается в Ипатьевской летописи в 1147 г. Сколько лет прошло от первого летописного упоминания Москвы?
Ответ: От первого летописного упоминания Москвы прошло 873 года.
13. Выполните действия:
14. Собираясь в гости к своей бабушке, Карлсон решил подкрепиться. Для этого на завтрак он съел 26 банок варенья, а на обед — на 16 банок больше. Сколько банок варенья съел Карлсон?
1) 26 + 16 = 42 (банки) — Карлсон съел на обед.
2) 26 + 42 = 68 (банок) — съел Карлсон
Ответ: Карлсон съел 68 банок варенья.
15. На одном участке растут 34 куста смородины, а на другом — на 18 кустов меньше. Сколько всего кустов смородины растёт на двух участках?
1) 34 — 18 = 16 (кустов) — растёт на втором участке.
2) 34 + 16 = 50 (кустов) — растёт на двух участках.
Ответ: На двух участках растёт 50 кустов.
Задача от мудрой совы
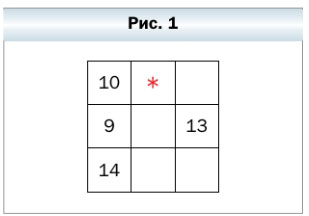
16. В квадрате (рис. 1) суммы чисел в каждом столбце, в каждой строке и диагоналях должны быть одинаковыми. Найдите число, которое должно быть записано вместо звёздочки.
1) Посчитаем сумму чисел в одном столбце. Все цифры у нас известны в первом столбце:
10 + 9 + 14 = 33
Это значит, что в кадом столбце, строке или диагонали сумма чисел должна равняться 33.
2) Рассмотрим вторую строку. У нас известно два числа и общая сумма. Найдём неизвестное число:
33 — (9 + 13) = 33 — 12 = 11 — число в середине второй строки.
3) Рассмотрим диагональ от нижнего левого угла до верхнего правого угла:
33 — (14 + 11) = 33 — 25 = 8 — число в верхнем правом углу.
4) Рассмотрим третий столбец:
33 — (8 + 13) = 33 — 21 = 12 — число в нижнем правом углу
5) Рассмотрим нижнюю строку:
33 — (14 + 12) = 33 — 26 = 7 — число в середине нижней строки.
6) Рассмотрим средний столбец:
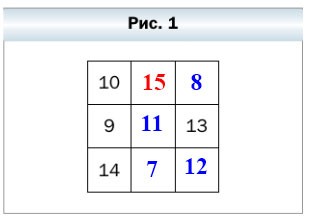
33 — (11 + 7) = 33 — 18 = 15 — искомое число на месте звёздочки.
Ответ: На месте звёздочки надо написать число 15.
Комментарий: На самом деле для поиска искомого числа достаточно было выполнить первые три действия, а затем вычислить искомое рассмотрев верхнюю строчку. Остальные неизвестные, согласно заданию, искать было не обязательно.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта