Тема: Как найти неизвестное слагаемое.
Цель: создать необходимые условия для вывода обучающимися правила нахождения неизвестного слагаемого.
Задачи:
Образовательная: познакомить с правилом, позволяющим находить корень уравнения, если неизвестным является одно из двух слагаемых.
Развивающая: совершенствовать вычислительные навыки; развивать логическое мышление и внимание;
Воспитательная: воспитывать любовь к предмету, дисциплинированность во время урока;
Регулятивные: получают возможность контролировать свою деятельность, адекватно оценивать свои достижения. Познавательные: слушать и читать, извлекая нужную информацию, а также самостоятельно находить правильное решение примеров.
Личностные УУД: формировать положительное отношение к учению, к познавательной деятельности, желание приобретать новые знания, умения, совершенствовать имеющиеся, осваивать новые виды деятельности.
Содержание урока
|
Этапы урока |
Деятельность учителя |
Деятельность обучающихся |
УУД |
|
-Здравствуйте, ребята! Быстро, но тихо садитесь. |
Приветствуют учителя. |
Коммуникативные: Планирование учебного сотрудничества с педагогом и со сверстниками. |
|
-Постарайтесь все понять, Учитесь тайны открывать, Ответы полные давать, Чтоб за работу получать Только лишь отметку «пять»! |
Настраиваются на плодотворную и эффективную работу на уроке. |
Личностные: Выражать положительное отношение к процессу познания, проявлять желание проявлять новое. |
|
-Урок наш начнем с устного счета. -Найдите значение первого выражения. 43-17=26 -Найдите значение второго выражения. 57-46=11 -Найдите значение третьего выражения. 30-16=14 -Найдите значение четвертого выражения. 37+42=79 -Найдите значение пятого выражения. 25+18=43 -Найдите значение шестого выражения. 78-65=13 -Найдите значение седьмого выражения. 82-46=36 -Найдите значение восьмого выражения. 23+15=38 |
43-17=26 57-46=11 30-16=14 37+42=79 25+18=43 78-65=13 82-46=36 23+15=38 |
Познавательные: Самостоятельно выделять и формулировать познавательные задачи; с помощью деятельностного метода исследования. |
|
Решите следующую задачу. -Я прочитаю сейчас задачу, а вы внимательно слушайте. «Одна тыква легче другой на 2 кг и весит 8 кг. Сколько весят обе тыквы?» -Что известно в задаче? -Что нужно найти в задаче? -Решите задачу. -Объясните решение этой задачи. |
Известно, что одна тыква легче другой на 2 кг и весит 8 кг. В задаче нужно найти сколько весят обе тыквы. 1)8+2=10 (кг)-весит вторая тыква. 2)10+8=18 (кг)-весят обе тыквы. Ответ: 18 килограмм. |
Коммуникативные: Развивать умение использовать речь для решения примеров и задач, задавать вопросы. |
|
-Следующая задача логическая, слушайте внимательно. «Велосипедист проехал на двухколёсном велосипеде 14 км. Сколько километров проехало каждое колесо?» -Решите задачу. -Почему? |
Каждое колесо проехало 14 километров. Потому что колеса на одном транспорте, они едут одновременно с одинаковой скоростью. |
Регулятивные: Прогнозировать результат решения практической учебной задачи. |
|
—Разгадайте ребус. — Какое слово зашифровано? Как вы рассуждали? — Что такое уравнение? -Что такое корень? -Способом подбора найдите корень уравнения х+10=30 — Как называются числа при сложении? Какой компонент неизвестен в этом уравнении? |
Зашифровано слово уравнение. Равенство, содержащее неизвестное, называется уравнением. Корень уравнения – это число, чему равен х. Корнем уравнения является число 20. Первое слагаемое, второе слагаемое, значение суммы. Неизвестно первое слагаемое. |
|
|
-На устном счете активно работали … — Остальным желаю быть активнее! |
||
|
— Как вы думаете, открытию, какой закономерности будет посвящён урок? — Откройте учебник на странице 77 и прочитайте тему урока. -Определите цель урока. |
Нахождение неизвестного слагаемого. Научиться находить неизвестное слагаемое. Вывести правило для нахождения неизвестного слагаемого. |
Познавательные: Самостоятельно формулировать тему урока. |
|
-Откройте свои рабочие тетради и запишите число и классную работу. Сегодня 3 апреля. |
Записывают число и классную работу. |
|
|
-Найдите задание №1. Громко и четко прочитает задачу… -Что известно в задаче? -Что требуется узнать? -Составим краткую запись к этой задаче. -Сколько тетрадей было в I пачке? -Ставим 17 т. -Сколько тетрадей было во II пачке? -Обозначим число тетрадей во II пачке, т.к. неизвестно через х. -Что еще нам известно в задаче? -Объединяем 2 пачки фигурной скобкой и ставим 42 т. -Составим круговую схему по этой задаче. -Какое число поставим в синее окно? -Почему? -Какое число поставим в желтое окно? —Что нужно узнать? -В розовом окне какие будут тетради? -Мы знаем сколько тетрадей во II пачке? -Вместо вопроса мы поставим знак х. |
«В открытой пачке лежало 17 тетрадей, а число тетрадей во второй пачке неизвестно. Учительница сказала, что всего в двух пачках 42 тетради. Сколько тетрадей в двух пачках?» Известно, что в открытой пачке лежало 17 тетрадей, а всего в 2х пачках 42 тетради. Требуется узнать количество тетрадей во второй пачке. I пачка – 17 т. 42 т. II пачка – х т. Неизвестно. Известно, что всего было 42 тетради. 42 Потому что это сумма. 17 Сколько было тетрадей во II пачке. Которые находятся во II пачке. Нет. |
|
|
— Первое слагаемое 17, второе слагаемое – неизвестное число х, а значение суммы 42. Составьте и запишите соответствующее уравнение. -Какое запишем уравнение? |
17+х=42 х=42-17 х=25 |
|
|
-Знак какого действия стоит в уравнении между известным числом и неизвестным? |
Знак действия сложения. |
|
|
-Нам нужно найти неизвестное число. -Смотрим на круговую схему. -Как называются компоненты при сложении? -Определим каким знаком соединяет стрелка квадратики с известными числами. -Какой компонент нам неизвестен? -Записывают это так: второе слагаемое = из суммы 42 вычитаем первое слагаемое 17. Вычитаем. -42-17 сколько получаем? -25-это корень уравнения. -Ребята, как же найти неизвестное слагаемое? -Посмотрите на правило которое выделено розовым цветом на следующей странице. -Громко и четко правило прочитает… -Читаем все вместе хором. -Кто сможем повторить данное правило? |
Первое слагаемое, второе слагаемое, значение суммы. 17+… 42-… Второе слагаемое х 17+х=42 х=42-17 х=25 25 Из суммы вычесть известное слагаемое. |
|
|
Физминутка |
-Сейчас с вами немного отдохнем. Все встали. В уравненьях всё в порядке, Ну а нам нужна зарядка. Мы немножко отдохнём, Физкультминутку проведём. Мы семь раз в ладоши хлопнем, Восемь раз ногами топнем. Прибавляем три к семи Столько мы присесть должны. |
Повторяют движения за учителем. |
|
|
-Найдите задание №5, посмотрите на данную схему. -По данной схеме нам нужно составить и решить уравнение. -Назовите слагаемые и значение суммы. -Для нахождения неизвестного слагаемого составьте уравнение. -Как найди неизвестное слагаемое? -Найдите неизвестное слагаемое х + 25 = 60 используя новое правило. -К доске пойдет решить данное уравнение с объяснением пойдет… -Все остальные слушают внимательно и записывают решение уравнения в тетрадь. -Чтобы убедиться, что мы не ошиблись, нужно выполнить проверку. Для этого нужно вместо неизвестного числа подставить корень уравнения 35 и выполнить сложение. Если наша полученная сумма равняется сумме уравнения, то уравнение мы решили верно. Снизу записываем 60=60, знак равенства должно быть под знаком равенства. |
Слагаемые х и 25, значение суммы 60. х + 25 = 60 Из суммы вычесть известное слагаемое. х+25=60 х=60-25 х=35 35+25=60 60=60 |
|
|
-Найдите задание №6, громко и четко прочитает задание… -Какой компонент в первом уравнении нам неизвестен? -Как найти второе слагаемое? -К доске пойдет решать первое уравнение с объяснением пойдет… -На какие знания будем опираться? — Какое число можно назвать корнем уравнения? -Все остальные отступили 3 клеточки вправо и запишите уравнение. -Какой компонент неизвестен во втором уравнении? -Как найти первое слагаемое? — К доске пойдет решать следующее уравнение с объяснением пойдет… -Все остальные отступили 2 клеточки ниже и запишите уравнение. -Какой компонент неизвестен в последнем уравнении? -Как найти второе слагаемое? — К доске пойдет решать последнее уравнение с объяснением пойдет… -Все остальные отступили 3 клеточки вправо и запишите уравнение. |
Второе слагаемое. Из суммы вычесть первое слагаемое. Правило нахождения неизвестного слагаемого. Число является корнем уравнения, если при подстановке его вместо х в уравнение получаем верное равенство. 150+х=255 х=255-150 х=105 Первое слагаемое. Из суммы вычесть второе слагаемое. х+36=86 х=86-36 х=50 Второе слагаемое. Из суммы вычесть первое слагаемое. 10+х=20 х=20-10 х=10 |
|
|
-Найдите задание №7, громко и четко задание прочитает… -Выполнить данное задание к доске с объяснением пойдет… -Кто может рассказать нам правило нахождения неизвестного слагаемого? |
х+57=90 х=90-57 х=33 |
|
|
-Найдите задание №8, громко и четко задание прочитает… -Что известно в задании? -Какое действие выполняется? -Назовите компоненты действия сложения -Составить и решить уравнение пойдет к доске… -Что неизвестно в уравнении? -Как найти второе слагаемое? |
Что к 264 прибавили неизвестное число и получили 576. Действие сложения. Второе слагаемое. От суммы вычесть первое слагаемое. |
|
А) инструктаж по выполнению самостоятельной работы. |
-А сейчас проведём небольшую самостоятельную работу. Послушайте внимательно. -Работа по вариантам. Поднимите руки 1 варианта, опустите. Посмотрите внимательно на слайд. Вы решаете уравнение х + 18 = 93 вместе с проверкой. -Поднимите руки 2 варианта, опустите. -Посмотрите внимательно на слайд. Вы решаете уравнение 34 + х =60 вместе с проверкой. — Уравнение I варианта пойдет решать … — Уравнение II варианта пойдет решать … -Отступите 2 клеточки вниз и приступайте к работе. |
Слушают учителя. I вариант: х+18=93 х=93- 18 х=75 75+18=93 93=93 II вариант: 34+х=60 х=60-34 х=26 34+26=60 60=60 |
|
|
Б) проверка самостоятельной работы. |
-Проверим самостоятельную работу. — Ваше мнение, как выполнена самостоятельная работа? -У кого не так исправьте. -Молодцы, присаживайтесь. |
Проверяют как выполнили самостоятельную работу учащиеся у доски. |
Регулятивные: Совместно с учителем и одноклассниками давать оценку выполнения работы. |
|
— Подведём итог урока. — С каким правилом познакомились на уроке? — Где мы можем применить это правило? |
Научиться находить неизвестное слагаемое. Вывести правило для нахождения неизвестного слагаемого. Для решения уравнений. |
Регулятивные: Выделение и осознание обучающимися того, что уже усвоено. |
|
— Ребята, спасибо Вам за урок, за старание и стремление к знаниям, которые помогли нам сегодня вновь совершить новое открытие в математике. — Хочу поставить сегодня за урок оценку 5… |
Слушают учителя. |
Регулятивные: Совместно с учителем и одноклассниками давать оценку своей деятельности на уроке |
|
-Если вы считаете, что вы работали сегодня на уроке хорошо, все было ясно и понятно и чисто написано в тетради, то нарисуйте на полях простым карандашом веселый смайлик. -Если вы считаете, что вы не активно работали на уроке и у вас неопрятно в тетради, то нарисуйте на полях простым карандашом грустный смайлик. |
Самостоятельно оценивают себя на уроке. |
Личностные: рефлексия способов и условий действия, контроль и оценка процесса результатов деятельности. Регулятивные: Совместно с учителем и одноклассниками давать оценку своей деятельности на уроке |
|
-Запишите домашнее задание: тетрадь на печатной основе стр. 36 задания №1- №3. -Урок окончен, до свидания! |
Записывают домашнее задание. |
Конспект
урока по математике, проведенного в 2 «В» классе МБОУ КСОШ № 1 студенткой 2 «А»
уск. курса
ГБПОУ
РО «КонстПК», специальность 44.02.02 Преподавание в начальных классах
Патриной
Татьяной Александровной
Дата:
6.04.2017
Класс:
2 «В»
Тема:«Как найти
неизвестное слагаемое».
Цель:создать
необходимые условия для знакомства с правилом, позволяющим находить корень
уравнения, если неизвестным является одно из двух слагаемых;
Задачи:
Образовательные:
-совершенствование вычислительных навыков, навыков устного счёта;
-учить детей решать уравнения,
находить неизвестное слагаемое;
-закреплять умения выполнять
сложение и вычитание однозначных чисел с переходом через десяток.
Развивающие:
— развивать умение составлять уравнения, находить корень уравнения
и выполнять проверку правильности вычисления.
— развивать быстроту счета,
умение самостоятельно мыслить;
—
развивать умение самоконтроля, взаимоконтроля, математически
грамотную речь;
Воспитательные:
-воспитывать
познавательный интерес к предмету;
— чувства
взаимопомощи, взаимосотрудничества;
Формирование
УУД:
Познавательные УУД:
·
Умение выполнять, анализировать объекты с
целью выделения признаков, по заданным критериям;
Коммуникативные УУД:
·
Умение оформлять свою мысль в устной
форме; слушать и понимать речь других;
·
Умение планировать учебное сотрудничество
с учителем и со сверстниками;
Регулятивные УУД:
·
Умение организовывать свое рабочее место
под руководством учителя;
·
Умение высказывать свое предположение
(версию);
·
Умение вносить необходимые дополнения,
исправления в свою работу, если она расходится с образцом;
·
Умение работать по предложенному учителем
плану;
Личностные УУД:
·
Выполнять самооценку на основе критерия
успешности учебной деятельности;
Познавательные УУД:
·
Умение выполнять, анализировать объекты с
целью выделения признаков, по заданным критериям;
Метапредметные:
Коммуникативные УУД:
·
Умение оформлять свою мысль в устной
форме; слушать и понимать речь других;
·
Умение планировать учебное сотрудничество
с учителем и со сверстниками;
Регулятивные УУД:
·
Формировать
умения определять и формулировать цель на уроке с помощью учителя;
·
Работать по
коллективно составленному плану;
·
Оценивать
правильность выполнения действия на уровне адекватной ретроспективной оценки;
·
Вносить
необходимые коррективы в действие после его завершения на основе его оценки и
учета характера сделанных ошибок;
·
Высказывать
своё предложение;
Личностные УУД:
·
Выполнять самооценку на основе критерия
успешности учебной деятельности;
Методы обучения:
словесная, наглядная, частично-поисковая;
Формы организации познавательной
деятельности:
·
Фронтальная;
·
Индивидуальная;
План урока:
I.
Организационный момент.
1) Приветствие
2) Знакомство
II.
Устный счет.
1) Нахождение
значений выражений.
2) Решение
задачи в стихах
3) Решение
задач
4) Нахождение
значения выражения
5) Итого
устного счета
III.
Сообщение темы и цели урока
IV.
Изучение нового материала
1)Выполнение
зад. № 1 стр.77
2)Выполнение
зад. № 2 стр.77
3)Выполнение
зад. № 3 стр.77
4)Физминутка
5)
Выполнение зад. № 5 стр. 79
6)Выполнение
зад. № 6 стр.79
7)
Выполнение зад. № 7 стр.79
V.
Закрепление изученного материала
1)
Выполнение зад. № 1,2 стр.36 (рабочая тетрадь)
VI.
Итог урока
2)
Словесное оценивание
3)
Рефлексия
|
Этапы урока |
Формирование УУД |
Деятельность учителя |
Деятельность учащихся |
||||||||||||||||||
|
I. |
|||||||||||||||||||||
|
1.Самоопределение к деятельности. |
Регулятивные: организация рабочего Коммуникативные: планирование учебного |
— Здравствуйте, -Сегодня урок -Быстро, -Встало Заглянуло На урок Математика -Я -Улыбнитесь |
Проверяют готовность к |
||||||||||||||||||
|
II. |
|||||||||||||||||||||
|
1. Нахождение значений |
Познавательные: умение на основе анализа Коммуникативные: умение оформлять свои |
— А Выполним -Проверим -Я буду -Я -Как -В каком -Какое -Найди сумму -Найди -Найди -Какое -Как -Какое -Как |
81 84-3=81 47 69 58 90 53 23 23+7=30 30 30-9=21 |
||||||||||||||||||
|
2.Решение |
Познавательные:Ориентироваться в своей Регулятивные: учиться исправлять |
— Переходим к следующему заданию. -Решим задачу в стихах. «Мы И друзей Мама – пять Папа – Я с А теперь Сколько Для -Так сколько |
14 |
||||||||||||||||||
|
3. Решение задач |
Личностные: развивать Коммуникативные: правильно и точно |
-Теперь выполним -Решим -Слушайте 1. У трех бабушек -Сколько -Сколько -Сколько -Послушайте 2. Слушайте «Стоит в |
4 2 (Ответ: 12 ножек и 6 рожек.) (Ответ:Нисколько) |
||||||||||||||||||
|
4. |
Личностные: учиться обобщать и делать |
Выполним следующее задание. -Если вы правильно выполните вычисление, то разгадаете 23 – 17 = 6 У 57 – 46 = 11 Р 37 + 42 = 79 Е 25 + 18 = 38 – 6 = 32 Е 49 — 24 —Расставьте в порядке возрастания.
—Какое слово зашифровано? |
Уравнение |
||||||||||||||||||
|
5. Итог устного счета |
-Молодцы, отлично поработали, особенно мне понравилось, как -Все остальные включайтесь в активную работу класса. |
||||||||||||||||||||
|
III. |
|||||||||||||||||||||
|
Регулятивные:Определять Коммуникативные:планирование |
— Как в уравнении обычно обозначается неизвестное число? -Ребята, что такое уравнение? — Что такое корень уравнения? -Как вы думаете, какова тема нашего урока? —Сегодня на уроке мы продолжим -Тема урока: «Как найти неизвестное слагаемое?» |
(буквой Х) Уравнение-это числовое Значение Х-са |
|||||||||||||||||||
|
IV. |
|||||||||||||||||||||
|
1. Выполнение зад. № 1 стр.77. 2. Выполнение зад. № 3 стр.77 |
Регулятивные: организовать совместную Познавательные: развивать правильное чтение |
— -Сядьте -Положите — -Запишите -Откройте свои учебники на стр.77-ой, и найдите -Поставьте пальчик. -Вслух громко и четко прочитает задание… «В открытой пачке лежало 17 тетрадей, а число (Пересказываем текст задачи, демонстрируя – Что известно в задаче? — Что требуется узнать? -Что обозначим через Х? – Посмотрите на краткую запись к этой задаче. -Повторите условие задачи по краткой записи Краткая запись: 1п. – 17 т. 2 п. – х т. 17 + х = 42 -Составьте уравнение по условию задачи. -Запишите уравнение. -Назовите компоненты в уравнении. 2). Составить круговую схему для этого уравнения 17 + х = 42
— По уравнению нужно составить круговую схему. -Известное слагаемое вставим в квадрат жёлтого -Неизвестное слагаемое в квадрат красного — Какое число запишем в желтый квадрат? -Что запишем в красный квадрат? -Знак, какого действия стоит в уравнении 17 + х — Квадратики, какого цвета соединяет стрелка со — В какой квадратик должно быть вписано – По составленной круговой схеме найди — В результате его выполнения и будет найдено Записывают это так: 17 + х = 42 х = 25 -42-17 сколько получится? 25 – корень уравнения -Что такое 42? -Что такое 17? -Как нашли неизвестное слагаемое? – Как найти неизвестное слагаемое по значению -Найдите правило на странице 79 в розовом -Послушайте, я его прочитаю. Правило: Если из известного значения суммы вычесть известное -Повторим хором. -Поднимите руку, кто готов повторить -Правильно. Молодцы. — С каким правилом познакомились? |
Оформляют запись числа и (вторую пачку тетрадей) 17 + х = 42 Число 17 Х «+» Голубой — В уравнении 17 + х = 42 одно из слагаемых было неизвестно. Мы нашли Читают правило на стр.79. 25 Сумма Известное слагаемое (Из суммы 42 вычли известное слагаемое 17) Если из известного значения суммы вычесть известное слагаемое, то |
||||||||||||||||||
|
4. |
Личностные: учатся переключать |
—Вы наверное устали, поэтому предлагаю немного В уравненьях всё в порядке, Ну а нам нужна зарядка. Мы немножко отдохнём, Физкультминутку проведём. Мы семь раз в ладоши хлопнем, Восемь раз ногами топнем. Прибавляем три к семи Столько мы присесть должны —Садитесь очень тихо. |
Повторяют за учителем |
||||||||||||||||||
|
5. Выполнение задания №5стр79. |
Познавательные: повторяют компоненты , Регулятивные: вспоминают Коммуникативные: учатся с легкостью Личностные: проверяют свои качества |
—В учебнике найдите № 5 на странице 79-ой.(Устно) -Рассмотрите круговую схему в учебнике. Назовите слагаемые (х и -Для нахождения неизвестного слагаемого составьте уравнение. -Какой компонент неизвестен? -Найди неизвестное слагаемое х + 25 = 60 , используя новое Х + 25 = 60 х = 60 – 25 х = 35 -А как убедиться в том, что мы не ошиблись при вычислении и Записываем на доске: х + 25 = 60 х = 60 – 25 х = 35 35 +25 =60 60=60 -60=60 ,значит уравнение решили верно. |
(Х и 25) (60) Необходимо — Надо вместо х + 25 = 60 х = 60 – 25 х = 35 35 +25 =60 60=60 |
||||||||||||||||||
|
6. 7. |
Коммуникативны: Познавательные: учатся Коммуникативны: Личностные: учатся Коммуникативные: учатся |
Найдите Задание -Первое -Отступите 150+х=255 х=255-150 х=105 150+105=255 255=255 -Какое Как Найдите «Чтобы х+57=90 х=90-57 х=33 33+57=90 90=90 |
105 50 10 (второе) (Из суммы вычесть Х+57=90 Х=90-57 Х=33 33+57=30 90=90 |
||||||||||||||||||
|
V. |
|||||||||||||||||||||
|
1.Выполнение 2.. |
Личностные: Регулятивные: учатся |
-Откройте -Найдите Вслух Задание 1)Рассмотрите 2) Х+12=54 Х=54-12 Х=42Х=5 42+12=54 54=54 — В — Куда -Куда -Найдите -Прочитайте Задание По
|
42- 5- Верхнее(голубое) В правое В левое 1)Х+18=93 Х=75 75-+18=93 93=93 2)34+Х=60 Х=26 34+26=60 60=60 |
||||||||||||||||||
|
VI. |
|||||||||||||||||||||
|
1. 2. |
Познавательные: поиск и Регулятивные:прогнозируют результаты |
— Итак, наш урок подошел к концу. — Чему — Как — —
-Результат — — Как вы |
Мы |
Методист_______________Елжова
В.Н.
Учитель
_____________ Стряпчева О. В.
— Начинаем урок с математической разминки.
Вставь пропущенные числа в «окошечки», чтобы равенства были верными.
40 + … = 56 … + 15 = 55
70 + … = 89 … + 17 = 47
— Найди среди математических записей уравнения. Как узнали? Докажите.
12- 4 128 + 2 = 130
25 • 3 х + 10 = 30
х – 96 4 + х
х + 318 = 921
— Что такое корень уравнения?
— Какое число является корнем уравнения х + 10 = 30? Как узнали?
— Подберите корень к следующему уравнению: х + 318 = 921. Можно ли воспользоваться этим способом, чтобы найти корень этого уравнения?
— Как называются числа при сложении? Какой компонент неизвестен в этом уравнении?
— Как вы думаете, открытию, какой закономерности будет посвящён урок?
— Откройте учебник, отметьте закладкой страницу учебника и прочитайте тему урока. Определите цель урока.
В открытой пачке лежало 17 тетрадей, а число тетрадей в закрытой пачке неизвестно, то есть – х. Всего в двух пачках 42 тетради. Сколько тетрадей в двух пачках?
(Пересказываем текст задачи, демонстрируя лежащие на столе пачки тетрадей).
– Что известно? Что требуется узнать?
– Сделайте краткую запись к этой задаче, обозначив неизвестное число через х.
Запись:
Пачка № 1 – 17 т.
Пачка № 2 – х т.
Всего – 42 т.
— Составьте круговую схему по этой задаче, записав
вместо вопросительного знака букву х.
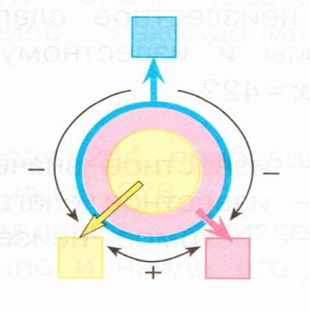
— По круговой схеме составьте и запишите соответствующее уравнение: первое слагаемое 17, второе – неизвестное число, а значение суммы 42.
-Закрась известное слагаемое жёлтым цветом, а неизвестное – красным.
-Знак, какого действия стоит в уравнении 17 + х = 42 между известным числом и неизвестным х? Подчеркни его.
— Квадратики, какого цвета соединяет стрелка со знаком «+» на круговой схеме?
— В какие квадратики должны быть вписаны слагаемые суммы 17+х?
— В какой квадратик должно быть вписано известное значение суммы 42?
-На круговой схеме обведите цветным карандашом стрелку, соединяющую квадратики с известными числами.
– По составленной круговой схеме найди неизвестное число. Для этого определи, каким знаком соединяет стрелка квадратики с известными числами? Запишите действие, на которое указывает эта стрелка. В результате его выполнения и будет найдено искомое неизвестное.
Записывают это так: 17 + х = 42
х = 42 – 17
х = 25
25 – корень уравнения 17 + х = 42
– Как найти неизвестное слагаемое по значению суммы и известному слагаемому в уравнении 17 + х = 42?
— Где мы можем найти подтверждение нашим предположениям? Найдите и прочитайте правило. Повторите его про себя. Перескажите его друг другу.
-Расскажите правило.
— Какое правило сформулировали?
Работа по учебнику. У.2, стр.79 № 5
— Вернёмся к уравнению, которое мы записали в начале урока х + 318 = 921.Самостоятельно найдите неизвестное слагаемое этого уравнения.
-На какие знания будем опираться?
— Выполните проверку правильности нахождения корня уравнения.
— Какое число можно назвать корнем уравнения?
Мы научим решать уравнения быстро и быть уверенными в правильном и успешном результате. Для начала, выучим простые правила и рассмотрим примеры. Самый лёгкий тип уравнений — это у которых слева размещена разность, произведение, частное или сумма чисел и одно неизвестное, а справа — известное число. Если проще, нам надо найти в уравнении одно неизвестное. Неизвестное делимое с делителем, слагаемое или уменьшаемое с вычитаемым. Такие типы уравнений мы рассмотрим далее в статье.
Распишем основные правила для поиска неизвестных слагаемых, множителей, делимых и так далее. Для закрепления теории, мы подобрали конкретные примеры под каждое правило и каждую ситуацию, с которой вы можете столкнуться при решении уравнений такого типа.
Как найти неизвестное слагаемое, правило
Представим, что на столе стоит две вазы. В этих вазах в общей сложности лежит 7 яблок. В одной вазе лежит 2 яблока. Как узнать сколько яблок лежит во второй вазе и есть ли они там вообще? Посмотрим, как выглядит эта задача в математическом виде, отметив неизвестное число яблок во второй вазе как x. Согласно условиям выше, это неизвестное вместе с числом 2 образовывают 7. Значит, наше уравнение будет выглядеть как: 2 + x = 7. Справа имеем значение суммы, а слева — сумма чисел с одним неизвестным слагаемым. Для решения уравнения надо найти число x. В таких случаях используют правило:
Правило 1
Чтобы найти неизвестное слагаемое в уравнении, надо из суммы вычесть известное.
В ситуации, где происходит математическое нахождение неизвестного слагаемого, вычитание является обратный действием по смыслу, относительно сложения. Другими словами, между действиями вычитания и сложения есть математическая связь, и правило нахождения неизвестного слагаемого благодаря этой связи можно отобразить в буквенном виде: если в условии a + b = c, то c − b = a и c − a = b. А если вы видите обратные примеры, такие как c − a = b и c − b = a, то можете быть уверенны в том что a + b = c. Благодаря определению и математической связи, мы можем узнать неизвестное слагаемое, имея только его сумму с известным слагаемым. От перестановки слагаемых, значение не меняется, поэтому неважно какое надо найти слагаемое — первое или второе. Давайте используем это правило на практике, для лучшего понимания теории.
Пример 1
Давайте решим уравнение, которое мы составили выше: 2 + x = 7. С учётом правила, мы должны из суммы обоих слагаемых, 7, вычесть известное, 2. В решении это будет выглядеть так: 7 − 2 = 5.
В решении математических задач и примеров очень важно знать и использовать правильный алгоритм записи таких уравнений:
- Запишем исходное уравнение, на базе математической задачи.
- Применяем подходящее правило и записываем следующее уравнение на его основании.
- Записываем финальное уравнение, где указываем значение ранее неизвестного.
Запись решения по этой последовательности, отображает последовательные замены изначального уравнения равносильными ему по значениям. В итоге мы сможем увидеть в решении весь процесс нахождения неизвестного. Правильная форма записи нашего уравнения будет в виде такого решения:
2 + x = 7,
x = 7 – 2,
x = 5.
Четвертой строкой в решении примера может стать проверка решения, которая даст уверенность в правильности найденного ответа. Подставим найденное значение в исходное уравнение. Берем число 5 и подставляем в пример 2 + x = 7. У нас получится:
2 + 5 = 7.
Так как мы получили правильное исходное уравнение, значит мы решили пример верно. Если бы у нас получило неверное равенство в проверочном примере, например, 2 + 8 = 7, мы бы вернулись к первому пункту алгоритма решения примера. Неверное равенство при проверке указывает на допущенную ошибку в расчётах или неверно подобранном или использованном правиле.
Находим неизвестное уменьшаемое или вычитаемое
Итак, в математических примерах в процессе вычитания и сложения существует нерушимая связь. Эта связь сформулировала правила, благодаря которым можно быстро найти неизвестное — уменьшаемое, если нам известны разность и вычитаемое, или вычитаемое, если мы знаем разность и уменьшаемое. Для каждого случая есть правило, которое мы сейчас рассмотрим вместе с решением примера.
Правила 2 — 3 + примеры
Если прибавить к разности вычитаемое, получим неизвестное уменьшаемое.
Возьмем для примера уравнение x – 1 = 4. В качестве неизвестного сейчас выступает уменьшаемое. Исходя из правила выше, мы к разности 4 добавляем вычитаемое 1. В сумме получаем 5. Значит, изначальное неизвестное уменьшаемое равно 5. Запишем решение по правильному алгоритму:
x – 1 = 4,
x = 4 + 1,
x = 5.
Не лишним будет проверить правильность решения примера путём подстановки найденного числа 5 в исходный пример:
5 – 1 = 4.
Мы получили верное уравнение, значит решение правильное. Можно переходить к изучению следующего правила.
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Используем это правило для нахождения неизвестного вычитаемого в примере 5 – x = 2. Для решения этого уравнения мы определили, что неизвестное является вычитаемым, а значит, в этом случае будем использовать Определение 3. Вычтем из числа 5 известную разность 2 и получим 5 – 2 = 3. Вот так выглядит полная правильная запись решения:
5 – x = 2,
x = 5 – 2,
x = 3.
Давайте убедимся, что мы правильно решили уравнение. Для этого подставим найденное число в исходный пример.
5 – 3 = 2.
Полученное уравнение верное, значит мы правильно нашли неизвестное вычитаемое. Теперь, когда вы выучили базовые правила нахождения неизвестных, мы поделимся с вами более простым способ решения примеров. Для нахождения неизвестного, нам нужно перенести неизвестное по одну сторону знака равности в уравнении, чаще левую, а известные — по другую, например, правую. При этом, когда переносите известное или неизвестное через знак равности, меняете его знак на противоположный. Если на одной из сторон ничего не остаётся, значит там будет стоять число 0. Мы покажем, как это работает на практике.
Есть пример 5 – x = 2, перенесём известные по правую сторону от знака уравнения:
– x = 2 – 5
При решении, получим уравнение:
– x = – 3
Так как в уравнениях всегда ищется неизвестное с положительным знаком, сменим знаки на противоположные в обеих частях уравнения, как бы перенося известное и неизвестное через знак равности, получим:
x = 3
Как видим, найденное значение неизвестного вычитаемого совпадает с тем значением, которое мы нашли при использовании Определения 3. Правило переноса чисел через знак равности со сменой их знака на противоположный работает для всех уравнений без исключения. Можем использовать это правило вместо всех вышеперечисленных.
Находим неизвестный множитель
Рассмотрим два уравнения: 3 ⋅ x = 9 и x ⋅ 2 = 6. И в первом, и во втором примере нужно найти один из неизвестных множителей. Второй множитель и производное — известны. Давайте запомним правило для решения подобных примеров.
Правило 4 + пример
Чтобы найти неизвестный множитель, нужно разделить производное на другой, известный множитель. Смысл этого правила базируется на обратном смысле к операции умножения. Между операциями деления и умножения также есть связь, которая выражается в следующем: если a ⋅ b = c и при этом ни a, ни b не равны 0, то c : a = b и, наоборот, c : b = a.
Найдём неизвестный множитель из уравнения 3 ⋅ x = 9 путём деления известного частного 9 на известный множитель 3. Запишем решение по алгоритму:
3 ⋅ x = 9,
x = 9 : 3,
x = 3.
Выполним подстановку, чтобы проверить правильность результата:
3 ⋅ 3 = 9
Уравнение правильное, это значит, мы верно установили значение неизвестного множителя. Обратите внимание, правило невозможно использовать в случае, если известный множитель равен 0. К примеру, если вам попадётся уравнение x ⋅ 0 = 8, вы не сможете его решить с помощью этого правила. Само уравнение x ⋅ 0 = 8 бессмысленно, так как для его решения нужно было бы разделить 8 на 0, а делить на 0 нельзя.
Подобные ситуации детально рассмотрены в статье о линейных уравнениях. В случае использования Определения 4, по факту мы делим обе части примера на известный множитель, за исключением 0. Согласно более сложному правилу, мы можем делить обе части уравнения на любой множитель, отличный от 0 и это не повлияет на правильность уравнения и на значение его корня. Оба правила согласованы между собой и отражают математическую связь между обеими частями уравнения.
Нет времени решать самому?
Наши эксперты помогут!
Находим неизвестный делитель или делимое
Последний случай, с которым вы можете столкнуться в решении простых математических примеров — как найти неизвестное делимое при известном частном и делителе, и наоборот, как найти делитель, если из уравнения известно значение только делимого и частного. Используя знакомую связь между делением и умножением, сформируем правило для решения подобных примеров.
Правило 5 + пример
Если мы ищем неизвестное делимое, то умножаем частное на делитель. Давайте рассмотрим, как использовать правило при решении практических примеров.
Возьмем для решение уравнение типа x : 2 = 4. Перемножаем делитель 2 и частное 4 между собой, получаем ответ 8. Вот мы и нашли неизвестное делимое. Последовательная запись решения будет выглядеть в виде:
x : 2 = 4,
x = 4 · 2,
x = 8.
Также запишем проверочный пример, подставив найденное делимое 8 в исходное уравнение:
8 : 2 = 4.
Правильность проверочного уравнения указывает на правильность найденного ответа.
Определение 5 можно связать с умножением обеих частей уравнения на один и тот же множитель, отличный от 0. Такие изменения в примере никаким образом не повлияют на корни обеих частей уравнения или итоговое значение его неизвестного. Давайте ознакомимся со следующим правилом.
Правило 6 + пример
Чтобы найти неизвестный делитель, нужно делимое разделить на известное частное. Разберем простой пример ниже.
Возьмём уравнение 10 : x = 5. Разделим делимое 10 на известное частное 5. Получим ответ 2, что и будет значением неизвестного делителя в этом уравнении. В любом случае, уравнение нельзя решать в уме, а нужно обеспечить запись процесса решения по алгоритму:
10 : x = 5,
x = 10 : 5,
x = 2.
Завершаем решение примера проверкой результата:
10 : 2 = 5.
Мы получили верное уравнение, значит нашли корень правильно. Обратите внимание, если частное равно 0, мы не может применять это Определение, так как придётся делить делимое на 0. И в таком случае найти делимое невозможно. Но число 0 может выступать в роли частного в уравнении 0 : x = 0. В этом случае, неизвестное x может быть любым положительным или отрицательным числом, то есть равняться бесконечному количеству вариантов значения.
На практике вы будете встречать более сложные примеры и задачи на нахождение неизвестного слагаемого, вычитаемого или множителя/делимого, в которых будете последовательно применять вышеперечисленные правила.
Вот заданье, вот мученье! Я решаю уравненье!
Привет, ребята! Сегодня мы с вами поговорим об
уравнениях. О тех уравнениях, в которых надо найти неизвестное
слагаемое. Давайте прежде всего вспомним, как надо находить неизвестное
слагаемое. Вот перед вами формула действия сложения, где, как вы видите, сумма
является целым, а слагаемые – частями.
Ну
а если нам известны одно из
слагаемых и сумма, то как найти неизвестное слагаемое?
Чтобы
найти неизвестное слагаемое надо из суммы вычесть
известное слагаемое.
Поэтому
неизвестное слагаемое в уравнениях мы находим вычитанием.
Вот
перед вами уравнение:
х
+ 29 = 11 · 4
Ух
ты! Это что-то новенькое! Вы привыкли к уравнениям, в которых обычно есть три
числа – два известных и одно неизвестное. Например, вот такое уравнение:
А
в этом после знака равно стоит не одно число, а числовое выражение. Какое-то усложнённое
уравнение получилось.
С
чего же начать? Пожалуй, прежде всего надо наше уравнение сделать обычным,
простым. А для этого надо что сделать? Правильно, выполнить то действие,
которое стоит справа от знака равно. Перемножаем числа одиннадцать и четыре и
получаем число сорок четыре. А теперь переписываем уравнение в уже привычном
для нас виде: икс плюс двадцать девять равно сорок четыре. Вот теперь решаем
его.
Надо
найти неизвестное слагаемое. Находим его
вычитанием. Из сорока четырёх вычитаем двадцать девять. Икс равен пятнадцати.
Под чертой выполняем проверку – переписываем наше уравнение, заменяя букву икс
на число, которое у нас получилось. Выполняем действия слева и справа от знака
равно.
х
+ 29 = 44
х
= 44 – 29
х
= 15
15
+ 29 = 11 · 4
44
= 44
В
обеих частях получится сорок четыре. Значит, уравнение решено верно.
А
теперь решим вот такое уравнение:
17
+ у = 96 : 4
Вы
обратили внимание на то, что и здесь, прежде чем найти неизвестное, уравнение нужно
упростить. Надо выполнить действие, которое находится справа от знака
равно. Частное чисел девяносто шесть и четыре равно двадцати четырём.
Записываем
уравнение, заменив числовое выражение в правой его части значением этого
выражения. В уравнении надо найти неизвестное второе слагаемое. Находим его
вычитанием. Игрек равен семи.
17
+
у
=
24
у
= 24 – 17
у
= 7
17
+ 7 = 96 : 4
24
= 24
Проверяем.
Переносим уравнение под черту. Не забудьте! Не упрощённое, а именно то, которое
было дано первоначально. Находим значения его левой и правой частей. Они между
собой равны. Значит, корень уравнения найден верно.
А
теперь я предлагаю вам решить и проверить самостоятельно два уравнения.
х
+ 43 = 24 + 76 28 + у = 96 : 3
Не
забывайте: Чтобы найти неизвестное слагаемое, надо из суммы
вычесть известное слагаемое.
И
при проверке не ленитесь – обязательно выполняйте действия в левой и правой
части уравнения. Это поможет вам вовремя обнаружить ошибку, если вы случайно её
допустите.
Ну
а теперь проверим, так ли вы решили уравнения.
х
+ 43 = 100 28 + у = 32
х
= 100 – 43 у = 32 – 28
х
= 57 у = 4
57
+ 43 = 24 + 76 28 + 4 = 96 : 3
100
= 100 32 = 32
Я
надеюсь, вы не забыли, что при проверке записывается данное в начале уравнение,
но вместо буквы подставляется корень уравнения, который мы нашли. Обязательно
пересчитайте левую и правую части уравнения. Если их значения равны, то
уравнение решено верно. Ну и, конечно, вы знаете:
Чтобы
найти неизвестное слагаемое, надо из суммы вычесть
известное слагаемое.
А
я сегодня прощаюсь с вами, ребята! До новых встреч!










