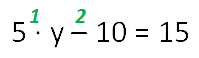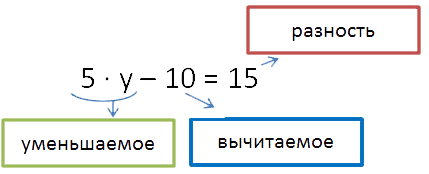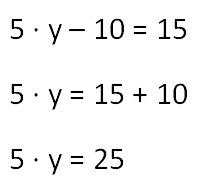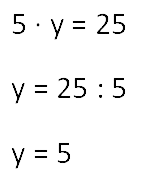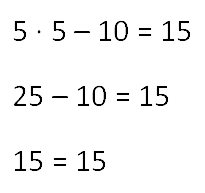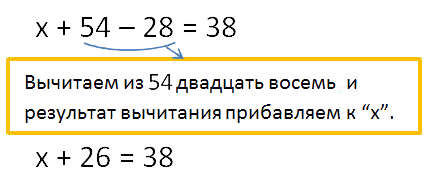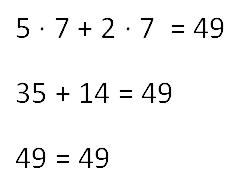Как найти неизвестное сложное уравнение - Исправление недочетов и поиск решений вместе с Examum.ru

Уравнение с одним неизвестным

Уравнение вида ax = b, где x — неизвестное, a и b — числа, называется уравнением с одним неизвестным или линейным уравнением.

Число a называется коэффициентом при неизвестном, а число b — свободным членом.

Если в уравнении ax = b коэффициент не равен нулю (a ≠ 0), то, разделив обе части уравнения на a, получим . Значит, уравнение ax = b, в котором a ≠ 0, имеет единственный корень .

Если в уравнении ax = b коэффициент равен нулю (a = 0), а свободный член не равен нулю (b ≠ 0), то уравнение не имеет корней, так как равенство 0x = b, где b ≠ 0, не является верным ни при каком значении x.

Если в уравнении ax = b и коэффициент, и свободный член равны нулю (a = 0 и b = 0), то уравнение имеет бесконечное множество корней, так как равенство 0x = 0 верно при любом значении x.

Решение уравнений с одним неизвестным

Все уравнения с одним неизвестным решаются одинаково с помощью преобразований, которые могут выполняться в любом порядке. Список возможных преобразований, которые могут быть использованы для решения уравнений:

освобождение от дробных членов;
раскрытие скобок;
перенос всех членов, содержащих неизвестное, в одну часть, а известные — в другую (члены с неизвестными, как правило, переносят в левую часть уравнения);
сделать приведение подобных членов;
разделить обе части уравнения на коэффициент при неизвестном.

Пример 1. Решить уравнение

Освобождаем уравнение от дробных членов:

20x — 28 — 24 = 9x + 36.

20x — 9x = 36 + 28 + 24.

Выполняем приведение подобных членов:

Делим обе части уравнения на коэффициент при неизвестном (на 11):

Делаем проверку, подставив в данное уравнение вместо x его значение:

Уравнение обратилось в верное равенство, следовательно, корень был найден верно.

Пример 2. Решить уравнение

Это уравнение проще решить, не раскрывая скобок, поэтому делим обе части уравнения на 5:

Выполняем приведение подобных членов:

Делаем проверку, подставив в данное уравнение вместо x его значение:

5(11 — 2) = 45;
5 · 9 = 45;
45 = 45.

Обычно все рассуждения при решении уравнения производят устно, а само решение записывается так:

Решение уравнений с одним неизвестным (переменной)

В данной публикации мы рассмотрим определение и общий вид записи уравнения с одним неизвестным, а также приведем алгоритм его решения с практическими примерами для лучшего понимания.

Определение и запись уравнения

Математическое выражение вида ax + b = 0 называется уравнением с одним неизвестным (переменной) или линейным уравнением. Здесь:

Уравнение можно представить в равнозначном виде . После этого мы смотрим на коэффициенты.

При a ≠ 0 единственный корень .

При a = 0 уравнение примет вид . В таком случае:

если b ≠ 0 , корней нет;
если b = 0 , корнем является любое число, т.к. выражение верно при любом значении x .

Алгоритм и примеры решения уравнений с одим неизвестным

Простые варианты

Рассмотрим простые примеры при a = 1 и наличии всего одного свободного коэффициента.

» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Пример	Решение	Объяснение
слагаемое	от суммы отнимается известное слагаемое
уменьшаемое	разность прибавляется к вычитаемому
вычитаемое	из уменьшаемого вычитается разность
множитель	произведение делится на известный множитель
делимое	частное умножается на делитель
делитель	делимое делится на частное

Сложные варианты

При решении более сложного уравнения с одной переменной, очень часто требуется сначала его упростить, прежде чем находить корень. Для этого могут применяться следующие приемы:

раскрытие скобок;
перенос всех неизвестных в одну сторону от знака “равно” (обычно в левую), а известных в другую (правую, соответственно).

Пример: решим уравнение .

Раскрываем скобки:
6x + 18 – 3x = 2 + x .
Переносим все неизвестные влево, а известные вправо (не забываем при переносе менять знак на противоположный):
6x – 3x – x = 2 – 18 .
Выполняем приведение подобных членов:
2x = -16 .
Делим обе части уравнения на число 2 (коэффициент при неизвестной):
x = -8 .

Решение сложных уравнений. 3 класс.

Овладение детьми способом решения уравнений в начальной школе создает прочную основу для дальнейшего обучения алгебры, химии, физики и других предметов.

Начиная с 3-го класса, ученикам встречаются сложные уравнения, но справиться с ними очень просто.

Дети уже умеют решать простые уравнения, читай об этом здесь.

А эта статья будет посвящена решению сложных уравнений в 2-3 действия.

Очень часто родители, желая помочь, объясняют так: вот смотри, сейчас вот это число перенести в другую часть от знака равенства, надо поменять знак на противоположный: было умножение, меняем на деление; было сложение меняем на вычитание.

В начальной школе это объяснение не срабатывает, т.к. ребенок не знаком с законами алгебры.

Как сложное уравнение привести к тому, которые мы уже умеем решать, а именно к уравнению в 1 действие?

Рассмотрим уравнение в 2 действия:

х + 56 = 98 — 2 — оно достаточно легкое.

Здесь особого труда не будет в решении, потому что ребенок сразу догадается, что сначала надо 98-2.

х + 56 = 98 — 2

х + 56 = 96 – это простое уравнение. А его решаем очень быстро!

Сейчас мы рассмотрим уравнение:

Такое уравнение можно решить несколькими способами.

У нас здесь неизвестное число х. Мы не знаем, что спрятано за этим числом.

А когда к х + 5 – это число тоже известно.

Закроем его и пусть это будет другое число, например b .

Мы видим, что у нас получилось самое простое уравнение в 1 действие.

2 • b = 30

А чтобы найти а, нам нужно 30 : на 2.

А b не что иное, как х + 5.

х + 5 = 30 : 2

х + 5 = 15

х = 15 – 5

х = 10

Проверку делаем как обычно: переписываем первое уравнение: 2 • (10 + 5) = 30.

30 – переписываем, а левую часть считаем — будет 30.

30 = 30, значит, уравнение решили правильно.

При решении таких сложных уравнений самое главное – понять, что заменить на другое неизвестное число. Когда в уравнении всего 2 действия – это очень просто.

Более удобно и понятно, как показывает практика, если использовать решение сложных уравнений на основе зависимости между компонентами действий.

Наше уравнение 2 • (х + 5) = 30 читаем так: число 2 умножить на сумму х и пяти, получится 30. В данном случае – нам неизвестна сумма, чтобы ее найти, надо 30:2.

48 : (16 – а) = 4.

Если опять заменять часть уравнения другим неизвестным числом, можно запутаться. Поэтому легче использовать взаимосвязи компонентов и результата действия: число 48 разделить на разность.

Нам неизвестна разность, поэтому сначала нужно узнать чему она равна. Надо 48 : 4.

16 — а = 48 : 4

16 — а = 12 – это простое уравнение.

а = 16 — 12

а = 4

Проверка: 48 : (16 — 4) = 4

Давайте посмотрим еще одно:

Из 96 надо вычесть разность с и 16. Чтобы найти разность, надо 96-94.

Проверка: 96 — (16 — 14) = 94

А сейчас мы переходим к тем уравнениям, у которых не 2, а 3 действия. Как же нам поступать в этом случае? При решении таких сложных уравнения используем знания порядка выполнения действий в выражениях со скобками и без них.

Рассмотрим уравнение: 36 – (8 • у + 5) = 7

Прежде всего, нужно внимательно оценить левую часть уравнения: ту, которая с неизвестным числом. Вы должны четко себе представить какое вы будете делать действие первым, какое – вторым, какое – третьим: сначала делается умножение, потом сложение и последним – вычитание.

И вот то, которое вы будете делать третьим, с него и начнем, т.е. начинаем упрощать уравнение с последнего действия. Последнее действие – вычитание. С него и начнем: из числа 36 вычесть то, что в скобках и получим 7.

Значит, то что в скобках – вычитаемое, чтобы его найти, надо 36 — 7.

По правилам математики в данной записи скобки – не ставим.

8 • у + 5 = 29 – уравнение сложное. Нужно его упростить. Данное уравнение читаем так: к произведению 8 и у прибавили 5 и получилось 29. Нам неизвестно произведение, чтобы его найти, надо 29-5.

8 • у = 24 – это уравнение простое.

Проверка: 36 — (8 • у + 5) = 7 . Правую часть – 7 — переписываем, а левую считаем.

Итак: 7 = 7. Значит, уравнение решили правильно.

(36 + d) : 4 + 8 = 18. Определяем порядок действий: первое – сложение в скобках, второе – деление, третье сложение вне скобок. Значит, все, что до 8 – это первое слагаемое, чтобы его найти, надо 18 — 8

(36 + d) : 4 = 18 — 8

(36 + d) : 4 = 10 – уравнение сложное, теперь последнее действие — :, значит

36 + d = 40 – уравнение простое и его мы решаем легко!

Для удобства и быстроты решения сложных уравнений можете пользоваться данной памяткой

Дело в том, что при кажущейся сложности, если внимательно изучить все приемы, которые я вам сегодня показала, эти уравнения дети будете щелкать как семечки. Обязательно напишите в комментариях, какой способ вам более удобен.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 58

источники:

Решение уравнений с одним неизвестным (переменной)

Решение сложных уравнений. 3 класс.

Источник

Под сложными (составными) уравнениями мы понимаем
уравнения, которые содержат два или более арифметических действия.

Решение таких уравнений выполняется по тем же правилам, которые мы
рассмотрели на странице «Решение простых уравнений 5 класс» в этой же теме.

Но решение составных уравнений производится в определённой
последовательности.

Рассмотрим уравнение:

1. Расставляем
порядок действий в уравнении.

2. Определяем
неизвестное по последнему действию. Последнее действие в данном
уравнении — это вычитание. Обращаем ваше внимание, что на этом этапе наше
неизвестное — это «5y», и именно его мы рассматриваем как уменьшаемое.

3. Решаем
как простое уравнение и находим «5y». Вспомним правило для нахождения
неизвестного уменьшаемого.

Чтобы найти неизвестное
уменьшаемое, надо к разности прибавить вычитаемое.

4. Теперь
перед нами простое уравнение. Необходимо найти неизвестный множитель. Решаем
уравнение по следующему правилу.

Чтобы найти неизвестный
множитель, надо произведение разделить на известный множитель.

5. Не
забудем выполнить проверку.

Всё верно. Значит уравнение решено правильно.

Другой
способ решения сложных уравнений

Некоторые сложные (составные уравнения) можно решать другим
способом. Зная и умея применять свойства сложения и вычитания, а также свойства
умножения и деления, уравнения решаются следующем образом.

Рассмотрим уравнение.

(x + 54) − 28 = 38

1. Упрощаем
выражение, стоящее в левой части уравнения, используя одно из свойств
вычитания.

Чтобы из суммы отнять число,
нужно это число вычесть из одного слагаемого и прибавить результат вычитания к
другому слагаемому.

2. Далее
решаем простое уравнение, пользуясь правилом нахождения неизвестного
слагаемого.

x = 38 − 26

x = 12

3. Выполняем
проверку.

(12 + 54) − 28 = 38

66 − 28 = 38

38 = 38

Упрощение
выражений в уравнениях

Запомните!

Если в
уравнении встречается выражения, которые можно упростить, то вначале упрощаем
выражения, и только после этого решаем уравнение.

Решить уравнение.

5x + 2x = 49

Левую часть уравнения можно упростить. Сделаем это.

7x = 49

Теперь решим простое уравнение по правилу нахождения неизвестного
множителя.

x = 49 : 7

x = 7

Завершив пример, выполним проверку.

Источник

Метод замены переменной
Метод разложения на множители
Метод группировки слагаемых
Подбор целого корня и деление многочлена на многочлен уголком
Однородные уравнения
Выделение полного квадрата
Метод оценки
Использование свойств функций
Графический метод решения уравнений

Что делать, если вам – например, на Профильном ЕГЭ по математике – встретилось не квадратное уравнение, а кубическое? Или даже уравнение четвертой степени? Ведь для уравнений третьей, четвертой и более высоких степеней нет таких простых формул, как для квадратного уравнения.

В этой статье – способы решения сложных алгебраических уравнений. Замена переменной, разложение на множители, группировка, использование симметрии, однородности, деление многочлена на многочлен. Они вполне могут встретиться на ЕГЭ и олимпиадах в уравнениях, неравенствах и задачах с параметрами.
Также мы рассматриваем применение свойств функций, метод оценки, выделение полного квадрата, графический способ.

Вспомним основные понятия.

Корень уравнения – такое число, которое мы можем подставить вместо переменной в уравнение и получить истинное равенство.

Например, число 3 – корень уравнения 2x = 6.

Решить уравнение – значит найти его корни или доказать, что их нет.

Равносильными называются уравнения, множества решений которых совпадают. Другими словами, у них одни и те же корни.

Например, уравнения $left ( x^{2}-1 right )left ( x^{2}+3 right)=0$ и $x^{2}=1$ равносильны. Их корни совпадают: x=1 или x=-1.

В этой статье мы рассмотрим рациональные уравнения. В них переменная х входит в целой степени. Стандартный вид такого уравнения: слева многочлен, справа ноль.
Например, уравнение первой степени имеет вид ax+b=0 , где По-другому оно называется линейным уравнением, и вы с ним хорошо знакомы.

Уравнение второй степени приводится к виду , где Это квадратное уравнение, и с ним тоже все просто.

Уравнение третьей степени имеет вид , где

В общем виде такие уравнения n-й степени можно записать так:
$ax^n+bx^{n-1}+cx^{n-2}+dots + mx+p=0$ , где х — переменная, — некоторые числа, причём

Теорема. Уравнение n-й степени имеет не более n действительных корней.

Это значит, что у квадратного уравнения не более двух корней. У уравнения третьей степени не более трех корней.
Как же найти эти корни?

к оглавлению ▴

Метод замены переменной

Замена переменной – ключ к решению многих задач.

Самый простой пример – биквадратное уравнение.

Так называется уравнение вида . Оно решается с помощью замены x^2=t , где

1. Решим уравнение .

Решение:

Сделаем замену , тогда

$t_{1,2}=frac{37pm35}{18};$ t=4 или $t=-frac{1}{9}$

Значение переменной $t=-frac{1}{9}$ не удовлетворяет условию замены, так как $-frac{1}{9}<0.$

Значит,

Ответ: x=pm 2

2.Решим уравнение

Решение:

Пусть Это уравнение имеет два корня: t=-9 или t=-1 . Оба корня отрицательны и не удовлетворяют условию . Значит, исходное уравнение не имеет действительных корней.

Ответ:

Такой символ означает, что корней нет, множество корней исходного уравнения является пустым.

3. Решим уравнение:

$frac{x^{2}+1}{x}+frac{x}{x^{2}+1}=2,9$

Решение:

Если приводить обе части к одному знаменателю, получим уравнение четвертой степени. Вряд ли мы с ним справимся.

Сделаем замену $frac{x^{2}+1}{x}=t.$ Тогда $frac{x}{x^{2}+1}=frac{1}{t},tneq 0.$

С новой переменной уравнение стало проще:

$t+frac{1}{t}=2,9$

$t+frac{1}{t}-2,9=0$

Умножим обе части на 10t. Получим квадратное уравнение:

$10t^{2}-29t+10=0$

Корни этого уравнения: $t=frac{5}{2}$ или $t=frac{2}{5}.$

Вернемся к переменной

Если $t=frac{2}{5}$ , то $frac{x^{2}+1}{x}=frac{2}{5}.$

Отсюда $5x^{2}-2x+5=0.$

Дискриминант этого уравнения отрицателен, корней нет.

Если $t=frac{5}{2}$ , то $frac{x^{2}+1}{x}=frac{5}{2}.$ Получим квадратное уравнение для : $2x^{2}-5x+2=0.$

У этого уравнения два корня: x=2 или x=0,5. Это ответ.

4. Решим уравнение

Решение:
Мы видим, что выражение 4x^2-5x в уравнении встречается дважды. Хорошо бы обозначить его новой переменной, сделать замену.

Введем новую переменную

Уравнение примет вид: или t=-3.

Возвращаемся к переменной х:

$left[ begin{gathered} 4x^2-5x=-1 \ 4x^2-5x=-3 end{gathered} right.$

У нас появилось новое обозначение: — знак совокупности.
Такой знак означает «или».

Мы получили совокупность из двух квадратных уравнений.

$left[ begin{gathered} 4x^2-5x+1=0 \ 4x^2-5x+3=0 end{gathered} right.$

Решим эти уравнения по очереди.

$1)~~4x^2-5x+1=0; D = 25-16=9;x_{1,2}=frac{5pm3}{8}; left[ begin{gathered} x=1 \ x=0,25 end{gathered} right.$

2) Уравнение не имеет корней. Его дискриминант отрицателен.

Ответ: 1; 0,25

5. Решим уравнение

Решение:

Не будем спешить раскрывать скобки. Ведь раскрыв их, мы получили бы уравнение четвертной степени.

Посмотрим на уравнение внимательно.

На координатной прямой точки 1; 3; –5; –7 расположены симметрично относительно точки x=-2.

Сделаем замену x+2=t , тогда x=t-2 .

Тогда:

x-1=t-3

x-3=t-5

x+5=t+3

x+7=t+5

Мы выразили все «скобки», то есть все множители, через новую переменную. Вот что это дает:

$left ( t^{2}-9 right )cdot left ( t^{2}-25 right )=297$

И еще одна замена: $t^{2}-9=z$ .

$z^{2}-16z-297=0.$ Обычное квадратное уравнение. Замечательно!

Подберем его корни по теореме Виета. Заметим, что

$left{begin{matrix} z_{1}+z_{2}=16\ z_{1}cdot z_{2}=-297 end{matrix}right.$ ; отсюда $z_{1}=27$ , $z_{2}=-11$ .

Если $z=t^{2}-9=-11$ , то $t^{2}=-2,$ нет решений.

Если $z=t^{2}-9=27$ , то $t^{2}=36.$ Тогда t=6 или t=-6

Если x+2=6 , то x=4 .

Если x+2=-6 , то x=-8 .

Ответ: 4; –8.

Дальше – еще интереснее.

6. Решите уравнение $frac{x^{2}}{3}+frac{48}{x^{2}}=10cdot left ( frac{x}{3}-frac{4}{x} right )$

Решение:

Сделаем замену $frac{x}{3}-frac{4}{x} =t$ . То, что в правой части в скобках, заменили на новую переменную.

$t^{2}=left ( frac{x}{3}-frac{4}{x} right )^{2}=frac{x^{2}}{9}+frac{16}{x^{2}}-frac{8}{3}=frac{1}{3}left ( frac{x^{2}}{3}+frac{48}{x^{2}}-8 right )$

$frac{x^{2}}{3}+frac{48}{x^{2}}-8=3t^{2}Rightarrow frac{x^{2}}{3}+frac{48}{x^{2}}=3t^{2}+8$ .

Получили квадратное уравнение:

$3t^{2}+8=10t$

$3t^{2}-10t+8=0$

$D=10^{2}-4cdot 3cdot 8=100-96=4$

$t_{1}=frac{10-2}{6}=frac{4}{3}$

$t_{2}=frac{10+2}{6}=2$

Если $frac{x}{3}-frac{4}{x}=frac{4}{3}$ , то $x^{2}-4x-12=0 Rightarrow x_{1}=-2, ; x_{2}=6.$

Если $frac{x}{3}-frac{4}{x}=2$ , то $x^{2}-6x-12=0.$

$x_{3,4}=frac{6pm sqrt{84}}{2}=frac{6pm 2sqrt{21}}{2}=3pm sqrt{21}.$

Ответ:

к оглавлению ▴

Метод разложения на множители

Этот метод удобен, когда в правой части уравнения стоит ноль, а в левой – выражение, зависящее от переменной.

Произведение двух или нескольких множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а остальные при этом не теряют смысла.

7. Решим уравнение .

Конечно, не нужно перемножать все «скобки». Левая часть уравнения равна нулю, если х=0 или х=2 или х=3 или х=5. Все эти значения переменной – корни уравнения.

Ответ: 0; 2; 3; 5.

8. Решим уравнение

Решение:

Вынесем за скобки x^3 ,то есть разложим левую часть на множители.

$x^3(x^3+8)=0 Leftrightarrow left[ begin{gathered} x^3=0 \ x^3+8=0 end{gathered}right. Leftrightarrow left[ begin{gathered} x=0 \ x=-2 end{gathered}right.$

Ответ: {-2;0}

Мы записали корни уравнения в виде множества из двух значений переменной, -2 и 0. Это одна из возможных форм записи ответа.
Метод разложения на множители часто применяется вместе с методом группировки.

к оглавлению ▴

Метод группировки слагаемых

9. Решите уравнение $x^{3}-3x^{2}-6x+8=0$

Решение:

Разложим левую часть уравнения на множители. Сгруппируем слагаемые:

$x^{3}+2^{3}-3x^{2}-6x=0$

Первые два слагаемых – сумма кубов. Применим формулу: $a^{3}+b^{3}=left ( a+b right )left ( a^{2}-ab+b^{2} right )$ . Получим:

$left ( x+2 right )left ( x^{2}-2x+4 right )-3xleft ( x+2 right )=0$

$left ( x+2 right )left ( x^{2}-2x+4 -3xright )=0$

$left ( x+2 right )left ( x^{2}-5x+4right )=0$ .

Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Записывается это так:

$left ( x+2 right )left ( x^{2}-5x+4 right )= 0 Leftrightarrow left[ begin{array}{ccc} x+2=0 \ x^{2}-5x+4 = 0 \ end{array} right.$

Ответ: -2; 1; 4.

Здесь мы тоже использовали знак совокупности.

Запись $left[ begin{array}{ccc} x=-2 \ x=4 \ x=1 \ end{array} right.$ читается как « x=-2 или x=4 или x=1 ».

Решая уравнения и особенно неравенства, мы будем постоянно пользоваться знаками системы и совокупности. Мы записываем решения в виде цепочки равносильных переходов. Для сложных уравнений и неравенств это единственный способ прийти к ответу и не запутаться.

10. Решите уравнение

Решение:

Разложим левую часть уравнения множители методом группировки.

$9x^2(x-1)-(x-1)=0 Leftrightarrow (x-1) cdot (9x^2-1)=0 Leftrightarrow \ Leftrightarrow left[ begin{gathered} x-1=0 \ 9x^2-1=0 end{gathered} right. Leftrightarrow left[ begin{gathered} x=1 \ x=pm frac{1}{3} end{gathered} right.$

Ответ: $pmfrac{1}{3}; 1$

11. Решите уравнение $x^{2}+2x+frac{2}{x}+frac{1}{x^{2}}=1$

Решение:

Сгруппируем слагаемые:

$x^{2}+frac{1}{x^{2}}+2left (x+frac{1}{x} right )-1=0$

А если сделать замену $x+frac{1}{x}=t$ ?

Тогда $t^{2}=left ( x+frac{1}{x} right )^{2}=x^{2}+frac{1}{x^{2}}+2Rightarrow x^{2}+frac{1}{x^{2}}=t^{2}-2$ .

Получаем квадратное уравнение: $t^{2}-2+2t-1=0$ . Удачная замена!

$t^{2}+2t-3=0Leftrightarrow left[ begin{array}{ccc} t=-3 \ t=1 \ end{array} right.$

Если $x+frac{1}{x}=1$ , то , нет решений.

Если $x+frac{1}{x}=-3$ , то $x^{2}+3x+1=0$

D=9-4=5 , $x_{1,2}=frac{-3pm sqrt{5}}{2}$ .

Ответ: $frac{-3pm sqrt{5}}{2}$ .

к оглавлению ▴

Подбор целого корня и деление многочлена на многочлен уголком

Рассмотрим еще один метод решения уравнений третьей, четвертой и более высоких степеней.

12. Решите уравнение $x^{3}-9x^{2}+26x-24=0$

Решение:

Разложить левую часть на множители с первой попытки не удается.

Оказывается, если уравнение третьей (четвертой, пятой…) степени имеет целые корни, то находятся они среди делителей свободного члена (слагаемого, не содержащего x). В данном случае – среди целых делителей числа 24.

Выпишем целые делители числа 24:

1; –1; 2; –2; 3; –3; 4; –4; 6; –6; 8; –8; 12; –12; 24; –24

Подставляя их по очереди в уравнение, при x=2 получаем верное равенство:

$2^{3}-9cdot 2^{2}+26cdot 2-24=0$

Это значит, что левую часть уравнения можно разложить на множители:

$x^{3}-9x^{2}+26x-24=left ( x-2 right )cdot Pleft ( x right )$ , где $Pleft ( x right )=ax^{2}+bx+c$ .

Чтобы найти , поделим выражение $x^{3}-9x^{2}+26x-24$ на x-2 . В столбик. Так же, как мы делим друг на друга числа.

Немного непривычно, да? Потренируйтесь – у вас получится!

$x^{3}-9x^{2}+26x-24=left ( x-2 right )cdot left ( x^{2}-7x+12 right )Leftrightarrow left[ begin{array}{ccc} x-2=0 \ x^{2}-7x+12=0 \ end{array} right.Leftrightarrow left[ begin{array}{ccc} x=2 \ x=3 \ x=4 \ end{array} right.$

Ответ: 2; 3; 4.

13. Решите уравнение $x^{4}-5x^{3}+4x^{2}-5x+1=0$

Решение:

Разложить на множители? Но как? И замена не видна сразу. Посмотрим на уравнение внимательно. Его коэффициенты: 1, — 5, 4, — 5, 1.

Такое уравнение называется симметрическим, или возвратным.

Разделим обе его части на $x^{2}neq 0$ . Мы можем это сделать, поскольку x=0 не является корнем нашего уравнения.

$x^{2}-5x+4-frac{5}{x}+frac{1}{x^{2}}=0$

Теперь группируем слагаемые:

$x^{2}+frac{1}{x^{2}}-5left (x-frac{1}{x} right )+4=0$

Сделаем замену $x-frac{1}{x}=t$ .

Тогда $t^{2}=left ( x-frac{1}{x} right )^{2}=x^{2}+frac{1}{x^{2}}-2Rightarrow x^{2}+frac{1}{x^{2}}=t^{2}+2$

Получили уравнение $t^{2}+2-5t+4=0$ . Легко!

$x-frac{1}{x}=3Rightarrow x^{2}-3x-1=0, ;D_{1}=9+4=13,; x_{3,4}=frac{3pm sqrt{13}}{2}$

Ответ: $1pm sqrt{2}, frac{3pm sqrt{13}}{2}$

14. Решите уравнение

Решение:

Разделив обе части уравнения на , получим:

$x^2-5x+6-frac{5}{x}+frac{1}{x^2}=0.$

Группируем слагаемые:

$left(x^2+frac{1}{x^2}right)-5left(x+frac{1}{x}right)+6=0.$

Сделаем замену $x+frac{1}{x}=t$ , тогда $t^2=x^2+frac{1}{x^2}+2 Rightarrow x^2+frac{1}{x^2}=t^2-2.$

Наше уравнение примет вид:

$(t^2-2)-5t+6=0 Leftrightarrow t^2-5t+4=0 Leftrightarrow left[ begin{gathered} t=4 \ t=1 end{gathered} right.$

Обратная замена:

$1)~ x+frac{1}{x}=1 Leftrightarrow x^2-x+1=0; D = 1-4=-3<0 Rightarrow x in emptyset$

$2)~ x+frac{1}{x}=4 Leftrightarrow x^2-4x+1=0; D = 4-1=3; x_{1,2}=2pm sqrt{3}$

Ответ:

к оглавлению ▴

Однородные уравнения

В школьном курсе математики проходят однородные показательные и однородные тригонометрические уравнения. Однородные алгебраические уравнения решаются тем же методом: делением на старшую степень.

15. Решите уравнение

Решение:

Это однородное уравнение. Разделим каждое слагаемое на при условии .

Получим: $left(frac{x^2+2x}{2x-1}right)^2-frac{x^2+2x}{2x-1}-6=0$

Выполним замену: $frac{x^2+2x}{2x-1}=t.$

Получим уравнение:

$t^2-t-6=0 Leftrightarrow left[ begin{gathered} t=3 \ t=-2 end{gathered} right.$

Обратная замена приведет нас к совокупности квадратных уравнений:

$left[ begin{gathered} x^2-4x+3-0 \ x^2+6x-2=0 end{gathered} right.$

Решим эти квадратные уравнения.

$1)~x^2+6x-2=0; x=-3pm sqrt{11}$

$2)~x^2-4x+3=0 Leftrightarrow left[ begin{gathered} x=3 \ x=1 end{gathered} right.$

Мы сказали, что поделить обе части уравнения на 2x-1 можно, только если Проверим, что будет, если . Тогда x=0,5 . Такое значение переменной не является корнем уравнения.

Ответ:

Рассмотрим еще одно однородное уравнение.

16. Решите уравнение

Решение:

x=-8 не является корнем уравнения, поэтому разделим уравнение на (x+8) и получим

$left(frac{x^2+2x+2}{x+8}right)^2-4cdotfrac{x^2+2x+2}{x+8}+3=0.$

Замена $frac{x^2+2x+2}{x+8}=t$ приводит к квадратному уравнению:

Его корни t=3 и t=1.

Обратная замена дает совокупность квадратных уравнений:

$2)~x^2-4x+3=0 Leftrightarrow left[ begin{gathered} x^2-x-22=0 \ x^2+x-6=0 end{gathered} right.$

Решив эти квадратные уравнения, получаем корни:

$x=frac{1pm sqrt{89}}{2}; x=-3; x=2.$

Ответ: $frac{1pm sqrt{89}}{2}; -3; 2.$

Покажем еще несколько методов решения алгебраических уравнений. Они встречаются также в задачах с параметрами.

к оглавлению ▴

Выделение полного квадрата

17. Решите уравнение $x^2+frac{x^2}{(x+1)^2}=3$

Решение:

В правой части уравнения сумма двух квадратов. Добавим и вычтем удвоенное произведение двух выражений:

$x^2+2cdot xcdotfrac{x}{x+1}+frac{x^2}{(x+1)^2}-2cdot xcdotfrac{x}{x+1}=3.$

Свернем полный квадрат по формуле сокращенного умножения.

$left(x+frac{x}{x+1}right)^2-frac{2x^2}{x+1}=3; ~left(frac{x^2}{x+1}right)^2-frac{2x^2}{x+1}=3$

Замена $frac{x^2}{x+1}=t$ приведет уравнение к виду:

или t=-1.

Обратная замена дает совокупность двух квадратных уравнений:

$left[ begin{gathered} x^2-3x-3=0 \ x^2+x+1=0 end{gathered} right.$

Корни первого из этих уравнений:

$x_{1,2}=frac{3pmsqrt{21}}{2}$

Второе уравнение не имеет корней, его дискриминант отрицателен.

Ответ: $frac{3pmsqrt{21}}{2}$

к оглавлению ▴

Метод оценки

18. Решим уравнение

Решение:

Преобразуем правую часть уравнения:

Уравнение примет вид:

Оценим левую и правую части уравнения.

Так как то равенство выполняется, только если и левая, и правая его части равны нулю.

Уравнение равносильно системе:

$begin{cases} (x-3)^6=0 \ -(x-2)^2=0 end{cases}$ ; $begin{cases} x=6 \ x=2 end{cases}$

Система решений не имеет.

Ответ: корней нет.

При решении мы пользовались следующей теоремой:
Теорема. Если в уравнении функция y=f(x) ограничена сверху и , а функция y=g(x) ограничена снизу, причем , то уравнение равносильно системе:

$begin{cases} f(x)=m \ g(x)=m end{cases}$

Если система решений не имеет, то у данного уравнения корней нет.

Читайте о том, как метод оценки применяется в задачах с параметрами.

к оглавлению ▴

Использование свойств функций

Еще один нетривиальный метод решения уравнений – подобрать корень и доказать, что других корней нет.

Здесь нам поможет следующая теорема:
Теорема. Если в уравнении функция y=f(x) является монотонно возрастающей, а функция y=g(x) монотонно убывающей или постоянной, то уравнение не может иметь более одного корня.

19. Решите уравнение

Решение:

Левая часть уравнения представляет собой функцию, монотонно возрастающую при любом значении переменной х, т.к. является суммой монотонно возрастающих функций, а правая часть постоянна. Поэтому, если уравнения имеет корень, то он единственный.

Подбором находим, что x=-1 т.к.

Ответ: -1.

20. Решите уравнение

Решение:

Функция является возрастающей (как сумма двух возрастающих функций), а правая часть постоянна. Уравнение имеет не более одного корня. Подбором находим, что x=1 — корень, так как

Других корней быть не может.
Ответ: 1.

к оглавлению ▴

Графический метод решения уравнений

Чтобы решить графически уравнение , строим в одной системе координат графики функций y=f(x) и y=g(x) и находим точки пересечения этих графиков. Абсциссы точек пересечения графиков — это корни уравнения .

21. Решите графически уравнение

Решение:

Запишем уравнение в виде x^3=x+6 . Построим в одной системе координат графики функций y=x^3 и y=x+6.

Графики функций пересекаются в единственной точке — корень уравнения, поскольку Других корней нет.
Ответ: 2.

Список литературы:

1. О. Ю. Черкасов, А. Г. Якушев. Домашний репетитор. Математика. Интенсивный курс подготовки к экзамену.

2. А. Г. Мордкович. Решаем уравнения.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Алгебраические уравнения и способы их решения. Уравнения третьей и четвертой степени» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Сложные уравнения

Определение и решение сложных уравнений

Решение таких уравнений производится в определенной последовательности:

расставляется порядок действий в уравнении;
неизвестная (выражение) определяется по последнему действию;
рассматривая выражение с неизвестной как «единое» выражение, решаем полученное простейшее уравнение;
шаги алгоритма повторять до тех пор, пока не будет определено значение неизвестной.

Примеры решения задач

Также некоторые сложные уравнения можно решать следующим образом, который основывается на свойствах арифметических действий.

Понравился сайт? Расскажи друзьям!

Источник

Под сложными (составными) уравнениями мы понимаем уравнения, которые содержат два или более арифметических действия.

Решение таких уравнений выполняется по тем же правилам, которые мы рассмотрели на странице «Решение простых уравнений 5 класс» в этой же теме.

Но решение составных уравнений производится в определённой последовательности.

Рассмотрим уравнение:

Расставляем порядок действий в уравнении.
Определяем неизвестное по последнему действию. Последнее действие в данном уравнении — это вычитание. Обращаем ваше внимание, что на этом этапе наше неизвестное — это «5y», и именно его мы рассматриваем как уменьшаемое.
Решаем как простое уравнение и находим «5y». Вспомним правило для нахождения неизвестного уменьшаемого.

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

Теперь перед нами простое уравнение. Необходимо найти неизвестный множитель. Решаем уравнение по следующему правилу.

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

Не забудем выполнить проверку.

Всё верно. Значит уравнение решено правильно.

Другой способ решения сложных уравнений

Некоторые сложные (составные уравнения) можно решать другим способом. Зная и умея применять свойства сложения и вычитания, а также свойства умножения и деления, уравнения решаются следующем образом.

Рассмотрим уравнение.

(x + 54) − 28 = 38

Упрощаем выражение, стоящее в левой части уравнения, используя одно из свойств вычитания.

Чтобы из суммы отнять число, нужно это число вычесть из одного слагаемого и прибавить результат вычитания к другому слагаемому.

Далее решаем простое уравнение, пользуясь правилом нахождения неизвестного слагаемого.

x = 38 − 26

x = 12
Выполняем проверку.

(12 + 54) − 28 = 38

66 − 28 = 38

38 = 38

Упрощение выражений в уравнениях

Запомните!

Если в уравнении встречается выражения, которые можно упростить, то вначале упрощаем выражения, и только после этого решаем уравнение.

Решить уравнение.

5x + 2x = 49

Левую часть уравнения можно упростить. Сделаем это.

7x = 49

Теперь решим простое уравнение по правилу нахождения неизвестного множителя.

x = 49 : 7

x = 7

Завершив пример, выполним проверку.

Источник