Решение уравнений с дробями
О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
-
Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
Как решать уравнения с дробями. Показательное решение уравнений с дробями.
Решение уравнений с дробями рассмотрим на примерах. Примеры простые и показательные. С их помощью вы наиболее понятным образом сможете усвоить, как решать уравнения с дробями.
Например, требуется решить простое уравнение x/b + c = d.
Уравнения такого типа называется линейным, т.к. в знаменателе находятся только числа.
Решение выполняется путем умножения обоих частей уравнения на b, тогда уравнение принимает вид x = b*(d – c), т.е. знаменатель дроби в левой части сокращается.
Например, как решить дробное уравнение:
x/5+4=9
Умножаем обе части на 5. Получаем:
х+20=45
Другой пример, когда неизвестное находится в знаменателе:
Уравнения такого типа называются дробно-рациональными или просто дробными.
Решать дробное уравнение бы будем путем избавления от дробей, после чего это уравнение, чаще всего, превращается в линейное или квадратное, которое решается обычным способом. Следует только учесть следующие моменты:
- значение переменной, обращающее в 0 знаменатель, корнем быть не может;
- нельзя делить или умножать уравнение на выражение =0.
Здесь вступает в силу такое понятие, как область допустимых значений (ОДЗ) – это такие значения корней уравнения, при которых уравнение имеет смысл.
Таким образом решая уравнение, необходимо найти корни, после чего проверить их на соответствие ОДЗ. Те корни, которые не соответствуют нашей ОДЗ, из ответа исключаются.
Например, требуется решить дробное уравнение:
Исходя из вышеуказанного правила х не может быть = 0, т.е. ОДЗ в данном случае: х – любое значение, отличное от нуля.
Избавляемся от знаменателя путем умножения всех членов уравнения на х
И решаем обычное уравнение
5x – 2х = 1
3x = 1
х = 1/3
Решим уравнение посложнее:
Здесь также присутствует ОДЗ: х -2.
Решая это уравнение, мы не станем переносить все в одну сторону и приводить дроби к общему знаменателю. Мы сразу умножим обе части уравнения на выражение, которое сократит сразу все знаменатели.
Для сокращения знаменателей требуется левую часть умножить на х+2, а правую — на 2. Значит, обе части уравнения надо умножать на 2(х+2):
Это самое обычное умножение дробей, которое мы уже рассмотрели выше
Запишем это же уравнение, но несколько по-другому
Левая часть сокращается на (х+2), а правая на 2. После сокращения получаем обычное линейное уравнение:
х = 4 – 2 = 2, что соответствует нашей ОДЗ
Для закрепления материала рекомендуем еще посмотреть видео.
Решение уравнений с дробями не так сложно, как может показаться. В этой статье мы на примерах это показали. Если у вас возникли какие то трудности с тем, как решать уравнения с дробями, то отписывайтесь в комментариях.
Памятка : «Решение уравнений», 5 класс
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
(Х – 87) – 27 = 36; Х-87 в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое
Х – 87 = 63; х в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое
Проверка: (150 – 87) – 27 = 36;
87- ( 41 + У ) = 22; 41 + У в уравнении является вычитаемым . Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность
41 + У = 65; У в уравнении является слагаемым. Чтобы найти неизвестное слагаемое , нужно из суммы вычесть известное слагаемое
Проверка: 87- ( 41 + 24 ) = 22;
(у – 35) + 12 = 32; у – 35 в уравнении является слагаемым. Чтобы найти неизвестное слагаемое , нужно из суммы вычесть известное слагаемое
у – 35 = 20; у в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое
(237 + х) – 583 = 149;
468 – ( 259 – х) = 382;
(237 + х) – 583 = 149;
237 + х = 149 + 583;
(237 + х) – 583 = 149;
237 + х – 583 = 149;
х – (583 – 237) = 149;
468 – ( 259 – х) = 382;
259 – х = 468 – 382;
468 – ( 259 – х) = 382; 468 – 259 + х = 382;
Решение уравнений, приведение подобных слагаемых
Пример 1: 8х-х=49 ; сначала запишем знаки умножения,
8*х-1*х=49 ; затем воспользуемся распределительным свойством (вынесем общую переменную за скобки)
Х*7=49 ; х является неизвестным множителем . Чтобы найти неизвестный множитель , нужно произведение разделить на известный множитель
Пример 2: 2х+5х+350=700 ; воспользуемся распределительным свойством (вынесем общую переменную за скобки)
Х*(2+5)+350=700 ; приведем подобные слагаемые (т.е. сложим числа в скобках)
7х является неизвестным слагаемым . Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое
7х=350; х является неизвестным множителем . Чтобы найти неизвестный множитель , нужно произведение разделить на известный множитель
2*50 + 5*50 + 350 = 700;
100 + 250 + 350 = 700;
Пример: 270: х + 2 = 47;
( 270 : х — является слагаемым.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое
( х является делителем . Чтобы найти неизвестный делитель , нужно делимое разделить на частное)
Пример: а : 5 – 12 = 23;
Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое )
( а является делимым. Чтобы найти неизвестное делимое , нужно частное умножить на делитель .
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 706 человек из 76 регионов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 856 человек из 77 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 45 человек из 20 регионов
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 849 220 материалов в базе
Материал подходит для УМК
«Математика», Виленкин Н.Я., Жохов В.И. и др.
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 09.12.2019
- 266
- 2
- 08.12.2019
- 264
- 0
- 19.11.2019
- 211
- 2
- 18.11.2019
- 963
- 7
- 18.11.2019
- 330
- 0
- 17.11.2019
- 330
- 0
- 17.11.2019
- 358
- 12
- 17.11.2019
- 239
- 6
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 15.12.2019 58987
- DOCX 17.4 кбайт
- 6539 скачиваний
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Кретинина Светлана Сергеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 4 года и 8 месяцев
- Подписчики: 0
- Всего просмотров: 63942
- Всего материалов: 9
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В каждом округе Москвы появятся школьные службы примирения
Время чтения: 3 минуты
В Госдуму внесли законопроект о возможности повторной сдачи ЕГЭ
Время чтения: 1 минута
Минпросвещения предлагает изменить форму для проведения ВОШ
Время чтения: 1 минута
В России выросло число детей с ОВЗ, поступающих в колледжи
Время чтения: 1 минута
25% школ выбрали компьютерный формат проведения ВПР
Время чтения: 1 минута
Вузы смогут разрешить студентам сдать выпускную работу на цифровом носителе
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
http://reshit.ru/Kak-reshat-uravneniya-s-drobyami
http://infourok.ru/pamyatka-reshenie-uravneniy-klass-4004064.html
Линейные уравнения с дробями не содержат переменной в знаменателе. Чтобы решить линейное уравнение с дробями, удобно избавиться от знаменателей.
Для этого нужно найти наименьший общий знаменатель всех входящих в уравнение дробей и обе части уравнения умножить на это число.
Наименьший общий знаменатель данных дробей равен 6. Дополнительный множитель к первой дроби равен 2, ко второй — 3, к 5 — 6. Умножаем обе части уравнения на наименьший общий знаменатель:
Можно, конечно, сразу же умножить дополнительный множитель на числитель каждой дроби. Но, к сожалению, наибольшее количество ошибок при решении линейных уравнений с дробями допускается именно на этом шаге. Скобки — друзья ученика :). Поэтому лучше воспользоваться их помощью:
-
- Особенно полезны скобки в случае, когда перед дробью стоит знак «минус».
- После раскрытия скобок можно сразу же перенести неизвестные в одну сторону уравнения, известные — в другую (не забыв при переносе изменить их знаки), а можно сначала упростить каждую часть, приведя подобные слагаемые, а потом уже переносить.
- Ответ: -34.
- Здесь наименьший общий знаменатель дробей равен 12. Находим дополнительный множитель к каждой дроби и умножаем обе части уравнения на 12:
- Раскрываем скобки и упрощаем
- Обе части уравнения делим на число, стоящее перед иксом:
- Ответ: -5.
- Уравнения такого вида можно решить, использовать основное свойство пропорции (в верной пропорции произведение крайних членов равно произведению средних членов):
- при делении двух отрицательных чисел получается положительное число, поэтому минусы можно сразу же не писать.
- Если это возможно, лучше ответ записать в виде десятичной дроби:
- Ответ: 0,1875.
Источник: http://www.algebraclass.ru/linejnye-uravneniya-s-drobyami/
Матвокс ⋆ решение дробных уравнений. пример 8 ⋆ энциклопедия математики
Для решения этого уравнения не будем применять основное свойство пропорций.
Перенесем все в левую часть уравнения:
- На этом шаге нужно приводить все слагаемые к общему знаменателю.
- Если внимательно посмотреть на знаменатели дробей, то можно увидеть, что один из них – это квадратный трехчлен.
- В таких ситуациях нужно всегда пытаться разложить его на множители, так как это может позволить упростить поиск общего знаменателя.
- Таким образом, разложим на множители:
Для этого приравняем к нулю и решим полученное квадратное уравнение:
Найдем дискриминант:
Корнями квадратного уравнения будут:
И:
Разложим уравнение на множители:
Уравнение примет вид:
Очевидно, данное разложение на множители сильно упростило дальнейшие вычисления.
Приведем слагаемые к общему знаменателю и запишем в виде одной дроби:
Отсюда:
- Упростим:
- Отсюда:
В числителе записано выражение, а не число, значит переходим к шагу 7.
- Приравняем числитель к нулю и решим полученное уравнение:
- Так как можно все элементы уравнения делить на любое число, отличное от нуля, то разделим их на -2:
- Это квадратное уравнение. Решим его с помощью дискриминанта:
- Корнями квадратного уравнения будут:
- и
- Полученные корни не сложные для дальнейших вычислений, и, если посмотреть на знаменатель, то и он не сложный для нахождения ОДЗ.
- Поэтому в данном случае можно выбрать любой из вариантов алгоритма.
Найдем ОДЗ изначального уравнения. Поэтому переходим к шагу 9 алгоритма.
- Найдем значения, при которых знаменатель изначального уравнения не равен нулю:
- Произведение не равно нулю, когда каждый из множителей не равен нулю:
- Отсюда:
- На этом шаге выберем корни уравнения, полученные на шаге 7, попадающие в ОДЗ.
- Итак:
- и
- При этом:
- и
- Таким образом, корень, равный -2 не попадает в ОДЗ, и значит его нужно исключить из ответа.
Можно провести проверку корня.
- Ответ:
- Корень дробного уравнения равен 1:
Источник: https://mathvox.ru/algebra/uravneniya-reshenie-uravnenii/glava-3-drobnie-uravneniya/reshenie-drobnih-uravnenii-primer-8/
Как решать уравнения с дробями. Показательное решение уравнений с дробями
Решение уравнений с дробями рассмотрим на примерах. Примеры простые и показательные. С их помощью вы наиболее понятным образом сможете усвоить, как решать уравнения с дробями.
Например, требуется решить простое уравнение x/b + c = d.
Уравнения такого типа называется линейным, т.к. в знаменателе находятся только числа.
Решение выполняется путем умножения обоих частей уравнения на b, тогда уравнение принимает вид x = b*(d – c), т.е. знаменатель дроби в левой части сокращается.
- Например, как решить дробное уравнение:
x/5+4=9
Умножаем обе части на 5. Получаем:
х+20=45 - x=45-20=25
- Другой пример, когда неизвестное находится в знаменателе:
- b/x + c = d
- Уравнения такого типа называются дробно-рациональными или просто дробными.
- Решать дробное уравнение бы будем путем избавления от дробей, после чего это уравнение, чаще всего, превращается в линейное или квадратное, которое решается обычным способом. Следует только учесть следующие моменты:
- значение переменной, обращающее в 0 знаменатель, корнем быть не может;
- нельзя делить или умножать уравнение на выражение =0.
Здесь вступает в силу такое понятие, как область допустимых значений (ОДЗ) – это такие значения корней уравнения, при которых уравнение имеет смысл.
Таким образом решая уравнение, необходимо найти корни, после чего проверить их на соответствие ОДЗ. Те корни, которые не соответствуют нашей ОДЗ, из ответа исключаются.
Например, требуется решить дробное уравнение:
1/x + 2 = 5
Исходя из вышеуказанного правила х не может быть = 0, т.е. ОДЗ в данном случае: х – любое значение, отличное от нуля.
- Избавляемся от знаменателя путем умножения всех членов уравнения на х
- 1 + 2x = 5х
- И решаем обычное уравнение
- 5x – 2х = 1
3x = 1 - х = 1/3
- Ответ: х = 1/3
- Решим уравнение посложнее:
Решая это уравнение, мы не станем переносить все в одну сторону и приводить дроби к общему знаменателю. Мы сразу умножим обе части уравнения на выражение, которое сократит сразу все знаменатели.
Для сокращения знаменателей требуется левую часть умножить на х+2, а правую — на 2. Значит, обе части уравнения надо умножать на 2(х+2):
Это самое обычное умножение дробей, которое мы уже рассмотрели выше
Запишем это же уравнение, но несколько по-другому
- Левая часть сокращается на (х+2), а правая на 2. После сокращения получаем обычное линейное уравнение:
- 4 = х + 2
- х = 4 – 2 = 2, что соответствует нашей ОДЗ
- Ответ: х = 2.
- Для закрепления материала рекомендуем еще посмотреть видео.
Решение уравнений с дробями не так сложно, как может показаться. В этой статье мы на примерах это показали. Если у вас возникли какие то трудности с тем, как решать уравнения с дробями, то отписывайтесь в х.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Источник: https://reshit.ru/Kak-reshat-uravneniya-s-drobyami
Уравнение неизвестный числитель дроби. Как решать уравнения с дробями по математике
Уравнение — это равенство, содержащее букву, значение которой надо найти.
В уравнениях неизвестное обычно обозначается строчной латинской буквой. Чаще всего используют буквы « x » [икс] и « y » [игрек].
— это значение буквы, при котором из уравнения получается верное числовое равенство.
— значит найти все его корни или убедиться, что корней нет.
Решив уравнение, всегда после ответа записываем проверку.
Информация для родителей
Уважаемые родители, обращаем ваше внимание на то, что в начальной школе и в 5 классе дети НЕ знают тему «Отрицательные числа».
Поэтому они должны решать уравнения, используя только свойства сложения, вычитания, умножения и деления. Методы решения уравнений для 5 класса приведены ниже.
Не пытайтесь объяснить решение уравнений через перенос чисел и букв из одной части уравнения в другую с изменением знака.
Освежить знания по понятиям, связанным со сложением, вычитанием, умножением и делением вы можете в уроке «Законы арифметики».
Решение уравнений на сложение и вычитание
- Как найти неизвестноеслагаемое
- Как найти неизвестноеуменьшаемое
- Как найти неизвестноевычитаемое
- Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое.
- Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
- Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность.
- x + 9 = 15x = 15 − 9x = 6
- Проверка
- x − 14 = 2x = 14 + 2x = 16
- Проверка
- 16 − 2 = 1414 = 14
- 5 − x = 3x = 5 − 3x = 2
- Проверка
Решение уравнений на умножение и деление
- Как найти неизвестныймножитель
- Как найти неизвестноеделимое
- Как найти неизвестныйделитель
- Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
- Чтобы найти неизвестное делимое, надо частное умножить на делитель.
- Чтобы найти неизвестный делитель, надо делимое разделить на частное.
- y · 4 = 12y = 12: 4y = 3
- Проверка
- y: 7 = 2y = 2 · 7y = 14
- Проверка
- 8: y = 4y = 8: 4y = 2
- Проверка
- Уравнение — это равенство, содержащее букву, знамение которой нужно найти.
Решение уравнения — это тот набор значений букв, при котором уравнение превращается в верное равенство:
- Напомним, что для решения уравнении
надо слагаемые с неизвестным перенести в одну часть равенства, а числовые слагаемые в другую, привести подобные и получить такое равенство: - Из последнего равенства определим неизвестное по правилу: «один из множителей равен частному, деленному на второй множитель».
- Так как рациональные числа а и Ь могут иметь одинаковые и разные знаки, то знак неизвестного определяется по правилам деления рациональных чисел.
Порядок решения линейных уравнений
- Линейное уравнение необходимо упростить, раскрыв скобки и выполнив действия второй ступени (умножение и деление).
- Перенести неизвестные в одну сторону от знака равенства, а числа — в другую сторону от знака равенства, получив тождественное заданному равенство,
- Привести подобные слева и справа от знака равенства, получив равенство вида ax
= b
. - Вычислить корень уравнения (найти неизвестное х
из равенства x
= b
: a
), - Выполнить проверку, подставив неизвестное в заданное уравнение.
- Если получим тождество в числовом равенстве, то уравнение решено верно.
Особые случаи решения уравнений
- Если уравнение
задано произведением, равным 0, то для его решения используем свойство умножения: «произведение равно нулю, если один из сомножителей или оба сомножителя равны нулю».
- 27 (x
— 3) = 0 27 не равно 0, значит x
— 3 = 0 - У второго примера два решения уравнения, так как это уравнение второй степени:
- Если коэффициенты уравнения являются обыкновенными дробями, то прежде всего надо избавиться от знаменателей.
Для этого:
- Найти общий знаменатель;
- Определить дополнительные множители для каждого члена уравнения;
- Умножить числители дробей и целые числа на дополнительные множители и записать все члены уравнения без знаменателей (общий знаменатель можно отбросить);
- Перенести слагаемые с неизвестными в одну часть уравнения, а числовые слагаемые — в другую от знака равенства, получив равносильное равенство;
- Привести подобные члены;
Основные свойства уравнений
- В любой части уравнения можно приводить подобные слагаемые или раскрывать скобку.
- Любой член уравнения можно переносить из одной части уравнения в другую, изменив его знак на противоположный.
- Обе части уравнения можно умножать (делить) на одно и то же число, кроме 0.
- В примере выше для решения уравнения были использованы все его свойства.
Как решить уравнение с неизвестным в дроби
Иногда линейные уравнения принимают вид, когда неизвестное
оказывается в числителе одной или нескольких дробей. Как, например, в уравнении ниже.
В таких случаях подобные уравнения можно решить двумя способами.
I способ решения Сведение уравнения к пропорции
При решении уравнений способом пропорции необходимо выполнить следующие действия:
Итак, вернемся к нашему уравнению. В левой части у нас и так стоит только одна дробь, поэтому в ней не нужны никакие преобразования.
Будем работать с правой частью уравнения. Упростим правую часть уравнения так, чтобы там осталась только одна дробь. Для этого вспомним правила сложения числа с алгебраической дробью.
Теперь используем правило пропорции и решим уравнение до конца.
Источник: https://svfan.ru/uravnenie-neizvestnyi-chislitel-drobi-kak-reshat-uravneniya-s-drobyami-po/
Действия с дробями 7 класс, повторение, сравнение, сокращение, решение уравнений
В начале первой четверти семиклассники на уроках математики активно повторяют все действия, как с обыкновенными, так и с десятичными дробями. И делают они это не просто так.
В 7 классе по программе обучения начинается алгебра. Дроби будут состоять уже из алгебраических выражений, многочленов. Все действия с такими уже дробями основываются на умении решать обыкновенные дроби в пятом шестом классе.
Дроби повторение 7 класс
Повторение начинается с самых простых примеров на все арифметические действия с обыкновенными дробями. Не забываем, что там где знаменатели разные следует найти общий, и только потом выполнять действия.
Сравнение дробей 7 класс
Для того, чтобы научиться сравнивать дроби, нужно узнать несколько способов по их сравнению, и выбрать для себя более понятный и удобный.
Основные правила сравнения дробей:
В первом правиле мы сравниваем только числители, так как знаменатели равны. Мы уже говорили, что знамен.-это общее количество долей, а числитель показывает сколько их взято из общего, следовательно, чем больше долей взято, тем и дробь соответственно больше.
При одинаковых числ-х сравнивают только знамен. Чем он меньше, тем больше дробь. Разберемся, почему так. К примеру разделите 10 на 5 и 10 на 2, очевидно, что второе частное больше первого. Поэтому, если сравнить 10/5 и 10/2, то 10/2 будет больше.
В десятичных дробях мы сравниваем их соответствующие целые части и дробные. Если первые равны, то мы сравниваем десятые, сотые и т.д. Поэтому для сравнения мы должны уравнивать количество дес.знаков.
Также можно сравнить две обыкн.дроби используя число, которое находится в ряду между ними. Какая из дробей окажется больше этого числа, та и будет большей в примере.
Вот несколько интересных способов, как можно сравнить дроби:
Если от вас требуется сравнить десятичную и обыкновенную дроби, можно перевести одну из них в более удобную для вас. И сравнивать вы уже будите либо обыкновенные, либо десятичные.
Еще один хороший способ, дополнить до единицы. Чем больше нужно добавить дроби, чтобы получить целое, тем она будет меньше.
Можно использовать и перекрестное правило, как в пропорции. Для этого умножаем смотрящие друг на друга числители и знаменатели.
Правила дробей 7 класс
- Начиная изучать рациональные дроби в седьмом классе, стоит познакомиться с рядом правил, которым подчиняются действия с ними.
- К рациональным дробям применяются те же правила, что и к обыкн-м.
- Для выполнения всех арифметических действий, следует знать несколько формул сокращенного умножения:
- Эти формулы понадобятся на уроках математики до 11 класса, поэтому их лучше выучить сразу в седьмом.
Действия с дробями 7 класс
Как в пятом и шестом, так же и в седьмом классе, дроби в основном складывают, вычитают, умножают и делят. Есть еще сокращение и сравнение. Рациональные дроби также называют алгебраическими.
Сложение и вычитание.
К примеру, b/3 + c/3. Это сумма рациональных или алгебраических дробей. Решением будет: b+c/3.
Еще пара примеров.
Умножение и деление.
Так же как и с обыкновенными дробями, умножать будем числитель на числитель, и знам. на знаменатель. Очень важно обратить внимание на то, что вы умножаете многочлены, поэтому каждый числитель и знаменатель лучше взять в скобки. Так вы сможете избежать ненужных ошибок.
И деление выполняется в точности также как и в обык.дробях. Первую дробь оставьте на месте без изменений, поменяйте частное на умножение, вторую дробь переверните.
Сложение и вычитание дробей 7 класс
Никогда не начинайте выполнять действия не упростив выражения. Выполните все возможные преобразования и пример решится намного легче и быстрее. Также числители второй и последующих дробей при сложении и вычитании стоит взять в скобки. Очень часто возникают ошибки только из-за одного неправильно поставленного знака. Будьте внимательны.
Если перед скобкой стоит , раскрываем ее, не меняя знаки внутри. Если >, то все меняем на противоположные.
Пример.
Знаменатели совершенно одинаковые, находим сумму числ. Приведите подобные, это с и 2с, d и -d, которые в свою очередь взаимно уничтожаются, так как имеют разные знаки. В итоге остается с+2с = 3с. Ответ: 3с/2а.
Все намного проще, если знам. одинаковые. С разными нужно немного подумать.
Пример.
В примере два знам. 15а и 3. Нам нужно найти общий. В этом случае проще домножить 3 так, чтобы получить 15а. Для этого 3 умножаем на 5а. Но чтобы действие было верным, применяем основное свойство дроби, и на 5а умножим еще и числитель. Далее складываем дроби с один.знам.
Деление и умножение дробей 7 класс
Разберем сразу примеры, так как правила уже обговорены выше.
В примере выше требуется разделить алгебраические дроби, содержащие выражения со степенью. Здесь важно вспомнить, что при сокращении степеней мы вычитаем из большей степени меньшую.
Первую дробь мы оставили без изменений, вторую перевернули, заменив действие на умножение. Теперь ищем, что можно сократить. Сначала смотри на числовые коэффициенты. Сокращаем 7 и 35, 9 и 18. Затем сокращаем буквенную часть.
Для удобства возьмите каждый многочлен в скобки. Мы видим, что сразу можно сократить скобку (7-х). Многие допускают ошибку, считая что (a-b) и (a+b) сократимы, это большая ошибка. Ведь к примеру, 5-2 и 5+2 совершенно разные выражения.
Конечные десятичные дроби 7 класс
Десятичные дроби отличаются друг от друга по количеству знаков (цифр) после запятой. Соответственно своему названию, у конечной десятичной дроби после запятой, конечное число знаков: 5, 0235; 2,3654; 0,12 и т.д.
Любую такую дробь можно перевести обратно в обыкновенную. 2,36 = 2 целых 36/100. Но не каждую обыкновенную можно представить в виде конечной дес.дроби. В таком случае уже получается бесконечная дес.дробь.
Уравнения с дробями 7 класс на примерах с пояснением
Уравнения с дробями можно решить используя пропорцию, или светси решение к этому. Первое уравнение и ему подобные очень просто и быстро решается пропорцией. Используем умножение .
Бывают и более сложные уравнения, которые нужно преобразовать.
Здесь уже нужно вспомнить правило умножения скобки на число или раскрытие скобок. На число перед скобкой умножаем каждое слагаемое в скобке. Значит 7 умножим и на 2, и на (-х). Далее решаем как обычное линейное уравнение.
В следующем уравнении разберем два способа решения.
Первый вариант решения основывается на избавлении от знаменателей, дабы превратить дробное уравнение в линейное. Для этого умножаем каждое слагаемое на общий для дробей знаменатель. В нашем случае 45.
Сокращаем и получаем линейное уравнение. Раскрываем в нем скобки, находим подобные слагаемые.
Вторым вариантом будет приведение к общему знаменателю в правой части, и сведению решения к пропорции.
Сокращение дробей 7 класс
При сокращении рациональных дробей используем правило сокращения обык.др. Числитель и знаменатель делим на один многочлен.
Запомните, что разные буквенные части мы не сокращаем, только одинаковые.
Дроби, в числ. и знамен. которых стоит выражение (многочлен) тоже сократимы. В таких дробях можно сокращать только одинаковые многочлены. Многочлены разделены между собой умножением.
Также можно использовать формулы сокращ. умножения.
Еще пара примеров:
Источник: https://luckclub.ru/dejstviya-s-drobyami-7-klass-povtorenie-sravnenie-sokrashhenie-reshenie-uravnenij
10 Методы решения уравнений, содержащих целые или дробные части
К
числу нестандартных относятся методы
решения уравнений, которые содержат
целые и (или) дробные части действительных
чисел. В программе школьной математики
методы решения таких уравнений не
изучаются. В настоящем разделе применение
существующих методов и приемов
иллюстрируется на примерах решения
ряда уравнений.
Целой
частью действительного числа (илиАнтье)
называется
наибольшее целое число, не превосходящее
,
и это число обозначается.
Очевидно, что
png»>Разностьназывается дробной частью числа(илиМантисса)
и
обозначается через Из определения следует, что
png»>Кроме того, справедливо равенство
Отметим
некоторые свойства введенного выше
понятия целой части действительного
числа.
Перейдем
теперь к рассмотрению уравнений,
содержащих целую и (или) дробную части
неизвестной переменной.
Задачи
и решений
Пример
10.1. Решить
уравнение
Решение.
Поскольку
являются целым числом, то- тоже целое число. Следовательно, число
png»>также является целым. В таком случаеи уравнение (10.3) принимает видЦелыми корнями последнего уравнения
являются
qmhj/img-Aj5vlr.png»>
Пример
10.2. Решить
уравнение
Решение.
Рассмотрим
последовательно три случая.
Если
,
т.е. решением уравнения (10.4) могут быть
только
Пусть
тогда из уравнения (10.4) следует, чтоТак
как,
то получаем систему неравенств
Если
Следовательно, уравнение (10.4) не имеет
корней среди
Пример
10.3. Решить
уравнение
Решение.
Используя
свойство (10.2), можно записать
Отсюда,
принимая во внимание уравнение (10.5),
следуют неравенства
Поскольку
в этом случае следует,
что.
Так как- целое число, то отсюда получаем, что
png»>Следовательно, имеем
Из
уравнения (10.5) следует, что – целое число. Так как
png»>то остается лишь проверить целые значенияНетрудно установить, что решениями
(10.5) являются
qmhj/img-kYkNrI.png»>
Пример
10.4. Решить
уравнение
(10.7)
Решение.
Из
формулы (10.1) следует, что В этой связи уравнение (10.7) можно
переписать, как
Отсюда
следует уравнение
(10.8)
Очевидно,
что является корнем уравнения (10.8). Положим,
чтоТогда разделим обе части уравнения
(10.9) наи получим уравнение
Рассмотрим
последовательно несколько случаем.
Если
В таком случае
Пример
10.5. Решить
уравнение
Решение.
Решая
тригонометрическое уравнение (10.10),
получаем
(10.11)
где
– целое число. Из уравнения (10.11) получаем
совокупность двух уравнений
png»>Левые части обоих уравнений являются
целыми числами, в то время как их правые
части (за исключением случая
png»>в первом уравнении) принимают иррациональные
значения.
Следовательно,
равенство в уравнениях совокупности
может иметь место только в том случае,
когда правые их части являются
рациональными (точнее, целыми) числами.
А это возможно лишь в первом уравнении
при условии, что В этом случае получаем уравнение
png»>откуда следует
Ответ:
Пример
10.6. Решить
уравнение
Решение.
Левая
часть уравнения (10.12) принимает только
целые значения, поэтому число является целым.
Так
как то при любом целоммногочленпредставляет собой произведение трех
последовательно расположенных на
числовой оси
qmhj/img-b1a3G_.png»>целых чисел, среди которых имеется хотя
бы одно четное число и число, кратное
трем. Следовательно, многочленделится набез остатка, т.е.
png»>является целым числом.
В
этой связи и уравнение (10.12) принимает видили
Так
как то корнями уравнения (10.13) являются
Ответ:
Пример
10.7. Доказать
равенство
Доказательство.
Любое число можно представить или какгде- целое число и
Рассмотрим
два возможных случая.
-
Пусть Так как
Таким
образом, равенство (10.14) выполняется для
каждого из двух рассмотренных выше
случаем. Следовательно, равенство
(10.14) доказано.
Заключение
В
результате работы над дипломным проектом
был проведен анализ решения нестандартных
типов решения тестовых задач. Все
рассмотренные задачи, решаемые
нестандартными методами, классифицированы
по следующим типам:
-
метод функциональной подстановки
-
методы, основанные на применении численных неравенств,
-
метод тригонометрической подстановки;
-
методы, основанные на монотонности функций,
-
методы решения функциональных уравнений,
-
методы, основанные на применении векторов,
-
комбинированные методы,
-
методы, основанные на использовании ограниченности функций,
-
методы решения симметрических систем уравнений,
-
методы решения уравнений, содержащих целые или дробные части числа.
-
В
каждом из этих типов рассмотрены
конкретные примеры и методы их решения. -
Материал,
содержащийся в дипломной работе,
представляет собой основу методического
пособия, которое можно при определенной
доработке, внедрять как в школьный
процесс, так и при подготовке абитуриентов
к поступлению. -
Список
использованных источников
-
Азаров, В.И. Функциональные методы решения задач [текст] : учебное пособие / В.И. Азаров, О.П. Тавгень, В.С. Федосенко. – Мн. :БГУ,1994.
-
Азаров, А.И Экзамен по математике: руководство к решению задач [текст] : справочное пособие / С.В. Пруцко, В.С. Федосенко. – Мн. :ТетраСистем, 2001.
-
Ивлев, Б.М. Задачи повышенной трудности по алгебре и началам анализа [текст] : учебное пособие / Б.М. Ивлев, А.М.Абрамов, Ю.П. Дудницин, С.И. Шварцбург. -М. :Просвещение, 1990.
-
Габринович, В.А. Решим любую задачу [текст] : учебное пособие / В.А. Габринович, В.И. Громак. – Мн. :Асар, 1996.
-
Мандрик, П.А. Экзамен по математике на пять [текст] : учебное пособие / П.А. Мандрик, В.И. Репников. – Мн. :тетраСистемс, 1999.
-
Олехник, С.Н. Нестандартные методы решений уравнений и неравенств [текст] : учебное пособие / С.Н. Олехник, М.К. Потапов, П.И. Пасаиченуо. – М. :МГУ, 1991.
-
Пруцко, С.В. Экзамен по математике [текст] : руководство к решению задач : учебное пособие / С.В. Пруцко, А.И. Азаров, В.С. Федосенко. – МН. :тетраСистемс, 2001.
-
Пруцко, С.В. руководство к решению конкурсных задач по математике [текст] : учебное пособие / С.В. Пруцко, А.И. Азаров, В.С. Федосенко. – МН. :тетраСистемс, 1999.
-
Сборник задач по математике для поступающих во втузы [текст] / под редакцией М.И.Сканави. – Мн. :Высшая школа, 1990.
-
Супрун, В.П. Избранные задачи повышенной сложности по математике [текст] / В.П. Супрун. Мн. :Полымя, 1998.
-
Супрун, В.П. Нестандартные методы решения задач по математике [текст] / В.П. Супрун. –Мн. :Полымя, 2000.
Источник: https://studfile.net/preview/5792561/page:8/
Линейные уравнения с дробями в 6 классе можно решать по обычной схеме: неизвестные — в одну сторону, известные — в другую, изменив при этом их знак. Другой путь — предварительно упростить уравнение, превратив его из линейного уравнения с дробями в линейное уравнение с целыми числами.
Сначала на примере одного линейного уравнения с дробями рассмотрим оба способа решения.
1 способ: Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Приводим к общему знаменателю дроби в каждой части уравнения:
Это — простейшее линейное уравнение. Обе части уравнения делим на число, стоящее перед иксом:
При делении чисел с разными знаками получаем отрицательное число. По правилу деления дробей:
После сокращения имеем:
(В данном случае ответ можно записать и в виде десятичной дроби: х=-0,8).
2 способ:
Обе части уравнения умножим почленно на наименьший общий знаменатель всех входящих в него дробей, в данном случае он равен 24:
При умножении на знаменатель дроби сокращаются, в знаменателе остается единица, которую не пишем. От линейного уравнения с дробями перешли к линейному уравнению с целыми числами:
Неизвестные — в одну сторону, известные — в другую с противоположными знаками:
Обе части уравнения делим на число, стоящее перед иксом:
Ответ: -4/5.
Как видите, второй способ существенно упрощает решение линейного уравнения с дробями.
Обе части уравнения умножаем почленно на наименьший общий знаменатель всех входящих в него дробей. Здесь он равен 60:
Вместо линейного уравнения с дробями получили линейное уравнение с целыми числами. Неизвестные переносим в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Сокращаем дробь на 3:
Ответ: 5/11.
Обе части уравнения умножаем почленно на наименьший общий знаменатель всех входящих в него дробей:
В результате линейное уравнение с дробями заменили на линейное уравнение с целыми числами:
Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Ответ: 2,9.
В следующий раз рассмотрим линейные уравнения с смешанными дробями.
Методы решения уравнений, содержащих дроби
В этой статье я расскажу методики решения рациональных уравнений, содержащих дроби.
Что такое рациональное уравнение? Это уравнение, которое содержит в себе такие действия как сложение, вычитание, умножение, деление, возведение в степень с целым показателем. Извлечение корня — это недопустимое действие для рационального уравнения. Корень делает уравнение иррациональным, как, собственно, и дробный показатель степени.
В свою очередь рациональные уравнения делятся на два вида: целые рациональные и дробные рациональные.
К целым рациональным уравнениям относятся линейные и квадратные уравнения. Рассмотрим пример:
Это уравнение является…попробуешь угадать?…линейным. Его можно запросто увидеть, если деление на 2 и на 6 заменить умножением на 1/2 и 1/6 соответственно. Но оно все-таки содержит в себе знаменатель, поэтому мы его и рассматриваем в данной статье.
К дробным рациональным уравнениям относятся уравнения, которые содержат икс в знаменателе. Например, это уравнение дробное рациональное:
Методика решения приведенных примеров, в принципе, одинакова. Разница состоит в том, что в дробных рациональных уравнениях знаменатель не должен равняться нулю, поэтому при их решении оговаривают ограничения для икса. По-научному говорят, что находят область допустимых значений (ОДЗ).
Но давайте начнем с простого.
Целое рациональное уравнение.
Сначала решим целое рациональное уравнение.
Если ты в уравнении видишь дроби, то надо от них избавится, ведь уравнение без дробей решается намного приятнее)
В этом уравнении находим общий знаменатель. Он равен 6. Это значит, что обе части уравнения надо умножить на 6 (одинокий икс тоже).
Обычно этот шаг пропускают и переходят к следующему, но я его все равно распишу:
Числители и знаменатели сокращаются и получается элементарное уравнение:
Приводим подобные слагаемые:
Чтобы найди икс надо -10 разделить на 10 (произведение делим на известный множитель). Получаем ответ:
Готово!
Дробное рациональное уравнение.
Теперь решим дробное рациональное уравнение.
Я уже писала о том, что в дробных рациональных уравнениях знаменатели не должны равняться нулю. Знаменатель второй дроби нас устраивает, ведь 3 не равно 0) А вот знаменатель первой дроби требует от нас, чтобы мы нашли ОДЗ.
А дальше по накатанной: надо обе части уравнения умножить на общий знаменатель. Общим знаменателем будет выражение 3(х + 9).
Снова распишу подробно, но если ты шаришь, то следующую запись можешь не писать.
В первой дроби сокращаем (х + 9), а во второй — тройки. Получаем такое уравнение:
Здесь можно раскрыть скобки, потом перенести известные в одну сторону, а неизвестные — в другую… Но делать я этого не стану, а просто обе части уравнения разделю на -2. А еще поменяю местами левую и правую части уравнения, чтобы привести его к привычному виду.
Чтобы найти неизвестное слагаемое надо из суммы вычесть известное слагаемое, т.е. из -9 вычесть 9.
Ответ таков:
Сравниваем с ОДЗ… Всё отлично. Корень уравнения подходит.
Альтернативный метод решения уравнения с дробями.
Но нельзя пройти мимо другого метода решения данного уравнения: с помощью пропорции. Помнишь, как она раскрывается? Правильно, крест-накрест. И не надо искать общий знаменатель)
Перемножаем….и о чудо! Получаем уравнение, которое мы уже решали!
Дальнейшее решение расписывать не буду, оно есть выше.
Такой способ решения уравнений хорош, когда в уравнении имеются две дроби.
В завершении решу еще одно уравнение предложенными выше способами.
Только ты решаешь какой способ выбрать.
Твой персональный препод Васильева Анна)
Со всеми числами в математике можно производить основные арифметические действия: складывать, вычитать, умножать, делить, сравнивать.
Исключением не являются обыкновенные дроби.
Сегодня мы на уроке научимся складывать и вычитать обыкновенные дроби с одинаковыми знаменателями.
Эта информация доступна зарегистрированным пользователям
В общем виде запишем правила сложения и вычитания таких дробей.
Выясним, как с помощью координатной прямой можно найти сумму и разность обыкновенных дробей с одинаковыми знаменателями.
Вспомним названия компонентов арифметических операций сложения и вычитания и по каким правилам находится каждое из них.
Рассмотрим примеры решения уравнений и текстовых задач с использованием правил сложения и вычитания дробей с одинаковыми знаменателями.
Вы уже достаточно хорошо знакомы с обыкновенными дробями.
Вам известно, что дробь- это часть некоторой рассматриваемой величины, часть от целого.
Вы умеете правильно читать и записывать обыкновенные дроби.
Мы выяснили, что дробное число состоит из двух частей (двух чисел), разделенных дробной чертой.
Нижнюю часть дроби называют знаменателем, он показывает на сколько равных частей (долей) разделили целое, верхнюю часть дроби называют числителем, он показывает сколько частей взяли.
Вы уже умеете сравнивать обыкновенные дроби, находить часть целого и целого по части.
Попробуем сегодня выяснить возможно ли обыкновенные дроби складывать и вычитать.
Сложение- это арифметическая операция, в результате которой происходит объединение исчисляемых объектов в единое целое.
Результат операции сложения называют суммой.
Складываемые числа называют слагаемыми.
В общем виде операция сложения выглядит так:
Эта информация доступна зарегистрированным пользователям
Выясним, как и по каким правилам складывают дроби с одинаковыми знаменателями.
Рассмотрим пример.
Целое яблоко разрезали на две равные части- две доли, каждая из которых равна ½ яблока.
Первая доля яблока- ½ яблока (первое слагаемое).
Вторая доля яблока- ½ яблока (второе слагаемое).
Эта информация доступна зарегистрированным пользователям
Одно целое яблоко будет представляет собой сумму этих двух половинок.
(mathbf{frac{1}{2} + frac{1}{2} = frac{2}{2} = 1}) (две доли из двух представляют одно целое яблоко).
Рассмотрим ситуацию посложнее.
Два друга, Саша и Миша, разделили яблоко на четыре равные части- 4 доли, каждая из которых равна ¼ яблока.
Эта информация доступна зарегистрированным пользователям
Миша съел три дольки яблока, т.е. три доли из четырех или ¾ яблока.
Саша съел одну дольку яблока, т.е. одну долю из четырех или ¼ яблока.
Для того чтобы определить сколько всего долей съели друзья, нам нужно сложить все доли, которые съел каждый из них.
¾ яблока, которые съел Миша- первое слагаемое.
¼ яблока, которые съел Саша- второе слагаемое.
Всего мальчики съели 4 доли яблока (3 доли + 1 доля) из четырех.
Эта информация доступна зарегистрированным пользователям
(mathbf{frac{3}{4} + frac{1}{4} = frac{3 + 1}{4} = frac{4}{4} = 1}) (четыре доли из четырех представляют одно целое яблоко).
Саша и Миша съели целиком все яблоко, т.е. (mathbf{frac{4}{4} = 1}).
Заметим следующее: при сложении обыкновенных дробей в первом и во втором примере, мы складывали только числители дробей, а знаменатель слагаемых в результате сложения оставался прежним.
Правило сложения обыкновенных дробей с одинаковыми знаменателями сформулируем так:
При сложении обыкновенных дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же.
Запишем данное правило в буквенном виде.
Эта информация доступна зарегистрированным пользователям
Причем n ≠ 0.
Эта информация доступна зарегистрированным пользователям
Рассмотрим несколько примеров.
1. Найдите значение суммы (mathbf{frac{3}{15} и frac{4}{15}}).
У дробей (mathbf{frac{3}{15} и frac{4}{15}}) одинаковый знаменатель, следовательно, чтобы сложить эти дроби, нужно сложить их числители, а знаменатель оставить без изменения.
(mathbf{frac{3}{15} + frac{4}{15} = frac{3 + 4}{15} = frac{7}{15}})
2. Найдите значение суммы (mathbf{frac{12}{26} и frac{8}{26}}).
У дробей (mathbf{frac{12}{26} и frac{8}{26}}) одинаковый знаменатель, следовательно, чтобы сложить эти дроби, нужно сложить их числители, а знаменатель оставить без изменения.
(mathbf{frac{12}{26} + frac{8}{26} = frac{12 + 8}{26} = frac{20}{26}})
Правило сложения обыкновенных дробей справедливо как для правильных, так и неправильных дробей.
3. Найдите сумму правильной и неправильной дроби (mathbf{frac{8}{17} и frac{17}{17}}).
Так как знаменатель первой и второй дроби равны, найдем сумму числителей этих дробей, а знаменатель оставим без изменения.
(mathbf{frac{8}{17} + frac{17}{17} = frac{8 + 17}{17} = frac{25}{17}})
4. Найдите сумму неправильных дробей(mathbf{frac{14}{5} и frac{9}{5}}).
Так как знаменатель первой и знаменатель второй дроби равны, найдем сумму числителей этих дробей, а знаменатель оставим без изменения.
(mathbf{frac{14}{5} + frac{9}{5} = frac{14 + 9}{5} = frac{23}{5}})
Сложение дробных чисел с одинаковыми знаменателями можно проиллюстрировать с помощью координатной луча.
Эта информация доступна зарегистрированным пользователям
На координатном луче сложение дробных чисел представляет собой ряд последовательных действий.
Рассмотрим сложение дробных чисел с одинаковыми знаменателями с помощью координатного луча на примере.
Найдем сумму дробей (mathbf{frac{2}{7} и frac{3}{7}}).
1. Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Эта информация доступна зарегистрированным пользователям
Так как знаменатели суммируемых дробных чисел одинаковы и равны семи, то единичный отрезок выгоднее всего разбить на семь равных частей (долей).
Каждая такая доля будет равна (mathbf{frac{1}{7}}) единичного отрезка ОЕ.
2. Найдем точку с координатой (mathbf{frac{2}{7}}), назовем ее точкой А.
Дробь (mathbf{frac{2}{7}}) представляет собой две части (доли) из семи, следовательно, точка А с координатой (mathbf{frac{2}{7}}) будет удалена от начала координат на расстояние двух долей единичного отрезка ОЕ.
3. К числу (mathbf{frac{2}{7}}) прибавим число (mathbf{frac{3}{7}}).
От найденной точки А((mathbf{frac{2}{7}})) отложим вправо (по направлению координатного луча) 3 доли единичного отрезка ОЕ, попадем в точку, координатой которой является число (mathbf{frac{5}{7}}), назовем ее точкой В.
Две доли, да еще три доли, в результате получаем пять долей из семи.
(mathbf{frac{2}{7} + frac{3}{7} = frac{2 + 3}{7} = frac{5}{7}})
Эта информация доступна зарегистрированным пользователям
Осуществлять вычитание дробей с одинаковыми знаменателями так же просто, как находить их сумму.
Вычитанием называют математическую операцию, в результате которой происходит уменьшение общего количества исчисляемых объектов.
Результат вычитания называют разностью (остаток при вычитании).
Число, из которого вычитают (которое уменьшают), называют уменьшаемым.
Число, которое вычитают из уменьшаемого- это вычитаемое.
В общем виде операция сложения выглядит следующим образом:
Эта информация доступна зарегистрированным пользователям
Рассмотрим простой пример.
Вишневый пирог разрезали на 6 равных частей, (mathbf{frac{3}{6}}) этого пирога съели.
Какая часть пирога осталась?
Для данной задачи целый вишневый пирог- это уменьшаемое.
Так как пирог разрезали на 6 долей, то дробь (mathbf{frac{6}{6}}) будет представлять собой один целый пирог.
Эта информация доступна зарегистрированным пользователям
По условию съели от целого пирога ((mathbf{frac{6}{6}}) пирога) его некоторую часть ((mathbf{frac{3}{6}}) пирога).
Следовательно, дробь (mathbf{frac{3}{6}})— это вычитаемое.
Получаем следующее: из шести возможных долей съели три.
Эта информация доступна зарегистрированным пользователям
Определим разность- остаток (часть пирога, которая осталась нетронутой).
По рисунку мы можем заметить, что целый пирог разделили на шесть долей и из них съели три, ровно половину, вторая половина (столько же сколько съели) осталась, т.е. осталось три доли из шести.
(mathbf{frac{6}{6} — frac{3}{6} = frac{6 — 3}{6} = frac{3}{6}}) пирога осталось.
Запишем правило вычитания дробей с одинаковыми знаменателями.
При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют прежним.
Данное правило с помощью букв можно записать следующим образом:
Эта информация доступна зарегистрированным пользователям
Причем n ≠ 0.
Эта информация доступна зарегистрированным пользователям
Рассмотрим несколько примеров.
Выполним вычитание обыкновенных дробей с одинаковыми знаменателями.
1. Найдите значение разности (mathbf{frac{16}{45} и frac{7}{45}}).
Дроби (mathbf{frac{16}{45} и frac{7}{45}}) имеют одинаковые знаменатели, следовательно, нам следует из числителя уменьшаемого вычесть числитель вычитаемого, знаменатель необходимо оставить прежним.
(mathbf{frac{16}{45} — frac{7}{45} = frac{16 — 7}{45} = frac{9}{45}})
Правило вычитания дробей с одинаковыми знаменателями справедливо для всех видов обыкновенных дробей как для правильных, так и неправильных.
2. Найдите разность(mathbf{frac{15}{17} и frac{13}{17}}).
Дроби (mathbf{frac{15}{17} и frac{13}{17}}) имеют одинаковые знаменатели, следовательно, из числителя уменьшаемого вычтем числитель вычитаемого, а знаменатель оставим тем же.
(mathbf{frac{15}{17} — frac{13}{17} = frac{15 — 13}{17} = frac{2}{17}})
3. Найдите разность(mathbf{frac{25}{13} и frac{7}{13}}).
Из неправильной дроби (mathbf{frac{25}{13}}) вычтем правильную (mathbf{ frac{7}{13}}).
Дроби (mathbf{frac{25}{13} и frac{7}{13}}) имеют одинаковые знаменатели, следовательно, из числителя уменьшаемого вычтем числитель вычитаемого, а знаменатель оставим тем же.
(mathbf{frac{25}{13} — frac{7}{13} = frac{25 — 7}{13} = frac{18}{13}})
4. Найдите разность (mathbf{frac{35}{35} и frac{3}{35}}).
Из неправильной дроби (mathbf{frac{35}{35}}) вычтем правильную (mathbf{frac{3}{35}}).
Дроби (mathbf{frac{35}{35} и frac{3}{35}}) имеют одинаковые знаменатели, следовательно, из числителя уменьшаемого вычтем числитель вычитаемого, а знаменатель оставим тем же.
(mathbf{frac{35}{35} — frac{3}{35} = frac{35 — 3}{35} = frac{32}{35}})
5. Найдите разность(mathbf{frac{52}{35} и frac{40}{35}}).
Найдем разность двух неправильных дробей.
Дроби (mathbf{frac{52}{35} и frac{40}{35}}) имеют одинаковые знаменатели.
Из числителя уменьшаемого вычтем числитель вычитаемого, а знаменатель оставим тем же.
(mathbf{frac{52}{35} — frac{40}{35} = frac{52 — 40}{35} = frac{12}{35}})
Вычитание дробных чисел с одинаковыми знаменателями можно продемонстрировать с помощью координатного луча.
Как это происходит, рассмотрим на примере.
Найдем разность дробей (mathbf{frac{6}{7} и frac{2}{7}}).
1. Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Эта информация доступна зарегистрированным пользователям
Так как знаменатели уменьшаемого и вычитаемого одинаковы и равны семи, то единичный отрезок выгоднее всего разбить на семь равных частей (долей).
Каждая такая доля будет равна (mathbf{frac{1}{7}}) единичного отрезка ОЕ.
2. Отметим на координатном луче точку А с координатой (mathbf{frac{6}{7}}).
Дробь (mathbf{frac{6}{7}}) представляет собой шесть долей единичного отрезка ОЕ из семи.
Следовательно, точка А должна быть удалена от начала координат вправо (по направлению координатного луча) на расстояние шести долей единичного отрезка ОЕ.
3. Найдем разность дробей (mathbf{frac{6}{7} и frac{2}{7}}).
Из (mathbf{frac{6}{7}})вычтем (mathbf{frac{2}{7}}), для этого переместим полученную точку А((mathbf{frac{6}{7}})) на 2 доли единичного отрезка ОЕ влево (против направления координатного луча), получим точку В с координатой (mathbf{frac{4}{7}}).
(mathbf{frac{6}{7} — frac{2}{7} = frac{6 — 2}{7} = frac{4}{7}})
Эта информация доступна зарегистрированным пользователям
Уравнения и задачи, содержащие обыкновенные дроби, решают по тем же правилам и используя те же методы, которые применяют при решении уравнений и задач с натуральными числами.
Эта информация доступна зарегистрированным пользователям
Рассмотрим на примерах решение уравнений, содержащих обыкновенные дроби.
Эта информация доступна зарегистрированным пользователям
Уравнение- это равенство, которое включает в себя неизвестные числа, обозначенные буквами, значение которых можно определить.
Важно помнить, что при нахождении корней уравнения, с правой и левой частью уравнения можно производить различные действия и преобразования, однако, эти действия не должны нарушать равенство между ними.
Нам хорошо известно каким образом связаны между собой компоненты каждой арифметической операции, воспользуемся данными знаниями при решении уравнений.
- Решение уравнения с неизвестным слагаемым.
Неизвестным может быть любое слагаемое.
Правило: чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Пример №1.
Решим уравнение (mathbf{x + frac{7}{12} = frac{12}{12}}).
Выражение, стоящее в левой части уравнения, является суммой.
В этом выражении неизвестно первое слагаемое х.
(mathbf{x + frac{7}{12} = frac{12}{12}})
(mathbf{x = frac{12}{12} — frac{7}{12}})
(mathbf{x = frac{5}{12}})
Проверка: в исходное уравнение (mathbf{x + frac{7}{12} = frac{12}{12}}) вместо неизвестного х нужно подставить найденное значение (mathbf{x = frac{5}{12}}).
(mathbf{frac{5}{12} + frac{7}{12} = frac{12}{12}})
(mathbf{frac{12}{12} = frac{12}{12}}) получили верное равенство, следовательно, корень уравнения найден верно.
Ответ: (mathbf{x = frac{5}{12}}).
- Решение уравнения с неизвестным уменьшаемым.
Правило: если неизвестно уменьшаемое число, необходимо сложить два неизвестных компонента операции вычитания, т.е. нужно разность сложить с вычитаемым.
Пример №2.
Решим уравнение (mathbf{x — frac{10}{17} = frac{7}{17}}).
Выражение, стоящее в левой части уравнения, является разностью, а неизвестная х— уменьшаемым.
Найдем значение х, при которой исходное уравнение обратится в верное равенство.
(mathbf{x — frac{10}{17} = frac{7}{17}})
(mathbf{x = frac{7}{17} + frac{10}{17}})
(mathbf{x = frac{17}{17}})
Проверка: в исходное уравнение (mathbf{x — frac{10}{17} = frac{7}{17}}) вместо неизвестного х нужно подставить найденное значение (mathbf{x = frac{17}{17}}).
(mathbf{frac{17}{17} — frac{10}{17} = frac{7}{17}})
(mathbf{frac{7}{17} = frac{7}{17}}) получили верное равенство, следовательно, корень уравнения найден верно.
Ответ: (mathbf{x = frac{17}{17} = 1}).
- Решение уравнения с неизвестным вычитаемым.
Правило: чтобы найти вычитаемое, необходимо от уменьшаемого отнять разность.
Пример №3.
Решим уравнение (mathbf{frac{15}{31} — x = frac{9}{31}}).
Выражение, стоящее в левой части уравнения, является разностью, в данном выражении неизвестная х— это вычитаемое.
Найдем значение х, при которой исходное уравнение обратится в верное равенство.
(mathbf{frac{15}{31} — x = frac{9}{31}})
(mathbf{x = frac{15}{31} — frac{9}{31}})
(mathbf{x = frac{6}{31}})
Проверка: в исходное уравнение (mathbf{frac{15}{31} — x = frac{9}{31}}) вместо неизвестного х нужно подставить найденное значение (mathbf{x = frac{6}{31}}).
(mathbf{frac{15}{31} — frac{6}{31} = frac{9}{31}})
(mathbf{frac{9}{31} = frac{9}{31}}) получили верное равенство, следовательно, корень уравнения найден верно.
Ответ: (mathbf{x = frac{6}{31}}).
Рассмотрим решение более сложного уравнения, которое содержит несколько арифметических операций.
Пример №4.
Решим уравнение (mathbf{(frac{24}{18} — x) — frac{5}{18} = frac{12}{18}}).
Первым делом упростим данное уравнение.
Определим арифметическую операцию, которая будет выполнятся в последнюю очередь.
Последним действием будет нахождение разности между выражением в скобках (mathbf{(frac{24}{18} — x)}) и дробью (mathbf{frac{5}{18}})
За неизвестное примем целое выражение, стоящее в левой части уравнения в скобках.
В таком случае х (на данном этапе решения) является частью неизвестного уменьшаемого.
Чтобы найти неизвестное уменьшаемое, нужно разность сложить с вычитаемым.
(mathbf{(frac{24}{18} — x) = frac{12}{18} + frac{5}{18}})
(mathbf{frac{24}{18} — x = frac{12 + 5}{18}})
(mathbf{frac{24}{18} — x = frac{17}{18}})
В результате получили простое уравнение, в котором неизвестно вычитаемое.
(mathbf{x = frac{24}{18} — frac{17}{18}})
(mathbf{x = frac{24 — 17}{18}})
(mathbf{x = frac{7}{18}})
Проверка: в упрощенное уравнение (mathbf{frac{24}{18} — x = frac{17}{18}}) вместо неизвестного х нужно подставить найденное значение (mathbf{x = frac{7}{18}}).
(mathbf{frac{24}{18} — frac{7}{18} = frac{17}{18}})
(mathbf{frac{17}{18} = frac{17}{18}}) получили верное равенство, следовательно, корень уравнения найден верно.
Ответ: (mathbf{x = frac{7}{18}}).
Рассмотрим на примерах решение задач на сложение и вычитание обыкновенных дробей с одинаковыми знаменателями.
Нам известны различные виды арифметических задач на сложение и вычитание: задачи на нахождение суммы, разности, вычитаемого, уменьшаемого, слагаемого, задачи на разностное сравнение, задачи на увеличение или уменьшение на несколько единиц.
Сегодня рассмотрим только некоторые из них.
Задача №1.
В первый день засеяли (mathbf{frac{2}{7}}) поля, а во второй день (mathbf{frac{3}{7}}) этого поля.
Какую часть поля засеяли за эти два дня?
Эта информация доступна зарегистрированным пользователям
Кратко запишем условие задачи.
Эта информация доступна зарегистрированным пользователям
Общую часть поля, которую засеяли за два дня, найдем с помощью операции сложения.
Решение:
Из условия задачи известно первое слагаемое ((mathbf{frac{2}{7}})) и второе слагаемое ((mathbf{frac{3}{7}})).
Найдем сумму двух слагаемых.
(mathbf{frac{2}{7} + frac{3}{7} = frac{2 + 3}{7} = frac{5}{7}})(поля) засеяли за два дня.
Ответ: (mathbf{frac{5}{7}}) (поля).
Задача №2.
Мама купила один кочан капусты.
Для приготовления супа она потратила (mathbf{frac{3}{5}}) кочана.
Какая часть кочана капусты осталась?
Эта информация доступна зарегистрированным пользователям
Мы знаем, что единицу можно представить в виде дроби, в которой числитель равен знаменателю.
Чтобы решить данную задачу, единицу (один кочан капусты) нужно представить в виде дроби со знаменателем 5, так будет удобнее производить вычисления.
Получим дробь (mathbf{frac{5}{5}})- это целый кочан капусты, который купила мама.
Известно, чтобы найти остаток чего-либо (разность чисел), нужно от уменьшаемого отнять вычитаемое.
В нашем случае, уменьшаемое- это дробь (mathbf{frac{5}{5}}) (целый кочан капусты).
Вычитаемое в данной задаче- это дробь (mathbf{frac{3}{5}}) (часть капусты, которая пошла на приготовление супа).
Запишем кратко условие задачи.
Было: 1 кочан капусты ((mathbf{frac{5}{5}}) кочана)
Израсходовали: (mathbf{frac{3}{5}}) кочана
Осталось- ?
Решение:
(mathbf{frac{5}{5} — frac{3}{5} = frac{5 — 3}{5} = frac{2}{5}}) (кочана) осталось.
Ответ: (mathbf{frac{2}{5}}) (кочана)
Попробуем решить более сложную задачу на сложение и вычитание дробей с одинаковыми знаменателями, в которой необходимо выполнить несколько арифметических операций.
Задача №3.
В магазин привезли ананасы.
В первой половине дня продали (mathbf{frac{1}{4}}) всех ананасов, а после обеда- (mathbf{frac{2}{4}}) привезенных ананасов, и осталось продать еще 40 ананасов.
Сколько ананасов привезли в магазин?
Эта информация доступна зарегистрированным пользователям
Выясним, какую часть от привезенных ананасов составляет число 40.
Общее количество ананасов примем за единицу, вычтем из этого количества часть ананасов, которые удалось продать.
Далее по известной части оставшихся ананасов найдем исходное их количество.
(mathbf{1 — frac{1}{4} — frac{2}{4} = frac{4}{4} — frac{1}{4} -frac{2}{4} = frac{4 — 1 — 2}{4} = frac{3 — 2}{4} = frac{1}{4}}) (ананасов) осталось продать.
40 ананасов- это остаток ананасов, которые не удалось продать, составляет (mathbf{frac{1}{4}}) всех привезенных ананасов.
Если известно сколько составляет часть от целого, то по известной части можно найти целое.
Воспользуемся правилом нахождения целого по его части.
40 ананасов, составляющие (mathbf{frac{1}{4}}) часть всех привезенных ананасов, разделим на числитель и полученный результат умножим на знаменатель дроби, которая выражает эту часть.
40 ÷ 1 • 4 = 40 • 4 = 160 (ананасов) всего привезли в магазин.
Ответ: 160 (ананасов).
Эта информация доступна зарегистрированным пользователям






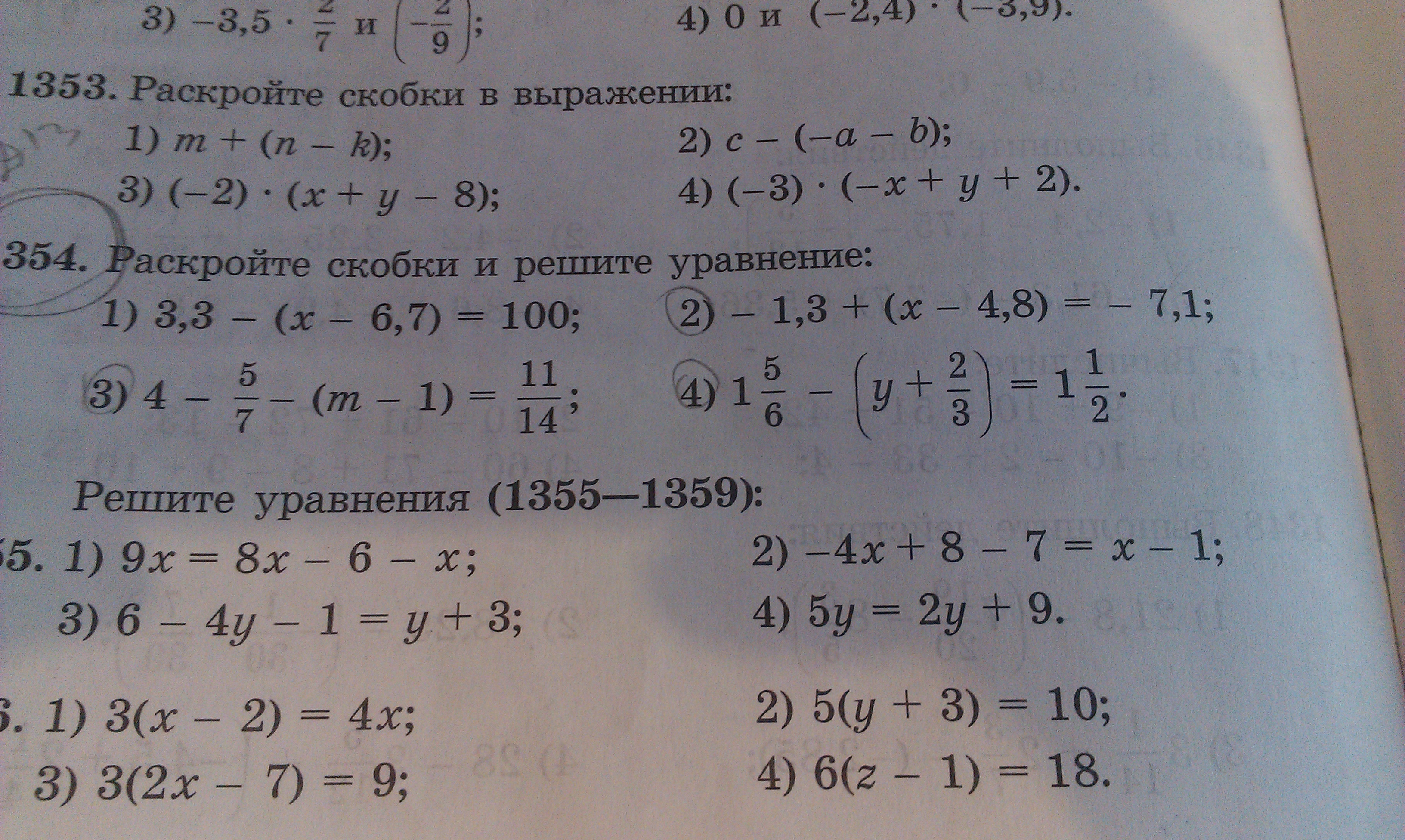










![Rendered by QuickLaTeX.com [x = - frac{{1 cdot mathop {24}limits^4 }}{{mathop 6limits_1 cdot 5}}]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-b277148ea87346868250dc5cb394589b_l3.png)