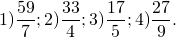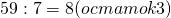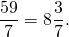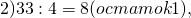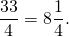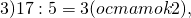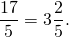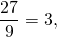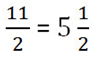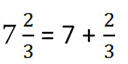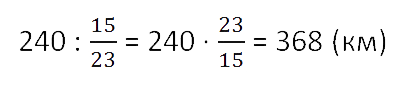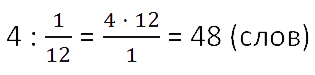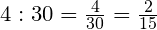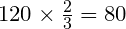Как найти неизвестную часть дроби - Исправление недочетов и поиск решений вместе с Examum.ru

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

обыкновенный вид — ½ или a/b,
десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = −b : а; если а равно нулю, а b не равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Линейное уравнение выглядит так

ах + b = 0, где a и b — действительные числа.

Что поможет в решении:

если а не равно нулю, то у уравнения единственный корень: х = −b : а;
если а равно нулю, а b не равно нулю — у уравнения нет корней;
если а и b равны нулю, то корень уравнения — любое число.

Квадратное уравнение выглядит так:

ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

подобрать число, которое можно разделить на каждый из знаменателей без остатка;
умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

если значение переменной обращает знаменатель в 0, значит это неверное значение;
делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

Область допустимых значений: х ≠ −2.
Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.

Урок по теме «Решение дробных рациональных уравнений». 8-й класс

Разделы: Математика

Класс: 8

Цели урока:

формирование понятия дробных рационального уравнения;
рассмотреть различные способы решения дробных рациональных уравнений;
рассмотреть алгоритм решения дробных рациональных уравнений, включающий условие равенства дроби нулю;
обучить решению дробных рациональных уравнений по алгоритму;
проверка уровня усвоения темы путем проведения тестовой работы.

развитие умения правильно оперировать полученными знаниями, логически мыслить;
развитие интеллектуальных умений и мыслительных операций — анализ, синтез, сравнение и обобщение;
развитие инициативы, умения принимать решения, не останавливаться на достигнутом;
развитие критического мышления;
развитие навыков исследовательской работы.

воспитание познавательного интереса к предмету;
воспитание самостоятельности при решении учебных задач;
воспитание воли и упорства для достижения конечных результатов.

Тип урока: урок – объяснение нового материала.

Ход урока

1. Организационный момент.

Здравствуйте, ребята! На доске написаны уравнения посмотрите на них внимательно. Все ли из этих уравнений вы сможете решить? Какие нет и почему?

Уравнения, в которых левая и правя часть, являются дробно-рациональными выражениями, называются дробные рациональные уравнения. Как вы думаете, что мы будем изучать сегодня на уроке? Сформулируйте тему урока. Итак, открываем тетради и записываем тему урока «Решение дробных рациональных уравнений».

2. Актуализация знаний. Фронтальный опрос, устная работа с классом.

А сейчас мы повторим основной теоретический материл, который понадобиться нам для изучения новой темы. Ответьте, пожалуйста, на следующие вопросы:

Что такое уравнение? (Равенство с переменной или переменными.)
Как называется уравнение №1? (Линейное.) Способ решения линейных уравнений. (Все с неизвестным перенести в левую часть уравнения, все числа — в правую. Привести подобные слагаемые. Найти неизвестный множитель).
Как называется уравнение №3? (Квадратное.) Способы решения квадратных уравнений. (Выделение полного квадрата, по формулам, используя теорему Виета и ее следствия.)
Что такое пропорция? (Равенство двух отношений.) Основное свойство пропорции. (Если пропорция верна, то произведение ее крайних членов равно произведению средних членов.)
Какие свойства используются при решении уравнений? (1. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному. 2. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.)
Когда дробь равна нулю? (Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.)

3. Объяснение нового материала.

Решить в тетрадях и на доске уравнение №2.

Какое дробно-рациональное уравнение можно попробовать решить, используя основное свойство пропорции? (№5).

х 2 -4х-2х+8 = х 2 +3х+2х+6

х 2 -6х-х 2 -5х = 6-8

Решить в тетрадях и на доске уравнение №4.

Какое дробно-рациональное уравнение можно попробовать решить, умножая обе части уравнения на знаменатель? (№6).

Теперь попытайтесь решить уравнение №7 одним из способов.

Дробно-рациональные уравнения

Что такое дробно-рациональные уравнения

Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:

при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.

Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.

9 x 2 — 1 3 x = 0

1 2 x + x x + 1 = 1 2

6 x + 1 = x 2 — 5 x x + 1

Уравнения, которые не являются дробно-рациональными:

Как решаются дробно-рациональные уравнения

В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.

Алгоритм действий при стандартном способе решения:

Выписать и определить ОДЗ.
Найти общий знаменатель для дробей.
Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
Записать уравнение со скобками.
Раскрыть скобки для приведения подобных слагаемых.
Найти корни полученного уравнения.
Выполним проверку корней в соответствии с ОДЗ.
Записать ответ.

Пример 1

Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:

x x — 2 — 7 x + 2 = 8 x 2 — 4

Начать следует с области допустимых значений:

x 2 — 4 ≠ 0 ⇔ x ≠ ± 2

Воспользуемся правилом сокращенного умножения:

x 2 — 4 = ( x — 2 ) ( x + 2 )

В результате общим знаменателем дробей является:

Выполним умножение каждого из членов выражения на общий знаменатель:

x x — 2 — 7 x + 2 = 8 x 2 — 4

x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )

После сокращения избавимся от скобок и приведем подобные слагаемые:

x ( x + 2 ) — 7 ( x — 2 ) = 8

x 2 + 2 x — 7 x + 14 = 8

Осталось решить квадратное уравнение:

Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:

Примеры задач с ответами для 9 класса

Требуется решить дробно-рациональное уравнение:

x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0

Определим область допустимых значений:

О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2

x 2 + 7 x + 10 ≠ 0

D = 49 — 4 · 10 = 9

x 1 ≠ — 7 + 3 2 = — 2

x 2 ≠ — 7 — 3 2 = — 5

Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:

a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )

x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0

Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:

x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0

Сократим дроби, избавимся от скобок, приведем подобные слагаемые:

x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —

— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0

x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0

x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0

2 x 2 + 9 x — 5 = 0

Потребуется решить квадратное уравнение:

2 x 2 + 9 x — 5 = 0

Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.

Дано дробно-рациональное уравнение, корни которого требуется найти:

4 x — 2 — 3 x + 4 = 1

В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:

4 ( x + 4 ) x — 2 — 3 ( x — 2 ) x + 4 — 1 ( x — 2 ) ( x + 4 ) = 0

4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0

4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0

x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0

Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:

— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0

Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:

( x — 2 ) ( x + 4 ) ≠ 0

Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:

— x 2 — x + 30 = 0 _ _ _ · ( — 1 )

Получилось квадратное уравнение, которое можно решить:

Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.

Нужно решить дробно-рациональное уравнение:

x + 2 x 2 — 2 x — x x — 2 = 3 x

На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:

x + 2 1 x ( x — 2 ) — x x x — 2 — 3 ( x — 2 ) x = 0

x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0

x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0

— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0

Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.

— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )

Корни квадратного уравнения:

x 1 = — 4 ; x 2 = 2

Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.

Найти корни уравнения:

x 2 — x — 6 x — 3 = x + 2

Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:

x 2 — x — 6 1 x — 3 — x ( x — 3 ) — 2 ( x — 3 ) = 0

x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0

x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0

0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0

Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:

Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.

Ответ: х — любое число, за исключением 3.

Требуется вычислить корни дробно-рационального уравнения:

5 x — 2 — 3 x + 2 = 20 x 2 — 4

На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:

5 ( x + 2 ) x — 2 — 3 ( x — 2 ) x + 2 — 20 1 ( x — 2 ) ( x + 2 ) = 0

5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0

5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0

2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0

( x — 2 ) ( x + 2 ) ≠ 0

Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.

Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.

Ответ: корни отсутствуют

Нужно найти корни уравнения:

x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )

Начнем с определения ОДЗ:

— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0

При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:

x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )

( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )

( x — 3 ) x + x = x + 5

Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:

x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0

Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:

x 1 · x 2 = — 10 x 1 + x 2 = 3

В этом случае подходящими являются числа: -2 и 5.

Второе значение не соответствует области допустимых значений.

источники:

http://urok.1sept.ru/articles/559882

http://wika.tutoronline.ru/algebra/class/9/drobnoraczionalnye-uravneniya

Источник

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Понятие дроби

обыкновенный вид — ½ или a/b,
десятичный вид — 0,5.

Дроби бывают двух видов:

Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Понятие уравнения

Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = −b : а; если а равно нулю, а b не равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Линейное уравнение выглядит так

ах + b = 0, где a и b — действительные числа.

Что поможет в решении:

если а не равно нулю, то у уравнения единственный корень: х = −b : а;
если а равно нулю, а b не равно нулю — у уравнения нет корней;
если а и b равны нулю, то корень уравнения — любое число.

Квадратное уравнение выглядит так:

ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Понятие дробного уравнения

Как решать уравнения с дробями

1. Метод пропорции

Итак, у нас есть линейное уравнение с дробями:

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

подобрать число, которое можно разделить на каждый из знаменателей без остатка;
умножить на это число каждый член уравнения.

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

если значение переменной обращает знаменатель в 0, значит это неверное значение;
делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Примеры решения дробных уравнений

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

Область допустимых значений: х ≠ −2.
Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.

Как выделить целую часть дроби

Как неправильную дробь перевести в правильную? Для этого надо выделить из нее целую часть. А как выделить целую часть дроби? Рассмотрим, как это следует делать, в теории и на примерах.

Чтобы из неправильной дроби выделить целую часть, нужно:

1) Разделить с остатком числитель на знаменатель.

2) Неполное частное записать в целую часть.

3) Остаток (если он есть) записать в числитель.

4) Знаменатель оставить тот же.

Теперь рассмотрим, как выделить целую часть дроби, на конкретных примерах.

Перевести неправильные дроби в правильные:

1) Делим с остатком числитель на знаменатель:

Неполное частное равно 8. Это — целая часть. Остаток от деления равен 3. Его записываем в числитель. Знаменатель 7 переписываем без изменения:

так как числитель делится на знаменатель нацело.

—>Школа математики для всех, кто учиться и преподает —>

Каталог статей

Смешанные числа. Выделение целой части

Среди обыкновенных дробей различают два разных вида.
Правильные и неправильные дроби
Рассмотрим дроби.

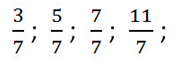
Обратите внимание, что в двух первых дробях (3/7 и 5/7) числители меньше знаменателей. Такие дроби называют правильными.

У правильной дроби числитель меньше знаменателя. Поэтому правильная дробь всегда меньше единицы.

Рассмотрим две оставшиеся дроби.
Дробь 7/7 имеет числитель равный знаменателю (такие дроби равны единицы), а дробь 11/7 имеет числитель больший знаменателя. Такие дроби называют неправильными.

У неправильной дроби числитель равен или больше знаменателя. Поэтому неправильная дробь или равна единице или больше единицы.

Любая неправильная дробь всегда больше правильной.

Как выделить целую часть
У неправильной дроби можно выделить целую часть. Рассмотрим, как это можно сделать.

Чтобы из неправильной дроби выделить целую часть надо:
1. разделить с остатком числитель на знаменатель;
2. полученное неполное частное записываем в целую часть дроби;
3. остаток записываем в числитель дроби;
4. делитель записываем в знаменатель дроби.

Пример. Выделим целую часть из неправильной дроби 11/2.
• Разделим в столбик числитель на знаменатель.

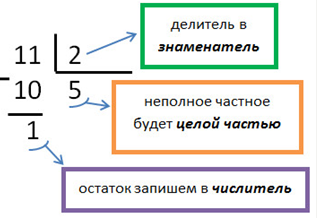
• Теперь запишем ответ.

Полученное число выше, содержащее целую и дробную часть, называют смешанным числом.

Мы получили смешанное число из неправильной дроби, но можно выполнить и обратное действие, то есть представить смешанное число в виде неправильной дроби.
Чтобы представить смешанное число в виде неправильной дроби надо:
1. умножить его целую часть на знаменатель дробной части;
2. к полученному произведению прибавить числитель дробной части;
3. записать полученную сумму из пункта 2 в числитель дроби, а знаменатель дробной части оставить прежним.
Пример. Представим смешанное число в виде неправильной дроби.
• Умножаем целую часть на знаменатель.

3 • 5 = 15
• Прибавляем числитель.

15 + 2 = 17
• Записываем полученную сумму в числитель новой дроби, а знаменатель оставляем прежним.

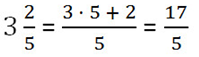
Любое смешанное число можно представить как сумму целой и дробной части.

Любое натуральное число можно записать дробью с любым натуральным знаменателем.

Частное от деления числителя на знаменатель такой дроби будет равно данному натуральному числу.
Примеры.

источники:

http://www.for6cl.uznateshe.ru/kak-vydelit-celuyu-chast-drobi/

http://matematik.3dn.ru/publ/3-1-0-26

Источник

На уроке математики, на улице, в магазине, в быту и профессиональной деятельности, науке и технике часто приходится встречаться с дробями и решать различные задачи с ними.

Эта информация доступна зарегистрированным пользователям

Так, например, в кулинарии очень часто используют дробные числа, отмеряя те или иные ингредиенты в соответствии с рецептом: пол чайной ложки соли, треть стакана, четверть пачки, полкилограмма сахара и т.д.

Определяя время по часам, приходится находить часть от часа, от минуты, например, 30 минут равняется ½ часа, четверть часа (15 минут)- это ¼ часа, 30 секунд равняются ½ минуты, 15 секунд составляют ¼ минуты.

Эта информация доступна зарегистрированным пользователям

В медицине и фармацевтике используют дробные числа.

В состав лекарственного средства чаще всего включают дробное количество различных действующих и вспомогательных веществ.

Эта информация доступна зарегистрированным пользователям

Для корректного лечения врач устанавливает эффективную дозировку лекарственного препарата, которая иногда представлена в виде дробного числа.

Дозировку или концентрацию лекарственного средства приходится выражать в виде дроби: полтаблетки (1/2), четверть (1/4) таблетки и т.д.

Особенно важно учитывать количество медицинского препарата для пациентов детского возраста.

Часто дозировку лекарства для детей рассчитывают относительно взрослой дозы на основе данных о массе ребенка, количестве лет и др.

Обыкновенные дроби широко используются в строительстве и архитектуре.

Создавая надежную конструкцию, важно соблюдать соизмеримость и определенные соотношения частей сооружения.

Эта информация доступна зарегистрированным пользователям

Начертить чертеж, построить здание, возвести мост, положить асфальт, приготовить бетонную смесь невозможно без знаний о дробях.

В спортивных состязаниях вам, наверное, не раз приходилось слышать такие фразы: «состоялся четверть финал» или «полуфинал чемпионата», «одна восьмая финала».

Дроби используют в искусстве, например, в музыке, живописи и др.

Одним из примеров внедрения дробей в музыкальное искусство может служить нотная грамота.

Еще древнегреческий ученый Пифагор установил связь между длительностью музыкального звучания и дробей.

Дроби применяют для обозначения длительности нот.

Так, например, существует длинная нота.

Кроме нее есть половинная нота, четвертная, восьмая, шестнадцатая и т.д.

Эта информация доступна зарегистрированным пользователям

Такое обозначение нот удобно, так как явно видно насколько одна нота длиннее или короче другой.

Существует еще одна важная роль дробного числа в музыке.

Музыкальный размер (количество ритмических единиц в такте) так же обозначают в виде дроби (только без дробной черты) вначале нотной строки.

Эта информация доступна зарегистрированным пользователям

С помощью музыкального размера музыканты понимают с каким ритмом и темпом нужно играть музыкальное произведение.

В картографии и географии с помощью дроби указывают масштаб карты.

Деление целого на доли встречается в юридической практике при делении наследства.

В повседневной жизни мы часто делим целое на части, например, плитку шоколада ломаем на дольки, чтобы угостить друзей, режем на кусочки торт на празднике, делим мандарин на дольки и т.д.

Мы можем привести бесконечное множество примеров деления чего-либо на части.

Сегодня на уроке вспомним, что называют долей числа и, что представляет собой дробь от числа.

Эта информация доступна зарегистрированным пользователям

Научимся решать задачи, в которых необходимо находить часть от целого и целое по его части.

Рассмотрим алгоритм и примеры решения таких задач.

В математике дробью обозначают часть некоторой рассматриваемой величины, часть от целого.

Каждую равную часть одного целого называют долей числа.

Дробь представляет собой число, которое состоит из одной или нескольких долей (равных частей) целого.

Математическая запись обыкновенной дроби оформляется в виде двух чисел, разделенных чертой, которая называется дробной (она может быть горизонтальной и наклонной).

Число, стоящее над дробной чертой, называют числителем.

Числитель показывает, сколько долей взяли от целого.

Число, стоящее под дробной чертой, называют знаменателем.

Знаменатель показывает, на сколько всего равных долей разделили целое.

Зная целое, можно найти его часть.

Рассмотрим такую задачу.

Эта информация доступна зарегистрированным пользователям

Ленту, длиной 12 дм, разрезали на 2 равные части.

Что значит разрезать на две равные части?

Это значит, что ленту нужно разделить на две доли, каждая из которых является половиной этой ленты.

Эта информация доступна зарегистрированным пользователям

Итак, каждая доля- это половина всей ленты, по-другому такую часть от целого называют одна вторая часть ленты, обозначают ½.

В нашем примере половина всей ленты, т.е. одна вторая часть ее составляет 6 дм.

Запишем равенство: 12 ÷ 2 = 6 (дм).

Ленту такой же длины разделим на четыре равные части.

Эта информация доступна зарегистрированным пользователям

Получим 4 доли, каждая из которых равна одной четвертой всей длины ленты, обозначается 1/4.

Четверть (одна четвертая) ленты составляет: 12 ÷ 4 = 3 (дм).

Попробуем найти одну шестую ленты все той же длины- 12 дм.

Эта информация доступна зарегистрированным пользователям

1/6 доля этой ленты будет составлять: 12 ÷ 6 = 2 (дм).

Итак, нам становится ясно, чтобы найти долю от числа, необходимо разделить это число на количество долей (равных частей).

Рассмотрим ситуацию посложней.

Полоску бумаги, длиной 15 см, разделим на 5 равных частей (пять долей).

Эта информация доступна зарегистрированным пользователям

Определим, чему будет равны (mathbf{frac{3}{5}}) этой полоски бумаги.

Одна доля ((mathbf{frac{1}{5}}) этой полоски)- это 15 ÷ 5 = 3 (см).

Возьмем три таких доли.

Так как одна доля составляет 3 см, то три доли будут равны 3 ∙ 3 = 9 (см).

В данном случае получилось, что три пятых полоски бумаги составляют 9 см.

Сформулируем правило нахождения части от целого.

Чтобы найти несколько долей целого (дробь от числа), необходимо найти величину одной доли, затем умножить ее на количество долей.

Запишем алгоритм нахождения части от числа (несколько долей целого).

1. Найти величину одной доли.

2. Величину одной доли умножить на количество взятых долей.

В буквенном виде данное правило можно представить так:

Пусть А— это исходное число.

В— неизвестная часть числа А, выраженная дробью (mathbf{frac{m}{n}}).

m— числитель, показывает сколько долей взяли.

n— знаменатель, показывает на сколько долей разделили число А.

Чтобы найти часть числа А, необходимо это число А разделить на знаменатель (n) и умножить на числитель (m) дроби, которая выражает эту часть.

Эта информация доступна зарегистрированным пользователям

В качестве примера рассмотрим решение нескольких задач.

Задача №1.

Туристы за все время своего путешествия из пункта А в пункт В должны пройти 54 км.

Туристы прошли (mathbf{frac{1}{2}}) всего пути по лесу.

Сколько километров прошли туристы по лесу? Сколько им осталось пройти?

Решение:

Вспомним правило.

Чтобы найти долю от числа, необходимо число разделить на количество долей.

Прошли (mathbf{frac{1}{2}}) всего пути- это значит туристы преодолели половину своего пути.

Разделим весь путь на 2 равные доли, т.е. на 2, в результате получим (mathbf{frac{1}{2}}) пути, которую туристы прошли по лесу.

Этот путь будет составлять: 54 ÷ 2 = 27 (км).

Определим путь, который им осталось пройти, для этого из общего пути вычтем пройденный по лесу путь:

54 — 27 = 27 (км) туристам осталось пройти.

Ответ: 27 (км), 27 (км).

Задача №2

За три дня туристы прошли 54 километра.

За первый день они прошли половину всего пути.

За второй день преодолели (mathbf{frac{2}{3}}) оставшегося пути.

Сколько километров туристы прошли в каждый из трех дней?

Решение:

Весь трехдневный путь туристов составляет 54 км.

Первый день туристы прошли половину- это (mathbf{frac{1}{2}}) всего пути.

Выше в задаче №1 мы уже находили (mathbf{frac{1}{2}}) от 54 (км), у нас получился следующий результат:

54 ÷ 2 = 27 (км) прошли туристы в первый день.

Так как в первый день пройдена половина пути, то вторая половина- это оставшийся путь.

Он будет равен: 54 — 27 = 27 (км).

Второй день- это (mathbf{frac{2}{3}}) оставшегося пути, т.е. (mathbf{frac{2}{3}}) от 27 (км).

Чтобы найти дробь от числа, необходимо найти величину одной доли, затем умножить ее на количество частей (долей).

Найдем величину одной доли, для этого весь оставшийся путь (27 км) разделим на знаменатель дроби (в нашем случае это число 3), данное выражение будет описываться выражением 27 ÷ 3.

Полученный результат умножим на количество, пройденных туристами долей, на которые нам указывает числитель дроби (он равен 2).

В результате получим равенство:

27 ÷ 3 ∙ 2 = 9 ∙ 2 = 18 (км) туристы прошли во второй день.

Так как во второй день туристы прошли 18 км от пути, оставшегося после первого туристического дня (т.е. 18 км из 27 км), то за третий день им осталось пройти:

27 — 18 = 9 (км) туристы прошли в третий день.

Проверим полученные результаты.

Найдем весь туристический путь за три дня, он должен быть равен 54 км.

Для этого сложим путь первого, второго и третьего дня.

27 + 18 + 9 = 45 + 9 = 54 (км) прошли туристы за три дня.

Задача решена верно.

Ответ: 27 (км), 18 (км), 9 (км).

Эта информация доступна зарегистрированным пользователям

Если известно сколько составляет часть от целого, то по известной части можно найти целое.

Рассмотрим задачу:

Пусть длина (mathbf{frac{1}{2}}) ленты составляет 10 дм.

Определим, чему равна длина всей ленты.

Эта информация доступна зарегистрированным пользователям

Так как (mathbf{frac{1}{2}}) ленты- это ее половина, и она составляет 10 дм, то вторая половина так же равна 10 дм.

В таком случае, чтобы найти длину всей ленты, мы можем сложить длины этих двух половинок или, заменив сложение одинаковых слагаемых умножением, можем по 10 дм взять два раза, в результате получим равенство:

10 ∙ 2 = 20 (дм) длина всей ленты.

Ответ: 20 (дм).

Рассмотрим еще одну задачу, в которой будет известна длина одной четвертой части ленты.

Ленту подарочную разделили на четыре части.

Длина (mathbf{frac{1}{4}}) ленты составляет 5 дм.

Эта информация доступна зарегистрированным пользователям

Определим, чему равна длина всей ленты.

Целое, т.е. всю ленту разделили на 4 доли.

Известно, что одна доля- это (mathbf{frac{1}{4}}) ленты, она составляет 5 дм.

Чтобы найти длину всей ленты, необходимо длину одной доли (в нашем случае 5 дм) умножить на количество долей (в нашем примере их 4).

Получим следующее равенство:

5 ∙ 4 = 20 (дм) длина всей ленты.

Ответ: 20 (дм).

Рассмотрев эти два примера, можно сделать вывод:

Чтобы найти неизвестное число по его доле, необходимо долю этого числа умножить на число долей.

Усложним задачу про ленту и попробуем ее решить.

Пусть подарочную ленту разделили на 5 равных частей.

Определим, какова длина всей ленты, если (mathbf{frac{3}{5}}) этой ленты составляет 12 дм.

Эта информация доступна зарегистрированным пользователям

Из условия задачи известно, что разделили ленту на 5 долей, а 3 таких доли составляют 12 дм.

Для того чтобы найти длину всей ленты, необходимо найти длину одной доли.

Следовательно, известную длину трех долей (12 дм) разделим на количество этих долей (3 доли).

Данное действие будет описывать следующее выражение: 12 ÷ 3.

Затем умножим длину одной доли на количество всех долей (в нашем случае всю ленту разделили на 5 долей).

В результате получим равенство:

12 ÷ 3 ∙ 5 = 4 ∙ 5 = 20 (дм) длина всей ленты.

Ответ: 20 (дм).

Сформулируем правило нахождения целого по его части.

Чтобы найти целое по его части, необходимо определить величину одной доли, затем полученный результат умножить на общее количество долей (на которое поделено целое).

Запишем алгоритм нахождения числа по его дроби.

1. Найти величину одной доли.

2. Величину одной доли умножить на количество всех долей, на которое разделено число.

В буквенном виде данное правило можно представить так:

Пусть А— это исходное число, оно неизвестно.

В— часть числа А, выраженная дробью (mathbf{frac{m}{n}}).

m— числитель, показывает сколько долей взяли.

n— знаменатель, показывает на сколько долей разделили число.

Чтобы найти исходное число А, необходимо число В, соответствующее части числа А, разделить на числитель (m) и полученный результат умножить на знаменатель (n) дроби, которая выражает эту часть.

Эта информация доступна зарегистрированным пользователям

Рассмотрим, как данное правило применяется при решении задач.

Задача №1.

Дима потратил на сладости 120 рублей, что составляет (mathbf{frac{2}{4}}) всех накопленных им денег.

Сколько всего денег было у Димы накоплено?

Решение:

Общее количество денег, которое было у Димы не известно.

Известно только то, что 120 рублей- это часть всех денег Димы.

Эта же часть денег выражена дробью (mathbf{frac{2}{4}}) от всех денег.

Знаменатель данной дроби показывает на то, что все накопленные деньги разделены на 4 части, а числитель дроби указывает на то, что две части из четырех составляют 120 рублей.

Найдем величину одной доли (одной части из четырех), т.е. сколько составляет (mathbf{frac{1}{4}}) (четверть) всех денег Димы.

120 ÷ 2 = 60 (руб.) составляет четверть всех денег Димы.

Чтобы найти общее количество денег, которые накопил Дима (а это четыре части по 60 рублей), нужно:

4 ∙ 60 = 240 (руб.) было накоплено у Димы.

Кратко решение данной задачи можно записать следующим образом:

120 ÷ 2 ∙ 4 = 240 (руб.) было накоплено у Димы.

Ответ: 240 (руб.)

Очень часто задачи такого типа имеют более сложные условия и их приходится решать в несколько действий.

Задача №2.

Дима купил шоколадку. Он за нее заплатил 60 рублей, что составило (mathbf{frac{1}{3}}) всех его денег.

От оставшейся суммы (mathbf{frac{2}{3}}) он потратил на мороженное, остальные деньги положил в копилку.

Сколько денег Дима положил в копилку?

Решение:

Первым делом определим первоначальную сумму, которая была у Димы.

Будем считать, что искомое число состоит из трех долей.

По условию задачи одна доля составляет 60 рублей.

Чтобы найти число (целое) по его доле, необходимо долю этого числа умножить на число долей.

В таком случае получаем:

60 ∙ 3 = 180 (руб.) всего было накоплено у Димы- это первоначальная сумма, которая у него была.

Следующим действием найдем часть денег, которые потратил Дима на мороженное.

Из общей суммы денег вычтем 60 рублей, которые были потрачены на шоколадку.

180 — 60 = 120 (руб.) оставшееся сумма денег у Димы.

От полученного остатка найдем (mathbf{frac{2}{3}})

Чтобы найти (mathbf{frac{2}{3}}) от 120 (дробь от числа), нужно число 120 разделить на знаменатель и умножить на числитель этой дроби.

120 ÷ 3 ∙ 2 = 40 ∙ 2 = 80 (руб.) Дима потратил на мороженное.

Из первоначальной суммы (180 рублей) вычтем деньги, потраченные на шоколадку, (60 рублей), вычтем деньги, потраченные на мороженное, (80 рублей) и получим остаток денег, который Дима положил в копилку.

180 — 60 — 80 = 100 — 60 = 40 (руб.) Дима положил в копилку.

Ответ: 40 (руб.)

Эта информация доступна зарегистрированным пользователям

Сложные задачи на нахождение числа по его части

Часто задачи данного типа сложнее, чем рассмотренная задача выше, и более сложные задачи приходиться решать в
несколько действий.

Рассмотрим задачу.

При подготовке к диктанту по английскому языку Оля
выучила четверть всех слов, заданных учителем.
Если бы она выучила ещё 4 слова, то была
бы выучена треть всех слов.
Сколько всего слов надо было выучить Оле?

Решение. Как обычно подчеркнём в условии задачи все важные данные.

Как видно из условия, четыре невыученных слова — это часть от всех слов, которую можно найти в виде
разности дробей.

Такую часть всех слов составляют 4 слова.

Итак, 4 слова — это

от всех слов (целого). Теперь по правилу нахождения
числа по его части данное числовое значение разделим на соответствующую ему дробь

Ответ: всего 48 слов надо было выучить к диктанту.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Задачи на дроби

Выражение части в долях целого
Нахождение дроби от числа
Нахождение числа по его дроби

Выражение части в долях целого

Чтобы выразить часть в долях целого, нужно часть разделить на целое.

Задача. В классе 30 учащихся, отсутствуют четверо. Какая часть учащихся отсутствует?

Решение:

Ответ: В классе отсутствует 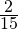учащихся.

Нахождение дроби от числа

Для решения задач, в которых требуется найти часть целого справедливо следующее правило:

Если часть целого выражена дробью, то чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на её числитель.

Задача 1. Было 600 рублей, этой суммы истратили. Сколько денег истратили?

Решение: Чтобы найти от 600 рублей, надо эту сумму разделить на 4 части, тем самым мы узнаем, сколько денег составляет одна четвёртая часть:

600 : 4 = 150 (р.).

Ответ: Истратили 150 рублей.

Задача 2. Было 1000 рублей, этой суммы истратили. Сколько денег было истрачено?

Решение: Из условия задачи мы знаем, что 1000 рублей состоит из пяти равных частей. Сначала найдём сколько рублей составляет одна пятая часть от 1000, а затем узнаем сколько рублей составляют две пятых:

1) 1000 : 5 = 200 (р.) — одна пятая часть.

2) 200 · 2 = 400 (р.) — две пятых части.

Эти два действия можно объединить:

1000 : 5 · 2 = 400 (р.).

Ответ: Было истрачено 400 рублей.

Второй способ нахождения части целого:

Чтобы найти часть целого, можно умножить целое на дробь, выражающую эту часть целого.

Задача 3. По уставу кооператива, для правомочности отчётного собрания на нём должно присутствовать не менее членов организации. В кооперативе 120 членов. При каком составе может состояться отчётное собрание?

Решение:

Ответ: Отчётное собрание может состояться при наличии 80 членов организации.

Нахождение числа по его дроби

Для решения задач, в которых требуется найти целое по его части справедливо следующее правило:

Если часть искомого целого выражена дробью, то чтобы найти это целое, можно данную часть разделить на числитель дроби и результат умножить на её знаменатель.

Задача 1. Потратили 50 рублей, это составило от первоначальной суммы. Найдите первоначальную сумму денег.

Решение: Из описания задачи мы видим, что 50 рублей в 6 раз меньше первоначальной суммы, т. е. первоначальная сумма в 6 раз больше, чем 50 рублей. Чтобы найти эту сумму, надо 50 умножить на 6:

50 · 6 = 300 (р.).

Ответ: Первоначальная сумма — 300 рублей.

Задача 2. Потратили 600 рублей, это составило от первоначальной суммы денег. Найдите первоначальную сумму.

Решение: Будем считать, что искомое число состоит из трёх третьих долей. По условию две трети числа равны 600 рублей. Сначала найдём одну треть от первоначальной суммы, а затем сколько рублей составляют три третьих (первоначальная сумма):

600 : 2 · 3 = 900 (р.).

Ответ: Первоначальная сумма — 900 рублей.

Второй способ нахождения целого по его части:

Чтобы найти целое по величине выражающей его часть, можно разделить эту величину на дробь, выражающую данную часть.

Задача 3. Отрезок AB, равный 42 см, составляет 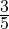длины отрезка CD. Найти длину отрезка CD.

Решение:

Ответ: Длина отрезка CD 70 см.

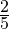
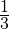
Задача 4. В магазин привезли арбузы. До обеда магазин продал , после обеда — привезённых арбузов, и осталось продать 80 арбузов. Сколько всего арбузов привезли в магазин?

Решение: Сначала узнаем, какую часть от привезённых арбузов составляет число 80. Для этого примем за единицу общее количество привезённых арбузов и вычтем из неё то количество арбузов, которое получилось реализовать (продать):

Итак, мы узнали, что 80 арбузов составляет от общего количества привезённых арбузов. Теперь узнаем сколько арбузов от общего количества составляет , а затем сколько арбузов составляют (количество привезённых арбузов):

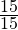
2) 80 : 4 · 15 = 300 (арбузов).

Ответ: Всего в магазин привезли 300 арбузов.

Источник

Решение уравнений с дробями

Понятие дроби

Основные свойства дробей

Понятие уравнения

Понятие дробного уравнения

Как решать уравнения с дробями

1. Метод пропорции

2. Метод избавления от дробей

Что еще важно учитывать при решении

Универсальный алгоритм решения

Примеры решения дробных уравнений

Урок по теме «Решение дробных рациональных уравнений». 8-й класс

Дробно-рациональные уравнения

Что такое дробно-рациональные уравнения

Как решаются дробно-рациональные уравнения

Примеры задач с ответами для 9 класса

Решение уравнений с дробями

Понятие дроби

Основные свойства дробей

Понятие уравнения

Понятие дробного уравнения

Как решать уравнения с дробями

1. Метод пропорции

2. Метод избавления от дробей

Что еще важно учитывать при решении

Универсальный алгоритм решения

Примеры решения дробных уравнений

Как выделить целую часть дроби

—>Школа математики для всех, кто учиться и преподает —>

Каталог статей

Читайте также

Сложные задачи на нахождение числа по его части

Ваши комментарии

Задачи на дроби

Выражение части в долях целого

Нахождение дроби от числа

Нахождение числа по его дроби