Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c — стороны произвольного треугольника
α, β, γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
Есть следующие формулы для определения катета или гипотенузы
a, b — катеты
c — гипотенуза
α, β — острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

a — сторона, основание
b, c — стороны
β, γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c1 , c2 — отрезки полученные от деления гипотенузы, высотой
α, β — углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
L— биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b — стороны треугольника
с — сторона на которую опущена биссектриса
d, e — отрезки полученные делением биссектрисы
γ — угол ABC , разделенный биссектрисой пополам
p — полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
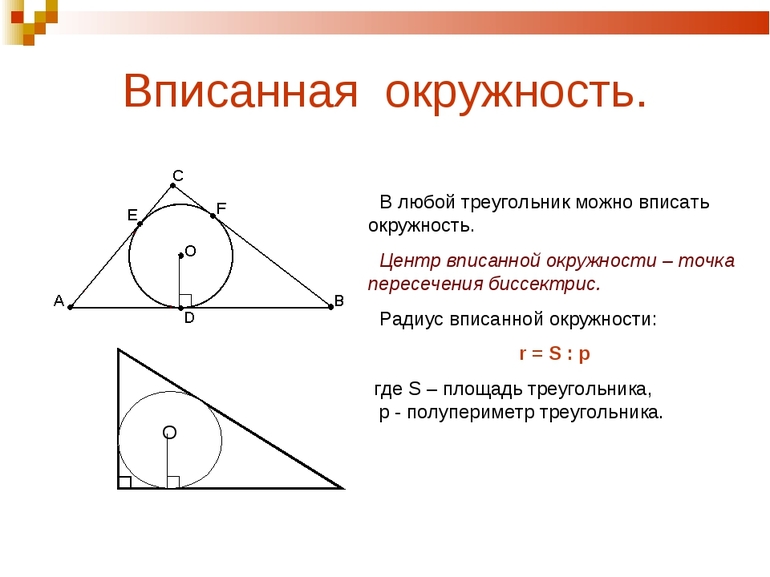
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
L — высота = биссектриса = медиана
a — одинаковые стороны треугольника
b — основание
α — равные углы при основании
β — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L — высота=биссектриса=медиана
a — сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
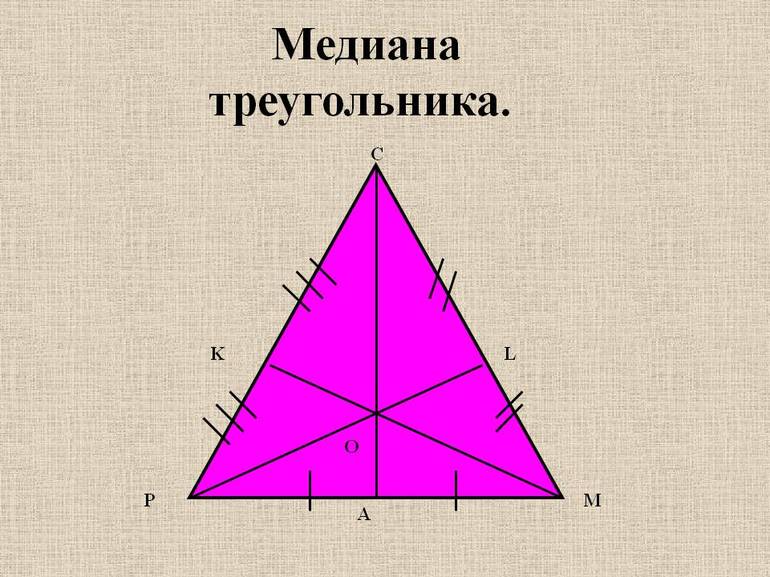
Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M — медиана, отрезок |AO|
c — сторона на которую ложится медиана
a, b — стороны треугольника
γ — угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M — медиана
R — радиус описанной окружности
O — центр описанной окружности
с — гипотенуза
a, b — катеты
α — острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:
- Найти все стороны треугольника.
- Найти все углы треугольника.
- Найти площадь (S) и периметр (P) треугольника.
- Найти радиус (r) вписанной окружности.
- Найти радиус (R) описанной окружности.
- Найти высоту (h) треугольника.
Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.
Как найти длину стороны треугольника?
Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
Для прямоугольного треугольника:
1) Найти катет через гипотенузу и другой катет
где a и b — катеты, с — гипотенуза.
2) Найти гипотенузу по двум катетам
где a и b — катеты, с — гипотенуза.
3) Найти катет по гипотенузе и противолежащему углу
где a и b — катеты, с — гипотенуза,α° и β° — углы напротив катетов.
4) Найти гипотенузу через катет и противолежащий угол
где a и b — катеты, с — гипотенуза,α° и β°- углы напротив катетов.
Для равнобедренного треугольника:
1) Найти основание через боковые стороны и угол между ними
где a — искомое основание, b — известная боковая сторона,α° — угол между боковыми сторонами.
2) Найти основание через боковые стороны и угол при основании
где a — искомое основание,b — известная боковая сторона,β° — угол при осноавнии.
3) Найти боковые стороны по углу между ними
где b — искомая боковая сторона, a — основание,α° — угол между боковыми сторонами.
4) Найти боковые стороны по углу при основании
где b — искомая боковая сторона, a — основание,β° — угол при осноавнии.
Для равностороннего треугольника:
1) Найти сторону через площадь
где a — искомая сторона, S — площадь треугольника.
2) Найти сторону через высоту
где a — искомая сторона,h — высота треугольника.
3) Найти сторону через радиус вписанной окружности
где a — искомая сторона,r — радиус вписанной окружности.
4) Найти сторону через радиус описанной окружности
где a — искомая сторона,R — радиус описанной окружности.
Для произвольного треугольника:
1) Найти сторону через две известные стороны и один угол (теорема косинусов)
где a — искомая сторона, b и с — известные стороны, α° — угол напротив неизвестной стороны.
2) Найти сторону через одну известную сторону и два угла (теорема синусов)
где a — искомая сторона, b — известная сторона, α° и β° известные углы.
Скачать все формулы в формате Word
Загрузить PDF
Загрузить PDF
Периметр треугольника — это общая длина всех его сторон.[1]
Самый простой способ найти периметр треугольника заключается в том, чтобы сложить длины всех его сторон, однако если вы не знаете длину хотя бы одной стороны треугольника, необходимо сначала найти ее. В первом разделе данной статьи рассказано, как вычислить периметр треугольника по трем известным сторонам — это наиболее простой и распространенный метод. Затем показано, как найти периметр прямоугольного треугольника, если известны длины двух сторон. И наконец, описано, как с помощью теоремы косинусов рассчитать периметр любого треугольника, если даны две стороны и угол между ними.
-
1
Запомните формулу, которая позволяет вычислить периметр треугольника. Если треугольник имеет стороны a, b и c, его периметр P равен: P = a + b + c.
- Таким образом, чтобы найти периметр треугольника, следует сложить длины всех трех его сторон.
-
2
Посмотрите на треугольник и узнайте длины всех трех сторон. Предположим, треугольник имеет следующие стороны: a = 5, b = 5 и c = 5.
- Рассматриваемый треугольник называется равносторонним, так как все три его стороны имеют одинаковую длину. Тем не менее формула для расчета периметра справедлива для любого треугольника.
-
3
Сложите длины всех трех сторон, чтобы найти периметр. В нашем примере 5 + 5 + 5 = 15, то есть P = 15.
- Рассмотрим другой пример: a = 4, b = 3 и c=5. В этом случае периметр равен: P = 3 + 4 + 5 = 12.
-
4
В ответе не забывайте указывать единицу измерения. Если стороны измеряются в сантиметрах, окончательный ответ также должен быть приведен в сантиметрах. Ответ должен быть в тех же единицах, в которых приведены длины сторон в условии задачи.
- В приведенном примере длина каждой стороны составляет 5 сантиметров, поэтому периметр равен 15 сантиметрам.
Реклама
-
1
Запомните, что такое прямоугольный треугольник. Прямоугольным называется такой треугольник, один из углов которого является прямым, то есть равен 90 градусам. Самая длинная сторона такого треугольника всегда лежит напротив прямого угла и называется гипотенузой. Две другие стороны, образующие прямой угол, называются катетами. Прямоугольные треугольники очень часто встречаются в задачах по математике. К счастью, есть формула, с помощью которой всегда можно рассчитать длину неизвестной стороны!
-
2
Вспомните теорему Пифагора. Эта теорема гласит, что в любом прямоугольном треугольнике с катетами a и b и гипотенузой c стороны связаны следующим соотношением: a2 + b2 = c2.[2]
-
3
Нарисуйте прямоугольный треугольник и обозначьте стороны как a, b и c. Самая длинная сторона прямоугольного треугольника — это гипотенуза. Она лежит напротив прямого угла. Обозначьте гипотенузу как c, а более короткие стороны — как a и b. Неважно, какой катет вы обозначите буквой a, а какой — буквой b, так как это не повлияет на конечный результат.
-
4
Подставьте в формулу значения известных сторон. Помните, что a2 + b2 = c2. Вместо букв подставьте числа, данные в условии задачи.
- Предположим, в условии дано, что a = 3 и b = 4, тогда получаем: 32 + 42 = c2.
- Если катет a = 6 и гипотенуза c = 10, тогда можно записать: 62 + b2 = 102.
-
5
Решите полученное уравнение, чтобы найти неизвестную сторону. Для этого сначала возведите в квадрат известные длины сторон (просто умножьте данное число само на себя, например 32 = 3 * 3 = 9). Если вы ищете гипотенузу, сложите квадраты двух сторон и из полученной суммы извлеките квадратный корень. Если необходимо найти катет, вычтите квадрат известного катета из квадрата гипотенузы и из полученного числа извлеките квадратный корень.
- В первом примере складываем квадраты сторон 32 + 42 = c2 и получаем 25= c2. После этого извлекаем квадратный корень из 25 и находим c = 5.
- Во втором примере складываем квадраты сторон 62 + b2 = 102 и получаем 36 + b2 = 100. Переносим 36 в правую сторону уравнения: b2 = 64. Извлекаем квадратный корень из 64 и находим b = 8.
-
6
Сложите длины трех сторон, чтобы найти периметр. Как мы помним, периметр вычисляется по формуле: P = a + b + c. После того как мы нашли длины сторон a, b и c, необходимо сложить их, чтобы определить периметр.
- В первом примере: P = 3 + 4 + 5 = 12.
- Во втором примере: P = 6 + 8 + 10 = 24.
Реклама
-
1
Выучите теорему косинусов. Эта теорема позволяет вычислить неизвестную сторону треугольника, если даны длины двух других сторон и величина угла между ними. Теорема косинусов очень полезна, она справедлива для всех треугольников. Эта теорема гласит, что для любого треугольника со сторонами a, b и c и противолежащими им углами A, B и C справедлива следующая формула: c2 = a2 + b2 – 2ab cos(C).[3]
[4]
-
2
Дайте обозначения сторонам и углам треугольника. Обозначьте первую известную сторону как a, а противоположный ей угол — как A. Вторую известную сторону и противолежащий ей угол обозначьте соответственно b и B. Известный угол между этими сторонами обозначьте как C, а противолежащую ему сторону, длину которой необходимо найти, — как c.
- Предположим, дан треугольник со сторонами 10 и 12 и углом между ними 97°. В этом случае имеем: a = 10, b = 12, C = 97°.
-
3
Подставьте известные значения в формулу и найдите неизвестную сторону с. Сначала возведите в квадрат длины известных сторон и сложите полученные значения. Затем найдите косинус угла С с помощью обычного или онлайн-калькулятора.[5]
Умножьте cos(C) на 2ab и вычтите полученное число из суммы a2 + b2. В результате вы получите c2. Извлеките квадратный корень, чтобы найти длину неизвестной стороны c. В нашем примере имеем:- c2 = 102 + 122 – 2 × 10 × 12 × cos(97°).
- c2 = 100 + 144 – (240 × -0,12187) (мы округлили значение косинуса до 5 знаков после запятой).
- c2 = 244 – (-29,25).
- c2 = 244 + 29,25 (два минуса дают плюс!).
- c2 = 273,25.
- c = 16,53.
-
4
Используйте вычисленную длину стороны c, чтобы найти периметр треугольника. Напомним, что периметр вычисляется по формуле: P = a + b + c, то есть следует прибавить к известным величинам сторон a и b найденную длину стороны c.
- В нашем примере получаем: 10 + 12 + 16,53 = 38,53. Итак, периметр треугольника равен 38,53!
Реклама
Об этой статье
Эту страницу просматривали 270 082 раза.
Была ли эта статья полезной?
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
(1) |
 |
(2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:


Далее, из формулы

 . . |
(3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c — стороны произвольного треугольника
α , β , γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b — катеты
c — гипотенуза
α , β — острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

a — сторона, основание
b, c — стороны
β , γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Элементы треугольника — формулы вычисления основных параметров
Общие сведения
Произвольное множество точек называют геометрической фигурой. На плоскости они соединены замкнутыми линиями, образующими контур тела. В трёхмерном пространстве многоугольник, состоящий из трёх отрезков, не принадлежащих одной прямой, носит имя треугольник. Его линии называют сторонами или боковыми гранями, а место их пересечения — вершинами.
Треугольник — замкнутое геометрическое тело, состоящее из трёх сторон и такого же количества углов. Боковые грани принято обозначать маленькими латинскими буквами. Углы на рисунке показывают маленькой дугой, а в записи — символом ∠ с указанием соответствующей вершины. Точки же пересечения линий подписывают большими буквами.
Например, если имеется треугольник ABC, у него есть углы A, B, C и стороны a, b, c. Боковые грани могут обозначать и как отрезки, тогда в их имени учитываются ограничивающие точки. Например, AB, BC, CA. Строгого требования в виде обозначений нет, но существуют негласные правила, которых всё же рекомендуется придерживаться.
Хотя определение треугольника и его элементов одинаковое, выделяют 3 класса фигур:
- остроугольный — любой из углов тела не превышает 90 градусов;
- тупоугольный — форма одного из разворотов тупоугольная;
- прямоугольный — размер одного из трёх углов составляет 90 градусов.
Кроме этого, многоугольник классифицируют по числу равных сторон. Разносторонним он считается в том случае, если все они разной длины, равнобедренным — треугольник, имеющий 2 равные стороны, а равносторонним — у которого все стороны равны. Последний в литературе может ещё называться правильным.
На основании классификационных групп треугольники можно сравнивать между собой. Они считаются подобными, если 2 угла одного соответственно равны двум углам другого, или когда 2 стороны одного пропорциональны двум сторонам другого, а углы, заключённые между этими сторонами, равны. Эти правила называют признаками подобия. Они особенно популярны среди физиков. Их часто используют при вычислении элементов прямоугольников, квадратов, трапеций.
Элементы треугольника
Кроме сторон и вершин, фигура имеет различные точки и линии, называемые замечательными. Такое имя они получили из-за своих свойств. Но перед тем как их перечислить, нелишним будет привести основные величины, характеризующие фигуру, способы их нахождения и теоремы.
Периметр многоугольника можно определить, сложив все стороны: P = a + b + c. Площадь треугольника находится как половина произведения двух граней, умноженных на синус угла между ними: S = (a * b * sinC) / 2. Сумма углов равна 180 градусов, при этом напротив равных сторон лежат одинаковые углы.
К замечательным линиям относят:
- Медиану — линию, проходящую через вершину к середине противолежащей стороны. Всего в треугольнике можно провести 3 таких отрезка. Точка их пересечения является центром массы. Если считать от вершины, в ней она делится в отношении 2 к 1. Каждая медиана разделяет фигуру на 2 объекта с одинаковой площадью.
- Биссектрису — отрезок, построенный к стороне из угла и делящий его на 2 равные части. Она делит грань на 2 замкнутые линии, пропорциональные прилежащим сторонам. Точка, в которой пересекаются биссектрисы, является началом диаметра вписанной в треугольник окружности.
- Высоту — перпендикуляр, опущенный из угла на противоположную сторону. Все они пересекаются в одной точке.
- Срединную линию — проходит всегда параллельно одной из граней и соединяет середины двух оставшихся сторон. 3 таких линии разделят многоугольник на 4 равных треугольника.
При измерениях используют и «особенные» точки фигуры. Если в треугольник вписать окружность, её центр совпадёт с местом скрещивания перпендикуляров. А если поместить в круг, середина будет совпадать с пересечением биссектрис. Для других замечательных линий точки их соприкосновения также имеют свои названия: ортоцентр (высот) и центроид (медиан). Первая может принадлежать как внутренней площади фигуры, так и внешней (тупоугольный треугольник).
В равнобедренном треугольнике медиана, высота и биссектриса совпадают. При этом их центр является серединой как вписанной окружности, так и описанного круга. А угол, из которого построен один из таких отрезков, будет разделён на 2 одинаковых разворота равных 30 градусам.
Основные формулы
Найти любой элемент треугольника можно по специальным формулам. Чаще всего приходится искать стороны фигуры. Зная их, можно найти практически любые параметры, просто подставив в выражения значения размеров граней.
Найти длину отрезка, формирующего контур фигуры, можно, зная длины двух сторон и угла или значения двух углов и одной стороны. Для первого случая формула имеет вид a = b * sin (a) / sin (b) = b * sin (a) / sin (a + c), а второго: a = √(b 2 + c 2 — 2bc * cos (a)). Если имеется тупой угол, косинус будет отрицательный. Это необходимо учитывать при расчётах.
Это общие формулы, подходящие для любого типа треугольника. Но в то же время для прямоугольного существует своё правило, связывающее все 3 грани в одну формулу: c = √(b 2 + a 2 ). Называется оно теоремой Пифагора. В равнобедренном вычислить сторону можно, зная любую другую и угол. Для основания используют равенство b = 2a * cos (a), а для равных граней: a = b / 2 * cos (a).
Из множества других существующих формул для определения различных элементов фигуры, можно указать на те, что чаще всего используются при решении примеров:
- Высота: h = (2 / a) * √(p * (p — a) * (p — b) * (p — c)) или h = b * sin© = c * sin (b). Отрезок можно найти, зная площадь и сторону h = 2 * S / a или радиус описанной окружности: h = (b * c) / 2 * R.
- Биссектриса: L = √(a * b * (a + b + c) * (a + b — c)) / (a + b). Формулу можно упростить, используя периметр: L = 2 * √ (a * b * P) * (P — c)) / (a + b), где P = p /2 (полупериметр).
- Медиана: М = √(2 * a 2 + 2b 2 — c 2 ) / 2. Линию можно определить, зная только 2 стороны и лежащий между ними угол: М = √(a 2 + b 2 — 2 * a * b * cos (с)) / 2. В прямоугольном треугольнике она равняется радиусу описанного круга или половине гипотенузы: М = R = c / 2.
Существуют и упрощённые выражения. Формула Герона позволяет высчитать площадь, используя полупериметр и длины сторон: S = √(P * (P — a) * (P — b) * (P — c)). Также величину можно определить, зная высоту и длину основания: S = (a * H) / 2.
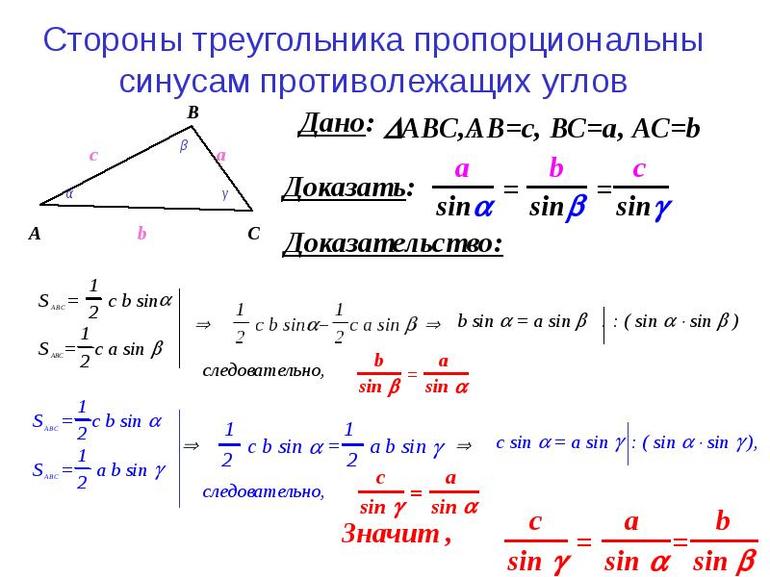
Для нахождения элементов треугольника в 7 классе ученикам дают ещё 2 фундаментальные теоремы: косинусов и синусов. Первая сообщает, что квадрат грани фигуры равен удвоенному произведению двух сторон и косинуса угла между ними, вычтенному из сумы квадратов: a 2 = b 2 + c 2 — 2 * b * c * cos (a). Согласно же второй, стороны пропорциональны синусам противолежащих углов: a / sin (a) = b / sin (b) = c / sin©.
Решение примеров
Формул для вычисления элементов треугольников можно насчитать несколько десятков. Запомнить их довольно сложно, поэтому нужно выучить основные определения и выражения, а сделать это лучше всего, решая практические примеры. Вот некоторые из них:
- В треугольнике проведено 2 высоты. Одна равняется 63 см, а другая 56 см. Найти истинный отрезок, если основание AC = 84 см, а размер медианы BK совпадает с длиной стороны BC. Так как точка K делит отрезок AC пополам, AK = KC = AC / 2 = 84 /2 = 42 см. В треугольнике BKC 2 стороны равны друг другу, согласно условию, значит, он равнобедренный. Следовательно, высота является одновременно и медианой. KH = HC = MC /2 = 42 / 2 = 21 см. Искомый отрезок будет равен: h = AK + KC = 42 + 21 = 63 см. Следовательно, правильный первый вариант.
- Пусть дан треугольник ABC. Найти возможный отрезок BN, на который биссектриса поделит сторону BC, если AB = 6 см, BC = 7 см, AC = 8 см. Для решения понадобится вспомнить свойство биссектрисы. Из него следует, что BN / NC = AB / AC = 6 / 8. Если искомый отрезок принять за икс, будет верным равенство KC = 7 — x. Значит: x / (7 — x) = 6 / 8. Отсюда можно выразить неизвестное: x = 42 / 14 = 3 см. Теперь останется подставить найденное число и найти искомое значение: KC = 7 — 3 = 4 см.
- Завод начал выпускать новую серию объёмных фигур. Определить, какой тип многоугольника лежит в их основании, если её стороны равны 3, 2 и √3. Чтобы найти ответ, нужно проанализировать исходные данные. Так как сумма двух меньших сторон больше третей боковой грани, в основании лежит треугольник. 3 в квадрате не равно 2 2 + (√3) 2 . Следовательно, геометрическое тело непрямоугольное. По теореме косинусов можно записать: a 2 = b 2 + c 2 — 2 * b * c * cos (a). Исходя из того, что cos (a) = -1/ √ 3, то есть он отрицательный, можно утверждать, что разворот угла тупой. Значит, треугольник у основания тупоугольный.
Проверить правильность вычислений можно, воспользовавшись онлайн-калькуляторами. Это сервисы, предоставляющие услуги по расчёту различных математических величин. Воспользоваться ими сможет любой, даже тот, кто не знает ни одной формулы и теоремы. Всё, что требуется от пользователя — правильно ввести исходные данные в специальную форму и нажать кнопку «Рассчитать». Через несколько секунд ответ, а в некоторых случаях и решение, появится на экране.
http://www-formula.ru/2011-10-09-11-08-41
http://nauka.club/matematika/geometriya/vychislenie-elementov-treugolnika.html
Как найти натуральную величину треугольника
Геометрическая фигура может быть изображена вращающейся, то есть занимающей определенное положение по отношению к неподвижной системе плоскостей проекции. В качестве оси вращения может использоваться любая прямая. Зная исходные данные вращающейся фигуры, можно определить ее натуральную величину, а также найти расстояние от заданной точки до треугольника.
Вам понадобится
- — учебник «Геометрия»;
- — линейка;
- — простой карандаш;
- — тетрадь.
Инструкция
Решите данную задачу путем замены плоскостей проекции. Прямые плоскости, проходящие перпендикулярно к линиям уровня данной плоскости, в геометрии получили название линий наибольшего наклона плоскости к соответствующей ей плоскости проекций. Проведите на рисунке горизонталь h и фронталь f. Ввиду того, что линия наибольшего наклона плоскости является перпендикулярной плоскости проекции П1 (эта перпендикулярность сохранена на горизонтальной проекции), ее горизонтальная проекция будет проходить через точку С1, то есть перпендикулярно проекции h1. Поскольку линия наибольшего наклона перпендикулярна к проекции плоскости П2, фронтальная проекция треугольника должна быть перпендикулярна проекции f2.
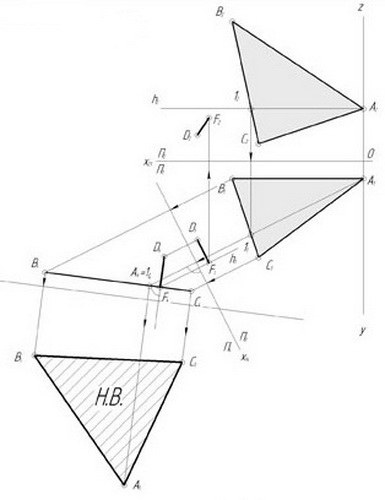
Для того чтобы преобразовать проецирующую плоскость в плоскость уровня, постройте еще одну плоскость проекций: она должна располагаться параллельно проекции треугольника с вершинами А4, В4 и С4. Затем проведите связующие линии и отложите координаты точек, которые взяты из плоскости П1. Полученная на рисунке проекция треугольника А5В5С5 будет соответствовать натуральной величине треугольника АВС.
Найдя натуральную величину треугольника ABC, с легкостью сможете определить расстояние от некой точки D до треугольника. Для этого опустите перпендикуляр из точки D на плоскость той проекции, которая является проецирующей. После этого найдите длину опущенного перпендикуляра.
Видео по теме
Обратите внимание
Помните: параллельный перенос геометрических фигур не изменяет ориентацию плоскости и не сохраняет неподвижных точек.
Полезный совет
Плоскости считаются параллельными, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым, принадлежащим другой плоскости. В то же время две прямые являются параллельными в том случае, если их одноименные проекции параллельны между собой.
Источники:
- Начертательная геометрия – решение задачи №3
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.