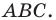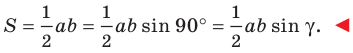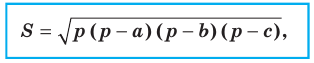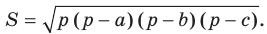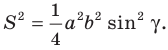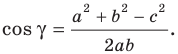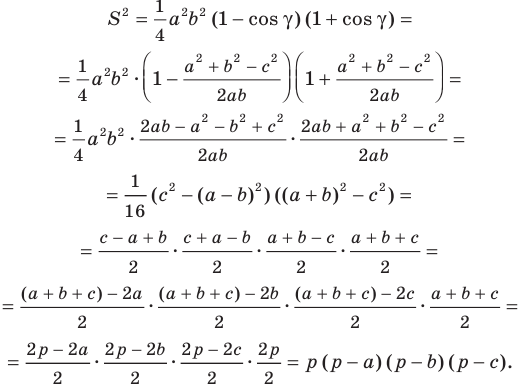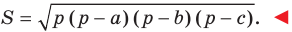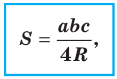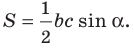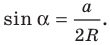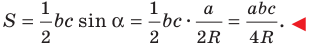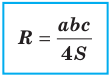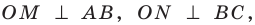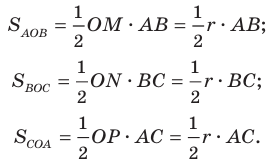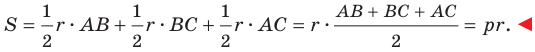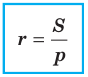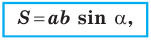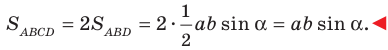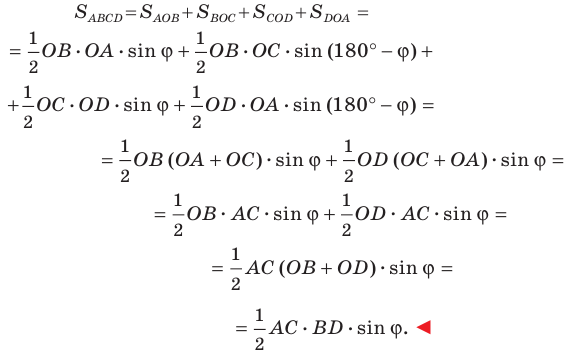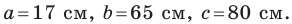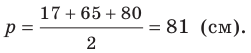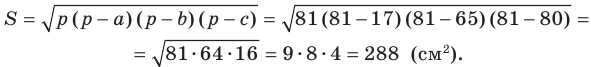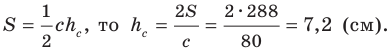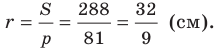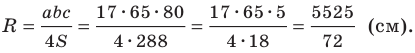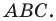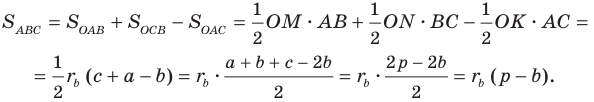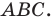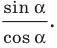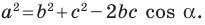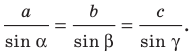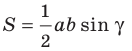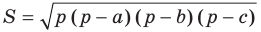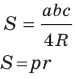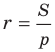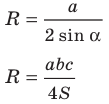Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
Решение:
Из теоремы косинусов имеем:
Откуда
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
Используя онлайн калькулятор для arcsin и arccos находим углы A и B:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Решение:
Найдем сторону c используя теорему косинусов:
Далее, из формулы
найдем cosA:
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:
Вычисления выше легко производить инженерным онлайн калькулятором.
Из формулы (3) найдем cosA:
Используя онлайн калькулятор для arcsin и arccos или инженерный онлайн калькулятор находим угол A:
Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Решение:
Так как, уже известны два угла, то можно найти третий:
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Откуда
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
Ответ:
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
(1) |
 |
(2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:


Далее, из формулы

 . . |
(3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
Углы треугольника
Геометрическая фигура из трех отрезков, соединенных между собой тремя точками, не лежащими на одной прямой, называется треугольником. Это — многоугольник с тремя углами. Сумма всех углов треугольника равна 180°. Если известна величина двух из них, третий угол определяем вычитанием из 180° величины двух известных углов.
α = 180°-β-γ
Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.
a 2 = b 2 + c 2 + 2abc cos (α)
Отсюда, косинус искомого угла равняется сумме квадратов смежных сторон (b, с) минус квадрат третей стороны треугольника (а), противолежащей искомому углу, и все это делится на удвоенное произведение смежных сторон:
cos (α) = (b 2 + c 2 — a 2 ) / 2bc
,
где а, b, с — стороны треугольника.
Используя теорему косинусов, определяем косинусы остальных углов. Величины углов в градусах находим по тригонометрической таблице.
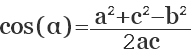
Углы прямоугольного треугольника
Калькулятор расчёта углов прямоугольного треугольника
Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).
Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.
Формула тангенса
- tg α — тангенс угла α
- a — противолежащий катет
- b — прилежащий катет
Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x . Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.
Углы треугольника
Сумма углов треугольника всегда равна 180 градусов:
Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.
Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:
Острый угол — угол, значение которого меньше 90°.
У прямоугольного треугольника один угол прямой, а два других угла — острые.
http://kalk.top/sz/corners-pr-triangle
Загрузить PDF
Загрузить PDF
В геометрии угол — это фигура, которая образована двумя лучами, которые выходят из одной точки (она называется вершиной угла). В большинстве случаев единицей измерения угла является градус (°) — помните, что полный угол или один оборот равен 360°. Найти значение угла многоугольника можно по его типу и значениям других углов, а если дан прямоугольный треугольник, угол можно вычислить по двум сторонам. Более того, угол можно измерить с помощью транспортира или вычислить с помощью графического калькулятора.
-
1
Сосчитайте число сторон многоугольника. Чтобы вычислить внутренние углы многоугольника, сначала нужно определить, сколько у многоугольника сторон. Обратите внимание, что число сторон многоугольника равно числу его углов.[1]
- Например, у треугольника 3 стороны и 3 внутренних углов, а у квадрата 4 стороны и 4 внутренних углов.
-
2
Вычислите сумму всех внутренних углов многоугольника. Для этого воспользуйтесь следующей формулой: (n — 2) x 180. В этой формуле n — это количество сторон многоугольника. Далее приведены суммы углов часто встречающихся многоугольников:[2]
- Сумма углов треугольника (многоугольника с 3-мя сторонами) равна 180°.
- Сумма углов четырехугольника (многоугольника с 4-мя сторонами) равна 360°.
- Сумма углов пятиугольника (многоугольника с 5-ю сторонами) равна 540°.
- Сумма углов шестиугольника (многоугольника с 6-ю сторонами) равна 720°.
- Сумма углов восьмиугольника (многоугольника с 8-ю сторонами) равна 1080°.
-
3
Разделите сумму всех углов правильного многоугольника на число углов. Правильный многоугольник это многоугольник с равными сторонами и равными углами. Например, каждый угол равностороннего треугольника вычисляется так: 180 ÷ 3 = 60°, а каждый угол квадрата находится так: 360 ÷ 4 = 90°.[3]
- Равносторонний треугольник и квадрат — это правильные многоугольники. А у здания Пентагона (Вашингтон, США) и дорожного знака «Стоп» форма правильного восьмиугольника.
-
4
Вычтите сумму всех известных углов из общей суммы углов неправильного многоугольника. Если стороны многоугольника не равны друг другу, и его углы также не равны друг другу, сначала сложите известные углы многоугольника. Теперь полученное значение вычтите из суммы всех углов многоугольника — так вы найдете неизвестный угол.[4]
- Например, если дано, что 4 угла пятиугольника равны 80°, 100°, 120° и 140°, сложите эти числа: 80 + 100 + 120 + 140 = 440. Теперь вычтите это значение из суммы всех углов пятиугольника; эта сумма равна 540°: 540 — 440 = 100°. Таким образом, неизвестный угол равен 100°.
Совет: неизвестный угол некоторых многоугольников можно вычислить, если знать свойства фигуры. К примеру, в равнобедренном треугольнике две стороны равны и два угла равны; в параллелограмме (это четырехугольник) противоположные стороны равны и противоположные углы равны.
Реклама
-
1
Помните, что в любом прямоугольном треугольнике один угол всегда равен 90°. Это так, даже если прямой угол никак не отмечен или его значение не указано. Таким образом, один угол прямоугольного треугольника всегда известен, а другие углы можно вычислить с помощью тригонометрии.[5]
-
2
Измерьте длину двух сторон треугольника. Самая длинная сторона прямоугольного треугольника называется гипотенузой. Прилежащая сторона это сторона, которая находится возле неизвестного угла. Противолежащая сторона — это сторона, которая находится напротив неизвестного угла. Измерьте две стороны, чтобы вычислить неизвестные углы треугольника.[6]
Совет: воспользуйтесь графическим калькулятором, чтобы решить уравнения, или найдите онлайн-таблицу со значениями синусов, косинусов и тангенсов.
-
3
Вычислите синус угла, если вам известны противолежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: sin(x) = противолежащая сторона ÷ гипотенуза. Например, противолежащая сторона равна 5 см, а гипотенуза равна 10 см. Разделите 5/10 = 0,5. Таким образом, sin(x) = 0,5, то есть x = sin-1 (0,5).[7]
- Если у вас есть графический калькулятор, введите 0,5 и нажмите клавишу sin-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 30°.
-
4
Вычислите косинус угла, если вам известны прилежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: cos(x) = прилежащая сторона ÷ гипотенуза. Например, прилежащая сторона равна 1,67 см, а гипотенуза равна 2 см. Разделите 1,67/2 = 0,83. Таким образом, cos(x) = 0,83, то есть x = cos-1 (0,83).[8]
- Если у вас есть графический калькулятор, введите 0,83 и нажмите клавишу cos-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 33,6°.
-
5
Вычислите тангенс угла, если вам известны противолежащая и прилежащая стороны. Для этого подставьте значения в уравнение: tg(x) = противолежащая сторона ÷ прилежащая сторона. Например, противолежащая сторона равна 75 см, а прилежащая сторона равна 75 см. Разделите 75/100 = 0,75. Таким образом, tg(x) = 0,75, то есть x = tg-1 (0,75).[9]
- Если у вас есть графический калькулятор, введите 0,75 и нажмите клавишу tg-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 36,9°.
Реклама
Советы
- Названия углов соответствуют их значениям. Угол в 90° — это прямой угол. Угол в 180° — это развернутый угол. Угол, который лежит между 0° и 90° — это острый угол. Угол, который лежит между 90° и 180° — это тупой угол. Угол, который лежит между 180° и 360° — это невыпуклый угол.
- Если сумма двух углов равна 90°, они называются дополнительными. Запомните: два острых угла прямоугольного треугольника всегда являются дополнительными. Если же сумма двух углов равна 180°, они называются смежными.
Реклама
Об этой статье
Эту страницу просматривали 237 750 раз.
Была ли эта статья полезной?
Содержание:
В этой лекции вы узнаете, что представляют собой синус, косинус и тангенс угла
Решение треугольников
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам).
Синус, косинус и тангенс угла от 0 до 180
Понятия синуса, косинуса и тангенса острого угла вам известны из курса геометрии 8 класса. Расширим эти понятия для произвольного угла 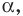
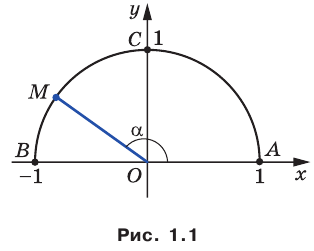
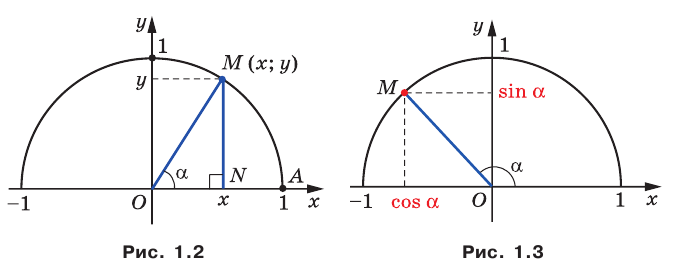
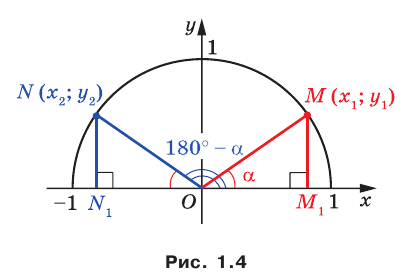
В верхней полуплоскости координатной плоскости рассмотрим полуокружность с центром в начале координат, радиус которой равен 1 (рис. 1.1). Такую полуокружность называют единичной.
Будем говорить, что углу 
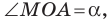
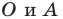
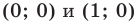

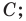
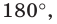
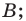
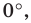
Пусть 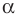
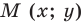
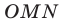
Поскольку 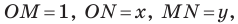
Итак, косинус и синус острого угла 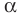
Полученный результат подсказывает, как определить синус и косинус произвольного угла 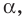
Определение. Косинусом и синусом угла 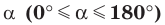
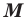
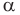
Пользуясь этим определением, можно, например, установить, что
Если 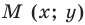
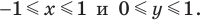
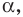
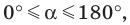
Если 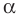
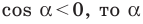
Из курса геометрии 8 класса вы знаете, что для любого острого угла а выполняются равенства:
Эти формулы остаются справедливыми также для 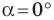
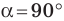
Пусть углам 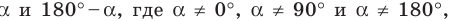
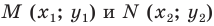
Прямоугольные треугольники 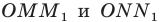
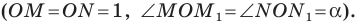
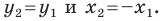
Убедитесь самостоятельно, что эти равенства остаются верными для
Если 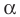
Это равенство остается верным для 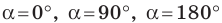
Пусть 
Следовательно, равенство 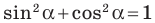
Определение. Тангенсом угла 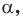
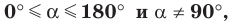
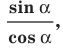
Поскольку 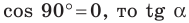
Очевидно, что каждому углу 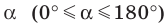
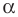
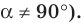
Функции 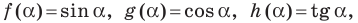
Пример №1
Докажите, что
Решение:
Пример №2
Найдите
Решение:
Имеем:
Теорема косинусов
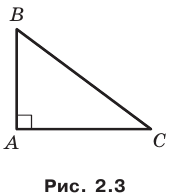
Из первого признака равенства треугольников следует, что две стороны и угол между ними однозначно определяют треугольник. А значит, по указанным элементам можно, например, найти третью сторону треугольника. Как это сделать, показывает следующая теорема.
Теорема 2.1 (теорема косинусов). Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними.
Доказательство: Рассмотрим треугольник 
Возможны три случая:
- угол
острый;
- угол
тупой;
- угол
прямой.
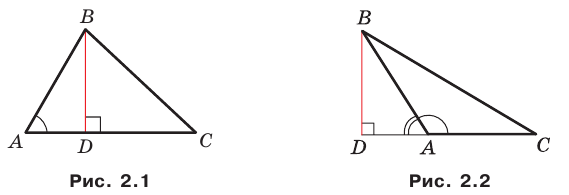
Первый случай. Пусть угол 
Пусть 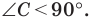
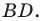
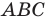
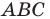
В прямоугольном треугольнике
Пусть 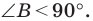
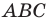

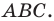
Второй случай. Пусть угол 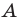
В прямоугольном треугольнике
В прямоугольном треугольнике BDC:
Третий случай. Пусть угол 
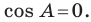
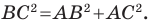
Доказательство теоремы косинусов показывает, что теорема Пифагора является частным случаем теоремы косинусов, а теорема косинусов является обобщением теоремы Пифагора.
Если воспользоваться обозначениями для длин сторон и величин углов треугольника 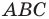
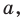
С помощью теоремы косинусов, зная три стороны треугольника, можно определить, является ли он остроугольным, тупоугольным или прямоугольным.
Теорема 2.2 (следствие из теоремы косинусов). Пусть 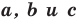
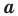
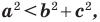
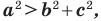
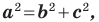
Доказательство: По теореме косинусов
Отсюда
Пусть 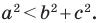
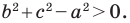

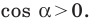
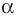
Поскольку 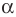
Пусть 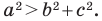
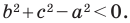

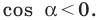
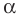
Пусть 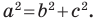

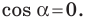
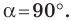
Пример №3
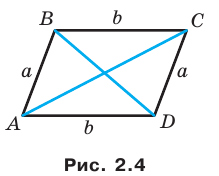
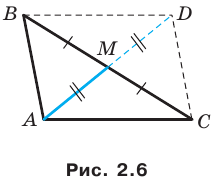
Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Решение:
На рисунке 2.4 изображен параллелограмм 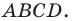
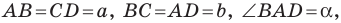
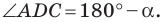
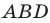
Из треугольника 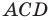
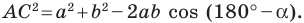
Сложив равенства (1) и (2), получим:
Пример №4
В треугольнике 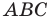
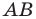
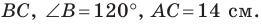
Решение:
По теореме косинусов
Пусть 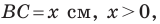
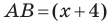
Имеем:
Корень -10 не удовлетворяет условию
Следовательно,
Ответ:
Пример №5
На стороне 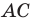
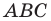
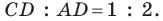
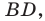
Решение:
По теореме косинусов из треугольника 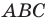
Отсюда
Поскольку 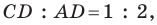
Тогда из треугольника 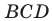
Следовательно,
Ответ:
Пример №6
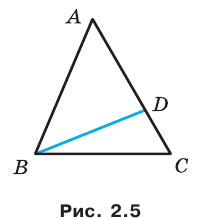
Две стороны треугольника равны 23 см и 30 см, а медиана, проведенная к большей из известных сторон, — 10 см. Найдите третью сторону треугольника.
Решение:
Пусть в треугольнике 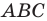
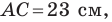
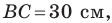
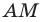
На продолжении отрезка 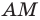
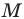
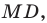
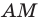
В четырехугольнике 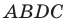
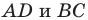
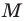
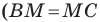
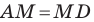
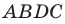
Так как сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон (см. ключевую задачу 1), то
Тогда
Ответ: 11 см.
Теорема синусов
При доказательстве ряда теорем и решении многих задач применяют следующую лемму.
Лемма. Хорда окружности равна произведению диаметра и синуса любого вписанного угла, опирающегося на эту хорду.
Доказательство: На рисунке 3.1 отрезок 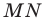
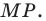
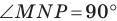
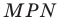
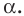
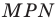
Все вписанные углы, опирающиеся на хорду 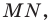
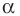
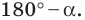
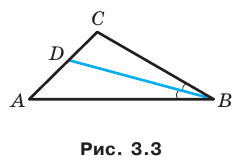
Из второго признака равенства треугольников следует, что сторона
и два прилежащих к ней угла однозначно определяют треугольник. Следовательно, по указанным элементам можно найти две другие стороны треугольника. Как это сделать, подсказывает следующая теорема.
Теорема 3.1 (теорема синусов). Стороны треугольника пропорциональны синусам противолежащих углов.
Доказательство: Пусть в треугольнике 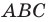
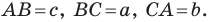
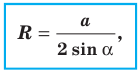
Пусть радиус описанной окружности треугольника 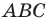
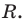
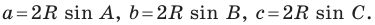
Следствие. Радиус окружности, описанной около треугольника, можно вычислить по формуле
где 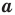
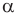
Пример №7
В треугольнике 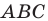
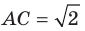
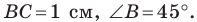
Решение:
По теореме синусов
Тогда
Поскольку 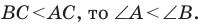
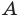
Отсюда, учитывая, что 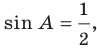
Ответ:
Пример №8
В треугольнике 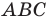
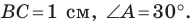
Решение:
По теореме синусов 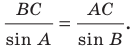
Поскольку 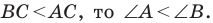
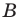
Ответ:
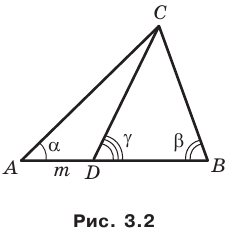
Пример №9
На стороне 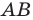
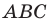
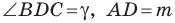
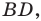
Решение:
Угол 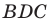
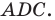
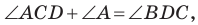
Из треугольника 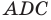
Следовательно,
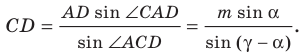
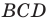
Следовательно,
Ответ:
Пример №10
Отрезок 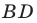
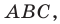
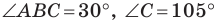
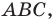
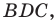
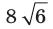
Решение:
Пусть 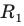
Поскольку отрезок 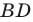
Из треугольника 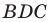
По следствию из теоремы синусов 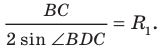
Из треугольника 
Пусть 
Тогда 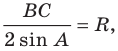
Ответ:
Как решать треугольников
Решить треугольник — это значит найти неизвестные его стороны и углы по известным сторонам и углам
Теоремы косинусов и синусов позволяют решить любой треугольник.
В следующих задачах значения тригонометрических функций будем находить с помощью калькулятора и округлять эти значения до сотых. Величины углов будем находить с помощью калькулятора и округлять эти значения до единиц. Вычисляя длины сторон, результат будем округлять до десятых.
Пример №11
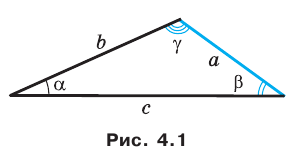
Решите треугольник (рис. 4.1) по стороне 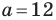
Решение:
Используя теорему о сумме углов треугольника, получаем:
По теореме синусов
Отсюда
Имеем:
Вновь применяя теорему синусов, запишем:
Отсюда
Имеем:
Ответ:
Пример №12
Решите треугольник по двум сторонам 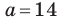
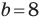
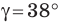
Решение:
По теореме косинусов
Отсюда
Далее имеем:
Отсюда
Используя теорему о сумме углов треугольника, получаем:
Ответ:
Пример №13
Решите треугольник по трем сторонам 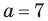
Решение:
По теореме косинусов 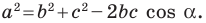
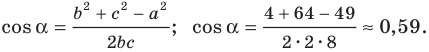
Пo теореме синусов 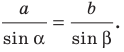
Поскольку 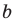
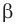
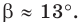
Ответ:
Пример №14
Решите треугольник по двум сторонам и углу, противолежащему одной из сторон:
Решение:
1) По теореме синусов
Отсюда
Поскольку угол 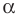
Используя теорему о сумме углов треугольника, получаем:
По теореме синусов
Отсюда
Ответ:
2) По теореме синусов
Отсюда 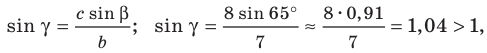
Ответ: задача не имеет решения.
3) По теореме синусов 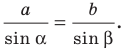
Возможны два случая: 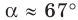
Рассмотрим случай, когда
Используя теорему о сумме углов треугольника, получаем:
Пo теореме синусов
Отсюда 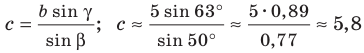
Рассмотрим случай, когда
Используя теорему о сумме углов треугольника, получаем:
Поскольку 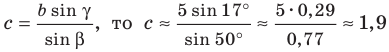
Ответ:
Тригонометрия наука об измерении треугольников
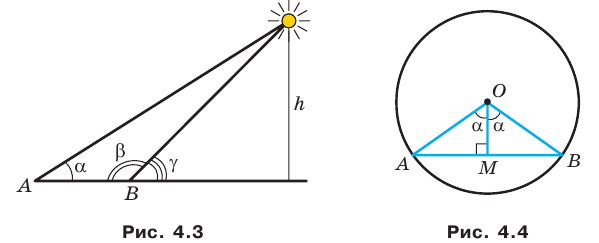
Вы знаете, что древние путешественники ориентировались по звездам и планетам. Они могли достаточно точно определить положение корабля в океане или каравана в пустыне по расположению светил на небосклоне. При этом одним из ориентиров служила высота, на которую поднималось над горизонтом то или иное небесное светило в данной местности в данный момент времени.
Понятно, что непосредственно измерить эту высоту невозможно. Поэтому ученые стали разрабатывать методы косвенных измерений. Здесь существенную роль играло решение треугольника, две вершины которого лежали на поверхности Земли, а третья являлась звездой (рис. 4.3) — знакомая вам задача 3.17.
Для решения подобных задач древним астрономам необходимо было научиться находить взаимосвязи между элементами треугольника. Так возникла тригонометрия — наука, изучающая зависимость между сторонами и углами треугольника. Термин «тригонометрия» (от греческих слов «тригонон» — треугольник и «метрео» — измерять) означает «измерение треугольников».
На рисунке 4.4 изображен центральный угол 
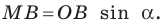
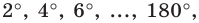
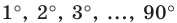
Измеряя длины полухорд, древнегреческий астроном Гиппарх (II в. до н. э.) составил первые тригонометрические таблицы.
Понятия синуса и косинуса появляются в тригонометрических трактатах индийских ученых в IV-V вв. н. э. В X в. арабские ученые оперировали понятием тангенса, которое возникло из потребностей гномоники — учения о солнечных часах (рис. 4.5).
В Европе первой работой, в которой тригонометрия рассматривалась как отдельная наука, был трактат «Пять книг о треугольниках всех видов», впервые напечатанный в 1533 г. Его автором был немецкий ученый Региомонтан (1436-1476). Этот же ученый открыл и теорему тангенсов:
где 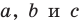
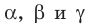
Современный вид тригонометрия приобрела в работах великого математика Леонарда Эйлера.
Леонард Эйлер
(1707-1783) Выдающийся математик, физик, механик и астроном, автор более 860 научных работ. Член Петербургской, Берлинской, Парижской академий наук, Лондонского королевского общества, многих других академий и научных обществ. Имя Эйлера встречается почти во всех областях математики: теоремы Эйлера, тождества Эйлера, углы, функции, интегралы, формулы, уравнения, подстановки и т. д.
Формулы для нахождения площади треугольника
Из курса геометрии 8 класса вы знаете, что площадь 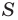
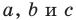
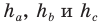
Теперь у нас появилась возможность получить еще несколько формул для нахождения площади треугольника.
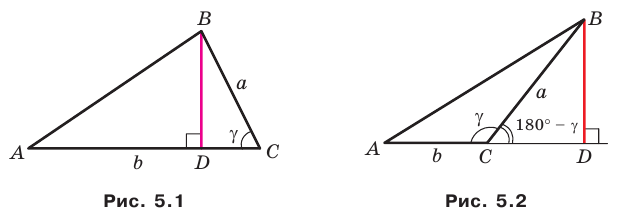
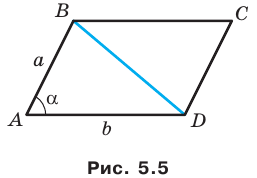
Теорема 5.1. Площадь треугольника равна половине произведения двух его сторон и синуса угла между ними.
Доказательство: Рассмотрим треугольник 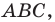
Возможны три случая:
- угол
острый (рис. 5.1);
- угол
тупой (рис. 5.2);
- угол
прямой.
На рисунках 5.1 и 5.2 проведем высоту 
Тогда
Из прямоугольного треугольника 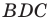
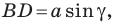
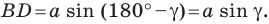
Если угол 
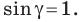
Теорема 5.2 (формула Герона
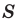
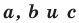
где 
Доказательство: Рассмотрим треугольник 
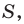
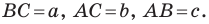
Пусть 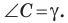
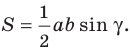
По теореме косинусов 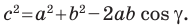
Поскольку 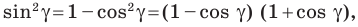
Отсюда
Теорема 5.3. Площадь 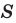
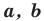
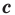
где 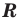
Доказательство: Рассмотрим треугольник 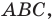
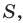
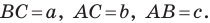
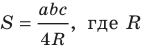
Пусть 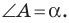
Из леммы п. 3 следует, что
Тогда
Заметим, что доказанная теорема позволяет находить радиус описанной окружности треугольника по формуле
Теорема 5.4. Площадь треугольника равна произведению его полупериметра и радиуса вписанной окружности.
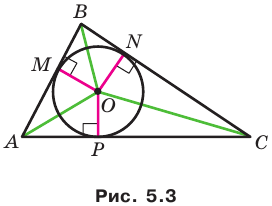
Доказательство: На рисунке 5.3 изображен треугольник 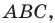
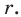
где 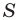
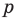
Пусть точка 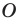
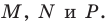
Проведем радиусы в точки касания. Получаем: 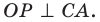
Следовательно,
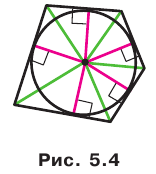
Теорему 5.4 обобщает следующая теорема.
Теорема 5.5. Площадь описанного многоугольника равна произведению его полупериметра и радиуса вписанной окружности.
Докажите эту теорему самостоятельно (рис. 5.4).
Заметим, что теорема 5.5 позволяет находить радиус вписанной окружности многоугольника по формуле
Пример №15
Докажите, что площадь 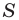
где 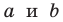
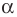
Решение:
Рассмотрим параллелограмм 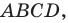
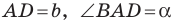
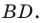
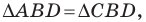
Пример №16
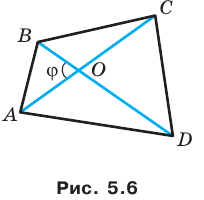
Докажите, что площадь выпуклого четырехугольника равна половине произведения его диагоналей и синуса угла между ними.
Решение:
Пусть угол между диагоналями 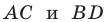
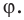
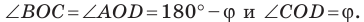
Пример №17
Стороны треугольника равны 17 см, 65 см и 80 см. Найдите наименьшую высоту треугольника, радиусы его вписанной и описанной окружностей.
Решение:
Пусть
Найдем полупериметр треугольника:
Площадь треугольника вычислим по формуле Герона:
Наименьшей высотой треугольника является высота, проведенная к его наибольшей стороне, длина которой равна
Поскольку
Радиус вписанной окружности
Радиус описанной окружности
Ответ:
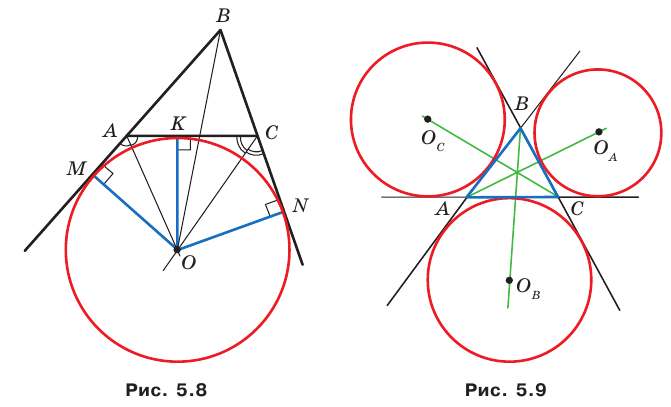
Вневписанная окружность треугольника
Проведем биссектрисы двух внешних углов с вершинами 
Проведем три перпендикуляра: 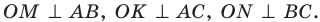
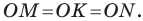
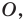
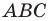
Поскольку 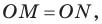
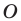
Любой треугольник имеет три вневписанные окружности. На рисунке 5.9 их центры обозначены 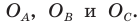
По свойству касательных, проведенных к окружности через одну точку, имеем: 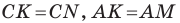
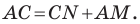
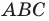
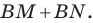
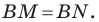
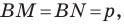
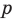
Имеем:
Отсюда 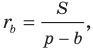
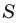
Аналогично можно показать, что
Справочный материал
Косинус и синус
Косинусом и синусом угла 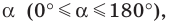
Тангенс
Тангенсом угла 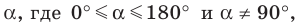
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними:
Следствие из теоремы косинусов
Пусть 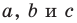
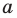
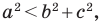
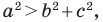
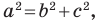
Лемма о хорде окружности
Хорда окружности равна произведению диаметра и синуса любого вписанного угла, опирающегося на эту хорду.
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов:
Формулы для нахождения площади треугольника
Формула Герона:
Формула для нахождения радиуса окружности, вписанной в треугольник
Формулы для нахождения радиуса окружности, описанной около треугольника
Площадь многоугольника, описанного около окружности
Площадь многоугольника, описанного около окружности, равна произведению его полупериметра и радиуса вписанной окружности.
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг
- Основные фигуры геометрии и их расположение в пространстве
- Пространственные фигуры — виды, изображения, свойства
- Взаимное расположения прямых на плоскости
- Треугольник
Как найти углы прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти углы прямоугольного треугольника
Чтобы найти углы прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для угла α:
- угол β
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
- для угла β:
- угол α
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
Введите их в соответствующие поля и получите результат.
Найти угол α зная угол β и наоборот
Если ∠β = , то ∠α =
0
Если ∠α = , то ∠β =
0
Формула
α = 90° — β
β = 90° — α
Найти углы прямоугольного треугольника зная катеты
Катет a =
Катет b =
∠α =
0
∠β =
0
Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?
Формулы
или так:
α = arctg(a/b)
β = arctg(b/a)
Пример
Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:
∠α = arctg(5/2) = arctg(2.5) ≈ 68.2°
∠β = arctg(2/5) = arctg(0.4) ≈ 21.8°
Найти углы прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет =
∠α =
0
∠β =
0
Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?
Формулы
sin(α) = a/c
sin(β) = b/c
cos(α) = b/c
cos(β) = a/c
или так:
α = arcsin(a/c) = arccos(b/c)
β = arcsin(b/c) = arccos(a/c)
Пример
Для примера определим чему равны углы α и β в градусах если гипотенуза c = 6 см, а катет b = 3 см:
∠α = arccos(3/6) = arccos(0.5) = 60°
∠β = arcsin(3/6) = arcsin(0.5) = 30°







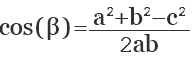
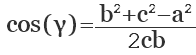









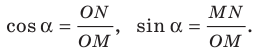
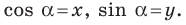
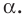

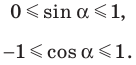




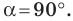
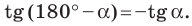
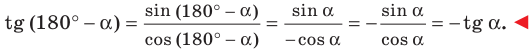
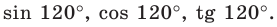
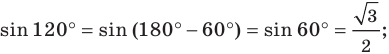
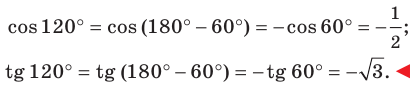
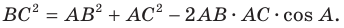
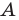 острый;
острый;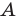 тупой;
тупой;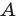 прямой.
прямой.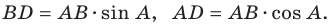
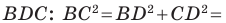
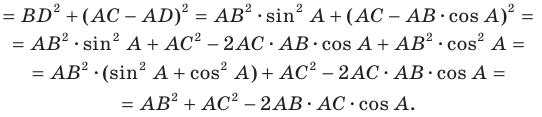
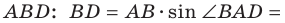
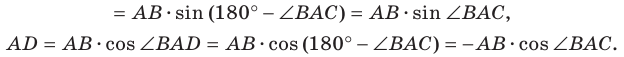
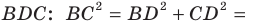
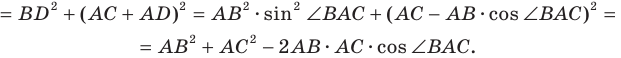
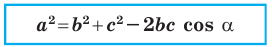
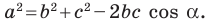
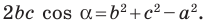
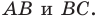
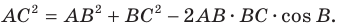
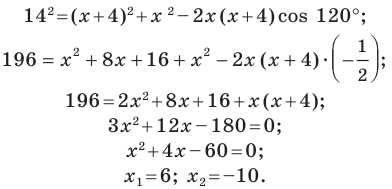
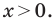
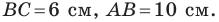
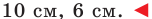
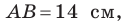
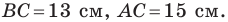
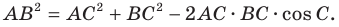
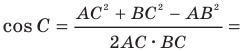
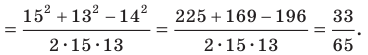
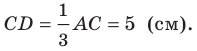
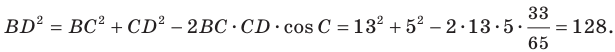
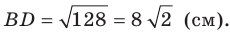
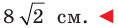
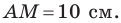
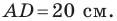
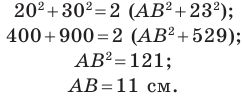

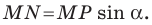
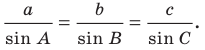
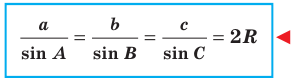
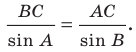
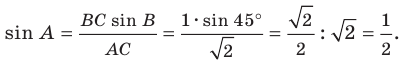
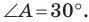
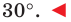
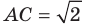
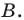
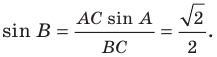
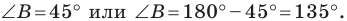
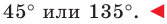
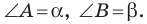
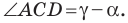
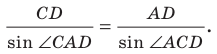
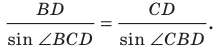
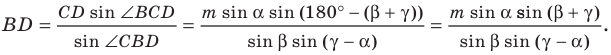
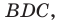
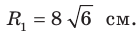
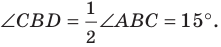
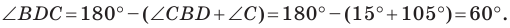
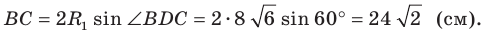
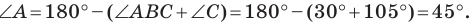
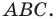
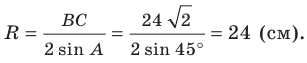
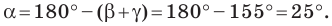
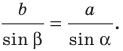
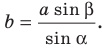
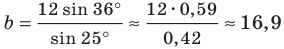
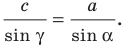
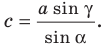
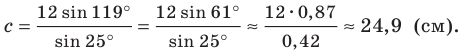
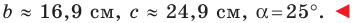
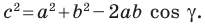
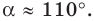
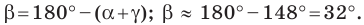
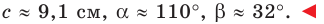
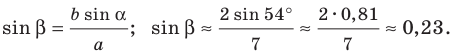
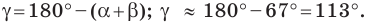
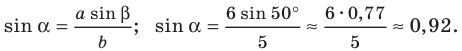
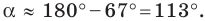
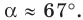
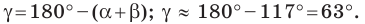
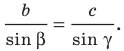
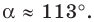
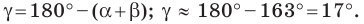
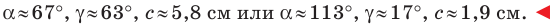

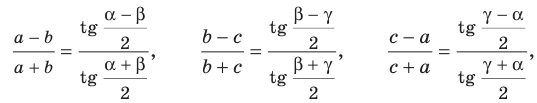
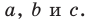

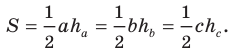
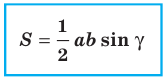
 острый (рис. 5.1);
острый (рис. 5.1); тупой (рис. 5.2);
тупой (рис. 5.2); прямой.
прямой.