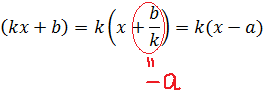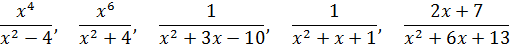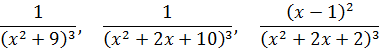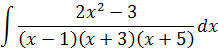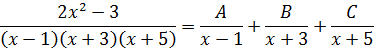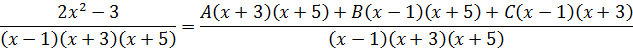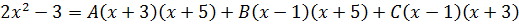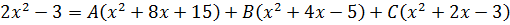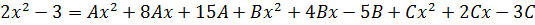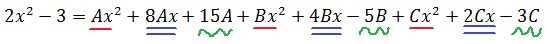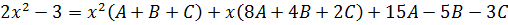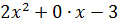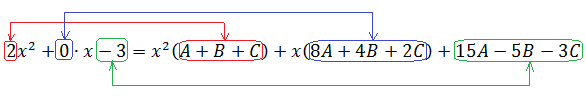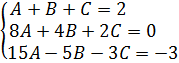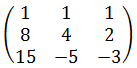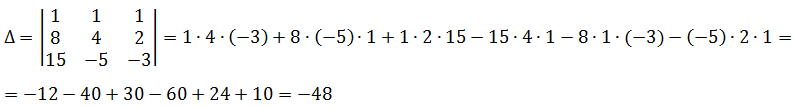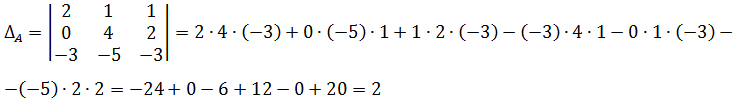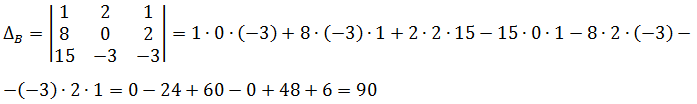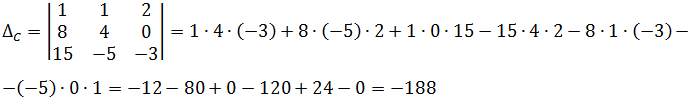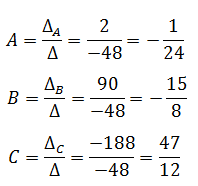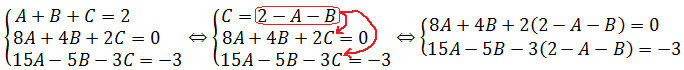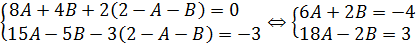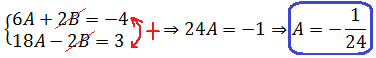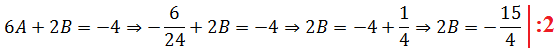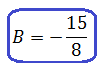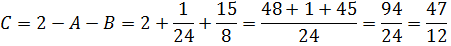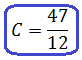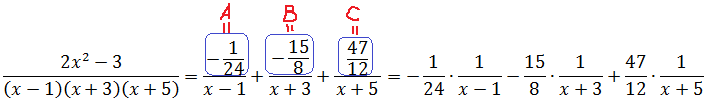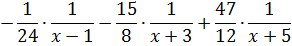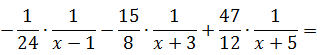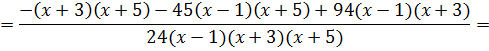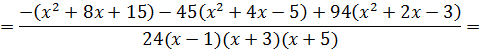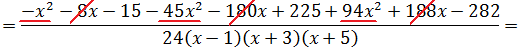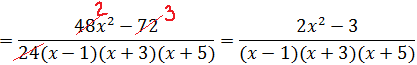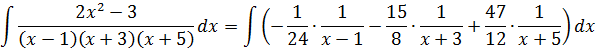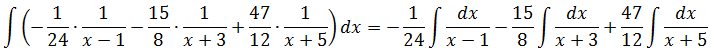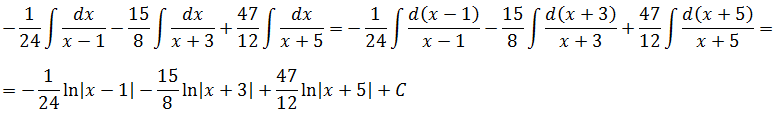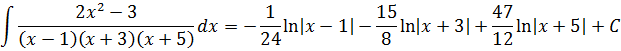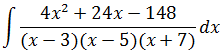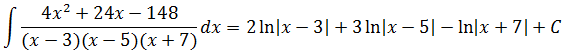Как найти неизвестный числитель в степени

Как решать
показательные уравнения?

Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Это поможет решить задания №5, 13 и 15 из профильного уровня математики.

Одна из их разновидностей – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие переменной (х) не в основании степени, а в самом показателе. Как это выглядит:

Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:

Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение (х). Познакомиться с понятием степени и ее свойствами можно тут и тут.

И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:

И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением. Кроме самой показательной функции в уравнении могут быть любые другие математические конструкции – тригонометрические функции, логарифмы, корни, дроби и т.д. Если вы видите степень, значит перед вам показательное уравнение.

Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.

Простейшие показательные уравнения

Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:

Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (х) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:

Значит, если (х=3), то мы получим верное равенство, а значит мы решили уравнение.

Решим что-нибудь посложнее.

Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:

Мы применили свойство отрицательной степени по формуле:

Теперь наше уравнение будет выглядеть так:

Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные – слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:

Такое мы решать умеем, ведь это обыкновенное линейное уравнение.

Поздравляю, мы нашли корень нашего показательного уравнения.

Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:

Воспользуемся одним из свойств степеней ((a^n)^m=a^):

И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:

И еще один пример:

Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.

Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.

Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.

Общий метод решения показательных уравнений

Пусть у нас есть вот такой пример:

Где (a,b) какие-то положительные числа. ((a>0, ; b>0).

Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.

Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:

Раз основания одинаковые, то мы можем просто приравнять степени:

Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:

Замечаем, что (16=2*2*2*2=2^4) это степень двойки:

Основания одинаковые, значит можно приравнять степени:

$$x=4.$$
Пример 6 $$5^<-x>=125 Rightarrow 5^<-x>=5*5*5 Rightarrow 5^<-x>=5^3 Rightarrow –x=3 Rightarrow x=-3.$$
Пример 7 $$9^<4x>=81 Rightarrow (3*3)^<4x>=3*3*3*3 Rightarrow(3^2)^<4x>=3^4 Rightarrow 3^<8x>=3^4 Rightarrow 8x=4 Rightarrow x=frac<1><2>.$$

Здесь мы заметили, что (9=3^2) и (81=3^4) являются степенями (3).

Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:

(3) и (2) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число (b>0), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице (a>0, ; a neq 1):

Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим (2) в виде (3) в какой-то степени, где (a=3), а (b=2):

Подставим данное преобразование в наш пример:

Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:

Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.

Кто забыл, что такое логарифм, можно посмотреть здесь.

Рассмотрим еще несколько аналогичных примеров.

Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:

Все эти варианты ответа верные, их можно смело писать в ответ.

И так, мы с вами научились решать любые показательные уравнения вот такого вида: (a^x=b), где (a>0; ; b>0).

Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа (a^x=b), где (a>0; ; b>0). Рассмотрим типы сложных уравнений, которые могут попасться:

Решение показательных уравнений при помощи замены

Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.

Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^<2x>=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^). Подставим:

Обратим внимание, что во всем уравнении все (х) «входят» в одинаковую функцию — (3^x). Сделаем замену (t=3^x, ; t>0), так как показательная функция всегда положительна.

Квадратное уравнение, которое решается через дискриминант:

Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:

И второй корень:

И еще один пример на замену:

Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Но если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):

Подставим в исходное уравнение:

Теперь показательные функции одинаковы и можно сделать замену:

Обратная замена, и наше уравнение сводится к простейшему:

И второе значение (t):

Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на (3^x):

Здесь нам придется воспользоваться свойствами степеней:

Разберем каждое слагаемое:

Теперь подставим получившееся преобразования в исходное уравнение:

Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену (t=(frac<7><3>)^x):

Сделаем обратную замену:

И последний пример на замену:

Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:

Разберем каждое слагаемое нашего уравнения:

Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!

И последнее слагаемое со степенью:

Подставим все наши преобразования в исходное уравнение:

Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):

Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера. Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.

И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут

Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2), (5) и (10). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:

Воспользуемся формулой ((a*b)^n=a^n*b^n):

И перекинем все показательные функции с основанием (2) влево, а с основанием (5) вправо:

Сокращаем и воспользуемся формулами (a^n*a^m=a^) и (frac=a^):

Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.

Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
2. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

• Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
• Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = −b : а; если а равно нулю, а b не равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

• если значение переменной обращает знаменатель в 0, значит это неверное значение;
• делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

1. Область допустимых значений: х ≠ −2.
2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.

Рациональные уравнения с примерами решения

Содержание:

Рациональные уравнения. Равносильные уравнения

два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.

Так, например, равносильными будут уравнения

Уравнения — не равносильны, так как корнем первого уравнения является число 10, а корнем второго — число 9.

Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.

1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;

2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;

3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.

Левая и правая части каждого из них являются рациональными выражениями.

Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.

В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.

Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.

Применение условия равенства дроби нулю

Напомним, что когда

Пример №202

Решите уравнение

Решение:

С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду где и — целые рациональные выражения. Имеем:

Окончательно получим уравнение:

Чтобы дробь равнялась нулю, нужно, чтобы числитель равнялся нулю, а знаменатель не равнялся нулю.

Тогда откуда При знаменатель Следовательно, — единственный корень уравнения.

Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:

Значит, решая дробное рациональное уравнение, можно:

1) с помощью тождественных преобразований привести уравнение к виду

2) приравнять числитель к нулю и решить полученное целое уравнение;

3) исключить из его корней те, при которых знаменатель равен нулю, и записать ответ.

Использование основного свойства пропорции

Если то где

Пример №203

Решите уравнение

Решение:

Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то Имеем: то есть ОДЗ переменной содержит все числа, кроме 1 и 2.

Сложив выражения в правой части уравнения, приведем его к виду: получив пропорцию:

По основному свойству пропорции имеем:

Решим это уравнение:

откуда

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.

Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:

Таким образом, для решения дробного рационального уравнения можно:

1) найти область допустимых значений (ОДЗ) переменной в уравнении;

2) привести уравнение к виду

3) записать целое уравнение и решить его;

4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.

Метод умножения обеих частей уравнения на общий знаменатель дробей

Пример №204

Решите уравнение

Решение:

Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:

Областью допустимых значений переменной будут те значения при которых то есть все значения кроме чисел А простейшим общим знаменателем будет выражение

Умножим обе части уравнения на это выражение:

Получим: а после упрощения: то есть откуда или

Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.

Следовательно, число 12 — единственный корень уравнения. Ответ. 12.

Решая дробное рациональное уравнение, можно:

3) умножить обе части уравнения на этот общий знаменатель;

4) решить полученное целое уравнение;

5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.

Пример №205

Являются ли равносильными уравнения

Решение:

Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.

Первое уравнение имеет единственный корень а второе — два корня (решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.

Степень с целым показателем

Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:

где — натуральное число,

В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: кг. Как понимать смысл записи

Рассмотрим степени числа 3 с показателями — это соответственно

В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:

Число должно быть втрое меньше числа равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, Равенство справедливо для любого основания при условии, что

Нулевая степень отличного от нуля числа а равна единице, то есть при

Вернемся к строке со степенями числа 3, где слева от числа записано число Это число втрое меньше, чем 1, то есть равно Следовательно, Рассуждая аналогично получаем: и т. д.

Приходим к следующему определению степени с целым отрицательным показателем:

если натуральное число, то

        Приветствую всех, дорогие друзья!

        Ну что, поздравляю! Мы с вами благополучно добрались до основного материала в интегрировании рациональных дробей — метода неопределённых коэффициентов. Великого и могучего.) В чём же заключается его величество и могущество? А заключается оно в его универсальности. Имеет смысл ознакомиться, правда? Предупреждаю, что уроков по данной теме будет несколько. Ибо тема очень длинная, а материал крайне важный. )

        Сразу скажу, что в сегодняшнем уроке (и последующих тоже) мы будем заниматься не столько интегрированием, сколько… решением систем линейных уравнений! Да-да! Так что те у кого проблемы с системами, повторите матрицы, определители и метод Крамера. А тех товарищей, у кого и с матрицами туго, призываю, на худой конец, освежить в памяти хотя бы «школьные» методы решения систем — метод подстановки и метод почленного сложения/вычитания.

        Для начала нашего знакомства отмотаем плёнку немного назад. Ненадолго вернёмся к прошлым урокам и проанализируем все те дроби, которые мы с вами интегрировали до этого. Напрямую, безо всякого метода неопределённых коэффициентов! Вот они, эти дроби. Я рассортировал их по трём группам.

        Группа 1

        В знаменателе — линейная функция либо сама по себе, либо же в степени. Одним словом, в знаменателе стоит произведение одинаковых скобок вида (х-а).

        Например:

        (x+4)¹ = (x+4)

        (x-10)² = (x-10)(x-10)

        (2x+5)³ = (2x+5)(2x+5)(2x+5)

        И так далее. Кстати, пусть вас не смущают скобки (4х+5) или (2х+5)³ с коэффициентом k внутри. Это всё равно, по своей сути, скобки вида (х-а). Ибо это самое k из таких скобок всегда можно вынести наружу.

        Вот так:

        

        Вот и всё.) И неважно, что именно при этом стоит в числителе — просто dx или же многочлен какой. Мы всегда раскладывали числитель по степеням скобки (x-a), превращали большую дробь в сумму маленьких, подводили (где надо) скобку под дифференциал и интегрировали.

        Группа 2

        

        Что общего у этих дробей?

        А общее то, что во всех знаменателях стоит квадратный трёхчлен ax²+bx+c. Но не просто, а именно в единственном экземпляре. И неважно здесь, положительный у него дискриминант или отрицательный.

        Такие дроби всегда интегрировались одним из двух способов — либо разложением числителя по степеням знаменателя, либо выделением полного квадрата в знаменателе с последующей заменой переменной. Всё зависит от конкретной подынтегральной функции.

        Группа 3

        

        Это были самые нехорошие для интегрирования дроби. В знаменателе — неразложимый квадратный трёхчлен, да ещё и в степени n. Но, опять же, в единственном экземпляре. Ибо, кроме трёхчлена, других множителей в знаменателе нету. Такие дроби интегрировались по рекуррентной формуле. Либо напрямую, либо сводились к ней после выделения полного квадрата в знаменателе и последующей замены переменной.

        Однако, к сожалению, всё богатое многообразие рациональных дробей не ограничивается только лишь этими тремя рассмотренными группами.

        А как быть, если в знаменателе стоят разные скобки? Например, что-нибудь типа:

        (х-1)(х+1)(х+2)

        Или одновременно скобка (х-а) и квадратный трёхчлен, что-то типа (х-10)(х²-2х+17)? И в других подобных случаях? Вот, именно в таких случаях и приходит на помощь метод неопределённых коэффициентов!

        Сразу скажу: работать мы пока что будем только с правильными дробями. Теми, у которых степень числителя строго меньше степени знаменателя. Как быть с неправильными дробями, подробно рассказано в первом уроке по дробям. Надо выделять целую часть (многочлен). Делением уголком числителя на знаменатель или разложением числителя — как хотите. И даже пример разобран. А многочлен вы уж как-нибудь худо-бедно проинтегрируете. Не маленькие уже поди.) Но на неправильные дроби тоже порешаем примеры!

        А теперь начинаем знакомиться. В отличие от большинства учебников по высшей математике, наше знакомство мы начнём не с сухой и грузной теории про основную теорему алгебры, теорему Безу, про разложение рациональной дроби на сумму простейших (об этих дробях позже) и прочего занудства, а начнём мы с несложного примера.

        Например, нам требуется найти вот такой неопределённый интеграл:

        

        Первый взгляд на подынтегральную дробь. В знаменателе стоит произведение трёх скобок:

        (x-1)(x+3)(x+5) 

        Причём все скобки разные. Поэтому наша старая технология с разложением числителя по степеням знаменателя в этот раз уже не прокатывает: какую именно скобку выделять в числителе? (х-1)? (х+3)? Непонятно… Выделение полного квадрата в знаменателе — тоже не в кассу: там многочлен третьей степени (если перемножить все скобки). Что делать?

        При взгляде на нашу дробь возникает вполне естественное желание… Прямо-таки непреодолимое! Из нашей большой дроби, которую неудобно интегрировать, как-то сделать три маленьких. Хотя бы вот так:

        

        Почему именно такой вид надо искать? А всё потому, что в таком виде наша исходная дробь уже удобна для интегрирования! Подводим знаменатель каждой маленькой дроби под дифференциал и — вперёд.)

        А можно ли вообще получить такое разложение? Новость хорошая! Соответствующая теорема математики гласит — да, можно! Такое разложение существует и единственно.

        Но есть одна проблемка: коэффициенты А, В и С мы пока не знаем. И сейчас нашей основной задачей как раз и будет их определить. Узнать, чему же равны наши буковки А, В и С. Отсюда и название — метод неопределённых коэффициентов. Начнём наше сказочное путешествие!

        Итак, у нас есть равенство, от которого мы начинаем плясать:

        

        Давайте приведём справа все три дроби к общему знаменателю и сложим:

        

        Теперь можно смело отбросить знаменатели (ибо они одинаковы) и просто приравнять числители. Всё как в обычном дробно-рациональном уравнении:

        

        Следующим шагом раскрываем все скобки (коэффициенты А, В и С пока лучше оставить снаружи):

        

        Далее вставляем все коэффициенты внутрь скобок и избавляемся от этих самых скобок:

        

        А теперь (важно!) выстраиваем всю нашу конструкцию справа по старшинству степеней: сначала собираем в кучку все члены с х², потом — просто с иксом и, наконец, собираем свободные члены. Фактически, просто приводим подобные и группируем слагаемые по степеням икс.

        Вот так:

        

        

        А теперь осмысливаем результат. Слева — наш исходный многочлен. Второй степени. Числитель нашей подынтегральной дроби. Справа — тоже некоторый многочлен второй степени. Но с неизвестными коэффициентами. Данное равенство должно быть справедливо при всех допустимых значениях икс. Дроби-то слева и справа были одинаковые (по нашему условию)! Это означает, что их числители (т.е. наши многочлены) — тоже одинаковые. Стало быть, коэффициенты при одинаковых степенях икс у этих многочленов обязательно должны быть равны!

        Начинаем с самой старшей степени. С квадрата. Смотрим, что за коэффициенты у нас стоят при х² слева и справа. Справа у нас стоит сумма коэффициентов А+В+С, а слева — двойка. Так у нас рождается первое уравнение.

        Записываем:

        А+В+С = 2

        Есть. Первое уравнение готово.)

        Далее идём по снижающейся траектории — смотрим на члены с иксом в первой степени. Справа при икс у нас стоит 8А+4В+2С. Хорошо. А что у нас при икс стоит слева? Гм… Слева вообще никакого слагаемого с иксом нету! Там только 2х² — 3. Как быть? Очень просто! Это значит, что коэффициент при икс слева у нас равен нулю! Мы же можем записать нашу левую часть вот так:

        

        А что? Имеем полное право.) Отсюда второе уравнение выглядит так:

        8A+4B+2C = 0

        Ну вот, практически, и всё. Осталось приравнять свободные члены:

        15А-5В-3С = -3

        Одним словом, приравнивание коэффициентов при одинаковых степенях икса происходит по такой схеме:

        

        Все три наших равенства должны выполняться одновременно. Поэтому собираем из наших выписанных уравнений систему:

        

        Системка не самая трудная для прилежного студента — три уравнения и три неизвестных. Как хотите, так и решайте. Можно методом Крамера через матрицы с определителями, можно методом Гаусса, можно даже обычной школьной подстановкой.

        Для начала я решу эту систему так, как обычно решают такие системы культурные студенты. А именно — методом Крамера.

        Решение начинаем с составления матрицы системы. Напоминаю, что эта матрица — просто табличка, составленная из коэффициентов при неизвестных. 

        Вот она:

        

        А вот дальше начинаем вычислять определители. Муторно немного, но ничего не поделать. Не школьники уже поди.)

        Первым делом вычисляем определитель матрицы системы. Или, коротко, определитель системы. Обычно он обозначается греческой буквой ∆ («дельта»):

        

        Отлично, определитель системы не равен нулю (-48≠0). Из теории систем линейных уравнений этот факт означает, что наша система совместна и имеет единственное решение.

        Следующим шагом вычисляем определители неизвестных ∆_A, ∆_B, ∆_C. Напоминаю, что каждый из этих трёх определителей получается из основного определителя системы путём замены столбцов с коэффициентами при соответствующих неизвестных на столбец свободных членов.

        Вот и составляем определители и считаем:

        

        

        

        Подробно объяснять технику вычисления определителей третьего порядка я здесь не буду. И не просите. Это уже совсем отклонение от темы будет.) Кто в теме, тот понимает, о чём речь. И, возможно, уже догадался, каким именно способом я вычислил эти три определителя.)

        А дальше уже находим неизвестные А, B и С по формулам Крамера:

        

        Вот всё и готово.)

        Так обычно решают системы культурные студенты. Но… Не все студенты дружат с матрицами и определителями. К сожалению. Для кого-то эти простые понятия высшей математики так навсегда и остаются китайской грамотой и таинственным монстром в тумане…

        Что ж, специально для таких некультурных студентов предлагаю более привычный способ решения — метод последовательного исключения неизвестных. Фактически, это продвинутый «школьный» метод подстановки. Только шагов побольше будет.) Но суть та же самая. Первым делом я исключу переменную С. Для этого я выражу С из первого уравнения и подставлю во второе и третье:

        

        Упрощаем, приводим подобные и получаем новую систему, уже с двумя неизвестными:

        

        Теперь, в этой новой системе, тоже можно выразить одну из переменных через другую. Но самые внимательные студенты, возможно, заметят, что коэффициенты перед переменной B — противоположны. Два и минус два. Стало быть, очень удобно будет сложить между собой оба уравнения, чтобы исключить переменную В и оставить только букву А.

        Складываем левые и правые части, мысленно сокращаем 2B и -2B и решаем уравнение только относительно А:

        

        Есть. Первый коэффициент найден: А = -1/24.

        Определяем второй коэффициент В. Например, из верхнего уравнения:

        

        Отсюда получаем:

        

        Отлично. Второй коэффициент тоже найден: B = -15/8. Осталась ещё буковка С. Для её определения используем самое верхнее уравнение, где она у нас выражена через А и В:

        

        Итак:

        

        Ну вот и всё. Неизвестные коэффициенты найдены! Неважно, через Крамера или через подстановку. Главное, правильно найдены.)

        Стало быть, наше разложение большой дроби в сумму маленьких будет выглядеть вот так:

        

        И пусть вас не смущают полученные дробные коэффициенты: в данной процедуре (методе неопределённых коэффициентов) это самое обычное явление.

        А теперь крайне желательно проверить, правильно ли мы нашли наши коэффициенты A, B и С. Поэтому сейчас берём черновик и вспоминаем восьмой класс — складываем обратно все три наши маленькие дроби.

        

        Если мы получим исходную большую дробь — значит, всё хорошо. Нет — значит, бейте меня ищите ошибку.

        Общий знаменатель, очевидно, будет 24(х-1)(х+3)(х+5).

        Поехали:

        

        

        

        

        

        Йес!!! Получили исходную дробь. Что и требовалось проверить. Всё гуд. Так что прошу не бить.)

        А теперь возвращаемся к нашему исходному интегралу. Легче он за это время не стал, да. Но теперь, когда наша дробь разложена в сумму маленьких, её интегрирование стало сплошным удовольствием!

        Смотрите сами! Вставляем наше разложение в исходный интеграл.

        Получаем:

        

        Пользуемся свойствами линейности и разбиваем наш большой интеграл в сумму маленьких, все константы выносим за знаки интеграла.

        Получаем:

        

        А полученные три маленьких интеграла уже легко берутся подведением знаменателя под знак дифференциала.

        Продолжаем интегрирование:

        

        Вот и всё.) И не надо в данном уроке спрашивать меня, откуда в ответе взялись логарифмы! Кто помнит таблицу интегралов, тот в теме и всё поймёт. А кто не помнит — гуляем по ссылочкам. Я их не просто так ставлю.

        Окончательный ответ:

        

        Вот такая красивая троица: три логарифма — трус, бывалый и балбес. И попробуй, догадайся до такого хитрого ответа с ходу! Только метод неопределённых коэффициентов и выручает, да.) Собственно, с этой целью и разбираемся. Что, как и откуда.

        В качестве тренировочного упражнения, предлагаю вам попрактиковаться в методе и проинтегрировать вот такую дробь:

        

        Потренируйтесь, найдите интеграл, не сочтите за труд! Должен получиться вот такой ответ:

        

        Метод неопределённых коэффициентов — штука мощная. Спасает даже в самой безнадёжной ситуации, когда и так дробь преобразовываешь, и эдак. И вот тут у некоторых внимательных и интересующихся читателей, возможно, возник целый ряд вопросов:

        — Что делать, если многочлен в знаменателе вообще не разложен на множители?

        — КАК надо искать разложение любой большой рациональной дроби на сумму маленьких? В каком виде? Почему именно в таком, а не сяком?

        — Что делать, если в разложении знаменателя есть кратные множители? Или скобки в степенях типа (х-1)²? В каком виде искать разложение?

        — Что делать, если, помимо простых скобок вида (х-а), знаменатель одновременно содержит и неразложимый квадратный трёхчлен? Скажем, х²+4х+5 ? В каком виде искать разложение?

        Что ж, пришла пора основательно разбираться, откуда ноги растут. В следующих уроках.)

If you see the expressions 3² and 5³, you might announce with a flourish that these mean «three squared» and «five cubed,» and be able to go about finding equivalent numbers without exponents, the numbers represented by the superscripts to the upper right above. These numbers in this case are 9 and 125.

But what if, instead of, say, a simple exponential function such as y = x ³, you instead have to solve an equation like y = 3^x. Here x, the dependent variable, appears as an exponent. Is there a way to pull that variable down from its perch to more easily deal with it mathematically?

In fact there is, and the answer lies in the natural complement of exponents, which are fun and helpful quantities known as logarithms.

What Are Exponents?

An exponent, also called a power, is a compressed way of expressing repeated multiplications of a number by itself. 4⁵ = 4 × 4 × 4 × 4 × 4 = 1,024.

Exponents can be negative, producing the relationship x⁻ⁿ = 1/(xⁿ). They can also be expressed as fractions, e.g., 2^(5/3). If expressed as fractions, both the numerator and denominator must be integer numbers.

What Are Logarithms?

Logarithms, or «logs,» can be regarded as exponents expressed as something other than a power. That probably doesn’t help much, so perhaps an example or two will.

In the expression 10³ = 1,000, the number 10 is the base, and it is being raised to the third power (or power of three). You can express this as, «the base of 10 raised to the third power equals 1,000.»

An example of a logarithm is log₁₀(1,000) = 3. Note that the numbers and their relationships to each other are the same as in the previous example, but they have been moved around. In words, this means, «the log base 10 of 1,000 equals 3.»

The quantity on the right is the power that the base of 10 has to be raised to in order to equal the argument, or input of the log, the value in parentheses (in this case 1,000). This value has to be positive, because the base — which can be a number other than 10, but is assumed to be 10 when omitted, e.g., «log 4» — is also always positive.

Helpful Logarithm Rules

So how can you work easily between logs and exponents? A few rules about the behavior of logs can get your started on exponent problems.

log_{b}(xy) = log_{b}{x} + log_{b}y log_{b}(dfrac{x}{y}) = log_{b}{x} text{ − }log_{b}y log_{b}(x^A) = A⋅log_{b}(x) log_{b}(dfrac{1}{y}) = −log_{b}(y)

Solving for an Exponent

With the above information, you’re ready to try solving for an exponent in an equation.

Example: If 50 = 4^x, what is x?

If you take the log to the base 10 of each side and omit explicit identification of the base, this becomes log 50 = log 4^x. From the box above, you know that log 4^x = x log 4. This leaves you with

log 50 = x log 4, or x = (log 50)/(log 4).

Using your calculator or electronic device of choice, you find that the solution is (1.689/0.602) = 2.82.

Solving Exponential Equations With e

The same rules apply when the base is e, the so-called natural logarithm, which has a value of about 2.7183. You should have a button for this on your calculator as well. This value gets its own notation, too: log_ex is written simply «ln x.»

Example: Solve the equation 16 = e^2.7x.

As above, ln 16 = ln e^2.7x = 2.7x.

ln 16 = 2.77 = 2.7x, so x = 2/77/2.7 = 1.03.

Содержание

• — Как найти числитель в дроби?
• — Как вычислить неизвестный числитель?
• — Как найти общий числитель?
• — Где находится числитель и знаменатель дроби?
• — Как правильно сравнивать дроби?
• — Как дробь прибавить к дроби?
• — Как найти неизвестное уменьшаемое и вычитаемое?
• — Как найти неизвестный множитель 3 класс?
• — Как найти знаменатель?
• — Как найти общий делитель 2 чисел?
• — Как найти все общие делители двух чисел?
• — Как объяснить ребенку общий знаменатель?
• — Кто придумал обыкновенные дроби?
• — Как записывается обыкновенная дробь?
• — Что такое простые дроби?

Число, стоящее над дробной чертой, называется числителем. Числитель показывает, сколько долей взяли (закрасили) у целого. Число, стоящее под дробной чертой, называется знаменателем. Знаменатель показывает, на сколько равных долей разделено целое.

Как найти числитель в дроби?

Числитель и знаменатель дроби

Под чертой дроби пишут число, показывающее, на сколько долей (частей) разделена единица. Оно называется знаменателем дроби. Над дробной чертой пишут число, показывающее, сколько таких частей взято. Это число называется числителем дроби.

Как вычислить неизвестный числитель?

Для этого существует следующее правило: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. Это правило объясняется тем, что вычитанию придается смысл, обратный смыслу сложения.

Как найти общий числитель?

Общий числитель дробей находят так же, как общий знаменатель. Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. от деления НОК на исходный числитель каждой дроби. Пример.

Где находится числитель и знаменатель дроби?

Числитель дроби — это число, стоящее в записи обыкновенной дроби над дробной чертой, то есть сверху. Числитель показывает количество долей. Знаменатель дроби — это число, стоящее в записи дроби под дробной чертой, то есть снизу. Знаменатель показывает, какие это доли и на сколько равных частей разделена единица.

Как правильно сравнивать дроби?

Чтобы сравнить дроби с разными числителями и знаменателями, нужно привести их к общему знаменателю. Дроби приведены к общему знаменателю. Если знаменатели одинаковые — больше та дробь, числитель которой больше.

Как дробь прибавить к дроби?

Чтобы сложить две обыкновенные дроби, следует:

1. привести дроби к наименьшему общему знаменателю;
2. сложить числители дробей, а знаменатель оставить без изменений;
3. сократить полученную дробь;
4. Если получилась неправильная дробь преобразовать неправильную дробь в смешанную.

Как найти неизвестное уменьшаемое и вычитаемое?

Вспоминаем правило для его нахождения: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

Как найти неизвестный множитель 3 класс?

Если надо найти неизвестный множитель, то произведение разделим на известный множитель. x ⋅ 5 = 20 ; x = 20 : 5 ; x = 4 .

Как найти знаменатель?

1) Выбираем из всех знаменателей наибольшее число и проверяем, делится ли оно на остальные. Если делится, то это число и есть наименьший общий знаменатель (НОЗ) этих дробей. 2) Если наибольший знаменатель не делится на все остальные, умножаем его на 2 и проверяем, делится ли полученное число на все остальные.

Как найти общий делитель 2 чисел?

Алгоритм Евклида заключается в следующем: если большее из двух чисел делится на меньшее — наименьшее число и будет их наибольшим общим делителем. Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя. Формула НОД: НОД (a, b) = НОД (b, с), где с — остаток от деления a на b.

Как найти все общие делители двух чисел?

Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:

1. разложить их на простые множители;
2. из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
3. найти произ ведение оставшихся множителей.

Как объяснить ребенку общий знаменатель?

Общий знаменатель – это любое положительное общее кратное всех знаменателей данных дробей. Иными словами, общим знаменателем некоторого набора обыкновенных дробей является любое натуральное число, которое делится на все знаменатели данных дробей.

Кто придумал обыкновенные дроби?

Современную запись дробей предложили арабы. Фундамент теории обыкновенных дробей заложили греческие и индийские математики. Впервые в Европе данный термин употребил в 1202 году первый крупный математик средневековой Европы Леонардо Пизанский (1170 — 1250), более известный как Фибоначчи.

Как записывается обыкновенная дробь?

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа. Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Что такое простые дроби?

Часть единицы или несколько её частей называются обыкновенной или простой дробью. Количество равных частей, на которые делится единица, называется знаменателем, а количество взятых частей – числителем. Дробь записывается в виде: Здесь 3 – числитель, 7 – знаменатель.

Интересные материалы:

Как хранить наушники дома?
Как хранить овощи в морозильной камере?
Как хранить печенье с глазурью?
Как хранить приготовленные спагетти?
Как хранить рулоны ткани?
Как хранить старые картины?
Как классифицируют горные породы?
Как классифицируют текстильные товары?
Как клеить Абс пластик?
Как клеить кромочную ленту на дсп?