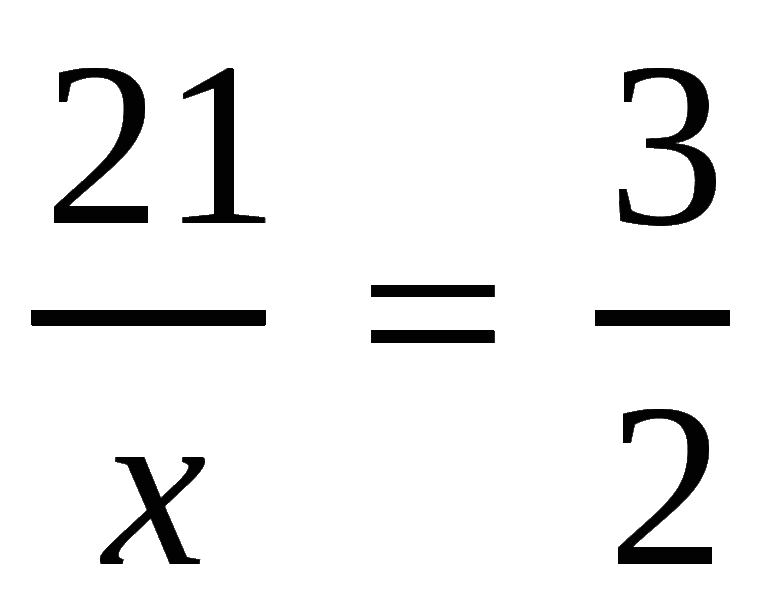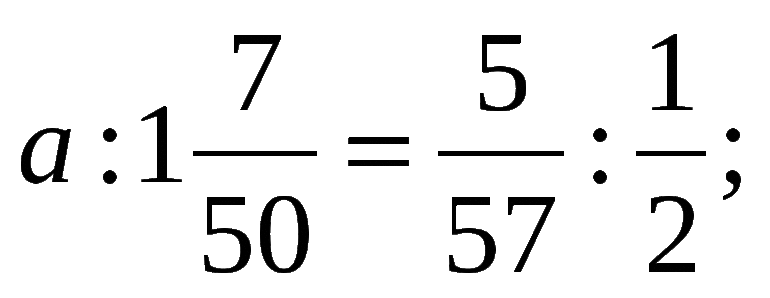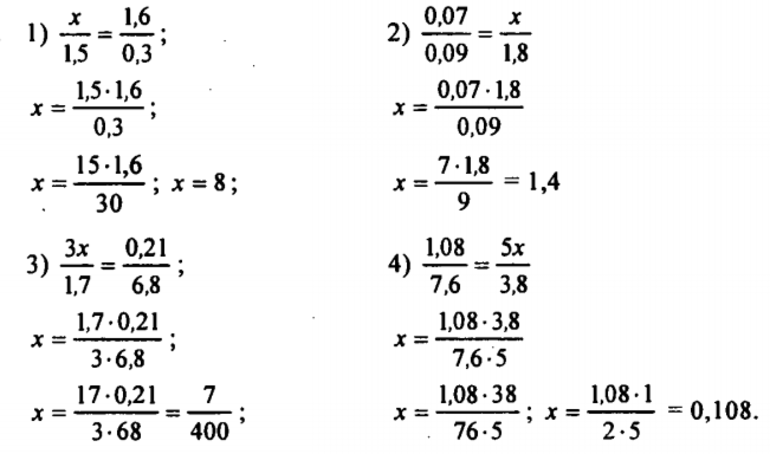Как найти неизвестный член пропорции правило

Пропорции

• Члены пропорции: крайние и средние
• Главное свойство пропорции
• Нахождение неизвестного члена пропорции

Равенство двух отношений называется пропорцией.

Пропорцию

a : b = c : d

или

можно прочитать так:  отношение  a  к  b  равно отношению  c  к  d,  или  a  относится к  b,  как  c  относится к  d.

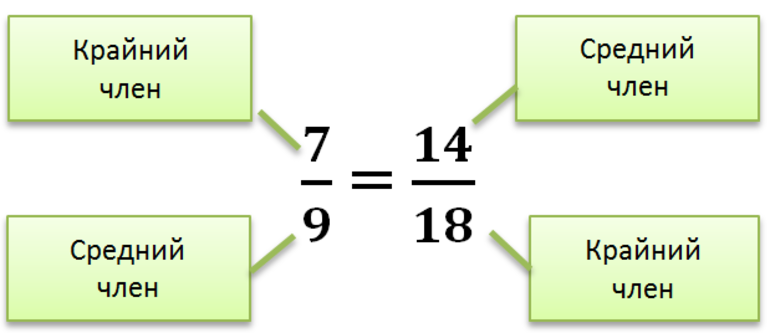
Члены пропорции: крайние и средние

Члены отношений, составляющих пропорцию, называются членами пропорции. Числа  a  и  d  называют крайними членами пропорции, а числа  b  и  c  — средними членами пропорции:

Эти названия условны, так как достаточно написать пропорцию в обратном порядке (переставить отношения местами):

c : d = a : b

или

и крайние члены станут средними, а средние — крайними.

Главное свойство пропорции

Произведение крайних членов пропорции равно произведению средних.

Из главного свойства пропорции следует:

1. Крайний член равен произведению средних, разделённому на другой крайний. То есть для пропорции   :

   

2. Средний член равен произведению крайних, разделённому на другой средний. То есть для пропорции   :

   

Нахождение неизвестного члена пропорции

Свойства пропорции позволяют найти любой из членов пропорции, если он неизвестен. Рассмотрим пропорцию:

x : 8 = 6 : 3.

Тут неизвестен крайний член. Так как крайний член равен произведению средних, разделённому на другой крайний, то

x = (8 · 6) : 3 = 16.

Математика

6 класс

Урок № 5

Пропорции

Перечень рассматриваемых вопросов:

• Понятие пропорции.
• Основное свойство пропорции.
• Как правильно составить пропорцию.
• Как найти неизвестный член пропорции.

Тезаурус

Равенство двух отношений называют пропорцией.

Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.

Основная литература

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.

Если один член пропорции неизвестен и необходимо его определить, то говорят, что нужно решить пропорцию.

Рассмотрим 3 способа нахождения неизвестного члена пропорции.

1 способ.

2 способ.

Способ 3.

Задача.

Решение:

Ответ:

1) можно;

2) можно;

3) нельзя;

4) нельзя.

Разбор решения заданий тренировочного модуля

№1. Тип задания: сортировка элементов по категориям.

№2. Тип задания: Подстановка элементов в пропуски в тексте.

Найдите неизвестный член пропорции.

Для нахождения неизвестного члена пропорции воспользуемся основным свойством пропорции, из которого следует: чтобы найти неизвестный средний член пропорции, надо произведение крайних членов разделить на известный средний член пропорции.

Ответ: 3.

Введение

Когда мы рисуем какой-нибудь объект, например дом, то стремимся нарисовать его похожим. Что это значит? Мы можем не знать ширину и высоту дома (см. Рис. 1), но мы всегда визуально оцениваем их соотношение.

Рис. 1. Соотношение ширины и высоты дома

Если высота дома в два раза больше его ширины, то на нашем рисунке это соотношение должно остаться таким же: если нарисовали дом шириной  клетки, то высота должна быть  клетки (см. Рис. 2).

Рис. 2. Правильное соотношение на рисунке

Если сделаем высоту дома  клеток, то он будет слишком «узкий», сделаем  клетки – снова непохоже, дом получается квадратным. (См. Рис. 3.)

Рис. 3. Слева направо: 1 – дом с неправильным соотношением ширины и высоты (ширина – 2 клетки, высота – 10); 2 – дом с верным соотношением ширины и высоты; 3 – дом с неправильным соотношением ширины и высоты (ширина – 2 клетки, высота – 2)

Записать это равенство можно с помощью дробей:

Или с помощью знака деления:

Эти записи эквиваленты.

Определение пропорции

Равенство двух отношений называют пропорцией.

 или

 и  называют крайними членами пропорции,  и  – средними членами.

Конечно, мы уже записывали пропорции раньше, просто не называли их так. Для любой дроби есть бесконечное количество эквивалентных, равных ей дробей. (Достаточно числитель и знаменатель умножить на одно и то же число.)

Раньше мы говорили «две третьих равно восемь двенадцатых» () или «два делить на три равно восемь делить на двенадцать» ().

Теперь мы можем еще сказать «два относится к трем, как восемь относится к двенадцати». То есть два отношения равны друг другу.

Случаи возникновения пропорции

Обычно пропорции возникают в двух случаях.

1. Мы знаем две величины. Их отношение можно записать дробью. Потом эту дробь можно записать более просто, например сократить. Получим равенство двух дробей, то есть пропорцию.

Пример 1. Высота дома  метров, ширина  метров. (См. Рис. 4.) Каково отношение этих размеров?

Рис. 4. Иллюстрация к примеру 1

Конечно, их отношение – это один размер, деленный на другой. То есть . Но эту дробь можно сократить, записать эквивалентной, более простой на вид. . То есть можно сказать, что высота относится к ширине, как  к , но проще сказать, как  к .

Можно и наоборот. Ширина относится к высоте, как  к  или как  к  ().

А если бы размеры были  м и  м?

Тогда мы бы записали отношение  и упростили его, умножив числитель и знаменатель на два: .

То есть обычно стараются получить несократимую дробь с целыми числителем и знаменателем.

2. Мы знаем две величины и их отношение. И еще две, которые связаны таким же отношением. Размеры дома –  и  метров и рисунка дома –  и  см. (См. Рис. 5.) Равенство этих двух отношений () и есть пропорция.

Рис. 5. Равенство отношений размеров предметов представляет собой пропорцию

Пример 2. Мы пошли в поход. В первый день мы шли  ч. Во второй день –  ч. Каково отношение пройденных расстояний в первый и второй день, если скорость была одинакова? (См. Рис. 6.)

Рис. 6. Иллюстрация к примеру 2

Во сколько раз времени мы больше затратили, во столько же раз мы больше и прошли.
То есть отношения времени и отношение пути в первый и второй день равны:

Получаем пропорцию:

И это будет справедливо для любых промежутков времени: . Отношение потраченного времени равно отношению пройденных расстояний.

Пример 3. Считается справедливым, что во сколько раз человек больше сделал, во столько раз и вознаграждение у него должно быть больше.

Введем обозначения: ,  – объем выполненной работы 1-м и 2-м человеком,

,  – вознаграждение каждого (см. Рис. 6).

Рис. 6. Иллюстрация к примеру 3

Тогда во сколько раз один объем отличается от другого, точно так же должны отличаться и вознаграждения. Два отношения равны, то есть получаем пропорцию: .

Математические действия с пропорцией

Теперь подробнее остановимся на арифметической части, какие математические действия мы можем производить с пропорцией.

Итак, пусть есть пропорция:

Так как левая и правая часть – это дроби, то мы можем делать все, что делали с дробями и раньше.

Приведем дроби к общему знаменателю (очевидно, что общим знаменателем является произведение ).

Две дроби равны. Знаменатели у них равны. Значит и числители их равны.

Запишем это: .

То есть если пропорция записана с помощью дроби, то можно перемножить ее члены крест-накрест и приравнять:

Если пропорция записана с помощью знака деления, то можно перемножить крайние и средние члены и приравнять:

Это одно и то же.

Это свойство иногда называют основным свойством пропорции.

Возьмем какую-нибудь простую пропорцию. Например, .

Легко увидеть, что это пропорция верная, так как обе дроби равны числу .

Перемножим крест-накрест ее члены, то есть воспользуемся основным свойством пропорции: . Получаем: .

Это свойство удобно при вычислениях, решении задач. Но если вы его не запомнили – ничего страшного. Всегда можно получить то же самое, просто выполняя эквивалентные преобразования дробей.

Приведем дроби к общему знаменателю:

Знаменатели равны, значит, числители тоже равны:

В качестве домашнего задания ответьте на следующие вопросы:

1. Почему в пропорции можно поменять местами два крайних члена?

Подсказка: воспользуйтесь основным свойством пропорции.

Какие еще члены можно поменять местами? (Для проверки возьмите любую пропорцию с конкретными числами.)

Пропорции в задачах

Итак, мы обсудили:

• Когда появляется пропорция.
• Какие арифметические действия мы можем с ней выполнять.

Осталось обсудить последний вопрос: как пропорция помогает нам решать задачи?

У пропорции  члена. Если три известны, а один нет, то мы можем его найти. Причем нет большой разницы, какой именно член неизвестен: , или , или , или .

Пример 1. Найти неизвестный член пропорции .

1. Первый способ.

Перемножим крест-накрест:

Выразим :

2. Второй способ 

После того как мы сократили правую дробь, поменять местами средние члены:

И сразу получаем ответ:

Ответ: .

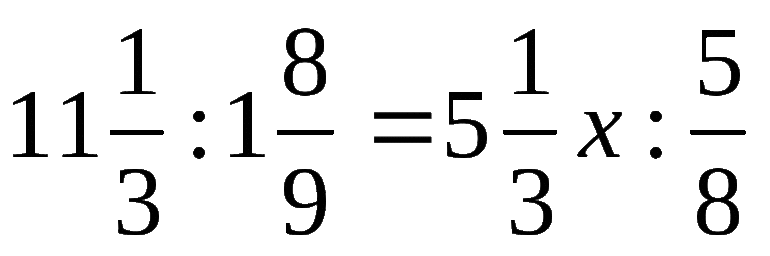
Пример 2. Найти неизвестный член пропорции: .

Перемножим крайние и средние члены:

Ответ: .

Задачи

Задача 1. В первый день участники похода прошли  км за  часов, во второй день –  км. (См. Рис. 7.) Сколько времени они шли во второй день, если скорость не менялась?

Рис. 7. Иллюстрация к задаче 1

Решение. Введем обозначения:  – пройденные пути;  – затраченное время.

Зачем вводить обозначения для тех величин, которые мы уже знаем? С такими обозначениями намного меньше шансов запутаться при записи условия, чем сразу записывать числами.

Итак, чем больше путь, тем больше затраченное время.

Запишем пропорцию:

Подставим известные величины:

Воспользуемся основным свойством, т. е. перемножим крест-накрест:

И выразим :

Ответ: во второй день они шли  часов.

Конечно, мы могли не применять здесь пропорцию.

Нам известны расстояние и время за первый день пути. Мы могли найти скорость движения. Так как скорость одинаковая и в первый, и во второй день и мы знаем расстояние за второй день, то можно найти требуемое время. Но так как в условии задачи не требовалось искать скорость, то мы сэкономили себе время, не вычисляя ее, тем самым сразу нашли неизвестное.

Задача 2. Первая бригада вскопала  поля и получила за это  рублей. Вторая бригада вскопала остальную часть поля. Сколько нужно заплатить второй бригаде? (См. Рис. 8.)

Рис. 8. Иллюстрация к задаче 2

Решение. Попробуем составить пропорцию сразу, используя известные значения, без введения дополнительных переменных. Понятно, что во сколько раз вторая бригада больше работала, во столько раз она и должна больше получить.

Запишем это в виде пропорции. Итак, если первая бригада вскопала , то вторая .

Отношение вскопанной площади (объема работ) равно: .

Отношения оплат должно быть равно отношению сделанной работы:

Выражаем :

Находим, что оплата второй бригады должна составить  рублей.

Ответ: второй бригаде нужно заплатить  рублей.

Заключение

Итак, кратко повторим.

Список литературы

1. Зубарева И.И., Мордкович А.Г. Математика. 6 класс. – М.: ИОЦ «Мнемозина», 2014 – 264 с.
2. Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Учебник в 3 частях. – 2-е изд., перераб. – М. «Просвещение», 2010; Ч. 2 – 128 с.
3. Виленкин Н.Я. и др. Математика. Учебник для 6 класса. – М.: ИОЦ «Мнемозина», 2013 – 288 с.

Дополнительные рекомендованные ссылки на ресурсы Интернет

1. Yaklass.ru (Источник).
2. Yaklass.ru (Источник).
3. School-assistant.ru (Источник).

Домашнее задание

1. Найдите неизвестный член пропорции: .
2. Верна ли данная пропорция: ?
3. За  кг картошки заплатили  руб. Сколько стоят  кг картошки?

Общие сведения

Изучение какого-либо термина в математике начинается с определения. Пропорцией вида x / y = v / z (x: y = v: z) называется равенство отношений двух чисел. Она представлена в виде правильной дроби, и состоит из следующих элементов, которые называются крайними (x и z) и средними (y и v) членами.

Следует отметить, что в некоторых сферах пропорциональная зависимость может быть представлена в немного другом виде. В этом случае знак равенства не указывается. Для удобства используется символ деления «:». Записывается в таком виде: a: b: c. Объяснение такой записи очень простое: для приготовления какого-либо вещества нужно использовать «а» частей одного компонента, b — другого и с — третьего.

Знак равенства не имеет смысла указывать, поскольку этот тип пропорциональной зависимости является абстрактным. Неизвестно, какой результат получится на выходе. Если взять за единицу измерения массу в кг, то и конечный результат получится в кг. В этом случае решать пропорцию не нужно — достаточно просто подставить данные, и получить результат.

Бывают случаи, когда следует посчитать пропорцию в процентах. Пример — осуществление некоторых финансовых операций.

Сферы применения

Пропорция получила широкое применение в физике, алгебре, геометрии, высшей и прикладной математике, химии, кулинарии, фармацевтике, медицине, строительстве и т. д. Однако ее нужно применять только в том случае, когда элементы соотношения не подчиняются какому-либо закону (методика исследования величин такого типа будет рассмотрена ниже), и не являются неравенствами.

В алгебре существует класс уравнений, представленных в виде пропорции. Они бывают простыми и сложными. Для решения последних существует определенный алгоритм. Кроме того, в геометрии встречается такие термин, как «гомотетия» или коэффициент подобия. Он показывает, во сколько раз увеличена или уменьшена фигура относительно оригинала.

Масштаб в географии является также пропорцией, поскольку он показывает количество см или мм, которые содержатся в какой-либо единице, зависящей от карты (например, в 1 см = 10 км). Специалисты применяютправило пропорции в высшей и прикладной математике. Расчет количества реактивов, вступающих в реакцию, для получения другого вещества применяется также пропорциональная зависимость.

Каждая хозяйка также применяет это соотношение для приготовления различных блюд и консерваций. В этом случае пропорция имеет немного другой вид: 1:2. Все компоненты берутся частями с одинаковыми размерностями или единицами измерения. Например, на 1 кг клубники необходимо 2 кг сахара. Расшифровывается такое соотношение следующим образом: 1 часть одного и 2 части другого компонентов.

В фармацевтике она также применяется, поскольку необходимо очень точно рассчитать массовую долю для каждого компонента лекарственного препарата. В медицине используется пропорциональная зависимость для назначения лекарства больному, дозировка которого зависит от массы тела человека.

Для приготовления различных строительных смесей она также используется, однако у нее такой же вид, как и для кулинарии. Например, для приготовления бетона М300 необходимы такие компоненты: цемент (Ц), щебень (Щ), песок (П) и вода (В). Далее следует воспользоваться таким соотношением, в котором единицей измерения является ведро: 1: 5: 3: 0,5. Запись расшифровывается следующим образом: для приготовления бетонной смеси необходимо 1 ведро цемента, 5 щебня, 3 песка и 0,5 воды.

Основные свойства

Для решения различных задач нужно знать основные свойства пропорции. Они действуют только для соотношения x / y = v / z. К ним можно отнести следующие формулы:

1. Обращение или обратное пропорциональное соотношение: [x / y = v / z] = [y / x = z / v].
2. Перемножение «крест-накрест»: x * z = y * v.
3. Перестановка: x / v = y / z и v / x = z / y.
4. Увеличение или уменьшение: x + у / y = v + z / z и x — у / y = v — z / z.
5. Составление через арифметические операции сложения и вычитания: (x + v) / (y + z) = x / y = v / z и (x — v) / (y — z) = x / y = v / z.

Первое свойство позволяет перевернуть правильные дроби соотношений двух величин. Это следует делать одновременно для левой и правой частей. Умножение по типу «крест-накрест» считается главным соотношением. С помощью его решаются уравнения и упрощаются выражения, в которых нужно избавиться от дробных частей. Найти неизвестный член пропорции можно также с помощью второго свойства, формулировка которого следующая: произведение крайних эквивалентно произведению средних элементов (членов).

Очень часто члены соотношения необходимо переставить для оптимизации вычислений. Для этого применяется свойство перестановки. При этом следует внимательно подставлять значения в формулу, поскольку неправильные действия могут существенно исказить результат решения. Этого можно не заметить. Для осуществления проверки следует подставить значение неизвестной в исходную пропорцию. Если равенство соблюдается, то получен верный результат. В противном случае необходимо найти ошибку или повторить вычисления.

Увеличение или уменьшение пропорции следует производить по четвертому свойству. Основной принцип: равенство сохраняется в том случае, когда уменьшение или увеличение числителя происходит на значение, которое находится в знаменателе. Нельзя отнимать от пропорции (от числителя и знаменателя равные числовые значения), поскольку соотношение не будет выполняться. Это является распространенной ошибкой, которая влечет за собой огромные погрешности при расчетах или неверное решение экзаменационных заданий.

Составить пропорцию можно с помощью вычитания и сложения. Этот прием применяется редко, но в некоторых заданиях может использоваться. Суть его заключается в следующем: отношение суммы крайнего и среднего элемента к суммарному значению других крайнего и среднего членов, которое равно отношению крайнего к среднему значению. Однако не ко всем выражениям можно применять свойства пропорции. Следует рассмотреть методику их определения.

Методика исследования

Пропорция применима только к линейным законам изменения величин. Примером этого является поведение простой тригонометрической функции z = sin (p). Величина «z» — зависимая переменная, которая называется значением функции. Переменная «p» — независимая величина или аргумент. В данном контексте она принимает значения углов в градусах. Для демонстрации того, что пропорция «не работает» необходимо подставить некоторые данные.

Кроме того, нужна таблица значений тригонометрических функций некоторых углов. Необходимо предположить, что p = 30, тогда z = sin (30) = 0,5. По свойству пропорции можно найти значение функции при р = 60, не используя таблицу. Для этого нужно составить пропорцию с неизвестным: 30 / 0,5 = 60 / х. Чтобы найти х («икс»), нужно воспользоваться свойством умножения «крест-накрест»: 60 * 0,5 = 30 * х. Уравнение решается очень просто: х = 60 * 0,5 / 30 = 30 / 30 = 1. Ответ получен очень быстро, и нет необходимости смотреть табличное значение.

В этом случае не так все просто. Если воспользоваться вышеописанной таблицей, то z = sin (60) = [3^(½)] / 2. Полученное значение не равно 1. Причина несоответствия — нелинейность функции. Математики для облегчения вычислений предлагают методику определения нелинейных выражений. Она состоит из следующих положений:

1. Записать функцию.
2. Рассмотреть составные части.
3. Если простой тип, перейти к 5 пункту.
4. Сложная — разложить на простые элементы, а затем перейти к 5 пункту.
5. Определить тип зависимости ее значения от аргумента: линейная или нелинейная. Если получен второй тип, то свойства пропорции применить невозможно.
6. Определить тип линейности, построив график.

По таким правилам были исследовано огромное количество функций. К нелинейным относятся следующие: прямые и обратные тригонометрические, гиперболические, показательные, логарифмические и сложные математические, состоящие из нелинейных зависимостей.

К прямым тригонометрическим относятся sin (p), cos (p), tg (p) и ctg (p), а к обратным — arcsin (p), arccos (p), arctg (p) и arcctg (p). Следует отметить, что гиперболическими являются sh, ch, th, cth, sech и csch. Показательная — z = a^y, а логарифмической — функция, имеющая операцию логарифмирования. Простые линейные могут объединяться с нелинейными. В таких случаях правило пропорции также не соблюдается.

Универсальный алгоритм

Алгоритм позволяет решать уравнения, и найти неизвестный член пропорции. Для его реализации следует знать теорию о пропорциях, и методику обнаружения нелинейных функций. Он состоит из нескольких шагов, которые помогут правильно вычислить необходимую величину:

1. Записать соотношение пропорции.
2. Проанализировать выражение в пункте под первым номером на наличие нелинейных функций и составляющих.
3. Применить свойство умножения «крест-накрест».
4. Перенести неизвестные в левую сторону, а известные — в правую. Необходимо обратить внимание на знаки: умножение — деление, сложение — вычитание и положительная величина становится отрицательной.
5. Решить уравнение.

Существуют различные приложения, позволяющие решить пропорцию. Онлайн-калькулятор позволяет вычислить неизвестный компонент очень быстро. Кроме того, результат вычислений отображается после проведения расчетов. Для реализации последнего пункта необходимо рассмотреть некоторые типы равенств с неизвестными.

Уравнения с пропорцией

Существуют уравнения в виде обыкновенной дроби, в которых необходимо найти неизвестную величину. Для этого нужно рассмотреть основные их виды:

1. Линейные.
2. Квадратные.
3. Кубические.
4. Биквадратные.

Различаются они степенным показателем. У первого типа степень переменной соответствует 1, второго — двойке, третьего — тройке и четвертого — четверке. При решении таких типов нужно выписать знаменатели отдельно, и решить их. Такие корни не являются решением исходной пропорции, поскольку знаменатели должны быть отличны от нулевого значения.

Решение линейного типа сводится к применению правила «крест-накрест». После чего нужно руководствоваться четвертым пунктом универсального алгоритма. Квадратное уравнение (ap ² + bp + c = 0) решается при помощи разложения на множители (существует высокая вероятность сокращения степени с последующим упрощением выражения) или с использованием дискриминанта (D = b ² — 4ac). Корни зависят от его значения:

1. Два корня, когда D > 0: р1 = (-b — [D]^(½)) / 2a и р2 = (-b + [D]^(½)) / 2a.
2. При D равном 0 (один): р = (-b) / 2a.
3. Если D < 0, то решений нет.

Решение уравнений кубического и биквадратного видов сводятся к разложению на множители. В результате этого происходит понижение степени до двойки. Кроме того, эффективным методом нахождения корней считается введение замены переменной.

Пример решения

Решение уравнений в виде пропорции осуществляется по такому же принципу. При этом рекомендуется использовать любые свойства. Необходимо проходить процесс обучения постепенно. Начинать нужно с простых примеров, а затем практиковаться на сложных заданиях. Первый тип был рассмотрен выше на примере sin (p).

Итак, необходимо решить уравнение [(t — 5) / (t — 2)] = [(t — 5) / (t — 1)]. Для начала следует определить тип функций каждого из элементов. Просмотрев список нелинейных выражений, можно сделать вывод о том, что все члены пропорции являются линейными. Далее нужно решить равенства с неизвестными, находящихся в знаменателях: t1 = 2 и t2 = 1. Корни не являются решениями уравнения.

Затем следует воспользоваться третьим пунктом алгоритма: (t — 5)(t — 1) = (t — 2)(t — 5). Если раскрыть скобки, то должно получиться такое равенство: t ² — t — 5t + 5 =t ² -5t -2t + 10. Перенести все слагаемые в левую сторону с противоположными знаками: t ² — t — 5t + 5 + 5t — t ² — 10 + 2t = 0. Приведя подобные слагаемые, выражение будет иметь такой вид: t = 5. Решением пропорции является значение t = 5.

Таким образом, для решения пропорций необходимо знать основные свойства, определение типа выражения по методике и алгоритм расчета.