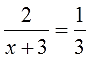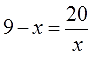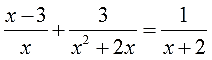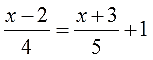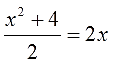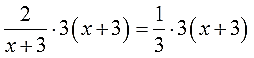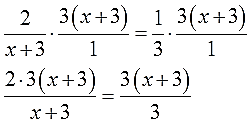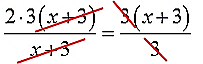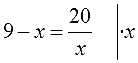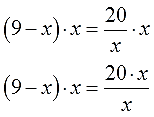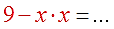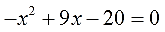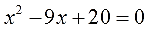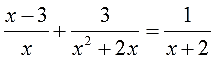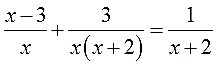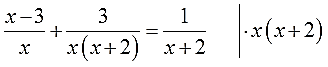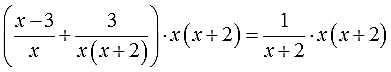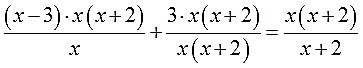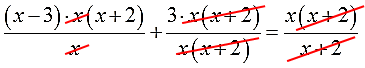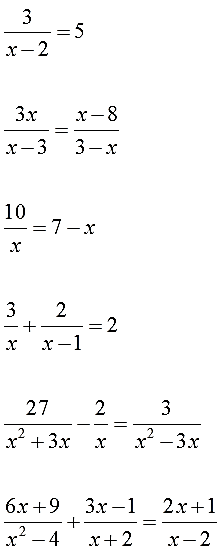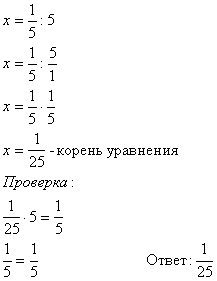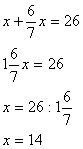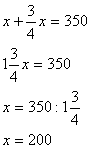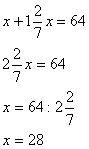Урок по теме «Решение дробных рациональных уравнений». 8-й класс
Разделы: Математика
Класс: 8
Цели урока:
- формирование понятия дробных рационального уравнения;
- рассмотреть различные способы решения дробных рациональных уравнений;
- рассмотреть алгоритм решения дробных рациональных уравнений, включающий условие равенства дроби нулю;
- обучить решению дробных рациональных уравнений по алгоритму;
- проверка уровня усвоения темы путем проведения тестовой работы.
- развитие умения правильно оперировать полученными знаниями, логически мыслить;
- развитие интеллектуальных умений и мыслительных операций — анализ, синтез, сравнение и обобщение;
- развитие инициативы, умения принимать решения, не останавливаться на достигнутом;
- развитие критического мышления;
- развитие навыков исследовательской работы.
- воспитание познавательного интереса к предмету;
- воспитание самостоятельности при решении учебных задач;
- воспитание воли и упорства для достижения конечных результатов.
Тип урока: урок – объяснение нового материала.
Ход урока
1. Организационный момент.
Здравствуйте, ребята! На доске написаны уравнения посмотрите на них внимательно. Все ли из этих уравнений вы сможете решить? Какие нет и почему?
Уравнения, в которых левая и правя часть, являются дробно-рациональными выражениями, называются дробные рациональные уравнения. Как вы думаете, что мы будем изучать сегодня на уроке? Сформулируйте тему урока. Итак, открываем тетради и записываем тему урока «Решение дробных рациональных уравнений».
2. Актуализация знаний. Фронтальный опрос, устная работа с классом.
А сейчас мы повторим основной теоретический материл, который понадобиться нам для изучения новой темы. Ответьте, пожалуйста, на следующие вопросы:
- Что такое уравнение? (Равенство с переменной или переменными.)
- Как называется уравнение №1? (Линейное.) Способ решения линейных уравнений. (Все с неизвестным перенести в левую часть уравнения, все числа — в правую. Привести подобные слагаемые. Найти неизвестный множитель).
- Как называется уравнение №3? (Квадратное.) Способы решения квадратных уравнений. (Выделение полного квадрата, по формулам, используя теорему Виета и ее следствия.)
- Что такое пропорция? (Равенство двух отношений.) Основное свойство пропорции. (Если пропорция верна, то произведение ее крайних членов равно произведению средних членов.)
- Какие свойства используются при решении уравнений? (1. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному. 2. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.)
- Когда дробь равна нулю? (Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.)
3. Объяснение нового материала.
Решить в тетрадях и на доске уравнение №2.
Какое дробно-рациональное уравнение можно попробовать решить, используя основное свойство пропорции? (№5).
х 2 -4х-2х+8 = х 2 +3х+2х+6
х 2 -6х-х 2 -5х = 6-8
Решить в тетрадях и на доске уравнение №4.
Какое дробно-рациональное уравнение можно попробовать решить, умножая обе части уравнения на знаменатель? (№6).
Теперь попытайтесь решить уравнение №7 одним из способов.
Решение уравнений с дробями
О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
-
Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
Дробно-рациональные уравнения
Что такое дробно-рациональные уравнения
Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:
при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.
Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.
9 x 2 — 1 3 x = 0
1 2 x + x x + 1 = 1 2
6 x + 1 = x 2 — 5 x x + 1
Уравнения, которые не являются дробно-рациональными:
Как решаются дробно-рациональные уравнения
В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.
Алгоритм действий при стандартном способе решения:
- Выписать и определить ОДЗ.
- Найти общий знаменатель для дробей.
- Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
- Записать уравнение со скобками.
- Раскрыть скобки для приведения подобных слагаемых.
- Найти корни полученного уравнения.
- Выполним проверку корней в соответствии с ОДЗ.
- Записать ответ.
Пример 1
Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:
x x — 2 — 7 x + 2 = 8 x 2 — 4
Начать следует с области допустимых значений:
x 2 — 4 ≠ 0 ⇔ x ≠ ± 2
Воспользуемся правилом сокращенного умножения:
x 2 — 4 = ( x — 2 ) ( x + 2 )
В результате общим знаменателем дробей является:
Выполним умножение каждого из членов выражения на общий знаменатель:
x x — 2 — 7 x + 2 = 8 x 2 — 4
x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )
После сокращения избавимся от скобок и приведем подобные слагаемые:
x ( x + 2 ) — 7 ( x — 2 ) = 8
x 2 + 2 x — 7 x + 14 = 8
Осталось решить квадратное уравнение:
Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:
Примеры задач с ответами для 9 класса
Требуется решить дробно-рациональное уравнение:
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
Определим область допустимых значений:
О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2
x 2 + 7 x + 10 ≠ 0
D = 49 — 4 · 10 = 9
x 1 ≠ — 7 + 3 2 = — 2
x 2 ≠ — 7 — 3 2 = — 5
Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:
a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Сократим дроби, избавимся от скобок, приведем подобные слагаемые:
x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —
— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0
x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0
x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0
2 x 2 + 9 x — 5 = 0
Потребуется решить квадратное уравнение:
2 x 2 + 9 x — 5 = 0
Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.
Дано дробно-рациональное уравнение, корни которого требуется найти:
4 x — 2 — 3 x + 4 = 1
В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:
4 ( x + 4 ) x — 2 — 3 ( x — 2 ) x + 4 — 1 ( x — 2 ) ( x + 4 ) = 0
4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0
4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0
x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0
Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:
— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0
Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:
( x — 2 ) ( x + 4 ) ≠ 0
Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:
— x 2 — x + 30 = 0 _ _ _ · ( — 1 )
Получилось квадратное уравнение, которое можно решить:
Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.
Нужно решить дробно-рациональное уравнение:
x + 2 x 2 — 2 x — x x — 2 = 3 x
На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:
x + 2 1 x ( x — 2 ) — x x x — 2 — 3 ( x — 2 ) x = 0
x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0
x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0
— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0
Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.
— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )
Корни квадратного уравнения:
x 1 = — 4 ; x 2 = 2
Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.
Найти корни уравнения:
x 2 — x — 6 x — 3 = x + 2
Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:
x 2 — x — 6 1 x — 3 — x ( x — 3 ) — 2 ( x — 3 ) = 0
x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0
x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0
0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0
Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:
Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.
Ответ: х — любое число, за исключением 3.
Требуется вычислить корни дробно-рационального уравнения:
5 x — 2 — 3 x + 2 = 20 x 2 — 4
На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:
5 ( x + 2 ) x — 2 — 3 ( x — 2 ) x + 2 — 20 1 ( x — 2 ) ( x + 2 ) = 0
5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0
5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0
2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0
( x — 2 ) ( x + 2 ) ≠ 0
Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.
Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.
Ответ: корни отсутствуют
Нужно найти корни уравнения:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )
Начнем с определения ОДЗ:
— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0
При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )
( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )
( x — 3 ) x + x = x + 5
Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:
x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0
Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:
x 1 · x 2 = — 10 x 1 + x 2 = 3
В этом случае подходящими являются числа: -2 и 5.
Второе значение не соответствует области допустимых значений.
http://skysmart.ru/articles/mathematic/reshenie-uravnenij-s-drobyami
http://wika.tutoronline.ru/algebra/class/9/drobnoraczionalnye-uravneniya
Иногда линейные уравнения принимают вид, когда неизвестное оказывается в числителе одной или нескольких дробей.
Как, например, в уравнении ниже.
В таких случаях подобные уравнения можно решить двумя способами.
I способ решения
Сведение уравнения к пропорции
Запомните!
При решении уравнений способом пропорции необходимо выполнить следующие действия:
- привести все дроби к общему знаменателю и сложить их как алгебраические дроби
(в левой и правой части должно остаться только по одной дроби); - полученное уравнение решить по правилу пропорции.
Итак, вернемся к нашему уравнению. В левой части у нас и так стоит только одна дробь, поэтому в ней не нужны
никакие преобразования.
Будем работать с правой частью уравнения.
Упростим правую часть уравнения так, чтобы там осталась только одна дробь.
Для этого вспомним правила сложения числа с алгебраической дробью.
Теперь используем правило пропорции и решим уравнение до конца.
II способ решения
Сведение к линейному уравнению без дробей
Рассмотрим уравнение выше еще раз и решим его другим способом.
Мы видим, что в уравнении присутствуют две дроби
«» и
«».
Наша задача сделать так, чтобы в уравнении не осталось ни одной дроби.
Другими словами, необходимо свести уравнение к обычному
линейному уравнению без неизвестного в дроби.
Запомните!
Чтобы избавиться от дробей в уравнении нужно:
- найти число, которое без остатка будет делиться на каждый из знаменателей;
- умножить каждый член уравнения на это число.
Давайте зададим себе вопрос: «Какое число без остатка делится на каждый из знаменателей дробей, то есть и на
«5», и на «9» ?».
Таким ближайшим наименьшим числом будет число «45».
Умножим каждый член уравнения на «45».
Важно!
При умножении уравнения на число нужно каждый член уравнения
умножить на это число.
Другие примеры решения уравнений с неизвестным в дроби
Решение уравнения I способом (через пропорцию)
-
+=
+
=
+
=
=
=
(49 − 23y) · 2 = 15 · (y + 6)
98 − 46y = 15y + 90
−46y − 15y = 90 − 98
−61y = −8 | :(−61)
y =
Ответ: y =
Решение уравнения II способом
(сведение к уравнению без дробей)
-
2 − +
= 0 | ·202 · 20 − +
= 0 · 2040 − 5 ·(3x − 7) + 4 · (x + 17) = 0
40 − 15x + 35 + 4x + 68 = 0
−15x + 4x + 40 + 35 + 68 = 0
−11x + 75 + 68 = 0
−11x + 143 = 0
−11x = −143 | :(−11)
x = 13
Ответ: x = 13
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
25 августа 2016 в 13:08
Виктория Лебеденко
Профиль
Благодарили: 0
Сообщений: 1
Виктория Лебеденко
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
3 сентября 2016 в 19:36
Ответ для Виктория Лебеденко
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
раскроем скобки x2+3x-x-3-x2-5=0(уничтожим x2 и-x2) получим 2x-8=0
2x=8
x=8 :2
x=4
0
Спасибо
Ответить
Линейные уравнения с дробями в 6 классе можно решать по обычной схеме: неизвестные — в одну сторону, известные — в другую, изменив при этом их знак. Другой путь — предварительно упростить уравнение, превратив его из линейного уравнения с дробями в линейное уравнение с целыми числами.
Сначала на примере одного линейного уравнения с дробями рассмотрим оба способа решения.
1 способ: Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Приводим к общему знаменателю дроби в каждой части уравнения:
Это — простейшее линейное уравнение. Обе части уравнения делим на число, стоящее перед иксом:
При делении чисел с разными знаками получаем отрицательное число. По правилу деления дробей:
После сокращения имеем:
(В данном случае ответ можно записать и в виде десятичной дроби: х=-0,8).
2 способ:
Обе части уравнения умножим почленно на наименьший общий знаменатель всех входящих в него дробей, в данном случае он равен 24:
При умножении на знаменатель дроби сокращаются, в знаменателе остается единица, которую не пишем. От линейного уравнения с дробями перешли к линейному уравнению с целыми числами:
Неизвестные — в одну сторону, известные — в другую с противоположными знаками:
Обе части уравнения делим на число, стоящее перед иксом:
Ответ: -4/5.
Как видите, второй способ существенно упрощает решение линейного уравнения с дробями.
Обе части уравнения умножаем почленно на наименьший общий знаменатель всех входящих в него дробей. Здесь он равен 60:
Вместо линейного уравнения с дробями получили линейное уравнение с целыми числами. Неизвестные переносим в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Сокращаем дробь на 3:
Ответ: 5/11.
Обе части уравнения умножаем почленно на наименьший общий знаменатель всех входящих в него дробей:
В результате линейное уравнение с дробями заменили на линейное уравнение с целыми числами:
Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Ответ: 2,9.
В следующий раз рассмотрим линейные уравнения с смешанными дробями.
Итак, друзья, продолжаем осваивать решение основных типов алгебраических уравнений. Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё одним основным типом уравнений — дробными уравнениями.
Иногда их называют более научно и солидно — дробные рациональные уравнения. Или дробно-рациональные уравнения. Это сути не меняет.)
Дробные уравнения — незаменимая вещь во многих других темах математики. Особенно — в текстовых задачах. Но для успешного их решения жизненно необходимо ориентироваться в трёх смежных темах:
1. Дроби и действия с дробями и дробными выражениями.
2. Тождественные преобразования уравнений.
3. Решение линейных и квадратных уравнений.
Без этих трёх китов браться за решение дробных уравнений слишком уж самонадеянно, я бы сказал. Почему? Да потому, что непонимание, как, скажем, работать с дробями (сокращать, приводить к общему знаменателю и т.д.) автоматически будет приводить к полному провалу и в дробных уравнениях. Намёк понятен?)
Так что тем, у кого проблемы хотя бы по одной из вышеперечисленных тем — настоятельно рекомендую освежить их в памяти, да и по ссылочкам пройтись.
Итак, вперёд!
Что такое дробное уравнение? Примеры.
Дробное уравнение, как следует непосредственно из названия, — это уравнение, в котором есть дроби. Обязательно. Причём (важно!) не просто дроби, а дроби, у которых есть икс в знаменателе. Хотя бы в одном.
Например, вот такое уравнение:
Или такое:
Или вот такое:
И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то такие уравнения к дробным не относятся. Либо это линейные уравнения, либо квадратные.
Например:
Это линейное уравнение, хотя тут тоже есть дроби. Почему? Да потому, что знаменатели дробей — четвёрка и пятёрка. Т.е. просто числа. И ни один из знаменателей не содержит иксов.
Или такое уравнение:
Это обычное квадратное уравнение, несмотря на двойку в знаменателе. Опять же, по причине того, что двойка — не икс, и деления на неизвестное в дроби нету.
В общем, вы поняли.
Как решать дробные уравнения? Убираем дроби!
Как это ни странно, дробные уравнения в большинстве своём решаются довольно просто. По чётким и несложным правилам. Каким же именно образом?
Первым делом надо избавиться от дробей! Это ключевой шаг в решении любого дробного уравнения, который должен быть освоен идеально. Ибо после того, как все дроби исчезли, уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы уже с вами знаем, что делать.)
Но… Как же нам избавиться от дробей?! Легко! Применяя всё те же старые добрые тождественные преобразования! В чём же суть?
Вникаем. Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится гораздо проще и приятнее.)
Это только на конкретном примере показать можно. Итак, решаем первое уравнение из нашего списка:
Первое, что приходит на ум — перенести всё в одну сторону, привести всё к общему знаменателю и т.д. Забудьте, как кошмарный сон! Так делают только в одном случае — при решении дробно-рациональных неравенств методом интервалов. Это отдельная большая тема.
А в уравнениях нам надо сразу умножить обе части на такое выражение, которое нам позволит сократить все знаменатели. И какое же это выражение?
Давайте его конструировать.) Смотрим ещё раз на уравнение:
Понятно, что в левой части для ликвидации знаменателя нам необходимо умножение на (х+3), а в правой — на 3. Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные — не катит. Ничего не поделать, так уж она устроена…)
Значит, нам надо скомбинировать такое выражение, которое одновременно делилось бы как на (х+3), так и на тройку. Причём очень важно — только с помощью умножения! И какое же это выражение? Очевидно, это 3(х+3). То есть, по сути, общий знаменатель обеих дробей.
Итак, для ликвидации всех дробей наше уравнение надо умножать на выражение 3(х+3).
Умножаем:
Это самое обычное умножение дробных выражений, но, так уж и быть, расписываю детально:
Прошу обратить внимание: скобки (х+3) я не раскрываю! Прямо так, целиком, их и пишу, как будто бы это одна буква. Ибо наша основная на данный момент задача — дроби убрать. Чего без произведения никак не сделаешь… И зачем же нам тогда париться с раскрытием скобок?!
А вот теперь мы видим, что в левой части сокращается целиком (х+3), а в правой 3. Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:
Вот и отлично. Дроби исчезли. После сокращения получилось безобидное линейное уравнение:
2∙3 = х+3
А его (надеюсь) уже решит каждый:
х = 3
Решаем следующий примерчик:
И опять избавляемся от того, что нам не нравится. В данном примере это дробь 20/х. Одна единственная. Для её ликвидации правую часть надо домножить на знаменатель. То есть, просто на х. Но тогда и левую часть тоже надо домножить на х: так уж второе тождественное преобразование требует.
Вот и домножаем! Всю левую часть и всю правую часть:
Напоминаю, что эта вертикальная чёрточка с умножением всего лишь означает, что обе части нашего уравнения мы умножаем на «х».
Вперёд!
А вот теперь — снова внимание! Очередные грабли. Заметьте, что при умножении левой части на икс, выражение (9 — х) я взял в скобки! Почему? Потому, что мы умножаем на икс всю левую часть целиком, а не отдельные её кусочки!
Дело всё в том, что частенько после умножения народ записывает левую часть вот так:
Это категорически неверно. Дальше можно уже не решать, да…)
Но у нас всё хорошо, будем дорешивать.
С чистой совестью сокращаем икс справа и получаем уравнение уже безо всяких дробей, в одну строчку.
(9 — х)∙х = 20
Вот и отлично. Все дроби исчезли напрочь, теперь можно и скобки раскрыть:
9х — х2 = 20
Переносим всё влево и приводим к стандартному виду:
Получили классическое квадратное уравнение. Но минус перед квадратом икса — нехорош. Забыть его проще простого! От него всегда можно избавиться умножением (или делением) уравнения на (-1). Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:
Решаем через дискриминант (или подбираем по теореме Виета) и получаем два корня:
х1 = 4
х2 = 5
И все дела.)
Как вы видите, в первом случае уравнение после преобразований стало линейным, а здесь — квадратным.
А бывает и так, что после ликвидации дробей вообще все иксы сокращаются и остаётся чистая правда. Что-нибудь типа 3=3. Это означает, что икс может быть любым. Какой икс ни возьми — всё равно всё посокращается и останется железное равенство 3=3.
Или наоборот, может получиться какая-нибудь белиберда, типа 3=4. А это будет означать, что корней нет. Какой икс ни возьми — всё сократится и останется бред…
Надеюсь, такие сюрпризы вас уже нисколько не удивят.) Если всё же удивят, то прогуляйтесь по ссылочке: Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее — особые случаи при решении линейных уравнений. Эти сюрпризы (полная пропажа иксов после преобразований) — они ко всем видам уравнений относятся. И дробные — не исключение.)
Разумеется, при попытке ликвидации дробей встречаются и неожиданности. И одну из них мы рассмотрим прямо сейчас.
Раскладываем на множители!
Решаем третье уравнение по списку:
А вот тут некоторые могут и зависнуть. На что же такое надо домножить всё уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, взять и тупо перемножить все три знаменателя, получить
x(x2+2x)(x+2)
и домножить на эту конструкцию всё уравнение. Математика не возражает.) Но… Может быть, есть выражение попроще?
Что ж, вскрою тайну: да, всё гораздо проще! Если в совершенстве владеть таким мощным приёмом, как разложение на множители. Привет седьмому классу!)
А попробуем-ка разложить на множители каждый из знаменателей? Ну, с х и х+2 точно ничего не сделать, а вот х2+2х вполне себе раскладывается! Выносим один икс за скобку и получаем:
х2+2х = х(х+2)
Отлично. Вставим наше разложение в исходное уравнение:
Вот теперь всё и прояснилось.) Теперь уже отчётливо видно, что гораздо проще будет умножать обе части уравнения на х(х+2). Это выражение гораздо короче и прекрасно делится на каждый из знаменателей: и на x, и на (х+2), и само на себя — на х(х+2).
Вот на х(х+2) и умножаем:
И снова расписываю подробно, дабы не запутаться. В левой части я буду использовать скобки: там сумма дробей. В правой части скобки не нужны: там одна дробь. Вот и пишем:
А теперь производим умножение. В левой части большие скобки умножаем на наше выражение х(х+2). Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем — вторую. Ну, а в правой части, по правилу умножения дробей, просто умножаем числитель:
Я уж не стал здесь рисовать единички в знаменателях, несолидно… И, опять же, малые скобки в числителях я не раскрываю! Они нам сейчас для сокращения понадобятся! И да… Откуда появились скобки (х — 3) в числителе первой дроби — думаю, уже не стоит объяснять?)
С удовольствием сокращаем все дроби:
(x-3)(x+2) + 3 = x
Раскрываем оставшиеся скобки, приводим подобные и собираем всё слева:
x2 + 2x — 3x — 6 + 3 — х = 0
x2 — 2x — 3 = 0
И снова получили квадратное уравнение.) Решаем и получаем два корня:
x1 = -1
x2 = 3
Вот и всё. Это и есть ответ.)
Из этого примера можно сделать важный вывод:
Если знаменатели дробей можно разложить на простые множители — обязательно делаем это! Пригодится при ликвидации дробей. Причём раскладываем всё до упора, используя все возможные способы из алгебры седьмого класса!
Как вы видите, всё просто и логично. Мы меняем исходное уравнение так, чтобы после наших преобразований из примера исчезло всё то, что нам не нравится. Или мешает. В данном случае это — дроби. И точно так же мы будем поступать и со всякими логарифмами, синусами, показателями и прочей жестью.) Мы всегда будем от всего этого избавляться.)
Ну что, порешаем?)
Решить уравнения:
Ответы (как обычно, вразброс):
x = 3
x1 = 0,5; x2 = 3
x = 2
х = 6
x = 2,6
x1 = 2; x2 = 5
Последнее задание не решается? Что ж, формулы сокращённого умножения всяко помнить надо, да…)
Всё решилось? Что ж, здорово! Значит, полпути в решении дробных уравнений мы с вами уже преодолели. Эта первая часть пути — избавление от дробей. Осталась вторая. Не менее важная!
Всё просто, но… Пришло время открыть вам горькую правду. Успешное решение дробных уравнений этого урока вовсе не гарантирует успех в решении всех остальных примеров этой темы. Даже очень простых, подобных этим. К сожалению…
Но об этом — дальше.)
Форма урока: объяснение нового
материала.
Цели урока:
- Обучающая: выработать навыки учащихся
умножать и делить обыкновенные дроби, решать и
оформлять задачи на уравнения. - Воспитательная: воспитывать
самостоятельность, аккуратность - Развивающая: развивать внимание,
математическую речь, вычислительные навыки
учащихся, интерес к математике.
Ожидаемые результаты: дети научаться
решать задачи и уравнения на дроби.
|
Этапы урока |
Время (мин) |
Слайды |
| Организационный момент. | 2 | Слайд 1 |
| Устная работа и повторение ранее изученного | 8 | Слайды 2, 3, 4, 5,6 |
| Формирование новых знаний и умений | 10 | Слайды 7, 8 |
| Физкультминутка | 2 | Слайды 9, 10 |
| Закрепление нового материала | 5 | Слайд 11 |
| Проверка знаний (с/р) | 10 | Слайд 12 |
| Постановка домашнего задания | 1 | Слайд 13 |
| Подведение итогов урока | 2 |
ХОД УРОКА
I. Организационный этап
– Здравствуйте, мы проведем сегодня урок по
теме «Деление дробей в уравнених». Откройте
тетради, запишите число, классная работа и тему
урока.
Целью нашего урока является закрепление и
проверка умений умножать и делить обыкновенные
дроби, а также повторить навыки решения задач и
уравнений.
II. Устный опрос учащихся
Чтобы умным в жизни стать
Надо дроби изучать
1) Переведите смешанную дробь в неправильную (Приложение 1, слайд 3)
2) Выделите целую часть (Приложение
1, слайд 4)
3) Умножьте дроби (Приложение 1,
слайд 5)
– Повторим правило умножения двух дробей:
Чтобы умножить дробь на дробь нужно перемножить
их числители и знаменатели и первое произведение
записать числителем, а второе знаменателем.
4) Выполните деление (в тетрадях с последующей
взаимопроверкой, сосед у соседа) (Приложение
1, слайд 6)
– Повторим правило деления двух дробей: Чтобы
разделить одну дробь на другую, нужно первую
дробь умножить на дробь, обратную второй.
III. Формирование новых знаний и умений
– При изучении темы деление большое значение
имеет умение решать уравнения. Рассмотрим пример
и запишем его в тетрадь. (Приложение
1, слайд 7)
– Чтобы решить уравнение необходимо
определить какой компонент в уравнении является
неизвестным.
– Какой?
– 1 множитель
– Правильно! Чтобы найти неизвестный множитель,
что нужно сделать?
– Чтобы найти неизвестный множитель необходимо
произведение разделить на известный множитель.
– Находим корень уравнения, выполняя деление.
Выполним проверку и запишем ответ.
– А теперь давайте проверим ваше умение решать
задачи.
№ 597 (Приложение 1,
слайд 7)
– Сколько всего прошел лыжник ? (26 км)
– Сколько километров прошел в первый день?
(неизвестно)
– Сколько километров прошел во второй день?
(неизвестно)
– Какую величину, с какой сравнивают?
– Что возьмем за х?
– Как найти дробь от числа?
– Сколько километров прошел за два дня?
– Как найти?
– Составим уравнение.
– 14 км лыжник прошел во второй день
26 – 14 = 12 км лыжник прошел в первый день.
№ 598 (Приложение 1,
слайд 
– Вспомним что такое 1% (одна сотая)
– Какой дробью запишем 75% (75/100 = 3/4)
– Сколько грибов собрала белка? (неизвестно)
– Сколько грибов собрал бельчонок? (неизвестно)
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе белка и бельчонок?
– Составим уравнение.
200 грибов собрала белка
350 – 200 = 150 грибов собрал бельчонок
IV. Физкультминутка
– Встаем и выполняем несколько упражнений.
А теперь, ребята, встали,
Быстро руки вверх подняли,
В стороны, вперёд, назад
Повернулись вправо, влево,
Тихо сели, вновь за дело.
V. Закрепление нового материала
№ 594
– Сколько собрал Митя?
– Сколько собрал Коля?
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе мальчики?
28 грибов собрал Митя
64 – 28 = 36 грибов собрал Коля
VI. «Математический выбор»
Уравнения, оцениваемые в 3
балла:
Уравнения, оцениваемые в 5 баллов:
1)
1)
2)
2)
3)

3)
4)
4)
Уравнения, оцениваемые в 6 баллов:
1)
2)
3)
4)
Оценки: 5 – 12 баллов; 4 – 9 баллов; 3 – 6 баллов.
Каждый выбирает себе уравнения по «плечу».
Учитель во время работы оценивает учеников.
VII. Итог урока
– С каким настроением вы сегодня работали на
уроке?
– Какая задача для вас была самой интересной?
– Ребята чему мы научились на сегодняшнем уроке?
– Как найти часть от числа?
– Как найти неизвестный множитель?
Оценки за урок.
VIII. Домашнее задание
– С листов решить любые три уравнения, из тех
которые не решали в классе.

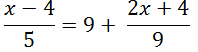
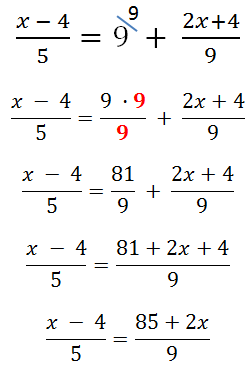
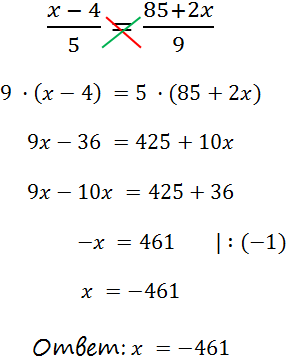
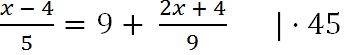

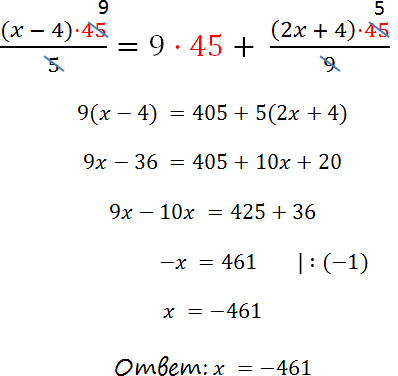



![Rendered by QuickLaTeX.com [x = - frac{{1 cdot mathop {24}limits^4 }}{{mathop 6limits_1 cdot 5}}]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-b277148ea87346868250dc5cb394589b_l3.png)