Как найти нейтральный элемент по операции - Исправление недочетов и поиск решений вместе с Examum.ru

Тема: Найдите нейтральный элемент (Прочитано 3216 раз)

0 Пользователей и 1 Гость просматривают эту тему.

Как найти нейтральный элемент для следующей операции *
х*у = ху+7х+7у+42

Знаю, что нейтральный элемент — это элемент Е удовлетворяющий условию А*Е=Е*А=А
Ну и как же найти этот нейтральный элемент?

« Последнее редактирование: 24 Мая 2011, 23:35:43 от NELL »

Не знаком с нейтральными элементами, но хорошо знаю алгебру. Чтобы выполнялось тождество, должно быть: 7х+7у+42=0 и, следовательно,
y=-x-6

За жизнью надо тщательно следить, все время избегая с ней разлуки.

xy сокращаются и остается 7х+7у+42=0. Отсюда y=-x-6

За жизнью надо тщательно следить, все время избегая с ней разлуки.

нееет! Вы не поняли.

В условии дается такая бинарная операция » * » (умножения), которая определяется выражением
х*у = ху+7х+7у+42

т.е. х * у — это не такое обычное умножение, а это операция, которая определяется этим вот большим выражением

« Последнее редактирование: 25 Мая 2011, 02:03:00 от NELL »

Тишина…

ex=e*x+7x+7e+42=x
e(x+7)=-42-6x
e = -(42+6x)/(x+7)
e = -6(x+7)/(x+7)
e = -6

Ого! Спасибо большое!

Источник

Нейтра́льный элеме́нт бинарной операции — это элемент, который оставляет любой другой элемент неизменным при применении к ним этой бинарной операции.

Содержание

1 Определение
2 Замечания
3 Примеры
4 См. также

Определение

Пусть — множество с определённой на нём бинарной операцией . Элемент называется нейтральным относительно , если

{displaystyle xcdot e=ecdot x=x,quad forall xin M.}

Иногда различают нейтральный слева элемент ${displaystyle e_{mathrm {l} }}$ , для которого

${displaystyle e_{mathrm {l} }cdot x=x,quad forall xin M,}$

и нейтральный справа элемент ${displaystyle e_{mathrm {r} }}$ , для которого

${displaystyle xcdot e_{mathrm {r} }=x,quad forall xin M.}$

Замечания

Если существует только левый или только правый нейтральный элемент, то в общем случае их может быть больше одного. Если одновременно существуют левый и правый нейтральный элементы, то они совпадают.

В приведённой выше мультипликативной нотации нейтральный элемент принято называть «единицей». Если для обозначения операции используется аддитивная нотация , то нейтральный элемент называют «нулём».

Примеры

Множество	Бинарная операция	Нейтральный элемент
Вещественные числа	(сложение)	0
Вещественные числа		1
Вещественные числа	${displaystyle a^{b}}$ (возведение в степень)	1 (нейтральный справа)
Матрицы размера	(матричное сложение)	нулевая матрица
Матрицы размера	(матричное произведение)	единичная матрица
Функции вида	(композиция функций)	Тождественное отображение
Функции вида	* (свёртка)	(дельта-функция)
Символьные строки	конкатенация	пустая строка
Расширенная числовая прямая	или
Расширенная числовая прямая	или
Подмножества множества	(пересечение множеств)
Множества	(объединение множеств)	(пустое множество)
Булева логика	(логическое и)	(истина)
Булева логика	(логическое или)	(ложь)

См. также

Обратный элемент;
Моноид;
Группа.

ar:عنصر حيادي
bg:Неутрален елемент
ca:Element neutre
cs:Neutrální prvek
et:Ühikelement
he:איבר יחידה
hu:Neutrális elem
lmo:Elemeent néutar
nl:Neutraal element
pl:Element neutralny
simple:Identity element
sk:Neutrálny prvok
sl:Nevtralni element
sr:Неутрал
sv:Neutralt element
uk:Нейтральний елемент
vi:Phần tử đơn vị
yi:נאטוראלע עלעמענט

Источник

Нейтральные элементы

Пусть

— бинарная операция на непустом множестве
А.

def.
Элемент е
из А
называется левым
нейтральным относительно
операции

,
если для любого а
из А
выполняется равенство е

а
= а.

def.
Элемент е
из А
называется правым
нейтральным относительно
операции

,
если для любого а
из А
имеем а

е
= а.

def.
Элемент е
из А
называется нейтральным
относительно
операции

,
если для любого элемента а
из А
верны равенства e

a
= a
= a

Теорема 1.
Если нейтральный элемент относительно
операции

существует, то он единственен.

Доказательство.

Следствие.
Если нейтральный элемент относительно
операции

существует, то все левые и правые
нейтральные элементы относительно

с ним совпадают.

Примеры.

1) Число 0 есть
нейтральный элемент относительно
сложения целых чисел. Число 1 есть
нейтральный элемент относительно
умножения целых чисел.

2) На множестве
Р(М)
относительно

нейтральный ;
относительно

нейтральный P(M).

Симметричные элементы

Пусть

– бинарная операция на множестве А,
обладающая нейтральным элементом е.

def.
Элемент v
из А
называется левым
симметричным
к элементу а

А
относительно операции

,
если v

a
= e.

def.
Элемент v
из А
называется правым
симметричным
к а
относительно операции

,
если а

v
= е.

def.
Элемент а’

А
называется симметричным
к элементу а

А относительно
операции

,
если а

a’
= е
= a’
a.
В этом случае элемент а
называется симметризуемым,
а элементы а
и а’
– взаимно
симметричными.

Примеры.

1) Относительно
сложения целых чисел симметричным к
данному целому числу является то же
число, взятое со знаком «минус».

2) Относительно
умножения рациональных чисел симметричным
к нулевому числу а
является

;
число нуль не имеет симметричного
относительного умножения.

Теорема 2.
Если операция

ассоциативна и элемент a
симметризуем, то существует единственный
элемент, симметричный к а.

Доказательство.

Следствие.
Если элемент a
имеет симметричный элемент а’
относительно ассоциативной операции

,
то все левые и все правые симметричные
к а
элементы совпадают с элементом а’.

Аддитивная и мультипликативная форма записи

Наиболее часто
используется аддитивная и мультипликативная
формы записи бинарной операции. При
аддитивной форме записи бинарную
операцию

называют сложением
и пишут а
+ b
вместо a

b,
называя элемент a
+ b
суммой
a
и b.
Элемент, симметричный элементу а,
обозначают (-а)
и называют противоположным
элементу а.
Нейтральный элемент относительно
сложения обозначают символом 0 и называют
нулевым
элементом
относительно сложения. При аддитивной
записи свойства ассоциативности и
коммутативности записывается в виде

a
+ (b
+ c)
= (a
+ b)
+ c,
a
+ b
= b
+ a.

При мультипликативной
форме записи бинарную операцию называют
умножением
и пишут a

b
(вместо а

b),
называется элемент a

b
произведением
а
и b.
Элемент, симметричный а,
обозначают а^-1
и называют обратным
элементу а.
Нейтральный элемент относительно
умножения обозначают через e
и 1 и называют единичным
элементом
или единицей
относительно умножения.
При мультипликативной записи свойства
ассоциативности и коммутативности
записываются в виде a

c)=(a

c,
a

b
= b

Свойство
дистрибутивности умножения относительно
сложения записываются в виде (a
+ b)

c
= a

c
+ b

c,
c

(a
+ b)
= c

a
+ c

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Алгебраические структуры и операции

Предметом рассмотрения в абстрактной алгебре являются произвольные множества с заданными на них операциями. При этом природа множеств и операций может существенно отличаться от привычных числовых множеств и известных операций над числами. Мы уже сталкивались с операциями над множествами и бинарными отношениями, которые оказались в чем-то похожими на операции над числами, но в то же время проявились и их существенные отличия.

В дискретной математике разрабатываются алгоритмы и вычислительные методы, позволяющие манипулировать сложно организованными нечисловыми структурами. Проблема работы с такими объектами возникла в связи с развитием современных информационных технологий и переходом от собственно вычислений (т.е. операций над числами) к обработке сложных структур данных. Так, проблемы программирования и машинного перевода привели к задачам работы с языковыми структурами, проблемы автоматизации проектирования — к задачам обработки графических объектов.

Современная дискретная математика проникнута алгебраическим духом, поскольку оказалось, что именно на алгебраической базе наиболее удобно разрабатывать общие подходы к работе с объектами различной природы.

Понятие алгебраической структуры

Множество векторов в пространстве с операцией сложения векторов, операцией векторного умножения, множество квадратных матриц с операциями сложения или умножения, множество функций с операцией сложения — вот примеры некоторых множеств с операциями, рассматривающихся в различных разделах математики. Выясним, что общего есть в свойствах операций на этих множествах и в чем их различие.

Определение 2.1. Пусть — произвольное непустое множество и — натуральное число. Любое отображение omegacolon A^nto A называют n-арной (или n-местной) операцией на множестве .

Таким образом, согласно приведенному определению, n-арная операция и каждому кортежу (a_1,ldots,a_n)in A^n однозначно сопоставляет элемент bin A . Компоненты кортежа называют при этом аргументами операции omega , а — результатом применения операции и к аргументам a_1,ldots,a_n .

Для n-арной операции используют обозначение

b=omega (a_1,ldots,a_n) или b= a_1ldots a_nomega .

Обычно, если n=2 , пишут a_1omega a_2 . При n=1 и n=2 говорят соответственно об унарной операции и бинарной операции.

Специально вводят понятие нульарной операции (т.е. для n=0 ). Под нульарной операцией на множестве понимают произвольный фиксированный элемент множества . Нульарные операции позволяют фиксировать элементы множества , обладающие некоторыми специальными свойствами. Примером выполнения нульарной операции является, например, фиксирование нуля в множестве целых чисел с операцией сложения. Примером унарной операции служит дополнение заданного множества до универсального множества.

Наиболее важными в алгебре и, следовательно, наиболее исследованными являются бинарные операции. Примерами таких операций могут служить сложение и умножение чисел, сложение и умножение матриц, сложение векторов линейного пространства.

Рассмотрим бинарную операцию на множестве , обозначив ее звездочкой (ast) . Эту операцию называют:

1) ассоциативной, если (xast y)ast z=xast (yast z) для любых x,y,zin A ;
2) коммутативной, если xast y=yast x для любых x,yin A ;
3) идемпотентной, если xast x=x для любого xin A .

Ассоциативность операции ast позволяет для любых элементов a_1,a_2,ldots,a_nin A однозначно трактовать результат выражения a_1ast a_2ast ldotsast a_n , так как

$a_1ast a_2ast ldotsast a_n= a_1ast (a_2ast ldotsast a_n)= (a_1ast a_2)ast (a_3ast ldotsast a_n)= (a_1ast ldotsast a_{n-1})ast a_n,.$

Операция сложения, заданная на множестве натуральных чисел, является ассоциативной и коммутативной. Операция умножения матриц ассоциативна, но не коммутативна. Идемпотентными являются операции объединения и пересечения множеств.

Элемент bold{0} множества называют левым (правым) нулем относительно данной операции ast , если bold{0}ast x=bold{0} (xastbold{0}=bold{0}) для любого xin A .

Если bold{0}' — левый нуль, а bold{0}'' — правый нуль, то они совпадают. Действительно, если и существуют, то они совпадают, так как bold{0}'= bold{0}'ast bold{0}''= bold{0}'' , и в этом случае говорят просто о нуле относительно операции. Из приведенных равенств следует, что нуль единственный и для него одновременно выполнены оба равенства bold{0}ast x= bold{0} и xast bold{0}= bold{0} .

Пример 2.1. а. На множестве целых чисел mathbb{Z} нулем относительно операции умножения будет число 0.

б. На множестве квадратных матриц вида $begin{pmatrix}a&0\b&1end{pmatrix}$ , где элементы и — действительные числа, любая матрица вида $begin{pmatrix} 0&0\d&1 end{pmatrix}$ будет правым нулем относительно операции умножения, поскольку

$begin{pmatrix}a&0\b&1end{pmatrix}! cdot! begin{pmatrix}0&0\d&1end{pmatrix}= begin{pmatrix}0&0\d&1end{pmatrix}!.$

Однако левого нуля в этом множестве нет, так как иначе он совпадал бы с правым нулем и был бы единственным. Но правых нулей имеется больше одного.

Нейтральные элементы относительно операции

Элемент bold{1} множества называют левым (правым) нейтральным элементом относительно операции ast , если bold{1}ast x=x (xastbold{1}=x) для любого элемента xin A . Для левого bold{1}' ; и правого bold{1}'' нейтральных элементов, если они оба существуют, выполнены равенства bold{1}'= bold{1}'ast bold{1}''= bold{1}'' , согласно которым они совпадают. В этом случае элемент bold{1} , который является и левым нейтральным, и правым нейтральным, единственный, и его называют просто нейтральным элементом.

Пример 2.2. Нейтральным элементом относительно операции умножения на множестве натуральных чисел является число 1. На множестве целых чисел нейтральным элементом относительно операции сложения будет число 0.

На множестве квадратных матриц вида $begin{pmatrix}a&0\b&0end{pmatrix}$ , где элементы и — действительные числа, любая матрица вида $begin{pmatrix} 1&0\d&0 end{pmatrix}$ будет правым нейтральным элементом по операции умножения, ибо

$begin{pmatrix} a&0\b&0end{pmatrix}! cdot! begin{pmatrix}1&0\d&0end{pmatrix}= begin{pmatrix} a&0\b&0end{pmatrix}!.$

Поскольку правых нейтральных элементов несколько, то левого нейтрального элемента по этой операции нет, так как иначе существовал бы единственный нейтральный элемент (левый и правый).

Следует заметить, что не для всякой бинарной операции нули и нейтральные элементы (левые и правые, в частности), существуют.

Примеры бинарных операций на множествах

Рассмотрим некоторые примеры бинарных операций на множествах.

Пример 2.3. а. Пусть — универсальное множество. Теоретико-множественные операции cup,,cap на множестве 2^U являются идемпотентными, ассоциативными и коммутативными, причем пустое множество является нулем относительно пересечения и нейтральным элементом относительно объединения

varnothingcap A=Acap varnothing= varnothing,quad varnothingcup A= Acup varnothing= A,

тогда как универсальное множество есть нуль относительно объединения и нейтральный элемент относительно пересечения

Ucap A=Acap U=A,quad Ucup A=Acup U=U

Операция setminus (разность множеств) не является ассоциативной, так как A setminus (B setminus C)ne (A setminus B)setminus C .

б. На множестве всех бинарных отношений на множестве операция композиции отношений является ассоциативной, но не коммутативной, а диагональ множества будет нейтральным элементом относительно этой операции.

в. Пусть — произвольное множество, содержащее не менее двух элементов. На множестве всех отображений из в с операцией композиции отображений постоянное отображение $varphi_{alpha}$ , переводящее любой элемент xin X в фиксированный элемент ain X , будет правым нулем, но не будет нулем относительно композиции отображений.

Действительно, для любого отображения fcolon Xto X и любого xin X имеем

$fcircvarphi_{alpha}(x)= varphi_{alpha}(f(x))= a= varphi_{alpha}(x)$ , то есть $fcircvarphi_{alpha}= varphi_{alpha}$ ,

что и означает, что $varphi_{alpha}$ — правый нуль относительно операции композиции на множестве отображений из в . Однако для любого xin X имеем

$varphi_{alpha}circ f(x)= f(varphi_{alpha}(x))= f(a),$

то есть $varphi_{alpha}circ f=varphi_{f(a)}$ — отображение, которое любой элемент переводит в элемент f(a) . Поскольку f(a) в общем случае не равно , то $varphi_{alpha}circ fne a$ . Значит, $varphi_{alpha}$ не является левым нулем относительно операции композиции.

Сигнатура алгебры

Рассмотренные выше примеры множеств с операциями приводят к следующим определениям.

Определение 2.2. Алгебра (универсальная алгебра, Ω-алгебра) считается заданной, если заданы некоторое множество , называемое носителем данной алгебры, и некоторое множество операций Omega на , называемое сигнатурой данной алгебры. Алгебру, носитель которой есть конечное множество, называют конечной алгеброй.

Поскольку алгебра задается ее носителем и сигнатурой, мы будем в записи обозначать алгебру как упорядоченную пару множеств mathcal{A}=(A,Omega) , полагая, что первая компонента этой пары есть носитель, а вторая — сигнатура. Подчеркнем, что алгебра — это не просто носитель и не просто сигнатура, а „синтез» этих двух объектов.

Замечание 2.1. Операции, включенные в сигнатуру, заданы как некоторые специальные отображения. Однако при этом не оговариваются свойства, которыми обладают операг ции на носителе. Например, они могут быть ассоциативными, коммутативными и т.д. При задании алгебр свойства операций обычно указывают дополнительно.

Если существует нейтральный элемент относительно операции, то его можно задать как нульарную операцию на носителе и включить в сигнатуру, а можно не включать и описать как свойство соответствующей операции.

Таким образом, одну и ту же алгебру можно задавать по-разному. Ниже приведены примеры различных описаний конкретных алгебр.

В ряде случаев указание носителя алгебры предполагает и задание определенной сигнатуры. В этом случае для упрощения пишут не mathcal{A}=(A,Omega) , а просто mathcal{A}=A и говорят «элемент алгебры «, имея в виду элемент носителя этой алгебры.

Пример 2.4. а. Рассмотрим алгебру

$mathcal{A}_1= bigl(2^M,, {cup,cap, setminus, triangle, overline{phantom{A}}, varnothing, M}bigr).$

Ее носителем является множество всех подмножеств произвольно фиксированного множества , а сигнатура состоит из следующих операций над множествами: объединения, пересечения, разности, симметрической разности, дополнения, пустого множества и множества (последние два элемента сигнатуры определяют нульарные операции).

б. Для любого множества можно определить алгебру

$mathcal{A}_2= bigl(2^{Mtimes M},, {cup, circ, phantom{|}^{-1}}bigr).$

носителем которой является множество всех подмножеств множества упорядоченных пар на , т.е. множество всех бинарных отношений на множестве , а сигнатура состоит из операций объединения, композиции бинарных отношений и взятия обратного отношения.

в. На множестве mathbb{R} действительных чисел можно, например, определить такую алгебру:

$mathcal{A}_3= bigl(mathbb{R},, {+, cdot, 0, 1}bigr),$

сигнатура которой состоит из операций сложения, умножения, а также двух нульарных операций, обозначающих два особых числа 0 и 1. Обратим внимание на то, что числа 0 и 1 в данном случае являются соответственно нулем и нейтральным элементом относительно умножения, а число 0 также играет роль нейтрального элемента относительно сложения. Мы применили понятие нульарнои операции, чтобы в обозначении алгебры отразить элементы со специальными свойствами.

г. Все предыдущие примеры алгебр были алгебрами с конечной сигнатурой, т.е. с сигнатурой, состоящей из конечного числа операций. Однако несложно построить пример алгебры с бесконечной сигнатурой. Например, алгебра

$mathcal{A}_4= bigl(mathbb{R},, {uparrow^ncolon, ngeqslant 2}bigr)$

на множестве действительных чисел mathbb{R} с операцией uparrow^n возведения в натуральную степень ngeqslant 2 имеет счетную сигнатуру. Далее будут приведены примеры алгебр и с несчетными сигнатурами.

Определяя алгебру, следует помнить, что результат применения любой операции обязательно должен принадлежать тому же множеству, что и ее аргументы. Например, пару из множества V_3 всех свободных векторов в пространстве и операции скалярного умножения векторов нельзя рассматривать как алгебру, так как скалярное произведение двух векторов не есть вектор. Заменив скалярное умножение векторным, получим алгебру.

Кроме того, нельзя забывать, что n-арная операция, как и всякое отображение, должна быть определена для любого кортежа длины n элементов множества. Поэтому не является алгеброй множество всех матриц с операциями сложения и умножения матриц, так как эти операции определены не для любой упорядоченной пары матриц. Если же при тех же операциях ограничиться множеством квадратных матриц фиксированного порядка , то получим алгебру.

Точно так же множество действительных чисел mathbb{R} с операцией {}:{} деления действительных чисел не является алгеброй, поскольку результат деления не определен при нулевом делителе. Пара же (mathbb{R}setminus{0}, {:}) есть алгебра.

Договоримся, определяя конкретную алгебру, записывать ее сигнатуру без фигурных скобок, перечисляя после обозначения носителя все операции. Так, в примере 2.4.а первая алгебра может быть записана как

$mathcal{A}_1= bigl(2^M,, cup,cap, setminus, triangle, overline{phantom{A}}, varnothing, Mbigr).$

Для алгебры mathcal{A}=(A,Omega) обозначим через $Omega^{(n)}$ подмножество сигнатуры Omega , состоящее из всех n-арных операций. Тогда $Omega=mathop{cup}limits_{ngeqslant 0}Omega^{(n)}$ . Так, для алгебры $mathcal{A}_1$ в примере 2.4.а будем иметь:

$Omega^{(0)}= {varnothing,M},quad Omega^{(1)}= {overline{phantom{A}}},quad Omega^{(2)}= {cup,cap,setminus,triangle},quad Omega^{(n)}= varnothing$ при n>2 .

Однотипные алгебры

Определение 2.3. Две алгебры $mathcal{A}_1=(A_1,Omega_1)$ и $mathcal{A}_2=(A_2,Omega_2)$ называют однотипными, если существует такая биекция Omega_1 на Omega_2 , при которой n-арная операция из Omega_1 для любого переходит в n-арную из Omega_2 .

Нередко сигнатуры однотипных алгебр и элементы этих сигнатур — операции — обозначают одинаково. Так, мы пишем (mathbb{R},+,cdot,0,1) и (mathbb{Q},+, cdot,0,1) , хотя первая алгебра задана на множестве всех действительных чисел, а вторая — на множестве рациональных чисел, и, например, сложение в первой алгебре, строго говоря, не есть та же самая операция, что сложение во второй алгебре. В общем случае мы часто будем говорить о различных (но однотипных) Ω-алгебрах, заданных на разных носителях, понимая, что Omega есть общее для всех этих алгебр обозначение их сигнатур.

Пример 2.5. Алгебра (2^M,cup,cap,varnothing,M) , заданная на множестве всех подмножеств множества , и алгебра $mathcal{A}_3=(mathbb{R}, +, cdot, 0,1)$ (см. пример 2.4.в), заданная на множестве действительных чисел, однотипны. Биекцию (взаимно однозначное соответствие) между их сигнатурами, которая сохраняла бы арность операций, можно определить и так: cupmapsto+, capmapstocdot, varnothingmapsto0, Mmapsto1 . Указанный способ задания биекции не единственный. Например, ее можно определить так:

cupmapstocdot,quad capmapsto+,quad varnothingmapsto1,quad Mmapsto0.

Алгебра (2^M,cup,cap,varnothing,M) и алгебра $mathcal{A}_1$ в примере 2.4.а не являются однотипными, так как их сигнатуры состоят из разного числа операций и между ними установить взаимно однозначное соответствие нельзя.

Не являются однотипными и алгебры $(2^M,overline{phantom{A}})$ и (mathbb{N},+) , ибо в первой алгебре единственная операция ее сигнатуры является унарной, а во второй — бинарной.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

то элемент называется
нейтральным относительно данной операции (другое название – единичный
элемент).

Примеры.

1. Число 1 является
нейтральным элементом множества относительно
операции умножения.

2. Матрица 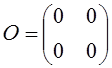— нейтральный элемент множества всех
матриц второго порядка относительно операции сложения матриц.

3. Множество натуральных
чисел не имеет нейтрального элемента относительно операции, задаваемой формулой
, т.к. иначе для некоторого числа и любого выполнялись
бы равенства: и , что
невозможно.

Эти примеры показывают, что может существовать один
нейтральный элемент и что нейтрального элемента может не быть вовсе.
Оказывается, других возможностей нет, т.е. не может быть более одного
нейтрального элемента.

Доказательство:

Пусть и — два нейтральных элемента относительно
операции *. Тогда (т.к —
нейтральный элемент), и (т.к — нейтральный элемент), откуда .

Пусть теперь множество содержит
нейтральный элемент относительно некоторой бинарной
операции *. Элемент называется правым обратным
для элемента , если ,
элемент называется левым обратным для , если . Если
операция ассоциативна, то левый и правый обратные элементы совпадают.

Доказательство:

(2)

(3)

Умножим равенство (2) слева на :

По ассоциативности: ,

из (3) следует: , но , а , значит
.

Таким образом, в случае ассоциативной операции можно
говорить просто об обратном элементе.

Обозначение: . Ясно, что .

Примеры.

1. Рассмотрим операцию умножения на множестве действительных чисел. Нейтральный элемент
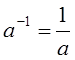
– число 1. Если , то обратный элемент существует. Для числа 0 обратного нет.
Если рассматривать операцию умножения только на множестве положительных действительных чисел, то все
элементы будут иметь обратные.

2. Множество с
операцией сложения. Каждый элемент имеет обратный, равный .

3. Множество квадратных матриц второго порядка с
операцией матричного умножения. Каждая невырожденная матрица обладает обратной,
а для вырожденной матрицы обратной не существует.

Рассмотренные примеры показывают, что некоторые элементы
обладают обратными, но могут существовать и элементы, не имеющие обратных.
Естественно возникает вопрос: может ли какой-нибудь элемент обладать
несколькими обратными? В рассмотренных примерах все элементы имели не более
одного обратного, и это не случайно, т.к справедливо утверждение:

Если операция ассоциативна, то никакой элемент не может
иметь более одного обратного.

Доказательство:

Пусть и — обратные элементы для элемента . Тогда и (совпадение левого и правого обратных уже
доказано).

Теперь получаем:

Подгруппы

Пусть множество является
группой относительно некоторой бинарной операции. Подмножество множества , являющееся группой относительно той же
операции, называется подгруппой группы .

Непосредственно из определения следует, что всякая группа
является своей подгруппой, и что множество, состоящее из одного элемента –
единицы группы, также будет ее подгруппой. У группы могут быть и другие
подгруппы. Подгруппа называется собственной,
если и .

Примеры.

1. Множество положительных рациональных чисел является группой относительно операции
умножения и поэтому подгруппой мультипликативной группы положительных
действительных чисел.

2. Множество целых чисел , будучи
группой относительно сложения, составляет подгруппу аддитивной группы
действительных чисел.

Чтобы установить, что непустое множество группы есть
подгруппа этой группы, достаточно проверить два условия:

1) Для любых двух элементов , их композиция принадлежит
.

2) Для любого элемента обратный
ему элемент также принадлежит .

Докажем это. Условие (1) означает, что операция на множестве
будет операцией и на множестве . Ассоциативность операции на следует из ее ассоциативности на . Из условий (1) и (2) следует, что : взяв какой-либо элемент , по условию (2) найдем в обратный ему элемент , а по условию (1) получим, что содержится в .

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

Источник