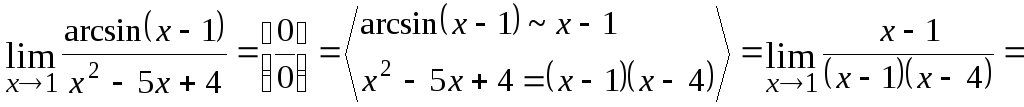Заказать задачи по любым предметам можно здесь от 10 минут
Как решать пределы для чайников?
Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что «скучная теория» должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.
Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.
Примеры решений
| Пример 1 |
| Вычислить а) $ lim_{x to 0} frac{1}{x} $; б)$ lim_{x to infty} frac{1}{x} $ |
| Решение |
|
а) $$ lim limits_{x to 0} frac{1}{x} = infty $$ б)$$ lim_{x to infty} frac{1}{x} = 0 $$ Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ text{a)} lim limits_{x to 0} frac{1}{x} = infty text{ б)}lim limits_{x to infty} frac{1}{x} = 0 $$ |
| Пример 2 |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} $$ |
| Решение |
|
Внимание «чайникам» $$ lim limits_{x to 1} frac{x^2+2 cdot x+1}{x+1}=frac{1^2+2 cdot 1+1}{1+1} = $$ $$ = frac{4}{2}=2 $$ Как видим в итоге у нас вычислился предел, результатом стала двойка. Хорошо, когда так получается, но бывает так, что результатом становятся неопределенности. Попробуем разобраться с ними — это не так страшно как кажется |
| Ответ |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} = 2 $$ |
Что делать с неопределенностью вида: $ bigg [frac{0}{0} bigg ] $
| Пример 3 |
| Решить $ lim limits_{x to -1} frac{x^2-1}{x+1} $ |
| Решение |
|
Как всегда начинаем с подстановки значения $ x $ в выражение, стоящее под знаком предела. $$ lim limits_{x to -1} frac{x^2-1}{x+1} = frac{(-1)^2-1}{-1+1}=frac{0}{0} $$ Что теперь дальше? Что же должно получиться в итоге? Так как это неопределенность, то это ещё не ответ и продолжаем вычисление. Так как в числители у нас многочлен, то разложим его на множители, помощью знакомой всем формулы ещё со школьной скамьи $$ a^2-b^2=(a-b)(a+b) $$. Вспомнили? Отлично! Теперь вперед и с песней применять её Получаем, что числитель $ x^2-1=(x-1)(x+1) $ Продолжаем решать учитывая вышеприведенное преобразование: $$ lim limits_{x to -1}frac{x^2-1}{x+1} = lim limits_{x to -1}frac{(x-1)(x+1)}{x+1} = $$ $$ = lim limits_{x to -1}(x-1)=-1-1=-2 $$ |
| Ответ |
| $$ lim limits_{x to -1} frac{x^2-1}{x+1} = -2 $$ |
| Пример 4 |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = frac{0}{0} = $$ $$ = lim limits_{x to 2}frac{(x-2)(x+2)}{(x-2)^2} = $$ $$ = lim limits_{x to 2}frac{x+2}{x-2} = frac{2+2}{2-2} = frac{4}{0} = infty $$ Бесконечность получилась в результате — это следует из примера 1. Когда число делится на 0 под знаком предела, то получается бесконечность. |
| Ответ |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = infty $$ |
Устремим предел в последних двух примерах к бесконечности и рассмотрим неопределенность: $ bigg [frac{infty}{infty} bigg ] $
| Пример 5 |
| Вычислить $ lim limits_{x to infty} frac{x^2-1}{x+1} $ |
| Решение |
|
$ lim limits_{x to infty} frac{x^2-1}{x+1} = frac{infty}{infty} $ Что же делать? Как быть? Не стоит паниковать, потому что невозможное — возможно. Нужно вынести за скобки и в числителе и в знаменателе икс, а потом его сократить. После этого предел попытаться вычислить. Пробуем… $$ lim limits_{x to infty} frac{x^2-1}{x+1} =lim limits_{x to infty} frac{x^2(1-frac{1}{x^2})}{x(1+frac{1}{x})} = $$ $$ = lim limits_{x to infty} frac{x(1-frac{1}{x^2})}{(1+frac{1}{x})} = $$ Используя определение из примера 2 и подставляя в место х бесконечность получаем: $$ = frac{infty(1-frac{1}{infty})}{(1+frac{1}{infty})} = frac{infty cdot 1}{1+0} = frac{infty}{1} = infty $$ |
| Ответ |
| $$ lim limits_{x to infty} frac{x^2-1}{x+1} = infty $$ |
| Пример 6 |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} $$ Чтобы устранить такую неопределенность нужно вынести за скобки икс в числителе и в знаменателе, далее их сократить. В полученное выражение подставить икс равное бесконечности. Пробуем… $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} = $$ $$ lim limits_{x to infty}frac{x^2(1-frac{4}{x^2})}{x^2(1-frac{4}{x}+frac{4}{x^2})} = $$ $$ lim limits_{x to infty}frac{1-frac{4}{x^2}}{1-frac{4}{x}+frac{4}{x^2}} = frac{1}{1} = 1 $$ |
| Ответ |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = 1 $$ |
Алгоритм вычисления лимитов
Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:
- Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: «ноль делить на ноль» или «бесконечность делить на бесконечность» и переходим к следующим пунктам инструкции.
- Чтобы устранить неопределенность «ноль делить на ноль» нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
- Если неопределенность «бесконечность делить на бесконечность», тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.
В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!
Правило. Для
вычисления предела функции
в точке
или при
надо применить теоремы о пределах и
подставить предельное значение аргумента.
Для всех основных
элементарных функций в любой точке их
области определения имеет место равенство

Примеры
Найти пределы
функций:
2.

3.

4.

5.

При вычислении
пределов функций формальная подстановка
вместо х
предельного значения
часто приводит к неопределенным
выражениям вида:,
,
,
,
,
,
.
Например,


Выражения вида
,
,
,
,
,
,
называютсянеопределенностями.
Вычисление предела
функции в этих случаях называют раскрытием
неопределенности.
Рассмотрим правила
раскрытия таких неопределенностей.
Неопределенность вида
Если
и
при
(
),
то говорят, что их частноепредставляет собой неопределенность
вида.
Правило. Чтобы
раскрыть неопределенность вида
,
заданную отношением двух многочленов,
надо и числитель и знаменатель разделить
на самую высокую входящую в них степеньх.
Например,

Рассмотрим
дробно−рациональную функцию

),
представляющую
собой отношение двух многочленов
относительно х
степеней m
и n
соответственно, и исследуем поведение
этой функции при
.
При нахождении
предела данной функции при
могут иметь место три варианта ответа:
|
1. |
|
|
2. |
|
|
3. |
|
Из этого следует,
что предел отношения двух многочленов
при
во всех случаях равен пределу отношения
их старших членов.
Примеры
Найти пределы
функций:
1.
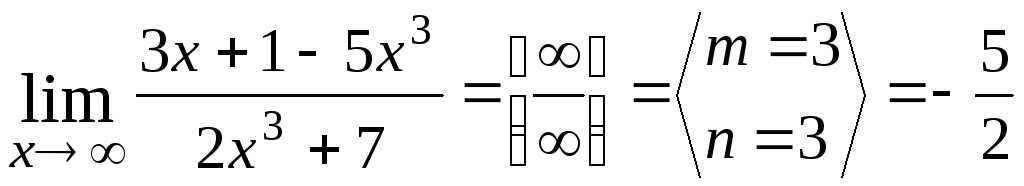
2.

3.

Неопределенность
вида
Если требуется
найти

гдеи
− бесконечно малые функции при
(
),
т.е.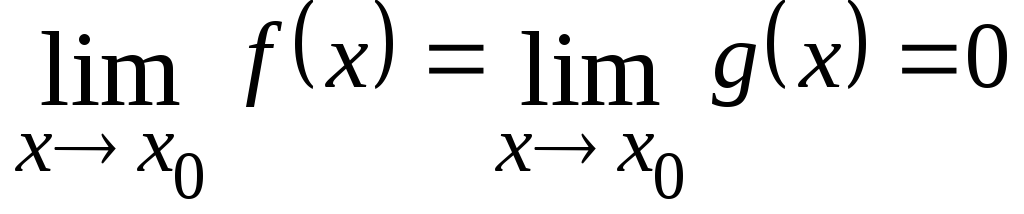
то в этом случае вычисление предела
называют раскрытием неопределенности
вида
.
Рассмотрим возможные
приемы раскрытия такой неопределенности.
Выделение критического множителя
Правило. Чтобы
раскрыть неопределенность вида
,
заданную отношением двух многочленов,
надо и в числителе и в знаменателе
выделить критический множитель и
сократить на него дробь.
Примеры
Найти пределы
функций:
1.

2.

Преобразование иррациональных
выражений
Правило. Чтобы
раскрыть неопределенность вида
,
в которой числитель или знаменатель,
или тот и другой иррациональны, надо:
− перенести
иррациональность из числителя в
знаменатель, или из знаменателя в
числитель, домножив дробь на сопряженные
выражения,
− либо сделать
замену переменной.
Замечание.
Если под знаком
предела делается замена переменной, то
все величины, входящие под знак предела,
должны быть выражены через эту новую
переменную. Из равенства, выражающего
зависимость между старой переменной и
новой, должен быть определен предел
новой переменной.
Примеры
Найти пределы
функций:
1.
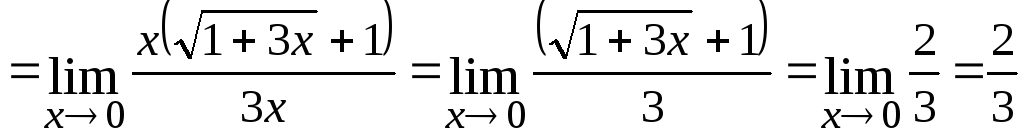
2.

3.

4.
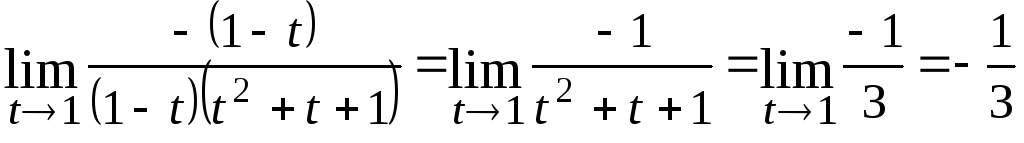
Применение первого замечательного
предела
Правило. Для
раскрытия неопределенности вида
,
содержащей тригонометрические выражения,
используют первый замечательный предел:


где
и
.
Примеры
Найти пределы
функций:
1.
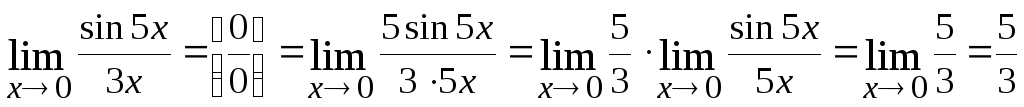
2.

4.

Применение эквивалентных бесконечно
малых величин
Правило. Для
раскрытия неопределенности вида
можно и числитель и знаменатель заменить
величинами им эквивалентными (п.2.12).
Примеры
Найти пределы
функций:
1.

2.

3.

4.
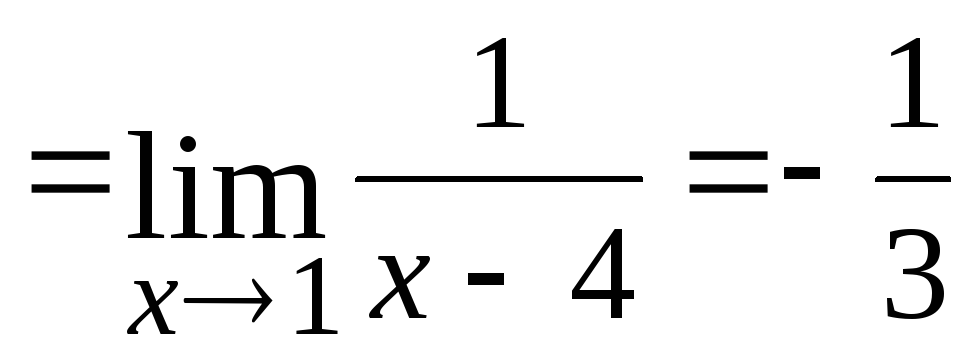
Неопределенности
вида
и
Если
и
при
,
то их разностьпредставляет собой неопределенность
вида
.
Если
и
при
,
то их произведение− это неопределенность вида
.
Правило.
Неопределенности
вида
и
раскрываются путем их преобразования
и сведения к неопределенностям видаили
.
Примеры
Найти пределы
функций:
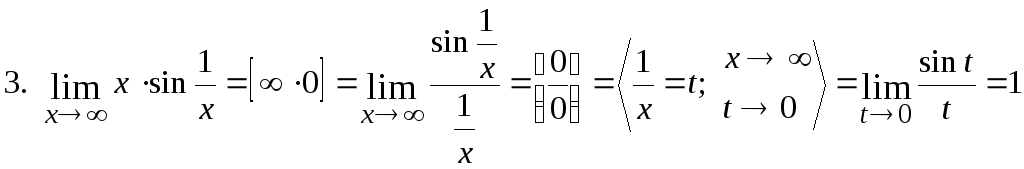
Неопределенности
вида
,
,
Пусть функция
имеет вид:
.
Если при
,
,
а,
то имеем неопределенность вида
.
Для раскрытия этой неопределенности
применяют второй замечательный предел:


или
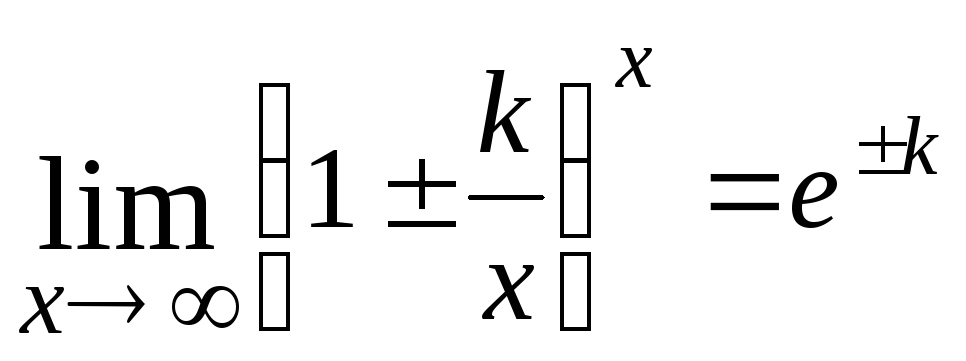
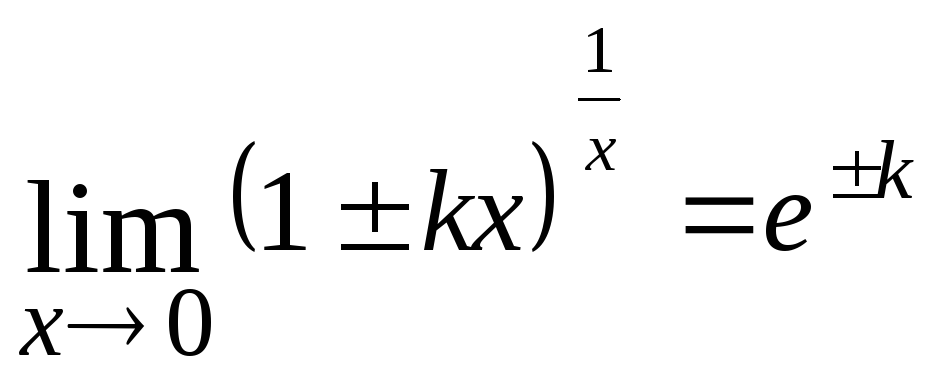
Примеры
Найти пределы
функций:
1.
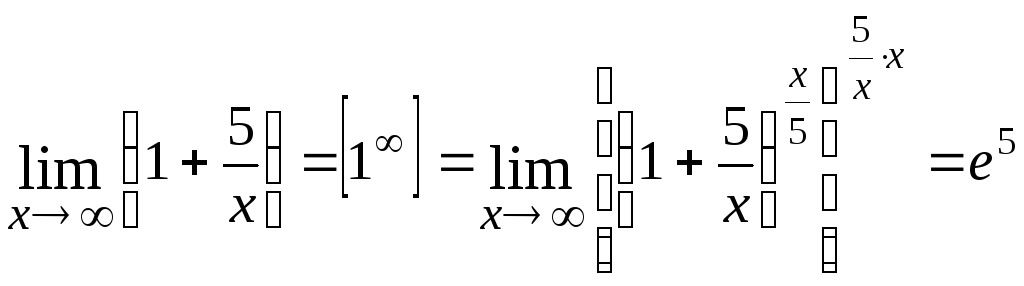
2.

3.
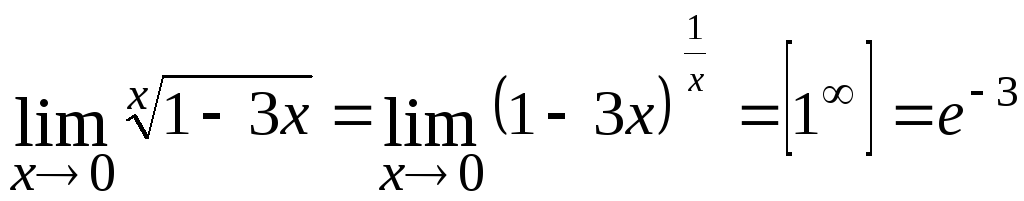
Если при
,
,
а,
то имеем неопределенность вида
.
Если
и
при
,
то имеет место неопределенность
.
Для раскрытия
неопределенностей вида
и
их преобразуют и сводят к неопределенности
видаследующим образом:

Примеры
Найти пределы
функций:
1.

2.

В заключение
отметим, что в дальнейшем будут рассмотрены
более эффективные методы вычисления
пределов функций, основанные на
использовании понятия производной.
Упражнения
Односторонние
пределы. Найти пределы:
1.

;

;
2.

;

0.
Непосредственное
вычисление пределов. Найти пределы:
3.
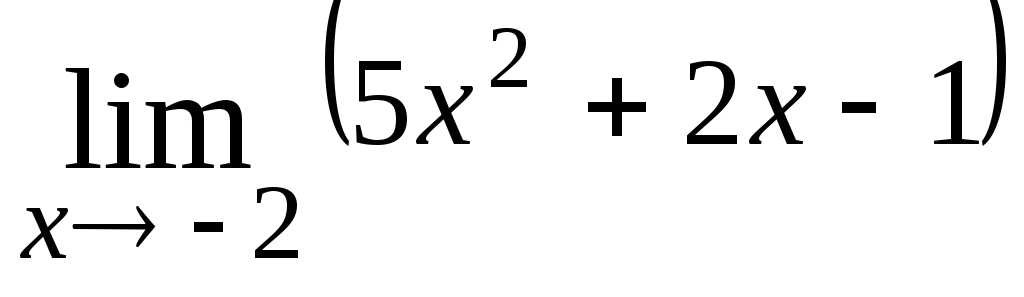
15;
4.

.
5.

0.
Раскрытие
неопределенности
.
Найти пределы:
6.
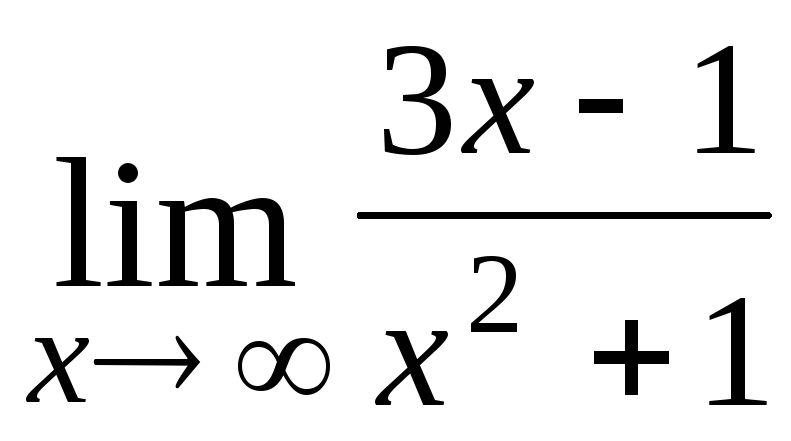
0;
7.
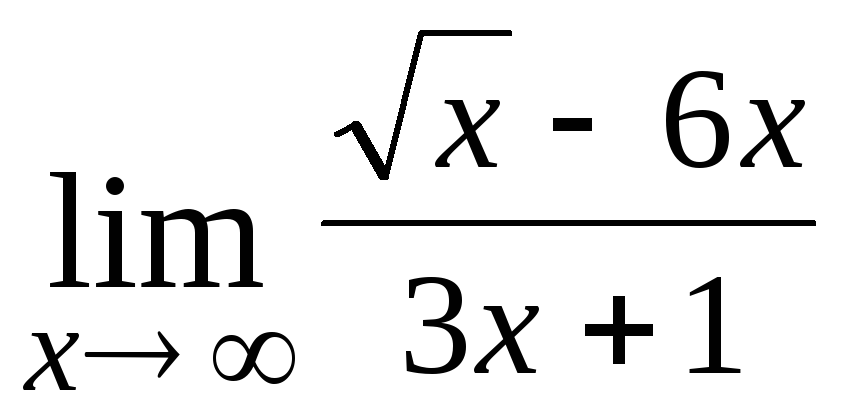
-2;
8.

;
9.

.
Раскрытие
неопределенности
.
Найти пределы:
10.

;
11.

-2;
12.
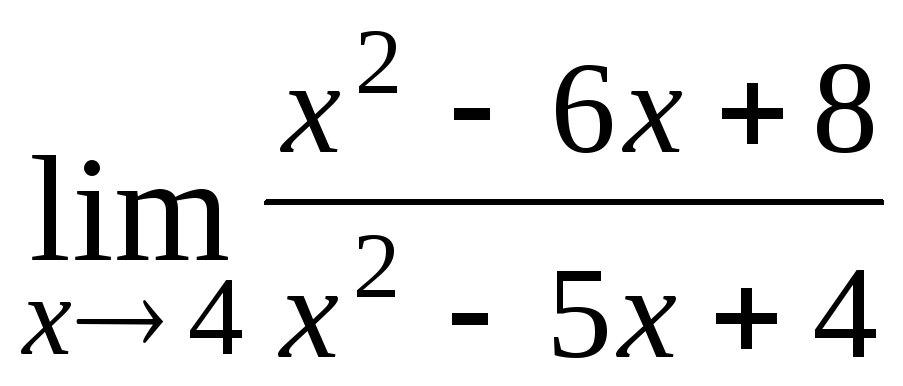
;
13.

;
14.

-12;
15.

.
16.
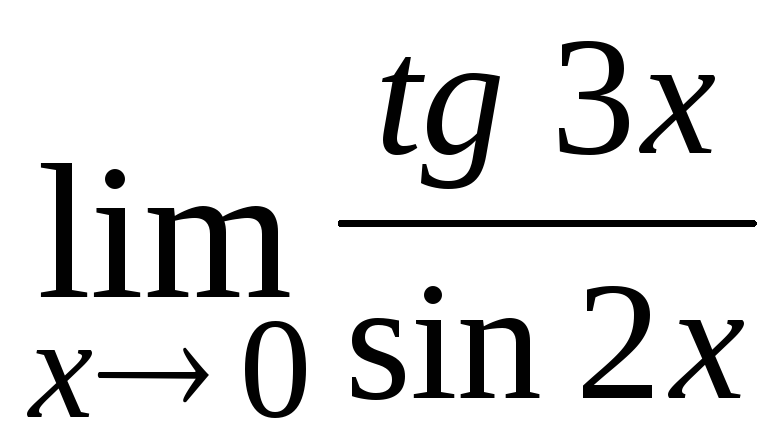
;
17.

;
18.

;
19.

;
20.

.
Раскрытие
неопределенностей
.
Найти пределы:
21.

;
22.

;
23.

0;
24.
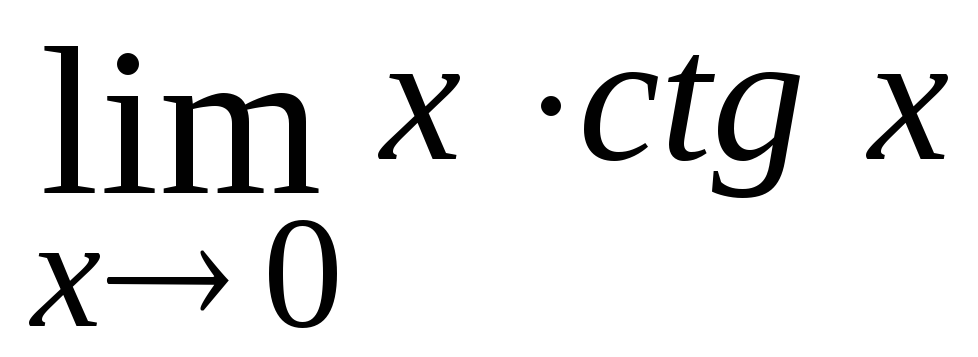
1.
Раскрытие
неопределенности.
Найти пределы:
25.
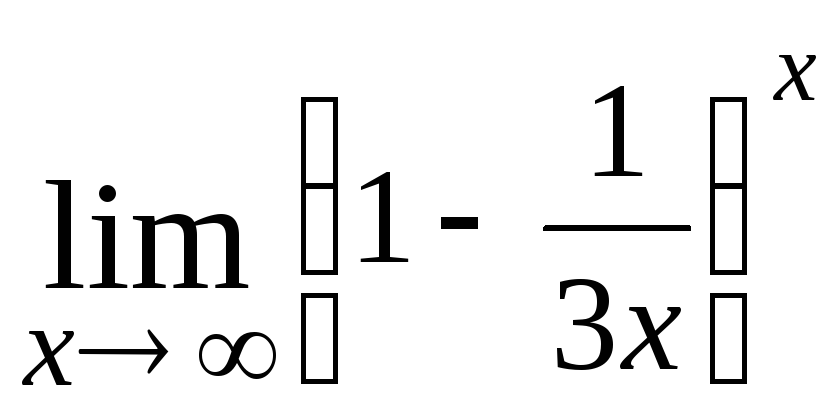
;
26.

;
27.

;
28.

.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Очень часто при вычислении пределов функций в какой-либо точке в результате упрощения получаются выражения, не несущие какой-либо информации об этой функции. Такие выражения носят название неопределённостей.
Виды неопредлённостей
-
$frac{0}{0}$ — деление нуля на нуль;
-
$frac{infty}{infty}$ — деление бесконечности на бесконечность;
-
$0 cdot infty$ — умножение нуля на бесконечность;
-
$1^{infty}$ — единица, возведённая в степень бесконечности;
-
$(infty-infty$) — разность бесконечностей;
-
$0^0$ — нуль в нулевой степени;
-
$infty^0$ — бесконечность в степени 0.
Неопределённости вида $frac{0}{0}$ и $frac{infty}{infty}$ называются основными и для их раскрытия применяется правило Лопиталя, тогда как остальные неопределённости сводятся путём тождественных преобразований также к основным или решаются иными способами.
Раскрытие неопределенностей
Сам по себе термин «неопределённость» не означает, что предела не существует. Во многих случаях для того чтобы прийти к конечному ответу можно использовать упрощения, правило Лопиталя и другие способы раскрытия математических неопределенностей.
Например, выражение вида $frac{x^2}{x}$ можно упростить до просто $x$ при любых значениях $x$, кроме нуля. Таким образом, предел этого выражения при приближении $x$ к нулю есть не что иное как $x$, а сам $x$ стремится к нулю, следовательно:
$lim_{xto 0}frac{x^2}{x}=lim_{xto 0} x=0$.
Наиболее универсальным способом для раскрытия неопределённостей является правило Лопиталя, но к нему не всегда возможно прибегнуть. Как было упомянуто выше, его возможно применять лишь к двум видам неопределённостей, тогда как остальные необходимо для начала привести к одной из форм основных неопределённостей.
В целом, при раскрытии неопредлённостей возможно использовать различные тождественные преобразования, замечательные пределы и замену одного бесконечно малого выражения на другое, подобное ему.
«Неопределенности пределов» 👇
Рассмотрим подробнее замену бесконечно малых выражений на аналогичное.
Таблица эквивалентных бесконечно малых выражений
Если две переменные $α$ и $β$ сходятся к нулю в одной точке и предел их отношения в этой точке равен единице, то эти переменные называются эквивалентными бесконечно малыми переменными.
Таблица эквивалентных бесконечно малых функций:
$x~sin x$;
$x~arcsin x$;
$x ~ tg x$;
$x ~ arctg x$;
$x ~ ln(1+x)$;
$1-cos x ~ frac{x^2}{2}$;
$ a^x-1 ~ x ln a$;
$e^x-1 ~ x$;
$(1+x)^a-1 ~ ax$.
Пример 1
Вычислите предел: $lim_{x to 0}frac{1}{x^3} cdot (frac{2+cosx}{3})^x-1)$.
Решение:
$lim_{x to 0}frac{1}{x^3} cdot (frac{2+cosx}{3})^x-1)=lim_{x to 0}frac{e^{xln frac{2+cosx}{3}}-1}{x^3}= lim_{x to 0}frac{1}{x^2} ln frac{2+cosx}{3}= lim_{x to 0}frac{1}{x^2} ln (frac{cosx-1}{3}+1=lim_{x to 0}frac{cosx-1}{3x^2}=-frac{1}{6}$
Раскрытие неопределённости, содержащей бесконечность в числителе и знаменателе
Для того чтобы раскрыть такую неопределённость, сначала находят в выражении старшую степень при переменной, а затем делят на эту переменную числитель и знаменатель.
Раскрытие неопределённости, содержащей нуль в числителе и знаменателе
При возникновении такого случая сначала производят разложение на множители числителя и знаменателя, а затем осуществляют сокращение дроби.
Правило Лопиталя для раскрытия неопределённостей
Данное правило является главным методом для вычисления неопределённостей вида $frac{0}{0}$ и $frac{infty}{infty}$. Суть метода состоит в том, чтобы вместо предела отношения двух функций находить предел производных двух функций:
$lim_{xto c} frac{f(x)}{g(x)}=lim_{xto c} frac{f’(x)}{g’(x)}$
Использование производных позволяет упростить выражения и найти, к чему стремится данный предел.
С помощью этого правила можно находить не только неопределённости, про которые сказано выше, но также и другие. Ниже приведена таблица, с помощью которой можно непределённости других видов приводить к форме, которую возможно упростить с помощью правила Лопиталя.
Рисунок 1. Преобразования неопределенностей пределов для применения правила Лопиталя
Пример 2
Вычислите предел, используя правило Лопиталя:
$lim_{x to 0} frac{x^2+5x}{3x}$
Решение:
$lim_{x to 0} frac{x^2+5x}{3x}= lim_{x to 0} frac{(x^2+5x)’}{(3x)’}=lim_{x to 0}frac{2x+5}{3}=frac{5}{3}$
Разложение неопределённостей в ряд Тейлора
Для оценки выражений, в результате вычисления которых образовались неопределённости вида $0^0$, $1^{infty}$, и $infty^0$ вычисляют предел натурального логарифма исследуемого выражения, а затем после получения результата от него берут экспоненту:
$0^0=e^{0 cdot (- infty)}$
$1^{infty}= e^{infty cdot ln1}= e^{infty cdot 0}$
$infty^0=e^{0 ln infty}= e^ { 0 cdot infty}$
Выражения, не являющиеся неопределённостями
Выражения вида $frac{1}{0}$ не считаются неопределённостями, также как неопределённости не рассматриваются все случаи, где знаменатель равен нулю, а числитель — любое число, отличное от нуля.
Другое выражение, не являющееся неопределённостью — это $0^{infty}$. Выражение вида $0^{+infty}$ стремится к нулю, тогда как выражение $0^{-infty}$ эквивалентно выражению $frac{1}{0}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim — от английского limit — предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача — найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент: предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

 Чтобы вычислить предел любого типа и вида нужно подставить значение x, указанное под пределом, в функцию, стоящую под знаком предела. Давайте попробуем это сделать:
Чтобы вычислить предел любого типа и вида нужно подставить значение x, указанное под пределом, в функцию, стоящую под знаком предела. Давайте попробуем это сделать:

 ,
, ,
, ,
,