Исследование СЛАУ. Общие сведения
В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.
Общие сведения (определения, условия, методы, виды)
Системы линейных алгебраических уравнений с n неизвестными могут иметь:
- единственное решение;
- бесконечное множество решение (неопределенные СЛАУ);
- ни одного решения (несовместные СЛАУ).
Пример 1
Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.
Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .
Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .
Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:
- Совместна ли система?
- Если система совместна, то, какое количество решений она имеет — одно или несколько?
- Как найти все решения?
Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:
- если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
- если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
- если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.
Ранг матрицы и его свойства
Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.
Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда
В математике выделяют следующие подходы к определению ранга матрицы:
- при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
- при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
- при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.
Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .
Свойства ранга матрицы:
- квадратная невырожденная матрица обладает рангом, который отличается от нуля;
- если транспонировать матрицу, то ранг матрицы не изменяется;
- если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
- при удалении нулевого столбца или строки ранг матрицы не изменяется;
- ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
- при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
- ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
- когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .
Пример 2
А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0
r ( A 1 ) = 1 , r ( B 1 ) = 1
А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6
Системы линейных алгебраических уравнений: основные понятия, виды
Определение СЛАУ
Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
$$left<begin a_ <11>cdot x_<1>+a_ <12>cdot x_<2>+ldots+a_ <1 n>cdot x_=b_ <1>\ a_ <21>cdot x_<1>+a_ <22>cdot x_<2>+ldots+a_ <2 n>cdot x_=b_ <2>\ ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots . . \ a_ cdot x_<1>+a_ cdot x_<2>+ldots+a_ cdot x_=b_ endright.$$
Упорядоченный набор значений $$left^<0>, x_<2>^<0>, ldots, x_^<0>right>$$ называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.
Задание. Проверить, является ли набор $<0,3>$ решением системы $left<begin 3 x-2 y=-6 \ 5 x+y=3 endright.$
Решение. Подставляем в каждое из уравнений системы $x=0$ и $y=3$:
$$5 x+y=3 Rightarrow 5 cdot 0+3=3 Rightarrow 3=3$$
Так как в результате подстановки получили верные равенства, то делаем вывод, что заданный набор является решением указанной СЛАУ.
Ответ. Набор $<0,3>$ является решением системы $left<begin 3 x-2 y=-6 \ 5 x+y=3 endright.$
Виды систем
СЛАУ называется совместной, если она имеет, хотя бы одно решение.
В противном случае система называется несовместной.
Система $left<begin 3 x-2 y=-6 \ 5 x+y=3 endright.$ является совместной, так как она имеет, по крайней мере, одно решение $x=0$, $y=3$
Система $left<begin 5 x+y=-6 \ 5 x+y=3 endright.$ является несовместной, так как выражения, стоящие в левых частях уравнений системы равны, но правые части не равны друг другу. Ни для каких наборов $$ это не выполняется.
Система называется определённой, если она совместна и имеет единственное решение.
В противном случае (т.е. если система совместна и имеет более одного решения) система называется неопределённой.
Система называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.
Система называется квадратной, если количество уравнений равно количеству неизвестных.
Система $left<begin 3 x-2 y=-6 \ 5 x+y=3 endright.$ квадратная, так как неизвестных две и это число равно количеству уравнений системы.
Матричная запись систем уравнений
Исходную СЛАУ можно записать в матричном виде:
Задание. Систему $left<begin x-y+z-4 t=0 \ 5 x+y+t=-11 endright.$ записать в матричной форме и выписать все матрицы, которые ей соответствуют.
Решение. Заданную СЛАУ записываем в матричной форме $A. X=B$ , где матрица системы:
$$A=left(begin 1 & -1 & 1 & -4 \ 5 & 1 & 0 & 1 endright)$$
то есть, запись СЛАУ в матричной форме:
$$left(begin 1 & -1 & 1 & -4 \ 5 & 1 & 0 & 1 endright)left(begin x \ y \ z \ t endright)=left(begin 0 \ -11 endright)$$
Расширенная матрица системы
Задание. Записать матрицу и расширенную матрицу системы $left<begin 2 x_<1>+x_<2>-x_<3>=4 \ x_<1>-x_<2>=5 endright.$
Решение. Матрица системы $A=left(begin 2 & 1 & -1 \ 1 & -1 & 0 endright)$ , тогда расширенная матрица $tilde=(A mid B)=left(begin 2 & 1 & -1 & 4 \ 1 & -1 & 0 & 5 endright)$
Метод Гаусса — определение и вычисление с примерами решения
Содержание:
Базисные и свободные переменные:
Пусть задана система
Элементарными преобразованиями системы линейных уравнений называются следующие преобразования:
- исключение из системы уравнения вида
- умножение обеих частей одного из уравнений системы на любое действительное число
;
- перестановка местами уравнений системы;
- прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число не равное нулю.
Элементарные преобразования преобразуют данную систему уравнений в эквивалентную систему, т.е. в систему, которая имеет те же решения, что и исходная.
Для решения системы т линейных уравнений с т неизвестными удобно применять метод Гаусса, называемый методом последовательного исключения неизвестных, который основан на применении элементарных преобразований системы. Рассмотрим этот метод.
Предположим, что в системе (6.1.1)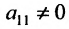
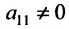
На первом шаге метода Гаусса исключим неизвестное 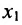
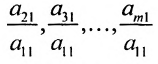
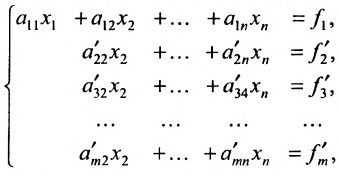
в которой коэффициенты 
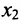
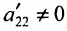
чтобы это условие было выполнено). Для исключения неизвестного 
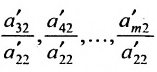
в которой коэффициенты 
Продолжая аналогичные преобразования, систему (6.1.1) можно привести к одному из видов:
Совокупность элементарных преобразований, приводящих систему (6.1.1) к виду (6.1.4) или (6.1.5) называется прямым ходом метода Гаусса.
Отметим, что если на каком-то шаге прямого хода метода Гаусса получим уравнение вида:
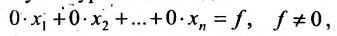
Итак, предположим, что в результате прямого хода метода Гаусса мы получили систему (6.1.4), которая называется системой треугольного вида. Тогда из последнего уравнения находим значение 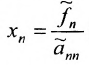
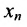
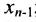
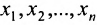
Если же в результате прямого хода метода Гаусса мы получим систему (6.1.5), которая называется системой ступенчатого вида, то из последнего уравнения этой системы находим значение неизвсстного 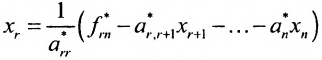
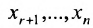
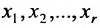
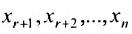
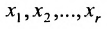
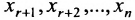
Таким образом, если система (6.1.1) путём элементарных преобразований приводится к треугольному виду (6.1.4), то она имеет единственное решение, если же она приводится к системе ступенчатого вида (6.1.5), то она имеет бесконечное множество решений. При этом неизвестные 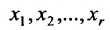
Практически удобнее преобразовывать не саму систему уравнений (6.1.1), а расширенную матрицу системы, соединяя последовательно получающиеся матрицы знаком эквивалентности
Формализовать метод Гаусса можно при помощи следующего алгоритма.
Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
1. Составьте расширенную матрицу коэффициентов системы уравнений так, чтобы 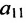
2. Выполните первый шаг метода Гаусса: в первом столбце начиная со второй строки, запишите нули, а все другие элементы вычислите по формуле
Матрица после первого шага примет вид
3. Выполните второй шаг метода Гаусса, предполагая, что 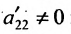
После второго шага матрица примет вид
4. Продолжая аналогичные преобразования, придёте к одному из двух случаев:
а) либо в ходе преобразований получим уравнение вида
тогда данная система несовместна;
б) либо придём к матрице вида:
где 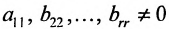
связано с тем, что в процессе преобразований матрицы исключаются строки, состоящие из нулей.
5. Использовав конечную матрицу, составьте систему, при этом возможны два случая:
Система имеет единственное,решение 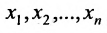
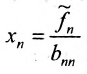
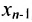
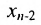
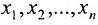
5.2. 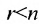
Тогда r неизвестных будут базисными, а остальные (n-r) — свободными. Из последнего уравнения выражаете неизвестное 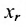
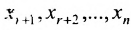
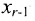
Система имеет в этом случае бесконечное множество решений.
Приведенный алгоритм можно несколько видоизменить и получить алгоритм полного исключения, состоящий в выполнении следующих шагов. На первом шаге:
- составляется расширенная матрица;
- выбирается разрешающий элемент расширенной матрицы
(если
, строки матрицы можно переставить так, чтобы выполнялось условие
);
- элементы разрешающей строки (строки, содержащей разрешающий элемент) оставляем без изменения; элементы разрешающего столбца (столбца, содержащего разрешающий элемент), кроме разрешающего элемента, заменяем нулями;
- все другие элементы вычисляем по правилу прямоугольника: преобразуемый элемент равен разности произведений элементов главной диагонали (главную диагональ образует разрешающий элемент и преобразуемый) и побочной диагонали (побочную диагональ образуют элементы, стоящие в разрешающей строке и разрешающем столбце):
— разрешающий элемент (см. схему).
Последующие шаги выполняем по правилам:
1) выбирается разрешающий элемент 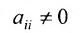
2) элементы разрешающей строки оставляем без изменения;
3) все элементы разрешающего столбца, кроме разрешающего элемента, заменяем нулями; • •
4) все другие элементы матрицы пересчитываем по правилу прямоугольника.
На последнем шаге делим элементы строк на диагональные элементы матрицы, записанные слева от вертикальной черты, и получаем решение системы.
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Из последней матрицы находим следующее решение системы
уравнении:
Ответ:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Система привелась к ступенчатому виду (трапециевидной форме):
в которой неизвестные 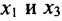
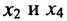
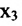
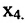
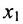
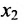
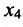
в котором 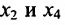
Если в общем решении положить 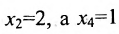
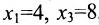
Ответ: система имеет бесконечное множество решений, общее решение которой записывается в виде:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом 
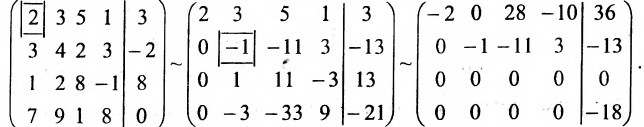
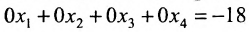
Ответ: система несовместна.
Замечание 1. Если дана система уравнений (6.1.1), в которой число уравнений m равно числу неизвестных n (m=n) и определитель этой системы 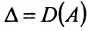
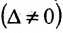
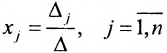
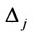
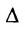
Если же такую систему (m-n) записать в матричной форме AX=F, то её решение можно найти по формуле 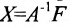
Замечание 2. Используя метод Гаусса, тем самым и алгоритм полного исключения, можно находить обратную матрицу. Для этого составляется расширенная матрица, в которой слева от вертикальной черты записана матрица А, а справа — единичная матрица. Реализовав алгоритм полного исключения, справа от вертикальной черты получаем обратную матрицу, а слева — единичную.
Пример:
Найти обратную матрицу для матрицы:
Решение:
то обратная матрица 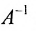
Покажем, что
ответ
Исследование совместности и определённости системы. Теорема Кронекера-Капелли
Рассмотрим систему (6.1.1) m линейных уравнений с n неизвестными при любых m и n (случай m=n не исключается). Вопрос о совместности системы решается следующим критерием.
Теорема 6.2.1. (критерий Кронкера-Капелли). Для того, чтобы система линейных уравнений(6.1.1) была совместна, необходимо и достаточно, чтобы ранг матрицы А системы был равен рангу расширенной матрицы 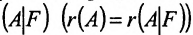
Доказательство и Необходимость:
Предположим, что система (6.1.1) совместна и 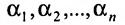
Из этих равенств следует, что последний столбец матрицы 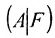
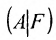
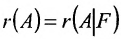
Достаточность. Пусть 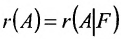
столбцов матрицы А, которые одновременно будут базисными столбцами и матрицы 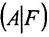
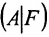
где 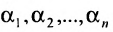
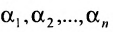
эта система совместна.
Совместная система линейных уравнений (6.1.1) может быть либо определенной, либо неопределенной.
Следующая теорема даст критерий определенности.
Теорема 6.2.2. Совместная система линейных уравнений имеет единственное решение тогда и только тогда, когда ранг матрицы А системы равен числу п ее неизвестных.
Таким образом, если число уравнений m системы (6.1.1) меньше числа ее неизвестных n и система совместна, то ранг матрицы системы 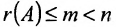
В случае 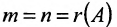
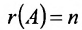
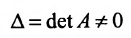
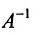
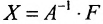
Следует отметить, что, решая систему (6.1.1) методом Гаусса, мы определяем и совместность, и определённость системы.
Пример:
Исследовать на совместность и определённость следующую систему линейных уравнений:
Решение:
Составим расширенную матрицу заданной системы. Определяя её ранг, находим тем самым и ранг матрицы системы. Для нахождения ранга матрицы применим алгоритм метода Гаусса.
Из последней матрицы следует, что ранг расширенной матрицы 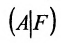
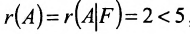
Однородные системы линейных уравнений
Система линейных уравнений (6.1.1) называется однородной, если все свободные члены 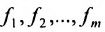
Эта система всегда совместна, так как очевидно, что она имеет нулевое решение
Для однородной системы важно установить, имеет ли она ненулевые решения. Этот факт устанавливается следующей теоремой.
Теорема 6.3.1. Для того, чтобы однородная система имела ненулевые решения, необходимо и достаточно, чтобы ранг г матрицы А системы был меньше числа неизвестных n (r
Доказательство. Необходимость. Пусть система (6.3.1) имеет ненулевое решение. Тогда она неопределённая, т.к. имеет еще и нулевое решение. В силу теоремы 6.2.2 ранг матрицы неопределённой системы не может равняться n потому что при r(А)=n система определённая. Следовательно, 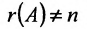
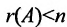
Достаточность. Если 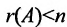
Следствие 1. Если число неизвестных в однородной системе больше числа уравнений, то однородная система имеет ненулевые решения.
Доказательство. Действительно, ранг матрицы системы (6.3.1) не может превышать m. Но так как по условию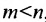
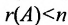
Следствие 2. Для того, чтобы однородная система с квадрат-ной матрицей имела ненулевые решения, необходимо и достаточно, чтобы её определитель 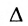
Доказательство. Рассмотрим однородную систему с квадратной матрицей:
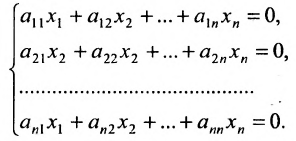
Если определитель матрицы системы 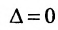
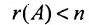
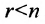
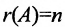
Пример:
Решить систему однородных линейных уравнений:
Решение:
Составим матицу системы и применим алгоритм полного исключения:
Из последней матрицы следует, что 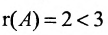
Используя последнюю матрицу, последовательно находим общее решение:
Неизвестные 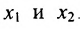
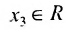
Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
Рассмотрим систему однородных линейных уравнений
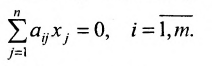
системы m линейных однородных уравнений с n неизвестными можно рассматривать как вектор-строку 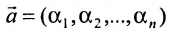
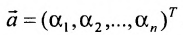
1) сумма двух решений также является решением системы, т.е.
если 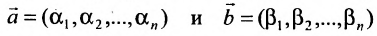
(6.4.1), то и 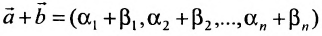
2) произведение решений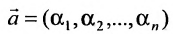
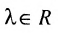
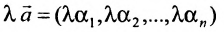
Из приведенных свойств следует, что
3) линейная комбинация решений системы (6.4.1) является решением этой системы.
В частности, если однородная система (6.4.1) имеет хотя бы одно ненулевое решение, то из него умножением на произвольные числа, можно получить бесконечное множество решений.
Определение 6.4.1. Фундаментальной системой решений для системы однородных линейных уравнений (6.4.1) называется линейно независимая система решений, через которую линейно выражается любое решение системы (6.4.1).
Заметим, что если ранг матрицы системы (6.4.1) равен числу неизвестных n (r(А)=n), то эта система не имеет фундаментальной системы решений, так как единственным решением будет нулевое решение, составляющее линейно зависимую систему. Существование и число фундаментальных решений определяется следующей теоремой.
Теорема 6.4.1. Если ранг матрицы однородной системы уравнений (6.4.1) меньше числа неизвестных (r(А)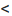
Сформулируем алгоритм построения фундаментальной системы решений:
- Выбираем любой определитель
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
- Свободным неизвестным придаём поочерёдно значения, равные элементам первой, второй и т.д. строк определителя
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
- Из полученных n-r решений составляют фундаментальную систему решений.
Меняя произвольно определитель 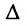
Пример:
Найти общее решение и фундаментальную систему решений для однородной системы уравнений:
Решение:
Составим матрицу системы и применим алгоритм полного исключения.
Для последней матрицы составляем систему:
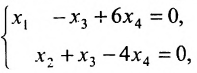
, из которой находим общее решение:
в котором 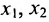
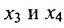
Построим фундаментальную систему решений. Для этого выбираем определитель 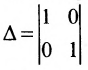
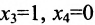
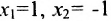
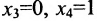
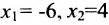
Таким образом, построенные два решения (1; -1; 1; 0) и (-6; 4; 0; 1) составляют фундаментальную систему решений.
Если ранг матрицы системы однородных линейных уравнений (6.4.1) на единицу меньше числа неизвестных: 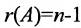
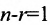
Рассмотрим теперь неоднородную систему m линейных уравнений с n неизвестными (6.1.1). Если в системе (6.1.1) положить 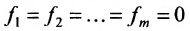
Решения системы (6.1.1) и её приведенной системы удовлетворяют свойствам:
- Сумма и разность любого решения системы (6.1.1) и любого решения её приведенной системы является решением неоднородной системы.
- Все решения неоднородной системы можно получить, прибавляя к одному (любому) её решению поочерёдно все решения её приведенной системы.
Из этих свойств следует теорема.
Теорема 6.4.2. Общее решение неоднородной системы (6.1.1.) определяется суммой любого частного решения этой системы и общего решения её приведенной системы.
Пример:
Найти общее решение системы:
Решение:
Составим расширенную матрицу (A|F) заданной системы и применим алгоритм полного исключения:
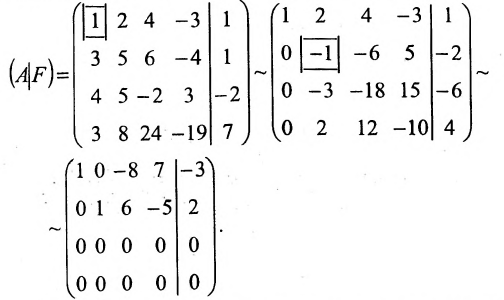
Преобразованной матрице соответствует система уравнений:
из которой находим общее решение системы:
, где 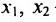
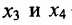
Покажем, что это общее решение определяется суммой любого частного решения заданной системы и общего решения приведенной системы.
Подставляя вместо свободных неизвестных 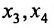
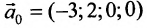
Очевидно, что общее решение приведенной системы имеет вид:
Суммируя частное решение заданной системы и общее решение приведенной системы, получим общее решение (6.4.2) исходной системы.
Отметим, что общее решение системы (6.1.1) можно представить в векторном виде:
где 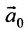
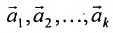
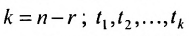
Формула (6.4.4) называется общим решением системы (6.1.1) в векторной форме.
Запишем общее решение системы примера 6.4.1 в векторной форме. Для этого определим фундаментальную систему решений приведенной системы. Возьмём определитель 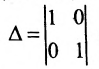
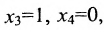
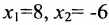
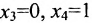
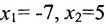
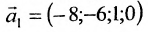
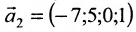
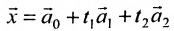
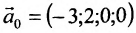
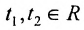
Определение метода Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример:
Решить систему уравнений методом Гаусса:
Решение:
Выпишем расширенную матрицу данной системы 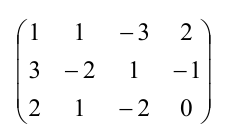
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
б) третью строку умножим на (-5) и прибавим к ней вторую:
В результате всех этих преобразований данная система приводится к треугольному виду:
Из последнего уравнения находим 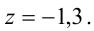
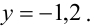
Вычисление метода Гаусса
Этот метод основан на следующей теореме.
Теорема:
Элементарные преобразования не изменяют ранга матрицы.
К элементарным преобразованиям матрицы относят:
- перестановку двух параллельных рядов;
- умножение какого-нибудь ряда на число, отличное от нуля;
- прибавление к какому-либо ряду матрицы другого, параллельного ему ряда, умноженного на произвольное число.
Путем элементарных преобразований исходную матрицу можно привести к трапециевидной форме
где все диагональные элементы 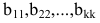
Пример:
Найти ранг матрицы
1) методом окаймляющих миноров;
2 ) методом Гаусса.
Указать один из базисных миноров.
Решение:
1. Найдем ранг матрицы методом окаймляющих миноров. Выберем минор второго порядка, отличный от нуля. Например,
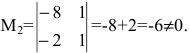
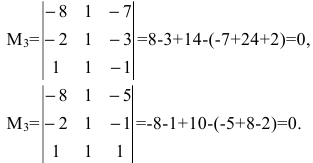
2. Найдем ранг матрицы методом Гаусса. Производя последовательно элементарные преобразования, получим:
- переставили первую и третью строки;
- первую строку умножили на 2 и прибавили ко второй, первую строку умножили на 8 и прибавили к третьей;
- вторую строку умножили на -3 и прибавили к третьей.
Последняя матрица имеет трапециевидную форму и ее ранг равен двум. Следовательно, ранг исходной матрицы также равен двум.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
- Ранг матрицы — определение и вычисление
- Определители второго и третьего порядков и их свойства
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://www.webmath.ru/poleznoe/formules_5_1.php
http://www.evkova.org/metod-gaussa
From Wikipedia, the free encyclopedia
In mathematics, particularly in algebra, an indeterminate system is a system of simultaneous equations (e.g., linear equations) which has more than one solution (sometimes infinitely many solutions).[1] In the case of a linear system, the system may be said to be underspecified, in which case the presence of more than one solution would imply an infinite number of solutions (since the system would be describable in terms of at least one free variable[2]), but that property does not extend to nonlinear systems (e.g., the system with the equation 
An indeterminate system by definition is consistent, in the sense of having at least one solution.[3] For a system of linear equations, the number of equations in an indeterminate system could be the same as the number of unknowns, less than the number of unknowns (an underdetermined system), or greater than the number of unknowns (an overdetermined system). Conversely, any of those three cases may or may not be indeterminate.
Examples[edit]
The following examples of indeterminate systems of equations have respectively, fewer equations than, as many equations as, and more equations than unknowns:
Conditions giving rise to indeterminacy[edit]
In linear systems, indeterminacy occurs if and only if the number of independent equations (the rank of the augmented matrix of the system) is less than the number of unknowns and is the same as the rank of the coefficient matrix. For if there are at least as many independent equations as unknowns, that will eliminate any stretches of overlap of the equations’ surfaces in the geometric space of the unknowns (aside from possibly a single point), which in turn excludes the possibility of having more than one solution. On the other hand, if the rank of the augmented matrix exceeds (necessarily by one, if at all) the rank of the coefficient matrix, then the equations will jointly contradict each other, which excludes the possibility of having any solution.
Finding the solution set of an indeterminate linear system[edit]
Let the system of equations be written in matrix form as
where 






where 



See also[edit]
- Indeterminate equation
- Indeterminate form
- Indeterminate (variable)
- Linear algebra
- Simultaneous equations
- Independent equation
- Identifiability
References[edit]
- ^ «Indeterminate and Inconsistent Systems: Systems of Equations». TheProblemSite.com. Retrieved 2019-12-02.
- ^ Gustafson, Grant B. (2008). «Three Possibilities (of a Linear System)» (PDF). math.utah.edu. Retrieved 2019-12-02.
{{cite web}}: CS1 maint: url-status (link) - ^ «Consistent and Inconsistent Systems of Equations | Wyzant Resources». www.wyzant.com. Retrieved 2019-12-02.
- ^ James, M., «The generalised inverse», Mathematical Gazette 62, June 1978, 109–114.
Further reading[edit]
- Lay, David (2003). Linear Algebra and Its Applications. Addison-Wesley. ISBN 0-201-70970-8.
Оценка сложных систем в условиях неопределенности
Неопределенность возникает в том случае, когда ситуация имеет несколько исходов и вероятность каждого исхода неизвестна. Если можно оценить вероятность каждого исхода, то говорят об условиях риска. Некоторые исследователи рассматривают риск и неопределенность – как равные категории. Однако при логическом анализе становится понятно, что эти понятия взаимосвязаны, легко переходят одна в другую, но существенно различаются друг от друга. В ситуации риска человек может не знать что точно произойдет, но имеет представление о вероятности будущих событий, в отличии от ситуаций неопределенности, когда нет достаточной информации о будущих событиях. Поэтому, прежде чем оценить ситуацию, необходимо продумать возможные варианты развития событий, провести анализ множества предположений и гипотез. Конкретный выбор варианта решения может привести к нескольким исходам с неизвестной вероятностью. Невозможность определения вероятности при таких случаях могут быть обусловлены двумя причинами:
— вероятности не могут быть рассчитаны в силу отсутствия необходимой статистической информации;
— ситуация не статистическая и об объективных вероятностях говорить вообще не имеет смысла. В этом случае говорят о ситуации «чистой неопределённости». Такая «чистая неопределённость» наиболее часто встречается в экономике.
Природа неопределенности – во всеобщей стохастичности и случайности событий. Неопределенность — это объективно существующая реальность пронизывающая все уровни организации материи и, в этом смысле, фатально неистребима. В то же время надо осознавать, что неопределенность является силой порождающей новое, следовательно, является реальным компонентом развития.
Неопределенность может рассматриваться в двух вариантах – как явление и как процесс. Этот взгляд хорошо обоснован в работах В.Ф.Капустина: «Как явление, неопределенность – это набор нечетких или размытых ситуаций, взаимоисключающей или недостаточной информации. К явлению относятся и форс-мажорные события, которые могут возникнуть помимо воли и сознания конкретного работника и изменить намеченный ход событий. Как процесс, неопределенность – это деятельность некомпетентного работника, принимающего ошибочные решения и т.д.»
Неопределенность как явление проявляется в различных сферах бытия и может обнаруживаться на уровне индивидуумов — неожиданными столкновениями сил, интересов, стремлений, на уровне социума — изменениями хода исторических событий, бессистемностью движения масс, на уровне биосферы — проявлением непреднамеренных действий и побочных продуктов деятельности человека.
Виды неопределенностей
Так как природа неопределенности весьма разнообразна, правомерно говорить о разных подходах к систематизации различных видов неопределенности в зависимости от критериев положенных в основу систематизации. Рассмотрим наиболее устоявшиеся классификации видов неопределенности.
Рекомендуемые материалы
1. Одна из наиболее распространенных классификаций видов неопределенности охватывает максимально возможную для логических умозаключений человека область. Эта классификация основывается на факторах порождаемых деятельностью человека и имеет четыре вида:
а) неопределенность целей — связана с неоднозначностью, а иногда и невозможностью выбора одной цели при принятии оптимального решения. Подразделяется на критериальные, ресурсные, модельные и экспертные неопределенности;
б) неопределенность природы – т.е. неопределенность наших знаний об окружающем мире и факторах действующих в данном явлении. В зависимости от возможности исследования и анализа подразделяется на статистические, интервальные и произвольные неопределенности;
в) неопределенности взаимодействия – определяются характером взаимодействий людей и могут быть структурированы в зависимости от психологических особенностей этих взаимодействий на неопределенности конфликтов, противодействия и кооперации (сотрудничества);
г) экспертные неопределенности — основываются на субъективных представлениях и суждениях экспертов.
2. В зависимости от возможности наступления ситуации неопределенности различают первичную и производную неопределенности.
а) Первичная неопределенность определяется природой событий и их возможных результатов. Одни события обуславливают, определяют одни результаты, другие — совершенно другие результаты. Соответственно, неопределенности связанные с одним и другим событием будут различны.
б) Произвольная неопределенность некоторого события обусловлена случайностью осуществления события из многообразия возможных.
3. В зависимости от направленности вектора времени можно также говорить о ретроспективной и перспективной неопределенности.
а) неопределенность прошлого (ретроспективная), порождающей причины настоящего и будущего;
б) перспективная неопределенность связанной с неоднозначностью взаимодействия причины и следствия, с тем, что последующее состояние системы не является единственным, а связано с необходимостью выбора из некоторого множества возможных состояний.
4. Полагая, что каждый исход имеет известную вероятность наступления и в зависимости от степени вероятности возможности наступления тех или других событий, потенциальная неопределенность может быть статистической и прогнозной.
а) Статистическая неопределенность задается характером действий системы и имеет достаточно высокую потенциальную возможность ее возникновения.
б) Прогнозная неопределенность возникает тогда, тогда невозможно оценить вероятность потенциальных результатов.
5. В отношении социально-экономических систем целесообразно рассматривать следующие виды неопределенности:
а) Неопределенности макросреды
— неопределенности, связанные с недостаточными знаниями о природе;
— неопределенности природных явлений;
— неопределенности, связанные с осуществлением действующих (неожиданные аварии) и проектируемых (возможные ошибки разработчиков или физическая невозможность осуществления процесса, которую заранее не удалось предсказать) технологических процессов;
— неопределенности, связанные с колебаниями цен, ставки процента, валютных курсов и других макроэкономических показателей;
— неопределенности, порожденные нестабильностью законодательства и текущей экономической политики, с политикой, экологическими проблемами в масштабе страны;
— внешнеэкономические неопределенности, связанные с ситуацией в зарубежных странах и международных организациях.
б) Неопределенности микросреды (неопределенности, связанные с ближайшим окружением сложной системы):
— неопределенности, связанные с деятельностью участников экономической жизни, с их деловой активностью, финансовым положением, соблюдением обязательств;
— неопределенность будущей рыночной ситуации, в том числе отсутствие достоверной информации о будущих действиях поставщиков в связи с меняющимися предпочтениями потребителей;
— неопределенности, связанные с социальными и административными факторами в конкретных регионах, в которых наша фирма имеет деловые интересы.
6. В зависимости от области исследования, понятие неопределенности приобретает специфические характеристики и виды. Так, например, в исследованиях социальной природы действий человека неопределенность может быть представлена двумя видами – имманентной и гетерономной.
а) Имманентная неопределенность порождается внутренней природой человека (Имманентный — филос. Внутренне присущий какому-нибудь предмету, явлению, проистекающий из его природы) и имеет место, когда горизонт предпочтений меняется, но типологическая узнаваемость событий и процессов сохраняется. Например, человек, избравший ту или иную профессию, может достичь в рамках своей профессии мастерства и высших ступеней, а может остаться на первоначально квалификационном уровне. Выбор вариантов и, соответственно, рождаемых этими вариантами неопределенностей, определяется характером самого человека.
б) Гетерономная неопределенность, в противоположность имманентной, приобретает принципиально другое качество. Выбор вариантов не во власти действий человека – обстоятельства определяют события и связанные с ними неопределенности. Примером могут служить исторические повороты судеб известных людей, которые при стечении обстоятельств менялись кардинальным образом и не могли быть прогнозируемыми.
Каждый из перечисленных видов неопределенности может быть детализирован более глубоко. Так, неопределенности связанные с авариями могут быть декомпозированы на ситуации при технологических авариях, в частности, на химических производствах и на атомных электростанциях и т.д.
Следует учитывать, что данная классификация видов неполная. В силу динамичного процесса познания и исследования природы неопределенностей стоит ожидать и новых интерпретаций, и новых классификаций.
Методы оценки сложных систем и принятия решений в условиях неопределенности
В практике деятельности сложных систем, неопределенности более всего встречаются в политической, социокультурной и научной средах. В социально-экономических сферах, например, в деятельности коммерческого предприятия, условия неопределенности часто нивелируются на административном уровне. Как правило, всегда есть возможность получить дополнительную информацию, проанализировать ситуацию еще раз, и уже на основе суждений, интуиции, накопленного опыта ЛПР (Лица принимающего решения) принять решения уменьшающие действия факторов неопределенности или переводя проблему в разряд определенных ситуаций.
Любая сложная система характеризуется множеством факторов неопределенности: неопределенность внешней среды, неопределенность, связанная с характером, вариантами и моделью развития, неопределенностью характеристик элементов составляющих данную систему их взаимоотношений и т.д. Факторы неопределенности социально-экономических систем определяют опасность потери ресурсов, упущения выгоды, появления дополнительных расходов. Следовательно, при проведении прогнозов развития таких систем необходимо учитывать факторы неопределенности, обуславливающие риск по различным показателям эффективности. В связи с этим, мы неминуемо сталкиваемся с проблемой исследования, оценки неопределенных составляющих и перевода их в формализованные показатели. Этот процесс может быть проведен на основе применения математических методов, позволяющих анализировать различные виды неопределенности.
Для оценки сложных систем в условиях неопределенности используются самые различные методы качественного и количественного анализа. К наиболее известным методам оценки в мировой практике следует мировой практике отнести такие методы как:
- метод сценариев;
- методы теории игр;
- метод Дерева решений;
- имитационное моделирование по методу Монте-Карло;
Методы сценариев. Основные характеристики этой группы методов были рассмотрены в лекциях раньше. Здесь уделим внимание только одному из вариантов этой группы – методу гарантированного прогноза. В его основе — определение верхнего, положительно влияющего на развитие исследуемой системы предела параметров и нижнего, препятствующего положительным изменениям предела показателей объекта. Полученный коридор сценариев и подвергается анализу. Исследование можно разделить на два этапа:
• предсценарный – работа с фактическими данными, формализация параметров, описание процессов, подготовка всей необходимой информации.
• сценарный этап – проведение расчетов по основным сценариям и составление подробного описаниия предлагаемых вариантов, а так же рекомендации для наиболее эффективного внедрения того или другого прогноза.
Стоит отметить, что недостатки этой группы методов — множество вариантов сценариев развития — субъективны и не дают достоверной вероятности и, следовательно, сложные системы не могут быть достоверно оценены.
Методы теории игр. В настоящее время нет универсального критерия по выбору решения для задач неопределенных статически. Разработаны лишь общие требования к критериям и процедурам оценки и выбора оптимальных систем.
Обычно задачи записываются в матрице вида:
|
а n |
n1 |
… |
n k |
K (aj) |
|
a1 . . a m |
k 11 |
… |
K mk |
a = (а1…аm) – вектор управляемых параметров, определяющий свойства систем
n = (n1…nk) – вектор неуправляемых параметров, определяющий состояние обстановки.
Кij – значение эффективности системы аi для состояния обстановки nj
Наиболее часто в неопределенной ситуации используются критерии:
- Среднего выигрыша
- Достаточного основания (критерий Лапласа)
- Осторожного наблюдателя (критерий Вальда)
- Пессимизма-оптимизма (критерий Гурвица)
- Минимального риска (критерий Севиджа)
Рассмотрим некоторые из них:
Критерий MAXIMAX – дает общую потенциальную характеристику развития системы, но не учитывает риска, связанного с неблагоприятным развитием внешней среды.
Критерий MAXIMIN (критерий Вальда) – позволяет минимизировать риски, но в то же время занижает эффективность, поэтому могут быть вычеркнуты высокоэффективные меры. Использование данного критерия целесообразно при условии необходимости достижения гарантированного результата.
Критерий MINIMAX (критерий Сэвиджа), в отличие от критерия MAXIMIN, минимизирует показатели высокой прибыли, таким образом, допускает получение дополнительной прибыли при разумном риске. В ситуации неопределенности этот критерий следует использовать в том случае, когда есть уверенность в том, что случайный убыток не приведет фирму к полному краху.
Критерий пессимизма-оптимизма Гурвица устанавливает два сценария развития событий, при которых возможно достижение минимальной и максимальной эффективности.
Рассмотренных критерии метода теории игр имеют один существенный общий недостаток – все они дают ограничения по выбору вариантов принятия решений по тому или иному показателю.
Пример. Необходимо оценить один из трех программных продуктов аi для борьбы с одним из четырех программных воздействий kj. Матрица эффективности выглядит следующим образом:
|
ак |
к1 |
к2 |
к3 |
к4 |
|
а1 |
0,1 |
0,5 |
0,1 |
0,2 |
|
а2 |
0,2 |
0,3 |
0,2 |
0,4 |
|
а3 |
0,1 |
0,4 |
0,4 |
0,3 |
- Критерий среднего выигрыша
Предполагает задание вероятностей состояния обстановки Рi. Эффективность систем оценивается как среднее ожидание (мат. ожидание) оценок эффективности по всем состояниям обстановки. Оптимальной системе будет соответствовать максимальная оценка.
К = ∑ РiКij
Предположим, что вероятность применения противником программных воздействий Р1 = 0,4; Р2=0,2; Р3=0,1; Р4=0,3
К(а1)=0,4*0,1+0,2*0,5+0,1*0,1+0,3*0,2=0,21
К(а2)=0,4*0,2+0,2*0,3+0,1*0,2+0,3*0,4=0,28
К(а3)=0,4*0,1+0,2*0,4+0,1*0,4+0,3*0,3=0,25
Оптимальное решение по данному критерию — программный продукт а2.
- Критерий Лапласа (достаточного основания)
Предполагается, что состояние обстановки равновероятно, так как нет достаточных оснований предполагать иное.
К=1/к∑Кij,
для каждого i, а оптимальное значение указывает максимальную сумму К.
Р1=0,25; Р2=0,25; Р3=0,25; Р4=0,25
К(а1)=0,25*(0,1+0,5+0,1+0,2)=0,225
К(а2)=0,25*(0,2+0,3+0,2+0,4)=0,275
К(а3)=0,25*(0,1+0,4+0,4+0,3)=0,3
Оптимальное решение — программа а3
Замечание – критерий Лапласа – это частный случай критерия среднего выигрыша.
- Критерий осторожного наблюдателя (критерий Вальда)
Это максимальный критерий (максимальные доходы, минимальные потери). Он гарантирует определенный выигрыш при худших условиях. Критерий использует то, что при неизвестной обстановке нужно поступать самым осторожным образом, ориентируясь на минимальное значение эффекта каждой системы.
Для этого в каждой строке матрицы находится минимальная из оценок систем
К(аi) min Кij.
j
Оптимальной считается система из строки с максимальным значением эффективности
Копт=max (minKij) для всех ij
i j
К(а1)=min(0,1;0,5;0,1;0,2)=0,1
К(а2)=min(0,2;0,3;0,2;0,4)=0,2
К(а3)=min(0,1;0,4;0,4;0,3)=0,1
Оптимальное решение – продукт а2
В любом состоянии обстановки выбранная система покажет результат не хуже найденного максимина. Однако такая осторожность является в ряде случаев недостатком критерия.
- Критерий пессимизма-оптимизма (критерий Гурвица)
Критерий обобщенного максимина. Согласно данному критерию при оценке и выборе систем не разумно проявлять как осторожность, так и азарт. Следует принимать во внимание самое высокое и самое низкое значение эффективности и занимать промежуточную позицию. Эффективность находится как взвешенная с помощью коэффициента α суммы максимальных и минимальных оценок.
К(ai) = α max Kij+(1- α)*min Kij
j j
0≤ α ≤1
Копт = max { α max Kij+(1- α)*min Kij}
i j j
α =0,6
К(а1)=0,6*0,5+(1-0,6)*0,1=0,34
К(а2)=0,6*0,4+(1-0,6)*0,2=0,32
К(а3)=0,6*0,4+(1-0,6)*0,1=0,28
Оптимальное решение – продукт а1
При α = 0 критерий Гурвица сводится к критерию максимина. На практике используются значения α из интервала (0,3÷0,7).
- Критерий минимального риска (критерий Севиджа)
Минимизирует потери эффективности при наихудших условиях. В этом случае матрица эффективности должна быть преобразована в матрицу потерь. Каждый элемент определяется как разность между максимальным и текущим значениями оценок эффективности в столбце.
∆ Кij = maxKij — Kij
После преобразования матрицы используется критерий минимакса, т.е. оптимального решения критерия.
K(ai)=max∆ Кij
j
Kопт=min (max∆ Кij)
i j
Таблица «Матрица потерь»
|
ак |
к1 |
к2 |
к3 |
к4 |
к(аi) |
|
а1 |
0,1 |
0 |
0,3 |
0,2 |
0,3 |
|
а2 |
0 |
0,2 |
0,2 |
0 |
0,2 |
|
а3 |
0,1 |
0,1 |
0 |
0,1 |
0,1 |
Итоговые результаты выписываем в таблицу «Форма записи результатов».
Таблица «Форма записи результатов»
|
ак |
к1 |
к2 |
к3 |
к4 |
Ср. выигр |
Лапласа |
Вальда |
Гурвица |
Севиджа |
|
а1 |
0,1 |
0,5 |
0,1 |
0,2 |
0,21 |
0,225 |
0,1 |
0,34 |
0,3 |
|
а2 |
0,2 |
0,3 |
0,2 |
0,4 |
0,28 |
0,275 |
0,2 |
0,32 |
0,2 |
|
а3 |
0,1 |
0,4 |
0,4 |
0,3 |
0,25 |
0,300 |
0,1 |
0,28 |
0,1 |
Тип критерия для выбора рационального варианта выбирается на аналитической стадии рассмотрения сложных систем.
Метод Дерева решений предлагает графическое отображение различных вариантов возможных будущих сценариев развития системы. Сходен с методом Дерева целей и методом Сценариев. От одного метода – четкие построения и структуризация проблем, от другого – вариативность возможных событий. Данный метод удобен в ситуациях, когда существует зависимость более поздние решений от решений, принятых ранее, и в свою очередь, определяющих сценарии дальнейшего дальнейших событий. Основными недостатками данного метода являются, во-первых, его субъективизм, во-вторых, громоздкость и техническая сложность обработки данных.
Последовательность действий при построении дерева решений
1. Структуризация проблемы — установление причинно-следственных связей в анализируемой проблеме. А именно, выбор предпочтительного варианта разрешения проблемы и менее предпочтительного (что можно отложить), а так же круг вопросов, информации необходимой для принятия решения, источников ее получения и возможных сроков необходимых для решения. Итогом этого этапа должна стать модель процесса принятия решений, в которой должны быть учтены следующие элементы:
— действия необходимые для принятия решений;
Обратите внимание на лекцию «24 Конфликты по вертикали».
— события, которые не зависят от ЛПР и являются результатом действия факторов неопреленности.
2. Построение диаграммы дерева решений
3. Оценка вариантов решений
4. Оценка вероятностей наступления событий и анализ неопределенности.
Имитационное моделирование по методу Монте-Карло некоторые исследователи считают эволюционным развитием метода сценариев, прежде всего потому, что в процессе реализации этого метода проигрываются достаточно большое количество вариантов. Это сложный и одновременно самый эффективный метод оценки систем.
Кроме рассмотренных выше методов для оценки эффективности сложных систем в условиях неопределенности могут быть применены и другие. Большинство этих методов строятся на субъективных и вероятностных оценках, и, следовательно, не могут быть идеальными с точки зрения точности и адекватности. Ограничения и недостатки формальных методов, многие специалисты чаще всего полагаются на свой личный опыт и интуицию, используя, в лучшем случае, только некоторые элементы расчетов прогнозных методов. Это объясняет продолжающийся поиск более эффективных и надежных методов зарубежными и отечественными исследователями. Одно из направлений этих работ – теория нечетких множеств в оценке экономической эффективности и риска в условиях неопределенности.
Система m
линейных алгебраических уравнений с n
неизвестными (или, линейная система,
также употребляется аббревиатура СЛА́У)
в линейной алгебре — это система
уравнений вида
Совместная
СЛУ– СЛУ, имеющая одно или несколько
решений.
Неопределенная
СЛУ– совместная СЛУ, имеющая более
одного решения.
Решается методом
Жордана – Гаусса. Решения выражаются
по средством свободных членов.
10) Однородные системы линейных уравнений
СЛАУ называется
однородной, если все её свободные члены
равны 0.
Теорема 1 (о
нетривиальных решениях однородной
системы)
Однородная
линейная система с квадратной матрицей
имеет нетривиальное решение тогда и
только тогда, когда определитель системы
равен нулю.
Доказательство
По теореме Крамера
тогда и только тогда, когда система с
квадратной матрицей имеет единственное
решение (т.е. векторы – столбцы системы
– линейно зависимы). В случае если задана
система линейных однородных уравнений,
это решение – тривиальное (0,0,…0). Значит,
нетривиальные решения имеются тогда и
только тогда, когда(т.е. решений системы бесконечное
множество).
Любое решение
СЛОУ выражается в виде линейной комбинации
векторов (если
):

…,
Покажем, что
вектора
– линейно независимы. Для этого составим
матрицуиз их координат:

Ниже черты
расположен минор порядка
,
отличный от нулястолбцов матрицы
линейно независимы.
Следовательно,
вектора
– линейно независимы, т.е. эти вектора
образуют базис подпространства.
Условие
нетривиальной совместности:
Для того, чтобы
однородная система имела нетривиальное
решение, необходимо и достаточно, чтобы
ранг ее основной матрицы был меньше
числа неизвестных
Теоре́ма
Кро́некера — Капе́лли— критерий
совместности системы линейных
алгебраических уравнений:
Система линейных
алгебраических уравнений совместна
тогда и только тогда, когда ранг её
основной матрицы равен рангу её
расширенной матрицы, причём система
имеет единственное решение, если ранг
равен числу неизвестных, и бесконечное
множество решений, если ранг меньше
числа неизвестных.
11. Векторы. Линейные операции над векторами
Геометрическим
вектором (или просто вектором) называетсянаправленный отрезок.
Вектор называется
нулевым, если начало и конец его совпадают.
Нулевой
вектор не имеет
определенного направления и имеет
длину, равную нулю. Это
позволяет при
записи отождествлять нулевой вектор с
вещественным числом
нуль.
Векторы
называются коллинеарными, если они
лежат либо на од-
ной прямой,
либо на параллельных прямых.
Два вектора
называются равными, если они коллинеарны,
имеют оди-
наковую длину
и одинаковое направление.
Линейные
операции над векторами.
Линейными
операциями принято называть операцию
сложения векторов и опе-
рацию умножения
векторов на вещественные числа.
Суммойa +
b двух векторов a и b называется вектор,
идущий
из начала
вектора a в конец вектора b при условии,
что вектор b
приложен к
концу вектора a.
1. a + b = b + a
(переместительное свойство);
2. (a + b) + c= a + (b +
c) (сочетательное свойство);
3. а+0=а
4. а+(-а)=0
Разностьюa — b вектора a и вектора b называется такой
вектор
c, который в
сумме с вектором b дает вектор a.
Произведениемα a (или aα) вектора a на вещественное
число α
называется
вектор b, коллинеарный вектору a, имеющий
длину,
равную |α|·|a| ,
и имеющий направление, совпадающее с
направле-
нием вектора
a в случае α > 0 и противоположное
направлению
вектора a в
случае α < 0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
29.05.20154.35 Mб56начерталка.rar.pdf
- #
- #
- #
- #
- #
- #
- #
- #
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Тарбокова Т.В.
1
1 ФГАОУ ВО «Национальный исследовательский Томский политехнический университет»
Решение систем линейных алгебраических уравнений (СЛАУ) «вручную» требует много времени, большого внимания, довольно громоздких преобразований и вычислений. Если допущена ошибка в решении СЛАУ, её бывает нелегко обнаружить. Целью применения пакета Mathcad в учебном процессе явилась потребность использования возможностей компьютеров для решения СЛАУ. Преимущества предлагаемого алгоритма заключаются в том, что решение СЛАУ осуществляется не формально, когда возвращается единственный вариант ответа. В процессе реализации алгоритма исследуются основные свойства СЛАУ: ранги основной и расширенной матриц системы, выбираются базисные неизвестные и свободные неизвестные, возвращаются общие решения при любом допустимом выборе базисных и свободных неизвестных. Заменяя столбцы основной матрицы СЛАУ столбцом свободных членов со свободными неизвестными, можно получать общее решение и методом Крамера, о чём в учебной литературе упоминаний нет.
Mathcad
системы линейных алгебраических уравнений
алгоритм
1. Кафедра высшей математики ТПУ. URL: http://portal.tpu.ru/departments/kafedra/vm/rabota/
2. Очков В.Ф. Mathcad 14 для студентов и инженеров: русская версия. – СПб.: БХВ-Петербург, 2009. – 512 с.: ил.
Линейное алгебраическое уравнение можно определить как уравнение, в которое искомые неизвестные входят в первой степени и между собой не перемножаются, т.е. в левой части линейного уравнения обычно записывается линейная комбинация искомых неизвестных, а в правой – свободный член. Совокупность таких уравнений образует систему линейных алгебраических уравнений (СЛАУ). Если СЛАУ имеет единственное решение, то она называется определённой. В случаях, когда решений бесконечное множество, СЛАУ называется неопределённой. Для решения определенных СЛАУ применяют методы Крамера, Гаусса, матричный, численные методы. Для неопределённой СЛАУ можно находить общее решение и какие-либо частные решения из их бесконечного множества.
В соответствии с ФГОС раздел «Линейная алгебра» модуля «Математика 1» входит в рабочие программы всех унифицированных образовательных математических кластеров дисциплины «Математика» [1]. В рабочие программы в обязательном порядке включаются индивидуальные домашние задания (ИДЗ) по всем разделам, в том числе и по разделу «Линейная алгебра». Решение СЛАУ «вручную» требует много времени, большого внимания, довольно громоздких преобразований и вычислений. Если допущена ошибка в решении СЛАУ, её бывает нелегко обнаружить. Целью применения пакета Mathcad в учебном процессе явилась потребность использования возможностей компьютеров для решения СЛАУ.
Квадратные СЛАУ с невырожденной основной матрицей системы, а также матричные уравнения в среде пакета Mathcad легко решаются матричным методом. Например, чтобы решить СЛАУ
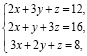
достаточно задать основную матрицу системы
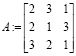
столбец свободных членов
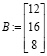
записав произведение обратной матрицы A–1 на матрицу В и воспользовавшись клавишей «=», получить решение:
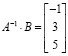
Проверка правильности решения также осуществляется в одно действие умножением матрицы А на найденную матрицу решения:
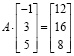
Можно предварительно записать найденную матрицу
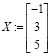
решения СЛАУ, тогда для проверки потребуется ввести с клавиатуры произведение 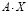
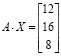
Начиная с шестой версии Mathcad, квадратные СЛАУ с невырожденной матрицей можно решать, используя встроенную функцию lsolve(A,B): X:= lsolve(A,B), и сразу получить решение
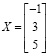
Для решения неопределенных СЛАУ в среде пакета Mathcad имеется несколько возможностей. Версия Mathcad 13/14 (в предыдущих версиях Mathcad основная матрица СЛАУ должна быть квадратной) позволяет находить одно из бесконечного множества частных решений СЛАУ при помощи встроенной функции lsolve(A,B) [2]. Например, так:
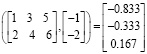
если решается СЛАУ
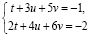
Замена знака равенства стрелкой из палитры символьных операций Symbolic возвращает частное решение в виде рациональных чисел:
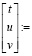
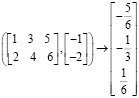
Но общее решение, применяя встроенную функцию lsolve(A,B), найти не удается.
Получить общее решение СЛАУ можно директивой solve палитры символьных операций Symbolic. Для этого надо в левую метку директивы solve записать матрицу из одного столбца и таким количеством строк, сколько уравнений в СЛАУ, отделяя свободные члены равенствами из палитры Boolean или вводя знаки «=» с клавиатуры вместе с клавишей Ctrl (получается «жирный» знак равенства). В правой метке следует перечислить имена всех неизвестных СЛАУ. Например,
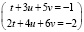
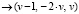
Возвращается общее решение, в котором t, u – базисные неизвестные, v – свободная неизвестная. Частное решение, возвращаемое встроенной функцией lsolve(A,B), соответствует свободной неизвестной 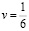
Недостаток применения директивы solve заключается в том, что в рассматриваемом примере базисные неизвестные выбираются единственным образом, хотя в качестве базисных неизвестных можно выбрать любую другую пару неизвестных, т.к. в рассматриваемом примере все миноры второго порядка основной матрицы системы отличны от нуля.
Обойти проблему можно, применяя предлагаемый наиболее близкий к классическому исследованию и решению СЛАУ алгоритм.
Ввести основную матрицу СЛАУ, обозначив ее A, например. В задаче исследовать СЛАУ на совместность задать расширенную матрицу системы А1.
Ввести столбец свободных членов, обозначив его, например, В.
Найти ранг основной матрицы системы: rank(A). Для СЛАУ больших размеров найти rank(A1). Если rank(A)≠rank(A1), СЛАУ несовместна, т.е. решений не имеет, и на этом исследование и решение СЛАУ заканчивается.
Если rank(A) = rank(A1), выбрать отличный от нуля базисный минор F (порядок базисного минора равен рангу основной матрицы СЛАУ) и базисные неизвестные, коэффициенты при которых вошли в базисный минор.
Оставшиеся свободные неизвестные перенести к свободным членам и ввести получившийся столбец С как функцию свободных неизвестных.
Получить общее решение, умножив обратную матрицу 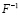
Присвоив свободным неизвестным числовые значения, получить соответствующее частное решение.
Для проверки надо матрицу А умножить на матрицу-столбец В1 решения, составленного из свободных и базисных неизвестных или из значений неизвестных частного решения.
Применение алгоритма рассмотрим на предыдущем примере
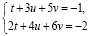
1. 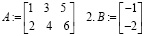
3. rank(A)=2
4. Выберем базисными неизвестными 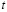
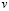
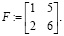
Определитель матрицы F отличен от нуля: 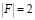
5. Составим матицу С:
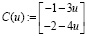
6. Получим общее решение
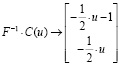
7. Пусть свободная неизвестная
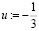
При этом значения базисных неизвестных 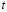
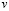
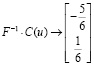
8. Составим столбец
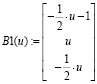
Тогда 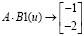
или сделаем проверку для частного решения:
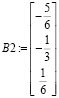
и получим 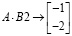
Преимущества предлагаемого алгоритма заключаются в том, что решение СЛАУ осуществляется не формально, когда возвращается единственный вариант ответа. В процессе реализации алгоритма исследуются основные свойства СЛАУ: ранги основной и расширенной матриц системы, выбираются базисные неизвестные и свободные неизвестные, возвращаются общие решения при любом допустимом наборе базисных и свободных неизвестных. Заменяя столбцы основной матрицы СЛАУ столбцом свободных членов со свободными неизвестными, можно получать общее решение и методом Крамера, о чём в учебной литературе упоминаний нет. Вот как это можно осуществить для СЛАУ
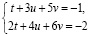
решенной выше матричным методом:
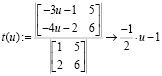
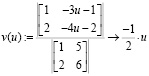
Таким образом, методом Крамера получено общее решение 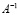
Библиографическая ссылка
Тарбокова Т.В. РЕШЕНИЕ НЕОПРЕДЕЛЕННЫХ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ В СРЕДЕ ПАКЕТА MATHCAD // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 6-2.
– С. 362-365;
URL: https://applied-research.ru/ru/article/view?id=6907 (дата обращения: 25.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)


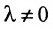 ;
;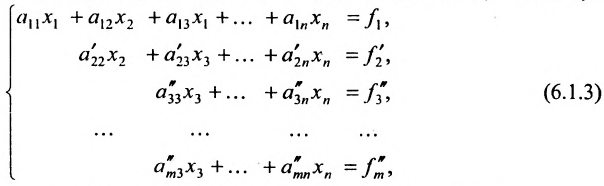
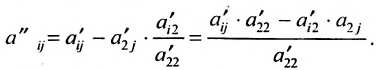
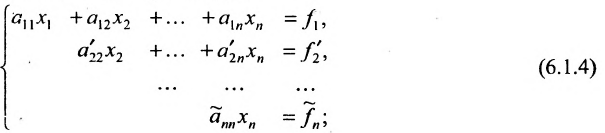
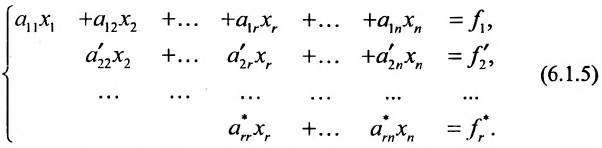

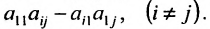
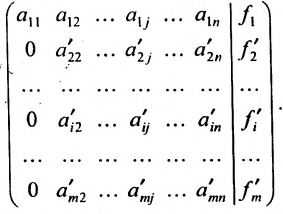
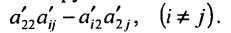

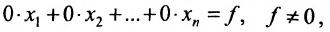
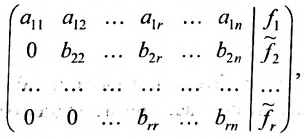
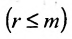
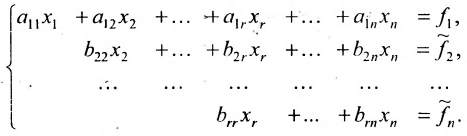
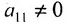 (если
(если 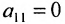 , строки матрицы можно переставить так, чтобы выполнялось условие
, строки матрицы можно переставить так, чтобы выполнялось условие 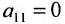 );
);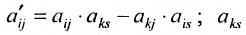 — разрешающий элемент (см. схему).
— разрешающий элемент (см. схему).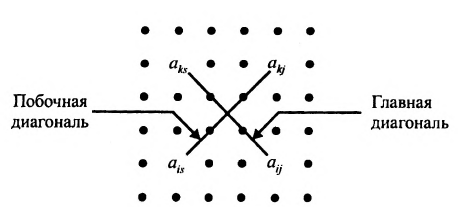
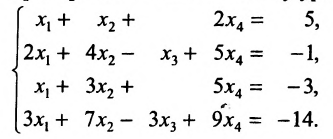


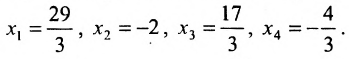
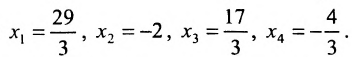

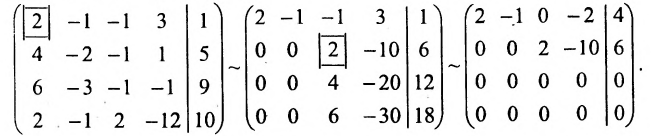

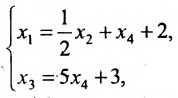
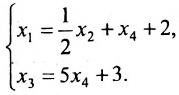
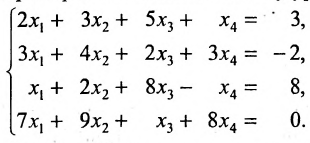
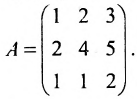
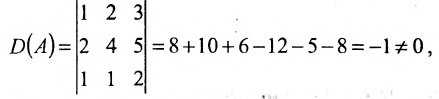

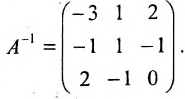
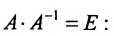
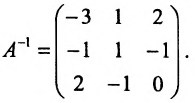
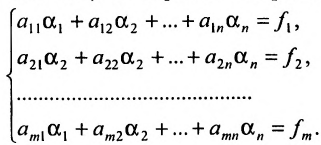
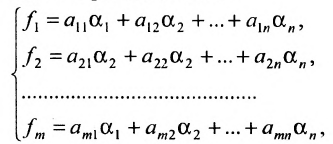
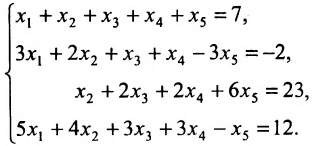

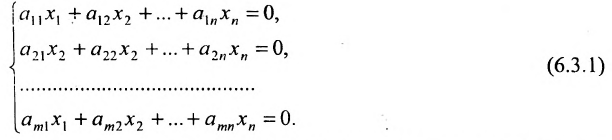
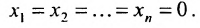
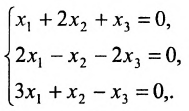
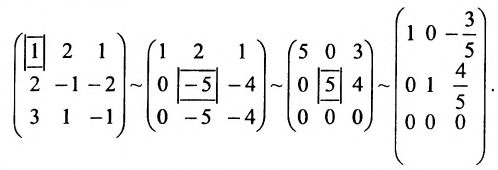
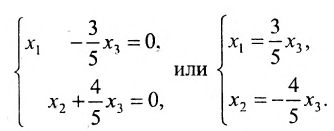
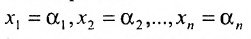
 порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули. , и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.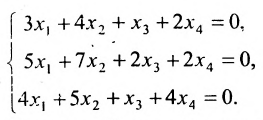
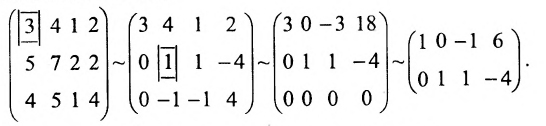
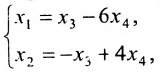
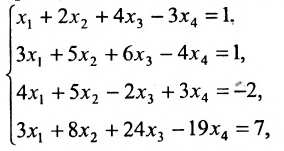
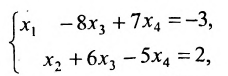



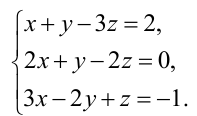
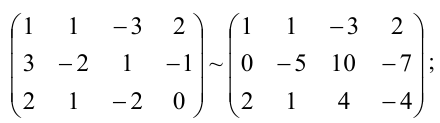
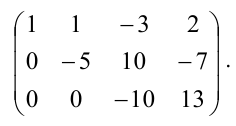
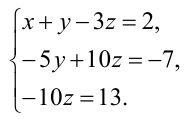
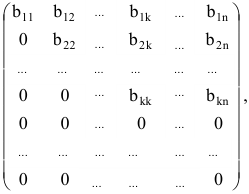
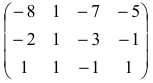
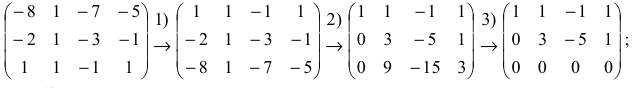




![{displaystyle x=A^{+}b+[I_{n}-A^{+}A]w}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46682e93ba613fa1164d2f7799343413534b1bb3)
