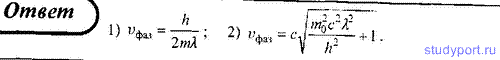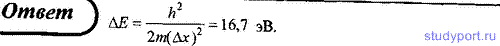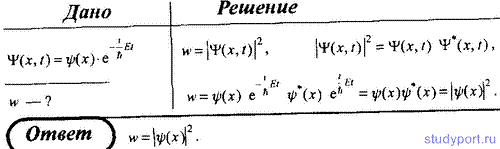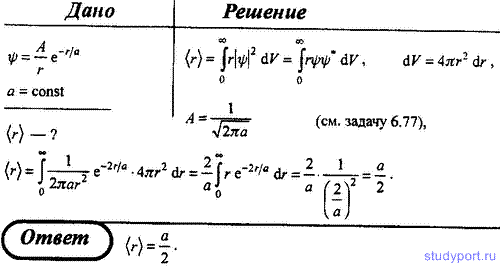Физические
величины никогда не могут быть измерены
абсолютно точно. Измеренное значение
любой физической величины всегда
отличается от ее истинного значения,
которое всегда неизвестно, так как при
выполнении любого измерения неизбежна
ошибка. Источников ошибок много. Они
связаны с несовершенством измерительных
приборов, с изменением условий опыта,
с неполнотой теоретической модели и
приближенным характером используемого
метода измерений, с округлением при
вычислениях и т.д.
Поэтому
необходимым условием выполнения любого
измерения является нахождение некоторого
интервала значений, в который с высокой
вероятностью должно попасть истинное
значение измеряемой величины. Измерение,
например, координаты
материальной точки должно сопровождаться
определением ошибки измерения,
измерение компоненты импульса— определением ошибки
.
В
классической физике не было принципиальных
ограничений на точность измерений.
Считалось, что при достаточно совершенной
аппаратуре все величины, характеризующие
физическую систему, могут быть измерены
со сколь угодно высокой точностью.
Однако
для микроскопических систем неограниченное
повышение точности получается не всегда.
В некоторых случаях существуют
принципиальные ограничения на точность
измерений. Эти ограничения не определяются
совершенством измерительной аппаратуры.
Каждое из этих ограничений является
фундаментальным свойством материи.
Проявляются эти свойства только в
микромире.
Принципиальные
ограничения на точность измерений
физических величин называются
соотношениями неопределенностей.
Впервые
соотношения неопределенностей были
сформулированы немецким физиком
Гейзенбергом в 1927 г.
Наиболее
важными являются два соотношения
неопределенностей. Первое устанавливает
ограничения на точность одновременного
определения координат частицы и
соответствующих компонентов ее импульса.
Для
—
координаты это соотношение записывается
в виде
(20.4)
(при
строгом применении формализма квантовой
механики получается соотношение
,
однако для качественных оценок используют
именно выражение (20.4)).
Второе
соотношение устанавливает предел
точности измерения энергии за данный
промежуток времени
, (20.5)
где
— длительность измерения энергии,
— неопределенность энергии.
Соотношения
неопределенностей обусловлены
корпускулярно-волновым дуализмом.
В
качестве примера рассмотрим движение
свободного электрона в пространстве.
Его движение описывается с помощью
плоской монохроматической волны, которая
обладает строго определенными значениями
частоты и волнового вектора. При этом
сопоставляемая электрону волна занимает
все пространство и имеет неограниченное
время существования. Докажем, что
одновременное «точное» определение
координаты и импульса электрона
невозможно.
Результат
прохождения световой волны через щель
хорошо известен из оптических
экспериментов. На экране наблюдается
дифракционная картина в виде чередующихся
светлых и темных полос. Можно предположить,
что и прохождение электронной волны
через щель приведет к аналогичным
результатам.
Так
как движения микрочастиц описываются
либо с волновых, либо с корпускулярных
позиций, то рассмотрим результаты
дифракции электронов с более привычной
корпускулярной точки зрения.
Пусть
до щели все электроны двигались
параллельно оси
с одинаковыми импульсами
(рис. 20.6).
Рис.20.6
Одинаковые
значения импульсов электронов можно
получить, разгоняя их в электрическом
поле, а затем производя селекцию по
скоростям. Однако о положении каждого
электрона ничего определенного сказать
нельзя. Координата
электронов до щели совершенно не
определена. Поэтому, в каком месте экранаокажется тот или иной электрон заранее
предсказать невозможно. На экранеполучается дифракционная картина,
аналогичная дифракции световой волны
на щели. Она свидетельствует о том, что
некоторые электроны прошли через щель
в экране.
Пусть ширина щели.
Эта щель представляет собой своеобразный
измерительный прибор, с помощью которого
можно определить в плоскости экранакоординату прошедшего электрона с
точностью.
Возникновение на экранедифракционной картины с корпускулярной
точки зрения следует трактовать, как
отклонение каждого электрона, прошедшего
через щель, на некоторый уголот направления своего первоначального
распространения, причём импульс электронапо абсолютной величине остается
неизменным. Каждый электрон после
прохождения через щель приобретет
составляющую импульса.
Причёмменяется непредсказуемым образом от 0
(электрон вообще не отклонился от
направления своего первоначального
распространения) до(угол
соответствует первому дифракционному
минимуму). Часть электронов будет
отклоняться на углы, большие чем,
однако этим числом можно пренебречь по
сравнению с количеством электронов,
отклоняющихся в пределах центрального
максимума. Таким образом, появляется
неопределенностьв нахождении проекции импульса на ось
. (20.6)
В
оптике дифракционных явлений известно,
что при падении на щель шириной
монохроматической волны длиной
,
первый минимум интенсивности света
появляется под углом,
для которого выполняется соотношение:.
Выражение (20.6) с учетом этого соотношения
запишется в виде:.
Используя формулу де Бройля,
получим:
. (20.7)
Увеличивая
ширину щели
,
можно уменьшить неопределенностьв нахождении проекции импульса на ось
и, наоборот, уменьшая неопределенность
в нахождении координаты электрона
(уменьшая ширину щели)
увеличиваем неопределенность.
Одновременное с заранее заданной
точностью определение координатыи проекции импульса электрона
вследствие наличия у электрона волновых
свойств, невозможно.
Таким
образом, предел ошибок (неопределенностей)
и
,
с которыми состояние микрочастицы можно
характеризовать классически, то есть
координатойи импульсом
,
определяется соотношением неопределенностей
Гейзенберга (20.4). В частном случае
неопределенностиможет и не быть. Так было при движении
электронов до экрана.
Но тогда, согласно соотношению
неопределенностей,.
Это означает, что частица может быть с
равной вероятностью обнаружена в любом
месте экрана.
Следует
особо отметить роль постоянной Планка
в соотношении
неопределенностей.
Отличие
от нуля исключает обращение в нуль
при заданном значении
.
Только переход к классической физике,
в которой,
снимает ограничения на точность
измерений.
При
произвольном движении частицы в
пространстве соотношения неопределенностей
выражаются тремя неравенствами:
,
,
.
(20.8)
Рассмотрим
несколько примеров:
1).
Электрон движется со скоростью V=103
м/с.
Пусть его
скорость
определена с точностю ΔV/V=0,10/0.
Чему равна неопределенность положения
электрона?
Из
соотношения (5.4) имеем:
,
но,
тогдам =
0,73 мм,
хотя
размер атомов или молекул ≈ 10-10
м.
Т.е. неопределенность в определении
координаты Δx
значительно
больше размеров самого атома. Здесь
электрон − классическая частица.
Такая
точность достаточна, чтобы можно было
говорить о движении электронов по
определенной траектории, иными словами,
описывать их движения законами
классической механики.
2).
Пуля массой 10 г
вылетает из винтовки со скоростью V
= 103
м/c.
Пусть
ΔV/V=0,10/0.
Чему равна неопределенность положения
пули?
м.
Т.е.
неопределенность в определении координаты
Δx
значительно
меньше
размеров
пули. Здесь пуля − классическая частица.
Ее координата определяется точно.
3).
Применим соотношение неопределенностей
к электрону, движущемуся в атоме водорода.
Допустим, что неопределенность координаты
электрона Δx
≈10-10
м (порядка размеров самого атома), тогда,
согласно (20.4),
.
Используя
законы классической физики, можно
показать, что при движении электрона
вокруг ядра по круговой орбите радиуса
r
≈ 0,5⋅10-10
м его скорость V
≈ 2,3⋅106
м/с. Таким
образом, неопределенность
скорости в несколько раз больше самой
скорости.
Очевидно,
что в данном случае нельзя говорить о
движении электронов в атоме по
определенной траектории. Иными словами,
для описания движения электронов в
атоме нельзя пользоваться законами
классической физики.
Теперь
обоснуем соотношение неопределенностей
(5.5) для энергии и времени. Для волнового
пакета (группы волн) справедливо
соотношение:
, (20.9)
смысл
которого заключается в том, что
ограниченный во времени волновой процесс
не может быть монохроматическим. Если
процесс длится в течение времени
,
то разброс частот(и соответственно разброс длин волн)
удовлетворяет соотношению (20.9). Поэтому
если для наблюдения даже монохроматического
процесса предоставлено некоторое время,
то частота процесса может быть определена
лишь с ошибкой,
подчиняющейся соотношению (20.9). Так как,
то соотношение (20.9) принимает вид:.
Это
означает, что чем меньше время
отведено для определения энергии
микрообъекта, тем с меньшей неопределенностью
можно говорить об энергии этого состояния.
Электрон в стационарном состоянии атома
может находиться сколь угодно долго
(),
поэтому энергия стационарного состояния
имеет вполне определенное значение ()
.
Принцип
неопределенностей − фундаментальный
принцип квантовой механики,
устанавливающий физическое содержание
и структуру ее математического аппарата.
Многие результаты задач, рассматриваемых
в квантовой механике, могут быть получены
и поняты на основе комбинации законов
классической механики с соотношением
неопределенностей. Важный тому пример
− проблема устойчивости атома. Рассмотрим
эту задачу для атома водорода.
Пусть
электрон движется вокруг ядра по круговой
орбите радиуса r
со
скоростью V.
По закону Кулона сила притяжения
электрона к ядру уравновешивается
центробежной силой,
гдеm
− масса электрона, ε0
− электрическая
постоянная, тогда радиус его орбиты
может быть сколь угодно малым, если
скоростьV
достаточно велика. Но в квантовой
механике должно выполняться соотношение
неопределенностей.
Если
допустить неопределенность положения
электрона ∆x
в пределах радиуса его орбиты r,
т.е. ∆x
= r,
а неопределенность скорости ∆V
в пределах
V,
т.е. ∆p=m∆V=mV,
то соотношение неопределенностей
примет вид: mVr
≥ ħ. Учитывая
связь между V
и r,
получим
и
.
Следовательно, движение электрона по
орбите радиусаr
< r0
=

м
невозможно. Таким образом, электрон не
может упасть на ядро, что объясняет
устойчивость атома. Величина r0
и является радиусом атома водорода.
Ему соответствует энергия связи атома
E0
(равная полной энергии электрона в
атоме, т.е. сумме кинетической энергии
и потенциальной энергии
),
что составляет
Это минимальное значение энергии E0
соответствует энергии основного
состояния атома водорода.
Таким
образом, квантовомеханические
представления впервые дали возможность
теоретически оценить размеры атома,
выразив его радиус через фундаментальные
физические постоянные ħ,
m, e, ε0.
Остановимся
в заключение на смысле, вкладываемом в
понятие «орбита электрона» в атоме. В
отличие от теории Бора, в квантовой
механике не существует определенных
орбит
электрона в атоме. Существование
определенных орбит, т.е. точно
известных
расстояний электрона от ядра, противоречит
соотношению неопределенностей. Под
термином «орбита электрона» в квантовой
механике понимается расстояние от ядра,
на котором вероятность обнаружить
электрон максимальна.
Еще
раз подчеркнем, что соотношения
неопределенностей не связаны с
несовершенством измерительной техники,
а являются объективным
свойством материи:
таких состояний микрочастиц, в которых
и координата, и импульс частицы имеют
определенное значение, просто не
существует
в
природе.
Вывод:
к волновому и корпускулярному описанию
следует относиться как к равноправным
и дополняющим друг друга точкам зрения.
Рубеж, разделяющий две концепции волн
и частиц определяется именно ограниченными
возможностями измерения.
Контрольные
вопросы:
1.
В чем состоит физический смысл волн де
Бройля?
2.
Каков физический смысл соотношений
неопределенностей Гейзенберга?
3.
В каком случае и почему можно говорить
о движении частицы по определенной
траектории?
4.
Как, исходя из соотношения
неопределенностей, объяснить наличие
естественной ширины спектральных
линий?
Страница 2 из 4
59. Докажите, что групповая скорость волн де Бройля равна скорости свободно движущейся частицы. Рассмотрите нерелятивистский и релятивистский случаи.
60. Докажите, что для свободно движущейся с постоянной скоростью v частицы выполняется соотношение vфаз u = c2 (u —групповая скорость).
61. Выведите закон дисперсии волн де Бройля, т.е. зависимость фазовой скорости волн де Бройля от их длины волны. Рассмотрите нерелятивистский и релятивистский случаи.
62. Ширина следа электрона (обладающего кинетической энергией T = 1,5 кэВ) на фотопластинке, полученного с помощью камеры Вильсона, составляет Δx = 1 мкм. Определите, можно ли по данному следу обнаружить отклонение в движении электрона от законов классической механики.
63. Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U = 1 кВ. Известно, что неопределенность скорости составляет 0,1% от ее числового значения. Определите неопределенность координаты электрона. Являются ли электроны в данных условиях квантовой или классической частицей?
64. Определите отношение неопределенностей скорости электрона, если его координата установлена с точностью до 10-5 м, и пылинки массой m = 10-12 кг, если ее координата установлена с такой же точностью.
65. Электронный пучок выходит из электронной пушки под действием разности потенциалов U = 200 В. Определите, можно ли одновременно измерить траекторию электрона с точностью до 100 пм (с точностью порядка диаметра атома) и его скорость с точностью до 10%.
66. Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределенность скорости составляет 10% от ее числового значения, определите неопределенность координаты электрона. Применимо ли в данном случае для электрона понятие траектории?
68. Используя соотношение неопределенностей в форме Δx Δpx >= h , оцените минимально возможную полную энергию электрона в атоме водорода. Примите неопределенность координаты равной радиусу атома. Сравните полученный результат с теорией Бора.
70. Воспользовавшись соотношением неопределенностей, оцените размытость энергетического уровня в атоме водорода: 1) для основного состояния; 2) для возбужденного состояния (время его жизни равно 10-8 с).
71. Длина волны λ излучаемого атомом фотона составляет 0,6 мкм. Принимая время жизни возбужденного состояния Δt = 10 с, определите отношение естественной ширины энергетического уровня, на который был возбужден электрон, к энергии, излученной атомом.
72. Принимая, что электрон находится внутри атома диаметром 0,3 нм, определите (в электрон-вольтах) неопределенность энергии данного электрона.
76. Волновая функция, описывающая некоторую частицу, может быть представлена в виде ψ(x, t) = ψ(x)*e –(i/h)*Et . Покажите, что плотность вероятности нахождения частицы определяется только координатной ψ-функцией.
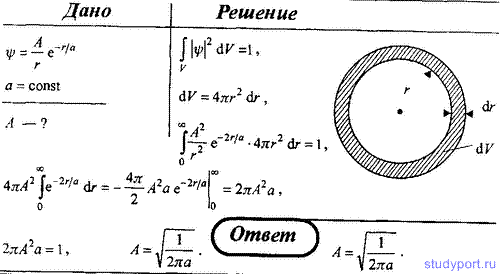
77. ψ-функция некоторой частицы имеет вид ψ = A/r*e—r/a, где r — расстояние этой частицы до силового центра; a — некоторая постоянная. Используя условие нормировки вероятностей, определите нормировочный коэффициент A.
78. Используя условие нормировки вероятностей, определите нормировочный коэффициент А волновой функции ψ = A*е—r/a, описывающей основное состояние электрона в атоме водорода, где r — расстояние электрона от ядра, a — первый боровский радиус.
79. Используя условие нормировки вероятностей, определите нормировочный коэффициент волновой функции ψ(r) = A*e—r^2/(2а^2), описывающей поведение некоторой частицы, где r — расстояние частицы от силового центра; a — некоторая постоянная.
80. Волновая функция ψ = A sin(2πx/l) определена только в области 0 <= x <= l . Используя условие нормировки, определите нормировочный множитель A.
81. ψ-функция некоторой частицы имеет вид ψ = A/r*е—r/a, где r — расстояние этой частицы до силового центра; a — некоторая постоянная. Определите среднее расстояние <r> частицы до силового центра.
82. Волновая функция, описывающая некоторую частицу, имеет вид ψ = A*e—r^2/(2a^2), где r — расстояние этой частицы до силового центра; a — некоторая постоянная. Определите среднее расстояние <r> частицы до силового центра.
При изучении волновых свойств света, например отражения или преломления, принято считать, что волна частично отражается, частично преломляется. Но при переходе к фотонным представлениям уже нельзя считать, что данный фотон «частично отразился», так как в этом случае изменилась бы частота отраженного света. Приходится говорить о том, что определенная часть фотонов отражается или что фотон имеет определенную вероятность от разиться. В такой трактовке амплитуда отраженного луча (или лучше энергия, пропорциональная квадрату амплитуды) определяется, как уже говорилось выше, вероятностью отражения фотона в данном направлении. Такое же рассмотрение возможно и для частиц вещества: квадрат модуля амплитуды волны де Бройля определяет вероятность нахождения частицы в том или ином месте (сама амплитуда есть функция координат и времени).
Итак, всякой движущейся частице следует сопоставить волновой процесс. Уравнение, описывающее ее движение, будет характеризоваться условиями распространения соответствующей волны де Бройля. Однако при этом решается задача не о положении данной частицы, а лишь о вероятности ее нахождения в некотором месте. Если речь идет о потоке частиц, то там, где вероятность их появления больше, они и окажутся в относительно большем числе; так, при дифракции электронов на щели наибольшая часть их попадет в участки, где вероятность их нахождения наибольшая,— соответствующие направления определяются формулой, характеризующей направления на максимум света:
где β — угол дифракции, Н — ширина щели.
Таким образом выясняется, что мы можем точно описать не характер движения отдельной микрочастицы, а лишь вероятность попадания ее в ту или иную область пространства. Это значит, что мы дошли до предела, за которым наши классические представления о характеристиках движения теряют свою полную определенность, привычную для классической механики. Это принципиальное положение, открытое Гейзенбергом и называемое соотношением неопределенностей, можно пояснить следующим примером. Пусть пучок электронов (рис. 12.2) со скоростью 
Эти электроны приобретут ранее отсутствовавшую у них составляющую импульса
модуль которой связан с шириной щели таким соотношением:
Отсюда получается:
или
Рис. 12.2
Более строгое рассмотрение задачи показывает, что полученное уравнение определяет наименьшее значение произведения ΔpxΔx, а более точное выражение имеет вид:

Здесь рх и х — импульс и координата, определяемые в одном и том же измерении. Величина Δх определяет неопределенность положения точки, через которую пролетел электрон (мы ведь знаем только лишь, что он прошел через щель). При этом неопределенность Δхпринципиально неустранима. Компонента импульса направлена по оси х, так как мы не можем указать, какому из электронов присущ тот или иной импульс Δрх.
Конечно, такие же соотношения, как (12.4), могут быть написаны для других координат:
Согласно (12.4) произведение неопределенностей не может быть ни в каком опыте сделано меньше постоянной Планка h. При этом весьма существенно, что, чем точнее определяется одна из величин, тем менее определенно будет значение другой величины. Так, при уменьшении Δx, т. е. ширины щели, дифракция проявляется более резко, следовательно, растет угол р, а с ним и неопределенность Δ рх.
Для опытов макроскопического масштаба это неравенство, оставаясь в принципе справедливым, уже не имеет значения. Докажем это. Вообразим электронный пучок диаметром dx= 10-3 м, летящий в вакууме. Этот диаметр определяет неопределенность в задании координаты электрона. Пусть скорость электрона vy = 107 м/с. Какова неопределенность в оценке скорости vx? Согласно (12.3) получаем:
т. е. ничтожно малую величину по сравнению со скоростью vy, поэтому обычно величиной Δvx и пренебрегают. Но при переходе к микромиру положение изменяется. Так, если мы знаем, что электрон находится внутри атома (неопределенность в задании координатыΔх=10-10 м), то неопределенность в определении скорости составит:
Но это величина того же порядка, какой можно приписать скорости электрона, предполагая, что он движется в атоме по законам классической физики. Поэтому внутри атома» в известной степени теряется определенность понятий координаты и импульса; классическое описание движения оказывается невозможным.
Так как неопределенность в определении скорости тем меньше, чем больше масса, то для более тяжелых частиц неопределенность бывает меньше.
Уравнение (12.4) можно представить в виде:
Так как нам важен лишь порядок величины, то напишем:

Здесь ΔW — неопределенность энергии частицы в некотором состоянии, At — время ее пребывания в данном состоянии (в нашем f примере речь шла о кинетической энергии, однако в действительности результат (12.5) верен и для полной энергии частицы). Таким образом, чем дольше частица пребывает в данном состоянии, тем более определенна ее энергия, и, наоборот, для состояний, существующих малый промежуток времени, энергия определяется с большой неопределенностью,
В случае фотона
W=hv,
и из (12.5) получается неопределенность частоты:
Из этого неравенства следует, что так как все реальные состояния ограничены во времени, то в природе не существует чисто монохроматических процессов (к этому вопросу мы вернемся позже при оценке ширины спектральных линий). Пока же мы отметим, что, например, чем продолжительнее импульс, заполненный высокочастотными колебаниями, тем он монохроматичнее.
В заключение добавим, что соотношение неопределенностей относится к некоторым парам физических величин, но не к любым: так, например, между неопределенностями координаты Δх и импульса Δру нет закономерных связей. Соотношение неопределенностей, как и представление о волнах де Бройля, является одним из основных положений квантовой механики.
Соотношение неопределенностей характеризует границы применимости классических представлений к микропроцессам. Но его ни в коем случае нельзя толковать как соотношение, определяющее границы нашего познания. Классические представления не являются единственно возможными, хотя они наиболее привычны для нас и необходимы при описании результатов опытов, производимых над микрочастицами при помощи макроскопических приборов.
Мы не можем указать, как именно будет развиваться в дальнейшем познание окружающего нас мира (в частности, микромира), но можно с полной определенностью утверждать, что границ этого развития не существует, что в природе есть еще очень много непознанного, но нет ничего непознаваемого. Этому учит диалектика развития науки, в частности физики.