Как найти неопределенные интегралы методом непосредственного интегрирования

В простейших примерах для применения непосредственного интегрирования достаточно разложить подынтегральную
функцию на слагаемые и постоянные величины вынести за знак интеграла.

При определенной практике интегрирования обычно эти действия проводят устно, записывая лишь результат интегрирования.

Примеры решения интегралов данным методом

В некоторых случаях выражение, стоящее под знаком интеграла, можно с помощью алгебраических
преобразований упростить так, чтобы можно было применить метод непосредственного интегрирования.

Читать дальше: интегрирование внесением под дифференциал.

Метод непосредственного интегрирования

Метод непосредственного интегрирования применяется, когда в интеграле присутствуют табличные элементарные функции, либо функции, сводящиеся к таким путём элементарных преобразований. Например, вынос константы за знак интеграла, разбиение интеграла на сумму интегралов так, чтобы подынтегральное выражение содержало готовую функция для интегрирования.

Пример 1

Найти неопределенный интеграл методом непосредственного интегрирования: $$ int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx $$

Решение

По свойству интеграл суммы есть сумма интегралов: $$ int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx = int x^3 dx + int frac{3 dx}{2sqrt{x}} + int frac{2 dx}{x} $$ Первый интеграл является табличным, поэтому используем непосредственное интегрирование: $$ int x^3 dx = frac{x^{3+1}}{3+1} = frac{x^4}{4} + C $$ Во втором интеграле есть константа, которую сразу можно вынести за знак, а далее интеграл превратится в табличный: $$ int frac{3dx}{2sqrt{x}} = 3 int frac{dx}{2sqrt{x}} = 3 sqrt{x} + C $$ В третьем интеграле выносим константу, а затем применяем метод непосредственного интегрирования: $$ int frac{2dx}{x} = 2int frac{dx}{x} = 2 ln x + C $$ Суммируем в одну запись и получаем: $$ int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx = frac{x^4}{4} + 3sqrt{x} + 2ln x + C $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx = frac{x^4}{4} + 3sqrt{x} + 2ln x $$

Пример 2

Вычислить неопределенный интеграл методом непосредственного интегрирования: $$ int_0^1 (sqrt{x} + x)^2 dx $$

Решение

Преобразуем выражение под интегралом для предстоящего интегрирования по частям. Для этого воспользуемся формулой: $$ (a+b)^2 = a^2 + 2ab + b^2 $$ Выполняем преобразование: $$ int_0^1 (sqrt{x} + x)^2 dx = int_0^1 (x + 2xsqrt{x} + x^2) dx = $$ По свойствам степеней дополнительно преобразуем второе слагаемое в вид: $$ 2xsqrt{x} = 2x cdot x^frac{1}{2} = 2x^{1+frac{1}{2}} = 2x^{frac{3}{2}} $$ Так как интеграл суммы равен сумме интегралов, то: $$ int_0^1 (sqrt{x} + x)^2 dx = int_0^1 x dx + int_0^1 2x^frac{3}{2} dx + int_0^1 x^2 dx = $$ Во слагаемом выносим за знак интеграла константу, чтобы интеграл стал табличным: $$ = frac{x^2}{2} bigg |_0 ^1 + 2 frac{x^{frac{3}{2}+1}}{frac{3}{2}+1} bigg |_0 ^1 + frac{x^3}{3} bigg |_0^1 = frac{x^2}{2} bigg |_0^1 + 2cdot frac{2}{5} x^frac{5}{2} bigg |_0^1 + frac{x^3}{3} bigg |_0^1 = $$ Применяя формулу Ньютона-Лейбница подставляем пределы интегрирования: $$ = frac{1}{2} + frac{4}{5} + frac{1}{3} = frac{15+24+10}{30} = frac{49}{30} $$

Ответ

$$ int_0^1 (sqrt{x} + x)^2 dx = frac{49}{30} $$

1. Неопределенный
   интеграл

Поскольку сейчас
речь пойдет только о неопределенном
интеграле, то для сокращения термин
«неопределенный» будем опускать.

Для того чтобы
научиться вычислять интегралы (или, как
говорят, интегрировать функции), нужно,
прежде всего, выучить таблицу интегралов:

Таблица1. Таблица
интегралов

1. . 2. (), u>0. 2a. (α=0); 2б. (α=1); 2в. (α=). 3. 3а. 4. 5. 5а) 6. 6а. 7. 7а.

8. 9. 10. 10а. 11. 11а. 12. 13. 13а.

Кроме того,
потребуется умение вычислять производную
от заданной функции, а значит, нужно
вспомнить правила дифференцирования
и таблицу производных основных
элементарных функций:

Таблица 2. Таблица
производных и правила дифференцирования:

( с) = 0 (cu) = cu ( u + v ) = u + v ( u — v ) = u — v ( u v) = uv + uv 6.а.

(sin и) = cos и  и (cos u) = – sin и и

А еще нам потребуется
умение находить дифференциал функции.
Напомним, что дифференциал функции

находят по формуле
,
т.е. дифференциал функции равен
произведению производной этой функции
на дифференциал её аргумента. Полезно
держать в памяти и следующие известные
соотношения:

Таблица 3. Таблица
дифференциалов

1. (b=Const) 2. () 3. 4. 5. (b=Const) 6. 7. 8. 9.

10. 11. 12. 13. 14. 15. 16. 17.

Причем использовать
эти формулы можно, как читая их слева
направо, так и справа налево.

Рассмотрим
последовательно три основных приема
вычисления интеграла. Первый из них
называют методом
непосредственного интегрирования. Он
основан на
использовании свойств неопределенного
интеграла, включает два основных приема:
разложение
интеграла на алгебраическую сумму
более простых и подведение
под знак дифференциала,
причем эти приемы могут быть использованы
как самостоятельно, так и в совокупности.

А)
Рассмотрим
разложение на алгебраическую сумму
– этот прием предполагает использование
тождественных преобразований
подынтегральной функции и свойств
линейности неопределенного интеграла:

и
.

а);
б)
;

в)

г)

д)
.

Решение.

а)
Преобразуем
подынтегральную функцию, разделив
почленно числитель на знаменатель:

.

Здесь использовано
свойство степеней:
.

б)
Сначала
преобразуем числитель дроби, затем
разделим почленно числитель на
знаменатель:

.

Здесь также
использовано свойство степеней:
.

в)

.

г)

.

Здесь использовано
свойство:
,
.

д)

.

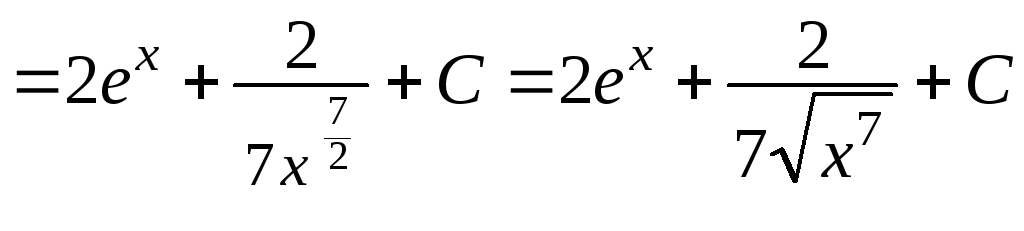
Здесь использованы
формулы 2 и 5 таблицы 1.

Пример
2.
Найти
интегралы:

а)
;
б)

;

в)


г)

д)

.

Решение.

а)
Преобразуем
подынтегральную функцию, используя
тригонометрическое тождество
:

.

Здесь вновь
использовано почленное деление числителя
на знаменатель и формулы 8 и 9 таблицы
1.

б)
Аналогично
преобразуем, используя тождество
:

.

в)
Сначала
разделим почленно числитель на знаменатель
и вынесем за знак интеграла константы,
затем используем тригонометрическое
тождество
:

.

г)
Применим
формулу понижения степени:

,

Получим:

.

д)
Используя
тригонометрические тождества, преобразуем:

.

.

Б)
Рассмотрим прием интегрирования,
который называют подведением под
знак дифференциала. В основе этого
приема лежит свойство инвариантности
неопределенного интеграла:

если
,
то для любой дифференцируемой функции
и = и(х) имеет место:
.

Это свойство
позволяет значительно расширить таблицу
простейших интегралов, так как в силу
этого свойства формулы таблицы 1
справедливы не только для независимой
переменной и, но и в случае, когда и
– дифференцируемая функция какой-либо
другой переменной.

Например,
,
но и
,
и
,
и
.

Или

и
,
и
.

Суть метода
заключается в выделении в заданном
подынтегральном выражении дифференциала
некоторой функции так, чтобы этот
выделенный дифференциал вместе с
остальным выражением составляли
табличную формула относительно этой
функции. В случае необходимости при
таком преобразовании можно соответствующим
образом добавлять константы. Например:

а)
;

б)

.

в)

(в последнем примере
записано ln(3 + x²)
вместо ln|3 + x²|
, так как выражение 3 + x²
всегда положительно).

Пример
3.
Найти
интегралы:

а)

;
б)

;
в);

г)
;
д)
;
е)
;

ж)
;
з)
.

Решение.

а)

.

Здесь
использованы формулы 2а, 5а и 7а таблицы
1, две последние из которых получены как
раз путем подведения под знак дифференциала:

,

.

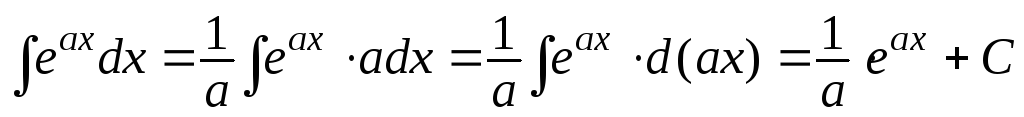
Интегрировать
функции вида

приходится очень часто в рамках вычисления
интегралов от более сложных функция.
Чтобы каждый раз не повторять описанные
выше действия, рекомендуем запомнить
соответствующие формулы, приведённые
в таблице 1.

б)

.

Здесь использована
формула 3 таблицы 1.

в)
Аналогично,
учитывая что
,
преобразуем:

.

Здесь
использована формула 2в таблицы 1.

г)

.

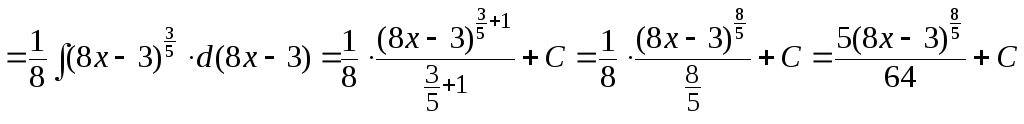
д)

;

е)

.

ж)

;

з)

.

Пример
4.
Найти
интегралы:

а)
б)

в)

.

Решение.

а)
Преобразуем:

.

Здесь так же
использована формула 3 таблицы 1.

б)
Используем формулу понижения степени
:

.

Здесь использованы
формулы 2а и 7а таблицы 1.

в)

.

Здесь наряду с
формулами 2 и 8 таблицы 1 использованы и
формулы таблицы 3:

,

.

Пример
5.
Найти
интегралы:

а)
;
б)

в);
г)
.

Решение.

а)
Произведение

можно дополнить (см. формулы 4 и 5 таблицы
3) до
дифференциала функции
,
где а
и b
– любые константы,
.
Действительно,
,
откуда
.

Тогда имеем:

.

б)
Используя формулу 6 таблицы 3, имеем
,
а также
,
значит, присутствие в подынтегральном
выражении произведения

означает подсказку: под знак дифференциала
нужно внести выражение
.
Поэтому получаем

.

в) Так
же как в пункте б), произведение

можно дополнить до дифференциала
функции
.
Тогда получим:

.

г)
Сначала воспользуемся свойствами
линейности интеграла:

.

Пример
6.
Найти
интегралы:

а)
;
б)
;

в) ; г)
.

Решение.

а)
Учитывая,
что

(формула 9 таблицы 3), преобразуем:

.

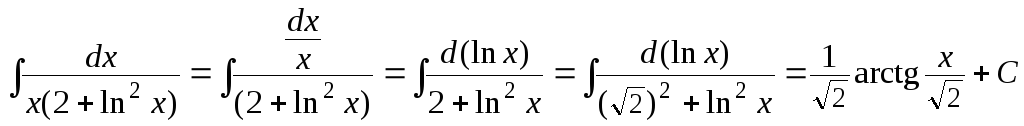
б)
Используя формулу 12 таблицы 3, получим

в)
Учитывая формулу 11 таблицы 3,
преобразуем

г) Используя формулу
16 таблицы 3, получим:

.

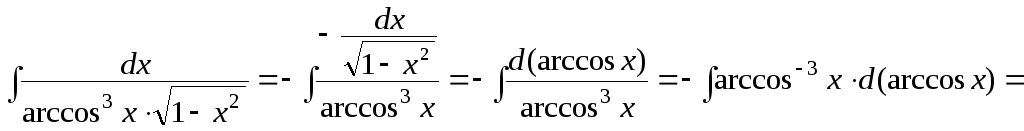
Пример
7.
Найти
интегралы:

а)
;
б)

;

в)
; г)

.

Решение.

а)
Все
представленные в этом примере интегралы
имеют общую особенность:
подынтегральная функция содержит
квадратный трехчлен. Поэтому и способ
вычисления этих интегралов будет основан
на одном и том же преобразовании –
выделении полного квадрата в этом
квадратном трехчлене.

.

б)

.

в)

.

г)

.

Прием подведения
под знак дифференциала является устной
реализацией более общего приема
вычисления интеграла, называемого
методом подстановки или заменой
переменной. Действительно, каждый раз,
подбирая подходящую формулу таблицы 1
к полученной в результате подведения
под знак дифференциала функции, мы
мысленно заменяли буквой и функцию,
внесенную под знак дифференциала.
Поэтому, если интегрирование путем
подведения под знак дифференциала не
очень получается, можно непосредственно
делать замену переменной. Подробнее об
этом – в следующем пункте.

Соседние файлы в папке Интегралы-Помощь

• #
• #
• #
• #

1. Основные понятия.

Для начала следует сказать, что интегралы бывают неопределённые и определённые. Нахождение простейшего интеграла сводится к нахождению общего вида первообразной. Результатом неопределённого интеграла является функция.

Вычисление простейшего определённого интеграла сводится к применению формулы Ньютона-Лейбница. Существует несколько методов нахождения интегралов:

• Непосредственное интегрирование
• Метод замены переменной
• Интегрирование почастям.

В общем виде определенный интеграл записывается так: ,где нижний предел интегрирования стандартно обозначается буквой , верхний предел интегрирования стандартно обозначается буквой . Отрезок называется отрезком интегрирования.

Ответим на следующие вопросы:

Что такое определенный интеграл?

Определенный интеграл – это число.

Есть ли у определенного интеграла геометрический смысл?

Есть. Самая популярная задача – вычисление площади с помощью определенного интеграла.

Что значит решить определенный интеграл?

Решить определенный интеграл – это значит, найти число.

Как решить определенный интеграл?

С помощью знакомой уже формулы Ньютона-Лейбница:

Этапы решения определенного интеграла следующие:

• Подставляем значение верхнего предела в первообразную функцию: .

Всегда ли существует определенный интеграл?

Нет, не всегда.

Рассмотрим пример вычисления интеграла , его не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными).

Может ли определенный интеграл быть равен отрицательному числу?

Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл.

Рассмотрим основные свойства определённого интеграла

Теорема 1.

Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.

Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница:

Теорема 2. Постоянный множитель можно выносить за знак определённого интеграла, т.е.

Теорема 3. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.

Теорема 4. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если

то

Теорема 5. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.

2. Рассмотрим примеры вычисления интегралов.

Пример 1. Вычислить определённый интеграл

Решение: Сначала найдём неопределённый интеграл, т.е. представим подынтегральную функцию в виде степени (заменив корень), получим х^1/3, а затем найдем первообразную этой функции:

Применяя формулу Ньютона-Лейбница к первообразной получим

Ответ: 12.

Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл.

Пример 2. Вычислить определённый интеграл

Решение: Вспомним, что е^2х — функция сложная, а значит при нахождении первообразной ( интеграла) нужно умножить на обратный коэффициент который стоит перед х, т.е. на ½. Используя формулу

получим,

Пример 3. Вычислить определенный интеграл

Решение:

Объяснение:

(1) Выносим константу за знак интеграла.

(2) Интегрируем по таблице с помощью самой популярной формулы . Появившуюся константу 1/3 целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?

(3) Используем формулу Ньютона-Лейбница . Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ 4²/₃

Ответ: 4²/₃

Пример 4. Вычислить определённый интеграл

Решение:

3. Далее рассмотрим еще примеры вычисления определённых интегралов, для этого посмотрите видео-урок https://videouroki.net/video/18-vychislenie-integralov.html. Если видео-урок будет пропущен, то будет намного сложнее выполнить домашнее задание.

Важно! Все интегралы, входящие в домашнюю работу, являютсяпростейшими интегралами.

Метод непосредственного интегрирования: примеры решения

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Метод непосредственного интегрирования заключается в применении простейших правил интегрирования, например, в применении табличных формул для раскрытия интегралов и правил, перечисленных сразу после таблицы.

Рисунок 1. Табличные интегралы для непосредственного интегрирования. Автор24 — интернет-биржа студенческих работ

Несколько основных правил, которые нужно помнить, вычисляя интеграл:

• Множитель-константу в подынтегральном выражении можно вынести перед знаком интегрирования;
• Интеграл суммы или разности нескольких функций равен сумме (разности) интегралов этих функций.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Пример 1

Найдите первообразную от $f(x) = 8 x^2 – 5x + 7$.

Решение:

Итак, начнём. Данная функция имеет в себе суммы и разности, а значит, интеграл от неё можно разложить:

$int ( 8 x^2 – 5x + 7)dx = int 8 x^2 dx — int 5x dx + int 7dx$.

Вынесем множители за знак интеграла. После этого всё решение сводится к использованию табличных значений:

$int 8 x^2 dx — int 5x dx + 7 int 7dx = 8 cdot int x^2 dx — 5 cdot int x dx + 7 int dx = frac83 cdot x^3 — frac52 cdot x^2 + 7x + C$.

Пример 2

Вычислить первообразную от функции $y=-frac{cos x}{3}$:

Ответ: $ int -frac{cos x}{3} = -frac13 int cos x = -frac13 sin x + C$.

Пример 3

Вычислите следующее выражение: $int (2x^2 + 1)^3 dx$.

Решение:

$int (2x^2 + 1)^3 dx = int (8x^6 + 12 x^4 + 6x^2 + 1) dx = frac87 x^7 + frac{12}{5} x^5 + 2x^3 + x + C$.

Пример 4

Очередной пример на нахождение интеграла: $int frac{(x — sqrt {x})(1 + sqrt{x})}{sqrt[3]{x}} cdot dx$.

Решение:

$int frac{(x — sqrt {x})(1 + sqrt{x})}{sqrt[3]{x}} cdot dx= int frac{x sqrt{x}- sqrt{x}}{sqrt[3]{x}} dx = int x^{frac76}dx — int x^{frac16}dx = frac{6}{13} x^{frac{13}{6}} — frac67 x^{frac76} + C$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 06.05.2023
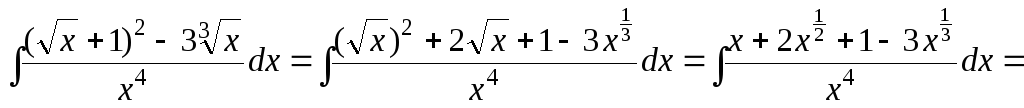
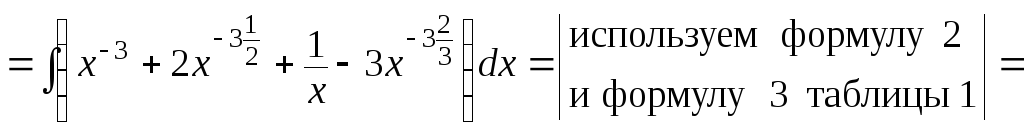
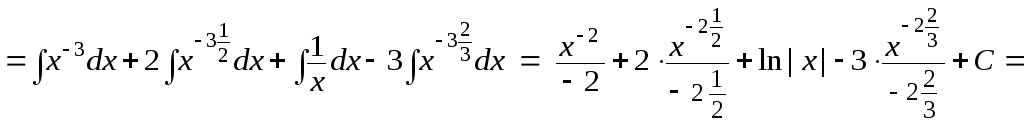
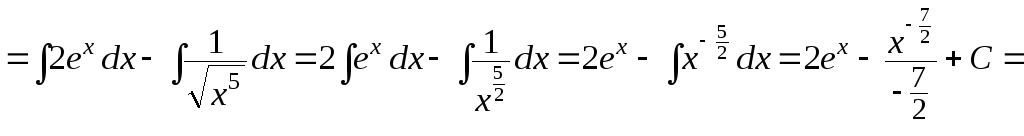
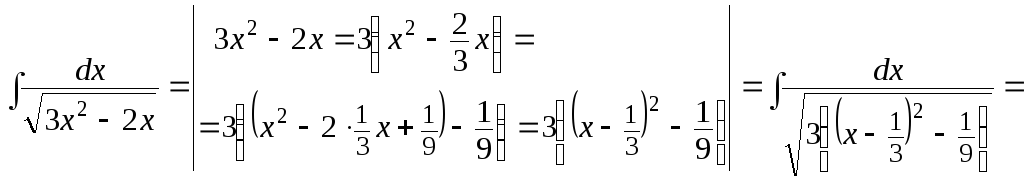
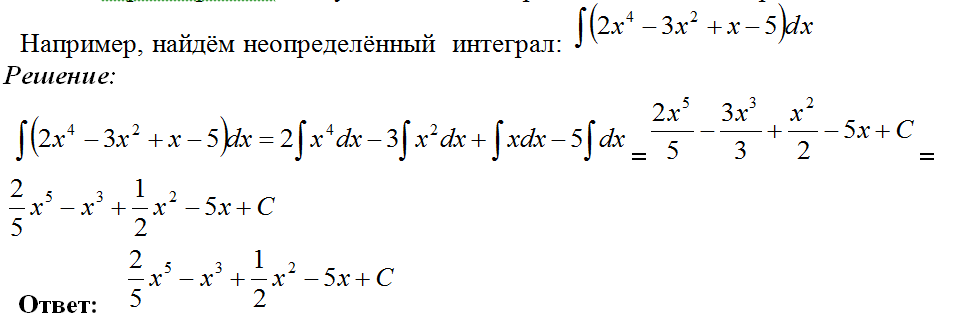