Как найти неопределенные интегралы в mathcad

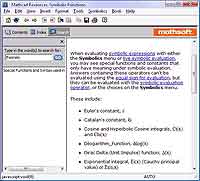
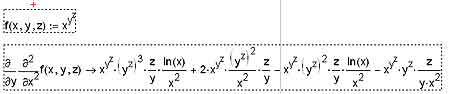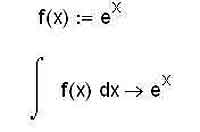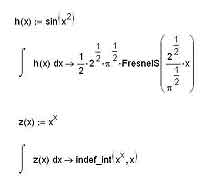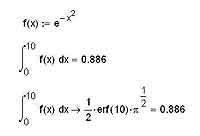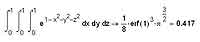В прошлый раз мы с вами научились использовать возможности мощнейшей математической среды MathCAD для вычисления различных вещей, относящихся к дифференциальному исчислению: пределов, производных, сумм сходящихся числовых и функциональных рядов. Сегодня мы с вами продолжим знакомство с тем, как в MathCAD вычислять многие важные вещи из ВУЗовского курса математического анализа. Надеюсь, что это будет для вас достаточно интересно.

Вычисление частных производных

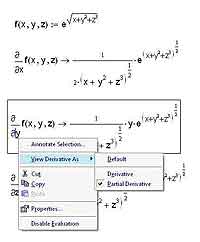
Напомню на всякий случай, что частными называются производные от функций нескольких переменных, берущиеся по одной или нескольким переменным. Для вычисления частных производных в MathCAD’е используются те же самые операторы, которые мы с вами уже весьма успешно применяли для вычисления полных производных. Единственное отличие — это, конечно же, оформление оператора взятия производной. В математическом анализе для отличия частных производных от полных используется специальная запись, в которой буква d, обозначающая производную, и сверху, и снизу пишется наклонной. MathCAD, как и во всех остальных случаях, позволяет пользователю применять привычную запись. Для того, чтобы изменить внешний вид оператора производной, выделите выражение и кликните по нему правой кнопкой мыши. В появившемся контекстном меню нужно выбрать пункт View Derivative As (Показывать производную как…), а в нем — Partial Derivative (Частная производная). Вы всегда можете вернуться к обычному отображению оператора производной, выбрав в том же самом меню пункт Derivative (Производная), который устанавливает для оператора производной вид оператора полной производной. Обратите внимание на то, что установка вида одного оператора взятия производной никак не влияет на все остальные операторы, как уже имеющиеся в вашей рабочей области, так и на те, которые будут добавлены в нее позднее.

Что касается такой весьма и весьма немаловажной вещи, как взятие смешанных производных, то она реализуется с помощью последовательного взятия частных производных по разным переменным. Хотя, конечно, в результате могут получаться и довольно громоздкие выражения, как, например, на иллюстрации, демонстрирующей применение нескольких операторов взятия производной для вычисления смешанных производных.

Неопределенные интегралы

Дифференцирование в математическом анализе неразрывно связано с интегрированием. Эти обратные друг другу действия — две стороны одной медали, а потому и мы с вами, поговорив об одном из них, перейдем к разговору о втором. У математиков есть шутка, что дифференцирование — это ремесло, а интегрирование — это искусство. MathCAD позволяет и интегрирование свести к уровню ремесла — если, конечно же, представлять себе, что в принципе может быть решаемо с помощью этой программы, а что нужно довести до того вида, в котором задачу уже можно «скармливать» MathCAD’у. Задача вычисления неопределенного интеграла обратна задаче нахождения производной функции. Неопределенный интеграл имеет также название первообразной, которое по ряду причин используется реже. Для вычисления неопределенных интегралов в среде MathCAD используется оператор, который можно легко найти на панели Calculus. Под знаком интеграла пользователь должен ввести функцию, для которой он хочет найти первообразную, а после знака дифференциала — переменную, по которой будет производиться интегрирование. Как видите, и здесь MathCAD верен себе, то есть дает пользователю возможность использовать, опять-таки, знакомые по математическому анализу обозначения неопределенных интегралов. Нужно отметить также, что для неопределенных интегралов необходимо применять символьное вычисление выражений, то есть знак «стрелочки», а не знак равенства.

Следует, впрочем, помнить, что многие интегралы просто принципиально не выражаются в элементарных функциях. В том случае, если вы подсунули MathCAD’у один из таких весьма распространенных интегралов, ситуация может иметь два различных финала: либо MathCAD успешно проинтегрирует выражение и выдаст результат с использованием каких-либо специальных функций, либо же честно признается, что его такое интегрировать не учили. Во втором случае вы увидите после «стрелочки», стоящей за интегралом, запись вида indef_int(f(x), x). Естественно, вместо f(x) и x будут соответственно стоять подынтегральная функция и та переменная, по которой вы хотели провести интегрирование. Оба возможных варианта продемонстрированы на иллюстрации ниже.

Со специальными функциями тоже все не так просто. Синтаксис, используемый для их записи в MathCAD’е, все же несколько отличается от принятого в математике, а потому, вполне вероятно, для того, чтобы разобраться в том, что за специальные функции скрываются за той или иной записью, придется воспользоваться справочной системой среды MathCAD. Для этого нажмите F1, в появившемся окне выберите вкладку Search, в поле рядом с кнопкой Go введите имя функции, информацию по которой вам нужно найти, а затем нажмите эту самую кнопку. Среди результатов поиска может оказаться и несколько разделов, и имеет смысл просмотреть их все.

В общем-то, даже в том случае, если MathCAD поднимает белый флаг при виде неопределенного интеграла, это не значит, что его вовсе невозможно вычислить в элементарных или специальных функциях. Вполне возможно, что с помощью каких-либо преобразований вам удастся привести его к виду, пригодному для решения в MathCAD. Также имеет смысл поискать решение в старых печатных справочниках или «погуглить» в интернете. Вполне возможно, что у MathCAD’а просто не хватило творческого воображения на то, чтобы до конца «раскрутить» ваш сложный интеграл.

Определенные интегралы

Неопределенные интегралы — это, конечно же, хорошо, но все же на практике куда как чаще используются интегралы определенные. И, думаю, для вас не окажется неожиданностью тот факт, что MathCAD прекрасно умеет справляться и с этим видом интегралов. Определенный интеграл, как вы понимаете, отличается от неопределенного наличием пределов интегрирования. Фактически неопределенный интеграл — это функция (первообразная подынтегральной функции), в то время как определенный интеграл — это просто какое-то число. То есть его мы можем вычислить не только аналитически, но и численно, что позволяет нам рассчитывать значения определенных интегралов даже тогда, когда первообразная рассчитана быть не может. Оператор для расчета определенных интегралов в MathCAD’е находится на панели Calculus недалеко от оператора расчета неопределенных интегралов и отличается от него, как я уже совсем недавно говорил, наличием пределов сверху и снизу от символа интеграла. После того, как вы запишете подынтегральное выражение, переменную интегрирования и собственно пределы, можно ставить знак равенства или стрелочку для вычисления определенного интеграла. В первом случае интеграл будет вычислен численно, во втором — аналитически.

Вопрос о том, какой способ вычисления интегралов использовать: численный или аналитический, — не такой надуманный и праздный, как может сначала показаться. Дело в том, что аналитически определенные интегралы вычисляются, во-первых, точнее, а во-вторых, быстрее, нежели численно. Правда, может возникнуть ситуация, аналогичная той, которую вы можете увидеть на иллюстрации выше — то есть символьный процессор не доведет процесс вычислений до конца, а оставит интеграл в виде смеси численных значений и функций. Впрочем, с этим всегда довольно просто справиться, как видите. Для вычисления кратных интегралов используется тот же прием, что и для вычисления смешанных частных производных для функций многих переменных. То есть мы последовательно интегрируем несколько раз функцию с заданными пределами, и в результате получаем именно то, что, в общем- то, и рассчитывали получить. Стоит отметить, что, поскольку при интегрировании кратных интегралов мы теряем при численном интегрировании особенно много времени, то здесь особенно желательно использовать именно аналитический способ вычисления интегралов.

В применении системы MathCAD для расчета определенных интегралов есть немало тонких моментов, которые не возникали при расчете интегралов неопределенных. Особенно это касается численных методов расчета интегралов. Как я уже говорил, эти методы позволяют рассчитать даже такие интегралы, которые не поддаются аналитическому вычислению. Однако за все надо платить, а потому использование численных методов интегрирования способно приводить к значительным погрешностям в результате, что, сами понимаете, при решении весьма значительного по своей распространенности класса задач не просто нежелательно, а часто даже совершенно недопустимо. О погрешностях при численном интегрировании в MathCAD’е и о том, как избежать того, чтобы они стали совсем уж гигантскими, мы с вами поговорим в следующий раз. А пока что давайте подведем итоги тому, о чем мы говорили сегодня.

Как видите, MathCAD с легкостью справляется с интегралами — пусть не со всеми, но с их значительной частью. Тех возможностей этой великолепной среды, о которых мы с вами уже успели поговорить в цикле статей «MathCAD — это просто!», на мой взгляд, как раз достаточно для того, чтобы прибавить вам энтузиазма в дальнейшем изучении этой программы.

SF, spaceflyer@tut.by

Как
и большинство математических операций,
интегрирование в MathCAD
может проводиться как численно, так и
в символьном виде. Каждый способ
вычислений имеет свои преимущества и
недостатки и, в отличие от дифференцирования,
здесь нельзя сказать однозначно, как
лучше всего проводить вычисления. Какой
способ интегрирования вы выберите для
той или иной функции в своих задачах,
будет зависеть от
вашего
опыта, интуиции, а также требований
конкретной задачи.

Численное
интегрирование.
Численно можно вычислить с большей или
меньшей точностью любой сходящийся
определенный интеграл с конечными или
бесконечными пределами интегрирования.
Пределы интегрирования обязаны быть
действительными, подынтегральная
функция может иметь и комплексные
значения, поэтому и значение интеграла
может быть комплексным.

Для
вычисления определенного интеграла
надо вставить в документ шаблон
оператора
определенного
интеграла с панели Calculus.
После заполнения всех полей ввода для
вычисления интеграла следует ввести
знак “=”.

При
численном интегрировании основная
проблема состоит в том, что интегрирование
с высокой точностью сложных функций
требует значительного времени. В таких
случаях приходится искать компромисс
между точностью и скоростью расчета. В
MathCAD
вы сами можете контролировать точность
проводимых вычислений. Для этого служит
встроенная переменная TOL.
Но нельзя сказать однозначно, какой
будет точность вычисления того или
иного интеграла при заданном значении
TOL.
Все численные методы интегрирования в
MathCAD
строятся на последовательных приближениях,
и значение переменной TOL
указывает, какой должна быть разница
между двумя последовательными
приближениями для остановки вычислений.
Поэтому не стоит воспринимать значение
этой переменной как точность вычисления
интеграла, можно лишь с уверенностью
сказать, точность будет не ниже значения
TOL.
Также следует помнить, что слишком
низкое значение TOL
может привести к тому, что MathCAD
не сможет вычислить интеграл и выдаст
ошибку, поэтому для большинства
однократных интегралов значение TOL
лучше выбирать в диапазоне 10^-3¸10^-4.

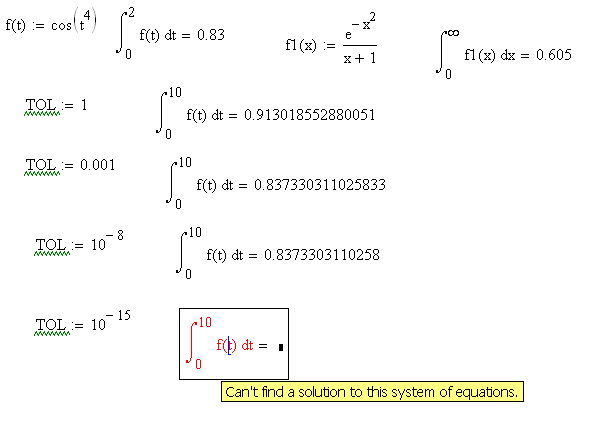
Точность
численного интегрирования также зависит
от численного метода, который используется
для вычисления интеграла. Существует
великое множество различных численных
методов интегрирования, и для того или
иного интеграла сложно заранее определить,
каким методом его можно вычислить
наиболее быстро и точно. В MathCAD
встроено несколько основных методов
численного интегрирования. Каждый из
этих методов предназначен для своего
класса интегралов. По умолчанию MathCAD
автоматически
выбирает тот или иной метод в зависимости
от введенной подынтегральной
функции и границ интегрирования
(вариант Auto
Select).
При желании можно выбрать численный
метод вручную, но в большинстве случаев
это только ухудшит результат. Для того,
чтобы выбрать численный метод для
вычисления интеграла, вызовите его
контекстное меню, которое содержит
кроме стандартных команд, еще и команды
выбора численного метода.

Символьное
интегрирование.
Символьный процессор MathCAD
позволяет вычислить как неопределенные,
так и определенные интегралы. Для
вычисления неопределенного интеграла
также существует свой оператор, как и
для определенного. Он находится на
панели Calculus
и позволяет вставить шаблон с двумя
полями ввода.

Командой
для символьных вычислений интегралов
является символьный оператор ®.
Результат (т.е. первообразная от
подынтегрального выражения) выводится
справа от стрелки. Если первообразную
функцию нельзя записать в аналитическом
виде, то справа от стрелки будет еще раз
переписан тот же интеграл.

Для
того, чтобы вычислить в символьном виде
определенный интеграл, MathCAD
сначала вычисляет первообразную, т.е.
повторяет действия неопределенного
интеграла. Далее, из значения первообразной
на верхней границе вычисляется ее
значение на нижней границе. Полученное
в результате выражение и возвращается
как ответ.

Значение
переменной TOL
не имеет никакого значения для символьных
вычислений.

Вычисление
интеграла – это, по-видимому, самая
сложная задача для символьного процессора
MathCAD.
Надо отметить, что символьное интегрирование
возможно только для небольшого круга
несложных подынтегральных функций.
Поэтому некоторые интегралы не могут
быть вычислены в символьном виде. Стоит
отметить, что существует несколько
интегралов, которые не имеют аналитического
выражения, но часто встречаются в
практических задачах. Эти интегралы в
математике носят определенные названия
и заданы в MathCAD
в виде специальных символьных функций
или констант. Таким образом, многие
интегралы, которые не имеют аналитического
выражения через элементарные функции,
будут все же вычислены символьным
процессором и записаны с использованием
специальных символьных функций MathCAD.

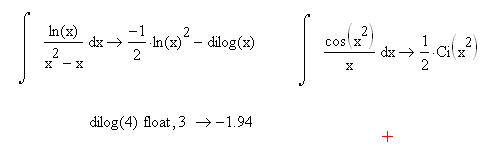
Однако
следует помнить, что результат символьного
интегрирования в данном случае является
лишь удобной записью того же интеграла.
Если понадобится определить значение
одной из этих функций в точке на числовой
оси, то придется вычислять соответствующий
интеграл численными методами.

Интегрирование
функций с параметром.
Следует помнить, что MathCAD
воспринимает все неопределенные
параметры в функциях как произвольные
комплексные функции. Поэтому интеграл
от функции с параметром будет вычислен
только в том случае, если он существует
при всех значениях параметра на
комплексной плоскости. Такое условие
выполняется далеко не для всех функций.
Решение данной проблемы является
использование модификатора символьных
вычислений assume.
С его помощью можно наложить определенные
ограничения на значения параметров,
входящих в подынтегральное выражение.

Вводится
интеграл, знак символьного вычисления
с полем ввода для модификатора, в которое
вводится ключевое слово assume
и через запятую условие, накладываемое
на параметр подынтегрального выражения
или несколько условий через запятую.

Расходящийся
интеграл.
Если интеграл расходится (равен
бесконечности), то вычислительный
процессор может выдать сообщение об
ошибке, а символьный процессор справляется
с этим интегралом, совершенно правильно
находя его бесконечное значение.

Кратные
интегралы.
Кроме однократных интегралов в MathCAD
есть возможность вычислять двойные,
тройные интегралы, а также интегралы
более высокой точности. Для вычисления
кратных интегралов не предусмотрено
отдельного оператора, для этого служит
уже знакомый оператор определенного
интеграла, в шаблоне которого в поле
ввода подынтегральной функции вводится
следующий шаблон определенного интеграла
ит.д.

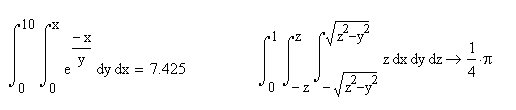
Кратные
интегралы являются сложной задачей как
для символьного процессора, так и для
численных расчетов. Стоит вначале
попытаться вычислить интеграл в
символьном виде, и если результат получен
не будет, вычислить его численно, задав
требуемое значение TOL.

Дополнительные
возможности символьного процессора.

1.
С помощью символьного процессора можно
рассчитать численное значение выражения
(действительное или комплексное). Иногда
такой путь считается более удобным, чем
применение численного процессора.

Вычисления
по команде complex
позволяют представить выражение в виде
a+jb.
Вышеприведенные действия можно
осуществить и с помощью соответствующих
команд из меню Symbolic.

2.
Последовательности символьных команд.

Символьные
вычисления допускается проводить с
применением цепочек из ключевых слов.
Для этого ключевые слова, соответствующие
последовательным символьным операциям,
должны быть введены по очереди с панели
Symbolic.
Последовательности символьных команд
допускают введение дополнительных
условий в расчеты, например, таких как
ограничения на действительную или
комплексную форму результата. Это
делается с помощью ключевого слова
assume.

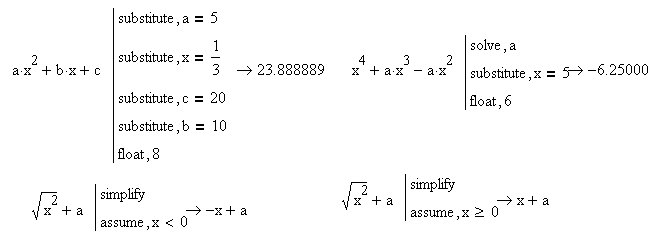
3.
Решение неравенств в символьной форме

4.
Решение систем уравнений в символьной
форме

Вопросы

1. Что
   такое символьные вычисления? Какие
   способы символьных вычислений имеются
   в системе MathCAD?
   В чем преимущество вычислений с помощью
   оператора символьного равенства перед
   вычислениями с помощью меню Symbolic?

2. Какой
   оператор осуществляет численные
   вычисления? И какой – символьные
   вычисления?

3. Какие
   алгебраические символьные вычисления
   может делать система MathCAD?
   Можно ли вычислить сумму или произведение
   ряда с помощью оператора численного
   вычисления, если верхний предел равен
   ¥
   ?

4. Какие
   матричные операции можно осуществить
   символьно?

5. Какие
   операторы предусмотрены для вычисления
   пределов в MathCADе?
   Можно ли вычислить предел численно?

6. Как
   осуществляется вычисление предела
   последовательности? Функции в точке,
   когда функция непрерывна, и в точках
   разрыва? Как можно обойти на графике
   особые точки функции (типа 0/0)?

7. Назовите
   три способа символьного дифференцирования.
   Приведите пример. Как можно определить
   производную в точке? Влияют ли константы
   TOL
   и CTOL
   на точность численного дифференцирования?
   Как можно определить производную вблизи
   точки разрыва?

8. Как
   вычисляются в MathCADе
   производные высших порядков и частные
   производные? Производные только каких
   порядков можно вычислить численно и
   почему?

9. Что
   такое численное интегрирование в
   MathCADе
   и как оно осуществляется? С помощью
   какой встроенной переменной можно
   контролировать точность численного
   интегрирования? От чего еще зависит
   точность численного интегрирования?

10. Назовите
    три способа символьного вычисления
    неопределенного интеграла в системе
    MathCAD.
    Приведите пример. Как осуществляется
    вычисление определенного интеграла с
    помощью оператора символьного равенства?

11. Как
    вычисляются интегралы с параметром,
    расходящиеся интегралы, кратные
    интегралы?

12. Как
    можно с помощью символьного процессора
    рассчитать численное значение выражения
    (вещественное или комплексное)?

13. Как
    создаются последовательности символьных
    команд? Приведите примеры.

14. Как
    решаются в MathCADе
    уравнения, неравенства и системы
    уравнений в символьной форме?

Лекция № 15

Решение дифференциальных
уравнений в MathCAD

Дифференциальные
уравнения являются основой огромного
количества расчетных задач из самых
различных областей науки и техники.

В
MathCAD
нет средств символьного (точного) решения
дифференциальных уравнений, но достаточно
хорошо представлены численные методы
их решения.

Дифференциальные
уравнения – это уравнения, в которых
неизвестные являются не
переменные
(т.е. числа), а функции
одной или нескольких переменных. Эти
уравнения (или системы) включают
соотношения между искомыми функциями
и их производными. Если в уравнения
входят производные только по одной
переменной, то они называются
обыкновенными дифференциальными
уравнениями (ОДУ). В противном случае
говорят об уравнениях в
частных производных.
Таким образом, решить
(иногда говорят проинтегрировать)
дифференциальное уравнение – значит,
определить
неизвестную функцию
на определенном интервале изменения
ее переменных.

Как
известно, одно обыкновенное дифференциальное
уравнение или система ОДУ имеет
единственное
решение, если помимо уравнения определенным
образом заданы начальные
или граничные
условия. Имеется два типа задач, для
которых возможно численное решение ОДУ
с помощью MathCAD:

• задачи
  Коши,
  для которых определены начальные
  условия на искомые функции, т.е. заданы
  значения этих функций в начальной точке
  интервала интегрирования уравнения;

• краевые
  задачи,
  для которых заданы определенные
  соотношения сразу на обеих границах
  интервала.

Из
дифференциальных уравнений в
частных производных
есть возможность решать только уравнения
с двумя
независимыми переменными:
одномерные
параболические
и гиперболические
уравнения, такие как уравнения
теплопроводности, диффузии, волновые
уравнения, а также двухмерные
эллиптические
уравнения (уравнения Пуассона и Лапласа).

В
MathCAD
нет универсальной функции для решения
дифференциальных уравнений, а есть
около двадцати функций для различных
видов уравнений, дополнительных условий
и методов решения. Эти функции можно
найти в библиотеке Insert/Function,
категория “Differential
Equation
Solving
(решение дифференциальных уравнений).

Решение
Обыкновенных Дифференциальных Уравнений
(ОДУ)

ОДУ
первого порядка.

ОДУ
первого порядка называется уравнение

F(x,y,y’)=0

F
– известная функция трех переменных;

x
– независимая переменная на интервале
интегрирования[a,b];

y
– неизвестная функция;

y’
– ее производная.

Функция
y(x)
является решением дифференциального
уравнения, если она при всех xÎ[a,b]
удовлетворяет уравнению

F(x,y(x),y’(x))=0

График
решения y(x)
называется интегральной кривой
дифференциального уравнения. Если не
заданы начальные условия, таких решений
y(x)
будет множество. При известных начальных
условиях y(x₀)=
y₀
решение y(x)
будет единственным.

Вычислительный
процессор MathCAD
может работать только с нормальной
формой
ОДУ. Нормальная
форма
ОДУ – это ОДУ, разрешенное относительно
производной

y’=f(x,y)

ОДУ
высших порядков.

Обыкновенным
дифференциальным уравнением n-го
порядка называется уравнение вида

F(x,y,y’,y’’,
…,y⁽ⁿ⁾)=0

F
– известная функция n+2
переменных;

x
– независимая переменная на интервале
интегрирования[a,b];

y
– неизвестная функция;

n
– порядок уравнения.

Функция
y(x)
является решением дифференциального
уравнения, если она при всех xÎ[a,b]
удовлетворяет уравнению

F(x,
y(x), y’(x), y’’(x),…, y⁽ⁿ⁾(x))=0

Нормальная
форма
ОДУ высшего порядка имеет вид

Y⁽ⁿ⁾
=f(x,
y,
y’,
…, y^(n-1))

Если
не заданы начальные условия, то
дифференциальное уравнение n
– го порядка имеет бесконечное множество
решений, при задании начальных условий
y(x₀)=
y₀,
y’(x₀)=
y_0,1,
y’’(x₀)=
y_0,2,
…, y^(n-1)(x₀)=
y_0,n-1
решение становится единственным (задача
Коши).

Задача
Коши для дифференциального уравнения
n
– го порядка может быть сведена к задаче
Коши для нормальной системы n
дифференциальных уравнений 1 го порядка,
которая в векторной форме имеет вид

Y’
= F(x,
Y),
Y(x₀)
= Y₀

Y(x₀)
= Y₀
– вектор начальных условий;

Y’=(y’₁,
y’₂,
…, y’_n)
– вектор первых производных;

F(x,
Y)
= (y₂,
y₃,
…, y_n,
f(x,y₁,
… , y_n)
– вектор правых частей;

Y
= (y₂,
y₃,
…, y_n)
– вектор искомого решения.

Эта
система получается в результате следующей
замены:

,где

Для
численного интегрирования ОДУ в MathCAD
имеется выбор – либо использовать
вычислительный блок Given/Odesolve,
либо встроенные функции. Оба способа
обладают одинаковыми возможностями,
но при использовании блока решения
запись уравнений более привычна и
наглядна, однако отдельная функция
может быть использована в составе других
функций и программ. Рассмотрим оба
варианта решения.

Вычислительный
блок Given/Odesolve

Ниже
приведены два примера для решения
дифференциальных уравнений первого и
второго порядка с использованием
вычислительного блока решения
Given/Odesolve.

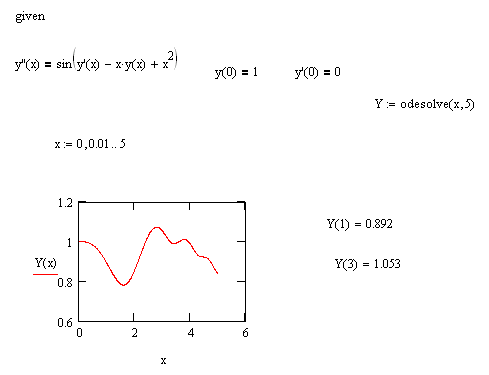
Вычислительный
блок для решения одного ОДУ состоит из
трех частей:

• ключевое
  слово given;

• ОДУ
  и начальные условия, записанные с
  помощью логического равенства;

• встроенная
  функция Odesolve(x,
  b)
  относительно независимой переменной
  x
  на интервале [a,
  b];
  b
  –
  верхняя
  граница отрезка интегрирования.
  Допустимо и даже предпочтительнее
  задание функции Odesolve(a,
  b,
  step)
  с тремя параметрами, где step
  – внутренний параметр численного
  метода, определяющий количество шагов;
  чем больше step,
  тем с лучшей точностью будет получен
  результат, но тем больше времени будет
  затрачено на его поиск.

Функция
Odesolve
возвращает решение задачи в виде функции.
Эта функция не имеет символьного
представления и может только вернуть
численное значение решения уравнения
в любой точке интервала интегрирования.

Функция
Odesolve
использует для решения дифференциальных
уравнений наиболее популярный алгоритм
Рунге-Кутта четвертого порядка, описанный
в большинстве книг по методам вычислений.
Он обеспечивает малую погрешность для
широкого класса систем ОДУ за исключением
жестких систем. Если щелчком правой
кнопки мыши на блоке формул с функцией
Odesolve
вызвать контекстное меню, то можно
изменить метод вычисления решения,
выбрав один из трех вариантов: Fixed
– метод Рунге-Кутта с фиксированным
шагом интегрирования (этот метод
используется по умолчанию), Adaptive
– также метод Рунге-Кутта, но с переменным
шагом, изменяемым в зависимости от
скорости изменения функции решения,
Stiff
– метод, адаптированный для решения
жестких уравнений и систем (используется
так называемый метод PADAUS).

Альтернативный
метод
решения ОДУ заключается в использовании
одной из встроенных функций: rkfixed,
Rkadapt,
или Bulstoer.
Все они решают задачу Коши для системы
дифференциальных
уравнений первого
порядка,
но каждая из них использует для этого
свой метод. Для простых
систем не играет большой роли, какой
метод использовать – все равно получите
решение достаточно быстро и с высокой
точностью. Но для сложных
или специфических
систем
бывает, что некоторые методы вообще не
могут дать удовлетворительного решения
за приемлемое время. Именно для таких
сложных, но не редких случаев в MathCAD
и введено несколько различных методов
решения систем ДУ.

• rkfixed
  – метод Рунге-Кутта с фиксированным
  шагом интегрирования. Самый простой и
  быстрый метод, но далеко не всегда самый
  точный. Полностью аналогичен использованию
  функции Odesolve
  с выбранным в контекстном меню методом
  Fixed.

• Rkadapt
  – метод Рунге-Кутта с переменным шагом
  интегрирования. Величина шага адаптируется
  к скорости изменения функции решения.
  Данный метод позволяет эффективно
  находить решения уравнений, в случае
  если оно содержит как плавные, так и
  быстро меняющиеся участки. Там, где
  решение меняется слабо, шаги выбираются
  более редкими, а в областях его сильных
  изменений – частыми. В результате для
  достижения одинаковой точности требуется
  меньшее число шагов, чем для rkfixed.
  Полностью аналогичен использованию
  функции Odesolve
  с выбранным в контекстном меню методом
  Adaptive.

• Bulstoer
  – метод Булирша – Штера. Этот метод
  более эффективен, чем метод Рунге-Кутта,
  в случае если решение является плавной
  функцией.

Имена
функций Rkadapt
и Bulstoer
начинаются с прописной буквы. В MathCAD
для некоторых имен функций неважно, с
какой буквы они записаны, но для
перечисленных функций это принципиально,
т.к. в MathCAD
также существуют функции с такими же
именами, только записанные с маленькой
буквы – rkadap,
bulstoer.
Эти функции используются в тех случаях,
когда важным является решение задачи
в конечной точке интервала интегрирования.

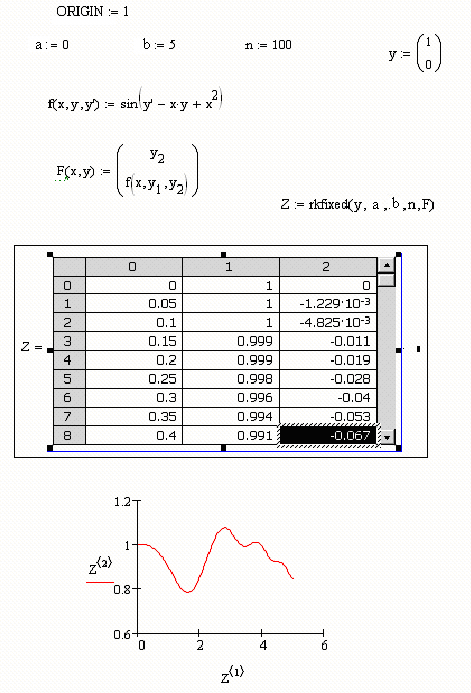
Выше
приведены примеры решения тех же
дифференциальных уравнений первого и
второго порядка, которые были решены с
использованием вычислительного блока
Given/Odesolve.

Применение
встроенных функций в документах MathCAD
выглядит сходным образом, т.е. функции
Rkadapt
и Bulstoer
имеют тот же синтаксис, что и выше
приведенная функция rkfixed.
Назначение аргументов в этих встроенных
функциях следующее:

• y
  – вектор начальных значений неизвестных
  функций, входящих в систему. В случае
  одного уравнения и одной неизвестной
  функции – это просто число.

• а
  – начало отрезка, на котором ищется
  решение системы (отрезка интегрирования).
  Именно в этой точке значения неизвестных
  функций принимаются равными элементам
  вектора y.

• b
  – конец отрезка интегрирования.

• n
  – количество частей, на которые
  разбивается отрезок [a,
  b]
  при решении системы. Чем больше это
  число, тем точнее получается решение,
  но расчет занимает больше времени.

• F(x,y)
  – векторная функция, элементы которой
  содержат правые части уравнений системы
  в нормальной
  форме
  (когда левые части – первые производные
  от соответствующих функций, а в правых
  частях производные отсутствуют).
  Аргументами этой функции являются
  вектор y,
  элементы которого соответствуют
  различным неизвестным функциям системы,
  и скалярный аргумент x
  , соответствующий независимой переменной
  в системе. В случае одного уравнения
  функция F
  может быть скалярной функцией, зависящей
  от двух скалярных переменных x
  и y.

Возвращаемым
значением всех вышеперечисленных
встроенных функций является матрица.
Первый столбец этой матрицы – это точки,
на которые разбивается отрезок [a,
b],
а остальные столбцы – это значения
функций системы в этих точках. Если в
аргументе функции rkfixed
было указано количество частей n
= 100, то матрица будет содержать 101 строку
вместе с начальной.

Решение
систем обыкновенных дифференциальных
уравнений.

Для
численного интегрирования систем ОДУ
в MathCAD
также имеется выбор – либо использовать
вычислительный блок Given/Odesolve,
либо встроенные функции rkfixed,
Rkadapt
и Bulstoer.

При
решении систем ОДУ MathCAD
требует, чтобы система ОДУ была
представлена в нормальной форме (когда
левые части – первые производные от
соответствующих функций, а в правых
частях производные отсутствуют):

где
Y
и Y’
– соответствующие неизвестные векторные
функции переменной t,
а F
– вектор правых частей системы уравнений
первого порядка. Именно векторное
представление используется для ввода
системы ОДУ в среде MathCAD.

Если
в систему ОДУ входят и уравнения
высших порядков,
то оно тоже сводится к системе уравнений
первого порядка, как было показано выше.
При этом количество нулевых условий
для вычислительного блока Given/Odesolve,
а также размер вектора начальных условий
y
и размер вектора правых частей F(x,y)
для встроенных функций rkfixed,
Rkadapt
и Bulstoer
должны быть равны сумме
порядков всех уравнений.

Вначале
покажем решение систем ОДУ первого
порядка с использованием вычислительного
блока Given/Odesolve

Функция
Odesolve
для системы ОДУ имеет несколько иной,
по сравнению с одним уравнением,
синтаксис. Теперь она возвращает вектор
функций, составляющих решение системы.
Поэтому в качестве первого аргумента
функции нужно ввести вектор, состоящий
из имен функций, использованных при
вводе системы. Второй и третий аргументы
то же самое, что и в задаче с одним ОДУ.

Решение
системы ОДУ показано на графике слева.
Как известно, решения ОДУ часто удобнее
изображать не в таком виде, а в фазовом
пространстве, по каждой из осей которого
откладываются значения каждой из
найденных функций (как показано на
рисунке справа). При этом аргумент входит
в них лишь параметрически. В рассматриваемом
случае двух ОДУ такой график – фазовый
портрет системы
– является кривой на фазовой плоскости.
В общем случае, если система состоит из
N
ОДУ, то фазовое пространство является
N
– мерным. При N
> 3 наглядность теряется, и для
визуализации фазового портрета приходится
строить его различные проекции.

Рассмотрим
решение этой же системы ОДУ первого
порядка с использованием встроенной
функции rkfixed.

Полученное
решение полностью соответствует
вышеприведенному решению с использованием
вычислительного блока Given/Odesolve.
Следует отметить, что начальные условия
здесь задаются в виде вектора y,
а функциям x(t)
и y(t)
соответствуют элементы этого вектора
y₁
и y₂.
Вектор начальных условий y
и вектор правых частей F
имеют размер равный двум, т.к. система
состоит из двух уравнений первого
порядка. Для системы ОДУ, состоящей из
двух уравнений второго порядка, размер
этих векторов будет равен четырем

Решение
жестких ОДУ и систем ОДУ
.

Сложно
дать математически точное определение
жесткости, поскольку задачи, входящие
в этот класс, весьма разнообразны. Чаще
всего жесткими дифференциальными
уравнениями называются уравнения, в
решении которых есть плавно меняющаяся
компонента, а также быстро затухающие
возмущения.

Для
жестких систем (stiff)
не работает обычный метод Рунге-Кутта
или Булирша-Штера. Наличие быстро
затухающего возмущения приводит к тому,
что эти численные методы дают расходящееся
решение. Для жестких задач разрабатываются
специальные методы. В MathCAD
предусмотрены три различные функции
для решения жестких задач:

• Radau
  – метод Radaus
  для жестких систем. Полностью аналогичен
  использованию функции odesolve
  с выбранным в контекстном меню методом
  Stiff.

• Stiffb
  – метод Булирша-Штера, адаптированный
  для жестких систем.

• Stiffr
  – метод Розенброка.

Краевые
задачи для ОДУ

Постановка
краевых задач для ОДУ отличается от
задач Коши, рассмотренных выше, тем, что
граничные условия для них ставятся не
в одной начальной точке, а на обеих
границах расчетного интервала. Если
имеется система N
ОДУ первого порядка, то часть из N
условий может быть поставлена на одной
границе интервала, а оставшиеся условия
– на противоположной границе. В связи
с тем, что условия поставлены не на
одной, а на обеих границах интервала,
краевые задачи нельзя решить изложенными
выше методами, предназначенными для
задач Коши. Для решения краевой задачи
в MathCAD
нет отдельной функции. Однако есть
функции, позволяющие превратить краевую
задачу в задачу Коши. Эти функции
«угадывают» недостающие начальные
условия, исходя из того, что решение
должно удовлетворять заданным условиям
в конечной точке интервала интегрирования.
Простейшей из функций, предназначенных
для приведения краевой задачи к задаче
Коши, является функция sbval.
Для того, чтобы решить двухточечную
краевую задачу с помощью этой функции,
следует выполнить следующие действия:

1. Задайте
   вектор v
   с количеством элементов равным количеству
   недостающих начальных условий. Значения
   элементов этого вектора – это начальные
   приближения, исходя из которых будет
   происходить поиск недостающих начальных
   условий. На данном этапе не конкретизируется,
   какой из элементов вектора будет
   соответствовать начальному значению
   той или иной неизвестной функции в
   задаче.

2. Задайте
   функцию F(x,y).
   Эта функция уже описывалась выше. Она
   представляет собой вектор, каждый
   элемент которого – это правая часть
   одного из уравнений системы.

3. Задайте
   еще одну векторную функцию load(x,v).
   Это функция от скалярного аргумента x
   и вектора v,
   который имеет столько же компонент,
   сколько недостающих начальных условий
   в системе. Сам вектор load
   должен содержать такое же количество
   элементов, как и вектор F,
   т.е. столько, сколько должно быть
   начальных условий в задаче. Если
   начальное значение какой-либо из функций
   известно, то соответствующий элемент
   вектора load
   должен содержать это значение. Для
   функций, начальное значение которых
   неизвестно, соответствующий элемент
   вектора load
   должен содержать один из элементов
   вектора v.

4. Следует
   задать еще одну некоторую функцию
   score(x,y).
   Аргументы этой функции – скаляр x
   и вектор y,
   который имеет столько элементов, сколько
   уравнений в системе. Количество компонент
   вектора score
   должно равняться количеству граничных
   условий, заданных в конечной точке
   отрезка интегрирования. На самом деле
   каждая компонента этого вектора задает
   одно из граничных условий в конечной
   точке. Например, если в задаче есть
   граничной условие y_i(b)=c,
   то один из элементов вектора score
   должен быть функцией, которая обращается
   в нуль при значениях x=b
   и y(b)=c.
   Конкретный вид этой функции не играет
   особой роли, поэтому проще всего задавать
   ее в таком виде: score_k(x,y):=y_i-c.
   Таким же образом должны быть заданы
   все элементы вектора score
   для всех конечных условий задачи.

5. Теперь
   все введенные величины нужно использовать
   как аргументы в функции sbval.
   Использование этой функции выглядит
   следующим образом: Y:=sbval(v,a,b,F,load,score).
   Аргументы a
   и b
   – это начало и конец отрезка интегрирования.

6. Результатом
   функции sbval
   будет вектор, содержащий недостающие
   начальные значения. Их последовательность
   задается той последовательностью, в
   которой были использованы компоненты
   вектора v
   в функции load.

7. Постройте
   вектор начальных значений, используя
   известные начальные значения, а также
   элементы вектора Y,
   там где значения были неизвестны.

8. Теперь
   можно решить полученную задачу как
   задачу Коши, с помощью, например, функции
   Rkadapt.

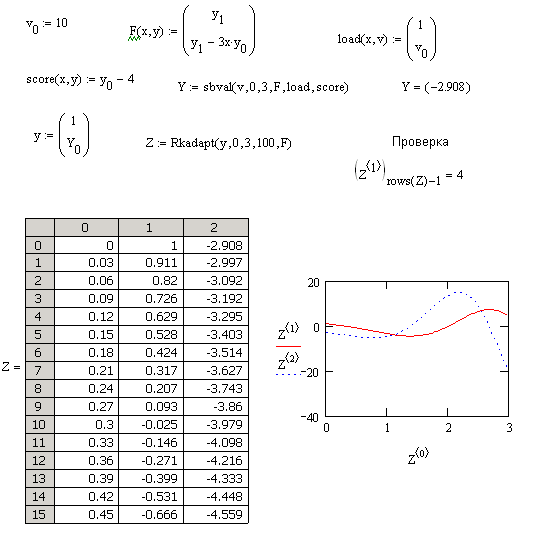
Ниже
приведено решение дифференциального
уравнения

на отрезке [0,3] с начальным условием
y(0)=1
и граничным условием y(3)=4.
Недостающее начальное условие – y’(0).

Решение
уравнений в частных производных.

Постановка
задач для уравнений в частных производных
включает определение самого уравнения
(или системы нескольких уравнений), а
также необходимого количества краевых
условий (число и характер которых зависит
от специфики уравнения). Согласно своему
названию, уравнения должны содержать
частные производные неизвестной функции
u
(или нескольких функций, если уравнений
несколько) по различным аргументам,
например, пространственной переменной
x
и времени t.
Соответственно, для решения задачи
требуется вычислить функцию нескольких
переменных, например, u(x,t)
в некоторой области определения
аргументов 0 £
x
£
L
и 0£
t
£
T.
Граничные условия определяются как
заданные временные зависимости функции
u,
или производных этой функции, на границах
расчетной области 0 и L,
а начальные – как заданная функция
u(x,0).

Сами
уравнения в частных производных
(несколько условно) можно разделить на
три основных типа:

• параболические
  – содержащие первую производную по
  одной переменной и вторую – по другой,
  причем все эти производные входят в
  уравнение с одинаковым знаком;

• гиперболические
  – содержащие первую производную по
  одной переменной и вторую – по другой,
  входящие в уравнения с разными знаками;

• эллиптические
  – содержащие только вторые производные,
  причем одного знака.

Средства
MathCAD
позволяют решать одномерные параболические
и гиперболические уравнения (с одной
пространственной и одной временной
переменной), а также двумерное уравнение
Пуассона. Такой, казалось бы, узкий круг
решаемых задач на самом деле охватывает
подавляющее большинство задач, возникающих
в физике и технике.

Дифференциальные
уравнения параболического типа.

Для
решения дифференциальных уравнений в
частных производных параболического
типа можно построить группу решения с
функцией pdesolve.
Такая группа решения состоит из следующих
элементов.

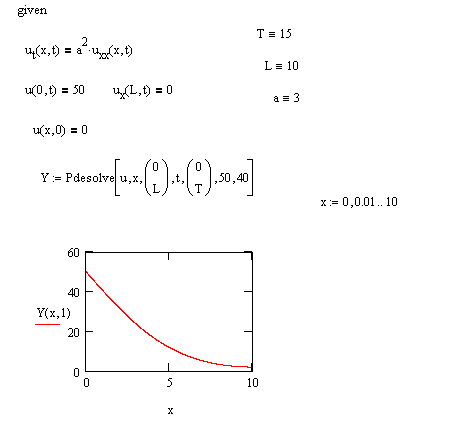
1. Ключевое
   слово given

2. Уравнение,
   которое нужно решить. Уравнение должно
   иметь такой вид:
   
   .
   Для ввода производных в данном случае
   нельзя пользоваться обычным оператором
   производной, а нужно пользоваться
   нижним индексом, как это обычно делается
   в литературе для записи уравнений в
   частных производных. При этом нижний
   индекс набирается не как числовой, а
   как буквенный (точка).

3. Граничные
   условия для функции u(x,t).
   Если уравнение второго порядка по x,
   то граничных условий должно быть два.
   Можно использовать как граничные
   условия Дирихле (u(x₀,t)
   = w(t)),
   так и граничные условия Неймана (u_x(x₀,t)
   = w(t))
   или их комбинацию, как в вышеприведенном
   примере.

4. Начальное
   значение для неизвестной функции –
   u(x,0).

5. функция
   pdsolve(u,x,xrange,t,trange,xpts,tpts). Ее
   аргументы имеют следующее назначение

   • u
     – имя функции, относительно которой
     решается уравнение. Для системы
     уравнений здесь должен быть вектор
     имен функций (как в odesolve).

   • X-
     имя
     пространственной переменной.

   • Xrange
     – двухкомпонентный вектор, задающий
     начало и конец интервала изменения
     пространственной переменной.

   • T
     – имя временной переменной. Основная
     разница между пространственной и
     временной переменными в данном случае
     – это то, что все уравнения могут
     содержать только первые производные
     по временной переменной.

   • Trange
     – еще один двухкомпонентный вектор.
     Этот вектор задает начало и конец
     временного интервала, на котором
     решается задача.

   • Xpts,
     tpts
     – количество точек, разбивающих для
     интегрирования пространственный и
     временной интервалы соответственно.
     Эти два параметра можно не указывать,
     тогда количество точек будет выбрано
     автоматически из соображений достаточной
     точности. Рекомендуется задавать эти
     параметры во всех задачах, кроме
     простых, поскольку во многих случаях
     высокая точность вычислений теряет
     смысл из-за погрешности, вносимой самим
     методом.

Выше
приведен пример решения одномерной
задачи теплопроводности для одного
бруска, один конец которого теплоизолирован,
а ругой поддерживается при определенной
температуре

Дифференциальные
уравнения гиперболического типа.

Функция
pdsolve
также позволяет решать системы ДУ в
частных производных первого порядка
по времени. Такая возможность может
быть использована для решения задач с
ДУ гиперболического типа. Ведь поскольку
уравнения гиперболического типа содержат
вторую производную по времени, то они
не могут быть напрямую введены для
решения функцией pdsolve.
ДУ гиперболического типа должно быть
приведено к системе из двух уравнений
первого порядка по времени (как это
делалось ранее для обычных ДУ высоких
порядков). А далее полученная задача
может быть решена с помощью функции
pdsolve
как система уравнений.

Помимо
вычислительного блока given/pdsolve,
для решения параболических и гиперболических
уравнений можно использовать встроенную
функцию numol.

Эллиптические
уравнения.

Решение
эллиптических уравнений в частных
производных реализовано только для
единственного типа задач – двумерного
уравнения Пуассона. Это уравнение
содержит вторые производные функции
u(x,y)
по двум пространственным переменным.
Для его решения в MathCAD
есть отдельные встроенные функции
multigrid
и relax.

Вопросы

1. Какие
   дифференциальные уравнения называются
   ОДУ первого порядка? Высшего порядка?
   Что такое нормальная форма ОДУ первого
   и высшего порядка? К чему сводятся ОДУ
   высшего порядка при решении?

2. Можно
   ли решить дифференциальные уравнения
   в MathCADе
   символьно?

3. Как
   решаются ОДУ с помощью вычислительного
   блока Given/Odesolve?
   Какой метод решения реализует функция
   Odesolve?
   Как можно изменить метод решения для
   этой функции?

4. Как
   решаются ОДУ с помощью встроенной
   функции rkfixed?
   Чем функция rkfixed
   отличается от функции Rkadapt?

5. Как
   осуществляется решение системы ОДУ с
   помощью вычислительного блока
   Given/Odesolve?
   Приведите примеры.

6. Как
   осуществляется решение системы ОДУ с
   помощью функции rkfixed?
   Приведите примеры.

Лекция №
16

Программирование
в MathCAD

MathCAD
– это система, ориентированная на
пользователя, который не обязан знать
абсолютно ничего о программировании.
Создатели MathCAD
изначально поставили перед собой такую
задачу, чтобы дать возможность
профессионалам – математикам, физикам
и инженерам самостоятельно проводить
сложные расчеты, не обращаясь за помощью
к программистам. Несмотря на блестящее
воплощение этих замыслов, выяснилось,
что совсем без программирования MathCAD
серьезно теряет в своей силе, в основном,
из-за недовольства пользователей,
знакомых с техникой создания программ.

В
очень ранних версиях MathCAD
встроенного языка программирования не
было. Чтобы применять привычные операции
проверки условий и организовывать
циклы, приходилось изобретать причудливую
смесь из встроенных функций if
и until,
а также комбинаций ранжированных
переменных. Но надо отметить, что
использование ранжированных переменных
– мощный аппарат MathCAD,
похожий на применение циклов в
программировании. В подавляющем
большинстве случаев намного удобнее
организовать циклы с помощью ранжированных,
чем заниматься для этого программированием.

И
тем не менее встроенный язык программирования
MathCADпозволяет
решать самые различные, в том числе и
довольно сложные, задачи и является
серьезным подспорьем для расчетов.
Поэтому последние версии MathCAD
имеют не очень мощный, но весьма элегантный
собственный язык программирования.

Для
вставки программного кода в документы
MathCAD
имеется
специальная
панель инструментов

.

Большинство
кнопок этой панели выполнено в виде
текстового представления операторов
программирования, поэтому их смысл
легко понятен. Операторы
программирования могут быть введены
только с этой панели, но никак не с
клавиатуры (можно еще их вводить с
помощью сочетаний клавиш, которые
приведены в тексте всплывающей подсказки).

Создание
программного блока начинается с команды

.
Нажатие
этой клавиши приведет к тому, что в
рабочей области документа появится
вертикальная черта, а справа от нее –
два пустые поля ввода

Вертикальная
черта означает, что строки, находящиеся
справа от нее, образуют линейную
программную последовательность операций.
Эта черта является особенностью программ
MathCAD.
В полях ввода можно ввести две первые
строки программы, а если требуется
большее число строк, то необходимо
нажимать клавишу

столько раз, сколько необходимо строк.
Не стоит забывать, что программа является
полноценным выражением MathCAD.
Это
выражение может быть использовано для
присвоения значения скалярной или
векторной переменной или определения
функции, или даже в составе другого
выражения, в том числе и другой программы.

Для
определения
функции
это будет выглядеть следующим образом:

Внутри
программы можно использовать глобальные
переменные документа, но изменить
их значение внутри программы никак
нельзя.
Можно создать в программе другие
переменные, доступ к которым может
осуществляться только из самой программы.
Эти переменные называются локальными
переменными. Локальные переменные «не
видны» извне. Локальная переменная
создается с помощью знака локального
присвоения

с панели Programming.
Для оператора локального присваивания,
так же как и для операторов обычного

и глобального

присваивания, можно изменить внешний
вид так, чтобы он выглядел как обычный
знак равенства. Для этого достаточно
вызвать контекстное меню этого оператора
и в нем выбрать команду View
Definition
As/Equal.

Последняя
строка любой программы не должна
содержать никаких управляющих операторов.
Эта строка задает значение, возвращаемое
программой. В качестве этого значения
может быть скаляр
(число или переменная), вектор или
матрица.
Таким образом, последняя строка программы
может содержать имя локальной переменной
либо некоторое математическое выражение,
куда входят как локальные, так и глобальные
переменные, либо вектор или матрицу.

Вставить
строку программного кода в уже созданную
программу можно в любой момент с помощью
той же самой кнопки Add
Line.
Для этого следует поместить на нужное
место внутри программы линии ввода.

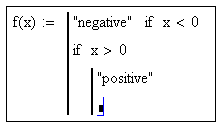
Если
вертикальная линия ввода находится в
начале текущей строки, то нажатие кнопки

приведет к появлению новой строки перед
текущей строкой, если вертикальная
линия ввода находится в конце строки,
то нажатие кнопки

приведет к появлению новой строки после
текущей. Можно выделить только часть
текущей строки, что повлияет на положение
новой строки в программе (например, если
необходимо для некоторого условия
выполнить не одно действие, а несколько).
Таким образом, основной принцип создания
программных модулей заключается в
правильном расположении строк кода.
Ориентироваться в их действии довольно
легко, т.к. фрагменты кода одного уровня
сгруппированы в программе с помощью
вертикальных черт.

Проверка
условий в программах.

Программы
в MathCAD
могут быть не только линейными, но и
разветвленными. Одним из вариантов
ветвления в программах является проверка
условия. Условия могут проверять значения
как локальных, так и глобальных переменных,
а также выражений, содержащих эти
переменные.

Для
проверки условий в программах MathCAD
служит оператор if

.
В поле
ввода справа
нужно ввести условие. Для ввода условий
служит панель Boolean.
На этой панели есть кнопки, предназначенные
для проверки условий


,
а также кнопки, предназначенные для
вставки логических операций

(логическое отрицание, операция «и»,
операция «или», операция «исключающее
или»). Вторые позволяют создавать сложные
условия. В поле
ввода слева
нужно ввести строку программы, которая
должна выполняться, если введенное
условие
истинно.

Если
для условия «истинно» необходимо
выполнение нескольких строк программы,
надо воспользоваться кнопкой

.

Если
невыполнение
условия должно привести к выполнению
какого-либо иного программного кода,
можно в строке, следующей за оператором
if,
вставить оператор

.
В поле
ввода слева
от этого оператора необходимо ввести
строку программы, которая будет
выполняться только в том случае, если
не выполнилось условие, заданное в
операторе if.

Следует
помнить, что если в программе введено
подряд несколько строк с оператором if

,

то
выражение слева от оператора otherwise
будет выполнено только в том случае,
если не выполняются условия, заданные
во всех операторах if.

Примеры:

Создание
циклов.

Другим
очень важным элементом при создании
нелинейных программ являются циклы.
Циклы позволяют повторять несколько
раз выполнение одного и того же
программного блока. Для создания циклов
в MathCAD
предусмотрено два оператора for
и while.

Цикл
for
– цикл со счетчиком.

В
таких циклах создается некоторая
переменная-счетчик, значение которой
изменяется после каждого выполнения
тела цикла. Выход из цикла происходит
при достижении этой переменной заданного
значения. Этот оператор вводится с
панели Programming
клавишей for

.
В поле
ввода после слова for
следует указать имя переменной –
счетчика. Это может быть любое имя,
которое не использовалось ранее в
программе. Внутри цикла можно использовать
эту переменную в любых выражениях,
нельзя только присваивать ей никакого
значения. В поле
ввода после знака

следует указать диапазон значений
переменной-счетчика. Вводить диапазон
в данном случае следует так же, как и
при
создании ранжированной переменной.
Вместо диапазона в данном поле ввода
можно указать
имя
некоторого массива (вектора
или матрицы). В этом случае переменная-счетчик
будет последовательно принимать значения
всех элементов этого массива. Возможность
перебора элементов массива не может
быть реализована с помощью цикла while,
поэтому именно в таких случаях цикл for
и является незаменимым. В поле ввода
под словом for
следует ввести тело цикла.

Пример:
Заполнить вектор числами от x_нач
до x_кон
с шагом h.
Затем определить сумму элементов этого
вектора и найти их среднее арифметическое
значение.

Цикл
while
– цикл, который выполняется до тех пор,
пока выполняется определенное условие.

В
поле
ввода справа
от слова while
следует ввести условие. Это условие
строится по тем же правилам, что и в
операторе if.
Оно будет проверяться после каждого
выполнения тела цикла и в тот момент,
когда условие перестанет выполняться,
повторение тела цикла прекратится. В
поле
ввода ниже
слова while
следует ввести тело цикла (напомним,
что для ввода нескольких строк в теле
цикла надо воспользоваться кнопкой Add
Line).

Пример1:
Вычислить сумму

с точностью е.

Пример2:
Найти первый элемент, превышающий
определенный порог.

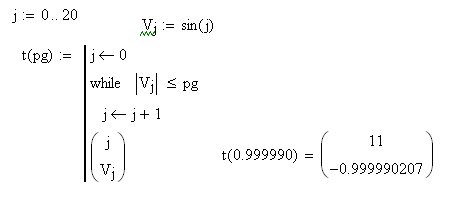
Использование
операторов break
и continue.

Иногда
возникает необходимость повлиять на
выполнение цикла некоторым образом,
например, прервать его выполнение по
какому-либо условию или выполнять
некоторые итерации не так, как другие.
Для этого и служат операторы break
и continue.

Оператор
break,
если он расположен внутри цикла, означает
немедленное прекращение выполнения
текущей итерации и выход из цикла. Если
есть необходимость прекратить выполнение
цикла по какому-либо условию, то следует
использовать конструкцию следующего
вида break
if
(условие).

Пример:
Выделить из массива все элементы от
начала и до первого вхождения в него
заданного числа.

Оператор
continue
используется для того, чтобы немедленно
перейти в начало цикла и начать следующую
итерацию. Этот оператор также обычно
используется в составе конструкции
вида continue
if
(условие).
Оператор continue
используется в случаях, когда необходимо
чтобы некоторые вычисления производились
для одних итераций и не производились
для других.

Пример:
Требуется заполнить элементы квадратной
матрицы в шахматном порядке.

Оператор
return
(возврат значения).

Как
мы уже указывали, результат выполнения
программного модуля помещается, как
правило, в последней его строке. Но можно
прервать выполнение программы в любой
ее точке (например, с помощью условного
оператора) и выдать некоторое значение,
применив оператор return.
В этом случае при выполнении указанного
условия значение, введенное в поле ввода
после return,
возвращается в качестве результата, и
никакой другой код больше не выполняется.
Вставляется в программу оператор return
с помощью одноименной кнопки панели
Programming

.
Пример:

Обработка
ошибок.

Система
MathCAD
предоставляет пользователю некоторый
контроль над ошибками, которые могут
возникнуть при вычислении выражений
или при выполнении программ. Для этой
цели служит оператор on
error,
который можно вставить с помощью
одноименной кнопки панели Programming

.
В поле
ввода справа
следует ввести выражение или программу,
которые необходимо вычислить (известно,
что это выражение может содержать ошибку
при определенных значениях входных
параметров). В поле
ввода слева
следует ввести выражение, которое будет
выполнено вместо правого выражения,
если при выполнении последнего возникнет
ошибка. Пример:
Если аргументу функции присвоено нулевое
значение, то в программе возникает
ошибка – деление на нуль. Но за счет
оператора on
error
сообщение не выводится, а функции в этой
точке присваивается значение, указанное
слева от оператора on
error
– значение машинной бесконечности.

В
поле ввода слева может быть введено
текстовое выражение, сообщающее об
ошибке

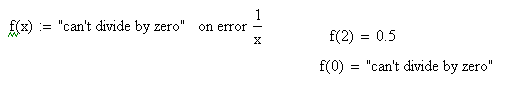
Конечно,
если программа содержит только простейшие
математические операции, то никаких
ошибок, кроме деления на нуль или
превышения наибольшего допустимого
числа в ней возникнуть не может. В таких
программах оператор on
error
используется редко. Но для более сложных
программ, которые содержат функции
решения дифференциальных уравнений,
аппроксимации или другие сложные функции
MathCAD,
использование on
error
может избавить от многих трудностей.

Иногда
может возникнуть ситуация обратная
той, которая была описана выше, т.е.
необходимо, чтобы при определенных
условиях результатом выражения было
сообщение об ошибке, хотя в действительности
при этом не возникает ни одной стандартной
ошибки MathCAD.
Для таких случаев в MathCAD
предусмотрена встроенная функция error.
В качестве аргумента этой функции нужно
в кавычках указать текст сообщения об
ошибке, который должен быть выведен.
Таким образом, если необходимо, чтобы
программа возвращала ошибку при
определенном условии, то следует
использовать конструкцию вида: error
(«текст ошибки») if
(условие).

Пример:

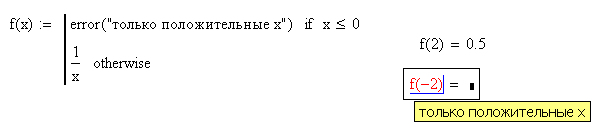
Для
того, чтобы иметь возможность нормально
вводить текст на русском языке в аргумент
функции error
(а также во все другие функции со
строками), следует изменить шрифт,
который используется во встроенном
стиле Constant.
Для того чтобы этот стиль правильно
отображал русские буквы, установите
курсор на любом числе или строковом
выражении в формульном блоке. При этом
в поле на панели инструментов Formatting,
отображающем текущий стиль, должно быть
написано – Constant.
Теперь выберите из раскрывающегося
списка шрифтов шрифт, поддерживающий
кириллицу.

Примеры
программирования.

1.
Вычислить функцию sin(x)
с точностью е.

2.
Даны массивы А(5) и В(5). Получить массив
С, в который записаны сначала элементы

массива
А в порядке возрастания, а затем элементы
массива В порядке убывания

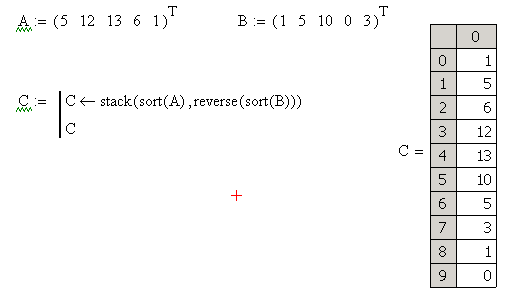
3.
По введенным значениям коэффициентов
А, В, С определить корни квадратного
уравнения

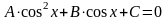
4.
Дан массив натуральных чисел В(10).
Определить, есть ли в нем 4 последовательных
числа (например, 1, 2, 3, 4, и т.п.). Напечатать
такие группы чисел.

Вопросы

1. Какая
   панель служит для вставки программного
   кода в документ MathCAD?
   Можно ли операторы программирования
   набрать с клавиатуры?

2. С
   какой команды начинается создание
   программного блока? Как с ее помощью
   можно создавать разветвленный программный
   блок?

3. Что
   такое определение программного блока?
   Обращение к программному блоку?

4. Что
   такое глобальные и локальные переменные
   для программного блока? Что может
   содержать последняя строка программного
   блока?

5. Как
   работает оператор if
   в программном блоке? Приведите пример.

6. Создание
   цикла с параметром в программном блоке.
   Приведите пример.

7. Создание
   цикла while
   в программном блоке. Приведите пример.

8. Для
   чего служат операторы break,
   continue
   в программном блоке? Приведите примеры.

9. Как
   работает оператор return
   в программном блоке? Приведите пример.

10. Как
    осуществляется обработка ошибок в
    программном блоке? Приведите пример.

Лекция №3

(установочная лекция)

Численные методы
решения задач.

Обработка
экспериментальных данных средствами
MathCAD

Развитие
электронной вычислительной техники,
создание алгоритмических языков
программирования и обширного
математического обеспечения ЭВМ
позволяет широко использовать численные
методы вычислительной математики при
решении различного рода прикладных
задач в науке, технике, производстве.

Численные
методы – это методы решения задач через
последовательность элементарных
операций, которые многократно повторяются
до тех пор, пока не будет получен конечный
результат с наперед заданной точностью.

Численными
методами часто приходится решать
следующие математические задачи:

1. решение
   нелинейных (алгебраических и
   трансцендентных) уравнений;

2. вычисление
   определенных интегралов;

3. решение
   обыкновенных дифференциальных уравнений;

4. решение
   дифференциальных уравнений в частных
   производных;

5. решение
   задач оптимизации;

6. обработка
   массивов числовых данных.

Каждая
из этих задач может представлять собой
самостоятельную прикладную задачу или
являться составной частью более сложных
прикладных задач.

Решение
нелинейных уравнений

Обычно
нелинейные уравнения делят на
трансцендентные и алгебраические.
Нелинейные уравнения, содержащие
тригонометрические функции или другие
специальные функции, например, lg(x)
или e^x,
называются трансцендентными. Методы
решения нелинейных уравнений такого
типа делятся на аналитические и численные.

Первые
позволяют найти решение непосредственно
с помощью формул и всегда обеспечивают
получение точного решения. Известным
примером такого рода является формула
корней квадратного уравнения. В численных
методах задается процедура решения в
виде многократного применения некоторого
алгоритма. Задача отыскания корней
нелинейного уравнения f(x)
= 0
считается решенной, если мы сумеем
определить корни с нужной степенью
точности.

Для
решения нелинейных уравнений известны
следующие численные методы: метод
половинного деления (метод дихотомии),
метод хорд, метод касательных (Ньютона),
метод секущих, метод простой итерации.
Рассмотрим метод половинного деления.

Графическая
интерпретация метода показана на рис.1.

Рис.1
Графическая интерпретация метода
половинного деления

В
этом методе отыскание корня уравнения
f(x)
= 0
проходит в два этапа. На первом этапе
необходимо отделить корень, т.е.выделить
интервал на оси абсцисс, на котором
функция f(x)
меняет свой знак. Для отделения корня
следует провести вычисление функции
f(x)
в точках, расположенных через равные
интервалы по оси x,
до тех пор, пока не будут найдены два
последовательных значения функции
f(x_n)
и f(x_n+1),
имеющие противоположные знаки.

На
втором этапе производится уточнение
корня. Найденный интервал [x_n,
x_n+1],
содержащий корень, делится пополам

Затем
по разности знаков функции на концах
интервала определяем, на каком из
полученных двух интервалов находится
корень уравнения. Найденный интервал
снова делится пополам и т.д.. В результате
интервал, на котором находится корень
сужается. Процесс повторяется до тех
пор, пока f(x_ср)
не станет достаточно близким к нулю.
Блок-схема алгоритма метода показана
на рис.2.

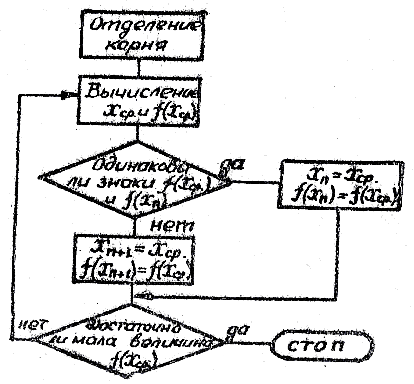
Рис.2
Блок-схема алгоритма метода половинного
деления

Численное
интегрирование

К
численному интегрированию обращаются,
когда нельзя через элементарные функции
аналитически записать первообразную
интеграла

или
когда подобная запись имеет сложный
вид.

Сущность
большинства численных методов вычисления
определенных интегралов состоит в
замене подынтегральной функции f(x)
аппроксимирующей функцией j(x),
для которой можно легко записать
первообразную в элементарных функциях,
т.е.

Используемые
на практике методы численного
интегрирования можно сгруппировать в
зависимости от способа аппроксимации
подынтегральной функции. Дадим краткую
характеристику групп наиболее
распространенных методов.

1.
Методы
Ньютона — Котеса.
Эти методы требуют, чтобы значения x
были заданы с постоянным шагом. Они
основаны на полиномиальной аппроксимации
подынтегральной функции. Алгоритмы
методов просты и легко поддаются
программной реализации.

2.
Методы
Гаусса – Кристоффеля
– методы наивысшей алгебраической
точности. Эти методы используют неравно
отстоящие узлы, расположенные по
алгоритму, обеспечивающему минимальную
погрешность интегрирования. Требуют
большего объема памяти, чем методы
первой группы.

3.
Методы
Монте-Карло.
В этих методах узлы выбираются с помощью
датчика случайных чисел. Ответ носит
вероятностный характер. Методы эффективны
при вычислении большой кратности.

Рассмотрим
методы первой группы. По этому методу
интервал разбивается на n
равных отрезков, длина каждого из которых

.
Для вычисления каждой элементарной
площади подынтегральную функцию на
данном отрезке заменяют с некоторой
степенью точности более простой функцией,
интеграл от которой можно вычислить,
используя только ординаты на концах
отрезка. Метод Ньютона -Котеса дает три
формулы для приближенного вычисления
определенного интеграла

1.
При замене f(x)
на каждом отрезке прямой, параллельной
оси x
(рис.3,а), получим формулу прямоугольников

2.
При замене f(x)
на каждом отрезке прямой, соединяющей
ординаты концов отрезка (рис.3,б), получим
формулу трапеций

3.
При замене f(x)
дугой параболы, проведенной через концы
трех ординат (рис.3,в), получим формулу
Симпсона. При этом число отрезков должно
быть четным

Точность
вычисления интеграла тем выше, чем
больше n
и меньше h,
и в пределе при n
®
¥
h
®
0 указанные формулы дадут точную величину
определенного интеграла.

Рис.3
Численное определение интеграла

Блок
схема алгоритма численного определения
интеграла с заданной степенью точности
представлена на рис. 4. На блок-схеме
a,b,e,n
– исходные данные, е – заданная точность,
n
– число разбиений, i1
– начальное значение интеграла, его
можно задать равным нулю, I
— вычисленное значение интеграла.

Для
достижения заданной точности число
разбиений удваивают до тех пор, пока
будет удовлетворено условие |i
– i1|<e.

Рис.4
Блок схема алгоритма численного
определения интеграла с заданной
степенью точности по формуле прямоугольников

Обработка
экспериментальных данных средствами
MathCAD.

Инженеру
на практике часто приходится сталкиваться
с необходимостью определения функции,
которая задана таблично. Т.е. известны
экспериментально снятые аргумент и
функция в узловых точках, а в промежутках
эта функция неизвестна и ее надо найти.

Для
анализа экспериментальных зависимостей
и приведения их к наглядному виду часто
используются такие средства, как
интерполяция, сглаживание и аппроксимация.
В некоторых задачах для анализа
зависимости бывает необходимо найти
ее Фурье-компоненту. Все перечисленные
средства анализа можно реализовать
средствами MathCad.

Интерполяция.

Интерполяцией
называют заполнение отрезками кривых
промежутков между заданными точками
по тому или иному закону. Для проведения
интерполяции в первую очередь должна
быть задана экспериментальная зависимость
в виде набора точек на плоскости. Для
этого должны быть заданы два одномерных
массива (вектора) – vx
и vy,
содержащие соответственно значения
координат x
и y
каждой точки. При этом важно,
чтобы значения в векторе vx
были заданы в
порядке возрастания.

Система
MathCad
позволяет проводить линейную
интерполяцию
и сплайн-интерполяцию
наборов экспериментальных точек.

Простейшим
вариантом интерполяции является линейная
интерполяция.
Она заключается в простом соединении
точек между собой отрезками прямых. Для
реализации такой интерполяции в MathCad
существует встроенная функция
linterp(vx,vy,x)
, где vx
vy
– уже известные векторы, содержащие
координаты последовательности точек,
x
– координата точки, в которой нужно
вычислить значение интерполирующей
функции. Пример построения линейной
интерполяции приведен на рис.5

Рис.5
Линейная интерполяция

На
практике линейная интерполяция
применяется редко.

Из
всех видов интерполяции наиболее часто
используется интерполяция, где
экспериментальные точки попарно
соединяются
отрезками полиномов.
Чаще всего для этого выбирают полиномы
третьей
степени(поэтому
такая кривая и называется кубическим
сплайном).
Для того чтобы найти коэффициенты
этих полиномов,
очевидно, недостаточно того условия,
что кривая должна проходить через
экспериментальные точки. Поэтому на
сплайн накладываются дополнительные
условия сшивки
– первая и вторая производные слева и
справа от каждой экспериментальной
точки должны быть равны между собой. Но
и после этого количество условий остается
на два меньше, чем количество неизвестных
коэффициентов. Дополнительные
два условия
должны быть наложены в начальной и
конечной экспериментальных точках,
поскольку в них нет условий сшивки. Эти
условия можно выбрать по-разному. В
MaqthCad
существуют три различных функции для
построения кубических сплайнов с
различными дополнительными
условиями.

• lspline(vx,vy)
  – в начальной и конечной точках
  накладывается условие линейности, т.е.
  вторая производная от функции равна
  нулю. Первая буква в названии функции
  – l
  , означает linear
  (линейный).

• pspline(vx,vy)
  – на первом и последнем интервале
  кривая является параболой, т.е.
  полиномиальный коэффициент при x³
  равен нулю. Буква p
  означает parabolic
  (параболический).

• cspline(vx,vy)
  – полиномиальные коэффициенты при x³
  на первых двух интервалах равны между
  собой точно так же, как на последних
  двух интервалах. Буква c
  означает cubic
  (кубический).

Результатом
каждой из перечисленных функций является
вектор, содержащий значения вторых
производных от интерполяционной кривой
во всех точках, заданных в массиве vx.
Для того чтобы исходя из этого вектора
построить кривую, нужно воспользоваться
встроенной функцией interp(v,vx,vy,x),
где vx
и vy
– массивы экспериментальных точек, v
– массив, полученный как результат
одной из трех функций, перечисленных
выше, x-
координата, в которой нужно вычислить
значение интерполяционной кривой.
Пример интерполяции кубическим сплайном
приведен на рис.6.

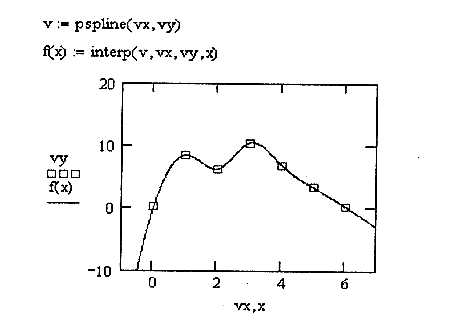
Рис.6
Интерполяция кубическим сплайном

В
приведенном примере использована
функция pspline.
В большинстве случаев от того, какую
функцию вы используете, слабо зависит
поведение кривой внутри интервала
экспериментальных значений. Заметное
отличие появляется лишь за границами
этого интервала.

Кубический
сплайн является эффективным средством
построения интерполяционной кривой в
подавляющем большинстве случаев. Но
иногда использование кубического
сплайна может привести к нежелательным
результатам. Чаще всего это происходит
в тех случаях, когда данные очень
неравномерно распределены вдоль оси
x.
В таких случаях на кривой кубического
сплайна могут появляться острые
экстремумы в промежутках между
экспериментальными точками. В некоторых
подобных случаях получить лучщую
интерполяционную кривую помогает
использование другого
вида интерполяции – В-сплайна.
Основное отличие В-сплайна от всех
описанных выше методов – сшивка
отрезков кривых происходит
не в экспериментальных точках, а
между ними, в специально заданных точках.
В MathCad
для реализации интерполяции В-сплайном
служит функция bspline(vx.vy,u,n),
где vx,vy
– векторы, содержащие координаты
экспериментальных точек, u
– вектор, содержащий координаты точек
сшивки, n
– порядок полинома. Результатом функции
bspline
является вектор, который далее следует
использовать как аргумент функции
interp.
В-сплайн в MathCad
можно построить из отрезков прямых,
парабол или кубических парабол, т.е.
допустимые значения параметра n
– 1,2 или 3. Количество точек сшивки не
является произвольной величиной и
должно быть всегда на n-1
меньше, чем количество экспериментальных
точек. Также на координаты точек сшивки
накладываются следующее условие: первая
точка сшивки должна быть не правее
первой экспериментальной точки, а
последняя не левее последней
экспериментальной точки. Остальные
точки сшивки могут произвольным образом
располагаться внутри отрезка. Пример
использования В-сплайна приведен на
рис.7.

Экстраполяция.

Интерполяция
дает возможность вычислять значения
неизвестной функции в промежутках между
экспериментальными точками, но иногда
возникает необходимость вычислять
значения функции вне области, ограниченной
этими точками. Для этого используют так
называемые методы
экстраполяции.

При
построении кубического сплайна, значение
интерполяционной кривой может быть
вычислено также и в любой точке за
пределами «пограничной» области.
Конечно, данный способ экстраполяции
можно использовать только на очень
небольшом расстоянии от «пограничных»
точек, поскольку кривая является
кубической параболой и быстро уходит
в область очень больших значений, не
имеющих ничего общего с реальной
зависимостью.

Рис.7
Сравнение эффективности кубического
сплайна и В-сплайна

Также
в MathCad
есть одна встроенная функция для
проведения экстраполяции – predict(v,m,n),
где v
– вектор значений функции на том отрезке,
где она известна (значения аргумента в
данной функции не задаются, и считается,
что точки распределены равномерно), m
– количество элементов вектора v,
на основании которых проводится
экстраполяция ( естественно, выбираются
точки, ближайшие к правой границе), n
– количество точек в рассчитываемом
векторе. Пример экстраполяции от
осциллирующей функции приведен на рис.8

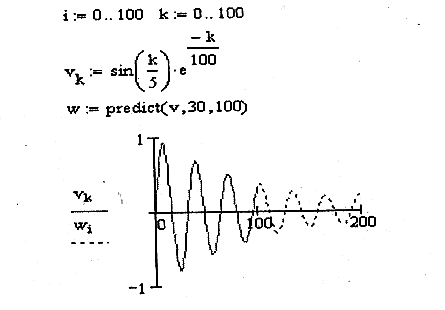
k,101+i

Рис.8
Экстраполяция с помощью функции predict

Результатом
функции predict
является вектор, состоящий из n
элементов и задающий значения функции
справа от границы выборки, т.е. в области,
где она была не известна. Алгоритм,
используемый в функции predict,
наилучшим образом подходит для
экстраполяции различного рода
осциллирующих зависимостей. В некоторых
случаях можно получить удовлетворительный
результат экстраполяции даже для
негладких зависимостей, таких как
пилообразный или прямоугольный сигнал.
Зато для непериодических зависимостей
приемлемый результат можно получить
очень редко и только на очень небольшом
расстоянии.

Регрессия

Результаты
экспериментов всегда содержат некоторую
случайную погрешность. Причем часто
погрешность оказывается величиной
одного порядка с измеряемой величиной.
В таких случаях интерполяционная кривая
будет весьма далека от истинной
зависимости. Поскольку подобные ситуации
возникают довольно часто, то интерполяция
редко используется при анализе результатов
экспериментов. Гораздо шире здесь
применяется регрессионный анализ.
Регрессией
называется подгон
параметров той или иной простой функции
для наилучшей аппроксимации
экспериментальных данных (от латинского
approximo
– приближаюсь). Если аппроксимирующая
функция выбрана удачно, то значения ее
параметров могут быть источником
разнообразной информации об измеряемой
величине.

Система
MathCad
содержит большое количество встроенных
функций для проведения регрессионного
анализа с использованием любых
аппроксимирующих функций и их комбинаций.
Все функции MathCad
для поиска оптимальных значений
параметров функций используют метод
наименьших квадратов, можно еще применить
метод медиан.

Линейная регрессия

Линейная
регрессия является наиболее простой,
но, тем не менее, используется чаще
любого другого вида регрессии. Она
заключается в нахождении таких значений
параметров a
и b,
чтобы прямая y
= a+bx
наилучшим образом аппроксимировала
заданной набор точек. Для проведения
линейной регрессии по методу наименьших
квадратов в MathCad
существует функция line(vx,vy).
Результатом функции line
будет вектор, содержащий значения
параметров a
и b
для построения регрессионной прямой.
Пример линейной регрессии представлен
на рис.9

Рис.9
Линейная регрессия с помощью функции
line

На
рис.9 для анализа эффективности линейной
регрессии построена псевдоэкспериментальная
последовательность точек. Для этого к
точным значениям линейной функции
прибавлены случайные числа, сгенерированные
с помощью функции rnorm.Затем
проведена линейная регрессия полученного
набора точек. Ее результат можно сравнить
с исходной прямой. Как видно из рис.,
параметры регрессионной прямой заметно
отличаются от исходных, но на графике
обе прямые проходят достаточно близко.

Для
линейной регрессии в MathCad
реализован также метод медиан с помощью
функции medfit(vx,vy).
Результатом этой функции является
вектор, аналогичный результату line.
Нельзя утверждать, что один из двух
методов регрессии более точен. Метод
наименьших квадратов является наиболее
универсальным, поэтому функция line
считается в MathCad
основной функцией для проведения
линейной регрессии.

Полиномиальная
регрессия.

Кроме
аппроксимации неизвестной функции с
помощью прямой,
широкое
применение находит и аппроксимация с
помощью полиномов различной степени.
Для этой цели в MathCad
существует функция regress(vx,vy,n).
Последний аргумент данной функции
задает степень полинома. Можно использовать
полином любой степени, но не большей,
чем число точек в выборке минус один.
При n
= 1 получится линейная регрессия. На
практике наибольшее применение находит
полиномиальная регрессия от второй до
пятой степени.

Результатом
функции regress
является вектор, содержащий коэффициенты
аппроксимирующего полинома. Эти
коэффициенты располагаются в векторе,
начиная с четвертого элемента в порядке
возрастания степеней. Первые три элемента
данного вектора являются служебными и
используются для того, чтобы результат
функции regress
можно было использовать как первый
аргумент функции interp
по аналогии со сплайн-интерполяцией.
Пример полиномиальной регрессии
представлен на рис.10.

Рис.10
Полиномиальная регрессия

На
рис.10 для иллюстрации полиномиальной
регрессии построена псевдоэкспериментальная
последовательность точек. В качестве
теоретической функции был использован
полином третьей степени с коэффициентами
0,1,-2,1. Как видно из примера, коэффициенты,
рассчитанные функцией regress,
значительно отличаются от коэффициентов
исходного полинома. Тем не менее в
области экспериментальных точек обе
кривые достаточно близки, но за пределами
этой области резко расходятся.

Аппроксимация
набора точек различными элементарными
функциями

Физические
величины зачастую подчиняются зависимостям
отличным от линейных или полиномиальных.
Поэтому в MathCad
существует несколько функций, позволяющих
выполнить регрессию с использованием
зависимостей, наиболее часто встречающихся
на практике. Таких функций в MathCad
всего шесть. Вот некоторые из них:

• expfit(vx,vy,vg)
  – регрессия экспоненциальной функцией
  y
  = a*e^b*x+c.

• sinfit(vx,vy,vg)
  – регрессия синусоидальной функцией
  y
  = a*sin(x+b)+c.

• pwrfit(vx,vy,vg)
  — регрессия степенной функцией e
  = a*x^b
  +c.

Перечисленные
функции используют трехпараметрическую
аппроксимирующую функцию, нелинейную
по параметрам. При вычислении оптимальных
значений трех параметров регрессионной
функции по методу наименьших квадратов
возникает необходимость в решении
сложной системы из трех нелинейных
уравнений. Такая система часто может
иметь несколько решений. Поэтому в
функциях MathCad,
которые проводят регрессию
трехпараметрическими зависимостями,
введен дополнительный аргумент vg.
Данный аргумент – это трехкомпонентный
вектор, содержащий приблизительные
значения параметров a,b
и c,
входящих в аппроксимирующую функцию.
Неправильный выбор элементов вектора
vg
может привести к неудовлетворительному
результату регрессии. На рис.11 приведен
пример проведения экспоненциальной
регрессии с помощью функции expfit,
регрессия проведена для двух различных
значений вектора vg.

Рис.11
Экспоненциальная регрессия

Аппроксимация
набора точек функциями, заданными
пользователем.

В
MathCad
существуют средства для проведения
регрессии самого общего вида. Это
означает, что можно использовать любые
функции в качестве аппроксимирующих и
находить оптимальные значения любых
их параметров, как линейных, так и
нелинейных. В том случае, если регрессионная
функция является линейной по всем
параметрам, т.е. представляет линейную
комбинацию жестко заданных функций,
провести регрессию можно с помощью
встроенной функции linfit(vx,vy,F).
Аргумегт F
– это векторная функция, из элементов
которой должна быть построена линейная
комбинация, наилучшим образом
аппроксимирующая заданную последовательность
точек. Результатом работы функции linfit
является вектор линейных коэффициентов.
Каждый элемент этого вектора – коэффициент
при функции, стоящей на соответствующем
месте в векторе F.
Таким образом, для того чтобы получить
регрессионную функцию, достаточно
скалярно перемножить эти два вектора.
Пример такой аппроксимации представлен
на рис.12.

Рис.12
Использование функции linfit

Сглаживание

Система
MathCad
применяется для обработки различного
рода сигналов. При этом очень важной
процедурой является очистка сигнала
от шумов. Один из вариантов решения
данной задачи – это использование
алгоритмов сглаживания (smoothig).
Существует множество алгоритмов
сглаживания данных, причем не всегда
можно заранее сказать, какой из них
будет наиболее эффективен для той или
иной задачи. В MathCad
реализовано три алгоритма сглаживания
и соответственно существует три функции
для их выполнения.

• medsmooth(vy,n)
  – реализует алгоритм «бегущих» медиан.
  Параметр n
  определяет ширину «окна» сглаживания,
  т.е. количество точек, которые используются
  при вычислении сглаженного значения
  в каждой точке. Параметр n
  должен быть целым нечетным числом.
  Данный алгоритм лучше всего подходит
  для сглаживания наборов точек, в которых
  лишь некоторые точки резко выбиваются
  из общей гладкой последовательности
  (см.рис.13).

• ksmooth(vx,vy,b)
  – алгоритм Гауссового ядра. В данном
  алгоритме сглаженное значение в каждой
  точке вычисляется как весовое среднее
  от всего набора данных с ядром в виде
  функции Гаусса. Параметр b
  — это параметр ширины функции ядра.
  Данный метод наилучшим образом подходит
  для фильтрации зашумленного сигнала
  (см.рис.14).

• supsmooth(vx,vy)
  – в данном алгоритме значение в каждой
  точке заменятся на значение регрессионной
  прямой, построенной с использованием
  некоторого количества близлежащих
  точек, причем данное количество
  выбирается по-разному для каждой точки
  с помощью адаптивного алгоритма.

Рис.13
Сглаживание сигнала с узкими
нерегулярностями

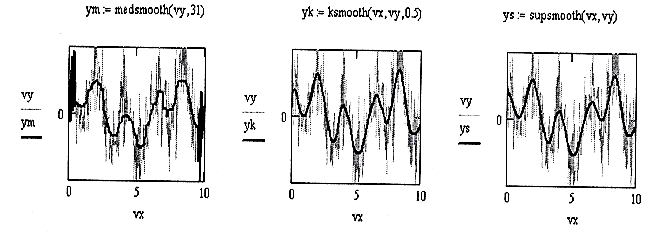
Рис.14
Сглаживание зашумленного сигнала

Дискретное
преобразование Фурье

Еще
одна операция, широко применяемая при
обработке сигналов , — вычисление
Фурье-спектра. Для проведения данной
операции с сигналами, заданными в виде
массивов данных, система MathCad
содержит численный алгоритм, называемый
быстрым преобразованием Фурье (Fast
Fourier
Transform
FFT).
Для реализации данного алгоритма в
MathCad
существует несколько различных функций.

• В
  том случае, если набор данных v
  состоит из 2^m
  элементов, а также все числа в наборе
  данных действительны, то для проведения
  Фурье-преобразования следует пользоваться
  функциями fft(v)
  или FFT(v).
  Обе эти функции выполняют
  Фурье-преобразование, а различие
  между ними заключается
  лишь в нормировке результата. Результатом
  функций fft
  и FFT
  будет массив из 2^{m
  -1}+1
  комплексных чисел.

• Если
  какое-либо из условий, перечисленных
  выше, не выполняется, т.е. массив содержит
  комплексные числа или не может быть
  расширен до размерности 2^m,
  то следует пользоваться функциями
  cfft(v)
  и CFFT(v).
  Результатом функций cfft
  и CFFT
  будет массив комплексных чисел той же
  размерности, что и исходный.

Результатом
каждой из перечисленных функций будет
массив комплексных чисел. Исходя из
этого массива, можно построить
амплитудно-частотную (АЧХ) или
фазово-частотную (ФЧХ) характеристику
сигнала. Для построения АЧХ следует
вычислить абсолютное значение каждого
элемента в массиве. Пример такого
построения приведен на рис.15.

Рис.15
Использование функции fft
для построения АЧХ — сигнала

На
рис 16 проведена фильтрация сигнала,
построенного на рис.15. Конечно, такой
метод фильтрации можно использовать,
только если уровень шума ощутимо ниже
уровня сигнала.

Рис.16
Амплитудная фильтрация сигнала

Здравствуйте, дорогие читатели!
По откликам на эмейл и статистики по скачиванием, я сделал выводы, что всё-таки интересуются люди программой Mathcad и вообще другими программами, что связанные с решением математических задач. Ну и так же я знаю, что тема «Интегралы» — это одна из наиболее тяжёлых в Высшей математике для студентов, особенно на первых порах.

Именно по этому я сделал ещё один видеоурок о Mathcad в котором рассказываю, как с помощью этой полезной программы можно находить интегралы. Так же для тех, кто не смотрел мои предыдущие видеоуроки по ней, то рекомендую ознакомиться с ними. Потому в этом уроке только конкретные примеры интегралов и способы их решение в Mathcad и вам может быть не понятно, что и от куда берётся, если вы не знаете первых шагов в этой программе.

И так, посмотрев этот видеоурок, вы узнаете, как в Mathcad решать:

• Неопределённые интегралы;
• Двойные или тройные интегралы;
• Определённые интегралы.

Приятного просмотра 🙂

P.S. Возникают любые вопросы, то пишите в комментариях!

Материалы по теме:

• Как легко решать интегралы вида: $$int e^{ax} cos(bx)dx$$???
• Что такое интеграл?
• Современный помощник на зимней сессии.
• Калькулятор XXI века «ЛовиОтвет»