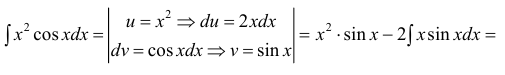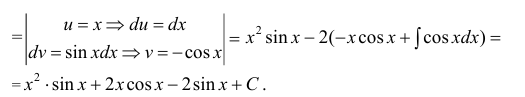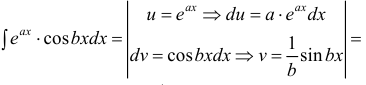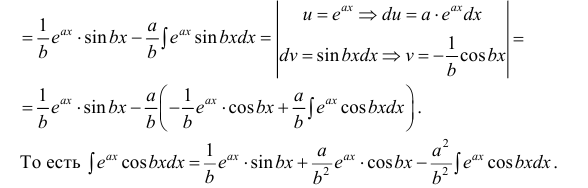Заказать задачи по любым предметам можно здесь от 10 минут
Замена переменной в неопределенном интеграле
Замена переменной в неопределенном интеграле используется при нахождении интегралов, в которых одна из функций является производной другой функции. Пусть есть интеграл $ int f(x) dx $, сделаем замену $ x=phi(t) $. Отметим, что функция $ phi(t) $ является дифференцируемой, поэтому можно найти $ dx = phi'(t) dt $.
Теперь подставляем $ begin{vmatrix} x = phi(t) \ dx = phi'(t) dt end{vmatrix} $ в интеграл и получаем, что:
$$ int f(x) dx = int f(phi(t)) cdot phi'(t) dt $$
Эта и есть формула замены переменной в неопределенном интеграле.
Алгоритм метода замены переменной
Таким образом, если в задаче задан интеграл вида: $$ int f(phi(x)) cdot phi'(x) dx $$ Целесообразно выполнить замену переменной на новую: $$ t = phi(x) $$ $$ dt = phi'(t) dt $$
После этого интеграл будет представлен в виде, который легко взять основными методами интегрирования: $$ int f(phi(x)) cdot phi'(x) dx = int f(t)dt $$
Не нужно забывать также вернуть замененную переменную назад к $ x $.
Примеры решений
| Пример 1 |
|
Найти неопределенный интеграл методом замены переменной: $$ int e^{3x} dx $$ |
| Решение |
|
Выполняем замену переменной в интеграле на $ t = 3x, dt = 3dx $: $$ int e^{3x} dx = int e^t frac{dt}{3} = frac{1}{3} int e^t dt = $$ Интеграл экспоненты всё такой же по таблице интегрирования, хоть вместо $ x $ написано $ t $: $$ = frac{1}{3} e^t + C = frac{1}{3} e^{3x} + C $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ int e^{3x} dx = frac{1}{3} e^{3x} + C $$ |
| Пример 2 |
|
Найти неопределенный интеграл методом замены переменной: $$ int sin^5 x cos x dx $$ |
| Решение |
|
Замечаем, что $ (sin x)’ = cos x $, поэтому выгодно сделать замену переменной $$ t = sin x, dt = cos x dx $$ Тогда после подставления её в интеграл будем иметь: $$ int t^5 dt = frac{t^6}{6} + C = frac{1}{6} sin^6 x + C $$ В самом конце очень важно не забывать возвращать замену назад, чтобы получить окончательный ответ. |
| Ответ |
| $$ int sin^5 x cos x dx =frac{1}{6}sin^6 x + C $$ |
| Пример 3 |
| Найти интеграл с помощью замены переменной: $$ int frac{cos sqrt{x}}{sqrt{x}} dx $$ |
| Решение |
|
Как обычно анализируем интеграл и замечаем, что в интеграле есть функция и её производная. А именно этой функцией является $ sqrt{x} $ и её производная $ frac{1}{2sqrt{x}} $. Поэтому замену переменной сделаем такой: $$ t = sqrt{x}, dt = frac{dx}{2sqrt{x}} $$ Подставляем в интеграл и решаем: $$ int frac{cos sqrt{x}}{sqrt{x}} dx = 2int cos t = 2sin t + C = $$ Выполняем обратную замену: $$ = 2sin sqrt{x} + C $$ |
| Ответ |
| $$ int frac{cos sqrt{x}}{sqrt{x}} dx = 2sin sqrt{x} + C $$ |
Итак, друзья, продолжаем наше знакомство с базовыми методами интегрирования! В прошлых уроках мы порешали простенькие интегралы на прямое применение таблицы, а также познакомились с первым базовым методом интегрирования — подведением функции под знак дифференциала. С этого урока уже начнётся серьёзное интегрирование и не менее серьёзные примеры. Так что, у кого пока проблемы с простыми интегралами — читайте предыдущие темы, пока не поздно. 
И в чём же заключается могущество сего метода? А в том, что в подавляющем большинстве случаев именно он позволяет превращать многие ужасные, на первый взгляд, примеры в белые и пушистые.) Например, интеграл с каким-нибудь страшным корнем или арксинусом после удачной замены может свестись к безобидному многочлену. Или к рациональной функции, которая всяко проще для интегрирования. Имеет смысл разобраться!
Итак, начнём.)
Суть замены переменной. Простейшие примеры.
Процедура замены переменной знакома всем вам ещё со школы. Например, решая жуткое тригонометрическое уравнение
sin2x — 2sin x — 3 = 0,
что вы обычно делаете? Правильно! Вы заменяете выражение sin x новой буквой — y, z, t — какой хотите. И дальше работаете уже с более простым квадратным уравнением — дискриминант считаете, тыры-пыры…
Всё то же самое и с интегралами.) Принцип тот же. Основная идея любой замены состоит в том, чтобы выражение, которое нам не нравится, заменить новой буквой. И все остальные части примера также выразить через эту самую новую букву. Тогда, если после всех преобразований пример упрощается, то, значит, основная цель данной замены выполнена. 
На прошлом уроке я уже говорил, что метод подведения функции под знак дифференциала — это простейший частный случай более общего метода замены переменной. Теперь настал черёд посмотреть, почему же это именно так и как работает сама процедура замены. Примеров в данном уроке будет не так много, но все они будут разобраны максимально подробно. Чтобы суть уловить.) Рассмотрим все проблемные места, исследуем каждую тонкость.
Начнём сразу с примера. Чтобы далеко не ходить, давайте вернёмся к нашему самому первому примеру из прошлого урока.
Пример 1
Что мы делали в прошлый раз, когда решали этот пример? Сначала мы добивались равенства выражений в показателе экспоненты и под дифференциалом. Для этого мы сначала выражали новый дифференциал d(3x) через старый dx, а уже в самом конце вводили новую переменную 3х = t и сводили наш интеграл к табличному.
Всё решение примера выглядело вот так:
d(3x) = (3x)’dx = 3dx
dx = d(3x)/3
Вспомнили? Отлично!
А теперь подойдём к данному примеру немного с другой стороны. Для начала вопрос: что вам больше всего не нравится в данном примере? 99 человек из 100 скажут: три икс! И будут правы. ) Вот и будем от этого самого 3х избавляться. Безопасно для самого примера.)
Для этого поступаем просто и элегантно. Нам ведь в примере не нравится 3х, верно? Вот и заменяем это самое 3х новой буквой! Да-да! Прямо сразу! Безо всяких дифференциалов. Дифференциалы будут потом.)
Так прямо и пишем:
3x = t
В результате данной замены наша подынтегральная функция превращается в простенькую табличную функцию et. И наш пример становится уже вот таким:
Но для применения табличной формулы этого пока мало. Почему? А потому, что, раз уж мы ввели новую переменную t, то, ясное дело, и весь пример целиком также должен быть выражен через t! А у нас в примере пока что торчит старый дифференциал dx. Надо бы его тоже как-то превратить в dt. Как? Очень просто!
Чтобы понять, во что же у нас превратится дифференциал dx, самым логичным было бы сначала выразить сам икс через новую переменную t. Здесь это проще простого. Для этого берём наше равенство 3x = t и выражаем из него икс через t. Вот так:
Отлично. Полдела сделано.) И теперь, чтобы выразить интересующий нас дифференциал dx через букву t, просто берём дифференциалы от обеих частей нашего равенства. Думаю, для этой процедуры комментарии уже излишни:
dx = d(t/3)
Вот и всё. Вставляем теперь в наш пример вместо dx выражение dt/3, выносим дробь 1/3 за знак интеграла и дорешиваем по таблице. Чистовое оформление примера теперь выглядит немного по-другому. Вот так:
Как видите, ответ получился тем же самым. Что вполне логично.)
Разберём ещё один пример с непосредственной заменой линейной конструкции. На закрепление.)
Пример 2
Напрашивается табличная формула с синусом:
Только э-э-э… в формуле стоит просто икс, а в нашем примере под синусом стоит сложный аргумент 11х+5. Неувязочка… А что, если заменить этот сложный аргумент 11х+5 новой буквой? Ведь именно это выражение нам и не нравится! Посмотрим…
На черновике так прямо и пишем вот такую заготовку:
Отлично! sin(11x+5) превращается в sin t, а dx превращается в dt/11. Жизнь налаживается.) Не пример, а сплошное удовольствие)
А теперь посмотрим на решение того же примера методом подведения выражения 11х+5 под дифференциал:
Получили тот же самый ответ, но оформление всё же немного другое. Почувствовали разницу?
В чём сходство этих двух способов? В том, что и там и тут мы заменяем новой буквой одно и то же выражение (в наших примерах это 3х и 11х+5). А отличие этих двух способов состоит лишь в том, на каком этапе решения вводится сама замена. Здесь мы сразу заменяем новой буквой то, что нам не нравится, потом связываем переменные старую с новой, а уж потом, в самом конце, находим связь и между их дифференциалами. А в методе подведения мы сначала связываем сами дифференциалы, а уже потом вводим замену. Или даже вообще не вводим, если уже «руку набили».:)
Как видите, и так и сяк решать можно. Тем, кто крепко дружит с дифференциалами, рекомендую сразу решать подобные интегралы методом подведения. Ибо такое решение гораздо короче. А этот способ, с изначальной заменой, хорош для тех студентов, кто с дифференциалами пока того… не очень…) Или если пример достаточно накрученный. Но зато этот способ более понятен, универсален и надёжен! Спасает в любой ситуации. Если, конечно, удачно выбрана сама замена.)
Это были самые простые примеры, где заменялась линейная конструкция — так, для разминки. Суть ясна, я думаю.)
А теперь разберём примеры посерьёзнее. Такие, где надо заменять не линейные, а более сложные выражения и подвести функцию под дифференциал уже не так-то просто, хоть и возможно. Как и в прошлом уроке, суть этой группы примеров будет заключаться в выделении из подынтегральной функции f(x) какой-то вспомогательной функции g(x) и её производной g’(x). И последующей замене g(x) = t. Здесь уже надо уметь чувствовать и узнавать в функциях производные других функций. В лицо! Зачем? А чтобы удачно подобрать замену! Ведь можно и неудачно подобрать, да. Особенно если плохо знать таблицу производных. Об этом мы уже подробно поговорили на прошлом уроке.)
Пример 3
Внимательно осматриваем пример и ищем в подынтегральной функции конструкцию, которая нам больше всего не нравится. Вот тут, в отличие от предыдущих примеров, уже возможны варианты. Кому-то не понравится корень, кому-то сам по себе корень будет по душе, но не понравится выражение 5х2+1, стоящее под корнем. Отдельным индивидуумам может не понравиться множитель x… Что именно заменять — пока не знаем. Всматриваемся дальше. У нас есть подкоренная конструкция 5х2+1 и есть множитель х, отдалённо похожий на её производную, так как
(5х2+1)’ = 10х
Именно это равенство и должно служить ключевой зацепкой!
А не попробовать ли заменить наше сложное подкоренное выражение 5х2+1 новой буквой? Что ж, попробуем и посмотрим, к чему это приведёт. Итак, делаем замену:
5х2+1 = t
Тогда наш корень после такой замены превратится в безобидную степенную конструкцию:
Так, с корнем расправились. Но, помимо корня, под интегралом у нас ещё осталось произведение xdx, которое тоже надо выразить через новую букву t, да.
Для этого немного схитрим. Не будем выражать «в лоб» икс через t, а затем искать dx. Это можно, но не нужно. Почему — объясню позже. Давайте сразу продифференцируем наше равенство для замены! Да-да! Целиком! Обе части. Вот так:
5х2+1 = t (это равенство — наша замена)
d(5х2+1) = dt (дифференцируем обе части)
(5х2+1)’dx = dt (раскрываем дифференциалы)
10xdx = dt
И что нам даёт эта запись? А то, что из неё теперь легко выражается нужная нам конструкция xdx:
Всё. Начинка интеграла теперь полностью выражена через t. Продолжаем наши игры.)
Подставляем теперь все данные в наш пример и получаем простенький табличный интеграл от степенной функции (n = 1/3, n+1 = 4/3):
Вот и все дела.) Пример разложили по полочкам. А можно ли решить данный интеграл через подведение под значок d? Можно! В одну строчку!
Другое дело, что догадаться, какую именно конструкцию надо подводить под дифференциал, уже гораздо сложнее: легко запутаться в коэффициентах. И под силу не каждому студенту. Поэтому те, кто пока не наловчился в подведении функции под дифференциал — решаем подобные примеры сразу через замену. Аккуратно. Чуть длиннее, зато надёжнее.)
А теперь ответ на вопрос, почему я не стал в явном виде выражать икс через t и затем находить dx. Не стал я этого делать по той причине, что наличие х2 в подкоренном выражении резко усложняет эту процедуру из-за того, что возникают корни.
Смотрите сами:
Тогда для дифференциала этого самого икса мы получим:
И, если теперь подставить в наш пример отдельные выражения для x и dx, то наши нехорошие корни благополучно сократятся и мы придём к тому же самому интегралу:
Как видите, получили всё то же самое, только выкладки более громоздкие. Поэтому, по возможности, сокращаем объём работы: ошибок меньше будет. 
Иногда встречаются и сюрпризы, когда замену переменной приходится проделывать более одного раза. Ничего страшного! Просто аккуратно заменяем неудобную конструкцию и последовательно упрощаем пример, шаг за шагом добираясь до табличного интеграла. И, конечно, после получения результата корректно осуществляем обратную замену. От новой переменной к предыдущей.)
Пример 4
Что, внушает? Минутку смотрим на пример, ужасаемся, после чего берём себя в руки и вспоминаем золотое правило всей математики:
Не знаешь, что нужно — делай, что можно!
И размышляем. Примерно так:
«Под интегралом нехорошая дробь. Сплошные синусы, аргументы разные — x и 2x. Да ещё и число «пи» затесалось… Кошмар! Но, очевидно, что чем больше одинаковых значков в примере и меньше разных, тем лучше. Поэтому первым делом упрощу-ка я синус двойного угла. По школьной формуле sin 2x = 2sin x·cos x. Поможет ли нам такое преобразование или нет — неясно. Но начинаем-то с самого простого! А там — видно будет.»
Если вы мыслите примерно так, то вы движетесь правильным курсом. Да! Сводим всё подынтегральное выражение к одному аргументу — к иксу. Два икс тут явно ни к чему.
Ну вот, уже лучше. В аргументах остались только иксы. А теперь снова пытаемся выявить родственные функции, опираясь на таблицу производных. Сразу же видно, что в получившейся дроби везде тусуются синусы, а в числителе в качестве множителя затесался косинус. Но косинус — ближайший родственник синуса! Родственник по производной. Ибо таблица производных гласит, что:
cos x = (sin x)’ .
Поэтому вводим напрашивающуюся замену sin x = t и продолжаем упрощать наш злой пример:
Отлично. Все синусы пропали напрочь, при этом суть примера не изменилась.
А дальше что делать с этой дробью? Таблица-то не катит! Нету пока подходящей формулы… Тупик? Вовсе нет! Опять внимательно осматриваем нашу дробь, выявляя родню по производной/дифференциалу, и… радостно замечаем, что в числителе стоит дифференциал знаменателя!
Вот так:
Мы же понимаем, что под дифференциал мы имеем право спрятать любую константу! В том числе и «пи».)
А вот теперь снова вводим замену! Да-да!
Тогда вообще красота получится!
Вот и всё. И нету больше никакого «пи»! Спряталось оно под дифференциал. Как и любая константа, да… А ведь как испугало в самом начале! 
Вот мы и свели ужасную дробь к безобидному табличному интегралу. По шагам, через две замены.) Но радоваться ещё рано, так как это ещё не ответ: нам икс нужен, а не z или t. Поэтому теперь последовательно проводим обратную замену. Тоже по шагам:
z = t2+π, где t = sin x
Итого z = sin2x + π.
Всё. Теперь со спокойной душой записываем окончательный ответ нашего злого примера:
Готово!
С опытом необходимость так подробно всё расписывать отпадёт сама собой. За ненадобностью. И особо продвинутые студенты этот интеграл легко вычислят в одну строчку вообще без замены! С помощью подведения под дифференциал, ага:
Быстро, правда? И вы тоже так сможете! Причём опыт нарабатывается достаточно скоро. Тренировка — залог успеха.)
Ну как, прониклись? Замена переменной (вкупе с подведением под дифференциал) — оч-чень мощный инструмент для интегрирования! И золотой ключик к успешному решению самых разнообразных примеров. 
А со следующего урока мы уже начнём копать глубже и познакомимся с отдельными специфическими видами замен — степенной заменой и тригонометрической заменой. И типовые примеры тоже обязательно порешаем. Посерьёзнее.)
А теперь несколько несложных примеров для тренировки.
Найти неопределённые интегралы
а) методом подведения функции под знак дифференциала,
б) непосредственной заменой переменной,
в) сравнить результаты и проверить ответ дифференцированием.
Ответов здесь тоже не дам. Не вижу смысла. Примеры довольно простые, и материала сегодняшнего и прошлого уроков вполне достаточно для успешной расправы с ними.) Проверяйте окончательный ответ обратным дифференцированием, не ленитесь! 
И тогда удача обязательно улыбнётся, поверьте! А у меня пока всё, продолжение следует!

Метод замены переменной или метод подстановки. Этот метод заключается во введении новой переменной интегрирования (то есть делается подстановка). При этом заданный интеграл приводится к новому интегралу, который является табличным или с помощью преобразований его можно свести к табличному.
|
Пусть требуется вычислить интеграл |
. Сделаем подстановку |
. |
||
|
Тогда |
и интеграл принимает вид: |
∫ ( ) |
, |
|
|
или |
||||
|
, т.е в подынтегральном выражении должна находиться некоторая |
||||
|
функция |
. После решения интеграла |
делаем |
||
|
∫ ( ) и её производная |
обратную подстановку t = x.
Общее правило: за t обозначаем саму функцию (а не её производную).
Находим dt следующим образом:
1)записываем формулу подстановки: ϕ(t) = f(x);
2)заключаем функции в скобки со знаком производной и домножаем на dx и dt
соответственно: (ϕ(t))’dt =(f(x))’dx;
3)берем производные и выражаем dx через dt.
Например подстановка: t2 = (2x-1) → ( t2)’ dt = (2x-1)’dx → 2tdt = 2dx →
→ dx = tdt Запомните это.
Пример 15.
Найти интеграл 

его. В конце решения делаем обратную замену.

Пример 16
Найти интеграл 
Упростим подынтегральную функцию, а потом сделаем замену переменной:
Пример 17
Найти неопределенный интеграл 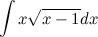
Заменим интеграл суммы на сумму интегралов и вынесем постоянные коэффициенты.
Полученные интегралы находим как интегралы от степенной функции:
Делая обратную замену, окончательно получим

Пример 18
Найти неопределенный интеграл 
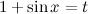
Сделаем обратную замену
Пример 19
Найти неопределенный интеграл 
Выполним обратную замену
Пример 20
Найти неопределенный интеграл 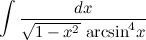
Выполним обратную замену и окончательно получим:
Содержание:
При решении многих практических задач таких, как вычисление длин линий, площадей, отыскание траекторий движения и других, вводится понятие интегрирования.
Определения
Определение: Первообразной функции
Теорема: (о существовании первообразной) Если функция f(x) непрерывна на сегменте 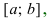
Теорема: Если F(x) — первообразная функции f(х), то функция F(x) + C (С -произвольная постоянная) также является первообразной функции f(х).
Доказательство:
ТЗ. Если 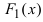
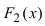
Доказательство: Пусть 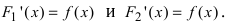
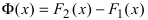
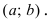
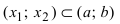
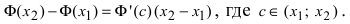
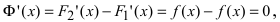
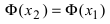
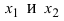
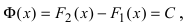
Пример:
Пусть дана функция 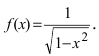
Решение:
В случае наличия двух первообразных показать, что они отличаются на постоянную величину.
Для функции существуют две первообразные 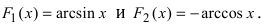
Определение: Совокупность всех первообразных функции 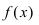
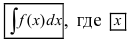
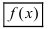
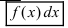
На основании теорем можно записать, что
Определение: Отыскание всех первообразных называется неопределенным интегрированием.
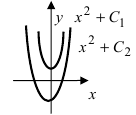
Выясним геометрический смысл неопределенного интеграла. Пусть дана функция 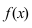
Пример:
Построить кривые, которые задаются неопределенным интегралом
Решение:
Первообразной для под интегральной функции f(х) = 2х будет функция 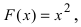
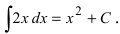
Рис. 1. Интегральные кривые
Свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна под интегральной функции
Доказательство: По определению неопределенного интеграла
2. Дифференциал неопределенного интеграла равен под интегральному выра- жению
Доказательство: По определению дифференциала от неопределенного интеграла имеем
3. Если под интегральное выражение является дифференциалом некоторой функции F(x), тo неопределенный интеграл равен
Доказательство: Так как
4. Неопределенный интеграл от линейной комбинации функций равен той же самой линейной комбинации неопределенных интегралов от этих функций
Частные случаи:
5. Формула неопределенного интеграла не зависит от обозначения переменной интегрирования
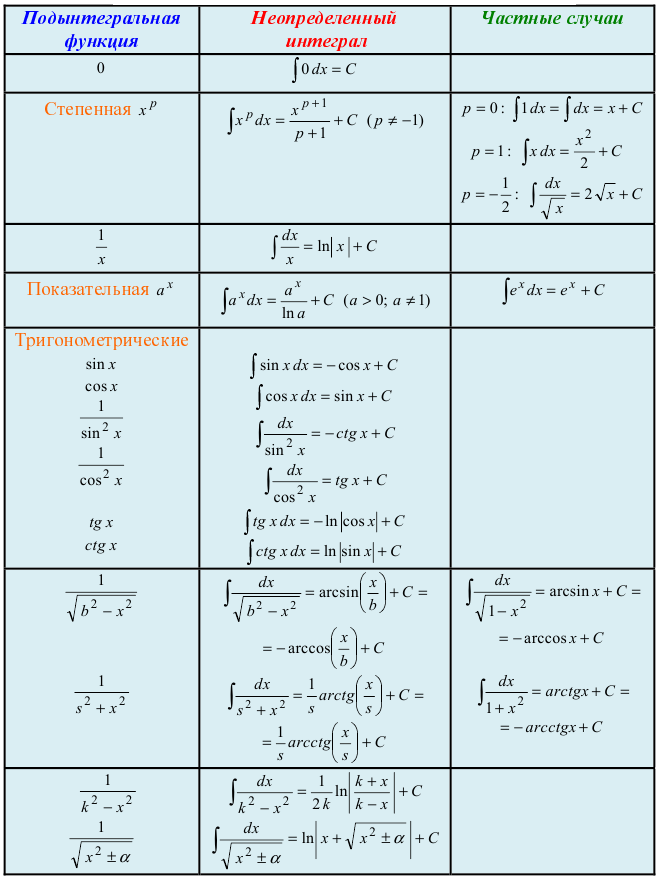
Таблица основных неопределенных интегралов
Методы интегрирования
Метод тождественных преобразований под интегральной функции
Данный метод основан на использовании простых приемов, алгебраических и тригонометрических формул, свойств подынтегральной функции, разложения полиномов на простые множители и свойств неопределенного интеграла. Рассмотрим этот метод на конкретных примерах.
1. Почленное деление числителя дроби на ее знаменатель
Замечание: Следует запомнить, что нет формулы почленного деления знаменателя дроби на ее числитель, т.е.
Пример:
Найти
Решение:
Выполним в под интегральной функции почленное деление числителя дроби на ее знаменатель и воспользуемся свойством линейности неопределенного интеграла
Замечание: Из этого примера видно, что слова «найти неопределенный интеграл” означают: за счет преобразований подынтегральной функции и использования свойств неопределенного интеграла данный интеграл надо привести к совокупности табличных интегралов и воспользоваться этой таблицей.
Замечание: Из примера также видно, что, несмотря на наличие двух табличных интегралов, константа интегрирования С пишется один раз, так как сумма или разность постоянных интегрирования все равно есть постоянная величина.
2. Использование противоположных арифметических операций (например, сложение-вычитание).
Пример:
Найти
Решение:
Анализ под интегральной функции показывает, что в числитель дроби надо добавить и вычесть 1 (при этом подынтегральная функция не изменится), а затем воспользоваться первым приемом (почленное деление числителя дроби на ее знаменатель)
3. Использование алгебраических и тригонометрических формул, например,
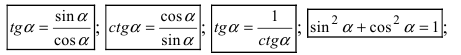
Пример:
Найти
Решение:
Воспользуемся формулой квадрата разности
Пример:
Найти
Решение:
4. Использование свойств функций, например,
Пример:
Вычислить
Решение:
Пример:
Вычислить
Решение:
5. Использование разложения полиномов на простые множители, например, 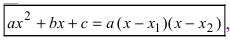
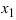
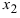
Пример:
Найти
Решение:
По теореме Виета уравнение 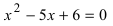
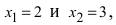
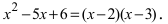
Метод замены переменной интегрирования
Данный метод основан на формуле
Метод замены переменной интегрирования применяется в двух случаях:
а) Если аргумент функции отличается от простого аргумента х, то этот сложный аргумент принимается в качестве новой переменной интегрирования t.
Пример:
Вычислить
Решение:
Так как показатель степени экспоненты отличается от простого аргумента х, то этот показатель степени принимаем в качестве новой переменной интегрирования, т.е.
Замечание: После нахождения первообразной с новой переменной интегрирования надо обязательно вернуться к старой переменной интегрирования.
Пример:
Вычислить
Решение:
Выражение, стоящее в круглых скобках, является аргументом степенной функции и отличается от простого аргумента х, поэтому принимаем его в качестве новой переменной интегрирования, т.е.
Пример:
Вычислить
Решение:
Выражение, стоящее в круглых скобках, является аргументом функции синус и отличается от простого аргумента х, поэтому принимаем его в качестве новой переменной интегрирования, т.е. 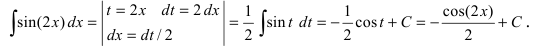
Пример:
Найти
Решение:
В подынтегральном выражении содержится элементарная функция tgx и в качестве множителя при dx присутствует ее первая производная 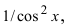
Пример:
Найти
Решение:
Данный пример объединяет первый метод с методом замены переменной интегрирования. Выполним почленное деление числителя дроби на ее знаменатель и разобьем интеграл на два интеграла, для которых применяются два случая замены переменной интегрирования
Замечание: Умение отыскивать подходящую замену вырабатывается в процессе многократных упражнений, однако можно указать ряд случаев, когда можно сразу увидеть необходимую замену переменной интегрирования при анализе подынтегрального выражения, например, 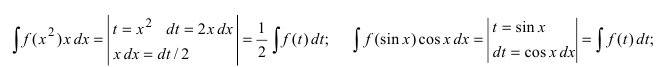
Метод интегрирования по частям
Интегрирование по частям основано на использовании формулы дифференциала от произведения двух функций 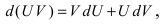
Таким образом, для неопределенного интеграла формула интегрирования по частям имеет вид:
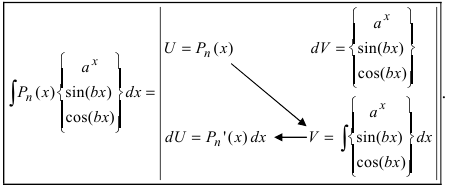
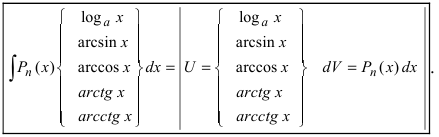
Для того чтобы знать, какую из функций принимать за U (все остальное в подынтегральном выражении принимается за dV), рассмотрим наиболее часто встречающиеся случаи:
1. 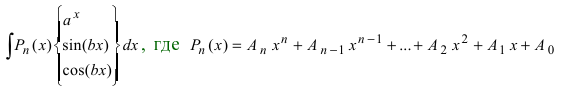
В этом случае
Замечание: Для нахождения функции dU используют определение дифференциала функции. При вычислении функции V интегрируют выражение dV, при этом постоянная интегрирования полагается равной нулю (С = 0). После выполнения этих действий применяют формулу интегрирования по частям.
Пример:
Вычислить
Решение:
Применим метод интегрирования по частям
Замечание: Из приведенного примера видно, что при необходимости метод интегрирования по частям применяется повторно.
2. Для интегралов вида
Пример:
Вычислить
Решение:
Действуя согласно методике, получим
3. Для интегралов вида 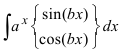
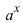
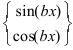
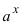
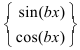
Пример:
Найти
Решение:
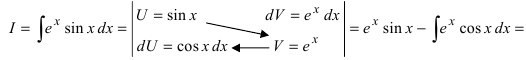
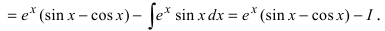
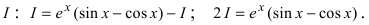
4. Нестандартные интегралы требуют для своего вычисления приобретения опыта на практических занятиях.
Пример:
Найти
Решение:
Неопределенный интеграл
Определение 1. Пусть Δ − промежуток действительной оси. Функция y=F(x) называется первообразной для функции y=f(x) на промежутке Δ, если F(x) − дифференцируема на Δ и 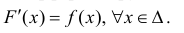
Пример:
Замечание. Первообразная функция определена не однозначно. А именно,
F(x) = x+C , где С – любая константа также будет первообразной для
В общем случае верна теорема:
Теорема 1. Две дифференцируемые на промежутке Δ функции 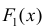
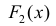
Доказательство. Необходимость.
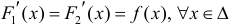
Тогда 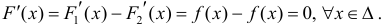
По теореме Лагранжа (теорема 4 § 12):
Достаточность. 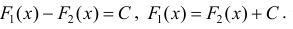
Тогда 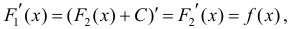
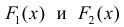
для одной и той же функции y=f(x), что и требовалось доказать.
Определение 2. Множество всех первообразных для функции y=f(x) на промежутке Δ называется неопределенным интегралом от функции f(x) и обозначается
Если F(x) — одна из первообразных, то , согласно теореме 1, 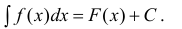
Свойства неопределенного интеграла
- Если ( ) F x — дифференцируема на Δ , то
(3) или
(4) здесь под записью
подразумеваем одну из первообразных.
- Если f (x) имеет первообразную на Δ, то λf(x) также имеет первообразную на Δ и ,если λ ≠ 0, то
(5)
- Если
имеют первообразную на Δ , тогда
также имеет первообразную на Δ и:
(6)
Свойства 1 – 4 легко выводятся из определения первообразной и интеграла
и соответствующих свойств производной.
Докажем, например, свойство 3.
Пусть F (x) — первообразная для f (x) на промежутке Δ. Тогда 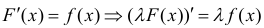
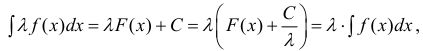
Из определений 1,2 следует, что интегрирование – действие обратное
дифференцированию (находится функция, производная которой равна данной).
- Заказать решение задач по высшей математике
Таблица интегралов
При вычислении интегралов в простых случаях применяют свойства 1 – 4.
Пример:
Пример:
Теорема 1. Если y=f(x) — непрерывна на промежутке Δ , то для нее ∃ первообразная функция y = F(x) на этом промежутке.
Замена переменной в неопределенном интеграле
Теорема 1. Пусть функция y = F(t) — первообразная для функции y = f(t) на промежутке 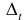
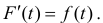
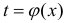
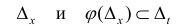
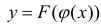
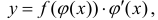
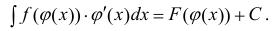
Доказательство. 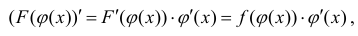
Замечание. Формулу (1) можно переписать в виде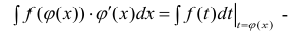
формула интегрирования с помощью подстановки 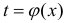
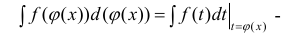
Формула интегрирования с помощью поднесения под дифференциал, когда
подынтегральную функцию 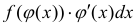
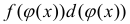
занося 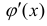
Пример:
Пример:
Пример:
При поднесении под дифференциал можно использовать свойства
дифференциала (см. § 6) 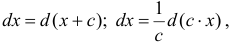
Пример:
Пример:
Пример:
Иногда в формуле (2) легче вычислять левую часть, чем правую:
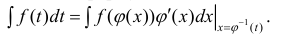
Формула (5) – формула интегрирования с помощью замены переменной 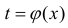
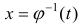
Пример:
Интегрирование по частям в неопределенном интеграле
Теорема 1. Пусть функция u(x) и v(x) – дифференцируемы на промежутке Δ и на этом промежутке 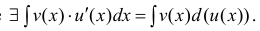
∃ и 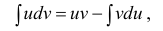
Доказательство. 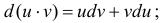
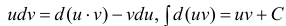
Пример:
Пример:
Замечание.
- При интегрировании выражений вида:
— многочлен степени n полагают:
После интегрирования по частям степень многочлена уменьшается на 1 (см. пример 1).
- При интегрирования выражений вида:
полагают:
(
— многочлен). После интегрирования по частям интеграл упрощается.
Пример:
Пример:
Таким образом, проинтегрировав дважды по частям, получили уравнение,
содержащее 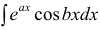
- Определённый интеграл
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Дифференциальное исчисление функций одной переменной
- Исследование функции
- Пространство R»
- Неопределённый интеграл
ПРЕДИСЛОВИЕ
Математика является важнейшей частью
профессионального образования, его фундаментом. Без овладения студентом
системой математических знаний, умений и навыков, приемов и методов познания
немыслимо воспитание и развитие качественного, конкурентоспособного
специалиста.
Цель обучения математике в учебных
заведениях профессионального направления в первую очередь предполагает
нахождение у каждого студента того места, где произошел разрыв базовой цепи
математических знаний, и задача преподавателя максимально быстро восстановить
потери. Во вторую очередь, заменить у студента негативное отношение к
дисциплине на понимание необходимости изучения данного раздела науки. Никакая
другая дисциплина не сможет так развить интуицию, пространственное воображение,
способность предвидеть результат и предугадывать пути решения.
Тема открытого занятия входит в
учебную программу дисциплины ЕН.01 «Математика».
Данная лекция-беседа была разработана
для студентов 2 курса, учитывая основные положения коллективного способа
обучения, объяснительно-иллюстративной технологии, технологии взаимного обучения
и ИКТ. Раздел «Интегральное исчисление» является одним из самых сложных для
восприятия разделов математики. Это обусловлено сложностью самого материала и
ограниченным количеством времени при изучении на первом и втором курсах. На
представленной лекции студенты обобщают основные теоретические положения,
закрепляют и систематизируют основные методы и приёмы нахождения неопределённого
интеграла, учатся применять знания при решении конкретных практических задач. Ход
занятия сопровождается демонстрацией слайдов по каждому этапу лекции. Для
закрепления нового материала предлагается тестирование с оригинальной
графической самооценкой. В конце студенты имеют возможность высказать свои
впечатления о занятии короткими фразами и пожелания на будущее.
ПЛАН ПРОВЕДЕНИЯ ЗАНЯТИЯ
Дисциплина: ЕН.01
Математика
Дата проведения: 13
декабря 2017г.
Группа: ПРМ.16
Специальность: 21.02.17
«Подземная разработка месторождений полезных ископаемых»
Тема: Метод замены переменных
в неопределённом интеграле.
Вид
занятия: лекция
Цель занятия:
методическая
— показать методику проведения интерактивной лекции-беседы;
учебная
— продолжить формирование умения интегрирования функций;
развивающая
— развивать аналитическое мышление, самостоятельность;
воспитательная
— воспитывать настойчивость в достижении поставленной цели.
Место проведения: аудитория
311
Продолжительность занятия: 80
мин
Межпредметные связи:
обеспечивающие:
математика, информатика и икт, физика;
обеспечиваемые:
высшая математика, геология и горное дело, техническая механика
Технические средства обучения:
ноутбук, мультимедийный проектор, экран
Методическое обеспечение занятия: презентация,
опорный конспект, тесты, лист самооценки
Литература:
1. Богомолов Н.В. Математика
/ Н.В. Богомолов. – М.: Дрофа. – 2006. – 300с.
2.
Богомолов Н.В. Практические занятия по математике / Н.В. Богомолов. – М.: Высш.
шк. – 1990. – 495с.
3.
Баврин И.И. Общий курс высшей математики / И.И. Баврин, В.Л. Матросов. — М.:
Просвещение. – 1995. – 608с.
СТРУКТУРА И ХОД ЗАНЯТИЯ
Структура занятия
1.
Организационный момент 2
мин
2.
Сообщение темы и цели занятия 1
мин
3.
Мотивация обучения 2
мин
4.
Актуализация опорных знаний 15
мин
5.
Изучение нового материала 35
мин
6.
Закрепление нового материала 20
мин
7.
Подведение итогов занятия 4
мин
8.
Домашнее задание 1
мин
Ход занятия
1. Организационный момент
1.1 Приветствие студентов.
1.2 Проверка наличия студентов.
1.3 Проверка готовности студентов,
аудитории и оборудования к занятию.
2. Сообщение темы и цели занятия
На экране с помощью проектора
включена презентация. На слайде 2 указана тема лекции и её цели.
3. Мотивация обучения
Наиболее интересны в рамках нашей
темы геометрические и физические приложения интегрального исчисления в горном
деле и геологии. С физической точки зрения с помощью интеграла можно вычислить
путь, пройденный ленточным конвейером до полной остановки, а используя тройной
интеграл, вычисляют, например, массу вывалившейся породы в кровле очистного
забоя (слайд 3).
Понятие интегрирования в большей степени
связаны с такими точными науками как физика, геометрия, техническая механика, и
даже экономика. Экологические основы природопользования в решении своих задач
использует другие методы подсчетов, однако есть одна область, в которой интегрирование
применяется — это оценка косвенного, прямого, и потенциального экологического
ущерба.
Без овладения студентом системой
математических знаний, умений и навыков, приемов и методов интегрирования,
немыслимо воспитание и развитие качественного, конкурентоспособного
специалиста.
Сегодня оценка на лекции будет складываться
из вашей работы в течение всего занятия. На столах у вас лежит «Лист
самооценки», подпишите его — ФИО (приложение 1)
4. Актуализация опорных знаний
Кто желает оформить на доске своё
решение домашних задач? Два студента на доске готовят демонстрацию домашних
примеров. В это время проводится фронтальный опрос (слайды 4-6).
1) Что называется первообразной?
2) Что называется неопределённым
интегралом?
3) Как обозначается, читается
неопределённый интеграл?
4) Что такое интегрирование?
5) Сформулировать 1 свойство
неопределённого интеграла.
6) Сформулировать 2 свойство
неопределённого интеграла.
7) Сформулировать 3 свойство
неопределённого интеграла.

9) Продолжить формулу
10) Продолжить формулу
11) Продолжить формулу
12) Продолжить формулу
13) Продолжить формулу
14) Продолжить формулу
15) Продолжить формулу
16) Продолжить формулу
17) Продолжить формулу
18) Продолжить формулу
19) Как называется метод
интегрирования с помощью таблицы первообразных и свойств неопределённого
интеграла?
20) С помощью какой формулы можно
вычислить определённый интеграл?
Слово предоставляем студентам у
доски. Выступают студенты с домашними примерами, проверяются их решения, каждый
сравнивает своё решение с решением на доске и выставляет самооценку.
5. Изучение нового материала
Метод интегрирования подстановкой
заключается во введении новой переменной интегрирования (т.е. подстановки). При
этом заданный интеграл приводится к новому интегралу, который является
табличным или к нему сводящимся (в случае «удачной» подстановки).
Общих методов подбора подстановок не существует. Умение правильно определить
подстановку приобретается практикой.
Пусть требуется найти интеграл . Сделаем подстановку
, где
— функция,
имеющая непрерывную производную. Тогда и на
основании свойства инвариантности формулы интегрирования получаем формулу
интегрирования подстановкой:
Эта формула называется также формулой
замены переменной в неопределенном интеграле. После нахождения интеграла в
правой части этого равенства следует перейти от новой переменной t к
переменной x.
Иногда целесообразно подбирать
подстановку в виде , тогда:
Примеры
Найти
неопределенный интеграл, используя метод замены переменной.
Решение
6. Закрепление нового материала
Для закрепления того, что мы с вами
изучили, выполним тест по вариантам №1 и №2 (приложение 2). Переверните листы
самооценки, обнаружите тест. В каждом вопросе выберите правильный ответ и
закрасьте ручкой соответствующие кружочки на рисунке. Строкам соответствуют
номера вопросов, а столбцам варианты ответов: первый столбец соответствует
ответу «а», второй – «б», третий – «в».
Затем соедините кружки линией.
Поднимите свои работы, и мы увидим рисунки, которые получились после решения
тестовых задач.
Посчитайте количество верных ответов
и заполните листы самооценки.
7. Подведение итогов занятия
Посчитайте общее количество баллов.
Поставьте оценку за занятие. Поднимите руки с оценкой «отлично», «хорошо»,
«удовлетворительно», «неудовлетворительно». Ваши впечатления о занятии?
а) Довольны ли вы своими баллами и своей
самооценкой?
б) Понравилась ли вам такая форма проведения
занятия?
в) Какой этап занятия более всего понравился?
г) Кто из ваших товарищей был на лекции самым
активным?
8. Домашнее задание:
Н.В.Богомолов
«Практические занятия по математике» Г.11 стр.198-201 №58(1), 59(1), 60(2),
63(1), 64(1,3)
ПРИЛОЖЕНИЯ
Приложение 1
|
ЛИСТ САМООЦЕНКИ СТУДЕНТА |
||
|
Ф.И.О |
||
|
Вид оценки (диапазон баллов) |
Пояснения к выставлению баллов |
Количество баллов |
|
Оценка |
Правильное |
|
|
Оценка фронтальном |
Один 2 |
|
|
Оценка |
Участие |
|
|
Оценка |
За |
|
|
Суммируйте все ваши баллы |
||
|
Максимально возможное количество баллов |
12 |
|
|
Если |
5 |
|
|
Если |
4 |
|
|
Если |
3 |
|
|
Если |
2 |
|
|
Ваша оценка |
Приложение 2
Тест I вариант
1.Найти
интеграл
а)
б)
в)
2.
Найти интеграл
а)
б)
в)
3.Найти
интеграл
а)
б)
в)
4.
Найти интеграл
а)
б)
в)
5.
Найти интеграл
а)
б)
в)
Тест
II вариант
1.Найти
интеграл
а)
б)
в)
2.
Найти интеграл
а)
б)
в)
3.Найти
интеграл
а)
б)
в)
4.
Найти интеграл
а)
б)
в)
5.
Найти интеграл
а)
б)
в)

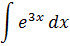
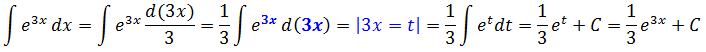
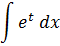
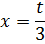
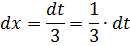
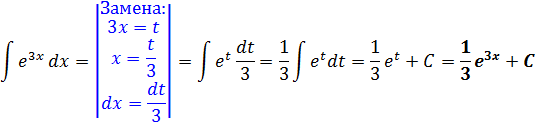
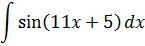
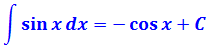
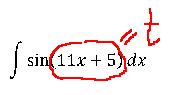
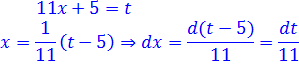
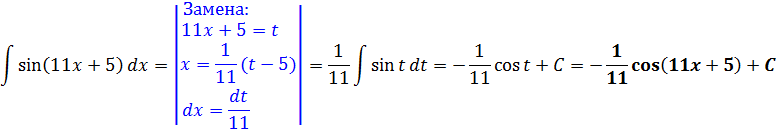
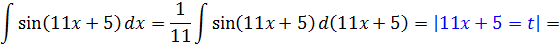
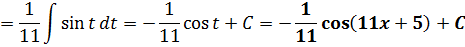
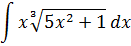
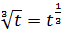
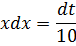
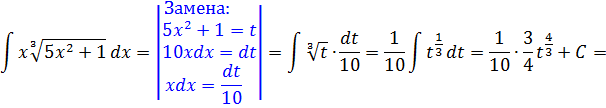
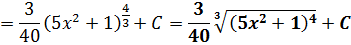
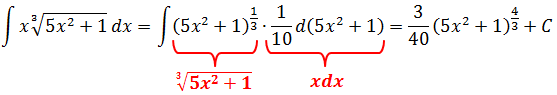
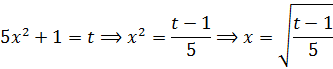
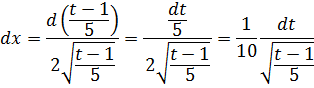
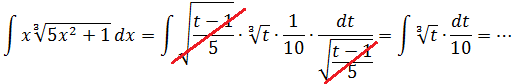
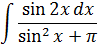
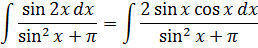
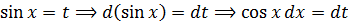
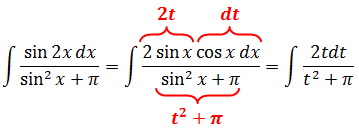
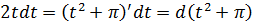
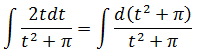
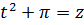
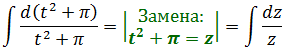
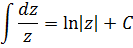
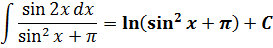
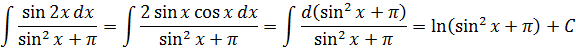
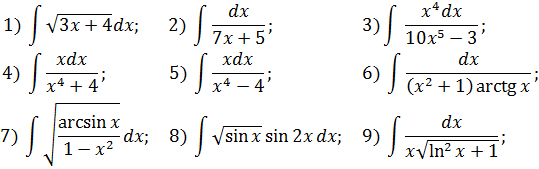


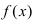
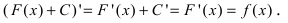
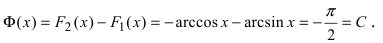
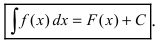
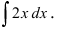
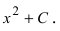
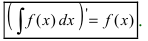
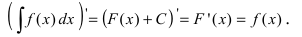
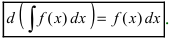
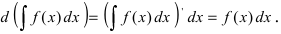
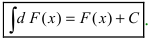
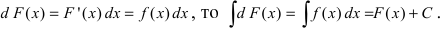
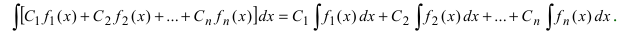
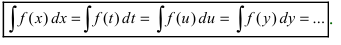
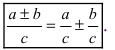
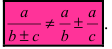
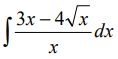
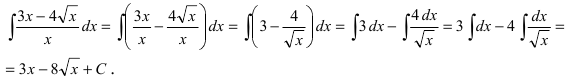
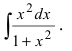
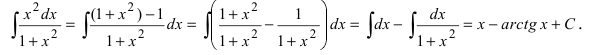
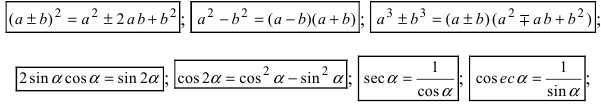
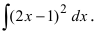
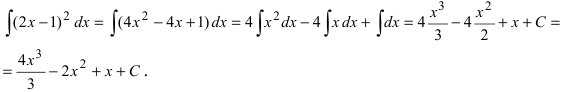
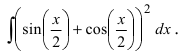
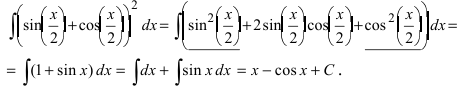
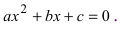
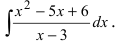
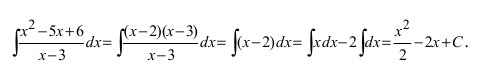
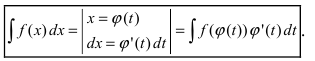
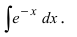
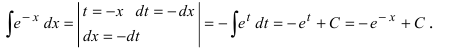
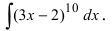
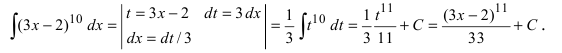
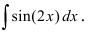
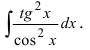
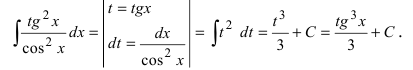
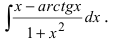
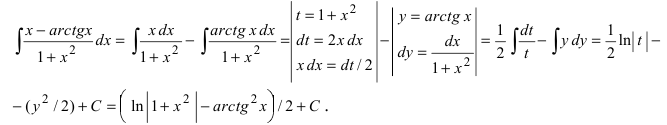
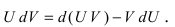
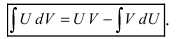
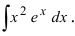
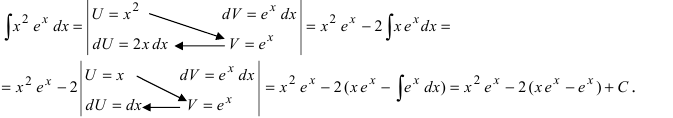
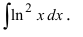
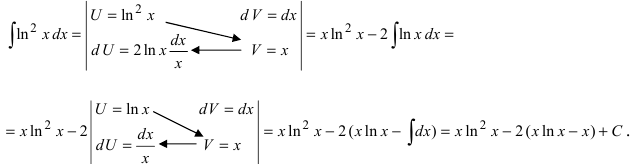
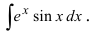
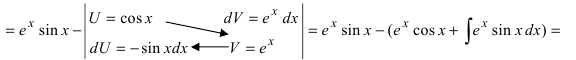
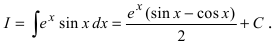
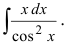
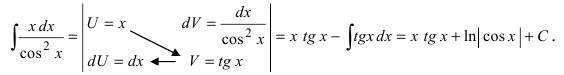
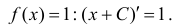
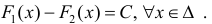
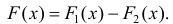
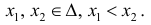
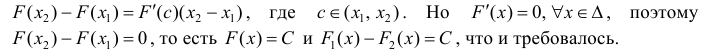
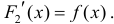
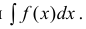
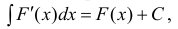 (3) или
(3) или 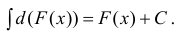
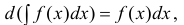 (4) здесь под записью
(4) здесь под записью 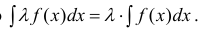 (5)
(5)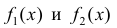 имеют первообразную на Δ , тогда
имеют первообразную на Δ , тогда 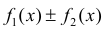 также имеет первообразную на Δ и:
также имеет первообразную на Δ и: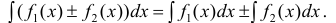 (6)
(6)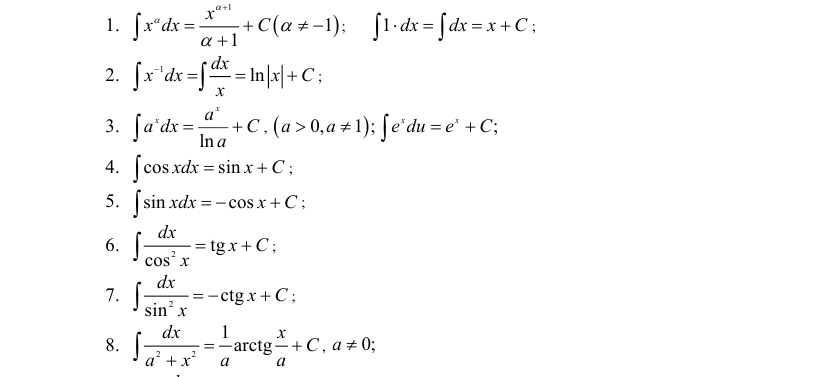
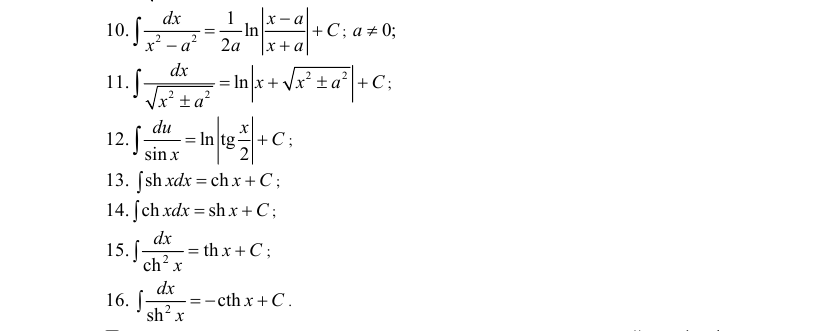
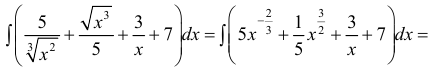
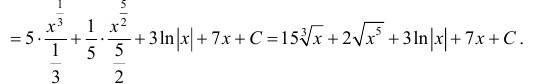
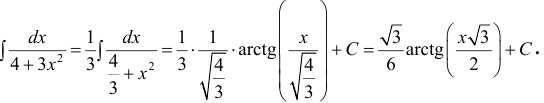
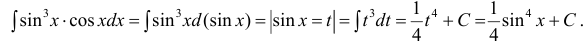
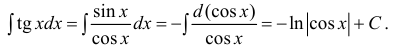
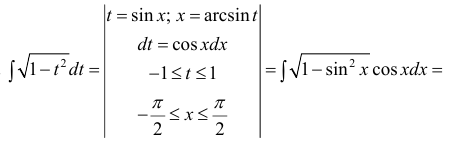
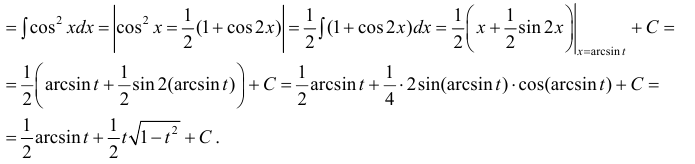
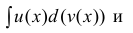
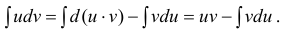
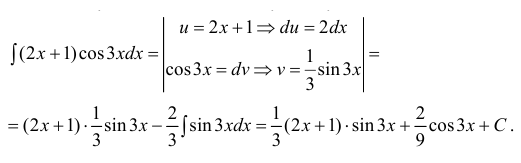
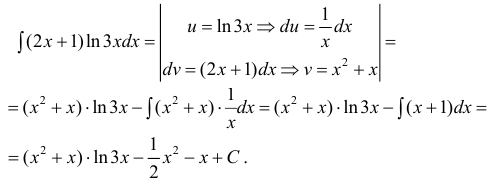
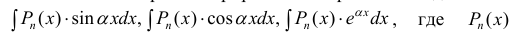 — многочлен степени n полагают:
— многочлен степени n полагают: 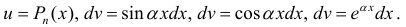 После интегрирования по частям степень многочлена уменьшается на 1 (см. пример 1).
После интегрирования по частям степень многочлена уменьшается на 1 (см. пример 1).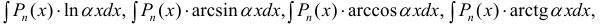
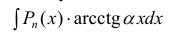 полагают:
полагают: 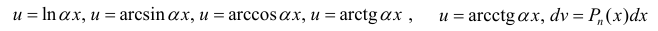 (
(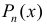 — многочлен). После интегрирования по частям интеграл упрощается.
— многочлен). После интегрирования по частям интеграл упрощается.