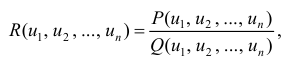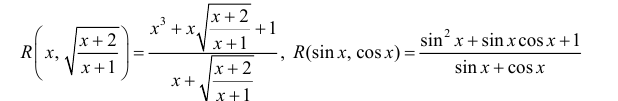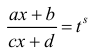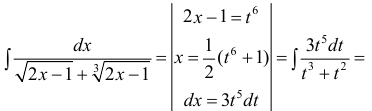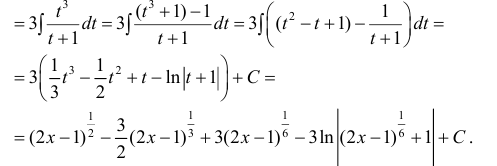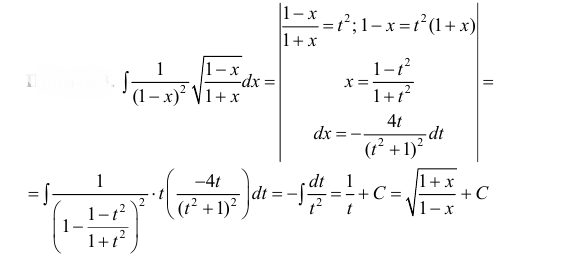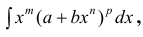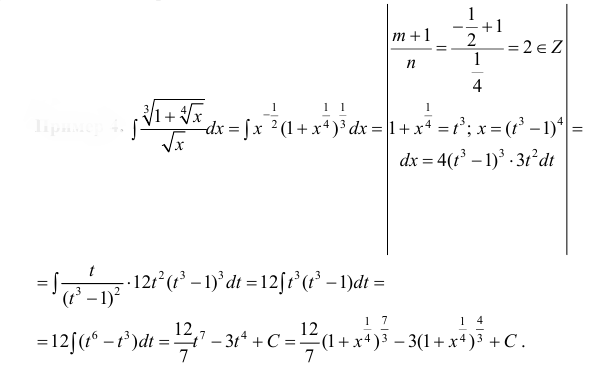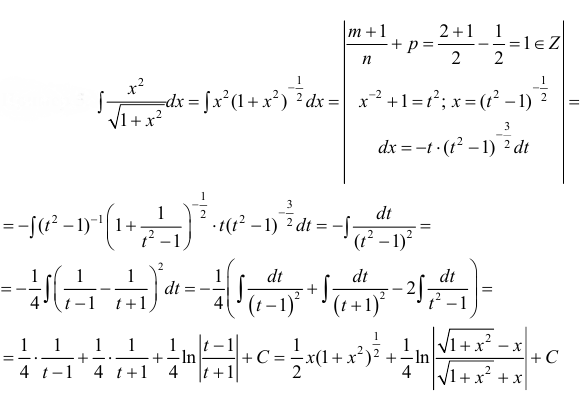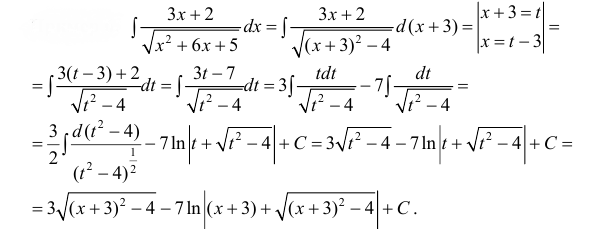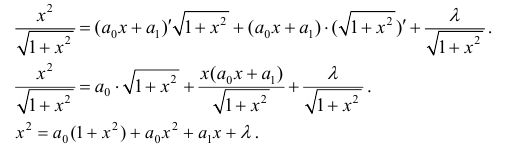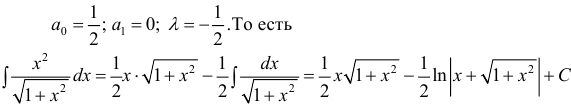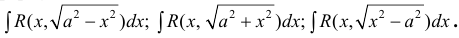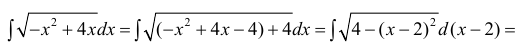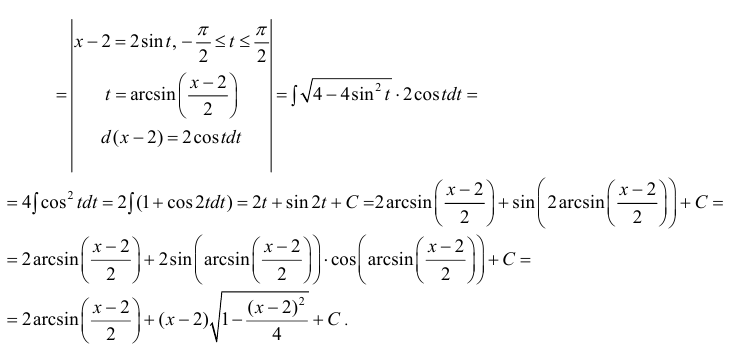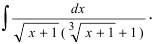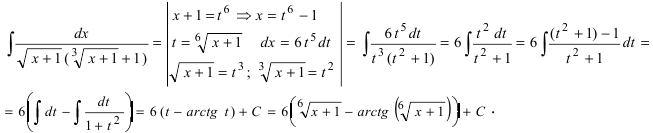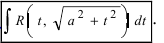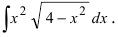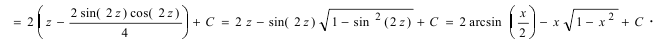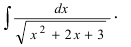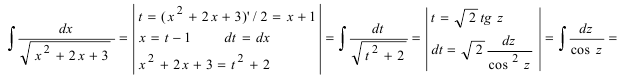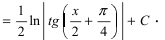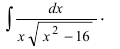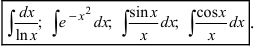Как найти неопределенный интеграл с корнями - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание:

Формула
Примеры вычисления интеграла корня

Формула

$$int frac{d x}{sqrt{x}}=2 sqrt{x}+C$$

Интеграл от единицы, деленной на корень, равен двум таким же корням плюс константа интегрирования.

$$int sqrt{x} d x=frac{2}{3} sqrt{x^{3}}+C$$

Заметим, что данные формулы сводятся к
интегралу от степенной функции при помощи следующих свойств:

$sqrt[m]{x^{n}}=x^{frac{n}{m}}$ и $frac{1}{x^{n}}=x^{-n}$

Примеры вычисления интеграла корня

Пример

Задание. Найти неопределенный интеграл $int frac{d x}{2 sqrt{x}}$

Решение. Согласно
свойствам неопределенного интеграла, константу можно выносить за знак интеграла, то есть получим:

$$int frac{d x}{2 sqrt{x}}=frac{1}{2} int frac{d x}{sqrt{x}}$$

А тогда, согласно формуле, будем иметь:

$$int frac{d x}{2 sqrt{x}}=frac{1}{2} int frac{d x}{sqrt{x}}=frac{1}{2} cdot 2 sqrt{x}+C=sqrt{x}+C$$

Ответ. $int frac{d x}{2 sqrt{x}}=sqrt{x}+C$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание.$int 2 sqrt{x} d x$

Решение. Константу выносим за знак интеграла:

$$int 2 sqrt{x} d x=2 int sqrt{x} d x$$

Далее интеграл находи по формуле:

$$int 2 sqrt{x} d x=2 int sqrt{x} d x=2 cdot frac{2}{3} sqrt{x^{3}}+C=frac{4 sqrt{x^{3}}}{3}+C$$

Ответ. $int 2 sqrt{x} d x=frac{4 sqrt{x^{3}}}{3}+C$

Читать дальше: интеграл обратной функции.

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Интегрирование иррациональных функций с примерами решения

Содержание:

Интегрирование иррациональных функций.

Определение 1. Функция вида

Пример 1.
— рациональная функция переменных u и v, при этом:

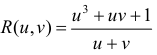
п.1. Интегралы вида:

Пусть s – общий знаменатель дробей 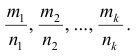Тогда подстановка
делает подинтегральную функцию рациональной.

Пример 2.

Пример 3

п.2. Интегралы вида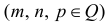— интегралы от дифференциального бинома.
Интегралы вида (1) выражаются через элементарные функции в следующих случаях:
а) p∈Z — интегралы рассмотрены в п.1.
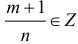
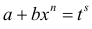
б) , тогда подстановка , где s – знаменатель р приводит интегральную функцию к рациональной.
в) , тогда подстановка , где s – знаменатель р приводит интегральную функцию к рациональной.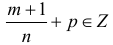
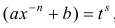
Во всех других случаях интегралы (1) выразить через элементарные функции нельзя (теорема Чебышева).

Пример 4.

Пример 5.

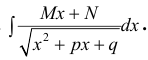
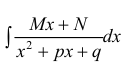
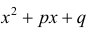
п.3. Интегралы вида Вычисление интегралов проводится аналогично интегралам выделением полного квадрата в трехчлене
(см. § 21, примеры 1, 2).

Пример 6.

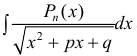
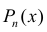
п 4. Интегралы вида , где — многочлен степени n.
Для вычисления интегралов используют равенство:
многочлен степени n−1 . Коэффициенты многочлена а также число λ находятся, если продифференцировать правую и левую часть равенства (2).

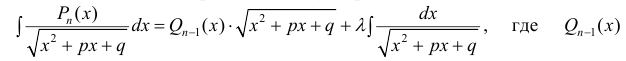
Заказать решение задач по высшей математике

Пример 7.
После взятия производной:

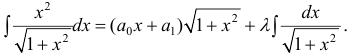
Приравниваем друг к другу коэффициенты при одинаковых степенях х в правой и левой частях.

Решив систему (3), получим :

(сравни с примером 5).

п.5. Интегралы вида
В данных интегралах можно избавиться от иррациональности, если применить подходящую тригонометрическую или гиперболическую подстановку.
— для первого интеграла,
— для второго,
— для третьего (см. § 23).

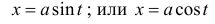
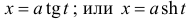
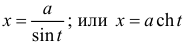
Пример 8.

Пример 9.

Интегрирование некоторых иррациональных функций

1. Интегралы вида .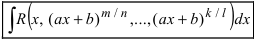

Интегралы такого типа вычисляются по следующей схеме:

В результате приведенных действий данный интеграл переходит в неопределенный интеграл от рациональной функции.

Пример:

Вычислить

Решение:

В данном примере 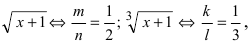следовательно, наименьший общий знаменатель этих дробей равен 6. Таким образом.

2. Интегралы вида .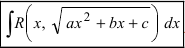

Такие интегралы путем замены 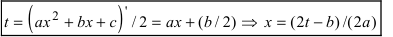приводятся к одному из интегралов вида:

1. 2. 3.

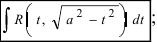
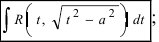
Для вычисления этих интегралов применяют следующие тригонометрические замены

1. 2. 3. — которые позволяют избавиться от квадратного корня.

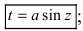
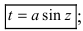
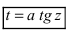
Пример:

Вычислить

Решение:

Данный интеграл соответствует интегралам типа 1., поэтому

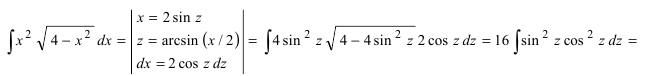
Пример:

Вычислить

Решение:

Воспользуемся указанной выше заменой

(интеграл вычислен в п. 2а)

Пример:

Вычислить

Решение:

Пример:

Вычислить

Решение:

Воспользуемся указанной выше заменой

Понятие о неберущихся интегралах

Определение: Интегралы, первообразные которых не выражаются через элементарные функции, называются неберущимися:

Прямоугольная система координат на плоскости и ее применение
Линии второго порядка
Полярные координаты
Непрерывность функции
Формула Тейлора и ее применение
Интегрирование рациональных дробей
Интегрирование тригонометрических функций
Интегрирование тригонометрических выражений

Источник

Заказать задачи по любым предметам можно здесь от 10 минут

Интегрирование иррациональных функций

Формула

Формула на интегрирование иррациональных функций зависит от типа предлагаемого к решению интеграла, в частности от подкоренного выражения:

Линейная функция: $$ sqrt[n]{ax+b}, (a neq 0) $$ Для решения такого интеграла удобно применить подстановку $ t = sqrt[n]{ax+b} $
Квадратный многочлен: $$ sqrt{ax^2+bx+c} $$ В этом случае необходимо дополнить многочлен до полного квадрата, а затем по одной из формул таблицы интегрирования решить полученный интеграл вида $ int frac{dx}{sqrt{alpha^2 pm x^2}} $
Разность квадратов: $$ sqrt{a^2-x^2} $$ Используем подстановку $ x = asin t $, затем по формуле $ 1-sin^2 t = cos^2 t $ продолжаем нахождение интеграла

Примеры решений

Пример 1

Найти интеграл иррациональной функции: $$ int frac{xdx}{sqrt[3]{x+1}} $$

Решение

Выполняем замену: $$ t = sqrt[3]{x+1} $$

Выражаем из замены $ x $: $$ x = t^3-1 $$

Находим $ dx $: $$ dx = 3t^2 dt $$

Подставляем в интеграл полученные данные:

$$ int frac{xdx}{sqrt[3]{x+1}} = int frac{(t^3-1)3t^2}{t} dt = $$

Выполняем разложение подынтегрального выражения на две дроби:

$$ = int 3t^4 dt — int 3t dt = frac{3t^5}{5} — frac{3t^2}{2} + C = $$

Возвращаем замену назад:

$$ = frac{3}{5}(sqrt[3]{x+1})^5 — frac{3}{2}(sqrt[3]{x+1})^2 + C = frac{3}{5}sqrt[3]{(x+1)^5}-frac{3}{2}sqrt[3]{(x+1)^2} + C $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ int frac{xdx}{sqrt[3]{x+1}} = frac{3}{5}sqrt[3]{(x+1)^5}-frac{3}{2}sqrt[3]{(x+1)^2} + C $$

Пример 2

Выполнить интегрирование иррациональных функций: $$ int frac{dx}{sqrt{x^2-6x+13}} $$

Решение

Замечаем, что под корнем находится квадратный многочлен. Это значит, что можно выделить под корнем полный квадрат, а затем решить интеграл по таблице интегрирования основных функций.

Выделяем полный квадртат:

$$ x^2-6x+13 = x^2 — 2cdot 3 + 3^2 + 4 = (x — 3)^2 + 4 $$

Подставляем полученное выражение под корень в интеграле:

$$ int frac{dx}{sqrt{x^2-6x+13}} = int frac{dx}{sqrt{(x-3)^2+4}} = $$

$$ = int frac{dx}{sqrt{x^2-6x+13}} = ln | x-3 + sqrt{x^2-6x+13}| + C $$

Ответ

$$ int frac{dx}{sqrt{x^2-6x+13}} = ln | x-3 + sqrt{x^2-6x+13}| + C $$

Пример 3

Решить интеграл с иррациональностью: $$ int sqrt{1-x^2} dx $$

Решение

Интеграл попадает под третий случай, в котором необходимо выполнить подстановку:

$$ x = sin t; dx = cos t; t = arcsin x $$

Записываем решение:

$$ int sqrt{1-x^2} dx = int sqrt{(1-(sin t)^2}) cos t dt = $$

Воспользовавшись тригонометрической формулой $ 1 — sin^2 t = cos^2 t $ получаем:

$$ = int sqrt{cos^2 t} cos t = int cos^2 t dt = $$

С учётом формулы понижения степени косинуса $ cos^2 t = frac{1+cos 2t}{2} $ имеем:

$$ = int frac{1+cos 2t}{2} dt = frac{1}{2} int (1+cos 2t) dt = $$

Воспользуемся свойством разложения интеграла:

$$ frac{1}{2} int dt + frac{1}{2} int cos 2t dt = frac{1}{2} t + frac{1}{4} sin 2t + C = $$

Выполняем обратную подстановку:

$$ = frac{1}{2} arcsin x + frac{1}{4} sin (2arcsin x) + C $$

Ответ

$$ int sqrt{1-x^2} dx = frac{1}{2} arcsin x + frac{1}{4} sin (2arcsin x) + C $$

Источник

Простое объяснение принципов решения интегрирования иррациональных функций и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения интегрирования иррациональных функций

Интегралы, подынтегральная функция которых представляет собой иррациональное выражение, не могут быть вычислены непосредственно. С помощью тождественных преобразований подынгегральной функции такие интегралы можно свести к табличным интегралам, либо к их алгебраической сумме.

При решении задач на вычисление интегралов от иррациональных функций, применяются методы подстановки и дробно-линейной подстановки.

Отдельным методом интегрирования иррациональных функций является использование формулы:

$[intfrac{P_{n}(x)}{sqrt{ax^{2} + bx + c}}dx = Q_{n-1}(x)cdotsqrt{ax^{2} + bx + c} + lambdaintfrac{dx}{sqrt{ax^{2} + bx + c}}]$

Примеры решений интегрирования иррациональных функций

Задача

Вычислить интеграл:

$[int frac{sqrt[3]{x}}{sqrt[3]{x^{2}} - sqrt{x}}dx]$

Решение

Представим интеграл в виде:

$[int frac{sqrt[3]{x}}{sqrt[3]{x^{2}} - sqrt{x}}dx = int frac{x^{frac{1}{3}}}{x^{frac{2}{3}} - x^{frac{1}{2}}}dx]$

Наименьшее общее кратное знаменателей дробей $frac{1}{3}, frac{2}{3}$ и $frac{1}{2}$ является 6.

Сделаем подстановку $x = y^{6}, dx = 6y^{5}dy$

$x^{frac{1}{3}} = (y^{6})^{frac{1}{3}} = y^{2}, x^{frac{2}{3}} = (y^{6})^{frac{2}{3}} = y^{4}, x^{frac{1}{2}} = (y^{6})^{frac{1}{2}} = y^{3}$

$[int frac{y^{2}}{y^{4} - y^{3}}6y^{5}dy = 6int frac{y^{7}}{y^{3}(y - 1)}dy = 6int frac{y^{4}}{y - 1}dy]$

Выделим целую часть в $frac{y^{4}}{y - 1}$ :

$frac{y^{4}}{y - 1} = y^{3} + y^{2} + y + 1 + frac{1}{y - 1}$

$[= 6left[frac{y^{4}}{4} + frac{y^{3}}{3} + frac{y^{2}}{2} + y + ln|y - 1|right] + C]$

Сделаем обратную подстановку

$6left[frac{y^{4}}{4} + frac{y^{3}}{3} + frac{y^{2}}{2} + y + ln|y - 1|right] + C = 6left[frac{sqrt[3]{x^{2}}}{4} + frac{sqrt{x}}{3} + frac{sqrt[3]{x}}{2} + sqrt[6]{x} + ln|sqrt[6]{x} - 1|right] + C$

Ответ

$[int frac{sqrt[3]{x}}{sqrt[3]{x^{2}} - sqrt{x}}dx = 6left[frac{sqrt[3]{x^{2}}}{4} + frac{sqrt{x}}{3} + frac{sqrt[3]{x}}{2} + sqrt[6]{x} + ln|sqrt[6]{x} - 1|right] + C]$

Задача

Вычислить интеграл:

$[int frac{sqrt{x}}{sqrt[3]{x^{2}} - sqrt{x}}dx]$

Решение

Представим интеграл в виде:

$[int frac{sqrt{x}}{sqrt[3]{x^{2}} - sqrt{x}}dx = int frac{x^{frac{1}{2}}}{x^{frac{2}{3}} - x^{frac{1}{2}}}dx]$

Наименьшее общее кратное знаменателей дробей $frac{1}{2}$ и $frac{2}{3}$ является 6.

Сделаем подстановку $x = y^{6}, dx = 6y^{5}dy$

$x^{frac{1}{2}} = (y^{6})^{frac{1}{2}} = y^{3}, x^{frac{2}{3}} = (y^{6})^{frac{2}{3}} = y^{4}$

$[int frac{y^{3}}{y^{4} - y^{3}}6y^{5}dy = 6int frac{y^{8}}{y^{3}(y - 1)}dy = 6int frac{y^{5}}{y - 1}dy]$

Выделим целую часть в $frac{y^{5}}{y - 1}$ :

$frac{y^{5}}{y - 1} = y^{4} + y^{3} + y^{2} + y + 1 + frac{1}{y - 1}$

$[6intfrac{y^{5}}{y - 1}dy = 6intleft[y^{4} + y^{3} + y^{2} + y + 1 + frac{1}{y - 1}right]dy =]$

$[= 6left[frac{y^{5}}{5} + frac{y^{4}}{4} + frac{y^{3}}{3} + frac{y^{2}}{2} + y + ln|y - 1|right] + C]$

Сделаем обратную подстановку

$6left[frac{y^{5}}{5} + frac{y^{4}}{4} + frac{y^{3}}{3} + frac{y^{2}}{2} + y + ln|y - 1|right] + C = 6left[frac{sqrt[6]{x^{5}}}{5} + frac{sqrt[3]{x^{2}}}{4} + frac{sqrt{x}}{3} + frac{sqrt[3]{x}}{2} + sqrt[3]{x} + ln|sqrt[6]{x} - 1|right] + C$

Ответ

$[int frac{sqrt{x}}{sqrt[3]{x^{2}} - sqrt{x}}dx = 6left[frac{sqrt[6]{x^{5}}}{5} + frac{sqrt[3]{x^{2}}}{4} + frac{sqrt{x}}{3} + frac{sqrt[3]{x}}{2} + sqrt[3]{x} + ln|sqrt[6]{x} - 1|right] + C]$

Задача

Вычислить интеграл:

$[int frac{sqrt[3]{x}}{x(sqrt{x} + sqrt[3]{x})}dx]$

Решение

Представим интеграл в виде:

$[int frac{sqrt[3]{x}}{x(sqrt{x} + sqrt[3]{x})}dxdx = int frac{x^{frac{1}{3}}}{x(x^{frac{1}{2}} + x^{frac{1}{3}})}dx = int frac{x^{frac{1}{3}}}{x^{frac{3}{2}} + x^{frac{4}{3}}}dx]$

Наименьшее общее кратное знаменателей дробей $frac{1}{2}$ и $frac{2}{3}$ является 6.

Сделаем подстановку $x = y^{6}, dx = 6y^{5}dy$

$x^{frac{1}{3}} = (y^{6})^{frac{1}{3}} = y^{2}, x^{frac{3}{2}} = (y^{6})^{frac{3}{2}} = y^{9}, x^{frac{4}{3}} = (y^{6})^{frac{4}{3}} = y^{8}$

$[int frac{y^{2}}{y^{9} + y^{8}}6y^{5}dy = 6int frac{y^{7}}{y^{9} + y^{8}}dy = 6int frac{1}{y^{2} + y}dy]$

Преобразуем подынтегральную функцию:

$[6int frac{1}{y^{2} + y}dy = 6int frac{y + 1 - y}{y(y + 1)}dy]$

$[6int frac{1}{y^{2} + y}dy = 6left[intfrac{dy}{y} - intfrac{dy}{y+1}right]]$

$[6left[intfrac{dy}{y} - intfrac{dy}{y+1}right] = 6left[ln|y| - ln|y + 1|right] + C]$

Сделаем обратную подстановку

$[= 6lnfrac{sqrt[6]{x}}{sqrt[6]{x} + 1} + C]$

Ответ

$[int frac{sqrt[3]{x}}{x(sqrt{x} + sqrt[3]{x})}dx = 6lnfrac{sqrt[6]{x}}{sqrt[6]{x} + 1} + C]$

Задача

Вычислить интеграл:

$[int frac{sqrt[6]{x}}{x(sqrt[3]{x} + sqrt[4]{x})}dx]$

Решение

Представим интеграл в виде:

$[int frac{sqrt[6]{x}}{x(sqrt[3]{x} + sqrt[4]{x})}dx = int frac{x^{frac{1}{6}}}{x^{frac{4}{3}} + x^{frac{5}{4}}}dx]$

Наименьшим общим кратным знаменателей дробей $frac{1}{6}, frac{4}{3}$ и $frac{5}{4}$ является 6.

Сделаем подстановку $x = y^{12}, dx = 12y^{11}dy$

$x^{frac{1}{6}} = (y^{12})^{frac{1}{6}} = y^{2}, x^{frac{4}{3}} = (y^{12})^{frac{4}{3}} = y^{16}, x^{frac{5}{4}} = (y^{12})^{frac{5}{4}} = y^{15}$

$[int frac{y^{2}}{y^{16} + y^{15}}12y^{11}dy = 12intfrac{y^{13}}{y^{15}(y + 1)}dy = 12intfrac{1}{y^{2}(y + 1)}dy]$

Преобразуем подынтегральную функцию:

$[12intfrac{1}{y^{2}(y + 1)}dy = -12intfrac{y^{2} - 1 - y^{2}}{y^{2}(y + 1)}dy =]$

$[-12left[intfrac{y - 1}{y^{2}}dy - intfrac{1}{y + 1}dyright] =]$

$[= -12left[intfrac{1}{y}dy - intfrac{1}{y^{2}}dy - intfrac{1}{y + 1}dyright] =]$

$[= -12left[ln{y} + frac{1}{y} + ln{(y + 1)}right] + C]$

Сделаем обратную подстановку

$-12left[ln{y} + frac{1}{y} + ln{(y + 1)}right] + C =-12left[ln{sqrt[12]{x}} + frac{1}{sqrt[12]{x}} + ln{(sqrt[12]{x} + 1)}right] + C = -12left[ln({sqrt[12]{x}cdot(sqrt[12]{x} + 1)}) + frac{1}{sqrt[12]{x}}right] + C = -12left[ln({sqrt[6]{x} + sqrt[12]{x})}) + frac{1}{sqrt[12]{x}}right] + C$

Ответ

$[int frac{sqrt[6]{x}}{x(sqrt[3]{x} + sqrt[4]{x})}dx = -12left[ln({sqrt[6]{x} + sqrt[12]{x})}) + frac{1}{sqrt[12]{x}}right] + C]$

Задача

Вычислить интеграл:

$[int frac{dx}{sqrt{4x^{2} + 2x + 1}}dx]$

Решение

Преобразуем $4x^{2} + 2x + 1$ :

$4x^{2} + 2x + 1 = 4(x^{2} + frac{1}{2}x + frac{1}{4}) = 4((x + frac{1}{4})^2 + frac{3}{16})$

$[intfrac{dx}{sqrt{4((x + frac{1}{4})^2 + frac{3}{16})}} = frac{1}{2}intfrac{dx}{sqrt{(x + frac{1}{4})^2 + frac{3}{16}}}]$

Подставим вместо $x + frac{1}{4}, t$ :

$x + frac{1}{4} = t, x = t - frac{1}{4}, dx = dt$

$[frac{1}{2}intfrac{dx}{sqrt{(x + frac{1}{4})^2 + frac{3}{16}}} = frac{1}{2}intfrac{dt}{sqrt{t^{2} + frac{3}{16}}}]$

$[frac{1}{2}intfrac{dt}{sqrt{t^{2} + frac{3}{16}}} = frac{1}{2}lnleft|t + sqrt{t^{2} + frac{3}{16}}|right| + C]$

Делаем обратную замену $t = x + frac{1}{4}$ :

$[frac{1}{2}lnleft|t + sqrt{t^{2} + frac{3}{16}}|right| + C = frac{1}{2}lnleft|x + frac{1}{4} + sqrt{(x + frac{1}{4})^{2} + frac{3}{16}}right| + C]$

Ответ

$[int frac{dx}{sqrt{4x^{2} + 2x + 1}}dx = frac{1}{2}lnleft|x + frac{1}{4} + sqrt{(x + frac{1}{4})^{2} + frac{3}{16}}right| + C]$

Задача

Вычислить интеграл:

$[int frac{x + 4}{sqrt{6 - 2x - x^{2}}}dx]$

Решение

Преобразуем $6 - 2x - x^{2}$ :

$6 - 2x - x^{2} = -(x^{2} + 2x - 6) = -((x + 1)^2 - 7) = 7 - (x + 1)^2$

Подставим вместо :

$[int frac{x + 4}{sqrt{6 - 2x - x^{2}}}dx = intfrac{t - 1 + 4}{sqrt{7 - t^{2}}}dt]$

$[intfrac{t - 1 + 4}{sqrt{7 - t^{2}}}dt = intfrac{tdt}{sqrt{7 - t^{2}}} + 3intfrac{dt}{sqrt{7 - t^{2}}} =]$

$[= -frac{1}{2}int(7 - t^{2})^{-frac{1}{2}}d(7 - t^{2}) + 3intfrac{dt}{sqrt{{(sqrt{7})^{2}} - t^2}} =]$

$[= -sqrt{7 - t^{2}} + 3arcsin{frac{t}{sqrt{7}}} + C]$

Делаем обратную замену :

$-sqrt{7 - t^{2}} + 3arcsin{frac{t}{sqrt{7}}} + C = 3arcsin{frac{x + 1}{sqrt{7}}} - sqrt{6 - 2x - x^{2}} + C$

Ответ

$[int frac{x + 4}{sqrt{6 - 2x - x^{2}}}dx = 3arcsin{frac{x + 1}{sqrt{7}}} - sqrt{6 - 2x - x^{2}} + C]$

Задача

Вычислить интеграл:

$[int frac{x^{2}}{sqrt{1 - 2x - x^{2}}}dx]$

Решение

Применим формулу

$[intfrac{P_{n}(x)}{sqrt{ax^{2} + bx + c}}dx = Q_{n-1}(x)cdotsqrt{ax^{2} + bx + c} + lambdaintfrac{dx}{sqrt{ax^{2} + bx + c}}]$

$[int frac{x + 4}{sqrt{6 - 2x - x^{2}}}dx = 3arcsin{frac{x + 1}{sqrt{7}}} - sqrt{6 - 2x - x^{2}} + C]$

$[int frac{x^{2}}{sqrt{1 - 2x - x^{2}}}dx = (Ax + B)sqrt{1 - 2x - x^{2}} + lambdacdotint frac{dx}{sqrt{1 - 2x - x^{2}}}]$

Дифференцируя равенство по , получаем:

$[int frac{x^{2}}{sqrt{1 - 2x - x^{2}}} equiv Acdotsqrt{1 - 2x - x^{2}} + (Ax + B)cdotfrac{-2 - 2x}{2sqrt{1 - 2x - x^{2}}} + frac{lambda}{sqrt{1 - 2x - x^{2}}}]$

$x^{2} equiv A(1 - 2x - x^{2}) + (Ax + B)(-1 - x) + lambda$

$x^{2} equiv A - 2Ax - Ax^{2}) - Ax - B - Ax^{2} - Bx + lambda$

Сопоставим коэффициенты слагаемых с в одинаковой степени:

– коэффициент при $x^{2}$

– коэффициент при

– коэффициент при $x^{0}$

Находим значения и :

$A = -frac{1}{2}, B = frac{3}{2}, lambda = 2$

Подставляем найденные значения в

$[int frac{x^{2}}{sqrt{1 - 2x - x^{2}}} equiv Acdotsqrt{1 - 2x - x^{2}} + (Ax + B)cdotfrac{-2 - 2x}{2sqrt{1 - 2x - x^{2}}} + frac{lambda}{sqrt{1 - 2x - x^{2}}}]$

Получаем

$[(-frac{1}{2}x + frac{3}{2})sqrt{1 - 2x - x^{2}} + 2intfrac{dx}{sqrt{2 - (x + 1)^{2}}} =]$

$[= (-frac{1}{2}x + frac{3}{2})sqrt{1 - 2x - x^{2}} + 2arcsin{frac{x + 1}{sqrt{2}}} + C]$

Ответ

$[int frac{x^{2}}{sqrt{1 - 2x - x^{2}}}dx = (-frac{1}{2}x + frac{3}{2})sqrt{1 - 2x - x^{2}} + 2arcsin{frac{x + 1}{sqrt{2}}} + C]$

Задача

Вычислить интеграл:

$[int frac{x^{2}}{sqrt{a^{2} - x^{2}}}dx]$

Решение

Для вычисления данного интеграла необходимо осуществить тригонометрическую подстановку

Найдём dx:

С учётом подстановки подынтегральная функция примет следующий вид:

$frac{x^{2}}{sqrt{a^{2} - x^{2}}} = frac{a^{2}sin^{2}t}{sqrt{a^{2} - a^{2}sin^{2}{t}}} = frac{a^{2}sin^{2}t}{sqrt{a^{2}(1 - sin^{2}{t})}} = frac{a^{2}sin^{2}t}{sqrt{a^{2}cos^{2}{t}}} = frac{a^{2}sin^{2}t}{acos{t}}$

В результате искомый интеграл преобразуется к следующему виду:

$[int frac{a^{2}sin^{2}t}{acos{t}}acos{t}dt = a^{2}int sin^{2}{t}dt]$

Данный интеграл относится к табличным и равен:

$[int sin^{2}{t}dt = frac{1}{2}(t - sin{t}cos{t}) + C]$

Поэтому:

$[a^{2}int sin^{2}{t}dt = a^{2}frac{1}{2}(t - sin{t}cos{t}) + C]$

Перейдём к переменной , для этого из подстановки выразим через :

$t = arcsin{frac{x}{a}}, sin{t} = frac{x}{a}, cos{t} = sqrt{1 - sin^{2}{t}} = sqrt{1 - frac{x^{2}}{a^{2}}} = frac{sqrt{a^{2} - x^{2}}}{a}$

В итоге получим:

$[a^{2}frac{1}{2}(t - sin{t}cos{t}) + C = frac{a^{2}}{2}(arcsinfrac{x}{a} - frac{x}{a}frac{sqrt{a^{2} - x^{2}}}{a}) + C]$

$[a^{2}frac{1}{2}(t - sin{t}cos{t}) + C = frac{a^{2}}{2}arcsinfrac{x}{a} - frac{x}{2}sqrt{a^{2} - x^{2}} + C]$

Ответ

$[int frac{x^{2}}{sqrt{2ax - x^{2}}}dx = frac{a^{2}}{2}arcsinfrac{x}{a} - frac{x}{2}sqrt{a^{2} - x^{2}} + C]$

Задача

Вычислить интеграл:

$[int frac{sqrt{4 - x^{2}}}{x^{2}}dx]$

Решение

Для вычисления данного интеграла необходимо осуществить тригонометрическую подстановку $x = 2sin{t}, t = arcsinfrac{x}{2}$

Найдём dx:

С учётом подстановки подынтегральная функция примет следующий вид:

$[frac{sqrt{4 - x^{2}}}{x^{2}} = frac{sqrt{4 - 4sin^{2}{t}}}{4sin^{2}{t}}cdot2cos{t}dt =]$

$[= intfrac{4cos^{2}{t}}{4sin^{2}{t}}dt = intfrac{1 - sin^{2}{t}}{sin^{2}{t}}dt = intfrac{dt}{sin^{2}{t}} - int dt =]$

Делаем обратную подстановку $t = arcsinfrac{x}{2}$ и учитываем, что $ctgt = frac{sqrt{1 - sin^{2}{t}}}{sin{t}} = frac{sqrt{1 - (frac{x}{2})^{2}}}{frac{x}{2}} = frac{sqrt{4 - x^{2}}}{x}$ :

$- ctgt - t + C = -frac{sqrt{4 - x^{2}}}{x} - arcsinfrac{x}{2} + C$

Ответ

$[int frac{sqrt{4 - x^{2}}}{x^{2}}dx = -frac{sqrt{4 - x^{2}}}{x} - arcsinfrac{x}{2} + C]$

Задача

Вычислить интеграл:

$[int frac{sqrt{x^{2} + 2x - 4}}{(x + 1)^{3}}dx]$

Решение

$x^{2} + 2x - 4 = (x + 1)^{2} - 5$

Сделаем подстановку :

$[int frac{sqrt{x^{2} + 2x - 4}}{(x + 1)^{3}}dx = intfrac{sqrt{t^{2} - 5}}{t^{3}}dt]$

Сделаем подстановку $t = frac{sqrt{5}}{sin{z}}, dt = frac{-sqrt{5}cdotcos{z}}{sin^{2}{z}}dz, z = arcsin{frac{sqrt{5}}{t}}$ :

$[intfrac{sqrt{t^{2} - 5}}{t^{3}}dt = intfrac{sqrt{frac{5}{sin^{2}{z}} - 5}}{frac{5sqrt{5}}{sin^{3}{z}}}cdotfrac{-sqrt{5}cos{z}}{sin^{2}{z}}dz = -frac{1}{sqrt{5}}intcos^{2}{z}dz =]$

$[= -frac{1}{sqrt{5}}cdotfrac{1}{2}int(1 + cos{2z})dz = -frac{5}{sqrt{10}}(z + frac{1}{2}sin{2z}) + C]$

Переходим к переменной через подстановку $z = arcsin{frac{sqrt{5}}{t}}$ :

$-frac{5}{sqrt{10}}(z + frac{1}{2}sin{2z}) + C = -frac{5}{sqrt{10}}(arcsin{frac{sqrt{5}}{t}} + frac{1}{2}sin{2arcsin{frac{sqrt{5}}{t}}}) + C$

Переходим к переменной через подстановку :

$-frac{5}{sqrt{10}}(arcsin{frac{sqrt{5}}{t}} + frac{1}{2}sin{2arcsin{frac{sqrt{5}}{t}}}) + C = -frac{5}{sqrt{10}}(arcsin{frac{sqrt{5}}{x + 1}} + frac{1}{2}sin{2arcsin{frac{sqrt{5}}{x + 1}}}) + C = -frac{5}{sqrt{10}}(arcsin{frac{sqrt{5}}{x + 1}} + frac{sqrt{5}cdotsqrt{x^{2} + 2x - 4}}{(x + 1)^2} + C$

Ответ

$[int frac{sqrt{x^{2} + 2x - 4}}{(x + 1)^{3}}dx = -frac{5}{sqrt{10}}(arcsin{frac{sqrt{5}}{x + 1}} + frac{sqrt{5}cdotsqrt{x^{2} + 2x - 4}}{(x + 1)^2} + C]$

Источник

Интеграл от корня

Интеграл от корня равен двум третям корня x в кубе плюс константа интегрирования.

(
int sqrt{x} d x=frac{2}{3} sqrt{x^{3}}+C
)

Эта формула может быть получена путем записи корня в виде показателя степени, а затем нахождения интеграла как степенной функции:

(
int x^{n} d x=frac{x^{n+1}}{n+1}+C
)

(
int sqrt{x} d x=int x^{frac{1}{2}} d x=frac{x^{frac{1}{2}+1}}{frac{1}{2}+1}=frac{x^{frac{1}{2}}}{frac{3}{2}}=frac{2}{3} sqrt{x^{3}}+C
)

Примеры решения проблем на тему «Интеграл от корня»

ПРИМЕР 1

Задача

Поиски Интеграла

(
int(2 sqrt{x}+1) d x
)

Решение.

Согласно свойствам интеграла интеграл от суммы равен сумме интегралов, а константу можно взять из знака интеграла. Тогда мы имеем:

(
int(2 sqrt{x}+1) d x=int 2 sqrt{x} d x+int d x=2 int sqrt{x} d x+x=2 cdot frac{2}{3} sqrt{x^{3}}+C=frac{4}{3} sqrt{x^{3}}+C
)

Ответ

(
int(2 sqrt{x}+1) d x=frac{4}{3} sqrt{x^{3}}+C
)

ПРИМЕР 2

Задача

Решить интеграл

(
int frac{x+1}{2 sqrt{x}} d x
)

Решение

разделит функцию подынтегральной функции:

(
int frac{x+1}{2 sqrt{x}} d x=int frac{x d x}{2 sqrt{x}}+int frac{d x}{2 sqrt{x}}=frac{1}{2} int sqrt{x} d x+sqrt{x}=frac{1}{2} cdot frac{2}{3} sqrt{x^{3}}+sqrt{x}+C=frac{sqrt{x^{3}}}{3}+sqrt{x}+C
)

Интеграл (
int frac{d x}{2 sqrt{x}}
) является табличным и равен

(
int frac{d x}{2 sqrt{x}}=sqrt{x}+C
)

Ответ

(
int frac{x+1}{2 sqrt{x}} d x=frac{sqrt{x^{3}}}{3}+sqrt{x}+C
)

Источник