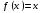Как найти неподвижную точку функции - Исправление недочетов и поиск решений вместе с Examum.ru

Теорема о неподвижной точке

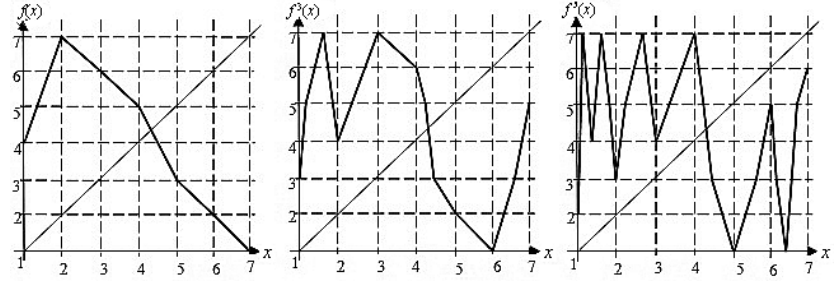
Определение 1.7. Элемент множества называют неподвижной точкой отображения fcolon Ato A , если f(a)=a .

Элемент упорядоченного множества называют наименьшей неподвижной точкой отображения fcolon Mto M , если он является наименьшим элементом множества всех неподвижных точек отображения .

Теорема 1.7 (теорема о неподвижной точке). Любое непрерывное отображение индуктивного упорядоченного множества (M,leqslant) в себя имеет наименьшую неподвижную точку.

Обозначим через mathbb{O} наименьший элемент множества . Полагаем $f^{0}(x)=x$ и $f^n(x)=f(f^{n-1}(x))$ для любого n>0 , т.е. f^n(x) означает результат n-кратного применения к . Рассмотрим последовательность элементов

$bigl{f^n(mathbb{O})bigr}_{ngeqslant0}= bigl{mathbb{O}, f(mathbb{O}), ldots, f^n(mathbb{O}),ldotsbigr}.$

(1.7)

Докажем, что последовательность (1.7) неубывающая. Используем метод математической индукции. Для элемента mathbb{O} , как наименьшего элемента множества , имеем $mathbb{O}-f^0(mathbb{O}) leqslant f(mathbb{O})$ . Пусть для некоторого натурального верно соотношение $f^{n-1}(mathbb{O})leqslant f^n(mathbb{O})$ . Согласно теореме 1.6, отображение монотонно, и поэтому

$f^n(mathbb{O})= f(f^{n-1}(mathbb{O})) leqslant f(f^n(mathbb{O}))= f^{n+1}(mathbb{O}),$

т.е. соотношение верно и для номера n+1 . Согласно методу математической индукции, $f^n(mathbb{O})leqslant f^{n+1}(mathbb{O})$ для любого $nin mathbb{N}_0$ , т.е. последовательность (1.7) неубывающая. Следовательно, по определению индуктивного упорядоченного множества, она имеет точную верхнюю грань. Обозначим ее через

$a=sup_{ngeqslant 0}f^n(mathbb{O}).$

(1.8)

Докажем теперь, что если у неубывающей последовательности отбросить любое конечное число начальных членов, то ее точная верхняя грань не изменится.

Действительно, если а есть точная верхняя грань неубывающей последовательности ${x_n}_{ngeqslant0}$ , то ageqslant x_n для всякого ngeqslant 0 . В частности, фиксируя произвольно k>0 , для любого ngeqslant k имеем , т.е. а будет верхней гранью подпоследовательности ${x_n}_{ngeqslant k>0}$ .

Докажем, что а является точной верхней гранью этой подпоследовательности. Пусть — какая-то ее верхняя грань, т.е. bgeqslant x_n для любого ngeqslant k . Так как последовательность ${x_n}_{ngeqslant0}$ неубывающая, то x_pleqslant x_k для каждого p=overline{0,k-1} . Поскольку x_kleqslant b , то в силу транзитивности отношения порядка x_pleqslant b и тем самым bgeqslant x_n для любого ngeqslant 0 , т.е. есть верхняя грань всей последовательности ${x_n}_{ngeqslant0}$ . Поскольку $a=mathop{sup_{ngeqslant0}x_n}limits^{phantom{A}^{.}}$ , то aleqslant b и $a=mathop{sup_{ngeqslant k>0}x_n}limits^{phantom{A}^{.}}$ . Следовательно, — точная верхняя грань последовательности ${x_n}_{ngeqslant k}$ .

В силу непрерывности получаем

$f(a)=f!left(sup_{ngeqslant0}f^n(mathbb{O})right)= sup_{ngeqslant0} f(f^n(mathbb{O}))= sup_{ngeqslant0}f^{n+1}(mathbb{O}).$ Но

$sup_{ngeqslant0}f^{n+1}(mathbb{O})= supbigl{f^1(mathbb{O}), f^2(mathbb{O}), ldotsbigr}= sup_{ngeqslant1}f^n(mathbb{O})=a.$

Таким образом, доказано, что является неподвижной точкой отображения .

Покажем теперь, что найденная неподвижная точка является наименьшей. Пусть для некоторого yin M имеем f(y)=y . Так как mathbb{O}leqslant y , а отображение , будучи непрерывным, монотонно, то

f(mathbb{O})leqslant f(y)=y,quad f(f(mathbb{O}))leqslant f(f(y))=y и т.д.

Следовательно, для любого ngeqslant 0 имеем $f^n(mathbb{O})leqslant y$ , т.е. элемент есть верхняя грань последовательности ${f^n(mathbb{O})}_{ngeqslant0}$ . Поскольку элемент (как точная верхняя грань) есть наименьший элемент на множестве всех верхних граней этой последовательности, то ygeqslant a . Таким образом, мы доказали, что произвольная неподвижная точка отображения не меньше элемента , то есть — наименьшая неподвижная точка отображения .

Нахождение неподвижной точки

Поиск неподвижной точки отображения fcolon Mto M можно рассматривать как задачу решения уравнения

x=f(x)

(1.9)

Теорему о неподвижной точке можно трактовать таким образом: для непрерывного отображения индуктивного упорядоченного множества в себя уравнение x=f(x) имеет решение, т.е. существует такой x_0in M , что выполняется равенство x_0=f(x_0) причем множество всех решений этого уравнения имеет наименьший элемент. Этот элемент и будет наименьшей неподвижной точкой отображения .

Отметим, что доказательство теоремы о неподвижной точке конструктивное: оно дает метод получения неподвижной точки. Для ее нахождения надо построить последовательность вида (1.7) и найти ее точную верхнюю грань.

Пример 1.20. Приведем простой пример вычисления наименьшей неподвижной точки. В качестве индуктивного упорядоченного множества возьмем отрезок [0;1] с естественным числовым порядком leqslant . Согласно примеру 1.19, это индуктивное упорядоченное множество.

Рассмотрим на этом множестве уравнение $x=frac{x}{2}+frac{1}{4}$ . Можно показать, что для индуктивного упорядоченного множества любая монотонная функция fcolon[0;1]to[0;1] , непрерывная в смысле определения из курса математического анализа, непрерывна и в смысле данного выше определения. Действительно, для любой неубывающей последовательности ${x_n}$ на множестве [0;1] справедливо равенство $sup{x_n}=lim_{nto+infty}x_n$ . В силу непрерывности функции в смысле определения из курса математического анализа имеем

$fBigl(lim_{nto+infty}x_nBigr)= lim_{nto+infty}f(x_n).$

Так как функция монотонна, то ${f(x_n)}_{ngeqslant0}$ — неубывающая последовательность и

$lim_{nto+infty}f(x_n)= sup f(x_n).$

В итоге получаем

$f(sup x_n)= fBigl(lim_{nto+infty}x_nBigr)= lim_{nto+infty}f(x_n)= sup f(x_n).$

Следовательно, правая часть данного уравнения непрерывна.

Заметим, что если бы в правой части стояла линейная функция с отрицательным коэффициентом при , то условие непрерывности функции в смысле приведенного выше определения было бы уже нарушено, поскольку такая функция не является монотонной в смысле определения 1.6.

Наименьшим элементом рассматриваемого множества является число 0. Вычисляем:

$begin{aligned}& f^0(0)= 0,,\ & f^1(0)= 1/4,,\ & f^2(0)= (1/2)cdot (1/4)+1/4=3/8,,\ & f^3(0)= (1/2)cdot (3/8)+1/4=7/16,,\ &cdots cdots cdots cdots cdots end{aligned}$

получая последовательность приближений к наименьшей неподвижной точке.

Можно проверить (например, с помощью метода математической индукции), что

$f^n(0)=frac{2^n-1}{2^{n+1}},,quad nin mathbb{N},.$

Предел этой последовательности равен 1/2 . Таким образом, наименьшая неподвижная точка отображения , определяемого правой частью уравнения, равна 1/2 . Это единственная в данном случае неподвижная точка отображения , что, конечно, очевидно и без теоремы 1.7 о неподвижной точке. Но здесь мы нарочно рассмотрели простой пример, показав, как можно решать подобные уравнения, основываясь на доказательстве теоремы. Мы не будем пока приводить более сложные примеры, так как интересные приложения теоремы о неподвижной точке имеются в теории графов и теории автоматов, и вернемся к этой теореме при решении задачи о путях в ориентированных графах.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

.Неподвижная точка отображения. Теорема о неподвижной точке.

Элемент
а множества А называют неподвижной
точкой
отображения
f:А→А,
если f(а)=а.
Элемент а упорядоченного множества М
называют наименьшей
неподвижной точкой
отображения f:М→М,
если он является наименьшим элементом
множества всех неподвижных точек
отображения f.
Теорема о
неподвижной точке Формулировка:
любое непрерывное отображение f
индуктивного упорядоченного множества
(М, <)
в себя имеет наименьшую неподвижную
точку. Доказательство: обозначим через
О наименьший элемент множества М.
Полагаем f⁰(х)=х
и fⁿ(х)=
f(fⁿ^-1(х))
для любой n˃0,
т.е. fⁿ(х)
означает результат n-кратного
применения f
к х. Рассмотрим последовательность
элементов М: {fⁿ(0)}n≥o
={0,f(0),
… fⁿ(0)
…}.
Докажем, что последовательность
неубывающая. Используем метод
математической индукции. Для элемента
О, как наименьшего элемента множества
М, имеем 0=f⁰(0)≤f(0).
Пусть для некоторых натуральных n
верно соотношение fⁿ^-1(0)≤fⁿ(0),
согласно теории о «отображении одного
индуктивного упорядоченного множества
в другом монотонно», отображение f
монотонно, и по этому
fⁿ(0)=f(fⁿ^-1(0))≤f(fⁿ(0))=fⁿ⁺¹(0),т.е.
соотношение верно для номера n+1.
Согласно методу математической индукции,
fⁿ(0)≤fⁿ⁺¹(0)
для любого nEN₀,
т.е. последовательность неубывающая.
Следовательно, по определению индуктивного
упорядоченного множества, она имеет
точную верхнюю грань. Обозначим ее
через а:а=sup_n_≥0fⁿ(0).
Докажем теперь, что если у неубывающей
последовательности отбросить любое
конечное число начальных членов, то ее
точная верхняя грань не изменится.
Действительно, если а есть точная
верхняя грань неубывающей последовательности
{х_n}≥0,
то а≥х_n
для всякого n≥0.
В частности фиксируя производную к˃0,
для любого n≥к
имеем а≥х_n,
т.е. а будет верхней гранью
подпоследовательности {х_n}n≥k≥0.
Докажем, что а является точной верхней
гранью этой подпоследовательности.
Пусть b
какая-то ее верхняя грань, т.е.b≥х_n
для любого n≥к.
Так как последовательность {x_n}≥0
x_k≤b,
то в силу транзитивности отношения
порядка x_p≤b
и тем самым b≥х_n
для любого n≥0,
т.е. b
есть верхняя грань всей последовательности
{x_n}_n_≥0.
Поскольку а=sup_n_≥0x_n,
то а≤b
и а=sup_n_≥_k_≥0x_n.
Следовательно, а – точная верхняя грань
подпоследовательности {x_n}_n_≥_k.
В силу непрерывности f
получим f(a)=f
(sup_n_≥0fⁿ(0))=sup_n_≥0f(fⁿ(0))=sup_n_≥0fⁿ⁺¹(o)
но sup
fⁿ⁺¹(0)=sup
{f¹(0),
f²(0)
… } = sup_n_≥₀fⁿ(0)=а

Таким
образом, доказано, что а является
неподвижной точкой отображения f.Покажем
теперь, что найденная неподвижная точка
является наименьшей. Пусть для некоторого
yEM
f(y)=y.
Т.к. 0<y,
а отображение f,
будучи непрерывным, монотонно, то f
(0)≤f(y)=y,
f(f(0))≤f(f(y))=y
и т.д. Следовательно, для любого n≥0,
fⁿ(0)≤y,
т.е. элемент y
есть верхняя грань последовательности
{fⁿ(0)}
_n_≥₀.
Поскольку а (как точная верхняя грань)
есть наименьший элемент на множестве
всех верхних граней этой последовательности,
то y≥а.
Таким образом мы доказали, что произвольная
неподвижная точка отображения f
не меньше элемента а, т.е. а – наименьшая
неподвижная точка отображения f.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Одномерные отображения

Неподвижная точка — точка, кот зад отобр переводит в неё же, иными сл, реш ур .

К прим, отобр имеет неподв точки x=1 и x=-3, т к f(1)=1 и f(3)=3.

Неподв есть не у всякого отобр — например, отобр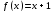 вещ прямой в себя непод точек не имеет.

Периодические точки — Точки, возвращающиеся в себя после конечного числа итераций, т е, решение ур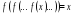

неподвижные точки — это периодические точки периода 1).

Теорема Шарковского. Пусть I – отрезок на числовой прямой, а f: I → I – непрерывное
отображение. Если f имеет точку периода p и , то найдется точка периода q

Пр1.Непрерывное отображение f: [1,5] → [1, 5], имеющее период 5, но не имеющее периода 3 Пусть f задано в точках 1, 2, 3, 4, 5 так :

а на промежуточные отрезки распространено по линейности (рис). а на промежуточные

отрезки распространено по линейности (рис. 1). Орбита точки x = 1 имеет вид 1, 3, 4, 2, 5, 1, …, т. е. f обладает периодом 5. Из графиков видим что нет орбиты периода 3

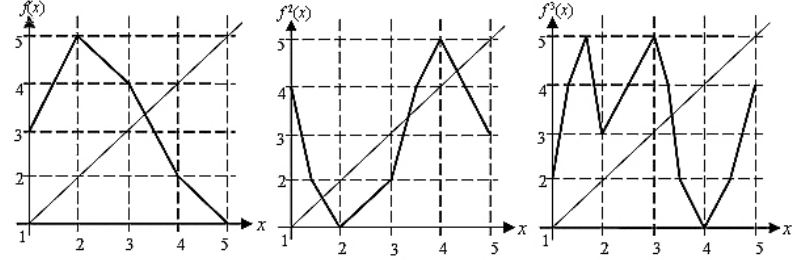
пр2 Непрерывное отображение f: [1,7] → [1, 7], спериод 7, не имеющее периоды 5 и 3.

Орбита точки x = 1 имеет вид 1, 4, 5, 3, 6, 2, 7, 1, т е имеет период 7

Из последнего рис решение уравнения есть только неподвижная точка. Значит, точек предыдущих периодов нет.

Задачи на одномерные отображения

пр Найти неподвижную точку отображения промежутка [0, 1] в себя, заданного ф-лой:

РЕШ: Неподвижная точка отображения промежутка [0, 1] соотв т пересеч графика

с биссектрисой коорд угла

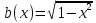
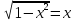
графиком явл окружность в ц нач к=т и с рад = 1ед измерения Неподвижная точка получ путем поворота т (1; 0) на угол 45◦, вокруг центра

1)Функция y = sign x не имеет обратной.

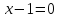
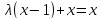
2) Дано уравнение преобразуем его к виду Найдите все , при которых применение теоремы возможно на отрезке [0,2]. Отв: -2  

3) Для каждого из следующих множеств указать пример непрерывного отображенияч этого множества в себя без неподвижных точек:

а) числовая прямая; б) полуинтервал (0,1]; в) пара отрезков [-2,-1] и [1,2].

4) указать пример разрывного (т.е. не непрерывного) отображения отрезка [0,1] в себя, не имеющего неподвижных точек

5)На числовой прямой R заданы функции. Какая из них отображает отрезок [0,1] в себя?

6) Пусть f – непрерывная функция на отрезке , отображающая каждый конец отрезка в себя, т. е. . Пусть g – непрерывная функция, отображающая отрезок в себя. Докажите, что тогда на этом отрезке найдется такая точка x0, что . Сохранится ли это в силе, если g – произвольная непрерывная функция на ?

7). Докажите, что непрерывное отображение f отрезка на (весь) отрезок , содержащий в себе отрезок А, имеет неподвижную точку. Верно ли это, если образ отрезка А не совпадает с В, а только лежит в нем?

8).Пусть f –непрерывное отображение отрезка на себя. Докажите, что отображение (композиция отображения f с самим собой) имеет по крайней мере две неподвижных точки. Верно ли это, если f отображает отрезок в себя, но не на себя?

9) Показать, что отображение оси Ох в себя имеет единственную неподвижную точку. В качестве приближенного значения корня уравнения взять 3й член посл-ти , полученной методом итерации, и оценить величину погрешности.

10) Отображение А на полупрямой переводит каждую точку в . Является ли оно сжимающим и имеет ли неподвижную точку?

Логистическое отображение (квадратичное отображение) — это полиномиальное отображение, описывающее изменение численности популяции с течением времени. 2 вида записи

Отобр Фейгенбаума	отобр Ферхюльста

описывает два эффекта:

1)когда численность популяции xn мала, она размножается со скоростью, пропорциональной этой численности, т к если

2) скорость размножения падает, возрастает конкуренция и смертность (нелинейное ограничение роста ) :

1)Найдите неподвижные точки логистического отображения и иссл их устойивость в зависимости от λ отв и

2). Найдите в явном виде элементы 2- цикла логистического отображения В каком интервале параметра λ существует 2й- цикл ?

3)Построить с помощью компьютера итерационные диаграммы для логистического отображения для значений параметра Какой процесс будет устанавливаться в каждом случае по прошествии достаточно большого времени ?

7)пример разрывного (т.е. не непрерывного) отобр отр [0,1] в себя, не имеющ неподвижных точек.

Инволюции

Непрерывное отображение f отрезка [0,1] в себя называют инволюцией, если оставляет неподв каждую точку отрезка. Иначе, это значит, что функция f обратна самой себе.

——————————————————————————————————————

1)Проверить что следующие функции являются инволюциями

2)Доказать что каждая нетривиальная инволюция имеет только 1 непод точку

3)Пусть f – непрерывная функция на отрезке , отобр каждый конец отрезка в себя, т.е. . Пусть g – любая непрер функция, отобр отрезок в себя. До, что тогда на этом отрезке найдется такая т x₀, что . Сохранится ли это утверждение в силе, если g – произвольная непрерывная функция на ?

Теорема о неподвижной точке.

Допустим, что некоторый шар заполнен песком. Если мы встряхнем этот шар, то все песч немн изменят свое положение. Но, оказывается, что есть такая песчинка, которая останется неподвижной.Пусть А – отрезок тонкой резинки. Б его деформир как уг, но без разрывов и склеивания. И в таком деформир виде заставим его занимать на пл=ти то же место, что и раньше (или часть места). Оказ, что при этом хотя бы одна точка займёт свое первона место.

Эти 2 примера дают понятие т о неподвижной точке. Л.Брауэра и причис к важн т в матем. Ещё прим этой т: если круг повернуть вокруг ц на угол 30о, то единств неподв точкой б центр круга.Но если то же отобр рассм на окружн, то она не б иметь неподвижных точек.

Каждое пост отобр произв пр=ва в себя имеет одну неподвижную т. А отобр некот множества в себя м иметь, а может и не иметь этой точки.

: Точка х, обл свойством, что f(x)=x, наз неподвижной точкой отображения.

Т БРАУЭРА: Каждое непрерывное отображение прямолинейного отрезка в себя имеет хотя бы 1 неподвижную точку.

Интуитивное доказательство

ДОК: В на прямой, содержащей этот отрезок, к-ты так, что отрезок превр в замкн промеж [a, b].

Тогда рассматриваемое отображение будет непрерывной функцией f, отображающей промежуток в себя (f :[a,b]→[a,c]). Опр новую ф q:[a,b]→R с усл, что q(x)=f(x) –x для x € [a,b] . Таким обр, функция q равна, взятому с определенным знаком, расстоянию между точкой Х и её образом f(x).

Если f(x) x, то f(x) — x= q 0, а если f(x)

а) Если неподвижен какой-н из концов промежeжутка, то доказывать нечего, т.к. этот конец и будет неподвижен точно.

б) Доп, что ни один из концов промежутка не неподвижен. Т к f(a) и f(b) принадлежат [a,b], то f(a)a и f(b)0 (f(a) – а = q0) и q (b)

Функция q непрерывна= она принимает все значения между q(a) и q(b). Следовательно, в некой точке х € [a, b] функция g(х) = 0. Эта точка и является искомой неподвижной точкой отображения .Ч т д.

Т Бореука-Улама для окружности. Пусть f : C R — непрерывная функция на окружности C. Тогда существует пара точек — антиподов x, x* такая, что f (x) = f (x*).

Следствие: на любой большой окружности земного шара (например, на экваторе) найдется пара антиподов, в которых температура воздуха одинакова.

Т (о блинах). Если A и B — ограниченные фигуры на плоскости, то существует прямая, которая делит каждую из этих фигур на две части равной площади.

Итерационный метод как применение сжатых отображений

Метод простой итерации — для уточнения корня уравнение f(x) = 0 (1) заменяется эквивалентным уравнением (2) Т е из следует и наоборот. Привести (1) к (2) можно многими способами, например, , где — непрерывная произвольная знакопостоянная функция. Геометрически на интервале отделения корня уравнение (1) представляется в виде двух пересекающихся линий и y = x

Условия сходимости достаточное f(x)- непрерывно дифференцируемая, при этом должна переводить отрезок [a,b] в себя.

Итерационная последовательность

Пример найти корень уравнения на отрезке [0,1]

1 способ но не непрерывно дифференцируема на [0,1]

Условие сжимаемости не выполнено

2 способ переводит [0,1] в себя и

Условие сжимаемости выполнено

Непрерывные отображения на квадрате

Задается уравнениями

Интуитивное доказательство теоремы Брауэра

Теорема о неподвижной точке формулируется для отрезка, квадрата. Она верна для круга и всякого выпуклого многоугольника

Лемма Шпернера — комбинаторный аналог теоремы Брауэра о неподвижной точке, один из основных результатов комбинаторной топологии. Утверждает, что при любой Шпернеровской раскраске вершин в триангуляции n-мерного симплекса найдётся ячейка триангуляции, вершины которой покрашены во все цвета. В 1мер сл, лемма Шпернера м рассм как дискр аналог т Больцано Коши.- если большой отрезок разбит на подотр и в вершинах отр расст 1 и 2, то при усл, что в верш большого отрезка стоят разные зн, сущ отрезок подразби, в верш кот стоят разные зн.

Есть триангуляция треугольника T. Вершины отмечены числами 1, 2 и 3 соот. Все вершины триангуляции от этими же числами с соблюдением след граничных условий: если такая вершина лежит на стороне треугольника T, то она получена в качестве отметки одно из тех 2 чисел, кот соотв концам этой стороны. Тогда есть хотя бы 1 грань с 3 разными отметками вершин (хорошая грань). Есть нечетное число хороших граней. , возможны пути 3 типов: 1) от гранич ребра (1,2) к хорошей грани (или в обратном направлении, что несущ), 2) от гранич ребра (1,2) к др такому же ребру, 3) от хорошей грани к другой такой же грани

Задачи на двумерные отображения и неподвижные точки

6) . К остову треугольника (рис.) применяется одно из следующих отображений: 1) каждый угол треугольника, состоящий из 4 граней, загибается внутрь, 2) весь треугольник поворачивается вокруг центра на угол 120 против часовой стрелки. В каждом из этих слу найтит неподвижные и почти неподвижные точки

двумерное отображение Эно

может служить для описания динамики ряда простых физических систем, таких как частица в вязкой среде под действием импульсных толчков, интенсивность которых зависит от координаты.

Параметр b характеризует степень диссипативности Параметр a -нелинейность (эквивалентен параметру λ в отображении Фейгенбаума).

1) Найти неподвижные точки отображения Эно

Отв

2) При выполнении какого условия в отображении появляются устойчивая и неустойчивая точки?

двумерное отображение с кубической нелинейностью Холмса

1. Найти аналитически координаты неподвижных точек периода 1 двумерного отображения Холмса и определить область их существования

метод простой итерации для системы двух уравнений

Рассмотрим систему двух уравнений

разными способами преобразуем к виду

Итерационный процесс

Достаточные условия сходимости

ф)(х, у) и ф2(х, у) определены и непрерывно дифференцируемы в заданной области;

начальные приближения х0, у0 и все последующие х,„ у„ принадлежат заданной области;

в рассматриваемой области выполняются неравенства:

или

Пример решить систему 2 уравнений

Преобразуем

Ограничимся положительным решением. Из рис за начальное приближение положительного решения системы можно принять

Точное решение системы имеет вид

Литература

1)Шашкин. Неподвижные точки, сер. Популярные лекции по математике, М.Наука,1989

2) Прошин Ю.Н., Шакиров М.А., Моделирование и визуализация нелинейных динамических систем, КФУ, Институт физики, 2017 г

3) Лемма Шпернера и справедливое деление, автореферат дипломной работы, СГУ им Чернышевского, каф. Компьютерной алгебры и теории чисел, Свратов, 2017

4) Данилов В.И., Лекции о неподвижных точках. —Российская экономическая школа, М, 2006 г

5) А.П. КузнецовА.В. Савин Л.В. Тюрюкина Введение в физику нелинейных отображений

6) Старостина В.В., Тепляков В.В. Вокруг теоремы Шарковского

Источник

Число x называется неподвижной точкой (fixed point) функции f, если оно удовлетворяет уравнению f(x) = x. Для некоторых функций f можно найти неподвижную точку, начав с какого-то значения и применяя f многократно:

f(x), f(f(x)), f(f(f(x))), . . .

— пока значение не перестанет сильно изменяться.

*-Нравится статья? Кликни по рекламе!

С помощью этой идеи мы можем составить процедуру fixed-point, которая в качестве аргументов принимает функцию и начальное значение и производит приближение к неподвижной точке функции. Мы многократно применяем функцию, пока не найдем два последовательных значения, разница между которыми меньше некоторой заданной чувствительности:

def fixedPoint(f, firstGuess):
    def closeEnaught(x,y):
        if abs(x-y)<0.001:
            return 1
        return 0
    def tryF(guess):
        next=f(guess)
        if closeEnaught(guess, next):
            return next
        return tryF(next)
    return tryF(firstGuess)

Подобным образом можно найти решение уравнения y = sin(y) + cos(y):

fixedPoint(lambda y: math.sin(y)+math.cos(y), 1.0)

Важно: нужно понимать, что для данного метода очень важно первое приближение, которое мы выберем. Это связано с направлением роста преобразований:

f(x), f(f(x)), f(f(f(x))), . . .

Этот процесс можно представить, как скольжение по графику. Для примера можно рассмотреть y=f(x)=x2. Сразу на ум приходит 2 стационарные точки — 0 и 1. Если возьмем первое приближение>1, то каждая такая подстановка будет больше предыдущей, что характеризует растущий график и мы не найдем стационарной точки. Если возьмем 0<приближение<1, то каждое новое значение будет меньше предыдущего и так мы найдем стационарную точку=0. Таким образом найти 1 можно лишь попав в неё сразу, т.е. выбрав приближение=1.0;

Процесс поиска неподвижной точки похож на процесс, с помощью которого мы искали квадратный корень. И тот, и другой основаны на идее последовательного улучшения приближений, пока результат не удовлетворит какому-то критерию. На самом деле мы без труда можем сформулироватьвычисление квадратного корня как поиск неподвижной точки. Вычислить квадратного корня из произвольного числа x означает найти такое y, что y² = x. Переведя это уравнение в эквивалентную форму y = x/y, мы обнаруживаем, что должны найти неподвижную точку функции
y → x/y, и, следовательно, мы можем попытаться вычислять квадратные корни так:

def sqrt(x):
    return fixedPoint(lambda y: x/y, 1.0)

К сожалению, этот поиск неподвижной точки не сходится. Рассмотрим исходное значение y₁. Следующее значение равно y₂ = x/y₁, а следующее за ним y3 = x/y₁ =x/(x/y₁) = y₁. В результате выходит бесконечный цикл, в котором два значения y₁ и y₂ повторяются снова и снова, прыгая вокруг правильного ответа.
Один из способов управлять такими прыжками состоит в том, чтобы заставить значения изменяться не так сильно. Поскольку ответ всегда находится между текущим значением y и x/y, мы можем взять новое значение, не настолько далекое от y, как x/y, взяв среднее между ними, так что следующее значение будет не x/y, а 1/2(y +x/y). Процесс получения такой последовательности есть всего лишь процесс поиска неподвижной
точки y →1/2(y + x/y).

def average(x, y):
    return (x+y)/2

def sqrt(x):
    return fixedPoint(lambda y: average(y,x/y), 1.0)

Интересно: Заметим, что y =1/2(y + x/y) всего лишь простая трансформация уравнения y = x/y; чтобы ее получить, добавьте y к обоим частям уравнения и поделите пополам.
Этот подход с усреднением последовательных приближений к решению, метод, который называют торможение усреднением (average damping), часто помогает достичь сходимости при поисках неподвижной точки.

Используемая литература:

http://mitpress.mit.edu/sicp/

Источник

По этой ссылке вы найдёте полный курс лекций по математике:

Пусть заданы отображения Теорема 2.4. Если gof = Ix : д сюръективно, а / инъективно. Бели д несюръективно, то в X найдется элемент- х € X, такой, что х $ д(У) 3g(f(X)) = Ix(X) = X. Это противоречие доказывает сюръективность д. Бели то по определению тождественного отображения Ix(zi) Ф 1х(х2)- Но тогда g(f(xi)) ф Ф 9{f(x*))* Отсюда с учетом определения 2.1 отображения нмеем f(xi) ф /(яг)» т.е. отображение / инъективно.

Теорема 2.6. Отображения / : X У и g : У X биективны и взаимно обратны тогда и только тогда, когда fof-Ix и fogzzly. 4 По теореме 2.2 имеем сюръективность и инъективность каждого из отображений / и д, т.е. их биективность. Обратно, биективность отображений / и д означает в данном случае, что они взаимно обратны, т.е. их композиции являются тождественными отображениями. Обсуждение этих вопросов имеет определенное практическое значение, так как они связаны с разрешимостью уравнений вида относительно х 6 X при заданном у 6 Y.

Если имеется отображение д : У Х) такое, что fog = Iy) то решение обязаг тельно существует, но необязательно единственное. Наоборот, существование такого отображения д: У -4 Х} что д of = 1хУ означает: если решение существует, то оно единственно. И лишь одновременное выполнение условий fog = Iy и gof = Ix гарантирует существование и единственность решения не только (2.10), но и обратного к нему уравнения д(у) = х относительно у € У при заданном х € X.

Итак, для однозначного решения (2.10) достаточно построить отображение д, такое, чтобы / и д были взаимно обратными отображениями. Но сделать это не всегда просто, а в слу-когда / небиективно, невозможно. Путем тождеств преобразований задачу можно свести к поиску так называемой неподвижной точки х* € X отображения : X X множества X в себя (см. 2.2), для которой х* = ). Отметим сразу, что в отличие от преобразования множества X на себя, которое является биекцией, отображение может быть произвольным.

Особенность неподвижной точки отображения состоит в том, что при отображении она переходит сама в себя, то- гда как прочие точки при отображении сдвигаются, например х переходит в x(х). (2.11) В частности, это множество может быть пустым (X* = 0) или содержать единственный элемент (3!х* € X* С X: х* =), т.е. решение (2.11) может отсутствовать или быть единственным. Многие задачи вычислительной математики можно свести к отысканию неподвижных точек отображений, для чего используют метод последовательных приближений, или метод итераций, суть которого состоит в построении итерационного алгоритма.

Бели задать первое приближение х 6 Х) то можно построить так называемую итерационную последовательность (см. рис. 2.13) элементов хп € X, п € N. Будут ли приближаться (или, как говорят, сходиться) элементы этой последовательности к неподвижной точке отображения ? Ответ на этот непростой вопрос зависит от свойств множества X, отображения и выбора элемента х € X в качестве первого приближения (см. Д.8.1 и Д.8.2). Здесь ограничимся лишь иллюстрацией. Пример 2.13. Пусть отображению в (2.11) отвечает функция 0.

Сразу видно, что одна из неподвижных точек этого отображения Xq = 0, а вторая х* = 1 — 1/А имеет смысл лишь при ^Х > 1. Но обратившись к методу итераций и выбрав в качестве первого приближения х € (0, 1), получим итерационную последовательность {зп}, для которой хп^ = Ххп(1-хп)у п€ N. (2.12) Отметим, что (2.12) можно рассматривать как упрощенную математическую модель эволюции биологической популяции с коэффициентом Л размножения особей, относительная численность хп которых уменьшается через равные промежутки времени пропорционально множителю (1 — хп) из-за ограниченности ресурсов при „перенаселении».

Возможно вам будут полезны данные страницы:

При А 1 и х € X график функции ) лежит ниже биссектрисы у = х координатного угла хОу (рис. 2.14) и V®! 6 (0, 1) элементы последовательности {хп} приближаются к точке „притяжения zjj = 0 (ломаная со стрелками), т.е. популяция гибнет из-за малости коэффициента размножения. Если Л > 1, то, как бы близко к точке Xq = 0 ни было элементы последовательности {хп} „уходят» от этой „гибельной» точки (она становится точкой „отталкива-ния»), и популяция выживает, причем возможны такие варианты:

1) для 1 ^ 2 численность хп популяции приближается к х9 монотонно, возрастая при х (при 1 — х п = 3) и убывая при х* — х* (рис. 2.15,а); а б в Рис. 2.15 2) для 2 Л ^ 3 хп приближается к х* немонотонно, ломаная спираль закручивается по часовой стрелке (рис. 2.15,5); 3) для 3 Л 4 Vari 6 (0, 1) хп не приближается к я*, причем в некоторых случаях итерационный алгоритм „зацикливается44 (рис. 2.15,б), т.е. число особей в популяции периодически повторяется; 4) для А^ 4 итерационный алгоритм (2.12) неработоспособен и может при некоторых п давать значения хп£Х.

Из этого примера видно, насколько важно располагать общим признаком наличия у отображения непо Неподвижная точка отображения движных точек и устанавливать еще до реализации итерационного алгоритма его работоспособность. Вопросы и задачи 2.1. Найти множество, на которое отображает множество X каждая из следующих функций: Для каждой функции найти график отображения и построить его. 2.2. Верны ли равенства f~l(f(A)) = A и /(/-1(5)) = 5, где А — множество из области определения функции /, а 5 — множество из области значений этой функции ? 2.3. Доказать, что п если /: Ak ->Y — взаимно однозначное отображение (к = = Т7п)- 2.4.

Пусть множества X и Y содержат соответственно тип элементов. Найти число отображений множества X в множество У, в том числе сюръекций, инъекций и биекций.

2.5. В каком случае справедливы равенства f(A П В) = жества из области определения функции / ? 2.6. Доказать дистрибутивность произведения произвольных множеств по отношению к операциям объединения, пересечения и разности. 2.7. Являются ли отношениями порядка: а) „х тяжелее у» в множестве гирь; б) „я старше у44 в множестве людей; в) „х подчинен у44 в множестве должностей; г) „я не превосходит Vй в множестве номеров домов на улице; д) „из х следует Vй в множестве высказываний; е) vx находится внутри в множестве окружностей на плоскости? Какие из этих множеств являются частично упорядоченными ?

2.8. В хоккейной команде 2 вратаря, 7 защитников и 10 нападающих. Сколькими способами тренер может образовать стартовую шестерку игроков, состоящую из вратаря, двух защитников и трех нападающих? 2.0. Замок сейфа имеет пять дисков с цифрами 0, 1, 2, …, 9 на каждом диске. Замок можно открыть при наборе на дисках шифра в виде определенной комбинации цифр. На набор одной комбинации цифр уходит пять секунд. Достаточно ли пяти суток для того, чтобы открыть сейф, не зная шифра?

2.10. Найти сумму квадратов биномиальных

коэффициентов для Vn Е N. 2.11. Существует ли система вложенных интервалов (вь М Э … D К, Ьп) Э (a„+i, 6n+i) Э п е N, имеющая общую точку ? Всякая ли система вложенных интервалов имеет непустое пересечение? 2.12. Доказать, что для конечного множества Л, содержащего п элементов, мощность cardP(y4) множества Р(А) всех подмножеств множества А равна 2П. 2.13. В каких случаях справедливы равенства: card (A U В) = card А card (А П В) = card Л; card (Л В) = card А card (А х В) = card А?

Неподвижная точка отображения 2.14. Для изображения цифр почтового индекса используют множество из девяти элементов, которые на рис. 2.16,а обозначены буквами а, 6, …, г (сами цифры изображены на рис. 2.16,5). а. Записать множества Л*, (А: = 0, 9) элементов, используемых для изображения каждой из десяти цифр. Есть ли среди этих множеств непересекающиеся ? б. Записать для каждого из элементов s ( s = а, 6, …, i) множество Ва цифр, в изображении которых использован элемент s.

Какие элементы использованы наиболее часто и наиболее редко? в. Указать цифры, наименее и наиболее близкие к цифре 3, считая мерой близости цифр число общих элементов в их изображении. Какой операции над множествами /Ц соответствует множество, определяющее меру близости цифр? г. Сколько различных фигур можно построить путем комбинации элементов исходного множества, считая, что в каждой комбинации может участвовать от 0 до 9 элементов?

Источник