Как найти неподвижные точки аффинного преобразования - Исправление недочетов и поиск решений вместе с Examum.ru

Неподвижных точек действительно нет, так как система $%x=y$%; $%y=z$%; $%z=x+1$% решений не имеет.

Рассмотрим уравнение плоскости: $%ax+by+cz+d=0$%, где хотя бы одно из чисел $%a,b,c$% отлично от нуля. Если эта плоскость инвариантна, то для любой её точки после замены координат должно иметь место равенство $%ay+bz+c(x+1)+d=0$%, то есть $%cx+ay+bz+c+d=0$%. Это уравнение той же плоскости, и оно не обязательно совпадает с предыдущим, но пропорционально ему с некоторым коэффициентом $%k$%, то есть $%c=ka$%, $%a=kb$%, $%b=kc$%, $%c+d=kd$%. Легко видеть, что $%a=0Rightarrow c=0Rightarrow b=0Rightarrow a=0$%, поэтому ни одно из чисел $%a,b,c$% нулю не равно. Тогда $%abc=k^3abc$%, и после сокращения на $%abcne0$% получается $%k^3=1$%, то есть $%k=1$%. (Здесь важно, что всё происходит над полем действительных чисел, потому что в комплексной области результат был бы другим.) Теперь из равенства $%c+d=d$% получается противоречие, из которого можно сделать вывод, что инвариантных плоскостей у нас нет.

Теперь рассмотрим вопрос об инвариантных прямых. Рассмотрим на прямой две различные точки с координатами $%(x_1,y_1,z_1)$% и $%(x_2,y_2,z_2)$%. Тогда $%(x_2-x_1,y_2-y_1,z_2-z_1)$% есть направляющий вектор прямой. После замены координат он превратится в $%(y_2-y_1,z_2-z_1,x_2-x_1)$%, и этот вектор пропорционален предыдущему. Как и выше, легко проверяется, что у него нет нулевых координат (в противном случае все нулевые), а произведение координат не изменилось, поэтому коэффициент пропорциональности равен 1, и все координаты равны. Это означает, что (1,1,1) является направляющим вектором инвариантной прямой (если таковая вообще есть).

Таким образом, прямая задаётся параметрически в виде $%x=x_0+t$%, $%y=y_0+t$%, $%z=z_0+t$%. После замены, сумма координат увеличивается на 1, и это значит, что значение параметра $%t$% увеличивается на $%frac13$%. Отсюда можно сделать вывод, что $%(x_0+frac13,y_0+frac13,z_0+frac13)=(y_0,z_0,x_0+1)$%. Точку $%x_0$% можно выбрать произвольно — например, полагая $%x_0=0$%. Тогда $%y_0=frac13$%, $%z_0=frac23$%, и прямая, заданная параметрически в виде $%x=t$%, $%y=frac13+t$%, $%z=frac23+t$% оказывается инвариантной. Точка $%(y,z,x+1)$% будет принадлежать той же прямой при замене значения параметра $%t$% на $%t+frac13$%.

Можно заметить, что эта прямая является пересечением двух плоскостей: $%y=x+frac13$% и $%z=y+frac13$%.

Источник

Задача
119.
Доказать, что линейное преобразование
плоскости тогда и только тогда будет
аффинным, когда образ каждого ненулевого
вектора будет отличен от нуля.

Задача 120
(с решением). Найти инвариантные прямые
линейного

преобразования,
заданного формулами

Образом прямой
при таком преобразовании является
прямая

или .
По условию, она должна совпасть с исходной
прямой .Две
прямые совпадут при условии
пропорциональности входящих в их
уравнения коэффициентов, т. е.

при условии ,
,
если и
условии,

если a=0.
Таким образом имеем 2 решения:
или для
первого случая и
для второго.

Задача
121.
Записать формулы, задающие произведение
и

данных аффинных преобразований (система
координат общая декартова)

Задача
122.
Записать формулы, задающие преобразование,
обратное к данному (система координат
общая декартова), если такое преобразование
существует.

Задача 123.
Доказать, что:

Если
А и В
— две
различные неподвижные точки аффинного
преобразования, то и все точки прямой
АВ неподвижны;

если аффинное
преобразование f
имеет единственную неподвижную точку,
то все инвариантные прямые (если они
существуют) проходят через эту точку;
точка пересечения
двух инвариантных прямых аффинного
преобразования неподвижна.

Задача 124.
Записать
формулы, задающие произведение и

данных аффинных преобразований (система
координат общая декартова)

Занятие 16 Элементы вычислительной геометрии. Триангуляция Делоне

Основные алгоритмы
вычислительной геометрии

Приведём часто
встречающиеся задачи вычислительной
геометрии и коротко обсудим их решение.

Отсечение
отрезка.

Необходимость
отсечения выводимого изображения по
границам некоторой области встречается
довольно часто. В простейших ситуациях
в качестве такой области, как правило,
выступает прямоугольник

Ниже рассматривается
достаточно простой и эффективный
алгоритм отсечения отрезков по границе
произвольного прямоугольника.

Четырьмя прямыми
вся плоскость разбивается на 9 областей
. По отношению к прямоугольнику точки
в каждой из этих областей расположены
одинаково. Определив, в какие области
попали концы рассматриваемого отрезка,
легко понять, где именно необходимо
произвести отсечение.

Классификация
точки относительно отрезка

Рассмотрим следующую
задачу: на плоскости заданы точка и
направленный отрезок. Требуется
определить положение точки относительно
этого отрезка

Расстояние от
точки до прямой

Пусть заданы точка

и прямая АВ, где ,

и требуется найти расстояние от этой
точки до прямой.

Найдем длину
отрезка АВ:
Опустим из точки С перпендикуляр на АВ.
Точку Р пересечения этого перпендикуляра
с прямой можно представить параметрически

где

Положение точки
С на этом перпендикуляре будет задаваться
параметром s, s < 0 означает, что С
находится слева от АВ, s >0, что С — справа
от АВ и s
= 0 означает, что С лежит на АВ.

Для вычисления S
воспользуемся следующей формулой:
и тогда искомое расстояние PC = sl.

Нахождение
пересечения двух отрезков

Пусть А, В, С и D —
точки на плоскости. Тогда направленные
отрезки АВ и CD
задаются следующими параметрическими
уравнениями:

Если отрезки АВ и
CD пересекаются, то
Перепишем это векторное соотношение в
координатном виде:

Эта система линейных
алгебраических уравнений при
имеет единственное решение:

Если оба получившихся
значения r
и s принадлежат отрезку [0,1], то отрезки
АВ и CD пересекаются и точка пересечения
может быть найдена из параметрических
уравнений. В случае, когда оба или одно
из полученных значений не принадлежат
отрезку [0,1], отрезки АВ и CD не пересекаются,
но пересекаются соответствующие прямые.
Равенство
означает, что отрезки АВ и CD параллельны.

Проверка
принадлежности точки многоугольнику

Для решения этой
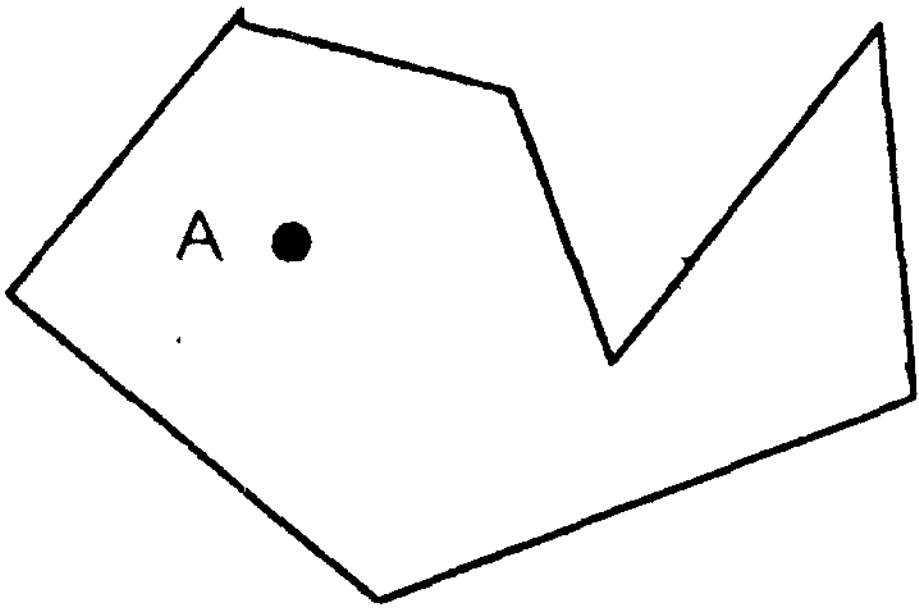
задачи выпустим из точки А(х,у) произвольный
луч и найдем количество точек пересечения
этого луча с границей многоугольника.
Если отбросить случай, когда луч проходит
через вершину многоугольника, то решение
задачи тривиально — точка лежит внутри,
если общее количество точек пересечения
нечетнечетно, и снаружи, если четно.

Ясно, что для любого
многоугольника всегда можно построить
луч, не проходящий ни через одну из
вершин. Однако построение такого луча
связано с некоторыми трудностями и,
кроме того, проверку пересечения границы
многоугольника с произвольным лучом
провести сложнее, чем с фиксированным,
например горизонтальным.

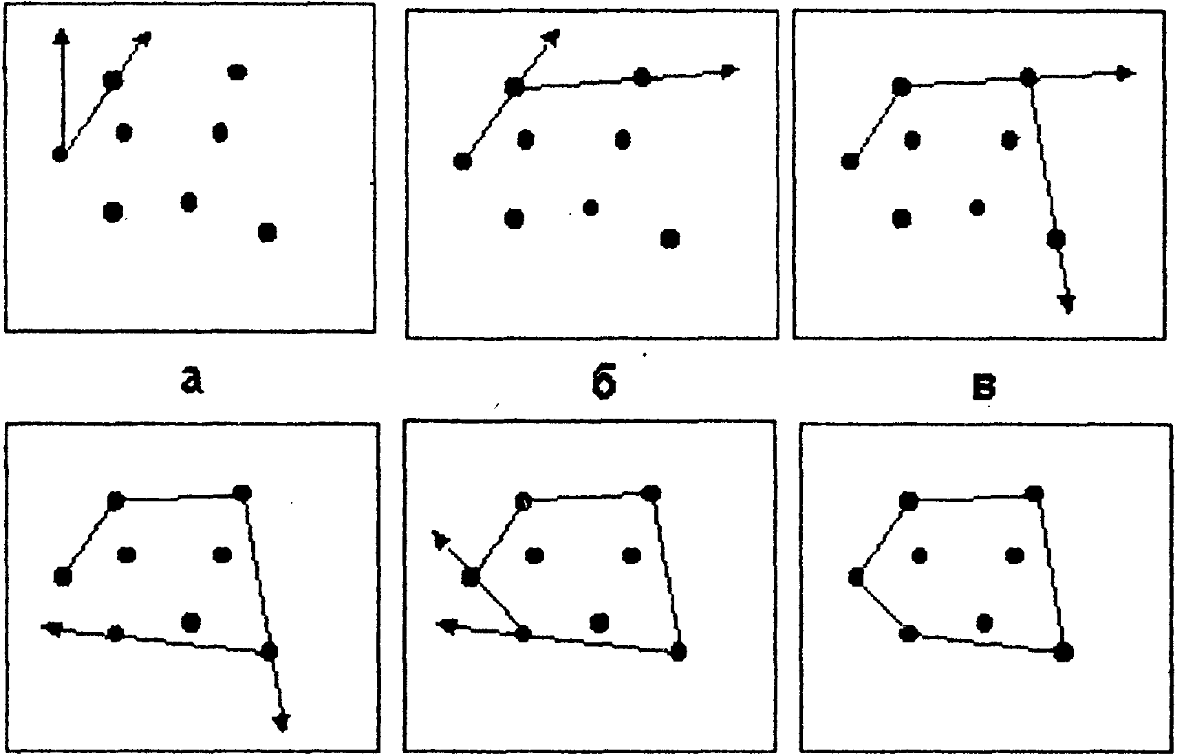
Возьмем луч,
выходящий из произвольной точки А, и
рассмотрим, к чему может привести
прохождение луча через вершину
многоугольника. Основные возможные
случаи изображены на рисунке.

В случае а, когда
ребра, выходящие из соответствующей
вершины, лежат по одну сторону от луча,
четность количества пересечений не
меняется.

Случай в, когда
выходящие из вершины ребра лежат по
разные стороны от луча, четность
количества пересечений изменяется. К
случаям б и г такой подход непосредственно
неприменим. Несколько изменим его,
заметив, что в случаях а и б вершины,
лежащие на луче, являются экстремальными
значениями в тройке вершин соответствующих
отрезков. В других же случаях экстремума
нет.

Исходя из этого,
можно построить следующий алгоритм:
выпускаем из точки А горизонтальный
луч в направлении оси Ох и все ребра
многоугольника, кроме горизонтальных,
проверяем на пересечение с этим лучом.
В случае, когда луч проходит через
вершину, т.е. формально пересекает сразу
два ребра, сходящихся в этой вершине,
засчитаем это пересечение только для
тех ребер, для которых эта вершина
является верхней.

Вычисление
площади многоугольника

Для площади s(P)
многоугольника Р, образованного вершинами

справедлива следующая формула:
Эта формула дает площадь многоугольника
со знаком, зависящим от ориентации его
вершин. В случае, когда вершины упорядочены
в направлении против часовой стрелки,
s(P) < 0.

Построение
выпуклой оболочки

Пусть S — конечный
набор точек на плоскости. Выпуклой
оболочкой
набора S называется пересечение всех
выпуклых многоугольников, содержащих
S. Ясно, что
— это выпуклый многоугольник, все вершины
которого содержатся в S (заметим, что не
все точки из S являются вершинами выпуклой
оболочки).

Один из способов
построения выпуклой оболочки конечного
набора точек S на плоскости напоминает
вычерчивание при помощи карандаша и
линейки. Вначале выбирается точка
заведомо являющаяся вершиной границы
выпуклой оболочки. В качестве такой
точки можно взять самую левую точку из
набора S (если таких точек несколько,
выбираем самую нижнюю). Затем вертикальный
луч поворачивается вокруг этой точки
по направлению часовой стрелки до тех
пор, пока не наткнется на точку
Тогда отрезок
будет ребром границы выпуклой оболочки.
Для поиска следующего ребра будем
продолжать вращение луча по часовой
стрелке; на этот раз вокруг точки b до
встречи со следующей точкой
Отрезок
будет следующим ребром границы выпуклой
оболочки. Процесс повторяется до тех
пор, пока мы снова не вернемся в точку
а. Этот метод называется методом
«заворачивания подарка».

Основным шагом
алгоритма является отыскание точки,
следующей за точкой, вокруг которой
вращается луч.

Временные затраты
данного алгоритма равны
где h — число вершин в границе искомой
выпуклой оболочки. Работа данного
алгоритма проиллюстрирована на рис.

Рассмотрим еще
один алгоритм для построения выпуклой
оболочки, так называемый метод обхода
Грэхема. В этом методе выпуклая оболочка
конечного набора точек S находится в
два этапа. На первом этапе алгоритм
выбирает некоторую экстремальную точку

и сортирует все остальные точки в
соответствии с углом направленного к
ним из точки
луча. На втором этапе алгоритм выполняет
пошаговую обработку отсортированных
точек, формируя последовательность
многоугольников, которые в конце концов
и образуют искомую выпуклую оболочку

Выберем в качестве
экстремальной точки точку с минимальной
у-координатой и поменяем ее местами с

Остальные точки сортируются затем в
порядке возрастания полярного угла
относительно точки
Если две точки имеют одинаковый полярный
угол, то точка, расположенная ближе к
должна стоять в отсортированном списке
раньше, чем более дальняя точка.

Для определения
того, какая именно точка должна быть
включена в границу выпуклой оболочки
после точки
используется тот факт, что при обходе
границы выпуклой оболочки в направлении
по часовой стрелки каждая ее вершина
должна соответствовать повороту влево.
Быстродействие данного алгоритма равно

Соседние файлы в папке Архив(1 курс)

Источник

Аффинные преобразования плоскости

Преобразование плоскости задается двумя скалярными функциями двух переменных:

$begin{cases}y_1=f_1(x_1,x_2),\y_2=f_2(x_1,x_2).end{cases}$ или, что то же самое, вектор-функцией $f(x)=begin{pmatrix}f_1(x)&f_2(x)end{pmatrix}^T.$

Формула аффинного преобразования плоскости

Пусть на плоскости фиксирована аффинная система координат $Ovec{e}_1vec{e}_2$ . Преобразование mathcal{A} плоскости называется аффинным, если координаты y_1,y_2 образа выражаются через координаты x_1,x_2 прообраза X~(Y=mathcal{A}(X)) по формулам

$begin{cases} y_1=a_1+ a_{11}x_1+ a_{12}x_2,\ y_2= a_2+a_{21}x_1+a_{22}x_2,end{cases} Leftrightarrowquad mathop{y}limits_{(vec{e})}= mathop{a}limits_{(vec{e})}+ mathop{A}limits_{(vec{e})}cdot mathop{x}limits_{(vec{e})},$

(2.11)

где $mathop{A}limits_{(vec{e})}= begin{pmatrix} a_{11}& a_{12}\ a_{21}&a_{22}end{pmatrix}$ — невырожденная матрица (матрица аффинного преобразования), $mathop{y}limits_{(vec{e})}= begin{pmatrix} y_1\y_2end{pmatrix},~mathop{x}limits_{(vec{e})}=begin{pmatrix}x_1\x_2end{pmatrix}$ координатные столбцы образа и прообраза (координатные столбцы радиус-векторов overrightarrow{OY} и overrightarrow{OX} ) соответственно, $mathop{a}limits_{(vec{e})}= begin{pmatrix}a_1\a_2end{pmatrix}$ — координатный столбец образа начала координат, или вектора переноса начала координат. В формулах аффинного преобразования (2.11) подчеркивается зависимость матрицы преобразования и координат векторов от выбранной системы координат. Обозначение системы координат в (2.11) будем опускать, если понятно, в какой системе координат задано преобразование.

Замечания 2.4

1. Столбец $a=begin{pmatrix}a_1\a_2end{pmatrix}$ в (2.11) определяет координаты образа O'=mathcal{A}(O) начала координат. Действительно, подставляя координаты x_1=x_2=0 точки в (2.11), получаем координаты y_1=a_1,,y_2=a_2 точки vec{a}=overrightarrow{OO'} . Можно сказать, что при аффинном преобразовании начало координат переносится на вектор а=00 , координатный столбец которого равен .

2. Аффинное преобразование (2.11) в любой другой аффинной системе координат $O'vec{e},'_1vec{e},'_2$ задается формулами того же вида.

Действительно, пусть известны: матрица $S= mathop{S}limits_{(vec{e})to (vec{e},')}$ перехода от старого базиса $(vec{e})=begin{pmatrix}vec{e}_1&vec{e}_2end{pmatrix}$ к новому базису $(vec{e},')=begin{pmatrix}vec{e},'_1&vec{e},'_2end{pmatrix}$ и координатный столбец вектора переноса начала координат vec{s}=overrightarrow{OO'} (рис.2.17). Тогда по формуле (2.8) имеем $begin{cases} x=s+Scdot x',\ y=s+Scdot y',end{cases}$ где x,y и x',y' — координатные столбцы точек X,Y (радиус-векторов overrightarrow{OX} , overrightarrow{OY} и overrightarrow{O'X} , overrightarrow{O'Y} ) в старой $Ovec{e}_1vec{e}_2$ и новой $O'vec{e},'_1 vec{e},'_2$ системах координат.

Координатный столбец вектора переноса начала координат

Подставляя в (2.11), получаем

$underbrace{s+ Scdot y'}_{y}= a+Acdot(underbrace{s+ Scdot x'}_{x}).$

Учитывая, что матрица обратимая (см. свойство 2 матриц перехода в разд.2.2.1), выражаем координатный столбец образа через координатный столбец прообраза в системе координат $O'vec{e},'_1vec{e},'_2$ :

$y'=underbrace{S^{-1}cdot(a+Acdot s-s)}_{a'}+underbrace{S^{-1}cdot Acdot S}_{A'}cdot x'=a'+A'cdot x'.$

В результате получили аффинное преобразование вида (2.11):

$mathop{y'}limits_{(vec{e},')}=mathop{a'}limits_{(vec{e},')}+mathop{A'}limits_{(vec{e},')}cdotmathop{x'}limits_{(vec{e},')}.$

с матрицей $A'=S^{-1}cdot Acdot S$ и координатным столбцом $a'=S^{-1}cdot(a+Acdot s-s)$ вектора переноса.

Таким образом, связь матриц одного и того же аффинного преобразования в разных базисах, а также координатных столбцов вектора переноса, имеет вид

$mathop{A'}limits_{(vec{e},')}=mathop{S^{-1}}limits_{(vec{e})to (vec{e},')}cdotmathop{A}limits_{(vec{e})}cdot mathop{S}limits_{(vec{e})to(vec{e},')},quadquad mathop{a'}limits_{(vec{e},')}=mathop{S^{-1}}limits_{(vec{e})to (vec{e},')}cdot! left(mathop{a}limits_{(vec{e})}+ mathop{A}limits_{(vec{e})}cdot mathop{s}limits_{(vec{e})}-mathop{s}limits_{(vec{e})}right),$

(2.12)

где $mathop{A}limits_{(vec{e})},, mathop{A'}limits_{(vec{e},')}$ — матрицы ( $mathop{a}limits_{(vec{e})},mathop{a'}limits_{(vec{e},')}$ — координатные столбцы вектора переноса) аффинного преобразования в старом и новом базисах, a $mathop{S}limits_{(vec{e})to(vec{e},')}$ — матрица перехода от старого базиса к новому.

3. Запишем (2.11), обозначив образ точки через X'=mathcal{A}(X) :

$begin{cases}x'_1=a_1+ a_{11}x_1+ a_{12}x_2,\x'_2= a_2 +a_{21}x_1+ a_{22}x_2,end{cases} Leftrightarrowquad x'=a+Acdot x,.$

(2.13)

Сравнивая формулы (2.13) аффинного преобразования плоскости с формулами (2.8) аффинного преобразования координат, заключаем, что эти соотношения: x'=a+Acdot x и x=s+Scdot x' будут равносильными, если положить $S=A^{-1}$ и $s=-A^{-1}cdot a$ . Действительно, умножая обе части равенства $x=-A^{-1}cdot a+A^{-1}cdot x'$ , следующего из первого соотношения, на матрицу слева, с учетом равенства $Acdot A^{-1}=E$ получаем $Acdot x=-Acdot A^{-1}cdot a+Acdot A^{-1}cdot x'$ , т.е. Acdot x=-a+x' , что равносильно x'=a+Acdot x . Таким образом, изменение координат точки будет одно и то же, подвергаем ли мы плоскость аффинному преобразованию, оставляя систему координат неизменной, или же оставляем плоскость неизменной, подвергая систему координат обратному преобразованию.

4. Аффинное преобразование плоскости порождает преобразование векторов на плоскости, если рассматривать векторы как упорядоченные пары точек, а именно: при аффинном преобразовании mathcal{A} каждому вектору vec{v} (рассматриваемому как упорядоченная пара точек vec{v}=overrightarrow{MN} ) ставится в соответствие вектор vec{v},' ( vec{v},'=overrightarrow{M'V'} , причем M'=mathcal{A}(M),~N'=mathcal{A}(N) ), координаты которого выражаются через координаты прообраза vec{v} no формулам:

v'=Acdot v,,

(2.14)

где v,v' — координатные столбцы векторов vec{v},,vec{v},' (относительно одного и того же базиса), — матрица аффинного преобразования (в том же базисе).

Это свойство следует из правила нахождения координат вектора, согласно которому из координат конца вектора надо вычесть координаты его начала. Если m,m',n,n' — координатные столбцы точек соответственно, то учитывая (2.13): m'=a+ Acdot m , n'=a+Acdot n и, получаем

$v'=n'-m'=underbrace{(a+Acdot n)}_{n'}-underbrace{(a+Acdot m)}_{m'}=Acdotunderbrace{(n-m)}_{v}=Acdot v,$

что и требовалось доказать.

Способы задания аффинного преобразования плоскости

Первый способ. Чтобы задать аффинное преобразование плоскости по определению, достаточно указать систему координат $Ovec{e}_1vec{e}_2$ и формулы (2.11), т.е. задать невырожденную матрицу преобразования и координатный столбец в (2.11).

Второй способ. Пусть на плоскости заданы две аффинные системы координат: старая $Ovec{e}_1vec{e}_2$ и новая $O'vec{e},'_1vec{e},'_2$ (рис.2.18). Тогда существует единственное аффинное преобразование mathcal{A} плоскости, которое каждой точке ставит в соответствие точку Y=mathcal{A}(X) , координаты которой в новой системе координат $O'vec{e},'_1vec{e},'_2$ совпадают с координатами точки в старой системе координат.

Аффинные системы координат (старая и новая) на плоскости

Действительно, пусть vec{s}=overrightarrow{OO'} — вектор переноса начала координат, $mathop{S}limits_{(vec{e})to(vec{e},')}$ — матрица перехода от старого базиса $(vec{e})=begin{pmatrix}vec{e}_1&vec{e}_2end{pmatrix}$ к новому базису $(vec{e},')=begin{pmatrix}vec{e},'_1&vec{e},'_2end{pmatrix}$ . Тогда, учитывая (2.8), имеем $mathop{y}limits_{(vec{e})}=mathop{s}limits_{(vec{e})}+mathop{S}limits_{(vec{e})to(vec{e},')}cdotmathop{y'}limits_{(vec{e},')}$ . Подставляя $mathop{y'}limits_{(vec{e},')}=mathop{x}limits_{(vec{e})}$ (координаты образа Y=mathcal{A}(X) в новой системе координат совпадают с координатами прообраза в старой системе координат), получаем аффинное преобразование

$mathop{y}limits_{(vec{e})}=mathop{s}limits_{(vec{e})}+mathop{S}limits_{(vec{e})to(vec{e},')}cdotmathop{x}limits_{(vec{e})}$

вида (2.11) с невырожденной матрицей $mathop{A}limits_{(vec{e})}=mathop{S}limits_{(vec{e})to(vec{e},')}$ и столбцом $mathop{a}limits_{(vec{e})}=mathop{s}limits_{(vec{e})}$ . Существование аффинного преобразования доказано. Докажем единственность от противного. Пусть преобразование mathcal{B} удовлетворяет тем же условиям, что и mathcal{A} , но для некоторой (хотя бы одной) точки образы mathcal{A}(X) и mathcal{B}(X) не совпадают. Тогда в новой системе координат $O'vec{e},'_2vec{e},'_2$ разные точки и будут иметь равные координаты (такие же, как координаты точки в старой системе координат $Ovec{e}_1vec{e}_2$ ), чего быть не может (см. пункт 1 замечаний 2.1). Полученное противоречие доказывает единственность аффинного преобразования.

Таким образом, аффинное преобразование (2.15) может быть задано указанием двух аффинных систем координат. Говорят, что аффинное преобразование задано переходом от одной аффинной системы координат к другой.

Третий способ. Аффинное преобразование плоскости вполне определяется образами трех данных точек, не лежащих на одной прямой, т.е. существует единственное аффинное преобразование, переводящее три точки O,A,B , не лежащие на одной прямой, в три точки O',A',B' , также не лежащие на одной прямой.

В самом деле, заданные точки O,A,B и O',A',B' порождают две аффинные системы координат $Ovec{e}_1vec{e}_2$ и $O'vec{e},'_1vec{e},'_2$ , где $vec{e}_1=overrightarrow{OA},,vec{e}_2=overrightarrow{OB}$ и $vec{e},'_1=overrightarrow{O'A'},,vec{e},'_2=overrightarrow{O'B'}$ — пары базисных (неколлинеарных) векторов, и тем самым однозначно определяют аффинное преобразование.

Пример 2.7. В прямоугольной системе координат Ovec{i}vec{j} заданы точки (рис.2.19):

Q(2,1),quad A(6,4),quad B(-2.4),quad Q'(10,3),quad A'(10,5),quad B'(6,6),quad X(2,7).

Требуется вывести формулы (2.11) аффинного преобразования mathcal{A} , отображающего точки Q,A,B в точки Q',A',B' , и найти координаты образа Y=mathcal{A}(X) точки :

Формулы аффинного преобразования, отображающего точки

а) в системе координат $Qvec{e}_1vec{e}_2,~vec{e}_1=overrightarrow{QA},~vec{e}_2=overrightarrow{QB}$ ;

б) в заданной прямоугольной системе координат.

Решение. а) Искомое преобразование mathcal{A} отображает систему координат $Qvec{e}_1vec{e}_2$ в систему координат $Q'vec{e},'_1vec{e},'_2$ , где $vec{e},'_1=overrightarrow{Q'A'}=mathcal{A}(vec{e}_1)$ , $vec{e},'_2=overrightarrow{Q'B'}=mathcal{A}(vec{e}_2)$ . Формулы, задающие такое преобразование , имеют вид (2.15), где — координатный столбец вектора vec{s}=overrightarrow{QQ'} в базисе $(vec{e})=begin{pmatrix}vec{e}_1&vec{e}_2end{pmatrix}$ , а $mathop{S}limits_{(vec{e})to(vec{e},')}$ — матрица перехода от базиса $(vec{e})=begin{pmatrix}vec{e}_1&vec{e}_2end{pmatrix}$ к базису $(vec{e},')=begin{pmatrix}vec{e},'_1&vec{e},'_2end{pmatrix}$ . По рис.2.19, учитывая, что $vec{i}=frac{1}{8}(vec{e}_1-vec{e}_2)$ и $vec{j}=frac{1}{6}(vec{e}_1+vec{e}_2)$ определяем разложения векторов $vec{s},vec{e},'_1,vec{e},'_2$ по базису (vec{e}) :

$begin{gathered}vec{s}=8cdotvec{i}+2cdotvec{j}=frac{8}{8}cdot(vec{e}_1-vec{e}_2)+frac{2}{6}cdot(vec{e}_1+vec{e}_2)=frac{4}{3}cdotvec{e}_1-frac{2}{3}cdotvec{e}_2;\[3pt]vec{e},'_1=2cdotvec{j}=frac{2}{6}cdot(vec{e}_1+vec{e}_2)=frac{1}{3}vec{e}_1+frac{1}{3}cdotvec{e}_2;quadvec{e},'_2=vec{e}_2=0cdotvec{e}_1+1cdotvec{e}_2.end{gathered}$

Следовательно, в системе координат $Qvec{e}_1vec{e}_2$ преобразование (2.15) имеет вид

поскольку согласно (2.2) матрица перехода формируется путем записи по столбцам координат векторов $vec{e},'_1,vec{e},'_2$ в базисе (vec{e}) .

Найдем координаты образа точки . В системе координат $Qvec{e}_1vec{e}_2$ точка имеет координаты x_1=1,~x_2=1 ,так как $overrightarrow{QX}=1cdotvec{e}_1+1cdotvec{e}_2$ . Подставляя в найденные формулы координаты прообраза, получаем искомые координаты образа:

$begin{pmatrix}y_1\[2pt]y_2end{pmatrix}=begin{pmatrix}dfrac{4}{3}\[8pt]-dfrac{2}{3}end{pmatrix}+begin{pmatrix}dfrac{1}{3}&0\[8pt]dfrac{1}{3}&1end{pmatrix}{cdot}begin{pmatrix}1\[2pt]1end{pmatrix}=begin{pmatrix}dfrac{5}{3}\[8pt]dfrac{2}{3}end{pmatrix},$ то есть $mathop{Y}limits_{(vec{e})}!left(frac{5}{3},frac{2}{3}right).$

Заметим, что в новой системе координат $Q'vec{e},'_1vec{e},'_2$ точка Y=mathcal{A}(X) имеет координаты $mathop{Y}limits_{(vec{e},')}(1,1)$ , которые совпадают с координатами точки $mathop{X}limits_{(vec{e})}(1,1)$ в старой системе координат $Qvec{e}_1vec{e}_2$ .

б) Подставляя в (2.11) координаты образов и прообразов, получаем:

$begin{aligned}Q'&=mathcal{A}(Q)colonquadbegin{pmatrix}10\3end{pmatrix}=begin{pmatrix}a_1\a_2end{pmatrix}+begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}end{pmatrix}{cdot}begin{pmatrix}2\1end{pmatrix},\[3pt]A'&=mathcal{A}(A)colonquadbegin{pmatrix}10\5end{pmatrix}=begin{pmatrix}a_1\a_2end{pmatrix}+begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}end{pmatrix}{cdot}begin{pmatrix}4\6end{pmatrix},\[3pt]B'&=mathcal{A}(B)colonquadbegin{pmatrix}6\6end{pmatrix}=begin{pmatrix}a_1\a_2end{pmatrix}+begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}end{pmatrix}{cdot}begin{pmatrix}-2\4end{pmatrix}.end{aligned}$

Вычитая первое уравнение из второго и третьего, получаем

$begin{pmatrix}0\2end{pmatrix}=begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}end{pmatrix}{cdot}begin{pmatrix}4\3end{pmatrix}$ и $begin{pmatrix}-4\3end{pmatrix}=begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}end{pmatrix}{cdot}begin{pmatrix}-4\3end{pmatrix},$ т.е. $left{!!begin{aligned}4a_{11}+3a_{12}&=0,\4a_{21}+3a_{22}&=2,\-4a_{11}+3a_{12}&=-4,\-4a_{21}+3a_{22}&=3.end{aligned}right.$

Решая эту систему, находим элементы матрицы $A= begin{pmatrix} 1/2& -2/3\-1/8& 5/6 end{pmatrix}$ , после чего определяем столбец $a=begin{pmatrix}a_1\a_2end{pmatrix}=begin{pmatrix}29/3\29/12end{pmatrix}$ . Таким образом, искомое преобразование mathcal{A} в заданной прямоугольной системе координат имеет вид

$begin{pmatrix}y_1\[2pt]y_2 end{pmatrix}= begin{pmatrix}a_1\[2pt]a_2 end{pmatrix}+ Acdot! begin{pmatrix}x_1\[2pt]x_2end{pmatrix}= begin{pmatrix} dfrac{29}{3}\[8pt] dfrac{29}{12}end{pmatrix}+begin{pmatrix}dfrac{1}{2}&-dfrac{2}{3}\[8pt]-dfrac{1}{8}&dfrac{5}{6}end{pmatrix}{cdot}begin{pmatrix}x_1\[2pt]x_2end{pmatrix}.$

Найдем координаты образа точки X(2,7) :

$begin{pmatrix}y_1\[2pt]y_2end{pmatrix}=begin{pmatrix}dfrac{29}{3}\[8pt]dfrac{29}{12}end{pmatrix}+begin{pmatrix}dfrac{1}{2}&-dfrac{2}{3}\[8pt]-dfrac{1}{8}&dfrac{5}{6}end{pmatrix}{cdot}begin{pmatrix}2\[2pt]7end{pmatrix}=begin{pmatrix}6\[2pt]8end{pmatrix},$ то есть Y(6,8) .

Получим теперь формулы аффинного преобразования mathcal{A} в системе координат $Qvec{e}_1vec{e}_2$ , используя связи (2.12). Учитывая, что переход от прямоугольной системы координат Ovec{i}vec{j} системе координат $Qvec{e}_1vec{e}_2$ определяется матрицей $S=begin{pmatrix}4&-4\3&3end{pmatrix}$ столбцом $s=begin{pmatrix}2\1end{pmatrix}$ поскольку vec{s}=overrightarrow{OQ} , $vec{e}_1=4vec{i}+3vec{j}$ , $vec{e}_2=-4vec{i}+3vec{j}$ находим

$begin{aligned}mathop{A'}limits_{(vec{e})}&=S^{-1}cdot Acdot S={begin{pmatrix}4&-4\[2pt]3&3end{pmatrix}!}^{-1}cdot!begin{pmatrix}dfrac{1}{2}&-dfrac{2}{3}\[8pt]-dfrac{1}{8}&dfrac{5}{6}end{pmatrix}!cdot!begin{pmatrix}4&-4\[2pt]3&3end{pmatrix}=\ &=frac{1}{24}cdot!begin{pmatrix}3&4\[2pt]-3&4end{pmatrix}!cdot!begin{pmatrix}0&-4\[2pt]2&3end{pmatrix}=frac{1}{24}cdot!begin{pmatrix}8&0\[2pt]-8&24end{pmatrix}=begin{pmatrix}dfrac{1}{3}&0\[8pt]dfrac{1}{3}&1end{pmatrix}!,end{aligned}$

$begin{aligned} mathop{a'}limits_{(vec{e})}&= S^{-1}cdot(a+Acdot s-s)= {begin{pmatrix} 4&-4\ 3&3 end{pmatrix}!}^{-1} cdot! left[begin{pmatrix}dfrac{29}{3}\[8pt]dfrac{29}{12}end{pmatrix}+begin{pmatrix}dfrac{1}{2}&-dfrac{2}{3}\[8pt]-dfrac{1}{8}&dfrac{5}{6}end{pmatrix}!cdot! begin{pmatrix}2\[2pt]1end{pmatrix}-begin{pmatrix}2\[2pt]1end{pmatrix}right]=\[2pt] &=frac{1}{24}cdot! begin{pmatrix}3&4\[2pt]-3&4end{pmatrix}!cdot! begin{pmatrix} dfrac{29}{3}+1-dfrac{2}{3}-2\[8pt]dfrac{29}{12}-dfrac{1}{4}+dfrac{5}{6}-1end{pmatrix}= frac{1}{24}cdot! begin{pmatrix}3&4\[2pt]-3&4end{pmatrix}!cdot!begin{pmatrix}8\[2pt]2end{pmatrix}= frac{1}{24}cdot!begin{pmatrix}32\[2pt]16 end{pmatrix}= begin{pmatrix} dfrac{4}{3}\[8pt]-dfrac{2}{3}end{pmatrix},end{aligned}$

что совпадает с результатами пункта «а».

Свойства аффинных преобразований плоскости

1. Аффинное преобразование взаимно однозначное, кроме того:

а) преобразование, обратное к аффинному, является также аффинным;
б) композиция аффинных преобразований является также аффинным преобразованием.

2. При аффинном преобразовании векторы преобразуются следующим образом:

г) равные векторы — в равные;
б) коллинеарные — в коллинеарные, причем отношение коллинеарных векторов сохраняется;
в) неколлинеарные — в неколлинеарные.

3. При аффинном преобразовании сохраняется отношение, в котором точка делит отрезок.

4. При аффинном преобразовании (2.11) площадь любого параллелограмма изменяется в одном и том же отношении, т.е. умножается на одно и то же число (называемое коэффициентом искажения площади): $S_{ast'}=vertdetvertcdot S_{ast}$ , где $S_{ast}$ — площадь параллелограмма, a $S_{ast'}$ — площадь образа этого параллелограмма. Другими словами, коэффициент искажения площади при аффинном преобразовании равен модулю определителя матрицы этого преобразования.

Первое свойство следует из обратимости матрицы аффинного преобразования, поскольку из (2.11) можно выразить координаты прообраза через координаты образа:

$x=-A^{-1}cdot a+A^{-1}cdot y.$

Заметим, что эти формулы имеют тот же вид, что и (2.11), т.е. преобразование, обратное к аффинному, является аффинным преобразованием с матрицей $A^{-1}$ и вектором переноса $(-A^{-1}cdot a)$ . Композиция аффинных преобразований y=a+Acdot x и z=b+Bcdot y :

$z=b+Bcdotunderbrace{(a+Acdot x)}_{y}=b+Bcdot a+Bcdot Acdot x$

также является аффинным преобразованием с матрицей Bcdot A (невырожденной в силу невырожденности и ) и вектором переноса b+Bcdot a .

Докажем второе свойство. Пусть ненулевые векторы vec{v} и vec{w} коллинеарны, причем $frac{vec{v}}{vec{w}}=lambda$ . Надо доказать, что их образы vec{v},'=mathcal{A}(vec{v}) и vec{w},'=mathcal{A}(vec{w}) также коллинеарны и $frac{vec{v},'}{vec{w},'}=lambda$ . Действительно, если { v} и — координатные столбцы векторов vec{v} и vec{w} , то v=lambdacdot w . Тогда для координатных столбцов и (векторов и ) по формуле (2.14) получаем (см. пункт 4 замечаний 2.4):

$v'=Acdot v=Acdotunderbrace{lambdacdot w}_{v}=lambdacdotunderbrace{Acdot w}_{w'}=lambdacdot w',$ то есть v'=lambdacdot w'.

Следовательно, vec{v},'=lambdacdotvec{w},' , т.е. векторы и коллинеарны и $frac{vec{v},'}{vec{w},'}=lambda$ . Если же хотя бы один из векторов нулевой, например, vec{v}=vec{o} , то его образ (по свойству 2) также нулевой вектор vec{v},'=vec{o} , который коллинеарен любому вектору vec{w},' . При lambda=1 получаем, что равные векторы преобразуются в равные. Наконец, неколлинеарные векторы не могут преобразоваться в коллинеарные, поскольку в этом случае при обратном преобразовании коллинеарные векторы преобразуются в неколлинеарные, что противоречит пункту 2,»б».

Третье свойство следует из второго (см. пункт 2,»б»). Действительно, пусть точки A,B,C отображаются в точки A',B',C' соответственно. Если точка делит отрезок в отношении AC:CB=alpha:beta , то векторы overrightarrow{AC} и overrightarrow{AB} коллинеарные и $overrightarrow{AC}=frac{alpha}{alpha+beta}cdotoverrightarrow{AB}$ . По свойству 2 пункта «б» векторы overrightarrow{A'C'} и overrightarrow{A'B'} также коллинеарны и $overrightarrow{A'C'}=frac{alpha}{alpha+beta}cdotoverrightarrow{A'B'}$ , т.е. точка делит отрезок A'B' в отношении Параллелограмм, построенный на базисных векторах, и его образ

A'C':C'B'=alpha:beta=AC:CB,.

Обсудим четвертое свойство. На рис.2.20 заштрихованы параллелограмм, построенный на базисных векторах $vec{e}_1vec{e}_2$ , и его образ (параллелограмм, построенный на базисных векторах $vec{e},'_1,vec{e},'_2$ ). Справедливость утверждения для параллелограммов следует из свойства 3 матрицы перехода от одного базиса к другому. Любой параллелограмм разбивается диагональю на два равных треугольника. Следовательно, утверждение справедливо для треугольников, а значит и для многоугольников, поскольку любой многоугольник разбивается на конечное число треугольников. Средствами математического анализа это свойство может быть распространено на произвольную измеримую плоскую фигуру.

Замечания 2.5

1. Третье свойство является характеристическим для аффинного преобразования и может быть взято в качестве эквивалентного определения.

2. Преобразование (2.11) для произвольной квадратной матрицы (быть может, вырожденной) называется линейным, при этом матрица называется матрицей линейного преобразования. Любое аффинное преобразование является линейным, но не всякое линейное преобразование является аффинным.

3. Квадратные матрицы и , связанные соотношением $A'=S^{-1}cdot Acdot S$ , называются подобными, а матрица — преобразующей. В силу (2.12) матрицы аффинного преобразования в разных базисах оказываются подобными, причем преобразующей матрицей служит матрица перехода от одного базиса к другому.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник