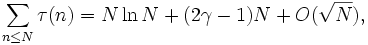Частное — это результат деления одного числа (делимое) на другое число (делитель). То есть по определению деления чисел «a» на «b» (a:b=c) — это такое число «с», что a = b•c
Но в целых числах результат деления не всегда будет целым числом. Например: 8:2 = 4, получим частное равное целому числу. А вот 7:2 — не получим целого числа.
Тогда в целых числах (в общем случае) деление «m» на «n» — это нахождение целых чисел «k» и «r», таких что:
m = k•n + r, где 0≤r<|n|, где m,n,k,n,r — целые числа и n≠0.
Число m — называется делимое
Число n — называется делитель
Число k — называется неполное частное
Число r — называется остаток.
Например: 7:2 = (3 и остаток 1), так как 7 = 3•2 + 1,
3 — будет неполным частным.
Или 7:(-2) = (-3 и остаток 1), так как 7 = -3•(-2) + 1
-3 — будет неполным частным.
Или -7:2 = (-4 и остаток 1), так как -7 = -4•2 + 1
-4 — будет неполным частным.
Или -7:(-2) = (4 и остаток 1), так как -7 = 4•(-2) + 1
4 — будет неполным частным.
Значение частного двух чисел в математике
Содержание:
- Что такое частное чисел
-
Деление как операция
- Основные свойства деления
- Неполное частное
- Изменение частного в зависимости от изменения делимого и делителя
-
Задачи, примеры вычисления частного
- Задача 1
- Задача 2
Что такое частное чисел
Частное чисел – это результат деления одного числа на другое. Оно показывает, сколько раз число a содержится в числе b.
Деление как операция
Деление – арифметическая операция, обратная умножению, суть которой заключается в нахождении одного из сомножителей по произведению и другому множителю. В данном случае произведение переходит в делимое, имеющийся сомножитель – в делитель, искомый сомножитель – в частное.
Подобно тому, как неоднократно прибавить число – это значит умножить, так и неоднократно вычесть – это значит разделить.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
На письме данную операцию можно обозначать разными символами:
- : двоеточием;
- ÷ обелюсом;
- / косой чертой (слеш);
- — горизонтальной чертой (знак дроби).
Процесс деления имеет следующий вид:
(frac{делимое}{делитель}=частное)
В цифрах данное выражение можно записать так:
(15 : 5 = 3,)
(15 ÷ 5 = 3,)
(15/5 = 3,)
(frac{15}{5}=3.)
Основные свойства деления
Деление не коммутативно, то есть не перестановочно – от перемены мест элементов операции частное изменяется:
(a : b ≠ b : a;)
Деление не ассоциативно – то есть при последовательном выполнении деления трех или более чисел последовательность операций имеет значение, при смене порядка выполнения изменится результат:
((a : b):c ≠ a : (b : c);)
Деление дистрибутивно справа – на одном и том же множестве две бинарные операции имеют свойство согласованности:
((a + b): x = (a : x)+(b : x);)
Имеется единственный нейтральный элемент – число 1, при делении на единицу результатом является исходное число (делимое):
(а : 1 = а;)
Имеется единственный обратный элемент – число 1, при делении единицы на число результатом является число, обратное исходному (делителю):
(1 : а = а^-1, а ≠ 0;)
Существует единственный нулевой элемент – число 0, при делении нуля на любое число результатом будет нуль:
(0 : а = 0, а ≠ 0;)
Деление на нулевой элемент не определено:
(а : 0 = ∞, а ≠ 0;)
Деление на противоположный элемент дает минус единицу:
(а : (-а) = -1.)
Неполное частное
Неполное частное – результат, который получился после деления с остатком.
Под делением с остатком понимается нахождение наибольшего целого числа, которое в произведении с делителем дает число, не превышающее делимое. Это искомое и называют неполным частным.
Разность между делимым и произведением делителя на неполное частное называется остатком, который всегда меньше делителя.
Например, 17 не делится без остатка на 5.
Наибольшее число, результат умножения которого на 5 не превосходит 17, это 3. 3 в данном случае является неполным частным.
Чтобы получить остаток, нужно из 17 вычесть произведение 3 и 5, то есть 17 – 3*5 = 2. Остаток – 2.
Изменение частного в зависимости от изменения делимого и делителя
Изменение делимого:
- увеличение делимого в несколько раз приведет к тому, что частное увеличится во столько же раз:
((а * x) : b = c * x;)
- уменьшение делимого в несколько раз приведет к тому, что частное уменьшится во столько же раз:
((a : x) : b = c : x.)
Изменение делителя:
- увеличение делителя в несколько раз приведет к тому, что частное уменьшится во столько же раз:
(а : (b * x) = c : x;)
- уменьшение делителя в несколько раз приведет к тому, что частное увеличится во столько же раз:
(а : (b : x) = c * x.)
Частное не изменится, если делимое и делить одновременно увеличить или уменьшить в одинаковое количество раз:
((а * x) : (b * x) = c;)
((а : x) : (b : x) = c;)
Задачи, примеры вычисления частного
Для того, чтобы проиллюстрировать данную арифметическую операцию, решим простые задачи.
Задача 1
В книге 891 страница. Она поделена на 9 равных глав. Узнайте, сколько страниц в одной главе.
Решение:
Для этого количество страниц разделим на количество глав:
891 : 9 = 99 (страниц)
Ответ: 99 страниц.
Задача 2
У Антона есть 22 апельсина. Он хочет приготовить из них компот. Для одного литра компота ему понадобится 3 апельсина. Нужно вычислить, сколько литров напитка сможет приготовить Антон и сколько апельсинов у него останется.
Решение:
22 : 3 = 7 (литров) (остаток 1)
Ответ: 7 литров, 1 апельсин останется.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Найти частное и остаток
Онлайн калькулятор зная делимое и делитель поможет найти неполное частное и остаток. При выполнении деления с остатком полученное число называется неполным частным, а разность между делимым и произведением делителя на неполное частное называется остатком. Остаток всегда меньше делителя. Определить остатки при делении.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также
Найдите частное чисел 9,647 и 0,1
- reply
Неполное частное
- Неполное частное
-
Делимость — одно из основных понятий арифметики и теории чисел, связаное с операцией деления.
Содержание
- 1 Определение
- 2 Обозначения
- 3 Связанные определения
- 4 Свойства
- 4.1 Число делителей
- 5 Обобщения
- 6 См. также
Определение
Если для некоторого целого числа a и целого числа
существует такое целое число q, что bq = a, то говорят, что число a делится нацело на b.
При этом число b называется делителем числа a, делимое a будет кратным числа b, а число q называется частным от деления a на b.
Обозначения
означает, что a делится на b
- b | a означает, что b делит a.
Связанные определения
- В этом соотношении число r называется остатком (от деления a на b), а число q — неполным частным (от деления a на b).
- Число a делится нацело на b тогда и только тогда, когда остаток от деления a на b равен нулю.
Свойства
- Любое натуральное число является делителем нуля;
- Единица является делителем любого целого числа;
- Любое натуральное число является делителем самого себя.
Число делителей
Число положительных делителей натурального числа n обычно обозначается τ(n), является мультипликативной функцией, для неё верна асимптотическая формула Дирихле:
Обобщения
Понятие делимости обобщается на произвольные кольца, например кольцо многочленов.
См. также
- Деление с остатком
- Признаки делимости
- Модульная арифметика
- Деление (математика)
- Конгруэнтность (алгебра)
- Сравнение по модулю
- Кольцо (математика)
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Неполное частное» в других словарях:
-
Дробь — Если делится какое нибудь целое число а на другое целое число b, т. е. ищется число x, удовлетворяющее условию bx=а, то могут представиться два случая: или в ряду целых чисел найдется число х, которое этому условию удовлетворит, или же окажется,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Деление с остатком — Деление c остатком (деление по модулю, нахождение остатка от деления, остаток от деления) арифметическая операция, результатом которой является два целых числа: неполное частное и остаток от деления целого числа на другое целое число.… … Википедия
-
Остаток от деления — в арифметике один из результатов операции деления с остатком. Образуется, если результат деления не может быть выражен целым числом, при этом остаток от деления должен быть по абсолютной величине меньше делителя. В случае, если числа… … Википедия
-
Фундаментальные алгоритмы — Два основных фундаментальных алгоритма это алгоритм деления и алгоритм Евклида Алгоритм деления предназначен для вычисления неполного частного и остатка от деления двух целых чисел. Алгоритм деления a делимое b делитель q неполное частное r –… … Википедия
-
ГОРНЕРА СХЕМА — прием для нахождения неполного частного и остатка при делении многочлена на двучлен , где все коэффициенты лежат в нек ром поле, напр., в поле комплексных чисел. Всякий многочлен единственным способом представим в виде где есть неполное частное,… … Математическая энциклопедия
-
Целая часть — График функции «пол» (целая часть числа) … Википедия
-
Преобразование Гаусса — В математике, преобразование Гаусса (измеримая) динамическая система на отрезке [0,1], заданная отображением где обозначает дробную часть числа. Это преобразование «стирает» первое неполное частное в разложении числа в цепную дробь: Кроме… … Википедия
-
Единая сетевая разметка — (ЕСР) система цифрового обозначения железнодорожных станций на территории стран СНГ и Балтии. С помощью кодов ЕСР кодируются станции, открытые для выполнения грузовых операций, производящие перевалку грузов с железнодорожного на речной или… … Википедия
-
ЗНАНИЕ В АРАБО-МУСУЛЬМАНСКОЙ ФИЛОСОФИИ — ЗНАНИЕ В АРАБО МУСУЛЬМАНСКОЙ ФИЛОСОФИИ. Благодаря слитости процессуального и субстанциального аспектов в категории масдара (отглагольного существительного) арабское языковое мышление имеет тенденцию рассматривать процесс и результат как нечто … Философская энциклопедия
-
ЗНАНИЕ В АРАБО-МУСУЛЬМАНСКОЙ ФИЛОСОФИИ. — ЗНАНИЕ В АРАБО МУСУЛЬМАНСКОЙ ФИЛОСОФИИ. Благодаря слитости процессуального и субстанциального аспектов в категории масдара (отглагольного существительного) арабское языковое мышление имеет тенденцию рассматривать процесс и результат как нечто… … Философская энциклопедия

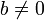 существует такое целое число
существует такое целое число 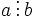 означает, что
означает, что