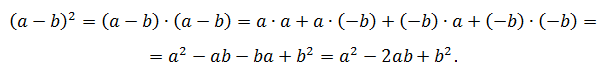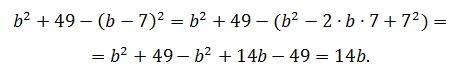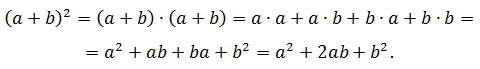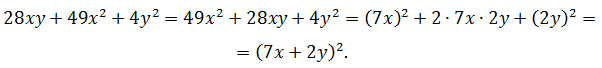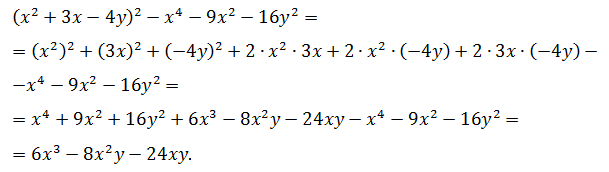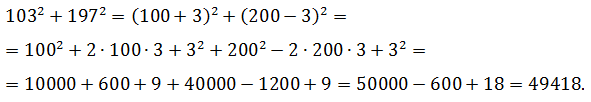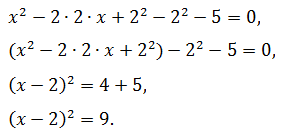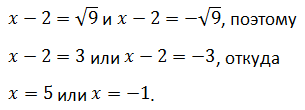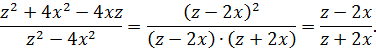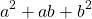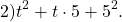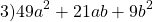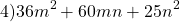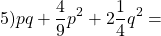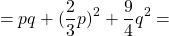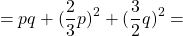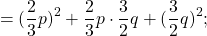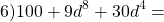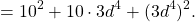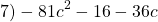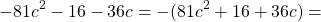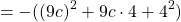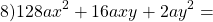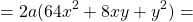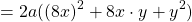Как найти неполный квадрат суммы

Формулы сокращённого умножения

• Разложение формул сокращенного умножения
• Неполный квадрат суммы
• Неполный квадрат разности

При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.

Формулы сокращённого умножения — это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.

a² + b² = (a + b)² — 2ab  —  сумма квадратов;

a² — b² = (a + b)(a — b)  —  разность квадратов;

(a + b)² = a² + 2ab + b²  —  квадрат суммы;

(a — b)² = a² — 2ab + b²  —  квадрат разности;

a³ + b³ = (a + b)(a² — ab + b²)  —  сумма кубов;

a³ — b³ = (a — b)(a² + ab + b²)  —  разность кубов;

(a + b)³ = a³ + 3a²b + 3ab² + b³  —  куб суммы;

(a — b)³ = a³ — 3a²b + 3ab² — b³  —  куб разности.

Обратите внимание, что  a  и  b  в формулах сокращённого умножения могут быть как числами, так и выражениями.

Разложение формул сокращенного умножения

Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения.

Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:

a² + b² = (a + b)² — 2ab.

Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)² — 2ab = (a + b)(a + b) — 2ab = a² + ab + ab + b² — 2ab = a² + b².

Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:

a² — b² = (a + b)(a — b).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)(a — b) = a² — ab + ab — b² = a² — b².

Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

(a + b)² = a² + 2ab + b².

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a + b)² = (a + b)(a + b) = a² + ab + ab + b² = a² + 2ab + b².

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:

(a — b)² = a² — 2ab + b².

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a — b)² = (a — b)(a — b) = a² — ab — ab + b² = a² — 2ab + b².

Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:

a³ + b³ = (a + b)(a² — ab + b²).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)(a² — ab + b²) = a³ — a²b + ab² + a²b — ab² + b³ = a³ + b³.

Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:

a³ — b³ = (a — b)(a² + ab + b²).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a — b)(a² + ab + b²) = a³ + a²b + ab² — a²b — ab² — b³ = a³ — b³.

Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:

(a + b)³ = a³ + 3a²b + 3ab² + b³.

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a + b)³ = (a + b)(a + b)² = (a + b)(a² + 2ab + b²) = a³ + 2a²b + ab² + a²b + 2ab² + b³ = a³ + 3a²b + 3ab² + b³.

Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:

(a — b)³ = a³ — 3a²b + 3ab² — b³.

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a — b)³ = (a — b)(a — b)² = (a — b)(a² — 2ab + b²) = a³ — 2a²b + ab² — a²b + 2ab² — b³ = a³ — 3a²b + 3ab² — b³.

Неполный квадрат суммы

Выражение:

a² + 2ab + b²

это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:

a² + ab + b²,

которое называется неполным квадратом суммы. Неполный квадрат суммы — это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.

Неполный квадрат разности

Выражение:

a² — 2ab + b²

это квадрат разности, который также называется полным квадратом разности относительно выражения:

a² — ab + b²,

которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.

Для успешного решения математических задач часто бывает необходимо уметь преобразовывать созданные выражения. Для этого применяют базовые знания, формулы сокращённого умножения, в том числе, квадрат суммы и квадрат разности.

Они помогают упрощать громоздкие записи, более рационально подходить к приведению дробей к одному знаменателю, решению уравнений и задач по геометрии, тригонометрии, математическому анализу, физике, химии, экономическим дисциплинам и многим другим наукам.

Поэтому среди многих разделов математики школьная алгебра занимает базовую приоритетную позицию, дающую основы вычислений для смежных предметов.

Формула квадрата разности

Для получения формулы применяют правило умножения многочлена на многочлен: нахождение суммы произведений каждого слагаемого одной скобки на каждое слагаемое второй скобки, учитывая, что квадрат отрицательного числа равен квадрату положительного:

Если запомнить правило, то необходимость постоянно прописывать эту цепочку равенств исчезает.

Квадрат разности двух выражений равен сумме квадратов каждого из выражений без их удвоенного произведения:

Примеры задач с решением

Задача №1

Требуется возвести в квадрат разность (8x — 3y).

Решение.

При использовании формулы получается:

Ответ: 64x² — 48xy + 9y².

Задача №2

Упростить выражение:

b² + 49 — (b — 7)²

Решение.

Ответ: 14b.

Формула квадрата суммы и неполного квадрата суммы

Также легко, как и в предыдущем случае, выводится эта формула:

Квадрат суммы двух выражений равен сумме квадратов каждого из них плюс их удвоенное произведение:

Многие школьники, начинающие знакомиться с этим материалом, часто теряют двойку во втором слагаемом правой части, получая

Однако, в этом случае, возникает неполный квадрат суммы (или разности), который на множестве действительных чисел не раскладывается на множители.

Обе формулы применяются не только для раскрытия скобок, но и для разложения на множители, что в свою очередь упрощает приведение к одному знаменателю, сокращение дробей, решение уравнений высоких степеней.

Примеры задач с решением

Задача №3

Преобразовать трёхчлен в квадрат двучлена:

28xy + 49x² + 4y²

Решение.

Поскольку квадраты находятся на втором и третьем местах, поменяем слагаемые между собой и подготовим выражение для применения формулы:

Ответ: (7x + 2y)². 

Возведение во вторую степень суммы трёх и более слагаемых выполняется аналогично: необходимо возвести в квадрат каждый элемент, записать все возможные удвоенные произведения и сложить полученные результаты.

Правила возведения в степени более высоких порядков возникают, когда выполняется умножение одинаковых многочленов несколько раз.

Возможность выполнять возведение в квадрат больших чисел, не используя калькулятор, является одним из преимуществ сокращённого умножения.

Задача №4

Выполнить раскрытие скобок и упростить:

(x² + 3x — 4y)² — x⁴ — 9x² — 16y²

Решение.

Ответ: 6x³ — 8x² — 24xy.

Задача №5

Вычислить:

103² + 197²

Решение.

Для каждого слагаемого применяется одно из правил возведения в квадрат, затем производится суммирование результатов:

Решая квадратные уравнения, вместо поиска дискриминанта выделяют полный (точный) квадрат среди слагаемых, расположенных в левой части. В правую сторону собираются оставшиеся элементы.

Задача №6

Решить уравнение:

x² — 4x — 5 = 0

Решение.

Первые два слагаемых левой части полностью удовлетворяют формуле квадрата суммы. Соотнеся их с соответствующими элементами правила, определяют, прибавляют и вычитают третье, затем сворачивают в точный квадрат, остальные члены алгебраической суммы переносят в правую сторону:

Решениями исходного уравнения являются корни уравнений

Ответ: x = 5 или x = -1.

Разность квадратов

Ещё одной формулой сокращённого умножения является разность квадратов. Она получается при умножении суммы двух выражений на их разность.

Читается справа налево.

Разность квадратов двух выражений равна произведению разности этих выражений на их сумму:

Применение последней записи справа налево есть раскрытие скобок более удобным способом, чем простое умножение многочленов.

Разложение на множители позволяет судить о наличии целых или натуральных корней квадратного уравнения.

Пример задачи с решением

Задача №7

Сократить дробь:

Решение.

В числителе записан квадрат разности, а в знаменателе – разность квадратов двух выражений. Применяя соответствующие формулы, получается искомый результат:

Ответ:

.

В большинстве случаев разницы, как сворачивать квадрат двучлена, не существует. Однако в данной ситуации, благодаря выражению в знаменателе, на первое место лучше поставить

, чтобы избежать игры с минусом при сокращении.

Онлайн калькуляторы помогают выполнять преобразования. Однако, поскольку формулы сокращённого умножения являются базовым материалом школьного курса, то лучше не просто получить результат, но и понять, каким образом к нему пришли.

План урока:

Разность квадратов

Квадрат суммы

Квадрат разности

Формулы для кубов

Треугольник Паскаля

Разность квадратов

Пусть есть два числа, одно из которых равно a, а другое – b. Их сумма будет равна a + b, а разность составляет a– b. Оба эти выражения являются многочленами.

Теперь перемножим сумму и разность, пользуясь правилами перемножения многочленов (см. урок 6) :

(a + b)(a — b) = a² — ab + ba — b²

Слагаемые – a b и b a являются подобными, их сумма равна нулю:

-ab + ab = -1ab + 1ab = ab(-1 + 1) = ab * 0 = 0

Поэтому в выражении их можно сократить:

(a + b)(a — b) = a² — ab + ba — b² = a² — b²

Получается, что произведение суммы двух чисел на их разность равно разности их квадратов. Естественно, как и любое другое математическое равенство, это можно переписать в обратном порядке:

a² — b²  = (a + b)(a — b)

Данное тождество называют формулой разности квадратов.

Вместо a и b в это тождество можно подставлять любые числа, выражения, одночлены, многочлены. Убедимся в ее справедливости на нескольких примерах. Вычислим значение выражения

7² — 5²

сначала напрямую, а потом с помощью формулы разности квадратов:

7² — 5² = 7*7 — 5*5 = 49 — 25 = 24

7² — 5² = (7 — 5)(7 + 5) = 2*12 = 24

Видно, что ответ не зависит от способа вычисления. Однако в ряде один из них представляется более удобным.

Пример. Вычислите разность двух квадратов: 2516² и 1516².

Решение. Возводить во вторую степень четырехзначные числа без калькулятора тяжело, поэтому используем сокращенное умножение:

2516² — 1516² = (2516 + 1516)(2516 + 1516) = 4032 * 1000 = 4032000

Ответ: 4032000

Пример. Вычислите 499•501.

Решение. Используем две простые замены:

499 = 500 — 1

501 = 500 + 1

С их помощью вычисления существенно упрощаются, так как произведение можно представить как разность квадратов двух чисел:

499 * 501 = (500 — 1)(500 + 1) = 500² — 1² = 250000 — 1 = 249999

Ответ: 249999.

Пример. Докажите, что число 765873² – 765864² делится на 9.

Решение. Разность квадратов равна:

765873² – 765864² = (765873 — 765864)(765873 + 765864) = 9*(765873 + 765864)

Даже не складывая слагаемые во второй скобке, мы можем сказать, что исходное число делится на 9, так как на 9 делится один из множителей, на которые мы разложили разность квадратов.

Теперь рассмотрим случаи, когда в формулу подставляются переменные. Пусть необходимо найти произведение полиномов 8u + 5v и 8u– 5v. С помощью формулы сокращенного умножения получаем:

(8u + 5v)(8u — 5v) = (8u)² — (5v)² = 64u² — 25v²

Конечно, мы могли бы выполнить эту операцию и без использования сокращенного умножения, просто раскрыв скобки методом «фонтанчика». Но тогда мы потратили бы больше времени, усилий и бумаги:

(8u + 5v)(8u — 5v) = (8u)² — 8u*5v + 5v*8u — (5v)² = 64u² — 25v²

Пример. Перемножьте полиномы x²z +2y³ и x²z– 2y³.

Решение.

(x²z +2y³)(x²z +2y³) = (x²z)² — (2y³)² = x⁴z² — 4y⁶

Пример. Упростите выражение

-3.5m² — (1.5n — 2m)(1.5n + 2m)

Решение:

-3.5m² — (1.5n — 2m)(1.5n + 2m) = -3.5m² — ((1.5n)² — (2m)²) = -3.5m² — 2.25n² + 4m² = 0.5m² — 2.25n²

Иногда с помощью сокращенного умножения можно разложить полином на множители. Например, двучлен x²– 25 можно представить как

x² — 25 = x² — 5² = (x — 5)(x + 5)

С помощью разложения разности квадратов на множители можно доказать, что разность вторых степеней двух последовательных натуральных чисел всегда является нечетным числом. Обозначим за n произвольное натуральное число. Тогда следующим за ним будет число n+1. Разность их квадратов равна

(n + 1)² = n²

Раскроем скобки:

(n + 1)² — n² = (n + 1 — n)(n + 1 + n) = 1*(2n + 1) = 2n + 1 = 1*(2n + 1) = 2n + 1

Число 2n +1 при делении на 2 дает остаток 1, то есть является нечетным.

Стоит отметить, что для суммы квадратов a² + b² аналогичной формулы разложения на множители не существует.

Квадрат суммы

Возведем во вторую степень сумму двух произвольных величин, которые обозначим буквами a и b:

(a + b)² = (a + b)(a + b) = a² + ab + ba + b² = a² + 2ab + b²

То есть верно тождество

(a + b)² = a² + 2ab + b²

Это тождество называют формулой квадрата суммы.

Покажем ее верность на числовом примере. Вычислим значение выражения (5 + 3)² двумя различными способами, с помощью формулы возведения суммы в квадрат и без нее:

(5 + 3)²  = 8² = 64

(5 + 3)² = 5² + 2 * 5 * 3 + 3² = 25 + 30 + 9 = 64

Выражение для квадрата суммы используется также, как и формула разности квадратов. В нее можно подставлять числа, полиномы и мономы, произвольные выражения. Тождество можно перевернуть, и тогда получится равенство:

a² + 2ab + b² = (a + b)²

которое является верным.

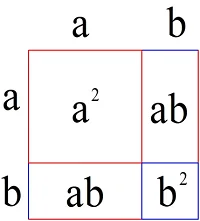
Тождество можно проиллюстрировать и геометрически. Построим квадрат со стороной a + b (отрезки длиной а выделены красным цветом, а длиной b– синим):

Площадь такой фигуры равна второй степени стороны:

S = (a + b)²

С другой стороны, этот квадрат составлен из двух прямоугольников площадью ab и квадратов со сторонами a и b:

S = a² + 2ab + b²

Пример. Вычислите 1010².

Решение. Представим число 1010 как сумму 1000 и 10. Тогда можно записать:

(1010)² = (1000 + 10)² = 1000² + 2 * 1000 * 10 + 10² = 1000000 + 20000 + 100 = 1020100

Пример. Докажите, что число 9060100 является второй степенью натурального числа.

Решение. Представим 9060100 как сумму слагаемых 9000000, 60000 и 100. В свою очередь верны следующие равенства:

3000² = 9000000

10² = 100

2 * 10 * 3000 = 60000

Тогда можно воспользоваться сокращенным умножением:

9060100 = 9000000 + 60000 + 100 = 3000² + 2 * 10 * 3000 + 10² = (3000 + 10)² = 3010²

Получили, что 9060100 – это вторая степень числа 3010. При этом нам не пришлось извлекать квадратный корень.

В тождество квадрата суммы можно подставлять не только числа, но и многочлены. Представим в виде произведения мономов выражение

(5h + ² — (4h + 10)²

Сначала по формуле квадрата суммы раскроем каждую из скобок:

(5h + ² — (4h + 10)² = (25h² + 80h + 64) — (16h² + 80h + 100) = 25h² + 80h + 64 — 16h² — 80h — 100

Далее приведем подобные слагаемые:

25h² + 80h + 64 — 16h² — 80h — 100 = (25h² — 16h²) + (80h — 80h) + (64 — 100) = 9h² — 36

оставшийся полином раскладывается на множители с помощью сокращенного умножения:

9h² — 36 = (3h)² — 6² = (3h — 6)(3h + 6)

Квадрат разности

Своя формула сокращенного умножения существует не только для квадрата суммы, но и для квадрата разности. Выведем её. Для этого возведем во вторую степень выражение a– b:

(a — b)² = (a — b)(a — b) = a² — ab — ba + b² = a² — 2ab + b²

Итак, мы получили тождество, называемое формулой квадрата разности:

(a — b)² = a² — 2ab + b²

Убедимся в верности тождества на примере. Для этого вычислим значение выражения (9 – 5)² двумя разными способами, с использованием формулы возведения разности в квадрат и без неё:

(9 — 5)² = 4² = 16

(9 — 5)² = 9² — 2 * 9 * 5 + 5² = 81 — 90 + 25 = 16

Заметим, что если поменять местами переменные aи b, то значение квадрата их разности не изменится:

(b — a)² = b² — 2ba + a² = a² — 2ab + b² = (a — b)²

Дело в том, что числа a– b и b – a являются противоположными. В предыдущем уроке «Разложение многочленов на множители» мы узнали, что

a — b = -(b — a)

Вторые же степени (как и вообще любые четные степени) противоположных чисел равны друг другу:

(-a)² = (-a)(-a) = (-1)*(-1)a² = a²

Можно заметить сходство между тождествами для вычисления квадрата разности и суммы. Действительно, они отличаются лишь одним знаком. Поэтому иногда эти два тождества записывают как единое целое:

Если в левой скобке стоит плюс, то и в правой должен быть именно он. Если в левой части тождества стоит минус, то справа также должен стоять минус.

Пример. Вычислите 999999².

Решение. Перемножать два шестизначных числа весьма сложно. Однако заметим, что число 999999 можно представить как разницу миллиона и единицы:

999999 = 1000000 — 1

Используем сокращенное умножение:

999999² = (1000000 — 1)² = 1000000² — 2*1*1000000 + 1 = 1000000000000 — 2000000 + 1

Несложно выполнить оставшиеся вычисления в столбик

1000000000000 — 2000000 + 1 = 999998000001

Ответ: 999998000001.

Пример. Раскройте скобки в выражении (4m– 3)²

Решение. Воспользуемся формулой сокращенного умножения:

(4m– 3)² = (4m)² — 2*4m*3 + 3² = 16m² — 24m + 9

Важно понимать, что вместо букв a и b могут стоять не только одночлены, но и полиномы. Пусть нам надо возвести во вторую степень полином

u² — 6u + 5

Если просто выполнить умножение методом «фонтанчика», то после раскрытия скобок получим 3•3 = 9 одночленов (так как исходный многочлен состоит из 3 мономов). Для упрощения представим исходный трехчлен как разность:

u² — 6u + 5 = u² — (6u — 5)

Тогда вторую степень можно найти так:

(u² — 6u + 5)² = (u² — (6u — 5))² = (u²)² — 2*u²(6u — 5) + (6u — 5)² = u⁴ — 12u³ + 10u² + 36u² — 60u + 25 = u⁴ — 12u³ + 36u² — 60u + 25 = u⁴ — 12u³ + 46u² — 60u + 25

Пример. Докажите, что квадратный трехчлен m²– 16m + 66 ни при каких значениях переменной m не принимает отрицательные значения.

Решение.

Известно, что вторая степень любого числа неотрицательна. Выделим в исходном трехчлене квадрат, содержащий переменную m. Для этого разложим число 66 как сумму 2 + 64:

m² — 16m + 65 = m² — 16m + 64 + 2 = m² — 2 * 8 * m + 8² + 2 = (m — ² + 2

При любом значении m выражение (m – ² неотрицательно, а значит, неотрицательно и значение (m – ² + 2. Более того, можно указать, что минимальное значение, которое может принимать исходный трехчлен, равно 2.

Заметим, что использованный в данном методе прием позволяет представить, по сути, любой квадратный трехчлен как разницу или сумму полного квадрата какого-то полинома и числа, что в свою очередь помогает оценить его максимальное или минимальное значение. Например, дан трехчлен 4v² + 12v – 10.Первое его слагаемое можно представить как квадрат какого-то числа:

(4v²) = (2v)²

Подобное действие в отношении трехчлена можно предпринять всегда, правда, иногда придется использовать квадратные корни, которые мы ещё не изучали детально. Далее второе слагаемое можно разложить на три множителя, одним из которых будет двойка, а вторым – тот самый одночлен, дающий при возведении во вторую степень первое слагаемое. Третий же множитель окажется каким-то числом:

12v = 2*2v*3

Теперь чтобы воспользоваться формулой квадрата суммы или квадрата разности, добавим к многочлену квадрат этого третьего множителя, а чтобы значение полинома не изменилось, сразу же его и вычтем. В данном случае третьим множителем оказалась тройка, а потому надо добавить 3² и сразу же отнять 3². Один из этих квадратов войдет в формулу сокращенного умножения, а другой – нет:

4v² + 12v — 10 = (2v)² + 2*2v*3 — 10 + 3² — 3² = ((2v)² + 2*2v*3 + 3²) — 10 — 3² = (2v + 3)² — 19

Так как выражение (2v + 3)² не может быть меньше нуля, то и минимальное значение трехчлена 4v² + 12v– 10 равно(– 19)

Пример. Оцените возможные значения трехчлена – 9с² + 15с + 8

Решение.

Воспользуемся таким же методом, но сначала вынесем знак минус за скобки, чтобы можно слагаемое 9c² представить как квадрат какого-то монома:

-9c² + 15c + 8 = -(9c² — 15c — = -((3c)² — 2 * 3c * 2.5 — 8 + 2.5² — 2.5²) = -((3c — 2.5)² — 8 — 6.25) = -(3c — 2.5)² + 14.25

Значение выражения – (3с – 2,5)² может быть только меньше или равным нулю. Значит, исходный трехчлен не может принимать значения, большие, чем 14,25.

Формулы для кубов

До этого мы познакомились с тождествами, в которых величины возводились во вторую степень. Их будет достаточно почти для всех школьных заданий, в том числе и на ЕГЭ, поэтому необходимо сосредоточиться именно на их изучении.Однако в алгебре есть и более сложные формулы сокращенного умножения, в которых переменные возводятся в куб.Их использование может пригодиться в задачах повышенной сложности. Выведем их.

Найдем значение куба суммы двух слагаемых. Для этого возведем в куб выражение a + b:

(a + b)³ = (a + b)²(a + b) = (a² + 2ab + b²)(a + b) = a³ + a²b + 2a²b + 2ab² + ab² + b³ = a³ + 3a²b + 3ab² + b³

Получили тождество

(a + b)³ = a³ + 3a²b + 3ab² + b³

которое называют формулой куба суммы.

Пример. Вычислите 101³

Решение.

101³ = (100 + 1)³ = 100³ + 3*100²*1 + 3*100*1² + 1 = 1000000 + 30000 + 300 + 1 = 1030301

Ответ: 1030301.

Пример. Представьте в виде многочлена выражение (4p + 3k)³.

Решение. Воспользуемся формулой куба суммы:

(4p + 3k)³ = (4p)³ + 3*(4p)²*3k + 3*4p*(3k)² + (3k)³ = 64p³ + 144p²k + 108pk² + 27k³

Выведем аналогичным образом и формулу куба разности чисел:

(a — b)³ = (a — b)²(a — b) = (a² — 2ab + b²)(a — b) = a³ — a²b — 2a²b + 2ab² — b³ = a³ — 3a²b + 3ab² — b³

Итак, мы получили ещё одно тождество

(a — b)³ = a³ — 3a²b + 3ab² — b³

Пример. Вычислите 498³.

Решение. Представим число 498 как разность 500 – 2. Тогда для вычисления можно воспользоваться выражением для вычисления куба разности:

498³ = (500 — 2)³ = 500³ — 3*500²*2 + 3 * 500 * 2² — 2³ = 125000000 — 1500000 + 6000 — 8 = 123505992

Ответ: 123505992.

Сложнее получить тождества для суммы и разности кубов, ведь напрямую найти разложить на множители выражение a³ + b³ довольно тяжело. К счастью, математикам удалось подобрать новые множители.

Сначала рассмотрим выражение

a² + ab + b²

Оно отличается от квадрата суммы только одним слагаемым. Вместо 2ab стоит ab. Из-за этой схожести его называют неполным квадратом суммы.

Аналогично определяют и такое понятие, как неполный квадрат разности.

Теперь попробуем перемножить неполный квадрат суммы чисел a и b и их разность:

(a — b)(a² + ab + b²) = a³ + a²b + ab² — a²b — ab² — b³ = a³ — b³

В результате нам удалось получить формулу разности кубов:

a³ — b³ = (a — b)(a² + ab + b²)

Теперь попробуем умножить сумму двух величин на неполный квадрат разности:

(a + b)(a² — ab + b²) = a³ — a²b + ab² + a²b — ab² + b³ = a³ + b³

Получили формулу суммы кубов:

a³ + b³ = (a + b)(a² — ab + b²)

Понятно, что запомнить все эти тождества нелегко, однако их всегда можно посмотреть в любом математическом справочнике.

Пример. Разложите на множители полином 8p³ + 0,001q³.

Решение. Здесь можно воспользоваться тождеством для куба суммы:

8p³ + 0.001q³ = (2p)³ + (0.1q)³ = (2p + 0.1q)((2p)² — 2p*0.1q + (0.1q)²) = (2p + 0.1q)(4p² — 0.2pq +0.01q²)

Применять формулы с кубами для вычислений значительно сложнее, чем со вторыми степенями, однако всё же иногда они могут помочь. Пусть надо вычислить значение выражения 55³ + 45³, не используя калькулятор или компьютер. Разложим его на множители:

53³ + 45³ = (55 + 45)(55² — 55*45 + 45²) = 100(55² — 55*45 + 45²)

Далее для упрощения расчетов добавим к значению в скобке произведение 55•45 и тут же отнимем его. Это позволит сделать «дополнить» неполный квадрат разности и воспользоваться соответствующей формулой сокращенного умножения:

100(55² — 55*45 + 45²) = 100((55² — 55*45 — 55*45 + 45² + 55*45) = 100((55² — 2*55*45 + 45²) + 55*45) = 100((55 — 45)² 55*45) = 100((10)² + 55*45) = 100(100 + 55*45)

В свою очередь произведение 55•45 можно также упростить:

100(100 + 55*45) = 100(100 + (50 + 5)*(50 — 5)) = 100(100 + (50² — 5²)) = 100(100 + 2500 — 25) = 100*2575 = 257500

Полученный результат можно проверить с помощью калькулятора:

55³ + 45³ = 257500

Треугольник Паскаля

До этого мы нашли формулы сокращенного умножения, которые позволяют возводить бином (a + b) во вторую и третью степень. Интересно, что есть быстрый способ составить подобное тождество для возведения выражения (a + b) в любую натуральную степень. Для этого используется так называемый треугольник Паскаля. Справедливости ради сразу отметим, что Блез Паскаль описал его лишь в 1653 году, в то время как упоминание о таком треугольнике содержится в трудах китайца Чжу Шицзе (1303 г.), перса Омара Хайяма (1100 г.) и индийца Халаюдхи (Xвек).

Выглядит треугольник Паскаля так:

На вершине (его условно считают нулевым, а не первым уровнем) стоит число 1. На следующем (первом) уровне стоит уже две единицы. Изучим уровень ниже. Здесь уже три числа. По краям снова единицы, а в центре двойка. Обратите внимание, что двойка равна сумме тех 2 цифр, которые расположены над ней (1 и 1).

На следующем уровне уже 4 числа. Снова по краям единицы, а в других ячейках стоят такие числа, что они равны сумме двух чисел над собой (2 + 1 = 3).

По такому же принципу построен весь треугольник. Количество уровней в нем не ограничено, хотя на рисунке последним показан 10-ый уровень.

Итак, при построении треугольника Паскаля используются следующие правила:

• на вершине стоит одна единица
• на каждом следующем уровне находится на одно число больше, чем на предыдущем;
• по бокам на каждом уровне стоят единицы;
• на всех остальных позициях стоят числа, которые равны сумме двух расположенных над ними чисел.

Какое же отношение треугольник Паскаля имеет к формулам сокращенного умножения? Запишем тождества для возведения в различные степени бинома a + b, а рядом – числа из соответствующего уровня треугольника (их называют биноминальными коэффициентами):

• (a + b)¹ = 1a + 1b, биноминальные коэффициенты 1 и 1;
• (a + b)² = 1a²+ 2ab+ 1b², биноминальные коэффициенты 1, 2, 1;
• (a + b)³ = 1a³ + 3a²b +3ab² + 1b³, коэффициенты равны 1, 3, 3, 1;

Можно заметить, что числа в треугольнике совпадают с теми коэффициентами, которые есть в формуле сокращенного умножения:

И такое соответствие будет верно для любой формулы вида (a + b)ⁿ, где n– натуральное число, хотя доказательство этого факта выходит за рамки 7 класса. Так, формула для возведения в 6-ую степень будет выглядеть так:

(a + b)⁶ = a⁶ + 6a⁵b + 15a⁴b² + 20a³b³ + 15a²b⁴ + 6ab⁵ + b⁶

Первым слагаемым идет a⁶, а далее слагаемое с буквенной частью a⁵b. У каждого следующего слагаемого числовой множитель берется из треугольника Паскаля, а в буквенной части у переменной a степень уменьшается, в то время как у b – увеличивается:

a⁶

6a⁵b

15a⁴b²

20a³b³

15a²b⁴

6ab⁵

b²

При этом степень каждого одночлена равна 6.

У треугольника Паскаля есть много других важных свойств, из-за которых он используется в иных разделах математики, в частности, в комбинаторике (она изучает количество способов, которыми можно расставить в определенном порядке предметы)и теории вероятностей. Например, можно заметить, что сумма всех чисел в строке n равна 2ⁿ:

1 + 2 + 1 = 4 = 2²

1 + 3 + 3 + 1 = 8 = 2³

1 + 4 + 6 + 4 + 1 = 16 = 2⁴

Более подробно использование треугольника Паскаля будет рассмотрено в старших классах.

Формулы сокращенного умножения

У истоков создания этого проекта лежит небольшая формула, которую я заметил в этом году. Если говорить точнее, это закономерность между числами. Я долго интересовался тем, что это за формула, но разные люди предполагали абсолютно разные варианты. Поскольку, безусловно, эта формула связана с квадратами чисел и я не знаю, придумал ли ее кто-то до меня, я решил сделать презентацию, в которой помимо этой закономерности рассказывалось о какой-нибудь интересной теме. Так я решил создать этот научно-исследовательский проект.

Квадрат суммы

Начнем с азов. Наверняка, каждый семиклассник (не говоря уже и о более старших школьниках) знает эту формулу. Но все же для закрепления материала стоит проверить эти знания.

Что читается, как >.

Квадрат разности

А вот на этой теме уже начинают встречаться сложности. К сожалению, не все ученики помнят эту формулу, некоторые путаются, но я надеюсь, что никто из нашего класса не ошибется ни в записи, ни в формулировке.

А читается эта формула: >.

Немного из истории. Вот мы и вспомнили первые две формулы сокращенного умножения. Как оказалось, ничего страшного в этом нет!

А задавались ли вы когда-нибудь вопросом, кто же все-таки придумал эти две формулы: квадрат суммы и квадрат разности? Некоторые источники говорят, что это был древнегреческий математик Евклид. Это было действительно уникальное открытие, поскольку мы знаем, что он жил еще в III веке до нашей эры.

Разность квадратов

Вот мы и дошли до последней формулы, связанной с квадратами чисел. В следующем слайде я докажу, почему она последняя. А пока что попытаемся вспомнить разность квадратов.

При этом следует помнить, что множители можно менять местами.

Разность квадратов двух чисел равна произведению суммы и разности этих чисел.

Сумма квадратов

Но в школьном курсе не дается понятие этой формулы сокращенного умножения, потому что ее попросту не существует. А сейчас мы рассмотрим, почему.

• Квадрат суммы и квадрат разности можно разложить не только по формуле, данной ранее. Их можно представить таким видом: (x+y)²=(x+y)(x+y) и (x-y)²=(x-y)(x-y).
• На основании того, что первые три формулы сокращенного умножения можно представить в виде произведения из двух многочленов, можно утверждать, что и сумму квадратов можно представить, как произведение из двух многочленов.
• Но все возможные комбинации уже использованы. Квадрат суммы — это произведение сумм этих чисел, квадрат разности — произведение разностей этих чисел, а разность квадратов — произведение суммы и разности. Значит, сумму квадратов нельзя представить в виде формулы сокращенного умножения.

Неполный квадрат

Для дальнейшего повторения формул сокращенного умножения мы должны также вспомнить еще один термин. Мы рассмотрели понятия квадрат суммы и квадрат разности ((x+y)²=x²+2xy+y² и (x-y)²=x²-2xy+y²). Так что же тогда такое неполный квадрат? Нам понадобятся неполный квадрат суммы и неполный квадрат разности. Неполный квадрат суммы — это x²+xy+y² (сумма квадрата первого числа, произведения первого числа на второе и второго числа), а неполный квадрат разности — это x²-xy+y² (квадрат первого числа минус произведение первого числа на второе плюс квадрат второго числа). Как мы видим, в обоих случаях вместо удвоенного произведения первого числа на второе появляется произведение первого числа на второе.

Сумма кубов

Вот мы и приступили к тому моменту, который, как я подозреваю, мало кто помнит. Время проверить знания.

Сумма кубов двух чисел равна произведению этих чисел и неполного квадрата их суммы.

Разность кубов

И сейчас мы вспомним еще одну, очень похожую на предыдущую, формулу.

Куб суммы

Эту формулу и следующую за ней немного сложно запомнить, но я все же надеюсь, что в нашем классе есть ученики с хорошей памятью, что мы сейчас и проверим.

Куб суммы двух чисел равен сумме квадрата первого числа, утроенного произведения квадрата первого числа на второе, утроенного произведения первого числа на квадрат второго и куба второго числа.

Куб разности

И вот наконец мы дошли до последней формулы, изучаемой в седьмом классе.

Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго числа.

Источник

Неполный квадрат разности

Неполный квадрат разности в алгебре важен в качестве составной части формулы суммы кубов. В процессе изучения формул сокращенного умножения важно научиться видеть формулы полных и неполных квадратов и различать их между собой.

Неполный квадрат разности — это сумма трех слагаемых, два из которых — квадраты некоторых выражений, а третье равно произведению этих выражений (со знаком «минус» перед ним).

В отличие от полного квадрата разности, произведение выражений не удваивается.

С помощью букв неполный квадрат разности можно записать так:

С помощью схемы — так:

Примеры неполных квадратов разности:

На практике неполный квадрат, как правило, свернут, поэтому, чтобы понять, является ли выражение неполным квадратом разности, его нужно проанализировать.

На этапе изучения новой темы есть смысл выражения подробно расписывать.

Как определить, является ли выражение неполным квадратом разности?

Признаки неполного квадрата разности

1) Выражение состоит ровно из трех слагаемых.

2) Два положительных слагаемых представляют собой квадраты некоторых выражений.

3) Третье слагаемое со знаком «минус» перед ним равно произведению этих выражений.

16x²=(4x)², 81y²=(9y)². Проверяем, равно ли третье слагаемое произведению 4x и 9y: 4x∙9y=36xy — да, равно. Следовательно, это выражение — неполный квадрат разности.

С помощью схемы это можно записать так:

100c²=(10c)², d² — уже представлен как квадрат, но 10c∙d≠20cd, поэтому выражение неполным квадратом разности не является (так как 20cd=2∙10c∙d, это выражение — полный квадрат разности).

Слагаемые могут стоять в произвольном порядке.

В некоторых случаях выражение, не являющееся неполным квадратом разности, может быть к нему приведено.

Здесь два слагаемых отрицательны, значит, неполным квадратом разности это выражение быть не может. Но если знак «минус» вынести за скобки, все знаки в скобках изменятся на противоположные:

В скобках — неполный квадрат разности.

В алгебре очень важно уметь раскладывать многочлены на множители и преобразовывать выражения (в том числе, по формуле суммы кубов, частью которой является неполный квадрат разности).

Источник

Неполный квадрат суммы

Неполный квадрат суммы в алгебре встречается в качестве составной части формулы разности кубов. Важно при преобразовании многочленов научиться видеть неполный квадрат и не путать его с полным квадратом суммы.

Неполный квадрат суммы — это сумма трех слагаемых, два из которых являются квадратами некоторых выражений, а третье равно произведению этих выражений.

У неполного квадрата суммы, в отличие от полного, произведение выражений не удваивается.

С помощью букв неполный квадрат суммы можно записать так:

С помощью схемы —

Примеры неполных квадратов —

На практике квадраты и произведение записаны в свернутом виде, поэтому, чтобы понять, является ли выражение полным либо неполным квадратом суммы, его надо проанализировать. На первых шагах изучения темы формулы имеет смысл подробно расписывать, в дальнейшем — делать это устно.

Как определить, является ли некоторое выражение неполным квадратом суммы?

Признаки неполного квадрата суммы

1) Выражение состоит ровно из трех положительных слагаемых.

2) Два слагаемых представляют собой квадраты некоторых выражений.

3) Третье слагаемое равно произведению этих двух выражений.

49y²=(7y)², 9b²=(3b)². Проверяем, равно ли третье слагаемое произведению 7y и 3b: 7y∙3b=21ab — да, равно. Значит, это выражение является неполным квадратом суммы.

С помощью схемы это можно записать так:

36m²=(6m)², 25n²=(5n)². Проверяем, равно ли третье слагаемое произведению 6m и 5n: 6m∙5n=30mn≠60mn. Значит, это выражение не является неполным квадратом суммы (60mn=2∙6m∙5n, то есть здесь есть полный квадрат суммы).

Слагаемые в выражении могут стоять в произвольном порядке (не обязательно в соответствии с формулой).

Иногда выражение, не являющееся неполным квадратом суммы, может быть к нему приведено. Например,

Здесь все три слагаемые — с «-«, то есть это выражение квадратом суммы быть не может. А что, если вынести «минус» за скобки? При этом знак каждого слагаемого в скобках изменится на противоположный:

В этом случае в скобках получили неполный квадрат суммы.

В скобках получили неполный квадрат суммы.

Умение раскладывать многочлены на множители и преобразовывать выражения, в том числе, содержащие разность кубов, в алгебре — обязательно.

Источник

Формулы сокращённого умножения

При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.

Формулы сокращённого умножения — это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.

Обратите внимание, что a и b в формулах сокращённого умножения могут быть как числами, так и выражениями.

Разложение формул сокращенного умножения

Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения.

Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:

Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:

Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

Неполный квадрат суммы

это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:

которое называется неполным квадратом суммы. Неполный квадрат суммы — это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.

Неполный квадрат разности

это квадрат разности, который также называется полным квадратом разности относительно выражения:

которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.

Источник