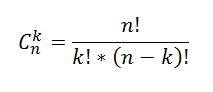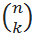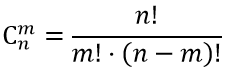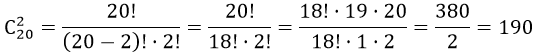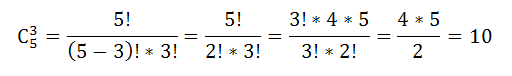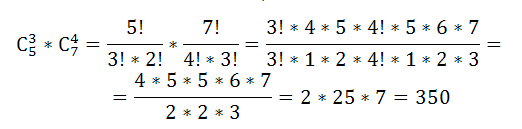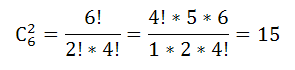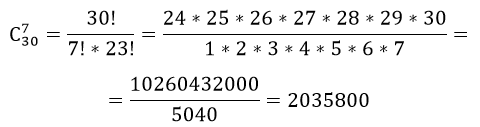Подсчитаем в MS EXCEL количество сочетаний из n элементов по k. С помощью формул выведем на лист все варианты сочетаний (английский перевод термина: Combinations without repetition).
Сочетаниями из n различных элементов по k элементов называются комбинации, которые отличаются хотя бы одним элементом. Например, ниже перечислены ВСЕ 3-х элементные сочетания, взятые из множества, состоящего из 5 элементов {1; 2; 3; 4; 5}:
(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)
Примечание
: Это статья о подсчете количества сочетаний с использованием MS EXCEL. Теоретические основы советуем прочитать в специализированном учебнике. Изучать сочетания по этой статье — плохая идея.
Отличие Сочетаний от Размещений
В отличие от
Размещений
следующие 3-х элементные комбинации (1; 2; 3); (1; 3; 2); (2; 1; 3); (2; 1; 3); (3; 2; 1); (3; 1; 2) считаются одинаковыми, и в набор
Сочетаний
включается только одна из этих комбинаций. Очевидно, что для тех же n и k число
Сочетаний
всегда меньше чем число
Размещений
(так как при размещениях порядок важен, а для сочетаний — нет), причем в k! раз.
Подсчет количества Сочетаний
Число всех
Сочетаний
из n элементов по k можно вычислить по формуле:
Например, количество 4-х элементных комбинаций из 6 чисел {1; 2; 3; 4; 5; 6} равно 15=6!/(4!(6-4)!)
Примечание
: Для
Сочетаний
из n элементов по k также используется и другая запись:
В MS EXCEL для подсчета количества комбинаций без повторов существует специальная функция ЧИСЛКОМБ() , английское название функции — COMBIN(). Для предыдущего примера формула =ЧИСЛКОМБ(6;4) , разумеется, также вернет 15. Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4) .
Очевидно, что k меньше или равно n, т.к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются). При k=n количество сочетаний всегда равно 1.
Примечание
: О Сочетаниях с повторениями (с возвращением элементов) можно прочитать в статье
Сочетания с повторениями: Комбинаторика в MS EXCEL
Вывод всех комбинаций Сочетаний
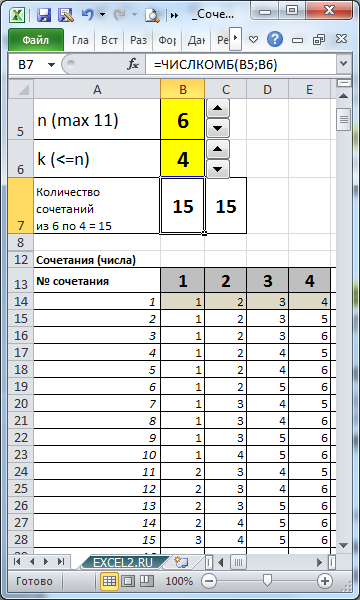
В файле примера созданы формулы для вывода всех Сочетаний для заданных n и k.
Задавая с помощью
элементов управления Счетчик
количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания.
В файле примера не забывайте увеличивать количество строк с формулами, чтобы поместились все ваши комбинации. Для этого выделите последние ячейки с формулами (сочетание №330) и скопируйте их вниз на нужно количество строк. При увеличении строк с формулами размер файла быстро растет, а скорости пересчета листа падает. Если строк 4 тысячи, то размер файла составляет около 2 Мб.
Задача
Автовоз может перевозить по 4 легковые машины. Необходимо перевезти 7 разных машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Сколькими различными способами можно заполнить первый автовоз? Конкретное место машины в автовозе не важно.
Нам нужно определить число
Сочетаний
7 машин на 4-х местах автовоза. Т.е. n=7, а k=4. Оказывается, что таких вариантов =ЧИСЛКОМБ(7;4) равно 35.
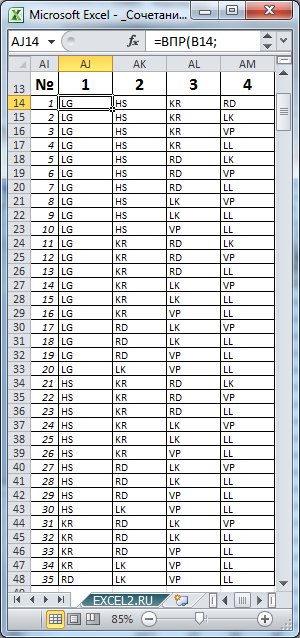
Воспользуемся файлом примера (ссылка внизу статьи) , чтобы наглядно убедиться, что мы решили задачу правильно.
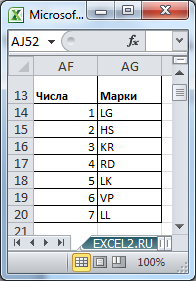
Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …
Выставив в ячейках
В5
и
В6
значения 7 и 4 соответственно, определим все варианты размещений машин в автовозе (см. столбцы AJ:AM).
Примечание
: О Перестановках можно прочитать в статье
Перестановки без повторений: Комбинаторика в MS EXCEL
, а о Размещениях в статье
Размещения без повторений: Комбинаторика в MS EXCEL
.
В комбинаторике сочетанием из N различных элементов по M называется набор M элементов, выбранных из множества N элементов. Такие наборы отличаются только вхождением в них M определенных элементов, порядок следования элементов в таком наборе не важен. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, и этим сочетания отличаются от размещений.
Сочетания без повторений
Задача: Найти все возможные сочетания без повторений из множества элементов {1,2,3} по 2.
Существуют следующие сочетания:
1: 1 2
2: 1 3
3: 2 3
Количество возможных сочетаний без повторений из N элементов по M можно определить по формуле (N≥M):
что в M! раз меньше соответствующего количества размещений без повторений (поскольку сочетания без повторений не зависят от порядка следования элементов).
Рассмотрим задачу получения всех сочетаний для чисел 1…N по M.
Реализация на С++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>
using namespace std;
bool NextSet(int *a, int n, int m)
{
int k = m;
for (int i = k — 1; i >= 0; —i)
if (a[i] < n — k + i + 1)
{
++a[i];
for (int j = i + 1; j < k; ++j)
a[j] = a[j — 1] + 1;
return true;
}
return false;
}
void Print(int *a, int n)
{
static int num = 1;
cout.width(3);
cout << num++ << «: «;
for (int i = 0; i < n; i++)
cout << a[i] << » «;
cout << endl;
}
int main()
{
int n, m, *a;
cout << «N = «;
cin >> n;
cout << «M = «;
cin >> m;
a = new int[n];
for (int i = 0; i < n; i++)
a[i] = i + 1;
Print(a, m);
if (n >= m)
{
while (NextSet(a, n, m))
Print(a, m);
}
cin.get(); cin.get();
return 0;
}
Результат выполнения
Сочетания с повторениями
Сочетаниями с повторениями называются наборы по M элементов, в которых каждый элемент множества N может участвовать несколько раз. При этом на соотношение значений M и N не накладывается никаких ограничений, а общее количество сочетаний с повторениями составляет
Примером такой задачи может служить выбор M открыток из N всеми возможными способами.
Для генерации сочетаний с повторениями воспользуемся решением для генерации размещений с повторениями, рассмотренным в этой статье.
Реализация на С++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
using namespace std;
bool NextSet(int *a, int n, int m)
{
int j = m — 1;
while (a[j] == n && j >= 0) j—;
if (j < 0) return false;
if (a[j] >= n)
j—;
a[j]++;
if (j == m — 1) return true;
for (int k = j + 1; k < m; k++)
a[k] = a[j];
return true;
}
void Print(int *a, int n)
{
static int num = 1;
cout.width(3);
cout << num++ << «: «;
for (int i = 0; i < n; i++)
cout << a[i] << » «;
cout << endl;
}
int main()
{
int n, m, *a;
cout << «N = «;
cin >> n;
cout << «M = «;
cin >> m;
int h = n > m ? n : m; // размер массива а выбирается как max(n,m)
a = new int[h];
for (int i = 0; i < h; i++)
a[i] = 1;
Print(a, m);
while (NextSet(a, n, m))
Print(a, m);
cin.get(); cin.get();
return 0;
}
Результат работы приведенного выше алгоритма:
Назад: Алгоритмизация
Сочетания
- Сочетания без повторений
- Сочетания с повторениями
- Биномиальные коэффициенты и их свойства
- Примеры
п.1. Сочетания без повторений
Сочетаниe без повторений – это неупорядоченная ⟨n,k⟩-выборка без повторений, k ≤ n. Общее количество сочетаний без повторений: $$ mathrm{ C_n^k=frac{n!}{(n-k)!k!} } $$
Внимание! Главным отличием сочетаний от размещений является неупорядоченность выборок. Если для размещения выборки (a,b)≠(b,a) не равны, то для сочетания (a,b)=(b,a) – одна и та же выборка.
Сочетания используются тогда, когда порядок выборки не важен.
Например:
Из 10 программистов нужно отобрать 4 для участия в проекте. Сколькими способами это можно сделать?
$$mathrm{ n = 10, k=4 }$$ В данном случае, порядок отбора не важен (выборка неупорядоченная); каждый кандидат может войти только один раз в выборку (выборка без повторений). Поэтому рассматриваем неупорядоченные ⟨10,4⟩ –выборки без повторений. Количество способов отбора равно: $$mathrm{ C_{10}^4=frac{10!}{6! 4!}=frac{10cdot 9cdot 8cdot 7}{1cdot 2cdot 3cdot 4}=210 }$$ Ответ: 210.
п.2. Сочетания с повторениями
Сочетаниe с повторениями – это неупорядоченная ⟨n,k⟩-выборка с повторениями. Общее количество сочетаний с повторениями: $$ mathrm{ overline{C}_n^k=frac{(n+k-1)!}{(n-1)k!} } $$
$$ mathrm{ overline{C}_n^k=C_{n+k-1}{k} } $$
Например:
Нужно отобрать 4 программистов для участия в проекте. Многочисленных претендентов можно разделить на две категории: желающих работать удаленно и предпочитающих работу в офисе. Сколько всего комбинаций из любителей офиса и удалёнки может оказаться в выбранной четвёрке? $$mathrm{ n = 2, k=4 }$$ Порядок отбора не важен; кандидатов из каждой категории может быть несколько или ни одного. Поэтому рассматриваем неупорядоченные ⟨2,4⟩ –выборки с повторениями: $$ mathrm{ overline{C}_2^4=frac{(2+4-1)!}{(2-1)4!}=frac{5!}{4!}=5 } $$ Всего – 5 комбинаций: OOOO,OOOD,OODD,ODDD,DDDD
где O – любитель офиса; D – любитель удалёнки. Напоминаем, что порядок не важен – важен только состав группы.
Ответ: 5.
п.3. Биномиальные коэффициенты и их свойства
Подробно о биноме – см. §28 справочника для 7 класса.
Для n-й степени бинома справедливо выражение: $$ mathrm{ (apm b)^n=a^n+C_n^1a^{n-1}bpm C_n^2a^{n-2}b^2+…+C_n^{n-1}b^n } $$ где (mathrm{C_n^k}) – биномиальные коэффициенты, к оторые одновременно являются количествами сочетаний без повторений из n по k: $$ mathrm{ C_n^k=frac{n!}{(n-k)!k!} } $$ Таким образом, биномиальные коэффициенты можно определять как с помощью треугольника Паскаля, так и с помощью данной формулы.
Заметим, что в литературе также часто встречается обозначение (mathrm{left(_k^nright)}) для биномиальных коэффициентов (mathrm{left(C_n^kright)}).
Свойства биномиальных коэффициентов
Свойство симметрии
$$mathrm{ C_n^k=C_n^{n-k} }$$
Свойство Паскаля
$$mathrm{ C_n^k=C_{n-1}^{k-1}+C_{n-1}^k }$$
Замена индексов
$$mathrm{ C_n^mC_m^{n-k}=C_{n}^{k}C_{k}^{n-m} }$$
Вынесение за скобки
$$mathrm{ C_n^k=frac{n}{k}C_{n-1}^{k-1} }$$
Рекуррентные формулы
begin{gather*}mathrm{ C_n^k=frac{n-k+1}{k}C_{n}^{k-1} }\ mathrm{ C_n^k=frac{n}{n-k}C_{n-1}^k } end{gather*}
Свойство суммы
$$mathrm{ C_n^0+C_n^1+C_n^2+…+ C_n^n=sum_{k=0}^nC_n^k=2^n }$$
Свойство разности
$$mathrm{ C_n^0-C_n^1+C_n^2-…+(-1)^nC_n^n=sum_{k=0}^n(-1)^kC_n^k=0 }$$
Свойства максимума
Если n – четное, то максимальное значение (mathrm{C_n^k}) имеет при (mathrm{k=frac{n}{2}}).
Если n – нечетное, то максимальное значение имеют два коэффициента (mathrm{C_n^k}), при (mathrm{k=frac{n-1}{2}}) и (mathrm{k=frac{n+1}{2}})
Свёртка Вандермонда
$$mathrm{ sum_{r=0}^kC_n^rC_m^{k-r}=C_{n+m}^k }$$
Сумма квадратов
$$mathrm{ sum_{k=0}^n(C_n^k)^2=C_{2n}^n }$$
Взвешенное суммирование
begin{gather*} mathrm{ sum_{k=0}^nnC_n^k=n2^{n-1} }\ mathrm{ sum_{k=0}^nn^2C_n^k=n(n+1)2^{n-2} } end{gather*}
Связь с числами Фибоначчи
$$mathrm{ C_n^0+C_{n-1}^1+…+C_{n-k}^{k}+…+C_{0}^{n}=F_{n+1} }$$
п.4. Примеры
Пример 1. На столе лежит 10 яблок и 5 груш.
1) Сколькими способами можно выбрать 7 фруктов?
2) Сколькими способами можно выбрать 7 фруктов, чтобы среди них было 3 груши?
1) Всего у нас n = 10 + 5 = 15 фруктов. Нужно выбрать k = 7 фруктов.
Порядок выбора не важен, т.е. выборка неупорядоченная. Находим: $$ mathrm{ C_n^k=C_{15}^7=frac{15cdot 14cdot 13cdot 12cdot 11cdot 10cdot 9}{1cdot 2cdot 3cdot 4cdot 5cdot 6cdot 7}=6435 } $$ Существует 6435 способов выбрать 7 фруктов из 15.
2) Выбираем 4 яблока из 10 и 3 груши из 5.
Для яблок: $$ mathrm{ C_{10}^4=frac{10cdot 9cdot 8cdot 7}{1cdot 2cdot 3cdot 4}=210 } $$ Для груш: $$ mathrm{ C_3^5=C_{5}^2=frac{5cdot 4}{1cdot 2}=10 } $$ По правилу произведения, общее количество способов выбрать 4 яблока и 3 груши: $$ mathrm{ C_{10}^3cdot C_{5}^3=210cdot 10=2100 } $$ Ответ: 1) 6435; 2) 2100.
Пример 2. В кондитерском магазине продаётся 4 вида пирожных. Сколькими способами можно купить 7 пирожных? $$ mathrm{ n=4, k=7 } $$ Порядок выбора пирожных неважен – выборка неупорядоченная; пирожные одного вида могут повторяться. Значит, находим количество сочетаний с повторениями: $$ mathrm{ overline{C}_4^7=C_{7+4-1}^7=C_{10}^7=C_{10}^3=frac{10cdot 9cdot 8}{1cdot 2cdot 3}=120 } $$ Ответ: 120
Пример 3. Рота состоит из 3 офицеров, 6 сержантов и 15 рядовых. Сколькими способами можно выбрать из них отряд, состоящий из 1 офицера, 2 сержантов и 5 рядовых?
По всем трём множествам делаем неупорядоченную выборку (т.е., сочетания) без повторений.
Выбираем офицеров: (mathrm{C_3^1=frac31=3})
Выбираем сержантов: (mathrm{C_6^2=frac{6cdot 5}{1cdot 2}=15})
Выбираем рядовых: (mathrm{C_{15}^6=frac{15cdot 14cdot 13cdot 12cdot 11}{1cdot 2cdot 3cdot 4cdot 5}=3003})
По правилу произведения, отряд можно выбрать:
(mathrm{3cdot 15cdot 3003=135135}) способами.
Ответ: 135135.
Пример 4. Найдите сумму
a) (mathrm{C_6^1+C_6^2+C_6^3+C_6^4+C_6^5+C_6^6})
По свойству суммы (mathrm{sum_{k=0}^6C_6^k=2^6}). Получаем: $$ mathrm{ C_6^1+C_6^2+C_6^3+C_6^4+C_6^5+C_6^6=sum_{k=0}^6C_6^k-C_6^0=2^6-1=64-1=63 } $$
б) (mathrm{C_n^1+6C_n^2+6C_n^3}) $$ mathrm{ C_n^1=n, C_n^2=frac{n(n-1)}{2}, C_n^3=frac{n(n-1)(n-2)}{6} } $$ Получаем begin{gather*} mathrm{ C_n^1+6C_n^2+6C_n^3=n+6cdot frac{n(n-1)}{2}+6cdot frac{n(n-1)(n-2)}{6}=}\ mathrm{ =n(1+3(n-1)+(n-1)(n-2))=n(3n-2+n^2-3n+2)=n^3 } end{gather*} Ответ: а) 63; б) n3.
Пример 5. Рассчитайте все (mathrm{C_{10}^k}) по рекуррентной формуле (mathrm{C_{n}^k=frac{n-k+1}{k}C_n^{k-1}}).
Постройте график (mathrm{C_{10}^k(k)}). Сделайте выводы.
Начальное значение (mathrm{C_{10}^0=1}).
|
0 $$mathrm{ C_{10}^0=1 }$$ 1 $$mathrm{ C_{10}^1=frac{10-1+1}{1}C_{10}^0=10 }$$ 2 $$mathrm{ C_{10}^2=frac{10-2+1}{2}C_{10}^1=45 }$$ 3 $$mathrm{ C_{10}^3=frac{10-3+1}{3}C_{10}^2=120 }$$ 4 $$mathrm{ C_{10}^4=frac{10-4+1}{4}C_{10}^3=210 }$$ 5 $$mathrm{ C_{10}^4=frac{10-5+1}{5}C_{10}^4=252 }$$ 6 $$mathrm{ C_{10}^6=frac{10-6+1}{6}C_{10}^5=210 }$$ 7 $$mathrm{ C_{10}^7=frac{10-7+1}{7}C_{10}^6=120 }$$ 8 $$mathrm{ C_{10}^6=frac{10-8+1}{8}C_{10}^7=45 }$$ 9 $$mathrm{ C_{10}^9=frac{10-9+1}{9}C_{10}^8=10 }$$ 10 $$mathrm{ C_{10}^{10}=frac{10-10+1}{10}C_{10}^9=1 }$$ |
 |
На графике видно симметрию коэффициентов: (mathrm{C_{10}^k=C_{10}^{10-k}}).
Т.к. n = 10 – чётное, максимальный коэффициент при (mathrm{k=frac{n}{2}=5, C_{10}^5=252}).
Можем также проверить свойство суммы: (mathrm{sum_{k=0}^{10}C_{10}^k=1024=2^{10}}).
Рейтинг пользователей
Сочетанием без повторений называют комбинации, составленные из n элементов по m элементам, которые отличаются друг от друга хотя бы одним элементом.
Обозначение: $С_n^m$
Допустим, имеется три буквы А, В и С.
Составим всевозможные комбинации только из двух букв, которые отличаются друг от друга хотя бы одним элементом: АВ, АС, ВС.
При подсчете числа сочетаний элементов — порядок не важен.
Запишем формулу сочетания
Пример 1
В классе 20 учащихся. Сколькими способами можно выделить двух человек для дежурства? Так как каждая группа учащихся в 2 человека должна отличаться хотя бы одним из учащихся. Отсюда, применим формулу комбинаторики — сочетание, имеем
Пример 2
Пусть имеется множество, содержащие 4 буквы: {А,В,С,D}.
Записать все возможные сочетания из указанных букв по три.
Решение
По формуле сочетания имеем,
$C_4^3 =frac{{4!}}{{left( {4 — 3} right)!cdot3!}} = frac{{4!}}{{3!}} = frac{{1cdot2cdot3cdot4}}{{1cdot2cdot3}} = 4$
Пример 3
В ящике 15 деталей, среди которых 6 бракованных. Наугад выбирается комплект из 5 деталей. Сколькими способами можно составить такой комплект, в котором 2 детали бракованные?
Решение
$C_{6}^2$ — количество способов выбора двух бракованных деталей из шести
$C_{9}^3$ — количество способов выбора трех исправных деталей из девяти
Тогда количество комбинаций по правилу умножения будет
$C_{6}^2·C_{9}^3=frac{{6!}}{{(6-2)!2!}}·frac{{9!}}{{(9-3)!3!}}=15·84=1260$
Пример 4
Сколькими способами можно распределить три путевки в один санаторий между пятью желающими?
Решение
Так как путевки предоставлены в один санаторий, то варианты распределения отличаются друг от друга хотя бы одним желающим. Поэтому число способов распределения равно
Пример 5
В научном конкурсе участвует 12 человек, из них 5 женщин и 7 мужчин. Сколькими способами можно сформировать группу из 7 человек, чтобы в ней было 3 женщины?
Решение
Из пяти женщин необходимо выбрать по три. Следователь, число таких способов отбора равно $С_5^3$
Число способов отбора мужчин, четырех из семи равно $С_7^4$
По формуле комбинаторики – сочетания, группу можно сформировать способами:
Пример 6
Сколькими способами можно составить суточный наряд по университету из одного офицера, двух сержантов и семи курсантов, если имеется 3 офицера, 6 сержантов и 30 курсантов?
Решение
Число способов выбора офицера: $С_3^1$
сержантов $С_6^2$
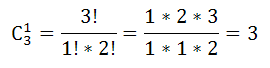
по аналогии, число комбинаций выбора курсантов, получаем $С_30^7$
Итак, получаем число способов составления суточного наряда
$$C_3^1cdot{C_6^2}cdot{C_{30}^7}=3cdot15cdot2035800=91611000$$
Есть массив:
array(
0 => 'один',
1 => 'два',
3 => 'три',
4 => 'четыре',
5 => 'пять',
6 => 'шесть'
);
Как можно найти все возможные неповторяющиеся комбинации из этих слов?
Т.е. например нужно получить подобное:
array(
0 => array('один', 'два', 'три', 'четыре', 'пять', 'шесть'),
1 => array('один', 'два', 'три', 'четыре', 'пять'),
3 => array('один', 'два', 'три', 'четыре'),
4 => array('один', 'два', 'три'),
5 => array('один', 'два'),
6 => array('один'),
7 => array('один', 'три', 'четыре', 'пять', 'шесть'),
8 => array('два', 'три', 'четыре', 'пять', 'шесть'),
9 => array('четыре', 'пять', 'шесть'),
//и т.д.
);Голову сломал уже всю. Не могу сообразить.