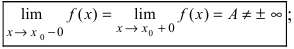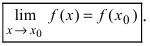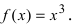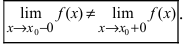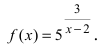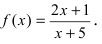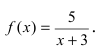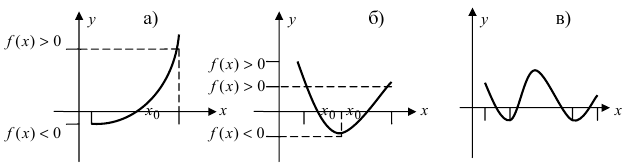Непрерывность функции и точки разрыва
- Приращение аргумента и приращение функции
- Непрерывность функции в точке
- Непрерывность функции на промежутке
- Односторонние пределы
- Классификация точек разрыва
- Точки разрыва первого рода
- Точки разрыва второго рода
- Алгоритм исследования функции на непрерывность
- Примеры
п.1. Приращение аргумента и приращение функции
Приращением аргумента называют разность $$ triangle x= x-x_0 $$ где x — произвольное число, которое мало отличается от начальной точки (x_0). Приращение аргумента может быть как положительным, так и отрицательным.
Приращением функции называют соответствующую разность $$ triangle y=f(x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.
Например:
 |
Пусть (y=3x-1) (x_0=1, x=1,1 ) Тогда begin{gather*} triangle x=x-x_0=0,1\ triangle y=(3x-1)-(3x_0-1)=\ =3(x-x_0 )=3triangle x=0,3 end{gather*} В данном случае приращение функции всегда в 3 три раза больше приращения аргумента. |
п.2. Непрерывность функции в точке и на промежутке
Функция (y=f(x)) непрерывна в точке (x_0), если в этой точке малому приращению аргумента (triangle x=x-x_0) соответствует малое приращение функции (triangle y=f(x)-f(x_0)): $$ lim_{triangle xrightarrow 0}triangle y=lim_{xrightarrow x_0}triangle y=0 $$
На «языке ε-δ» определение непрерывности будет следующим:
Функция (y=f(x)) непрерывна в точке (x_0), если для любого (varepsilongt 0) существует такое (delta(varepsilon)gt 0), что для любого (x, |x-x_0|ltdelta) выполняется (|f(x)-f(x_0)|ltvarepsilon:) $$ forall varepsilongt 0 existsdelta=delta(varepsilon)gt 0: forall x, |x-x_0|ltdeltaRightarrow |f(x)-a|ltvarepsilon $$
ε-δ определение непрерывности похоже на ε-δ определение предела функции, с той разницей, что модуль (|x-x_0|) может быть равен 0 для непрерывной функции, т.е. сама точка (x_0) входит в δ-окрестность.
Проанализируем предел приращения функции: begin{gather*} lim_{triangle xrightarrow 0}triangle y= lim_{triangle xrightarrow 0}left(f(x)-f(x_0)right)= lim_{triangle xrightarrow 0}f(x)-lim_{triangle xrightarrow 0}f(x_0)=\ =lim_{triangle xrightarrow 0}f(x)-f(x_0) end{gather*} т.к. (f(x_0)) — величина постоянная и от (triangle x) не зависит.
Для непрерывной функции: $$ lim_{triangle xrightarrow 0}triangle y =0 Leftrightarrow lim_{triangle xrightarrow 0}f(x)-f(x_0)=0Leftrightarrow lim_{triangle xrightarrow 0}f(x)=f(x_0) $$ Учитывая, что (triangle xrightarrow 0Leftrightarrow x-x_0rightarrow 0Leftrightarrow xrightarrow x_0)
получаем (lim{xrightarrow x_0}f(x)=f(x_0).)
Функция (y=f(x)) непрерывна в точке (x_0), если существует предел функции в этой точке и он равен значению функции в точке: $$ lim{xrightarrow x_0}f(x)=f(x_0) $$
Все три представленных определения непрерывности функции в точке эквивалентны.
Существуют и другие эквивалентные определения. Мы дадим ещё одно из них дальше, в этом же параграфе.
п.3. Непрерывность функции на промежутке
Промежуток – это интервал, отрезок, луч и т.п. (см. §16 справочника для 8 класса).
Функция (y=f(x)) непрерывна на промежутке, если она непрерывна в каждой точке этого промежутка.
График непрерывной функции – это непрерывная линия.
Кроме непрерывности, эта линия еще и «плавная», без «заломов».
При наличии заломов функция называется кусочно-непрерывной.
п.4. Односторонние пределы
Односторонний предел – это предел числовой функции при приближении к предельной точке с определенной стороны (слева или справа).
Обозначение односторонних пределов: begin{gather*} lim_{xrightarrow x_0 -0}f(x)=a — text{левый предел}\ lim_{xrightarrow x_0 +0}f(x)=b — text{правый предел} end{gather*}
Рассмотрим гиперболу (y=frac{1}{x-2}).
 |
У этой гиперболы две асимптоты (y=0) и (x=2). Точка (x_0=2) не входит в область определения. Если мы будем приближаться к (x_0=2) слева, начав, например с 1,5, мы будем постепенно опускаться по ветке гиперболы на минус бесконечность. Т.е., левый предел: $$ lim_{xrightarrow 2-0}frac{1}{x-2}=-infty $$ |
Если же мы будем приближаться к (x_0=2) справа, начав, например с 2,5, мы будем постепенно подниматься по ветке гиперболы на плюс бесконечность. Т.е., правый предел: $$ lim_{xrightarrow 2+0}frac{1}{x-2}=+infty $$ Левый и правый пределы в точке (x_0=2) для данной гиперболы не равны: $$ lim_{xrightarrow 2-0}frac{1}{x-2} ne lim_{xrightarrow 2+0}frac{1}{x-2} $$
Теперь рассмотрим параболу (y=x^2-2)
Областью определения параболы является вся числовая прямая (xinmathbb{R})
 |
В этом случае, если приближаться к (x_0=2) слева, мы получаем: $$ lim_{xrightarrow 2-0}(x^2-2)=2 $$ И если приближаться (x_0=2) справа, мы тоже получаем: $$ lim_{xrightarrow 2+0}(x^2-2)=2 $$ Левый и правый пределы равны: $$ lim_{xrightarrow 2-0}(x^2-2) =lim_{xrightarrow 2+0}(x^2-2) $$ |
Функция (y=f(x)) непрерывна в точке (x_0), если одновременно выполняются следующие три условия:
1) точка (x_0) принадлежит области определения функции (xin D);
2) левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ 3) предел функции в точке (x_0) равен значению функции в этой точке: $$ lim_{xrightarrow x_0}f(x)=f(x_0) $$
Это еще одно определение непрерывности, которым удобно пользоваться на практике.
п.5. Классификация точек разрыва
Точка (x_0) будет точкой разрыва для функции (y=f(x)), если выполняется хотя бы одно из условий:
1) точка (x_0) не принадлежит области определения функции (xnotin D);
2) левый и правый пределы в точке (x_0) не равны или бесконечны: $$ lim_{xrightarrow x_0 -0}f(x) nelim_{xrightarrow x_0 +0}f(x) text{или} lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=pminfty $$ 3) предел функции в точке (x_0) не совпадает со значением функции в этой точке: $$ lim_{xrightarrow x_0}f(x)ne f(x_0) $$
| Точки разрыва | 1-го рода Односторонние пределы существуют и конечны |
Устранимые Односторонние пределы равны между собой, но не равны (f(x_0)) |
| Неустранимые (скачок) Односторонние пределы не равны между собой |
||
| 2-го рода Хотя бы один из односторонних пределов бесконечен или не существует |
п.6. Точки разрыва первого рода
Устранимые точки разрыва 1-го рода
Левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x)=lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ НО:
либо точка (x_0) НЕ принадлежит области определения функции (xnotin D);
либо предел НЕ равен значению функции в точке (x_0): (lim_{xrightarrow x_0}f(x)ne f(x_0))
Например:
 |
(y=frac{x^2-4}{x-2}, x_0=2) Эта функция эквивалентна системе $$ y=frac{x^2-4}{x-2} Leftrightarrow begin{cases} y=x+2\ xne 2 end{cases} $$ При этом (lim_{xrightarrow 2-0}(x+2)=lim_{xrightarrow 2+0}(x+2)=4) В точке (x_0=2notin D) функция имеет устранимый разрыв. |
Разрыв можно устранить (функцию можно «склеить»), отдельно задав «гладкое» значение в особой точке: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} $$ В таком случае система станет эквивалентна всей прямой, т.е. станет непрерывной функцией: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} Leftrightarrow y=x+2 $$
Неустранимые точки разрыва 2-го рода (скачок)
Левый и правый пределы в точке (x_0) конечны, но не равны: $$ begin{cases} lim_{xrightarrow x_0 -0}f(x)=aneinfty\ lim_{xrightarrow x_0 +0}f(x)=bneinfty\ ane b end{cases} $$ Такой разрыв также называют скачком.
Величина скачка рассчитывается по формуле: $$ triangle y=lim_{xrightarrow x_0 +0}f(x)- lim_{xrightarrow x_0 -0}f(x)=b-a $$
Например:
 |
(y= begin{cases} x+1, xlt 2\ 3-x^2, xgeq 2 end{cases} , x_0=2) Односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}f(x)= lim_{xrightarrow 2-0}(x+1)=3\ lim_{xrightarrow 2+0}f(x)= lim_{xrightarrow 2+0}(3-x^2)=-1 end{gather*} Пределы не равны, но конечны. Функция в точке (x_0=2) делает скачок вниз. Величина скачка: $$ triangle y=-1-3=-4 $$ |
п.7. Точки разрыва второго рода
В точках разрыва 2-го рода хотя бы один из односторонних пределов бесконечен или не существует.
Например:
 |
(y=e^frac1x, x_0=0)
(x_0=0ne D) — точка не входит в ОДЗ Точка (x_0=0) – точка разрыва второго рода. |
На практике, при моделировании реальных процессов, разрывы 2-го рода в функциональных зависимостях встречаются довольно часто. Их положено заботливо анализировать и тщательно обходить, выбирая рабочие участки характеристических кривых, – чтобы «система не пошла в разнос».
п.8. Алгоритм исследования функции на непрерывность
На входе: функция (y=f(x))
Шаг 1. Найти ОДЗ функции, определить точки и промежутки, не принадлежащие ОДЗ.
Шаг 2. Составить множество точек, в которое входят точки и границы промежутков, не принадлежащие ОДЗ, а также – для кусочно-непрерывных функций – точки сшивания. Полученное множество состоит из точек, подозрительных на разрыв.
Шаг 3. Исследовать каждую из точек, подозрительных на разрыв, с помощью односторонних пределов. Если разрыв обнаружен, определить тип разрыва.
На выходе: список точек разрыва и тип разрыва для каждой точки.
п.9. Примеры
Пример 1. Исследуйте функцию на непрерывность:
a) ( y=frac{x+3}{x-1} )
ОДЗ: (x-1ne 0Rightarrow xne 1)
(x_0=1notin D) — точка не входит в ОДЗ, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 1-0}frac{x+3}{x-1}=frac{1-0+3}{1-0-1}=frac{4}{-0}=-infty\ lim_{xrightarrow 1+0}frac{x+3}{x-1}=frac{1+0+3}{1+0-1}=frac{4}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_0=1) — точка разрыва 2-го рода.
б) ( y=frac{x}{sqrt{x+2}-2} )
ОДЗ: ( begin{cases} x+2geq 0\ sqrt{x+2}-2ne 0 end{cases} Rightarrow begin{cases} xgeq -2\ sqrt{x+2}ne 2 end{cases} Rightarrow begin{cases} xgeq -2\ xne 2 end{cases} )
(x_0=-2) — левая граница ОДЗ
(x_1=2notin D)- точка не входит в ОДЗ
Точки (x_0) и (x_1) — подозрительные на разрыв
Исследуем (x_0=-2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} — text{предел не существует}\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{-2+0}{sqrt{-2+0+2}-2}=frac{-2}{-2}=1 end{gather*} Один из односторонних пределов не существует.
Точка (x_0=-2) — точка разрыва 2-го рода.
Исследуем (x_1=2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} =frac{2-0}{sqrt{2-0+2}-2}=frac{2}{-0}=-infty\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{2+0}{sqrt{2+0+2}-2}=frac{2}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_1=2) — точка разрыва 2-го рода.
в) ( y=frac{tgx}{3x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{tgx}{3x}=frac13lim_{xrightarrow -0}frac{tgx}{x}=frac13cdot 1=frac13\ lim_{xrightarrow +0}frac{tgx}{3x}=frac13lim_{xrightarrow +0}frac{tgx}{x}=frac13cdot 1=frac13 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) — точка разрыва 1-го рода, устранимый разрыв.
г) ( y= begin{cases} x+1, xlt 3\ x^2+3, xgeq 3 end{cases} )
ОДЗ: (xinmathbb{R})
(x_0=3)- точка сшивания, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 3-0}y=lim_{xrightarrow 3-0}(x+1)=3+1=4\ lim_{xrightarrow 3+0}y=lim_{xrightarrow 3+0}(x^2+3)=3^2+3=12 end{gather*} Односторонние пределы конечны, но неравны.
Точка (x_0=3) — точка разрыва 1-го рода, неустранимый разрыв (скачок).
Величина скачка: (lim_{xrightarrow 3+0}y-lim_{xrightarrow 3-0}y=12-4=8)
Пример 2. Доопределите функцию в точке разрыва так, чтобы она стала непрерывной в этой точке:
a) ( y=frac{2x^3-x^2}{7x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{2x^3-x^2}{7x}=frac{x^2(2x-1)}{7x}=frac{x(2x-1)}{7}) $$ y=frac{2x^3-x^2}{7x}Leftrightarrow y= begin{cases} frac{x(2x-1)}{7}\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{x(2x-1)}{7}=0, lim_{xrightarrow +0}frac{x(2x-1)}{7}=0 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) — точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=0).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{2x^3-x^2}{7x}, xne 0\ 0, x=0 end{cases} $$ б) ( y=frac{1-cos4x}{x^2} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{1-cos4x}{x^2}=frac{2sin^2 2x}{x^2}=frac{2sin^2 2x}{frac{(2x)^2}{4}}=8left(frac{sin2x}{2x}right)^2) $$ y=frac{1-cos4x}{x^2}Leftrightarrow y= begin{cases} 8left(frac{sin2x}{2x}right)^2\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8, lim_{xrightarrow +0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) — точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=8).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{1-cos4x}{x^2}, xne 0\ 8, x=0 end{cases} $$

|
БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
ст. преподавателя, к. физ.-мат. н. Поддубной О.H. |
го рода. Это – устранимая точка разрыва, т.к. возможно доопределить функцию
|
f(x)= |
sin x |
: |
||||
|
x |
||||||
|
sin x |
, |
при x ≠ 0 |
||||
|
x |
, которая является непрерывной при любом x . |
|||||
|
g(x) = |
||||||
|
при |
x = 0 |
|||||
|
1, |
|
График этой функции: |
|||
|
1 |
|||
|
0 |
.8 |
||
|
0 |
.6 |
||
|
0 |
.4 |
||
|
0 |
.2 |
||
|
-20 |
-10 |
10 |
20 |
|
-0.2 |
Точка х0 называется точкой разрыва 2-го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы
|
один из них бесконечен. |
1 |
||
|
Пример 5. Функция f(x)= |
имеет в точке х0=0 точку разрыва 2-го рода, т.к. |
||
|
х |
|||
|
lim f (x) = +∞; |
lim f (x) = −∞. |
||
|
x→0+0 |
x→0−0 |
7.5
5
2.5
-2.5
-5
-7.5
Непрерывность функции на интервале и на отрезке
Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
При этом на концах отрезка или интервала необходима только односторонняя непрерывность.
Пример 6. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
117

|
БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
|
ст. преподавателя, к. физ.-мат. н. Поддубной О.H. |
||
|
x + 4, |
x < −1 |
|
|
+ 2, |
−1 ≤ x ≤1 |
|
|
f (x) = x2 |
||
|
x >1 |
||
|
2x, |
Решение. Это составная функция, областью определения которой является вся числовая прямая, которая точками «стыка» x1 = −1 и x2 =1 разбивается на
интервалы, на которых функция меняет свое аналитическое представление. На каждом интервале (−∞, −1) , (-1,1), (1, +∞) функция f(x) определяется
элементарной степенной функцией, которая является непрерывной для любого x . Поэтому на каждом интервале (−∞, −1) , (-1,1), (1, +∞) функция f(x) является
непрерывной. Необходимо проверить непрерывность функции f(x) в точках «стыка» x1 = −1 и x2 =1:
|
lim |
f (x) = 3 |
lim |
f (x) = 3 |
|
x→−1−0 |
x→1−0 |
||
|
lim |
f (x) = 3 |
lim |
f (x) = 2 |
|
x→−1+0 |
x→1+0 |
||
|
f (−1) = (−1)2 + 2 = 3 |
f (1) =12 + 2 = 3 |
Таким образом, в точке х=-1 функция непрерывна, в точке х=1 имеет
разрыв 1-го рода. Так как lim f (x) = 3 = f (1) , то функция f(x) в точке х=1
x→1−0
непрерывна слева.
у
3
2
Пример 7. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
|
cos x, |
x ≤ 0 |
|
|
+1, 0 < x <1 |
||
|
f (x) = x2 |
||
|
x ≥1 |
||
|
x, |
Решение. Это составная функция, областью определения которой является вся числовая прямая, которая точками «стыка» x1 = 0 и x2 =1 разбивается на
интервалы, на которых функция меняет свое аналитическое представление. На
118

|
БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
ст. преподавателя, к. физ.-мат. н. Поддубной О.H. |
|
|
каждом интервале |
(−∞,0) , (0,1), (1, +∞) функция f(x) определяется |
элементарными тригонометрической и степенными функциями, которые являются непрерывными для любого x . Поэтому на каждом интервале (−∞,0) ,
(0,1), (1,+∞) функция f(x) является непрерывной. Необходимо проверить непрерывность функции f(x) в точках «стыка» x1 = 0 и x2 =1:
|
lim |
f (x) =1 |
lim |
f (x) = 2 |
|||
|
x→0−0 |
x→1−0 |
|||||
|
lim |
f (x) =1 |
lim |
f (x) =1 |
|||
|
x→0+0 |
x→1+0 |
|||||
|
f (0) = cos0 =1 |
f (1) =1 |
|||||
|
Таким образом, |
т.к. |
lim f (x) = lim f (x) = f (0) , то в |
точке х1=0 функция |
|||
|
x→0−0 |
x→0+0 |
|||||
|
непрерывна. В |
точке |
х2=1 |
lim f (x) ≠ lim f (x) = f (1) , |
поэтому это точка |
||
|
x→1−0 |
x→1+0 |
разрыва 1-го рода. В точке х2=1 функция f(x) непрерывна справа.
у
2
1
Свойства функций, непрерывных на отрезке Свойство 1: (Первая теорема Вейерштрасса ). Функция, непрерывная
на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M≤ f(x)≤ M.
Замечание: Свойство 1 не справедливо для промежутков другого вида, чем отрезок. В этом легко убедиться, построив соответствующие примеры.
Пример 8. Функция y = 1x непрерывна в каждой точке интервала (0,1) и вместе
с тем не ограничена на нем; функция y = x непрерывна на всей вещественной оси и неограниченна на ней.
Свойство 2: Функция, непрерывная на отрезке [a, b], имеет на нем как наибольшее так и наименьшее значение.
Т.е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причем
Карл Вейерштрасс (1815-1897) – немецкий математик
119

|
БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
ст. преподавателя, к. физ.-мат. н. Поддубной О.H. |
m ≤ f(x) ≤ M
Замечание 1: Отметим, что наибольшее и наименьшее значения функция может принимать на отрезке и несколько раз (например – f(x)=sinx).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Замечание 2: Если функция f непрерывна не на отрезке, а на
промежутке другого типа и даже, кроме того, ограничена на нем, она вообше говоря, не имеет наибольшего и наименьшего значения.
Свойство 3: (теорема Коши). Функция, непрерывная на отрезке [a, b] такая, что f (a) = A, f (b) = B , то для любого значения C , заключенного между
A и B , существует такая точка ξ [a,b], что f (ξ) = C .
Иначе говоря, непрерывная на отрезке функция, принимающая какиелибо два значения, принимает и любое промежуточное.
Свойство 4: Если функция f(x) непрерывна в точке х=х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.
Свойство 5: (теорема Больцано–Коши). Если функция f(x) непрерывна на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, в которой функция обращается в нуль.
Т.е. если sign(f(a)) ≠ sign(f(b)), то x0 [a,b] : f(x0)=0.
Функция f(x) называется равномерно непрерывной на отрезке [a, b], если для любого ε>0 существует δ >0 такое, что для любых точек х1 [a,b] и x2 [a,b] таких, что
|
x1 − x2 |
<δ |
||
|
верно неравенство |
f(x2) – f(x1) < ε |
Отличие равномерной непрерывности от “обычной” в том, что для любого ε существует свое δ , не зависящее от х, а при “обычной” непрерывности δ зависит от ε и х.
Свойство 6: (Теорема Кантора ). Функция, непрерывная на отрезке, равномерно непрерывна на нем.
Замечание: Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.
Кантор Георг (1845-1918) – немецкий математик
120

|
БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|||||
|
1 |
ст. преподавателя, к. физ.-мат. н. Поддубной О.H. |
|||||
|
Пример 9. |
y = sin |
|||||
|
x |
1 |
|||||
|
0 |
. 5 |
|||||
|
— 3 |
— 2 |
— 1 |
1 |
2 |
3 |
|
|
— 0 |
. 5 |
|||||
|
— 1 |
Функция y = sin 1x непрерывна на интервале (0, а), но не является на нем
равномерно непрерывной, т.к. существует такое число δ >0 такое, что существуют значения х1 и х2 такие, что f(x1) – f(x2) >ε, ε — любое число при условии, что х1 и х2 близки к нулю.
Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором (конечном или бесконечном) интервале (a,b) , где
|
c = lim f (x), |
d = lim f (x) , то и обратная ей функция х=g(y) так же |
|
x→a+0 |
x→b−0 |
однозначна, монотонна и непрерывна на интервале с концами c и d .
121
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция
- — она определена в этой точке и ее некоторой
-окрестности;
- — существуют конечные лево- и правосторонние пределы от функции в этой точке и они равны между собой, т.е.
— предел функции в точке 
Пример:
Найти область непрерывности функции
Решение:
Данная функция непрерывна 
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
Пример:
Доказать, что функция 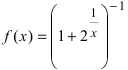
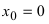
Решение:
Нарисуем график функции в окрестности нуля (Рис. 64): 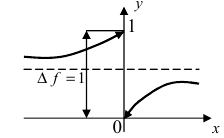
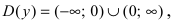
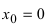
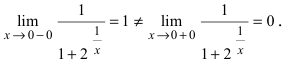
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция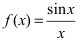
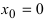
Решение:
В точке 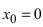
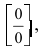
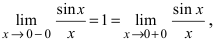
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен 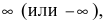
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 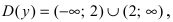
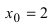
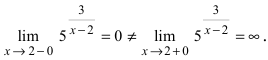
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 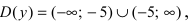
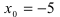
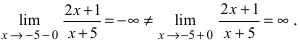
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций 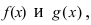
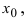
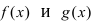
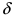
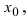
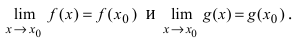
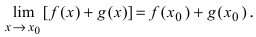
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций 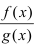
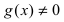
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
- Заказать решение задач по высшей математике
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
Пример:
Исследовать на непрерывность функцию
Решение:
Согласно схеме исследования функции на непрерывность имеем:
Рис. 65. Поведение графика функции 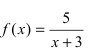
Из рисунка видно, что график функции 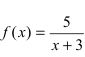
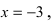
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке 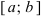
Определение: Замкнутый интервал 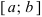
Приведем без доказательства свойства непрерывных функций на сегменте 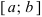
Теорема: Если функция 
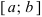
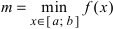
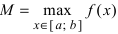
Пример:
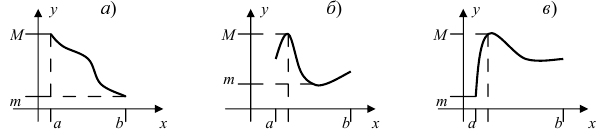
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 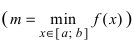
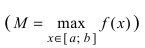
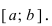
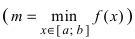
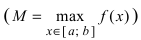
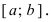
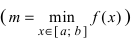
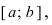
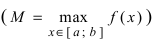
Тб. Если функция 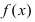
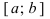
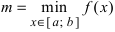
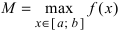
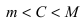
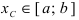
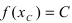
Пример:
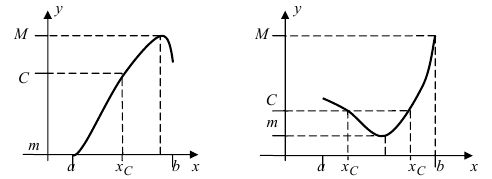
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция 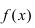
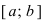
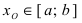
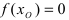
Пример:
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
Теорема Вейерштрасса о непрерывной функции на отрезке
30 декабря 2021
Теорема Вейерштрасса — фундаментальная теорема матанализа, которая состоит из двух частей:
- Теорема об ограниченности;
- Теорема о достижении максимума и минимума.
Сейчас мы сформулируем и докажем обе эти теоремы. Прежде всего дадим определения, на которые будем опираться:
Определение 1. Функция $fleft( x right)$ непрерывна в точке $x=a$, если $limlimits_{xto a}fleft( x right)=fleft( a right)$.
Определение 2. Функция $fleft( x right)$ непрерывна на интервале $left[ a;b right]$, если она непрерывна в каждой точке этого отрезка. При этом на концах отрезка речь идёт об односторонней непрерывности.
Всё это подробно разобрано в уроке про непрерывность функции в точке. Перейдём к теоремам.
1. Теорема Вейерштрасса об ограниченности функции
Теорема 1. (об ограниченности непрерывной функции) Функция, непрерывная на отрезке $left[ a;b right]$, ограничена на этом отрезке.
Другими словами, найдётся $Min mathbb{R}$ такое, что
[forall left( xin left[ a;b right] right)quad left| fleft( x right) right| lt M]
Приведу два доказательства — выбирайте то, которое больше нравится именно вам (или вашему преподу).
1.1. Доказательство методом Больцано
Предположим противное: пусть $fleft( x right)$ не ограничена на $left[ a;b right]$. Обозначим середину этого отрезка ${{c}_{1}}={left( a+b right)}/{2};$ и рассмотрим два новых отрезка:
[left[ a;{{c}_{1}} right]quad left[ {{c}_{1}};b right]]
Вместе эти отрезки покрывают отрезок $left[ a;b right]$. Следовательно, функция $fleft( x right)$ не ограничена как минимум на одном из них. Иначе если $fleft( x right)$ ограничена на обоих отрезках, то она будет ограничена и на из объединении, что противоречит нашему предположению.
Обозначим тот отрезок, на котором $fleft( x right)$ не ограничена, как ${{I}_{1}}=left[ {{a}_{1}};{{b}_{1}} right]$. Найдём середину этого отрезка ${{c}_{2}}={left( {{a}_{1}}+{{b}_{1}} right)}/{2};$. Вновь рассмотрим пару отрезков $left[ {{a}_{1}};{{c}_{1}} right]$ и $left[ {{c}_{1}};{{b}_{1}} right]$. Как минимум на одном из них функция $fleft( x right)$ будет не ограничена. Обозначим этот отрезок как ${{I}_{2}}=left[ {{a}_{2}};{{b}_{2}} right]$.
Проделаем эту операцию много раз. Получим последовательность стягивающихся отрезков:
[{{I}_{1}}supset {{I}_{2}}supset ldots supset {{I}_{n}}supset ldots ]
Длина отрезка ${{I}_{n}}$ равна $left| {{I}_{n}} right|=left| b-a right|cdot {{2}^{-n}}$ и стремится к нулю при $nto +infty $. По лемме о стягивающихся отрезках существует точка ${{x}_{0}}in mathbb{R}$ такая, что ${{x}_{0}}in {{I}_{n}}$ для любого $nin mathbb{N}$.
Кроме того, ${{x}_{0}}in left[ a;b right]$, поэтому функция $fleft( x right)$ непрерывна в т.ч. и в точке $x={{x}_{0}}$:
[limlimits_{xto {{x}_{0}}}fleft( x right)=fleft( {{x}_{0}} right)]
Вспомним определение предела функции в точке:
[begin{align} & limlimits_{xto {{x}_{0}}} fleft( x right)=fleft( {{x}_{0}} right)Rightarrow\ & forall left( varepsilon gt 0 right)quad exists left( delta =delta left( varepsilon right) gt 0 right): \ & xin {{overset{circ }{mathop{U}},}_{delta }}left( {{x}_{0}} right)Rightarrow left| fleft( x right)-fleft( {{x}_{0}} right) right| lt varepsilon\ end{align}]
Возьмём $varepsilon =1$. Следовательно, найдётся $delta =delta left( 1 right) gt 0$ такое, что в проколотой $delta $-окрестности точки ${{x}_{0}}$ выполняется условие $left| fleft( x right)-fleft( {{x}_{0}} right) right| lt 1$. Но тогда
[begin{align} left| fleft( x right) right|&=left| fleft( x right)-fleft( {{x}_{0}} right)+fleft( {{x}_{0}} right) right|le\ & le left| fleft( x right)-fleft( {{x}_{0}} right) right|+left| fleft( {{x}_{0}} right) right| lt \ & lt 1+left| fleft( {{x}_{0}} right) right| \ end{align}]
Получается, что внутри $delta $-окрестности функция ограничена числом $M=1+left| fleft( {{x}_{0}} right) right|$. Но поскольку $delta gt 0$ — фиксированное положительное число, а длины отрезков $left| {{I}_{n}} right|=left| b-a right|cdot {{2}^{-n}}$ стремятся к нулю, начиная с какого-то момента эти отрезки будут полностью лежать внутри этой $delta $-окрестности:
Мы даже можем приблизительно вычислить этот момент — достаточно потребовать, чтобы величина $delta $ оказалась больше длины $left| {{I}_{n}} right|$:
[begin{align} delta& gt left| b-a right|cdot {{2}^{-n}} \ {{2}^{n}} & gt {left| b-a right|}/{delta }; \ n& ge left[ {{log }_{2}}{left| b-a right|}/{delta }; right]+1 \ end{align}]
Здесь $left[ l right]$ следует понимать как «целая часть числа $l$» (подробнее об этом — в уроке «Что такое предел последовательности»).
Но тогда для всякого такого отрезка, полностью лежащего в $delta $-окрестности точки ${{x}_{0}}$, одновременно выполняется два условия:
- Функция $fleft( x right)$ ограничена на этом отрезке, потому что $left| fleft( x right) right| lt left| fleft( {{x}_{0}} right) right|+1$;
- Функция $fleft( x right)$ не ограничена на этом отрезке, потому что мы так выбрали ${{I}_{n}}$.
Получили противоречие. Следовательно, исходное предположение не верно. Теорема доказана.
1.2. Доказательство по Гейне
Рассмотрим более хитрое доказательство, которое опирается на теорема Больцано-Вейерштрасса о сходящейся подпоследовательности.
Итак, нужно доказать, что функция, непрерывная на отрезке $left[ a;b right]$, будет ограничена на этом отрезке. Вновь предположим, что это не так: пусть функция $fleft( x right)$ не ограничена, т.е.
[begin{align} & forall left( cin mathbb{R} right)quad exists left( xin left[ a;b right] right): \ & left| fleft( x right) right| gt c \ end{align}]
Рассмотрим натуральные значения $c$.
Пусть $c=1$. Тогда найдётся ${{x}_{1}}in left[ a;b right]$ такое, что $left| fleft( {{x}_{1}} right) right| gt 1$.
Пусть $c=2$. Тогда найдётся ${{x}_{2}}in left[ a;b right]$ такое, что $left| fleft( {{x}_{2}} right) right| gt 2$.
Продолжаем так много раз. Пусть $c=n$. Тогда найдётся ${{x}_{n}}in left[ a;b right]$ такое, что $left| fleft( {{x}_{n}} right) right| gt n$.
Получили последовательность $left{ {{x}_{n}} right}$, которая бесконечна и ограничена: $ale {{x}_{n}}le b$. По теореме Больцано-Вейерштрасса из неё можно выбрать сходящуюся подпоследовательность $left{ {{x}_{{{n}_{k}}}} right}$:
[limlimits_{kto +infty } {{x}_{{{n}_{k}}}}=xi ]
Но поскольку члены последовательности $ale {{x}_{{{n}_{k}}}}le b$, её предел $xi in left[ a;b right]$ (почему это так — смотрите свойства предела последовательности), и функция $fleft( x right)$, непрерывная на $left[ a;b right]$, будет непрерывна и в точке $x=xi $.
Согласно определению непрерывности функции по Гейне имеем
[limlimits_{kto +infty } fleft( {{x}_{{{n}_{k}}}} right)=fleft( xi right)]
С другой стороны, последовательность [left{ {{x}_{{{n}_{k}}}} right}] сконструирована таким образом, что
[left| fleft( {{x}_{{{n}_{k}}}} right) right| gt {{n}_{k}}ge k]
Но тогда предел
[limlimits_{kto +infty } fleft( {{x}_{{{n}_{k}}}} right)=infty ]
Получаем, что один и тот же предел одновременно равен и $fleft( xi right)in mathbb{R}$, и $infty notin mathbb{R}$. Чего не может быть, поскольку если предел существует, то он единственный.
Вновь получили противоречие. Следовательно, исходное предположение не верно. Теорема Вейерштрасса об ограниченности функции доказана.
1.3. Важное замечание
Эту теорему можно обобщить, рассмотрев вместо отрезка произвольный компакт.
С другой стороны, если вместо отрезка рассмотреть интервал (или любое другое открытое множество), то теорема будет не верна!
Пример 1. Функция $y= operatorname{tg}x$, где $xin left( -frac{pi }{2};frac{pi }{2} right)$.
Тангенс непрерывен в каждой точке указанного интервала, однако неограниченно возрастает при $xto {pi }/{2};$ и неограниченно убывает при $xto -{pi }/{2};$.
Принципиально важно, чтобы функция была определена на концах отрезка $left[ a;b right]$, т.е. принимала бы конкретные значения $fleft( a right)$ и $fleft( b right)$. И следовательно, была бы ограниченна в некоторой $delta $-окрестности этих концов.
2. Теорема Вейерштрасса о достижении максимума и минимума
В матанализе есть понятие локального максимума и минимума (смотрите раздел про производные), поэтому при формулировке теоремы Вейерштрасса лучше говорить о точной верхней грани и точной нижней грани значений функции на отрезке:
[suplimits_{xin left[ a;b right]}fleft( x right)quad inflimits_{xin left[ a;b right]}fleft( x right)]
Теорема 2. (о достижении точной верхней и нижней грани) Функция, непрерывная на отрезке $left[ a;b right]$, достигает своей точной верхней грани и точной нижней грани:
[begin{align} & exists left( {{x}_{1}}in left[ a;b right] right): & fleft( {{x}_{1}} right)=underset{xin left[ a;b right]}{mathop{sup }},fleft( x right) \ & exists left( {{x}_{2}}in left[ a;b right] right): & fleft( {{x}_{2}} right)=underset{xin left[ a;b right]}{mathop{inf }},fleft( x right) \ end{align}]
Докажем эту теорему только для точной верхней грани. Затем достаточно рассмотреть функцию $gleft( x right)=-fleft( x right)$ и заметить, что
[inflimits_{xin left[ a;b right]} fleft( x right)=-suplimits_{xin left[ a;b right]} gleft( x right)]
2.1. Доказательство для точной верхней грани
Пусть функция $fleft( x right)$ непрерывна на $left[ a;b right]$. Тогда по теореме Вейерштрасса об ограниченности, которую мы доказали выше, найдётся такое $Min mathbb{R}$, что
[forall left( xin left[ a;b right] right)quad left| fleft( x right) right| lt M]
Но тогда существует точная верхняя грань
[A=suplimits_{xin left[ a;b right]} fleft( x right)]
Докажем теорему от противного. Пусть $Ane fleft( x right)$ для любого $xin left[ a;b right]$. Тогда очевидно, что $A gt fleft( x right)$ при каждом $xin left[ a;b right]$.
Рассмотрим функцию $gleft( x right)=A-fleft( x right)$. Она непрерывна на отрезке $left[ a;b right]$. Кроме того для всякого $xin left[ a;b right]$
[gleft( x right)=A-fleft( x right) gt 0]
Следовательно, функция
[{{g}_{1}}left( x right)=frac{1}{gleft( x right)}=frac{1}{A-fleft( x right)} gt 0]
тоже непрерывна на отрезке $left[ a;b right]$ и принимает лишь положительные значения. Но тогда ${{g}_{1}}left( x right)$ ограничена на $left[ a;b right]$. Следовательно, найдётся число $B gt 0$ такое, что
[begin{align} left| {{g}_{1}}left( x right) right| & lt B \ 0 lt frac{1}{A-fleft( x right)}& lt B \ end{align}]
Но тогда
[begin{align} A-fleft( x right) & gt frac{1}{B} gt 0 \ fleft( x right) & lt A-frac{1}{B} \ end{align}]
Получается, что мы нашли верхнюю грань $A-{1}/{B};$, которая меньше точной верхней грани $A=suplimits_{xin left[ a;b right]} fleft( x right)$.
Но это противоречит определению точной меньшей грани. Следовательно, исходное предположение неверно. Теорема доказана.
Смотрите также:
- Теорема о промежуточном значении функции
- Непрерывность функции в точке
- Тест к уроку «Что такое логарифм» (средний)
- Тест к уроку «Площади многоугольников без координатной сетки» (средний)
- Как решать биквадратное уравнение
- Задача B4: экономика
Содержание:
- Непрерывность функции
- Непрерывность функции в точке
- Непрерывность функции в точке
- Задача пример №57
- Непрерывность функции на интервале
- Непрерывность функции на отрезке
- Задача пример №58
- Задача пример №59
- Задача пример №60
Непрерывность функции
Непрерывность функции часто можно легко объяснить следующим образом. Если график какой-либо функции можно построить не отрывая карандаш от бумаги, то эта функция непрерывна. В противном случае, у графика есть точки разрыва (скачка) и данная функция является разрывной функцией. График разрывной функции невозможно изобразить, не отрывая карандаш от листа.
Непрерывность функции в точке
Для того, чтобы функция была непрерывной в точке, ее график не должен прерываться, т.е. график не должен иметь «скачков». График функций на рисунках прерывается или имеет «скачок» в точке 



1. Функция не определена в точке 
2. В точке 

3. Предел функции 


Точка 
Если функция не удовлетворяет ни одному из указанных выше условий, то ее можно назвать непрерывной в точке 
Непрерывность функции в точке
Для того, чтобы функция 

1. Функция должна быть определена в точке 
2. Должен существовать предел 
3. Должно выполняться равенство 
Задача пример №57
Исследуйте непрерывность следующих функций.
Решение:
а) из графика функции 




Отметим, что во всех точках кроме 
b)
Как видно из графика, при стремлении значений 

Предел функции:
Значение функции: 




Непрерывность функции на интервале
Определение. Функция называется непрерывной на интервале 
Непрерывность функции на отрезке
Определение. Функция 




Любая функция — многочлен непрерывна на всей числовой оси. Рациональная функция непрерывна во всех точках, кроме тех, которые обращают знаменатель в 0. Функции 

Для функции, непрерывной на отрезке, справедлива следующая теорема.
Теорема Вейерштрасса. Функция, непрерывная на отрезке, принимает в нем наименьшее и наибольшее значения.
Теорема Коши. Если функция 


Следствие. Функция, непрерывная на отрезке, принимает все значения от наименьшего до наибольшего.
Применяя эту теорему, можно решить следующий тип задач.
Задача пример №58
Существует ли такое действительное число, куб которого больше самого числа на 1?
Решение:
искомое число 










Если какая-либо функция непрерывна на интервале 

Задача пример №59
Исследуйте непрерывность функции
Решение:
как видно из графика, при стремлении 
Т.е. в точке 



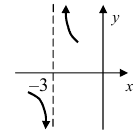
Задача пример №60
Определите точки разрыва функции
Решение: Линейная функция 





Сначала исследуем непрерывность функции в точке 
1. Значение функции. Функция определена в точке 

2. Существование предела. Для определения предела 






3. Значение и предел функции в точке. Так как 


Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Теорема о разложении на множители
- Экстремум функции многих переменных
- Пределы в математике
- Дифференциал функции
- Объемы подобных фигур
- Непрерывность функции
- Интервал сходимости степенного ряда
- Уравнение прямой через две точки
- Круги Эйлера фигуры, условно изображающие множества
- Тригонометрические комплексные числа

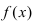
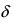 -окрестности;
-окрестности;