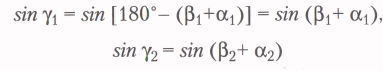Ф
агентство по образованию
САНКТПЕТЕРБУРГСКИЙ
Г
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ИНЖЕНЕРНАЯ
ГЕОДЕЗИЯ
Пособие
по учебной
геодезической практике
Учебное пособие
Санкт-Петербург
Издательство
Политехнического университета
2010
УДК 528.48 (075.8)
ББК
26
И
62
Авторы:
Е.Б. Михаленко, Н.Н. Загрядская, Н.Д.
Беляев,
В.В. Вилькевич, В.С. Ермаков,
А.А. Смирнов, С.В. Трофимов
Инженерная
геодезия. Пособие по учебной геодезической
практике :
учеб. пособие / Е. Б. Михаленко [и др.], под
научн. ред. Е. Б. Михаленко. – СПб. : Изд-во
Политехн. ун-та, 2011. – 86 с.
Пособие соответствует
государственному стандарту по направлению
270100 «Строительство».
В пособии излагаются
сведения, необходимые для выполнения
основных заданий учебной геодезической
практики студентов 1-го курса
инженерно-строительного факультета.
В первом разделе
рассмотрено решение ряда инженерных
задач – определение неприступного
расстояния, высоты и крена сооружения,
детальная разбивка кривых. В разделах
2-5 даны сведения о проведении геодезических
работ на начальной стадии строительства
(разбивочные работы) – составление
проекта вертикальной планировки
строительной площадки, расчет разбивочных
элементов для переноса проекта сооружения
в натуру, а также рекомендации по выносу
в натуру проектных горизонтальных
углов, расстояний и отметок точек. В
разделах 6-8 приведены инструкции по
использованию современных геодезических
приборов – электронных теодолитов VEGA
TEO и тахеометров Pentax.
В последнем 9-ом
разделе рассмотрены способы построения
горизонталей при помощи различных
программ CAD (Pythagoras,
Civil,
GeoniCS,
Credo)?
используемых для обработки результатов
топографических съемок (тахеометрической
и нивелировании площади).
Пособие предназначено
для студентов инженерно-строительного
факультета в пределах программы
бакалавриата.
Табл. 17. Ил. 61.
Библиогр.: 11 назв.
Печатается по
решению редакционно-издательского
совета Санкт-Петербургского государственного
политехнического университета.
Михаленко Е.Б.,
научное редактирование, 2011
Санкт-Петербургский
государственный
политехнический
университет, 2011
-
Решение некоторых инженерных задач
-
Определение неприступного расстояния
Неприступное
расстояние – это расстояние до объекта,
находящегося в поле зрения наблюдателя,
которое не может быть измерено
непосредственно. Это чаще всего связано
с наличием на местности каких-то
препятствий (забор, водоем и т.п.). В таком
случае прибегают к косвенному способу
измерений, когда измеряются какие-то
дополнительные величины (линейные или
угловые), а искомое расстояние вычисляется
с их помощью.
Неприступное
расстояние определяют, как правило, из
системы двух треугольников, построенных
на основе измеренных базисов. Базисы
разбивают на слабопересеченной местности,
длина их должна быть не менее половины
измеряемого расстояния. Базисные
расстояния измеряют лентой или рулеткой
с точностью 1/2000–1/3000, углы – теодолитом
полным приемом. Схема определения
неприступного расстояния показана на
рис. 1.1.
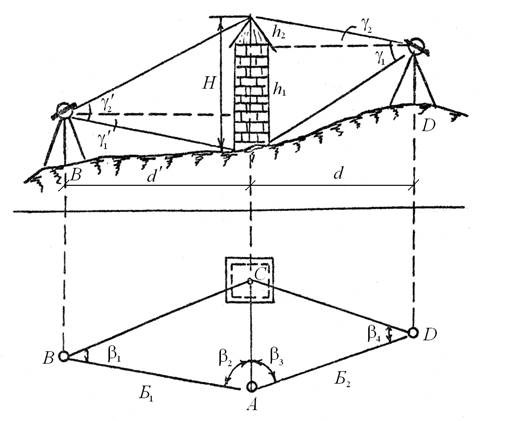
Рис. 1.1. Схема
определения неприступного расстояния
и высоты сооружения
Из
решения треугольников ABCиADCопределяют неприступное расстояние по
формулам:
;
(1.1)
.
(1.2)
Относительная
погрешность двух вычисленных значений
неприступного расстояния не должна
превышать 1/1000. При этом условии
неприступное расстояние принимается
равным среднему арифметическому двух
вычисленных.
Например,
м,
м,
,
,
,
.
Вычисляем неприступное расстоянием;
м. Среднее значение неприступного
расстояниям.
-
Определение высоты сооружения
Для
определения высоты сооружения башенного
типа на некотором расстоянии от него в
точке D
устанавливают теодолит и измеряют
вертикальные углы
и
при двух положениях вертикального
круга: КЛ и КП (см. рис. 1.1).Тогда
высота сооружения равна:
,
(1.3)
где
d
– горизонтальное проложение линии,
которое может быть измерено лентой,
рулеткой или дальномером. При невозможности
непосредственного измерения линии ее
вычисляют как неприступное расстояние,
разбив предварительно базисы.
Для
контроля проводят такие же измерения
и вычисления с точки B(см. рис. 1.1). Например,
м,
,
.
м;
м;
м.
Аналогично
обрабатывают результаты измерений со
станции на точке B.
-
Наблюдения за креном сооружения
-
Общие сведения
Креном
называется отклонение сооружения от
проектного положения в вертикальной
плоскости. Причиной его возникновения
обычно является неравномерная осадка
основания сооружения. Геометрическая
сущность измерения крена сводится к
определению взаимного положения двух
точек сооружения (например, точки A
и B
на рис.1.2),
которые по техническим условиям проекта
должны лежать на одной отвесной линии.
Наиболее простым способом полная угловая
величина крена
может быть получена проецированием
точки A
на горизонтальную плоскость. Измерив
высоту h
точки A
и длину проекции l,
можно найти
.
(1.4)
Рис. 1.2. Определение
крена сооружения
Другим
способом определения крена угла здания
является способ горизонтальных углов,
при котором с опорных пунктов, расположенных
на взаимно перпендикулярных осях,
измеряют горизонтальные углы между
опорным направлением и направлениями
на верхнюю и нижнюю точки угла здания.
По разнице измеренных углов и
горизонтальному проложению от станции
до наблюдаемой точки находят составляющие
крена по осям и полную величину крена.
Определение неприступного расстояния



Решение некоторых инженерных задач
Неприступное расстояние – это расстояние до объекта, находящегося в поле зрения наблюдателя, которое не может быть измерено непосредственно. Это чаще всего связано с наличием на местности каких-то препятствий (забор, водоем и т.п.). В таком случае прибегают к косвенному способу измерений, когда измеряются какие-то дополнительные величины (линейные или угловые), а искомое расстояние вычисляется с их помощью.
Неприступное расстояние определяют, как правило, из системы двух треугольников, построенных на основе измеренных базисов. Базисы разбивают на слабопересеченной местности, длина их должна быть не менее половины измеряемого расстояния. Базисные расстояния измеряют лентой или рулеткой с точностью 1/2000–1/3000, углы – теодолитом полным приемом. Схема определения неприступного расстояния показана на рис. 1.1.
Рис. 1.1. Схема определения неприступного расстояния и высоты сооружения
Из решения треугольников ABC и ADC определяют неприступное расстояние по формулам:
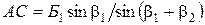
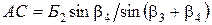
Относительная погрешность двух вычисленных значений неприступного расстояния не должна превышать 1/1000. При этом условии неприступное расстояние принимается равным среднему арифметическому двух вычисленных.
Например, 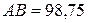
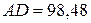
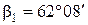
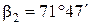
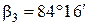
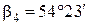
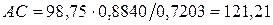
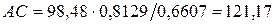
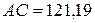
Источник
VII.5. Определение неприступного расстояния
Эта задача встречается при прокладке нивелирных, теодолитных, тахеометрических ходов через препятствия (реки, болота, загруженные транспортом магистрали и т.д.), а также при привязке запроектированных сооружений. Для выполнения полевых работ необходимо иметь: теодолит со штативом, мерную ленту, две вешки, топорик, пять колышков.
Определение неприступного расстояния производят косвенным способом – путем использования других измеренных величин.
Пусть требуется определить горизонтальное расстояние между точками В и Д (Рис.29).
По обе стороны от одной из точек разбивают два базиса (откладывают отрезки АВ и АС) и измеряют их с точностью не ниже 1/3000. Место закладки базисов выбирают наиболее ровное и горизонтальное. При наклоне местности более 2° в длины базисов вводят поправки на наклон. По длине и направлению базисы должны приближать треугольники АВД и ВДС к равносторонним, чем обеспечивается наибольшая точность определения искомого расстояния.
Далее по теореме синусов в обоих треугольниках определяют сторону ВД. Ошибку определения расстояния ВД находят как отношение разности результатов двух определений к среднему результату.
VII.6. Определение высоты недоступного сооружения
Для выполнения полевых работ при решении этой задачи используют те же инструменты и снаряжение, которые необходимы и для решения предыдущей задачи.
Требования к разбивке и измерению базиса те же, что и для решения предыдущей задачи.
Горизонтальные и вертикальные углы измеряют полными приемами и результаты измерений записывают в рабочей тетради. По измеренным величинам базиса и углов с помощью тригонометрических функций вычисляют высоту сооружения.
В зависимости от местных условий (возможности визировать на основание сооружения (точка О 3 ), наличия высотной отметки основания и высотных отметок точек А и В) постановка задачи может быть различной.
VII.7. Определение величины и направления крена инженерных сооружений башенного типа
Задача находит широкое применение при установке и выверке колонн, мачтовых опор, возведении дымовых труб и т.д.
Крен является наиболее характерным показателем совместной деформации сооружения башенного типа и его основания. В таких сооружениях крен вызывает
развитие дополнительного момента, который в свою очередь способствует увеличению крена и может привести к потере устойчивости и обрушению сооружения.
Под линейной величиной абсолютного крена понимается отрезок между проекциями центра подошвы фундамента и центра верхнего сечения сооружения на горизонтальную плоскость.
Определение крена в зависимости от требуемой точности, высоты сооружения, а также местных условий может быть осуществлено одним из следующих способов:
вертикального проектирования;зенитных расстояний;
высокоточного нивелирования осадочных марок;направления с одного опорного пункта;стереофотограмметрии.
Наибольшее распространение имеют первые четыре способа, наиболее универсальным и строгим из них является способ координат.
Способ координат заключается в определении прямой угловой засечкой координат центров верхнего и нижнего сечений сооружения в принятой системе координат. Для этого на каждом пункте наблюдения измеряются способом круговых приемов горизонтальные углы между направлениями на соседние пункты и на центры верхнего и нижнего сечений. За направление на центры принимают среднее из значений направлений на крайние точки сечений.
По результатам измерений можно определить координаты центров среднего верхнего (из двух – трех непосредственных измерений) и среднего нижнего сечений. Зная координаты центров верхнего и нижнего сечений, можно найти величину и направление крена для наблюдаемой по высоте части сооружения.
Для выполнения полевых работ необходимо иметь:
1) теодолит со штативом и буссолью;
2) мерную ленту со шпильками;
6) полевой журнал, подготовленный по приложению 25.
В качестве пунктов, с которых проводятся наблюдения, предпочтительно использовать пункты опорной геодезической сети, если расстояния между этими пунктами и от центра сооружения не менее полутора и не более двух высот сооружения. При отсутствии пунктов сети вблизи объекта, бригада самостоятельно назначает местоположение пунктов наблюдения, учитывая при этом, что с этих пунктов необходимо видеть не менее трех четвертей высоты сооружения, пункты должны быть расположены ориентировочно на одной высотной отметке и между ними обеспечена взаимная видимость. Расстояния между пунктами наблюдения и от центра сооружения до пунктов выбирают равными 1,5-2 Н – высоты сооружения.
Выбранные пункты бригада закрепляет колышками, забитыми вровень с поверхностью и рядом устанавливает сторожок с наименованием пункта наблюдения. В рабочей тетради зарисовывают абрис местности, на котором показывают объект наблюдения, схему расположения пунктов наблюдения и дают привязку этих пунктов к местным объектам. (Приложение 21)
Расстояние между пунктами наблюдения измеряют в прямом и обратном направлениях. Допустимая относительная погрешность измерения не более одной десятитысячной. Горизонтальное проложение этого расстояния вычисляют с учетом поправок за измеренный угол наклона или превышение между пунктами наблюдения, компарирование мерной ленты и температуру. Результаты измерений и вычислений записывают в рабочую тетрадь.
В приложении 21 приведен пример определения крена дымовой трубы и его направления.
Последовательно визируют и записывают в полевой журнал наблюдений отсчеты на вешку, установленную на втором пункте наблюдения, правый и левый края верхнего и нижнего сечения сооружения. Измерения горизонтальных углов производят методом круговых приемов, при этом в первом полуприеме теодолит поворачивают по часовой стрелке, а во втором против часовой стрелки. Таким же образом производят измерения и на втором пункте наблюдения.
При камеральной обработке результатов наблюдений вычисляют горизонтальные углы между направлениями на соседний пункт наблюдения и на центр выбранного сечения. Отсчет, приведенный к центру сечения, определяется как среднее арифметическое между отсчетами, взятыми при визировании на крайние точки соответствующего сечения.
Магнитный азимут базиса (линии между пунктами наблюдения), определенный при двух измерениях, усредняют и вычисляют дирекционный угол этого направления. В рамках учебной практики допускается принять дирекционный угол равным магнитному азимуту направления базиса.
Приняв координаты первого пункта равными нулю, вычисляют координаты второго пункта по формулам:
Источник
Решение некоторых инженерных задач
Определение неприступного расстояния
Неприступное расстояние – это расстояние до объекта, находящегося в поле зрения наблюдателя, которое не может быть измерено непосредственно. Это чаще всего связано с наличием на местности каких-то препятствий (забор, водоем и т.п.). В таком случае прибегают к косвенному способу измерений, когда измеряются какие-то дополнительные величины (линейные или угловые), а искомое расстояние вычисляется с их помощью.
Неприступное расстояние определяют, как правило, из системы двух треугольников, построенных на основе измеренных базисов. Базисы разбивают на слабопересеченной местности, длина их должна быть не менее половины измеряемого расстояния. Базисные расстояния измеряют лентой или рулеткой с точностью 1/2000–1/3000, углы – теодолитом полным приемом. Схема определения неприступного расстояния показана на рис. 1.1.
Рис. 1.1. Схема определения неприступного расстояния и высоты сооружения
Из решения треугольников ABCиADCопределяют неприступное расстояние по формулам:
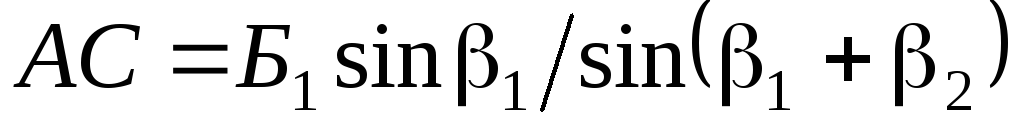
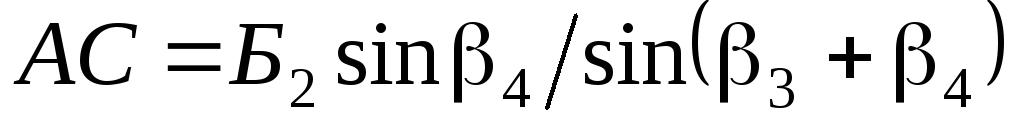
Относительная погрешность двух вычисленных значений неприступного расстояния не должна превышать 1/1000. При этом условии неприступное расстояние принимается равным среднему арифметическому двух вычисленных.
Например, 
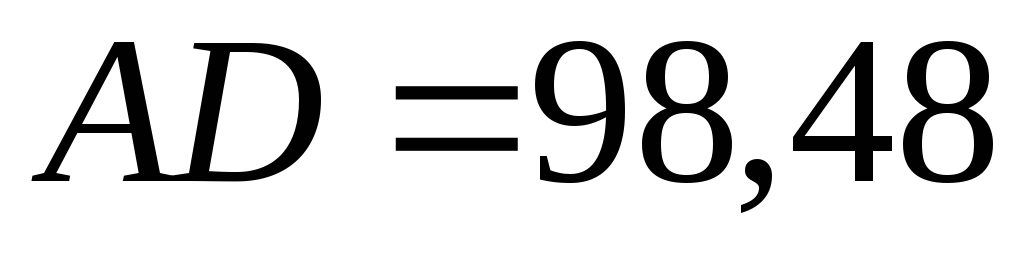
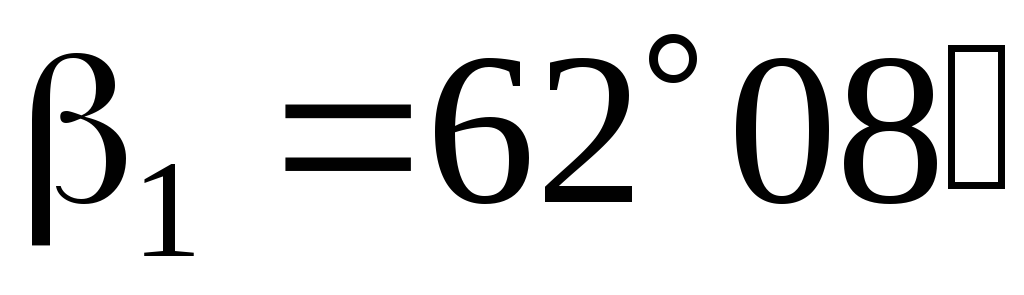

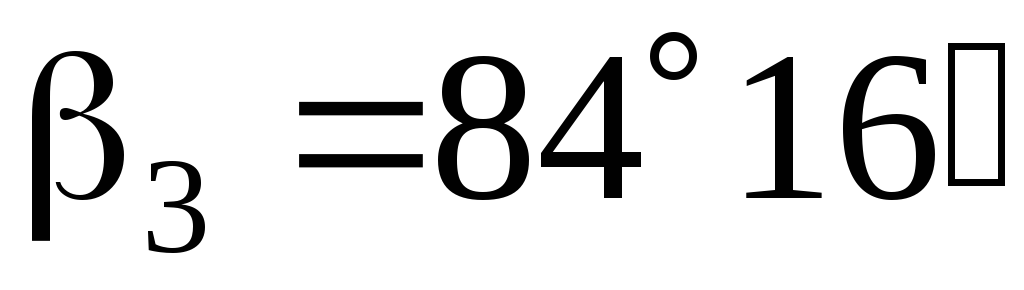
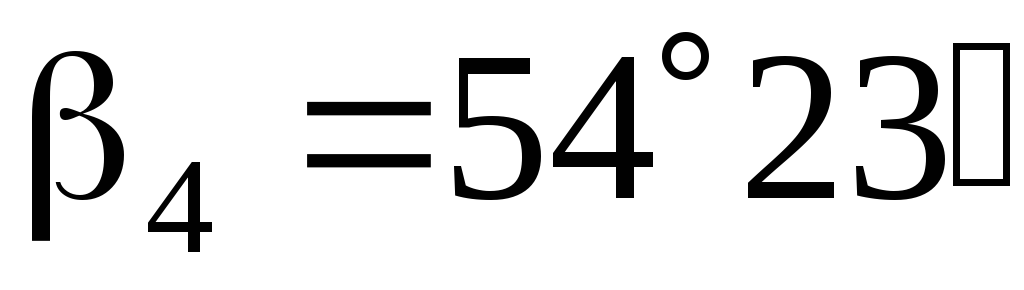



Определение высоты сооружения
Для определения высоты сооружения башенного типа на некотором расстоянии от него в точке D устанавливают теодолит и измеряют вертикальные углы 
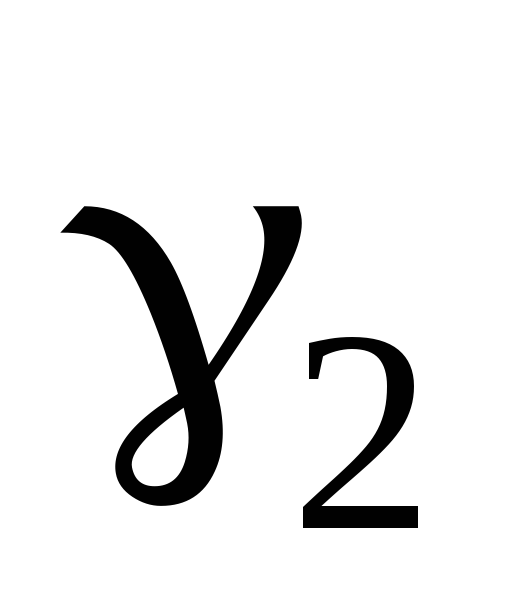
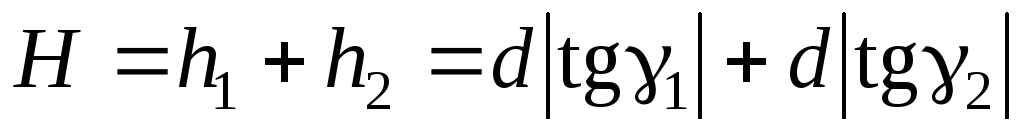
где d – горизонтальное проложение линии, которое может быть измерено лентой, рулеткой или дальномером. При невозможности непосредственного измерения линии ее вычисляют как неприступное расстояние, разбив предварительно базисы.
Для контроля проводят такие же измерения и вычисления с точки B(см. рис. 1.1). Например,




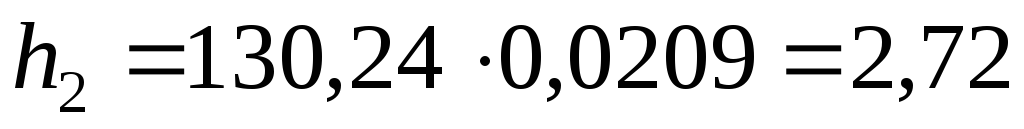

Аналогично обрабатывают результаты измерений со станции на точке B.
Наблюдения за креном сооружения
Общие сведения
Креном называется отклонение сооружения от проектного положения в вертикальной плоскости. Причиной его возникновения обычно является неравномерная осадка основания сооружения. Геометрическая сущность измерения крена сводится к определению взаимного положения двух точек сооружения (например, точки A и B на рис.1.2), которые по техническим условиям проекта должны лежать на одной отвесной линии. Наиболее простым способом полная угловая величина крена может быть получена проецированием точки A на горизонтальную плоскость. Измерив высоту h точки A и длину проекции l, можно найти

Рис. 1.2. Определение крена сооружения
Другим способом определения крена угла здания является способ горизонтальных углов, при котором с опорных пунктов, расположенных на взаимно перпендикулярных осях, измеряют горизонтальные углы между опорным направлением и направлениями на верхнюю и нижнюю точки угла здания. По разнице измеренных углов и горизонтальному проложению от станции до наблюдаемой точки находят составляющие крена по осям и полную величину крена.
Источник
Тема: Измерения расстояний
1. Приборы для измерения линий
_______ Линейные измерения на местности могут выполняться непосредственно (с помощью мерных приборов) и косвенно (с помощью дальномеров). В качестве мерных приборов используются следующие.
1.1. Стальные мерные ленты со шпильками
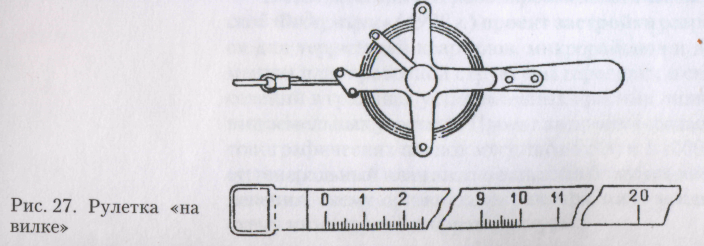
1.2. Стальные рулетки различной длины (от 2 до 100 м) в открытом или закрытом корпусе
1.3. Инварные ленты и проволоки (сплав железа и никеля в соотношении 64:36)
1.4. Дальномеры различной точности
_______ Для транспортировки лента наматывается на металлическое кольцо.
2. Подготовка линии местности к измерению
_______ Перед измерением линии конечные точки закрепляются. В конце линии ставится веха. При длине линии более 200 м она предварительно провешивается, то есть в створ линии ставятся дополнительные вехи.
3. Порядок измерения линии лентой
_______ Задний мерщик выставляет переднего в створ линии и собирает шпильки. Когда у заднего мерщика набирается 10 шпилек, он передает их переднему и записывает передачу.
_______ В результате длина линии вычисляется по формуле:

____ где N – количество передач по 10 шпилек;
_______ n – количество шпилек у заднего мерщика, не считая шпильки, которая в земле;
_______ r – остаток.
4. Учет поправок при линейных измерениях. Точность измерений
_______ В измеренное значение длины линии вводят поправки :
ΔDk – поправка за компарирование,
ΔDt – поправка за температуру,
ΔDv – поправка за наклон линии.
где D – длина измеренной линии,
___ Δl – поправка за компарирование.
_______ Тогда в общем виде:
_______ При измерении длин линий не только мерной лентой, но и другими мерными приборами (рулетками, инварными проволоками) вводятся те же поправки.
_______ Точность измерений линий лентой зависит главным образом от характера местности:
5. Определение неприступных расстояний
_______ В некоторых случаях, вследствие каких-либо препятствий, измерить линию продольного хода непосредственно лентой невозможно.
5.1. 1-й случай: (точка В недоступна для линейных измерений). По теореме синусов
6. Оптические дальномеры
Здесь p – расстояние между дальномерными нитями;
_____ n – количество делений дальномерной рейки между дальномерными нитями;
_____ p – коэффициент дальномера, который обычно равен 100 ;
_____ n – количество делений дальномерной рейки, видимых в трубу между дальномерными нитями.
_______ Расстояние с помощью нитяного дальномера определяется по формуле:
_______ При измерении наклонных расстояний дальномером визирный луч направлен наклонно.
_______ Считая, что скорость распространения электромагнитных волн V известна, можно записать:
_______ Прибор состоит из приемопередатчика, установленного на начальной точке, и отражателя, установленного на конечной точке линии.
_______ Скорость распространения электромагнитных волн в вакууме:
_______________________________________________ V = 2997925 ± 0,4 км/c
Источник
3.3. Определение неприступных расстояний
Длины линий, которые нельзя измерить непосредственно лентой или рулеткой (овраги, реки, насыпи и др.), можно определить косвенным путем. Например, при обмерах зданий
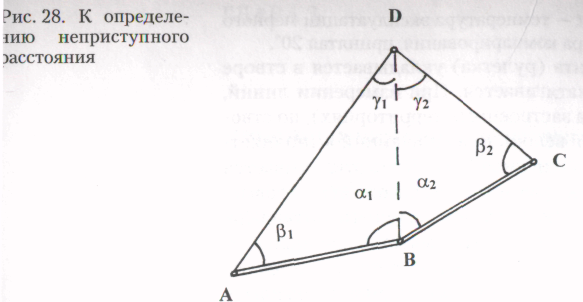
верхние части фасадов и интерьеров труднодоступны для измерений, целесообразно строить различные геометрические схемы, чтобы заменить линейные измерения угловыми и получить искомое значение расстояния аналитически. Наиболее распространенный способ — разбивка на местности двух треугольников, в которых измеряются все три угла (или в крайнем случае — два угла), а также два базиса с точностью не ниже 1:2 000 (рис. 28). Определяемое расстояние DВ подсчитывается по теореме синусов из треугольников АDВ и DВС:
Если угол γ измерить невозможно, то по формуле приведения имеем:
Расхождение полученных значений определяемого расстояния не должно превышать 1:2 000 величины этого расстояния.
3.4. Дальномеры
Дальномеры предназначены для измерения расстояний косвенным способом. Различают оптические и электронные дальномеры. Простейшим оптическим дальномером является нитяной дальномер, который имеется в теодолитах и нивелирах. В поле зрения зрительной трубы видна сетка нитей (рис. 29). Две крайние горизонтальные нити называются дальномерными. Для измерений применяется рейка, на которой нанесены сантиметровые деления. При наведении зрительной трубы на рейку можно определить число делений рейки п между дальномерными нитями, для этого берется отсчет по рейке по нижней и верхней горизонтальным ни-
тям, а затем подсчитывается разность отсчетов. Отсчет берется с точностью до 1 мм, при этом доли сантиметрового деления оцениваются «на глаз». Расстояние от инструмента до рейки определится из выражения:
где К — коэффициент дальномера, который в современных геодезических инструментах равен 100.
Это выражение верно, если рельеф ровный и угол наклона склона к горизонту не превышает 3°. В противном случае необходимо вычислить значение горизонтального проложения А по измеренному наклонному расстоянию В и углу наклона визирной линии к горизонту v:
Необходимо также учитывать погрешность отсчета по рейке за счет отклонения ее от перпендикуляра к визирному лучу:
Подставляя (1) в (2), получим:
Точность измерения линий нитяным дальномером равна 1/300 от длины линии. Например, при расстоянии 100 м погрешность измерения составит 0,3 м. Очевидно, что такая точность допустима в тех случаях, когда при съемке определяется положение так называемых нечетких контуров (границ лесов, болот и пр.) или при съемке рельефа местности.
Электронные дальномеры. Действие электронных дальномеров основано на измерении времени прохождения радио или световых излучений от начальной до конечной точек измеряемой линии и обратно. Радиодальномеры применяются, как правило, для измерения больших расстоя триангуляции, полигонометрии ). При выполнении инженерно-геодезических работ используются в основном светодаль-номеры. Отечественная промышленность выпускает электронные свето дальномеры: «Блеск-1» (СТ-5) и «Блеск-2» (2СТ-10). Точность измерения расстояний составляет: для «Блеск» — (10 + 5Вкм) мм при дальности измерений до 2 км; для «Блеск-2» — (5 + ЗОкм) мм при дальности измерений до 5 км. В комплект светодальномера входит: сам прибор, отражатели, штативы, термометр, барометр и др.
Выпускаются также электронные дальномеры в виде насадок на зрительную трубу теодолита.
Следует отметить, что в настоящее время дорогостоящие электронные дальномеры уступают место более современным приборам — электронным тахеометрам.
При измерении сравнительно коротких расстояний используются светодальномеры, работающие без отражателя по принципу пассивного отражения от предмета наведения. Получили распространение также ручные лазерные рулетки (рис. 30). Маркировка точек осуществляется видимым лазерным лучом. С помощью такой рулетки можно выполнять работу одному человеку и определять расстояния, недоступные для измерения обычными лентами и рулетками, например, при обмерах интерьеров зданий.
Лазерными рулетками фирмы «Бош»(Германия) измеряются расстояния от 0,2 до 60 м с погрешностью ± 3 мм. Рулетка «В18ТО» фирмы «Лейка» предназначена для измерения расстояний от 0,2 до 100 м с погрешностью ± 3 мм. Рулеткой «В15ТО» можно вычислять площади и объемы. К недостаткам лазерных рулеток следует отнести то, что они пригодны к работе при температуре не ниже минус 10°, кроме того, при ярком солнечном свете луч просматривается в пределах 20 м.
Источник
Недоступное (неприступное) расстояние – это расстояние до объекта, находящегося в поле зрения наблюдателя, которое не может быть измерено непосредственно.
Метод определения недоступного расстояния используется в тех случаях, когда надо измерить наклонное расстояние, горизонтальное проложение и разность высот между начальной точкой и любыми другими точками без перемещения инструмента.
Последняя измеренная точка может быть задана, как начальная для последующих измерений.
Результат измерений может быть выведен как градиент (уклон в %) между двумя точками.
Измерение расстояний между точками
Расстояние между двумя и более точками можно определить наблюдением визирных целей или вычислением по введенным координатам. Комбинация данных способов также возможна (например, наблюдение одной цели и ввод координат второй цели).
Определение с помощью наблюдения
1. На 3-й странице режима измерений нажмите [ОНР] и выберите «Опред-е HP».
2. Наведитесь на отражатель, установленный на начальной точке (ТЧК1) и нажмите [ИЗМЕР].
Если уже имеются результаты измерения расстояния, последнее значение берется в качестве начальной точки, и выводится экран, показанный на шаге 3.
Если инструмент находится вне диапазона работы компенсатора, выводится соответствующий экран. Приведите инструмент к горизонту.
3. Наведитесь на 2-й отражатель и нажмите клавишу [ОНР], чтобы начать измерения.
[ЗАП]: запись результата измерения первой цели.
На экране отображаются:
S : Наклонное расстояние между начальной и 2-й точками.
D : Горизонтальное проложение между начальной и 2-й точкой,
h : Превышение между начальной и второй точками.
Можно ввести высоту отражателя на начальной и 2-й точках. Нажмите [Выс_Ц] на 2-й стр.
Введите высоты отражателей и нажмите клавишу [ДА].
Нажмите [КООРД], чтобы ввести координаты.
При нажатии [ЗАП] отображается экран, показанный снизу.
Для сохранения результатов измерения на 2-й отражатель нажмите клавишу {Д А}.
Нажмите [ДА] для сохранения результатов определения недоступного расстояния и возврата к экрану с результатами измерений.
Для продолжения измерения без сохранения результатов измерения на 2-й отражатель или результатов определения недоступного расстояния нажмите {ESC}.
Результаты измерения недоступного расстояния нельзя сохранить, если отсутствуют имена точек, на которых установлены 1-й и/или 2-й отражатели. Введите имена точек.
4. Наведитесь на следующий отражатель и нажмите [ОНР], чтобы начать измерения. Таким способом можно определить наклонное расстояние, горизонтальное проложение и превышение между начальной точкой и несколькими отражателями. При нажатии клавиши [S/%] расстояние (S) между двумя точками выводится как градиент.
Для выполнения повторного наблюдения на начальную точку нажмите [ИЗМЕР]. Наведитесь на начальную точку и нажмите [ИЗМЕР].
При нажатии клавиши [СМЕНА] последняя измеренная точка становится новой начальной точкой при определении недоступного расстояния до следующего отражателя. «Смена начальной точки»
5. Для выхода из режима определения недоступного расстояния нажмите клавишу {ESC}.
Вычисление по введенным координатам
1. На 3-й странице режима измерений нажмите [ОНР] и выберите «Опред-е HP».
2. На 2-й странице нажмите клавишу [КООРД].
3. Введите координаты 1-го отражателя и нажмите [ДА].
Если нужно считать координаты из памяти, нажмите [СЧИТ].
Ввод данных о станции и дирекционного угла «Считывание координат из памяти»
4. Выберите «ТЧК2» и нажмите (ENT) для ввода координат 2-го отражателя.
5. Введите координаты 2-го отражателя и нажмите [ДА]. На экране отображаются значения:
S : Наклонное расстояние между начальной и 2-й точками.
D : Горизонтальное проложение между начальной и второй точками,
h : Превышение между начальной и второй точками.
Можно ввести высоту отражателя на начальной и 2-й точках. На 2-й странице нажмите клавишу [Выс_Ц]. Введите высоты отражателей и нажмите клавишу [ДА].
Нажмите клавишу [КООРД] для повторного ввода координат 1 -го и 2-го отражателей.
При нажатии клавиши [ЗАП] на экране отображаются результаты определения недоступного расстояния. Нажмите [ДА], чтобы сохранить результаты измерений.
При нажатии клавиши [S/%] расстояние (S) между двумя точками выводится как градиент.
Нажмите клавишу [ИЗМЕР], чтобы выполнить наблюдение на начальную точку. «Определение с помощью наблюдения»
При нажатии клавиши [СМЕНА] последняя измеренная точка становится новой начальной точкой при определении недоступного расстояния до следующего отражателя. «Смена начальной точки»
6. Для выхода из режима определения недоступного расстояния нажмите клавишу {ESC}.
Результаты измерения недоступного расстояния нельзя сохранить, если отсутствуют имена точек, на которых установлены 1-й и/или 2-й отражатели. Всегда вводите имена точек, на которых установлены отражатели.
Смена начальной точки
Последняя измеренная точка может быть задана, как начальная для последующих измерений.
1. Наблюдайте начальную точку и отражатель в соответствии с действиями, описанными в предыдущем разделе. «Измерение расстояний между точками»
2. После измерения визирных целей нажмите клавишу [СМЕНА], затем клавишу [ДА].
Для отмены измерения нажмите клавишу [НЕТ].
Последняя измеренная точка становится новой начальной точкой.
Выполните процедуру определения недоступного расстояния.