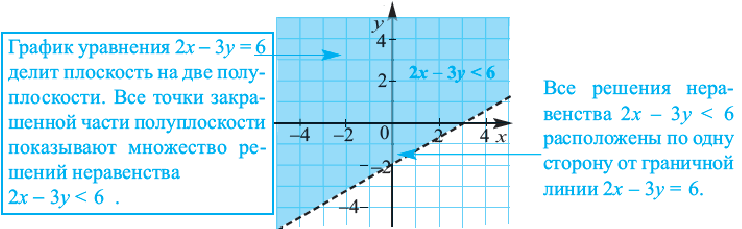
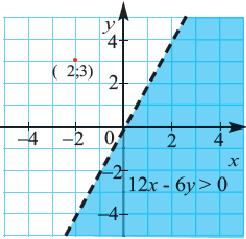
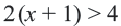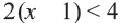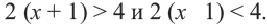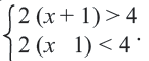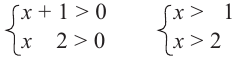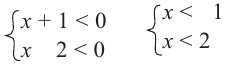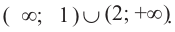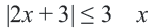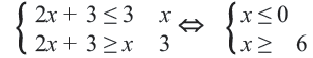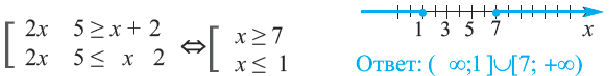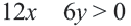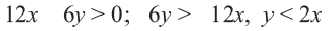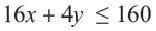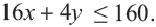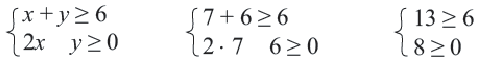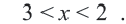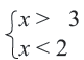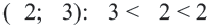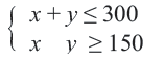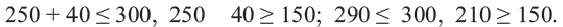Прежде чем перейти к разбору темы «Как решать
систему линейных неравенств» обязательно внимательно изучите
урок «Как решать неравенства».
Потренируйтесь в решении неравенств, тогда с системами неравенств у вас не возникнет трудностей.
Важно!
Системой неравенств называют два или более неравенства, которые объединены фигурной скобкой.
Рассмотрим пример системы неравенств.
Как видно на примере выше, систему неравенств легко определить по фигурной скобке.
Как решить систему неравенств
Запомните!
Чтобы решить систему неравенств нужно:
- решить отдельно каждое неравенство;
- сравнить полученные решения каждого неравенства и получить общий ответ системы.
Вернемся к нашему примеру системы неравенств.
Так как оба неравенства в системе уже решены и представляют собою готовый ответ, то
сразу переходим к поиску общего решения всей системы.
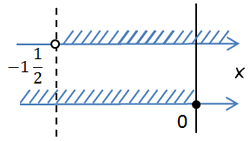
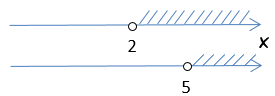
Для этого проведем две числовые оси (для каждого из неравенств свою). На осях заштрихуем результат решения неравенств.
Важно!
Числовые оси с решениями нужно располагать друг под другом.
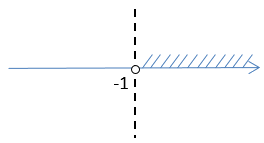
Числа на осях отмечают в порядке возрастания. То есть число «2» будет
находиться левее «5».
|
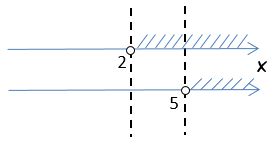
После того как мы построили числовые оси с решениями неравенств, необходимо провести через отмеченные
на осях числа перпендикулярные прямые.
Запомните!
При проведении прямых через точки на осях соблюдают следующие правила:
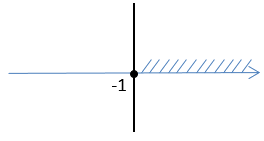
- если точка не входит в область решения («пустая» точка), то рисуют
пунктирную линию;
- если точка входит в область решения («заполненная» точка), то рисуют
сплошную линию.
Проведем прямые через числовые точки на осях.
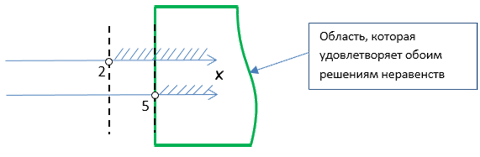
Для определения ответа найдем те области решения, которые удовлетворяют ответам обоим неравенствам.
Другими словами, те области, где в обоих случаях области решений заштрихованы.
Исходя из полученного анализа, мы получаем, что решением системы неравенств будет
«x > 5». Запишем полученный ответ.
|
Ответ: x > 5
Рассмотрим другой пример системы неравенств.
Так как неравенства в системе снова представляют собой готовые ответы — сразу перейдем к поиску общего
решения системы неравенств.
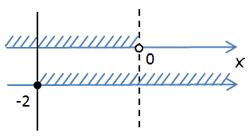
Нарисуем числовые оси для каждого неравенства и отметим на них решения. Проведем
через каждое отмеченное число на осях прямую по правилам, описанным выше.
|
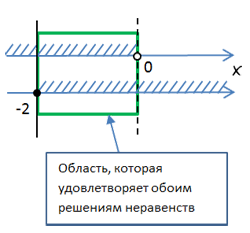
Выберем те области решений, которые удовлетворяют обоим неравенствам.
Как видно на рисунке выше, область решений, которая подходит для обоих неравенств, находится между числами
«−2» и «0».
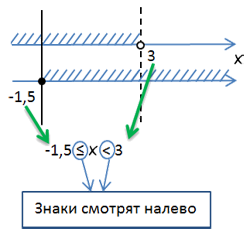
Когда область решений находится между двумя числами, принято записывать ответ с помощью двойного неравенства.

|
Ответ: −2 ≤ x < 0
Запомните!
Запись двойного неравенства используют, когда интервал решения системы неравенств лежит между числами.
Знаки сравнения («<» или «≤») в двойном
неравенстве всегда смотрят влево.
Числа записываются в том же порядке, что они расположены на оси.
Другие примеры решения систем неравенств
В отличии от примеров выше, как правило, в системах неравенств перед поиском общего решения всей системы необходимо
предварительно решить каждое из неравенств.
Рассмотрим и решим систему, где неравенства требуют предварительного решения.
Решим линейные неравенства по правилам, описанным в уроке
«Решение линейных неравенств». Затем найдем общий
ответ системы.
| 5(x + 1) − x > 2x + 2 | |
| 4(x + 1) − 2 ≤ 2(2x + 1) − x |
| 5x + 5 − x > 2x + 2 | |
| 4x + 4 − 2 ≤ 4x + 2 − x |
| 5x − x + 5 > 2x + 2 | |
| 4x + 4 − 2 ≤ 4x + 2 − x |
| 4x + 5 > 2x + 2 | |
| 4x + 2 ≤ 3x + 2 |
| 4x − 2x > 2 − 5 | |
| 4x − 3x ≤ 2 − 2 |
|
|
Ответ: −1 < x ≤ 0
При решении систем неравенств, в которых есть неравенства, содержащие пропорцию, используем
правило пропорции.
| 5(x + 1) ≤ 3(x + 3) + 1 | |
| ≤ |
| 5x + 5 ≤ 3x + 9 + 1 | |
| (2x − 1) · 2 ≤ (x + 1) · 7 |
| 5x − 3x ≤ 10 − 5 | |
| 4x − 2 ≤ 7x + 7 |
| 2x ≤ 5 | (:2) | |
| − 3x ≤ 9 | (:−3) |
| 2x (:2) ≤ 5 (:2) | |
| − 3x (:−3) ≥ 9 (:−3) |
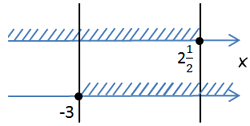
|
Ответ: −3 ≤ x ≤ 2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Неравенства
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
> больше,
≥ больше или равно,
< меньше,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x < b a x ≤ b a x > b a x ≥ b
где a и b – любые числа, причем a ≠ 0, x – переменная.
Примеры линейных неравенств:
3 x < 5 x − 2 ≥ 0 7 − 5 x < 1 x ≤ 0
Решить линейное неравенство – получить выражение вида:
x < c x ≤ c x > c x ≥ c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий > , < , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x < c |
|
x ∈ ( − ∞ ; c ) |
| x ≤ c |
|
x ∈ ( − ∞ ; c ] |
| x > c |
|
x ∈ ( c ; + ∞ ) |
| x ≥ c |
|
x ∈ [ c ; + ∞ ) |
Алгоритм решения линейного неравенства
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:
a x < b a x ≤ b a x > b a x ≥ b
- Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a > 0 то неравенство приобретает вид x ≤ b a .
- Если a < 0 , то знак неравенства меняется на противоположный, неравенство приобретает вид x ≥ b a .
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3 ( 2 − x ) > 18.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 − 3 x > 18
− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )
Делим обе части неравенства на (-3) – коэффициент, который стоит перед x. Так как − 3 < 0 , знак неравенства поменяется на противоположный. x < 12 − 3 ⇒ x < − 4 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ ( − ∞ ; − 4 )
№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x + 4 ≥ 3 x + 3 − 14
6 x − 3 x ≥ 3 − 14 − 4
3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на (3) – коэффициент, который стоит перед x. Так как 3 > 0, знак неравенства после деления меняться не будет.
x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ [ − 5 ; + ∞ )
Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).
Примеры:
№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x − 1 ≤ 6 x − 1
6 x − 6 x ≤ − 1 + 1
0 ≤ 0
Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
Ответ:
- x – любое число
- x ∈ ( − ∞ ; + ∞ )
- x ∈ ℝ
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
x + 6 − 9 x > − 8 x + 48
− 8 x + 8 x > 48 − 6
0 > 42
Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.
Ответ: x ∈ ∅
Квадратные неравенства
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c < 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий > , < , точки будут выколотые.
Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение a x 2 + b x + c вместо x.
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
- Записать ответ.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 ≥ x + 12
x 2 − x − 12 ≥ 0
x 2 − x − 12 = 0
a = 1, b = − 1, c = − 12
D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:
x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ .
Точки -3 и 4 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )
№2. Решить неравенство − 3 x − 2 ≥ x 2 .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
− 3 x − 2 ≥ x 2
− x 2 − 3 x − 2 ≥ 0
− x 2 − 3 x − 2 = 0
a = − 1, b = − 3, c = − 2
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1
x 1 = − 2, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:
− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет − .
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +.
Точки -2 и -1 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ [ − 2 ; − 1 ]
№3. Решить неравенство 4 < x 2 + 3 x .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
4 < x 2 + 3 x
− x 2 − 3 x + 4 < 0
− x 2 − 3 x + 4 = 0
a = − 1, b = − 3, c = 4
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1
x 1 = − 4, x 2 = 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:
− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 < 0
Это значит, что знак на интервале, в котором лежит точка 2, будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервалы со знаком − .
Точки -4 и 1 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )
№4. Решить неравенство x 2 − 5 x < 6.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 − 5 x < 6
x 2 − 5 x − 6 < 0
x 2 − 5 x − 6 = 0
a = 1, b = − 5, c = − 6
D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1
x 1 = 6, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком -.
Точки -1 и 6 будут в круглых скобках, так как они выколотые
Ответ: x ∈ ( − 1 ; 6 )
№5. Решить неравенство x 2 < 4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
x 2 < 4
x 2 − 4 < 0
x 2 − 4 = 0
( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2
x 1 = 2, x 2 = − 2
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:
x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком − .
Точки -2 и 2 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 2 ; 2 )
№6. Решить неравенство x 2 + x ≥ 0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.
x 2 + x ≥ 0
x 2 + x = 0
x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1
x 1 = 0, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:
x 2 + x = 1 2 + 1 = 2 > 0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )
Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x − 1 x + 3 < 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.
Алгоритм решения дробно рациональных неравенств:
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
- Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя.
- Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя.
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
- Нанести нули числителя и нули знаменателя на ось x.
Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые.
Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.
Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x − 1 x + 3 > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравниваем числитель к нулю f ( x ) = 0.
x − 1 = 0
x = 1 — это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
- Приравниваем знаменатель к нулю g ( x ) = 0.
x + 3 = 0
x = − 3 — это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.
Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
№2. Решить неравенство 3 ( x + 8 ) ≤ 5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Привести неравенство к виду f ( x ) g ( x ) ≤ 0.
3 ( x + 8 ) ≤ 5
3 ( x + 8 ) − 5 x + 8 ≤ 0
3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 x − 40 x + 8 ≤ 0
− 5 x − 37 x + 8 ≤ 0
- Приравнять числитель к нулю f ( x ) = 0.
− 5 x − 37 = 0
− 5 x = 37
x = − 37 5 = − 37 5 = − 7,4
x = − 7,4 — ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
- Приравнять знаменатель к нулю g ( x ) = 0.
x + 8 = 0
x = − 8 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.
Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )
№3. Решить неравенство x 2 − 1 x > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравнять числитель к нулю f ( x ) = 0.
x 2 − 1 = 0
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1
x 1 = 1, x 2 = − 1 — нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = 0 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )
Системы неравенств
Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств — это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
{ x + 4 > 0 2 x + 3 ≤ x 2
Алгоритм решения системы неравенств
- Решить первое неравенство системы, изобразить его графически на оси x.
- Решить второе неравенство системы, изобразить его графически на оси x.
- Нанести решения первого и второго неравенств на ось x.
- Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Примеры решений систем неравенств:
№1. Решить систему неравенств { 2 x − 3 ≤ 5 7 − 3 x ≤ 1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 3 ≤ 5
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 4 ;
Графическая интерпретация:
Точка 4 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
7 − 3 x ≤ 1
− 3 x ≤ 1 − 7
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 < 0, знак неравенства после деления меняется на противоположный.
x ≥ 2
Графическая интерпретация решения:
Точка 2 на графике жирная, так как знак неравенства нестрогий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.
Ответ: x ∈ [ 2 ; 4 ]
№2. Решить систему неравенств { 2 x − 1 ≤ 5 1 < − 3 x − 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 1 ≤ 5
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 3
Графическая интерпретация:
Точка 3 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
1 < − 3 x − 2
3 x < − 1 − 2
3 x < − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется.
x < − 1
Графическая интерпретация решения:
Точка -1 на графике выколотая, так как знак неравенства строгий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.
Ответ: x ∈ ( − ∞ ; − 1 )
№3. Решить систему неравенств { 3 x + 1 ≤ 2 x x − 7 > 5 − x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
3 x + 1 ≤ 2 x
3 x − 2 x ≤ − 1
x ≤ − 1
Графическая интерпретация решения:
- Решаем второе неравенство системы
x − 7 > 5 − x
x + x > 5 + 7
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x > 6
Графическая интерпретация решения:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
Ответ: x ∈ ∅
№4. Решить систему неравенств { x + 4 > 0 2 x + 3 ≤ x 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
x + 4 > 0
x > − 4
Графическая интерпретация решения первого неравенства:
- Решаем второе неравенство системы
2 x + 3 ≤ x 2
− x 2 + 2 x + 3 ≤ 0
Решаем методом интервалов.
− x 2 + 2 x + 3 = 0
a = − 1, b = 2, c = 3
D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16
D > 0 — два различных действительных корня.
x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.
Графическая интерпретация решения второго неравенства:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ .
Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.
Ответ: x ∈ ( − 4 ; − 1 ] ∪ [ 3 ; + ∞ )
Скачать домашнее задание к уроку 8.
При решении неравенств вы должны свободно владеть понятием числового неравенства, знать, что такое решение неравенства, что значит решить неравенство, помнить свойства неравенств. То же относится и к системам числовых неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в вузы.
Напомним свойства числовых неравенств.
1. Если а > b , то b < а; наоборот, если а < b, то b > а.
2. Если а > b и b > c, то а > c. Точно так же, если а < b и b < c, то а < c.
3. Если а > b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c < b – c). Т. е. к обеим частям неравенства можно прибавлять (или из них вычесть) одну и ту же величину.
4. Если а > b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.
Замечание.
Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
5. Если а > b и c < d, то а – c > b – d; если а < b и c > d, то а – c < b – d, т.е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак того неравенства, из которого вычиталось другое.
6. Если а > b и m – положительное число, то m а > m b и 
Если же а > b и n – отрицательное число, то n а < n b и 
7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а < b и c < d, где а, b, c, d > 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2, т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.
8. Если а > b, где а, b > 0, то 

Виды неравенств и способы их решения
1. Линейные неравенства и системы неравенств
Пример 1. Решить неравенство 
Решение:

Ответ: х < – 2.
Пример 2. Решить систему неравенств 
Решение:

Ответ: (– 2; 0].
Пример 3. Найти наименьшее целое решение системы неравенств
Решение:
Ответ:
2. Квадратные неравенства
Пример 4. Решить неравенство х2 > 4.
Решение:
х2 > 4 (х – 2)∙(х + 2) > 0.
Решаем методом интервалов.
Ответ:
3. Неравенства высших степеней
Пример 5. Решить неравенство (х + 3)∙(х2 – 2х + 1) > 0.
Решение:

Ответ: 
Пример 6. Найти середину отрезка, который является решением неравенства 4х2 – 24х + 24 < 4у2, где 
Решение:
Область определения неравенства: 
С учётом области определения 4х2 – 24х + 24 < 4у2 будет равносильно неравенству
Решаем методом интервалов.
Решение неравенства: 
Середина отрезка: 
Ответ: 
4. Рациональные неравенства
Пример 7. Найти все целые решения, удовлетворяющие неравенству 
Решение:

Методом интервалов:
Решение неравенства: 
Целые числа, принадлежащие полученным полуинтервалам: – 6; – 5; – 4; 1.
Ответ: – 6; – 5; – 4; 1.
5. Иррациональные неравенства
Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.
Пример 8. Решить неравенство 
Решение:
Область определения: 
Так как арифметический корень не может быть отрицательным числом, то 
Ответ: 
Пример 9. Найти все целые решения неравенства 
Решение:
Область определения 



Целыми числами из этого отрезка будут 2; 3; 4.
Ответ: 2; 3; 4.
Пример 10. Решить неравенство 
Решение:
Область определения: 
Преобразуем неравенство: 


Ответ: 
Пример 11. Решить неравенство 
Решение:
Раскрываем знак модуля.
Объединим решения систем 1) и 2): 
Ответ: 
6. Показательные, логарифмические неравенства и системы неравенств
Пример 12. Решите неравенство 
Решение:

Ответ: 
Пример 13. Решите неравенство 
Решение:

Ответ: 
Пример 14. Решите неравенство 
Решение:
Ответ: 
Пример 15. Решите неравенство 
Решение:
Ответ: 
Задания для самостоятельного решения
Базовый уровень
Целые неравенства и системы неравенств
1) Решите неравенство 2х – 5 ≤ 3 + х.
2) Решите неравенство – 5х > 0,25.
3) Решите неравенство 
4) Решите неравенство 2 – 5х ≥ – 3х.
5) Решите неравенство х + 2 < 5x – 2(x – 3).
6) Решите неравенство
.
7) Решите неравенство (х – 3) (х + 2) > 0.


9) Найдите целочисленные решения системы неравенств 
10) Решить систему неравенств 
11) Решить систему неравенств 
12) Найти наименьшее целое решение неравенства 
13) Решите неравенство 
14) Решите неравенство 
15) Решите неравенство 
16) Решите неравенство 
17) Найдите решение неравенства 

18) Решить систему неравенств 
19) Найти все целые решения системы 
Рациональные неравенства и системы неравенств
20) Решите неравенство 
21) Решите неравенство 
22) Определите число целых решений неравенства 
23) Определите число целых решений неравенства 
24) Решите неравенство 
25) Решите неравенство 2x<16 .
26) Решите неравенство 
27) Решите неравенство 
28) Решите неравенство 
29) Найдите сумму целых решений неравенства 
30) Решите неравенство 
31) Решите неравенство 
Иррациональные неравенства
32) Решите неравенство 
33) Решите неравенство
34) Решите неравенство 
Показательные, логарифмические неравенства и системы неравенств
35) Решите неравенство 
36) Решите неравенство 
37) Решите неравенство 
38) Решите неравенство 
39) Решите неравенство 
40) Решите неравенство 49∙7х < 73х + 3.
41) Найдите все целые решения неравенства 
42) Решите неравенство 
43) Решите неравенство 
44) Решите неравенство 7x+1-7x<42 .
45) Решите неравенство log3(2x2+x-1)>log32 .
46) Решите неравенство log0,5(2x+3)>0 .
47) Решите неравенство 
48) Решите неравенство 
49) Решите неравенство 
50) Решите неравенство logx+112>logx+12 .
51) Решите неравенство logx9<2.
52) Решите неравенство 
Повышенный уровень
53) Решите неравенство |x-3|>2x.
54) Решите неравенство 2│х + 1| > х + 4.
55) Найдите наибольшее целое решение неравенства 
56) Решить систему неравенств 
57) Решить систему неравенств 
58) Решите неравенство 
59) Решите неравенство 25•2x-10x+5x>25 .
60) Решите неравенство 
Ответы
1) х ≤ 8; 2) х < – 0,05; 3) х ≥ 5; 4) х ≤ 1; 5) х > –2; 6) х < 11; 7) 





20) (0; 2); 21) (0; 1,5); 22) 3; 23) 6; 24) (–1; 1,5); 25) х < 4; 26)
; 29) – 10; 30) (0; + ∞); 31)









.
Алгоритм решения линейного неравенства
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:
a x b a x ≤ b a x > b a x ≥ b
- Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a > 0 то неравенство приобретает вид x ≤ b a .
- Если a 0 , то знак неравенства меняется на противоположный , неравенство приобретает вид x ≥ b a .
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3 ( 2 − x ) > 18.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )
Делим обе части неравенства на ( -3 ) – коэффициент, который стоит перед x . Так как − 3 0 , знак неравенства поменяется на противоположный . x 12 − 3 ⇒ x − 4 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ ( − ∞ ; − 4 )
№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x + 4 ≥ 3 x + 3 − 14
6 x − 3 x ≥ 3 − 14 − 4
3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на ( 3 ) – коэффициент, который стоит перед x . Так как 3 > 0, знак неравенства после деления меняться не будет.
x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).
Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).
№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x − 6 x ≤ − 1 + 1
Получили верное неравенство, которое не зависит от переменной x . Возникает вопрос, какие значения может принимать переменная x , чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
Ответ:
- x – любое число
- x ∈ ( − ∞ ; + ∞ )
- x ∈ ℝ
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
x + 6 − 9 x > − 8 x + 48
− 8 x + 8 x > 48 − 6
Получили неверное равенство, которое не зависит от переменной x . Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.
Квадратные неравенства
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий > , , точки будут выколотые.
Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A ) и подставить её значение в выражение a x 2 + b x + c вместо x .
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства или ≤ в ответ выбираем интервалы со знаком -.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
a = 1, b = − 1, c = − 12
D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3
Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6 . Подставляем эту точку в исходное выражение:
x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ .
Точки -3 и 4 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )
№2. Решить неравенство − 3 x − 2 ≥ x 2 .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
a = − 1, b = − 3, c = − 2
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1
x 1 = − 2, x 2 = − 1
Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение:
− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0
Это значит, что знак на интервале, в котором лежит точка 0 будет − .
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +.
Точки -2 и -1 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ [ − 2 ; − 1 ]
№3. Решить неравенство 4 x 2 + 3 x .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
a = − 1, b = − 3, c = 4
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1
Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение:
− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0
Это значит, что знак на интервале, в котором лежит точка 2 , будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства , выбираем в ответ интервалы со знаком − .
Точки -4 и 1 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )
№4. Решить неравенство x 2 − 5 x 6.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
a = 1, b = − 5, c = − 6
D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1
Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства , выбираем в ответ интервал со знаком -.
Точки -1 и 6 будут в круглых скобках, так как они выколотые
Ответ: x ∈ ( − 1 ; 6 )
№5. Решить неравенство x 2 4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2
Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3 . Подставляем эту точку в исходное выражение:
x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства , выбираем в ответ интервал со знаком − .
Точки -2 и 2 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 2 ; 2 )
№6. Решить неравенство x 2 + x ≥ 0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.
x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1
Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1 . Подставляем эту точку в исходное выражение:
x 2 + x = 1 2 + 1 = 2 > 0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )
Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.
Алгоритм решения дробно рациональных неравенств:
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
- Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя .
- Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя .
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
- Нанести нули числителя и нули знаменателя на ось x .
Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые .
Если знак неравенства строгий ,
при нанесении на ось x нули числителя выколотые .
Если знак неравенства нестрогий ,
при нанесении на ось x нули числителя жирные .
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x − 1 x + 3 > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравниваем числитель к нулю f ( x ) = 0.
x = 1 — это ноль числителя . Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
- Приравниваем знаменатель к нулю g ( x ) = 0.
x = − 3 — это ноль знаменателя . При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства) .
- Наносим нули числителя и нули знаменателя на ось x .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.
Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
№2. Решить неравенство 3 ( x + 8 ) ≤ 5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Привести неравенство к виду f ( x ) g ( x ) ≤ 0.
3 ( x + 8 ) − 5 x + 8 ≤ 0
3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 x − 40 x + 8 ≤ 0
− 5 x − 37 x + 8 ≤ 0
- Приравнять числитель к нулю f ( x ) = 0.
x = − 37 5 = − 37 5 = − 7,4
x = − 7,4 — ноль числителя . Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = − 8 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.
Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )
№3. Решить неравенство x 2 − 1 x > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравнять числитель к нулю f ( x ) = 0.
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1
x 1 = 1, x 2 = − 1 — нули числителя . Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = 0 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )
Системы неравенств
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
Алгоритм решения системы неравенств
- Решить первое неравенство системы, изобразить его графически на оси x .
- Решить второе неравенство системы, изобразить его графически на оси x .
- Нанести решения первого и второго неравенств на ось x .
- Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Примеры решений систем неравенств:
№1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
Точка 4 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный.
Графическая интерпретация решения:
Точка 2 на графике жирная, так как знак неравенства нестрогий.
- Наносим оба решения на ось x .
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на отрезке от 2 до 4 . Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.
№2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
Точка 3 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
3 x − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется.
Графическая интерпретация решения:
Точка -1 на графике выколотая, так как знак неравенства строгий.
- Наносим оба решения на ось x .
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.
Ответ: x ∈ ( − ∞ ; − 1 )
№3. Решить систему неравенств < 3 x + 1 ≤ 2 x x − 7 >5 − x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
Графическая интерпретация решения:
- Решаем второе неравенство системы
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
Графическая интерпретация решения:
- Наносим оба решения на ось x .
- Выбираем подходящие участки и записываем ответ.
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
№4. Решить систему неравенств < x + 4 >0 2 x + 3 ≤ x 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
Графическая интерпретация решения первого неравенства:
- Решаем второе неравенство системы
Решаем методом интервалов.
a = − 1, b = 2, c = 3
D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16
D > 0 — два различных действительных корня.
x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.
Графическая интерпретация решения второго неравенства:
- Наносим оба решения на ось x .
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ .
Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.
http://infourok.ru/konspekt-uroka-po-algebre-i-nachalam-matematicheskogo-analiza-na-temu-ravnosilnost-uravneniy-i-neravenstv-sistemam-osnovnie-pony-3656526.html
Содержание:
Системы неравенств и совокупность неравенств
Исследование. Если альпинисты увеличат скорость на 1км/ч, то путь 4 км до вершины они преодолеют быстрее чем за 2 часа. Если же они уменьшат скорость на 1 км/ч, то не смогут добраться до вершины за 2 часа. С какой скоростью движутся альпинисты? Решение: Примем за
Если скорость увеличится на 1 км/ч, то длина пройденного пути будет больше 4-х км и соответствующее неравенство примет вид:
Если скорость уменьшится на 1 км/ч, то длина пройденного пути будет меньше 4-х км и соответствующее неравенство примет вид:
По условию задачи нужно найти такое значение 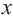
Неравенства, объединенные союзом 
В данной задаче нужно решить систему неравенств
Если каждое неравенство системы заменить на равносильное неравенство, то получим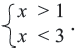
Для того, чтобы решить систему неравенств нужно найти множество решений каждого неравенства и найти пересечение этих множеств, то есть, общую часть.
Ответ: Решение системы промежуток 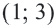
Совокупность неравенств
Задача. Наргиз и Эльшан играют в игру, построенную на числах. Каждый берег карточку с числом и прибавляет к нему 5. Если ответ будет меньше 10-ти или же больше 15-ти, то владелец карточки зарабатывает очко. Выразите с помощью неравенства ситуацию, когда Эльшан взяв одну карточку заработал очко.
Решение: Пусть число на карге будет 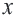
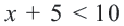
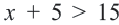
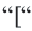
Решением данной совокупности неравенств будет множество: 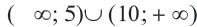
Пример.
Решите неравенство:
Решение: Для того, чтобы произведение двух множителей было положительным, нужно чтобы множители были одинакового знака. То есть, множители 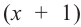

Данное неравенство сводится к решению совокупности:
Решение 1-ой системы совокупности:
Геометрическое изображение:
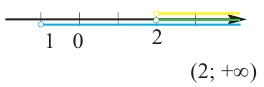
Геометрическое изображение:
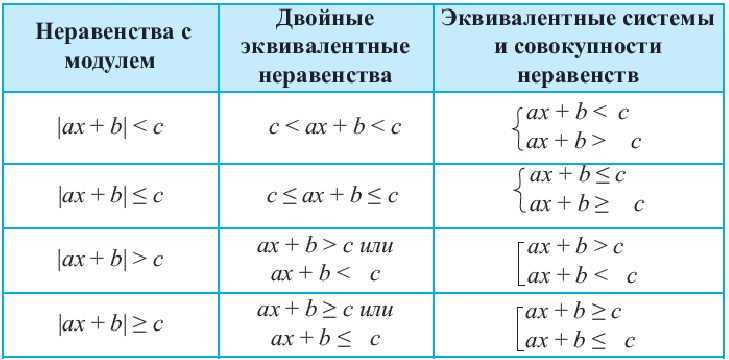
Неравенства, содержащие переменную под знаком модуля
Система неравенств, совокупность неравенств
Пример 2.
Решение:
Пример 3.
Решение:
Линейные неравенства с двумя переменными
Неравенства вида 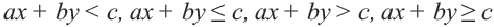
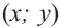
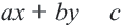
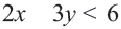
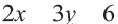
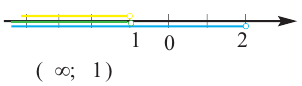
• Чтобы убедиться в правильности выбора полуплоскости, соответствующей решению неравенства, выбираются пробные точки в каждой из полуплоскостей. Закрашивается та полуплоскость, в которой расположена точка, удовлетворяющая данному неравенству.
• Если неравенство выражается знаками 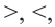
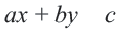
• Если неравенство выражается знаками 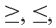
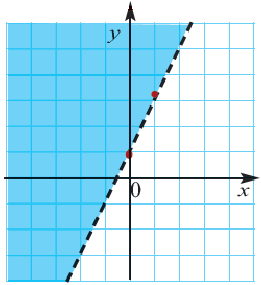
Пример 1.
1. Решим неравенство относительно переменной 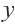
2. Нарисуем график уравнения 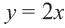
3. Проверим неравенство в точке 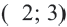
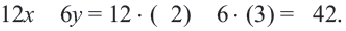
Пример 2. Напишите неравенство, соответствующее графику.
1. Определим уравнение 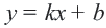
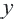
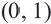
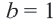
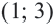
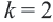
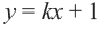
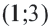
Уравнение линии границы: 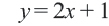
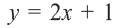
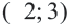
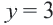
Левая часть 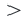
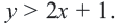
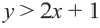
- Заказать решение задач по высшей математике
Прикладные задания.
Пример 1. Билет в театр для взрослых стоит 16 манат, а детский — 4 манат. Деньги, вырученные от продажи билетов в кассе, составляют не более 160 манат. Определите различные варианты количества проданных билетов. Числовые информации и переменные, соответствующие условию задачи:
Математическая запись:
1. Чтобы решить неравенство, выразим 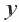
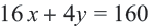
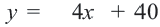
2. Закрасим фигуру, заданную графиком и осями координат.
3. Любые целые значения 
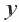
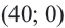
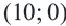
Системы линейных неравенств с двумя переменными
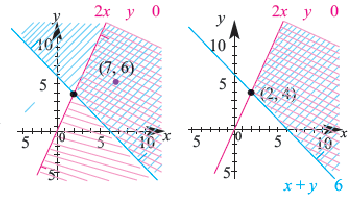
Решением системы линейных неравенств с двумя переменными называется множество пар чисел 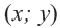
Пример 1.
1. С помощью граничной прямой 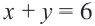
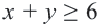
2. С помощью уравнения 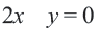
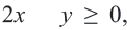
3. Множеством решений данной системы неравенств будет часть плоскости, закрашенная обоими цветами.
4. Выберем отсюда одну точку, например 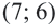
Каждая пара 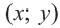
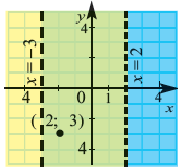
Пример 2. Изобразите графически на координатой плоскости неравенство
1. Запишем двойное неравенство 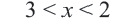
2. Изобразим неравенство 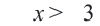

3. Изобразим неравенство 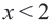
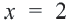
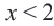
4. Часть плоскости, соответствующая неравенствам 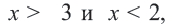
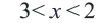
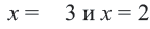
5. Проверка: проверим в точке
График системы линейных неравенств, соответствующий реальным жизненным ситуациям, в большинстве случаев строится в первой четверти координатной плоскости.
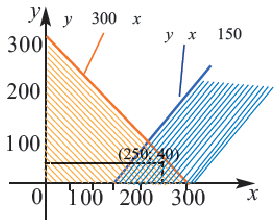
Пример 3. На одном из двух конвейеров производят кастрюли из нержавеющей стали, а на другом медные кастрюли. Если каждый из конвейеров работает на полную мощность, то ежедневно производится не более 300 кастрюль. Так как потребность в кастрюлях из нержавеющей стали больше, их ежедневно производят больше чем медных, но не меньше 150 штук. Напишите систему неравенств, показывающую ежедневное количество производимых кастрюль, и изобразите графически.
Решение: 1) Примем за 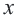
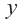
2) Решение неравенства 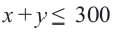
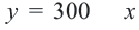
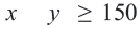
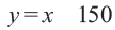
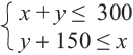
3. С помощью пробной точки 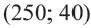
Решение системы неравенств найдено верно.
- Квадратные неравенства
- Точка, прямая и плоскость в пространстве
- Тригонометрические функции произвольного угла
- Теоремы синусов и косинусов
- Система координат в пространстве
- Иррациональные числа
- Действительные числа
- Решение уравнений высших степеней